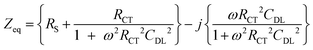Monitoring early zeolite formation via in situ electrochemical impedance spectroscopy

Abstract

Hitherto zeolite formation has not been fully understood. Although electrochemical impedance spectroscopy has proven to be a versatile tool for characterizing ionic solutions, it was never used for monitoring zeolite growth. We show here that EIS can quantitatively monitor zeolite formation, especially during crucial early steps where other methods fall short.

---

Classically, zeolite crystallization is achieved by aging a gel type hyperalkaline aluminosilicate synthesis mixture under hydrothermal conditions. While this approach has proven to be successful in initiating the highly complex zeolite crystallization process, the gel phase severely impedes the in situ investigation of the nucleation and growth processes. With the development of clear synthesis solutions and sols,^1–3in situ crystallization studies became possible. Though the crystallization processes of silicalite 1 and beta zeolite from clear solution are well-documented model systems for in situ investigation, a consistent model for its formation could not yet be formulated. Detailed knowledge of the shape, size and molecular level structure of emerging nano-sized species⁴ in clear synthesis mixtures is essential for the elucidation of the zeolite crystallization mechanism. Since in particular the early steps in zeolite formation consist of a complex interplay of (negatively charged) silicon oligomers and structure-directing cations in hyper alkaline solutions, monitoring the local ion interactions is one of the most crucial parameters to monitor. Traditionally exploited techniques such as small angle X-ray scattering (SAXS), dynamic light scattering (DLS) and nuclear magnetic resonance (NMR) spectroscopy fall short here. Electrochemical impedance spectroscopy (EIS) has already proven to be a versatile tool for the characterization of ionic solutions but has, to the authors' knowledge, never been used before to monitor zeolite growth.^5–7

Clear zeolite synthesis mixtures are typically prepared by the hydrolysis of a source of monomeric silicon in hyper alkaline media, directed by templating cations, the so-called structure-directing agents (SDAs). In this study, tetraethyl orthosilicate (TEOS, >99%, Aldrich) is used as monomeric silica source and tetraethylammonium hydroxide (TEAOH, 40%, Aldrich) as a SDA. Rimer et al.⁸ reported a ratio of silicon to hydroxide (Si/OH) of 1 to be a critical lower limit for zeolite growth. As demonstrated later by Castro et al.¹ nano-aggregate and nano-particle formation occurs only above this critical value for ethanol containing precursors.⁹

A range of beta zeolite clear solutions has been prepared with molar TEOS/TEAOH/H₂O ratios of x/9.0/9500, where x was varied from 0 to 40 moles. These sample compositions were chosen to be identical to the work presented earlier by Rimer.⁸ A relatively simple model of the chemical interactions in solution has been defined in PHREEQC v3 with the graphical user interface PHREEQCI 3.3.3, to describe the clear solution. This model accounts for the dissociation of TEAOH, the hydrolysis of TEOS and the acid–base silicic acid equilibria. An additional 9 reactions include the formation of dimers, trimers, tetramers and octamers, as well as larger silicate aggregates formulated as Si32 species. While this species formally is similar in Si-content to a precursor species previously suggested by the Leuven group¹⁰ and also similar in size to the earlier observed nano-aggregates^11,12 it simply assists to describe the experimental data in this context, and its composition should not be considered as definite. The reactions describing the formation of oligomers and nano-aggregates are shown in Table 1, together with the dimensionless equilibrium constants, log(K), as obtained from the literature¹³ and by parameter fitting.

Table 1 Oligomer and nano-aggregate formation reactions

Reaction	Log(K)
a From the literature.^13 b Obtained by parameter fitting.
Dimers
2H4SiO4 ↔ Si2O(OH)6 + H2O	0.82^a
2H4SiO4 ↔ Si2O2(OH)5^− + H2O + H^+	−8.13^a
2H4SiO4 ↔ Si2O3(OH)4^2− + H2O + 2H^+	−18.38^a
Trimers
3H4SiO4 ↔ Si3O6(OH)3^3− + 3H2O + 3H^+	−26.81^a
3H4SiO4 ↔ Si3O5(OH)3^5− + 2H2O + 3H^+	−25.78^a
Tetramers
4H4SiO4 ↔ Si4O8(OH)4^4− + 4H2O + 4H^+	−33.19^a
Octamers
2Si4O8(OH)4^−4 + 7H^+ ↔ Si8O13(OH)7^− + 4H2O	36.25^b
Ion pairing
Si8O13(OH)7^− + TEA^+ ↔ TEASi8O13(OH)7	47.00^b
Nano-aggregates
4TEASi8O13(OH)7 ↔ TEA4Si32O55(OH)22 + 3H2O	5.87^b

---

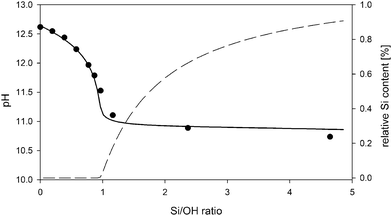
The reactions in Table 1 represent the simplest model capable of describing the experimental pH data fairly accurately. The experimental and simulated pH values as a function of Si/OH ratio in the clear solution samples are shown in Fig. 1.

Fig. 1 Experimental pH data (scatter plot) compared to pH simulated using the above described model in PHREEQC (full line). The relative fraction of nano-aggregates is displayed on the right axis (dotted line).

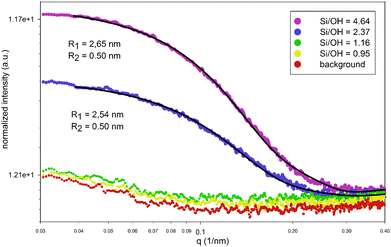
Interestingly, even this simple model predicts the formation of larger ion paired species and nano-aggregates only above the limit of Si/OH = 1. The relative fraction of these species, as calculated by the PHREEQC model, is shown on the right axis in Fig. 1. SAXS experiments, shown in Fig. 2, fully support the appearance of aggregates exclusively in systems with a Si/OH ratio exceeding 1. Intensity distributions obtained by multi-angle DLS measurements (ALV CGS-3 Compact Goniometer, Langen, Germany) shown in Fig. 3 reveal a decreasing population of ∼160 nm species with an increasing Si/OH ratio, while the population with a hydrodynamic radius of ∼4.5 nm increases. Below the limit of Si/OH = 1, the smaller population completely disappears. Note that an intensity distribution of the different populations is shown, and not a number distribution. In this case the scattering intensity of a single 160 nm particle is 2 × 10⁻¹² times larger than that of a 4.5 nm particle. As a consequence, even an extremely small number of the 160 nm species will effectively hide the more extensive population of 4.5 nm in the scattering data.

Fig. 2 Small angle X-ray scattering data of clear solutions. Dimensions of the fitted core–shell oblate ellipsoid model are displayed next to the curve; R₁ and R₂ are major and minor outer radii of the ellipse, respectively.

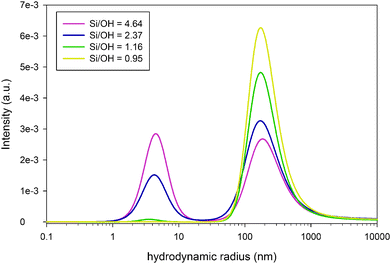Fig. 3 Intensity distribution in clear solutions with different Si/OH ratios, as determined by dynamic light scattering.

From the SAXS patterns (SAXSess, Anton Paar, Graz, Austria) shown in Fig. 2 however, only the smaller population can be monitored, growing in number with an increasing Si/OH ratio. Note that in DLS a hydrodynamic particle radius is obtained and not the actual particle radius. The SAXS data were modelled with a core–shell oblate ellipsoidal particle shape as proposed by Fedeyko et al.¹⁴ This model fits the higher q regions much better than simple models (e.g. spherical), especially for the highest Si/OH ratios (see ESI†). All models however indicate particle sizes that are in agreement with the DLS results obtained. The large population of approximately 160 nm, as observed by DLS, is not obvious from SAXS measurements. This may suggest that these are best described as local variations of the refractive index rather than being of particulate nature.

Since the time scales of DLS and SAXS are much smaller than those of NMR, the former are able to detect dynamic clusters of oligomers which remain undetected for most other techniques, provided there is scattering contrast.

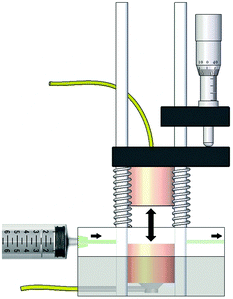
The impedance spectra were recorded continuously using an Agilent E4990A impedance analyser with a frequency range from 20 Hz to 110 MHz, in combination with a custom built impedance cell (Fig. 4). During the measurements, the cell was kept at a constant 25 °C in a climate chamber. The millimetre screw allows us to change the electrode gap, in order to account for double layer effects near the electrode surfaces. Increasing the electrode gap should increase the bulk resistance proportionally, yet not affect the double layer capacitance.

Fig. 4 Side view of the impedance cell designed for the measurements in highly ionic zeolite clear solutions. The double arrow indicates the electrode gap, which can be adjusted by means of the millimeter screw.

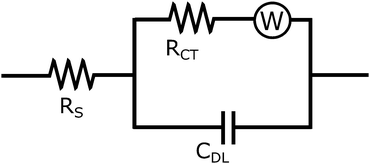
A Randles circuit (Fig. 5) is used as an equivalent circuit to describe the clear solution's electrochemical behaviour.¹⁵ The Warburg diffusion element is not considered due to the small effect of diffusion in the higher frequency range. The impedance behaviour (assuming time dependence exp(jωt)) of the earlier described beta zeolite clear solutions in the frequency range from 1 kHz to 1 MHz can be described as:

where ω (=2πf) is the angular frequency, R_S is the bulk resistance, R_CT is the charge transfer resistance or polarization resistance and C_DL is the double layer capacitance. With the current impedance measurement set-up and the simplified model description, the frequency range is limited to 1 MHz. Spurious electrical effects above that frequency require an adapted measurement set-up and extended equivalent circuit to account for non-ideal behaviour of the circuit.

Fig. 5 Equivalent Randles circuit for modeling the impedance data from zeolite clear solutions. The Warburg diffusion element (W) is not considered due to the small effect of diffusion in the higher frequency range.

The Bode plot is displayed below in Fig. 6. Bulk resistance values are obtained by fitting the equivalent Randles circuit to the experimentally obtained impedance spectra.

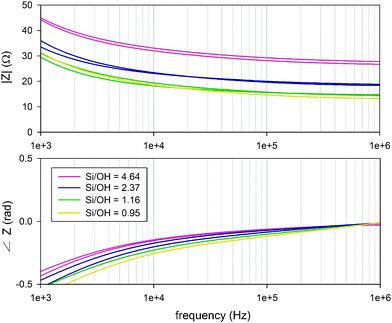Fig. 6 Bode plots of the zeolite clear solution impedance spectra with different Si/OH ratios, measured using an Agilent E4990A impedance analyser in combination with a custom built impedance cell.

As shown below in Fig. 7, the bulk resistance R_S shows a linear relation for the samples with the Si/OH ratio above 1. The conductivity consequently shows a linear decrease from 2.8 to 1.8 mS cm⁻¹, in accordance with data obtained earlier by Rimer et al.¹² for similar systems. This work focusses on the processes occurring during nano-aggregate formation, at Si/OH ratios above 1. It has been shown earlier by Fedeyko et al.¹⁴ that in silicalite-1 clear solutions, the conductivity drops drastically for Si/OH ratios below 1. In all clear solutions, the hydroxide content was kept constant, as can also be seen from the nearly constant pH curve in Fig. 1, in the range between Si/OH ratios from 1.0 to 5.0.

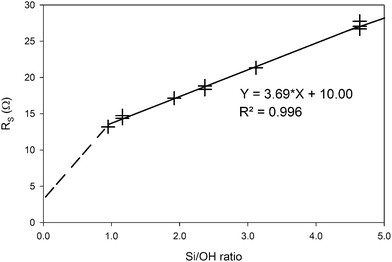Fig. 7 The bulk resistance R_S obtained from equivalent circuit fitting of the EIS spectra with the Randles circuit described earlier, as a function of the Si/OH ratio of each zeolite clear solution sample. The dotted line indicates the expected behaviour based on previous work on similar zeolite systems done by Fedeyko et al.¹⁴

Increasing the silica content in the zeolite beta clear solutions does not significantly alter the pH, but does influence its electrical properties. As more silica is added, the silica in solution leads to increased numbers of nano-aggregates. As can be seen from the DLS result, the nano-aggregates do not grow with higher Si-content, but the relative intensity of the scattered light increases drastically, indicating an increased number density. The dynamic clusters will not interfere with the observations by EIS at higher frequencies. These preliminary observations and their coherence and complementarity to other diagnostic means show that EIS is a viable tool for in situ monitoring zeolite formation in its early phases. Further studies that are currently in progress will allow us to qualitatively characterize also nano-aggregate growth by monitoring the electrical properties of the bulk liquid at later stages of zeolite formation. In this article, EIS is used only to investigate the bulk properties of the bulk liquid phase, and does not focus on the nano-aggregates yet. However, further research is being done to exploit EIS to the fullest for zeolite formation characterization. Via the double layer behaviour, EIS will be able to finally address the dielectric behaviour of zeolite clear solutions, separating the nano-aggregate properties from the bulk phase.

G. B. and C. E. A. K. acknowledge support from the Belgian Prodex office and ESA. C. E. A. K., E. B. and G. B. are supported by long term structural funding by the Flemish government (Methusalem grant of Professor J. Martens). F. T. acknowledges KU Leuven for an appointment as visiting professor. This work was in part supported by the Austrian COMET program (Linz Center of Mechatronics).

Notes and references

1. M. Castro, M. Haouas, F. Taulelle, I. H. Lim, E. Breynaert, G. Brabants, C. E. A. Kirschhock and W. Schmidt, Microporous Mesoporous Mater., 2013, 189, 158–162.
2. A. Aerts, L. R. A. Follens, M. Haouas, T. P. Caremans, M.-A. Delsuc, B. Loppinet, J. Vermant, B. Goderis, F. Taulelle, J. A. Martens and C. E. A. Kirschhock, Chem. Mater., 2007, 19, 3448–3454.
3. A. Aerts, M. Haouas, T. P. Caremans, L. R. A. Follens, T. S. Van Erp, F. Taulelle, J. Vermant, J. A. Martens and C. E. A. Kirschhock, Chem. – Eur. J., 2010, 16, 2764–2774.
4. M. Castro, M. Haouas, I. Lim, H. J. Bongard, F. Schüth, F. Taulelle, G. Karlsson, V. Alfredsson, E. Breynaert, C. E. A. Kirschhock and W. Schmidt, Chem. – Eur. J, 2016 , submitted.
5. H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670.
6. M. Sega, S. S. Kantorovich, A. Arnold and C. Holm, Recent Advances in Broadband Dielectric Spectroscopy, Springer, Netherlands, 2013, pp. 103–122.
7. M. Becchi, C. Avendaño, A. Strigazzi and G. Barbero, J. Phys. Chem. B, 2006, 109, 23444–23449.
8. J. D. Rimer, J. M. Fedeyko, D. G. Vlachos and R. F. Lobo, Chem. – Eur. J., 2006, 12, 2926–2934.
9. L. Van Tendeloo, M. Haouas, J. A. Martens, C. E. A. Kirschhock, E. Breynaert and F. Taulelle, Faraday Discuss., 2015, 179, 437–449.
10. C. E. A. Kirschhock, R. Ravishankar, P. Jacobs and J. A. Martens, J. Phys. Chem. B, 1999, 103, 11021–11027.
11. J. M. Fedeyko, J. D. Rimer, R. F. Lobo and D. G. Vlachos, J. Phys. Chem. B, 2004, 108, 12271–12275.
12. J. D. Rimer, R. F. Lobo and D. G. Vlachos, Langmuir, 2005, 21, 8960–8971.
13. S. Sjöberg, J. Non-Cryst. Solids, 1996, 196, 51–57.
14. J. M. Fedeyko, D. G. Vlachos and R. F. Lobo, Langmuir, 2005, 21, 5197–5206.
15. J. E. B. Randles, Faraday Discuss., 1947, 1, 11–19.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cc01106c

---