Tuning of molecular qubits: very long coherence and spin–lattice relaxation times

Abstract

We report a pulsed EPR study on different transition metal phthalocyanines, elucidating the dependence of spin relaxation on solvent, ligand and metal ion. Coherence times of >40 µs and spin–lattice relaxation times of up to 2 s were found. Minimization of SOMO-environment overlap leads to increased coherence times.

---

The realization of a quantum computer would change our world by boosting computation times¹ and cracking currently highly safe encryption algorithms.² In contrast to classical bits, quantum bits (qubits) can not only be in the states |0〉 and |1〉 but also in a coherent superposition of them. Among different physical systems proposed, molecular electron spin qubits are highly attractive.^3–5 Here the qubit interactions can be easily tuned by chemical modification of ligands and sample matrix.⁶ Electron spin qubits can be controlled and manipulated by pulsed electron spin resonance methods. The critical parameter for quantum computation is the coherence time of the superposition state which translates into the phase memory time T_M in EPR-measurements. T_M must be at least 10 000 times longer than the time required for an individual quantum operation,⁷ which is here a microwave pulse of typically 20 ns. So far, reported phase memory times in transition metal coordination compounds are typically around a few microseconds at cryogenic temperatures.^8–11 Although some systems with much longer coherence times are known,^12–14 systematic studies of electron spin relaxation are sparse.^15–17 In order to enable rational qubit design and predict phase memory times, a fundamental understanding of coherence-limiting factors and their relative importance for molecular qubits in different environments is required.

Transition metal phthalocyanines are very well known systems.^18,19 Their broad usage from cosmetics to technical applications has not only led to a detailed knowledge of their material properties, but also to availability of these complexes in ton-scale at low prices. Furthermore these compounds were recently proposed as qubits²⁰ and can be processed by molecular beam surface deposition, which is an important condition for implementing qubits in real devices.²¹ Nevertheless, surprisingly little has been published on electron spin relaxation behaviour of these compounds.^20,22 It has been reported that the utilized solvent influences the electronic properties of the central ion for phthalocyanines, such as energies and compositions of the molecular orbitals as well as g- and A-tensors.^23,24 In these extended studies, no coherence times were published.

The positive effect on coherence by deuterating the solvent has been reported several times.^9,25,26 Similarly, the effects of coordination geometry,¹⁵ ligand substitution²⁷ and spin–orbit coupling (SOC)^15,28 were reported in literature previously. No systematic study addressing all of these key questions in one comparative measurement series has appeared so far.

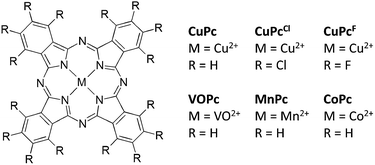
Here we present our results on tuning of molecular qubits. The key objectives were to reveal the influences of solvent, ligand and central ion on electron spin relaxation. We have chosen a series of transition metal phthalocyanines as target compounds for our study (Scheme 1). The compounds were measured with pulsed Q-band EPR spectroscopy (experimental data: Fig. S1–S10, fit parameters: Tables S1–S11, ESI†).‡

Scheme 1 Structures of investigated compounds.

The impact of solvent deuteration on electron spin relaxation was the first target of our investigation. Solutions of CuPc (0.5 mM) in H₂SO₄ and D₂SO₄ were employed to probe the interaction between solvent matrix and molecular qubit at 7 K.

Fig. 1 shows the resulting decay curves of the corresponding inversion-recovery- and Hahn-echo experiments. The former can be fitted for both samples with a biexponential decay according to eqn (1):

I(τ) = y₀ + A_f exp(−τ/T_1,f) + A_s exp(−τ/T_1,s) (1)

where f indicates a fast and s a slow process. The fast process is typically attributed to spectral diffusion in inversion recovery experiments and the slow process is usually assigned to the actual spin–lattice relaxation.^8,29 Within the experimental uncertainty, the times of fast and slow spin–lattice relaxation processes are insensitive to solvent deuteration for CuPc. The Hahn-echo decay curve shows stretched exponential behaviour in H₂SO₄ (eqn (2)):

I(2τ) = y₀ + A exp(−2τ/T_M)^k (2)

Fig. 1 Relaxation data of CuPc in H₂SO₄ (red triangles) and D₂SO₄ (blue circles) at Q-band and 7 K. (a) Inversion recovery experiment and biexponential fits (black lines). (b) Hahn echo experiment and biexponential fits (black lines).

Here the parameters have the same meaning as above and k is the stretch factor. The phase memory time is 7.78 ± 0.04 µs in the protonated solvent matrix and k = 1.66 ± 0.02. Stretch parameters between 1 and 2 have been reported to be characteristic of physical motion of nuclear spins,⁸ which here could involve the fluctuation of the proton positions in hydrogen bridges. In deuterated sulfuric acid, a biexponential decay according to eqn (3) was found:

I(2τ) = y₀ + A_f exp(−2τ/T_M,f) + A_s exp(−2τ/T_M,s) (3)

The slow component, T_M,s = 41 ± 4 µs, is 5 times longer than in normal sulfuric acid and almost 16 times longer than published values of CuPc in thin films.²⁰ This phase memory time gives a figure of merit (coherence time divided by the time for one operation) of Q_M = 2000. Here it must be noted that the slow process accounts for only about a third of the total relaxation. The fast process may be due to spin diffusion, as for the spin–lattice relaxation, or due to different species, e.g. two molecules being in relatively close proximity. Both phase memory times are orders of magnitude faster than the spin–lattice relaxation times, and the latter thus do not contribute to decoherence. Because of increased coherence times, D₂SO₄ was used as solvent matrix for the further investigations.

After probing the matrix of the molecular qubit, we focussed on the ligand. The key question here was if a change in ligand properties would modify the electron spin relaxation behaviour. We have chosen CuPc, CuPc^Cl and CuPc^F for this purpose. The nuclei of ¹H and ¹⁹F possess similar magnetic moments, but fluorine is much more electronegative. In contrast, the gyromagnetic ratio of ^35,37Cl is only about a tenth of the former ones. It has been shown before that changes in ligand substitution alter electronic and magnetic properties, e.g., in terms of g- and A-tensors and spin density distributions.²⁴

Fig. 2 displays the relaxation data which were extracted from the experimental decay curves. Inversion recovery experiments were fitted with biexponentials in all cases. CuPc and CuPc^Cl show very similar values for T_1,s of about 100 ms. This value is decreased to T_1,s = 60 ± 4 ms for CuPc^F. We attribute this decrease to changes in the phonon spectrum. T_1,f shows similar values in the lower two digit millisecond range for CuPc, CuPc^Cl and CuPc^F, but its contribution to the echo decay increases in the order H < F < Cl.

Fig. 2 Relaxation data of investigated compounds at Q-band and 7 K. (a) Fast and slow spin–lattice relaxation times (blue, open respectively filled squares) including standard deviation from fits, symbol size corresponds to contribution of process to echo decay. (b) Fast and slow phase memory times (red, open respectively filled circles) including standard deviation from fits, symbol size corresponds to contribution of process to echo decay.

Hahn echo measurements also show biexponential decay curves. We observe for CuPc, CuPc^Cl and CuPc^F similar values around 40 µs for T_M,s, leading to figures of merit of 2000, which is a rather high value for molecular qubits in solution at 7 K. Interestingly, the fast process is virtually absent in the case of CuPc^Cl whereas equal contributions or a dominant fast process can be found for CuPc and CuPc^F. Possibly the absence of the fast process in CuPc^Cl is due to inhibition of nuclear spin flip-flop transfer between solvent and ligand, in view of the very different nuclear magnetic moment and spin dynamics of ^35,37Cl compared to protons and deuterium.

The coherence time of CuPc^Cl (43 ± 1 µs) is among the highest values for transition metal compounds.^12–14 Monoexponential decay curves are uncommon for electron spin qubits. Also solid state qubits such as Si:P shows multi-component echo decay curves.³⁰ This is highly disadvantageous for quantum computation in real devices: numerous decay processes mean inferior controllability of the systems as well as less detectable intensity of relevant systems. In contrast to other proposed spin qubit systems, e.g. N@C₆₀,^31,32 the robust compound CuPc^Cl can be handled under atmospheric conditions and the complex is commercially available in ton-scale at low prices.

In order to compare the relaxation properties of various qubit cores, different transition metal phthalocyanines were investigated. VO²⁺, Mn²⁺, Co²⁺ and Cu²⁺ were selected as this series provides charge neutral compounds with increasing SOC. Furthermore the compounds possess only one unpaired electron except Mn²⁺ (S = 3/2).^33,34 Finally, different coordination geometries can be compared, as VOPc exhibits square-pyramidal shape whereas the others possess square-planar ones. Fig. 2 shows the results for the metal dependence. Spin–lattice relaxation involves a fast and a slow process with nearly equal relative contributions for all investigated central ions. T_1,s increases by one order of magnitude for each member of the series Mn²⁺ < Co²⁺ < Cu²⁺ < VO²⁺. We find an extraordinarily long T_1,s = 2.4 ± 0.3 s for VOPc. It is known from literature that switching from labile (tetrahedral) coordination geometries to more stable ones (octahedral and related) prolongs T₁.¹⁵ Spin reversal to the ground state occurs via crystal field oscillations involving energy transfer to the surrounding lattice. Hence for smaller SOC generally longer spin–lattice relaxation times are observed.²⁸ The ultra-slow spin–lattice relaxation of VOPc confirms these effects: Vanadium has one of the smallest SOCs of the transition metals and is present here in a robust, square-pyramidal coordination geometry. For Cu²⁺, Mn²⁺ and Co²⁺ no correlation between spin–lattice relaxation and SOC is apparent and other effects must be dominant. The difference between these metal ions is the localisation of the unpaired electrons for CoPc and MnPc on the one hand (d_z² and/or d_xz, d_yz),^35,36 and CuPc (d_x²−y²) and VOPc (d_xy) on the other.^35,37 Thus, in CoPc and MnPc, at least one unpaired electron is located in an orbital with contribution perpendicular to the molecular plane, whereas this is not the case for CuPc and VOPc. For electron spins in orbitals sticking out of the molecular plane stronger interactions with magnetic fluctuations in the surrounding matrix and therefore faster relaxation times are expected.

The very slow spin–lattice relaxation of VOPc motivated us to study the temperature dependence of electron spin relaxation (7–99 K, Fig. S10, ESI†). Spin–lattice relaxation shows biexponential behaviour with a stronger temperature dependence of the fast component. Spin–spin relaxation also exhibits two processes. T_M,s is around 20 µs and vanishes above 10 K in the spectrometer noise. Within the measurement uncertainty, the fast process is temperature independent.

The variations of phase memory times within the investigated transition metal series are more subtle compared to the large distribution in spin–lattice relaxation values. The slow components of spin–spin relaxation of CuPc (41 ± 4 µs) and VOPc (22 ± 5 µs) are significantly longer than those of MnPc and CoPc. This is attributed to the abovementioned influence of the nature of the SOMO on the spin dynamics.

The solvent-, ligand- and central ion dependent study of transition metal phthalocyanines revealed valuable information on electron spin relaxation properties of molecular qubits. Stable coordination geometries and small SOC open the possibility for ultra-long spin–lattice relaxation times, as shown with VOPc. CuPc^Cl shows a single component Hahn echo decay with a figure of merit of 2000, which makes it a promising qubit candidate. Finally, long coherence times can be expected when the molecular orbital bearing the electron spin qubit exhibits minimal contact with the environment.

We acknowledge the Fonds der Chemischen Industrie for funding.

Note and references

1. L. Grover, Pramana, 2001, 56, 333–348.
2. P. W. Shor, SIAM J. Comput., 1997, 26, 1484–1509.
3. D. Loss and D. P. DiVincenzo, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 120–126.
4. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
5. G. Aromí, D. Aguila, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546.
6. G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. L. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173–178.
7. D. P. DiVincenzo, Fortschr. Phys., 2000, 48, 771–783.
8. S. S. Eaton and G. R. Eaton, in Distance Measurements in Biological Systems by EPR, ed. L. J. Berliner, G. R. Eaton and S. S. Eaton, Springer US, Boston, MA, 2002, vol. 19, pp. 29–154.
9. A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201.
10. J. van Slageren, Top. Curr. Chem., 2012, 321, 199–234.
11. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844.
12. G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 136, 63–68.
13. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
14. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492.
15. A. J. Fielding, S. Fox, G. L. Millhauser, M. Chattopadhyay, P. M. H. Kroneck, G. Fritz, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 2006, 179, 92–104.
16. A. J. Fielding, B. Dong Bin, M. Engler, B. Baruah, D. C. Crans, G. R. Eaton and S. S. Eaton, Vanadium: The Versatile Metal, American Chemical Society, 2007, ch. 26, vol. 974, pp. 364–375.
17. M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626.
18. Phthalocyanines: Properties and Materials, The Porphyrin Handbook, Academic Press, San Diego, California, 2003, vol. 17, pp. 37–127.
19. Phthalocyanines: Spectroscopic and Electrochemical Characterization, The Porphyrin Handbook, Academic Press, San Diego, California, 2003, vol. 16, pp. 43–116.
20. M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508.
21. L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, A. Matteo, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016 10.1039/C5SC04295J.
22. K. J. Standley and J. K. Wright, Proc. Phys. Soc., 1964, 83, 361.
23. C. Finazzo, S. V. Doorslaer and A. Schweiger, J. Porphyrins Phthalocyanines, 2003, 07, 89–96.
24. C. Finazzo, C. Calle, S. Stoll, S. Van Doorslaer and A. Schweiger, Phys. Chem. Chem. Phys., 2006, 8, 1942–1953.
25. C. Schlegel, J. van Slageren, G. Timco, R. E. P. Winpenny and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134407.
26. C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204.
27. D. Kaminski, A. L. Webber, C. J. Wedge, J. Liu, G. A. Timco, I. J. Vitorica-Yrezabal, E. J. L. McInnes, R. E. P. Winpenny and A. Ardavan, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184419.
28. J.-L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1996, 119, 240–246.
29. S. Takahashi, J. van Tol, C. C. Beedle, D. N. Hendrickson, L.-C. Brunel and M. S. Sherwin, Phys. Rev. Lett., 2009, 102, 087603.
30. A. M. Tyryshkin, J. J. L. Morton, S. C. Benjamin, A. Ardavan, G. A. D. Briggs, J. W. Ager and S. A. Lyon, J. Phys.: Condens. Matter, 2006, 18, S783.
31. C. Meyer, W. Harneit, B. Naydenov, K. Lips and A. Weidinger, Appl. Magn. Reson., 2004, 27, 123–132.
32. J. J. L. Morton, A. M. Tyryshkin, A. Ardavan, K. Porfyrakis, S. A. Lyon and G. Andrew D. Briggs, J. Chem. Phys., 2006, 124, 014508.
33. H. Miyoshi, H. Ohya-Nishiguchi and Y. Deguchi, Bull. Chem. Soc. Jpn., 1973, 46, 2724–2728.
34. H. Miyoshi, Bull. Chem. Soc. Jpn., 1974, 47, 561–565.
35. M.-S. Liao and S. Scheiner, J. Chem. Phys., 2001, 114, 9780–9791.
36. N. Marom and L. Kronik, Appl. Phys. A: Mater. Sci. Process., 2009, 95, 165–172.
37. Y. Zhang, T. Learmonth, S. Wang, A. Y. Matsuura, J. Downes, L. Plucinski, S. Bernardis, C. O'Donnell and K. E. Smith, J. Mater. Chem., 2007, 17, 1276–1283.
38. I. Tkach, A. Baldansuren, E. Kalabukhova, S. Lukin, A. Sitnikov, A. Tsvir, M. Ischenko, Y. Rosentzweig and E. Roduner, Appl. Magn. Reson., 2008, 35, 95–112.
39. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.

---

Footnotes

† Electronic supplementary information (ESI) available: Details on electron spin relaxation fit parameters and further pulsed EPR measurements. See DOI: 10.1039/c6cc00300a

‡ The investigated compounds (Scheme 1) were purchased (Sigma Aldrich) and used without further purification. Solutions were prepared in 0.5 mM concentration by dissolution into sulfuric acid (95–98%; Merck) or D₂SO₄ (95–98% in D₂O, 99.5 atom% D; Aldrich). Pulsed Q-band EPR measurements were performed on a homebuilt spectrometer³⁸ equipped with an Oxford Instruments CF935 continuous flow Helium cryostat. The samples were degassed by three freeze–pump–thaw cycles and measured in flame-sealed quartz tubes. Electron spin echo detected EPR spectra were simulated with the Matlab toolbox “EasySpin”³⁹ (see Fig. S1–S7, fit parameters Tables S1, S4 and S7, ESI†). Spin dynamics experiments were performed at the field position of the most intense resonance line. Inversion recovery and Hahn echo pulse sequences were applied for detecting spin–lattice and spin–spin relaxation respectively (Fig. S1–S9, ESI†). The echo decay curves of all experiments were fitted with mono-, bi- or stretched exponentials (results see Tables S2, S3, S5, S6 and S8–S11, ESI†). Standard deviations of fit parameters are indicated as errors where appropriate. The reproducibility uncertainty of the pulsed measurements is around 10% due to instrument-specific instabilities in temperature, magnetic field and frequency/phase of the microwave pulses.

---