Molecular titanium–hydroxamate complexes as models for TiO₂ surface binding

Abstract

Hydroxamate binding modes and protonation states have yet to be conclusively determined. Molecular titanium(IV) phenylhydroxamate complexes were synthesized as structural and spectroscopic models, and compared to functionalized TiO₂ nanoparticles. In a combined experimental–theoretical study, we find that the predominant binding form is monodeprotonated, with evidence for the chelate mode.

---

Hydroxamates, as well as carboxylates and catecholates, chelate Fe(III) in natural siderophores (Greek: iron carriers).^1–3 These iron-chelating compounds are secreted by microbes, adsorb strongly to mineral surfaces, and gather iron from their environment. These attributes make hydroxamic acid derivatives (Fig. 1) particularly attractive for functionalization of semiconductive oxide surfaces.^4–8 They bind strongly⁹ and they are simple to synthesize from widely-available carboxylate precursors.^2,7

Fig. 1 Hydroxamic acid functional group, where R¹ and R² are H, alkyl, or aryl.

Hydroxamic acids are relatively new anchoring groups in the context of surface functionalization, with significant advantages over the more common carboxylic acids and phosphonic acids for photoelectrochemical devices. Most notable are the greater resistance to hydrolysis compared to carboxylic acids and greater electronic coupling over carboxylic and phosphonic aids that ensures efficient electron transport.^4–8

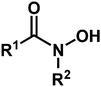
Hydroxamic acids of the form RCONHOH (R² = H, Fig. 1) have two potentially labile protons (O–H, N–H). Therefore, it has been unclear whether the surface-bound form is mono- (m) or dideprotonated (d) and how the protonation state affects the binding mode. Recent literature has focused on TiO₂ as the most widely used metal oxide for photoelectrochemical devices, and has suggested many possible modes for hydroxamate binding.^3,5,10,11 The most likely possibilities are shown in Fig. 2 where NH hydroxamic acids can chelate a single Ti (mc, dc) or bridge two Ti ions (mb and db).^5,10 The mc binding mode is analogous to that of a previously synthesized N-alkyl titanium hydroxamate complex, and in the natural product ferrichrome in which an N-alkyl hydroxamic acid chelates iron.^12,13 They could also bind as monodentate species, likely as the monodeprotonated monodentate species mm. Thus, they could bind in a monoanionic form via deprotonation at O (mc, mb, and mm), or dianionic form via deprotonation at O and N (db, dc). Herein, we show evidence for the monodeprotonated binding mode mc to TiO₂.

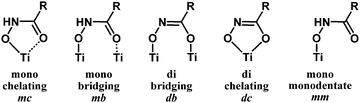Fig. 2 Surface binding schemes for NH hydroxamic acids. Mono = monodeprotonated. Di = dideprotonated.

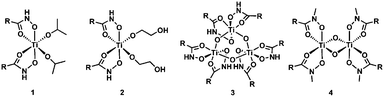
We analyzed hydroxamate binding by combining synthesis, IR spectroscopy and density functional theory (DFT) calculations of structure and IR spectra. Synthesis of a series of Ti-hydroxamate complexes from phenylhydroxamic acid precursors allowed for spectral comparisons to functionalized TiO₂ surfaces. This series included μ-oxo bridged Ti hydroxamate complexes prepared from NH- and N-methyl-phenylhydroxamic acids (Fig. 3), the latter being incapable of double deprotonation. We assigned the IR spectra and the composition of the functionalized TiO₂ surfaces by using DFT as described in the ESI.†

Fig. 3 Structures of synthesized compounds 1, 2, 3, and 4 where R = Ph.

Treatment of Ti(IV) isopropoxide with phenylhydroxamic acid (NH–PHA) forms the cis-bis-phenylhydroxamate-bis-isopropoxide Ti(IV) complex 1. We obtained the crystal structure of the monomeric titanium complex 2 (Fig. 4) by slow crystallization from 1 in ethylene glycol solvent, where labile isopropoxide ligands were replaced by ethylene glycol, which did not chelate in the system, but instead bound to Ti and formed a hydrogen bond with the NH group.

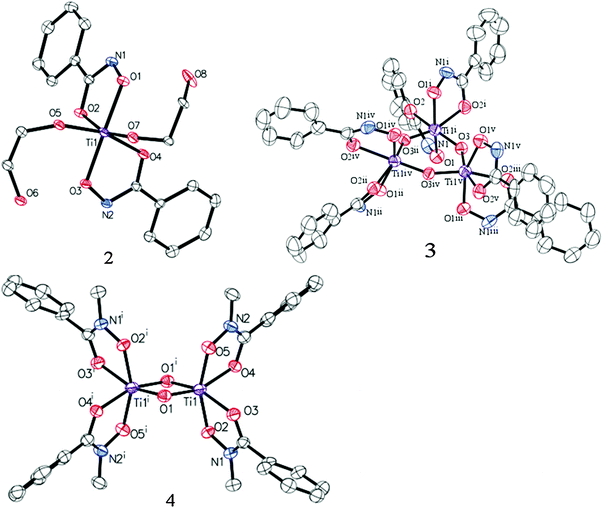Fig. 4 ORTEP diagrams of 2, 3, and 4 (50% probability) with H atoms and co-crystallized solvents omitted for clarity (see ESI†).

In moist DMSO solvent, the monomeric Ti complex 1 reacted with adventitious water to form the μ-oxo bridged trimer 3 (Fig. 3), having the crystal structure shown in Fig. 4. For comparison, N-methylphenylhydroxamic acid (NMe–PHA)¹⁴ gave the N-methyl analogue, which crystallized as the bis-μ-oxo dimer 4. These μ-oxo structures are the closest extant small molecule models for hydroxamate binding to TiO₂ and show substantial similarities to the possible coordination sphere around titanium when NH–PHA and NMe–PHA bind to TiO₂. We have, therefore, used them as the best available models for the surface-bound species.

The similarities between the NH–PHA and NMe–PHA structures follow from the comparison of the experimental and theoretical C–O, C–N, and N–O bond lengths, shown in Table S1 (ESI†). Doubly deprotonated coordination in the NH–PHA complexes would result in lengthened C–O bonds and shortened C–N bonds. Instead, the carbonyl bond lengths were 1.28, 1.26, and 1.28 Å for 2, 3, and 4, respectively, which are consistent with true C=O bonds as found in the prior literature.¹⁵ The C–N bond lengths are also similar for all the complexes, with bond-lengths of 1.31, 1.30, and 1.31 Å in good agreement with known metal–organic coordination compounds containing monodeprotonated hydroxamate ligands (Table S2, ESI†).¹⁵

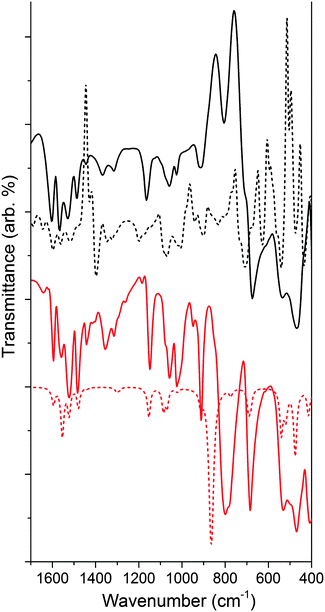
We calculated the lowest energy structures for the functionalized material modeled as NH–PHA, anchored to a slab of anatase TiO₂. We also computed the corresponding IR spectra of a {101} facet cluster model, obtained from a TiO₂ slab optimized with hydroxamate bound in various binding geometries. Fig. 5 compares the experimental and calculated spectra of NH–PHA bound to anatase TiO₂ and μ-oxo bridged model complex 3 (See Fig. S2 and S5 for complex 2 and ligand spectra, ESI†). A scaling factor of 0.975 was determined by matching the theoretical and experimental model complex spectra. Correlation of vibrational frequencies to specific vibrations is complicated by strong coupling of the skeletal vibrations, as previously discussed.^3,10,16 However, assignments can still be made using the theoretical spectra, especially for important bands involving carbonyl stretches (see Table S4 for a summary, ESI†). Significant contributions from the carbonyl stretches (ν_C=O) for NH–PHA on TiO₂ (vide infra) and for model complexes 2 and 3 occur at 1565/1604, 1566/1602, and 1558/1594 cm⁻¹, respectively. Similarly, the theoretical peak for ν_C=O for NH–PHA on TiO₂ and 2 and 3 occur at 1514/1562/1598, 1552/1593, and 1556/1594 cm⁻¹, respectively. These are shifted to lower frequency from the free NH–PHA, where the carbonyl in the solid-state hydrogen-bonded form appears at 1645 cm⁻¹. The ν_C=O for monodeprotonated PHA appears at 1605 cm⁻¹.¹⁷ Signals for the NH vibration are observed for NH–PHA bound to TiO₂ and in the spectra of 2 and 3 at 3193, 3189, and 3180 cm⁻¹, respectively (see Fig. S2, S3, S7, and S8, ESI†).

Fig. 5 Comparison of experimental (solid) and calculated (dashed) IR spectra of NH–PHA on TiO₂ (black) and model complex 3 (red). Theoretical calculation of NH–PHA on TiO₂ incorporates an equal mixture of mc via an oxygen vacancy, mb, and mm binding modes, and includes inverted peaks due to loss of surface hydration upon binding.

The IR data for 3 show striking overlap with the IR spectrum of the surface-bound NH–PHA (Fig. 5). Corresponding vibrational bands are within 20 cm⁻¹ of each other and have similar intensity ratios. This observation suggests that NH–PHA binds to TiO₂ in a monodeprotonated form as in the model complexes. Indeed, the presence of an NH stretch conclusively eliminates the dideprotonated forms as possibilities, leaving the only remaining possibilities as mc on a pristine surface or through an oxygen vacancy, as well as mm and mb. The similarity between the spectra of NH–PHA bound to TiO₂ and that of 3 provides good evidence for the chelating mode as a significant percentage of the surface-bound species. Bridging modes would be expected to cause significant changes in bond lengths and angles for the surface-bound species compared to the chelating modes, and thus significantly affect the spectra. In fact, in the theoretical geometries for mb and mc, we see a large difference in the O–N–C bond angle (133° and 115°, respectively), the N–C–O bond angle (126° and 116°, respectively), and the binding O–Ti bond length (∼2.17 Å and <2.08 Å, respectively) leading to mb as a higher energy surface binding mode. However, free energy calculations for the binding modes show mm, mb, and mc (via an oxygen vacancy) to be the most stable surface anchoring possibilities in that order, with mc being the least stable of those three modes (Table S3, ESI†). No single calculated binding geometry was found to reproduce the surface-bound spectra. Thus, a heterogeneous binding mixture utilizing all three binding modes was used to calculate the theoretical spectrum of NH–PHA on TiO₂ in Fig. 5.

Fig. 6 shows the IR analysis of 4 as compared to that of the ligand bound to TiO₂ (see Fig. S6 for ligand spectrum, ESI†). Much like for NH–PHA, the spectra of NMe–PHA bound to TiO₂ and model complex 4 have similarities. The ν_C=O are 1565/1595 cm⁻¹, 1564/1586 cm⁻¹, and 1597 cm⁻¹ for NMe–PHA on TiO₂, in 4, and for the ligand, respectively. The theoretical equivalents are 1424/1428/1584 cm⁻¹, 1551/1586 cm⁻¹, and 1646 cm⁻¹. The values for ν_C=O are similar to those of the NH–PHA analogues, described above. The trends in the free energy calculations for the binding modes mimic those of the NH–PHA analogues, and a similar mixture of mm, mb, and mc (via an oxygen vacancy) was used to model NMe–PHA bound to TiO₂.

Fig. 6 Comparison of experimental (solid) and calculated (dashed) IR spectra of NMe–PHA on TiO₂ (black) and model complex 4 (red). Theoretical calculation of NMe–PHA on TiO₂ incorporates an equal mixture of mc via an oxygen vacancy, mb, and mm binding modes, and includes inverted peaks due to loss of surface hydration upon binding.

Overall, there are more significant differences between the spectra of 4 with its surface-bound form than with the NH–PHA analogues, likely due to differences in the octahedral geometries of 3 and 4. TiO₂ anatase has a Ti–O–Ti bond angle¹⁸ of 156.2° compared to 140.8° for 3 and only 96.5° for 4, which is closer to octahedral. Thus, complex 3 could more closely match the chelating geometry of the NH–PHA ligand bound to the surface of anatase TiO₂ than the NMe–PHA analogues due to a greater degree of electronic similarity. UV-visible spectroscopy of the model complexes in solution and surface-bound to TiO₂ was performed (Fig. S9–S11, ESI†), but these data do not provide additional information on the binding geometry due to overlap of the UV absorption from TiO₂ with all the absorption bands of the model compounds.

The similarity of NH–PHA to both 4 and NMe–PHA on TiO₂ provides substantial evidence for the presence of the mc binding mode, as also found for the binding of N-alkylhydroxamates to metal ions in siderophores.¹² Our calculations suggest other binding modes are more energetically favorable, but for the calculations it must be assumed that the TiO₂ cannot undergo reconstruction to form a lower energy surface. As an experimental test, we compared the IR spectra of NH–PHA and NMe–PHA bound to commercially available nanoparticulate anatase and rutile TiO₂ (see Fig. S20 and S21, ESI†). The results show that all observable peaks are in alignment for each ligand on each crystal form, suggesting that the coordination of the ligand to the surface could cause significant bond rearrangement, ending in a lower energy surface that is similar between the two crystal phases of the starting materials. This hypothesis is additionally supported by the IR spectroscopic features of model complex 4, which should be more electronically similar to rutile than anatase, yet are dissimilar to both.

Our study provides new evidence on the binding of hydroxamates to TiO₂. The crystal structure data, supported by IR analysis and DFT calculations, show that the mc binding mode is present in the model complexes. For the binding of hydroxamates to TiO₂, we propose that there is likely a mixture of binding geometries on the surface, possibly due to surface reconstruction upon ligand binding. Our IR data suggest that mc is the main binding mode on the TiO₂ surface. The 5-membered chelate formed between the hydroxamate and Ti is a stable structural motif, providing a rationale for the tight binding and excellent hydrolytic stability of hydroxamates adsorbed to TiO₂ surfaces.

This material is based upon work supported as part of the Argonne-Northwestern Solar Energy Research (ANSER) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0001059. Additional funding was provided by a generous donation from the TomKat Charitable Trust. B. R. acknowledges support from the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1122492. V. S. B. acknowledges supercomputer time from NERSC and from the Yale HPC Center. Supporting information for this article is given via a link on the first page of the manuscript.

Notes and references

1. C. Cocozza, C. C. G. Tsao, S.-F. Cheah, S. M. Kraemer, K. N. Raymond, T. M. Miano and G. Sposito, Geochim. Cosmochim. Acta, 2002, 66, 431–438.
2. M. J. Miller, Chem. Rev., 1989, 89, 1563–1579.
3. J. Yang, P. J. Bremer, I. L. Lamont and A. J. McQuillan, Langmuir, 2006, 22, 10109–10117.
4. T. P. Brewster, S. J. Konezny, S. W. Sheehan, L. A. Martini, C. A. Schmuttenmaer, V. S. Batista and R. H. Crabtree, Inorg. Chem., 2013, 52, 6752–6764.
5. W. R. McNamara, R. C. Snoeberger III, G. Li, C. Richter, L. J. Allen, R. L. Milot, C. A. Schmuttenmaer, R. H. Crabtree, G. W. Brudvig and V. S. Batista, Energy Environ. Sci., 2009, 2, 1173–1175.
6. W. R. McNamara, R. L. Milot, H.-e. Song, R. C. Snoeberger III, V. S. Batista, C. A. Schmuttenmaer, G. W. Brudvig and R. H. Crabtree, Energy Environ. Sci., 2010, 3, 917–923.
7. C. Koenigsmann, T. S. Ripolles, B. J. Brennan, C. F. A. Negre, M. Koepf, A. C. Durrell, R. L. Milot, J. A. Torre, R. H. Crabtree, V. S. Batista, G. W. Brudvig, J. Bisquert and C. A. Schmuttenmaer, Phys. Chem. Chem. Phys., 2014, 16, 16629–16641.
8. L. A. Martini, G. F. Moore, R. L. Milot, L. Z. Cai, S. W. Sheehan, C. A. Schmuttenmaer, G. W. Brudvig and R. H. Crabtree, J. Phys. Chem. C, 2013, 117, 14526–14533.
9. E. Ahmed and S. J. M. Holmström, Microb. Biotechnol., 2014, 7, 196–208.
10. W. Li, L. G. C. Rego, F.-Q. Bai, C.-P. Kong and H.-X. Zhang, RSC Adv., 2014, 4, 19690–19693.
11. F. Ambrosio, N. Martsinovich and A. Troisi, J. Phys. Chem. Lett., 2012, 3, 1531–1535.
12. A. D. Ferguson, E. Hofmann, J. W. Coulton, K. Diederichs and W. Welte, Science, 1998, 282, 2215–2220.
13. N. Kongprakaiwoot, B. C. Noll and S. N. Brown, Inorg. Chem., 2008, 47, 11902–11909.
14. C. Punta, C. L. Rector and N. A. Porter, Chem. Res. Toxicol., 2005, 18, 349–356.
15. CSD search: there are 329 structures in the November 2014 database with organometallic compounds containing hydroxamic ligands similar to our system. These structures have average C–O, C–N, and N–O bond lengths of 1.276, 1.32, and 1.376 Angstroms, respectively (see ESI† for full table).
16. D. A. Brown, D. McKeith and W. K. Glass, Inorg. Chim. Acta, 1979, 35, 57–60.
17. A. I. Artemenko, E. K. Anufriev and I. V. Tikunova, J. Appl. Spectrosc., 1980, 32, 357–362.
18. M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and theoretical methods, ¹H and ¹³C NMR, full FT-IR spectra, experimental and theoretical UV-visible spectra, simulated (DFT) structures and coordinates, tables of frequencies, bond lengths and free energies, crystallographic data (CIF). CCDC 1402797–1402799. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5cc09857b

---