Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simultaneous quantification of ion pairs in water via infrared attenuated total reflection spectroscopy†
F.
Rauh
and
B.
Mizaikoff
*
Ulm University, Albert-Einstein-Allee 11, 89081 Ulm, Germany. E-mail: boris.mizaikoff@uni-ulm.de
First published on 10th February 2016
Abstract
In this study, ion pairs in aqueous solution were quantitatively and simultaneously determined via infrared attenuated total reflection (IR-ATR) spectroscopy. Seven salts that are occurring in natural seawater, i.e., NaCl, KCl, NaBr, KBr, MgCl2, CaCl2, and Na2SO4 were investigated. Multivariate data analysis was used to discriminate and assign the spectral information arising from each salt in calibration mixtures, each containing a mixture of all constituents in different concentrations. The algorithm was able to discriminate between NaCl/KCl, NaBr/KBr, MgCl2, CaCl2, and Na2SO4 with sodium and potassium chloride, and bromide being treated as sum parameters, respectively. An additional multivariate model was able to distinguish between NaCl, KCl, NaBr, and KBr including their simultaneous quantification. Finally, a sample of real seawater was analyzed, with the established model. MgCl2 could be correctly quantified at 0.5 ± 0.05% (w/v) in this sample, whilst the other ions obviously demand for a more precise and complex calibration model, which is more similar to real seawater.
Introduction
In this study, several salts occurring in seawater containing mostly IR-inactive ions (except SO42−) were analyzed using IR-ATR spectroscopy. The developed method enabled their simultaneous quantification based on the changes they are inducing within the IR-ATR spectrum of deionized water as a result of organization of the water molecules within the solvation shell of associated ions.1Ion association is affecting the molecular structure of water and thus influencing its' properties, e.g. viscosity, conductivity and the solubility of certain minerals.2 In general, the composition and behavior of seawater and the salts it is containing are of mayor importance for marine ecosystems, providing substantial contributions to human nutrition (e.g. fish, crustacea, algae, etc.). In this study, first results of the simultaneous detection and characterization of several ion pairs in artificial salt solutions, prepared in the laboratory, as well as a sample of real seawater via ATR ITR spectroscopy in combination with multivariate data evaluation are discussed. For real-time measurements (e.g. monitoring of seawater quality) on-ship or on buoys, FTIR spectroscopy offers a method for rapid detection of several ion pairs in water within a single measurement. For the best of our knowledge, this is the first study that deals with the determination of multiple ion pairs in one solution at a time.
Principal components analysis and regression (PCA/PCR) was applied to distinguish between seven different pairs of associated ions, and to predict their concentration within several test mixtures. Hence, the dataset was considered a matrix of p variables (i.e., absorbances at certain wavenumbers) measured at n objects (i.e., salt solutions). Such a dataset may be represented by n data points in a p-dimensional data space. Principal components analysis (PCA) then projects the data points into an eigenvector-based data space (i.e., directions of maximum variance), which goes along with a significant variable reduction. Hence, the first principal component (PC) is the eigenvector that covers the maximum variance in the dataset. Additional principal components need to be orthogonal to the first one, and comprise the remaining variance each with decreasing contribution to the total variance of the data set. During the principal components regression (PCR), these PCs are used as regressors for obtaining linear regressions serving e.g., as calibration functions.3–7
Practically, a calibration data set and a test data set (i.e., a so-called validation set) have to be prepared and analyzed. Each solution for both of these sets contains each analyzed salt. The calibration set consisted of 25 solutions containing each salt at a concentration of 0.8–4% (w/v). Sodium sulfate was contained at lower concentrations in order to avoid the precipitation of gypsum. Also, since the sulfate anion is IR-active, it is precisely detectable at low concentrations via distinct IR absorption features at approx. 1100 cm−1. The validation set comprised eight solutions with salt concentrations different from the samples within the calibration date set, yet within the same concentration range (see Table S1 of the ESI†).
The calibration set was used to establish a multivariate calibration and data evaluation model correlating measured concentrations with the concentrations predicted by the model. The predictive power of the model was successfully tested using quasi-unknown samples (i.e., the validation data set). It was shown that IR-ATR spectroscopy, albeit not at first sight the method of choice for analyzing IR-inactive ions, efficiently provides information on ion pairs in water complementary to conventionally applied techniques addressing their structure,8,9 solvation dynamics,10,11 and thermodynamic properties.2,12
Basic mathematical approaches for the equilibrium between free ions and ion pairs were published by N. Bjerrum in 192613 and R. M. Fuoss in 1934.12 Marcus and Hefter are giving a comprehensive and detailed overview on ion pairing in “Chemical Reviews” (2006).14
Max and Chapados have published several papers on infrared spectroscopy of dissolved ions, focusing on alkali halides. Their results show that a spectrum of a dissolved salt in water is a combination of two eigenspectra of pure water and “salt-solvated water” and that the ions stay closely associated in stable clusters, instead of being individually dissolved.15–20
Ion pairs in seawater were examined by Kester and Pytkowicz in the 1970s.21–23 For example, they developed a model that can explain the difference in activity coefficients in seawater and in single salt solutions, based on ion association.21
Katz and Ben-Yaakov studied the role of ion pairing concerning the diffusion of ions in seawater. They found a higher diffusive mobility of magnesium in an ion pair compared to the free ion.24
Jungwirth & Tobias carried out molecular dynamics studies including the effect of ion association, in order to explain the atmospheric reactivity of aqueous sea-salt microparticles.11
Experimental
Chemicals
NaCl, NaBr, KBr (each ACS-reagent grade), KCl (pro analysi grade), MgCl2·6H2O, and CaCl2·2H2O (both Ultra Grade) were purchased from Sigma-Aldrich (St Louis, MO, USA). Na2SO4·10H2O (pro analysi grade) was obtained from Merck (Darmstadt, Germany).All solutions were prepared by mixing concentrated solutions 28% (w/v) – except Na2SO4 at 1.05% (w/v) – of each salt at different ratios 0.8–4% (w/v) (Na2SO4: 0.03–0.15% (w/v)), and dilution with deionized water to a total volume of 7 mL. The mixtures were prepared according to Brereton.25
Instrumentation
For all measurements, a Vertex 70 FTIR spectrometer equipped with a temperature-controlled Bio-ATR II unit was used (both Bruker Optics, Ettlingen, Germany). The Bio ATR II measuring cell consists of a spherical zinc selenide crystal, covered by a very thin silicon wafer, which is in contact with the probed medium. This setup enables multiple total internal reflections in a very short distance (inside the silicon wafer), offering highly sensitive measurements with sample volumes as low as 10 μL. The temperature during IR-ATR experiments was stabilized using a thermostat (Lauda, Koenigshofen, Germany) at 22 ± 0.1 °C during all studies.Measurement procedure
Before the measurement was executed, the Si ATR crystal was thoroughly rinsed with deionized water. After drying, the lid of the ATR assembly was closed, and a background spectrum of ambient air was recorded. Thereafter, 20 μL of deionized water was pipetted into the sample cell and a spectrum was collected. Subsequently, all calibration mixtures were analyzed (20 μL each). After each analysis, the Si ATR waveguide was cleaned two times with 40 μL of pure water, and dried with a cotton swab. All spectra were collected at a spectral resolution of 1 cm−1 averaging 100 scans.Data processing
First, an atmospheric compensation algorithm was used to remove spectral features arising from atmospheric water vapor and CO2 within the IR beam path (OPUS 7 software package; Bruker Optics, Ettlingen, Germany). Thereafter, a spectrum of pure deionized water, recorded at the beginning of each test series, was subtracted from each salt solution spectrum obtaining a difference spectrum revealing only the changes induced within the water spectrum by the ion pairs (OPUS 7 software package). Then, the spectra were loaded into a Matlab environment (TheMathWorks, Nattick/MA, USA) for further analysis using the PSL Toolbox (Eigenvector Inc., Manson/WA, USA). All spectra were smoothed and mean centered prior to establishing a multivariate model. Also, spectral regions containing no or little information were excluded from the data analysis (i.e., spectral region selection; for more information see Fig. S1 within the ESI†). The first seven principal components (from a total of 20), covering 99.94% of the variance, were used for modelling the spectroscopically relevant variance. This is the minimal number of principal components yielding in good quality linear prediction curves. The remaining 13 principal components are supposed to represent only noise. The venetian blinds method was used to cross-validate the obtained model.Results & discussion
In an aqueous solution of a salt, two main ‘types’ of water are coexisting: (i) pure bulk water, and (ii) water within the solvation sphere around the dissolved salt ions. While the latter type of water may not be directly analytically addressed, its infrared spectrum may be derived via inter- and extrapolation of spectra of the respective aqueous salt solution with modulated concentration levels vs. the spectrum of pure deionized water. From thus obtained spectra of water associated with the solvation sphere around ions, information on the ions inducing the solvation sphere (i.e., ‘organizing’ the water molecules) can be collected, even if the ions per se are IR-inactive (e.g., dissolved monovalent ions such as Na+, Cl−, etc.). For example, it may be derived that certain ions are not individually solvated, but remain closely associated as ion pairs, which is the fundamental subject of the present study. Furthermore, the hydration number may be obtained.20Obviously, one anion and one cation of a solvated salt form a cluster in aqueous solution with a certain number of water molecules within the associated solvation sphere. Apparently, the number of water molecules is dependent on the ratio of the ionic radii. Max et al. have published several IR spectroscopic studies on the solvation of ions.15–20 For contrasting their results with the findings of the present study, a summary is provided in Table 1.
| Salt | Ratio of ionic radii | Hydration number |
|---|---|---|
| NaCl | 1.85 | 5 |
| KCl | 1.36 | 5 |
| NaBr | 2.00 | 5 |
| KBr | 1.47 | 5 |
| MgCl2 | 2.32 | 4 |
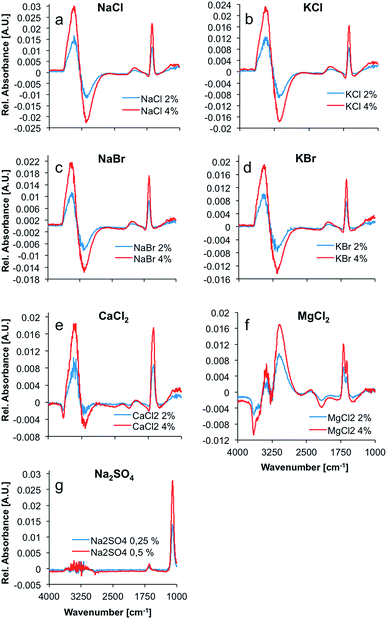
Max and Chapados reported the value of the hydration number of salts that have a ratio of ionic radii ranging from 1.33 to 2.00 to be five, and accordingly described these salts as ‘NaCl-like salts’. Consequently, it was anticipated that the difference spectra of NaCl, KCl, NaBr, KBr, and CaCl2 appear similar (see Fig. 1). The hydration shell of these salts is apparently quite similar, and comprises the same amount of water molecules. The difference spectrum of MgCl2 appears significantly different from these spectra with a calculated hydration number of four.
Table 2 provides an overview on some additional properties of ions that were taken into account during the present study. The hydration number of calcium chloride was calculated to five by using the given anion and cation radii (i.e., the ratio of ionic radii was calculated at 1.71). This is in excellent agreement with the spectral information, as the IR-ATR difference spectrum of the calcium chloride solution appears similar to the spectra of the other NaCl-like salt solutions. For sodium sulfate no hydration number was calculated, as the sulfate anion is polyatomic and cannot be described by the monoatomic model used herein.
| Ion | Radius26 [pm] | Volume [m3] | Charge density [A s m−3] | mol L−1 in seawater28 |
|---|---|---|---|---|
| Mg2+ | 78 | 1.99 × 10−19 | 1.61 | 0.0527 |
| Ca2+ | 106 | 4.99 × 10−19 | 0.64 | 0.0103 |
| Na+ | 98 | 3.94 × 10−19 | 0.41 | 0.4726 |
| K+ | 133 | 9.85 × 10−19 | 0.16 | 0.0103 |
| Cl− | 181 | 2.48 × 10−18 | −0.06 | 0.5451 |
| Br− | 196 | 3.15 × 10−18 | −0.05 | 0.0009 |
| SO42− | 290 (ref. 27) | 1.02 × 10−17 | −0.03 | 0.0282 |
As evident, Na+, K+, and Ca2+ cations are characterized by highly similar volume charge densities at an order of magnitude around 0.5 A s m−3. The magnesium cation has a significantly higher volume charge density of 1.61 A s m−3.
This higher volume charge density could play a significant role in the formation and structure of the hydration shell around MgCl2, as the electrostatic properties of the ion have a major effect on the water molecules surrounding the ions due to the dominating coulomb interactions. Ions with unusually high charge densities are obviously not only influencing the structure and dynamics of the first hydration shell, but also of the second hydration shell.29 Hence, the difference in volume charge density explains the distinct difference spectra of MgCl2 solutions, as compared to the spectra of solutions of NaCl-like salts (see Fig. 1).
The spectrum of liquid water in the mid-infrared (MIR) region is characterized by four main absorption features. The most prominent absorption is the O–H-stretching vibration centered at approx. 3350 cm−1. This band is a combination of a stretching vibration ν1, an overtone of the bending vibration 2ν2, and another stretching vibration ν3. The rather weak 3rd libration overtone feature (ν2 + νL) occurs at 2115 cm−1. At 1640 cm−1, the H–O–H bending vibration (ν2) shows a distinct feature. Another strong absorption band occurs at around 700 cm−1.30 This band was excluded from the analysis herein, as it is occurring near the cut-off of the applied mercury–cadmium–telluride (MCT) detector at 675 cm−1, and therefore appears distorted. The remaining absorption features of water show significant changes upon addition of several salts, as evident in Fig. 1. Principally, the OH stretching feature resembles a first deviation of a Gauss function in the difference spectra, whilst the shape of the H–O–H bending vibration looks like the second deviation of a Gauss function. These are the most prevalent changes in the spectrum of water upon addition of ions. Minor changes in intensity are induced in the combination band (ν2 + νL), revealing a small negative peak in the difference spectra of CaCl2 and MgCl2 solutions at ∼2100 cm−1. Since all changes are proportional to the ion concentration, the intensity of the peaks in the difference spectra representing those changes, are increasing with concentration. The difference spectrum of the MgCl2 solution shows two well resolved peaks between 3000 and 3400 cm−1 and a distinct negative peak at ∼3600 cm−1. Also, the peak at 1640 cm−1 is split, compared to the other spectra. It is anticipated that these differences are due to the more complex hydration shell of the magnesium cation, which is also influencing the second hydration shell, as stated before.29
The spectrum of dissolved sodium sulfate does not reveal significant spectral changes of the absorption features of H2O, unlike all other dissolved salts, which results from the significantly lower salt concentrations. Nevertheless, the distinct sulfate absorption feature at approx. 1100 cm−1 (triply degenerate asymmetric S–O stretching vibration (ν3) of SO42− in solution) remains pronounced for characterizing this salt.31
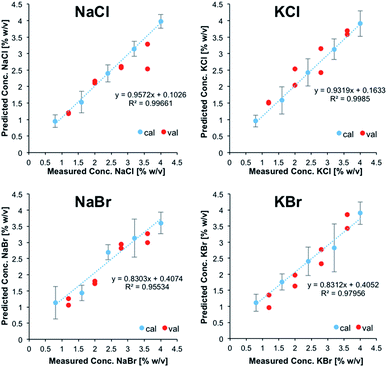
Fig. 2 illustrates the obtained linear calibration plots for the ion pairs contained in the calibration solutions, including the predicted concentrations for the ion pairs contained in the validation mixtures.
 | ||
| Fig. 2 Linear calibration functions for ion pairs derived from IR-ATR spectra. NaCl and KCl, as well as NaBr and KBr were treated as sum parameters. | ||
NaCl and KCl, as well as NaBr and KBr were treated as sum parameters. Apparently, these ion pairs form hydration shells that may not be differentiated with the developed model. For CaCl2, MgCl2, and Na2SO4, the standard deviation was calculated for each calibration point (i.e., five individual measurements each), and were used for illustrating positive and negative errors. For NaCl/KCl and NaBr/KBr, the standard deviation was used for describing the error associated with all calibration points, which were individually measured at least three times.
For all salts the predicted concentrations for the validation data (see red dots, Fig. 2) reveal good correlation with the experimental values, thus confirming the accuracy of the developed multivariate calibration model.
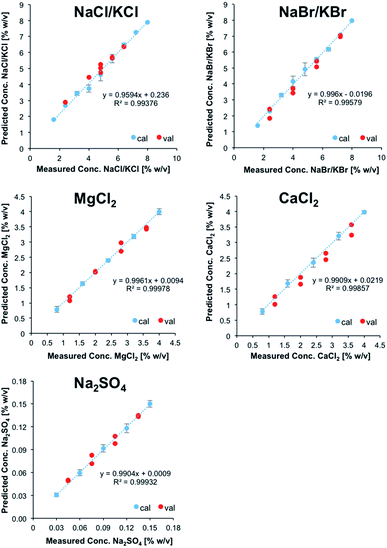
Subsequently, a refined model was established for further testing, if in fact NaCl, KCl, NaBr, and KBr may be discriminated and simultaneously quantified. For that purpose, 25 solutions containing all four salts at different concentrations were prepared and used as calibration data set. As described previously, a validation data set consisting of 8 solutions was prepared in addition. After PCA, 10 PCs were used for describing the analytically relevant variance data space. Then again, experimentally obtained vs. predicted values were plotted for each salt (Fig. 3). It was shown that a refined model for these particular species enabled the prediction of the concentrations of each salt within the validation mixtures, albeit with significantly higher errors associated with each calibration point compared to the previous model. Nonetheless, despite the fact that NaCl, KCl, NaBr, and KBr induce highly similar IR-ATR spectra and spectral changes within the water matrix, their discrimination and quantification in mixtures of reduced complexity is possible.
While clearly a more complex calibration model taking into account matrix effects would be more suitable, the (first) established calibration model was applied for analyzing a sample of real seawater from the Atlantic Ocean. Reference values were obtained via inductively coupled plasma-optical emission spectroscopy (ICP-OES) for all ions except Cl−; the concentration of sulfur was used for deriving the concentration of SO42−. The reference value for Cl− was obtained by titration with silver nitrate using potassium chromate as indicator.
The concentration of MgCl2 could be correctly predicted at 0.5 ± 0.05% (w/v), even though the calibration range does not cover this concentration in seawater. The predicted concentration of sodium sulfate (0.29 ± 0.01% (w/v)) was predicted 18% lower than derived by ICP-OES. Since ICP-OES determines the overall sulfur content in a sample, but not the content of the sulfate anion, this discrepancy might also include organic sulfur, dissolved in seawater. The concentration of NaCl/KCl was overpredicted by at least 34% (3.42 ± 0.21% (w/v)). Finally, the model was not able to predict the concentrations of NaBr/KBr and CaCl2, which are supposed to be present at concentrations significantly below the limits of detection of the developed method. While – as anticipated – the direct application of the developed IR-ATR method for simultaneously analyzing ion pairs in aqueous solution requires more sophisticated calibration samples representative for complex matrices when analyzing real-world seawater samples, this technique has certainly revealed its potential for rapidly and efficiently analyzing even IR-inactive ions in aqueous solution, and will be further refined for in-field applications during future studies.
Conclusions & outlook
A multivariate model using principal components analysis and regression (PCA/PCR) was established that enabled the simultaneous discrimination and quantification of five ion pairs in artificial aqueous ion solutions based on infrared attenuated total reflection (IR-ATR) spectroscopy. Thereby, MgCl2, CaCl2, Na2SO4 were determined along with NaCl/KCl and NaBr/KBr as sum parameters. In addition, a refined model distinguishing and quantifying NaCl, KCl, NaBr, and KBr proved the tailorability of this approach for moderately complex aqueous ion mixtures.The results of the present study confirm that ions are not individually solvated, but remain closely associated as clusters/ion pairs with a distinct number of water molecules within the inner solvation sphere, as anticipated by previous reports in literature. To the best of our knowledge, this is the first study that simultaneously confirms and quantifies such hydrated ion pairs via IR-ATR spectroscopy, which enables fast, reliable, and accurate measurements in minute sample volumes readily adaptable to a range of application scenarios.
Finally, real-world seawater samples were analyzed proving that some ion concentrations could be correctly predicted, yet revealing limitations due to the limited resemblance of the calibration samples with the complex background matrix in real seawater. The calibration matrix will be adapted to real seawater in further experiments in order to obtain good quality predictions of ion pairs in real world samples. Also, the influence of other parameters including temperature and pH will be determined and included in future models.
Acknowledgements
This work was in part funded by the European Union within project SCHeMA (Integrated in Situ Chemical Mapping Probes). Furthermore, Sylvia Mauthe and Juliana Fiechtner are thanked for measurements during their laboratory courses at IABC that have in part contributed to this study.References
- F. Vogt, M. Kraft and B. Mizaikoff, Appl. Spectrosc., 2002, 56, 1376–1380 CrossRef CAS.
- D. R. Kester and R. M. Pytkowicz, Geochim. Cosmochim. Acta, 1970, 34, 1039–1051 CrossRef CAS.
- S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52 CrossRef CAS.
- Chemometrik: Grundlagen und Anwendungen, ed. K. Danzer, H. Hobert, C. Fischbacher and K.-U. Jagemann, Springer, Berlin, 2001 Search PubMed.
- M. J. Adams, Chemometrics in analytical spectroscopy, Royal Society of Chemistry, Cambridge, 2nd edn, 2004 Search PubMed.
- R. G. Brereton, Chemometrics: data analysis for the laboratory and chemical plant, Wiley, Chichester, Repr., 2006 Search PubMed.
- W. Härdle and L. Simar, Applied multivariate statistical analysis, Springer, Berlin, New York, 2nd edn, 2007 Search PubMed.
- G. H. Peslherbe, B. M. Ladanyi and J. T. Hynes, Chem. Phys., 2000, 258, 201–224 CrossRef CAS.
- D. Laria and R. Fernández-Prini, J. Chem. Phys., 1995, 102, 7664–7673 CrossRef CAS.
- B. M. Pettitt and P. J. Rossky, J. Chem. Phys., 1986, 84, 5836–5844 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2000, 104, 7702–7706 CrossRef CAS.
- R. M. Fuoss, J. Am. Chem. Soc., 1958, 80, 5059–5061 CrossRef CAS.
- N. J. Bjerrum, K. Dan. Vidensk. Selsk., Mat.-Fys. Medd., 1926, 7, 9 Search PubMed.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CrossRef CAS PubMed.
- J.-J. Max, M. Trudel and C. Chapados, Appl. Spectrosc., 1998, 52, 234–239 CrossRef CAS.
- J.-J. Max and C. Chapados, Appl. Spectrosc., 1999, 53, 1045–1053 CrossRef CAS.
- J.-J. Max and C. Chapados, Appl. Spectrosc., 1999, 53, 1601–1609 CrossRef CAS.
- J.-J. Max and C. Chapados, J. Chem. Phys., 2000, 113, 6803–6814 CrossRef CAS.
- d. B. Serge Max, J. Joseph, A. Veilleux and C. Chapados, Can. J. Chem., 2001, 79, 13–21 CrossRef.
- J.-J. Max and C. Chapados, J. Chem. Phys., 2001, 115, 2664–2675 CrossRef CAS.
- D. R. Kester and R. M. Pytkowicx, Limnol. Oceanogr., 1969, 14, 686–692 CrossRef CAS.
- D. R. Kester and R. M. Pytkowicz, Geochim. Cosmochim. Acta, 1970, 34, 1039–1051 CrossRef CAS.
- D. R. Kester and R. M. Pytkowicz, Mar. Chem., 1975, 3, 365–374 CrossRef CAS.
- A. Katz and S. Ben-Yaakov, Mar. Chem., 1980, 8, 263–280 CrossRef CAS.
- R. G. Brereton, Analyst, 2000, 125, 2125–2154 RSC.
- J. Emsley, The elements, Clarendon Press, Oxford University Press, Oxford, New York, 3rd edn, 1989 Search PubMed.
- X. Lefebvre, J. Palmeri and P. David, J. Phys. Chem. B, 2004, 108, 16811–16824 CrossRef CAS.
- M. E. Q. Pilson, An introduction to the chemistry of the sea, Cambridge University Press, New York, 2013 Search PubMed.
- A. V. Verde, M. Santer and R. Lipowsky, Phys. Chem. Chem. Phys., 2016, 18, 1918–1930 RSC.
- S. Y. Venyaminov and F. G. Prendergast, Anal. Biochem., 1997, 248, 234–245 CrossRef CAS PubMed.
- S. J. Hug, J. Colloid Interface Sci., 1997, 188, 415–422 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ay02874d |
| This journal is © The Royal Society of Chemistry 2016 |