Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Low-cost microarray thin-film electrodes with ionic liquid gel-polymer electrolytes for miniaturised oxygen sensing
Junqiao
Lee
and
Debbie S.
Silvester
*
Nanochemistry Research Institute, Department of Chemistry, Curtin University, GPOBox U1987, Perth 6845, Western Australia. E-mail: d.silvester-dean@curtin.edu.au; Fax: +61 (0)892662300; Tel: +61 (0)892667148
First published on 25th February 2016
Abstract
A robust, miniaturised electrochemical gas sensor for oxygen (O2) has been constructed using a commercially available Pt microarray thin-film electrode (MATFE) with a gellified electrolyte containing the room temperature ionic liquid (RTIL) 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([C2mim][NTf2]) and poly(methyl methacrylate) (PMMA) in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mass ratio. Diffusion coefficients and solubilities for oxygen in mixtures of PMMA/RTIL at different PMMA doping concentrations (0–50% mass) were derived from potential step chronoamperometry (PSCA) on a Pt microdisk electrode. The MATFE was then used with both the neat RTIL and 50% (by mass) PMMA/RTIL gel, to study the analytical behavior over a wide concentration range (0.1 to 100 vol% O2). Cyclic voltammetry (CV) and long-term chronoamperometry (LTCA) techniques were employed and it was determined that the gentler CV technique is better at higher O2 concentrations (above 60 vol%), but LTCA is more reliable and accurate at lower concentrations (especially below 0.5% O2). In particular, there was much less potential shifting (from the unstable Pt quasi-reference electrode) evident in the 50% PMMA/RTIL gel than in the neat RTIL, making this a much more suitable electrolyte for long-term continuous oxygen monitoring. The mass production and low-cost of the electrode array, along with the minimal amounts of RTIL/PMMA required, make this a viable sensing device for oxygen detection on a bulk scale in a wide range of environmental conditions.
50 mass ratio. Diffusion coefficients and solubilities for oxygen in mixtures of PMMA/RTIL at different PMMA doping concentrations (0–50% mass) were derived from potential step chronoamperometry (PSCA) on a Pt microdisk electrode. The MATFE was then used with both the neat RTIL and 50% (by mass) PMMA/RTIL gel, to study the analytical behavior over a wide concentration range (0.1 to 100 vol% O2). Cyclic voltammetry (CV) and long-term chronoamperometry (LTCA) techniques were employed and it was determined that the gentler CV technique is better at higher O2 concentrations (above 60 vol%), but LTCA is more reliable and accurate at lower concentrations (especially below 0.5% O2). In particular, there was much less potential shifting (from the unstable Pt quasi-reference electrode) evident in the 50% PMMA/RTIL gel than in the neat RTIL, making this a much more suitable electrolyte for long-term continuous oxygen monitoring. The mass production and low-cost of the electrode array, along with the minimal amounts of RTIL/PMMA required, make this a viable sensing device for oxygen detection on a bulk scale in a wide range of environmental conditions.
1. Introduction
The detection and monitoring of gases is important for industrial, medicinal, security and health and safety applications.1 Various techniques are used to detect gases, but those based on electrochemical methods are often the most widely employed.1 Amperometric gas sensors (AGSs) based on “Clark electrodes” have been around for several decades and are available to purchase commercially from a range of companies.2 They typically consist of three electrodes connected by an electrolyte (usually water/H2SO4 mixture) and covered by a gas permeable membrane.1–3 Room temperature ionic liquids (RTILs) have been investigated significantly as a replacement solvent in AGSs due to their non-volatile nature (eliminating the need for a membrane),3 in addition to other advantageous properties such as wide electrochemical windows, good intrinsic conductivity, good solvating abilities and high chemical and thermal stability.4–7 A number of reviews on gas sensing in RTILs are available.2,8–11The gas that appears to be the most widely investigated in RTILs so far is oxygen (O2).11 Various studies on oxygen reduction in RTILs have used microdisc electrodes for the obvious advantages of higher current densities and lower ohmic drop effects.12–16 From an analytical point of view, employing an array of microdiscs can increase currents, whilst maintaining the benefits of a single microelectrode.17 However, due to the relatively expensive fabrication processes, there have only been limited investigations with microelectrode arrays, particularly for gas sensing in RTILs. Huang et al.18 proposed a membrane-free oxygen gas sensor consisting of a thin layer of the RTIL tris(n-hexyl)tetradecylphosphonium trifluorotris(pentafluoroethyl)phosphate ([P14,6,6,6][FAP]) dropcast onto an electrode array with 80 microdiscs in a square pattern (10 by 8). The microdiscs were patterned by photolithography onto a silicon wafer, and were 12 μm in diameter, recessed by ca. 1.6 μm and separated by 150 μm (centre-to-centre distance). Oxygen concentrations from 2–13 vol% O2 were studied, and linear calibration graphs were obtained (current vs. vol% O2) from continuous cyclic voltammograms. However, concentrations of O2 higher than 13 vol% were not investigated. The electrolyte was also a pure RTIL in the liquid state, so there are limitations on how such a “membrane-free” electrode can be employed in certain situations e.g. movement, shaking or tilting of the electrode, where loss of the RTIL might occur.
To overcome this, in our recent work,19 we mixed a pure RTIL with increasing amounts of poly(methyl methacrylate) (PMMA) to make a gel polymer electrolyte (GPE) that is mechanically stable (i.e. does not flow). At 50% mass of PMMA relative to the total mass (PMMA and RTIL), defined as 50% mPMMA/mTot. GPE, no electrolyte flow was evident. Oxygen reduction currents on 1 mm diameter Pt thin film electrodes (TFEs) were linear vs. concentration over the range 10–100 vol% O2 using cyclic voltammetry (CV), but suffered from some ohmic drop effects on the macro-sized electrode. The robustness of the electrode was demonstrated by the observation of identical CVs on the electrode at different geometries (e.g. upright, sideways, upside down), whereas CVs in the neat RTIL were significantly altered.19
In this work, we have employed the same GPE with a Pt microarray thin film electrode (MATFE) as a robust sensor for long-term continuous monitoring of oxygen. The microarray TFE has obvious advantages over the TFE, such as higher current density and lower ohmic drop contributions. Importantly, the MATFEs are commercially available, mass produced and low cost (just over 4 EURO per device), making the possibility of commercializing such oxygen sensors highly favourable. The results will show that good analytical responses can be obtained on these devices, and that more stable and reproducible results are obtained in the GPE compared to the neat RTIL. Ultimately, these cheap, robust, miniaturised electrodes, when used in conjunction with a layer of PMMA–RTIL GPE, could be employed in a range of applications for oxygen monitoring, even at high O2 concentrations and while being subjected to agitation, acceleration or positioned at different orientations during operation.
2. Experimental
2.1 Chemical reagents
The RTIL 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([C2mim][NTf2]) was purchased from Merck (Kilsyth, Vic, Australia) at ultra-high purity electrochemical grade, and used as received. Poly(methyl methacrylate) (PMMA, average MW ca. 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich Pty Ltd, NSW, Australia), tetra-N-butylammonium perchlorate (TBAP, >99.0%, Sigma-Aldrich) and ferrocene (Fc, 98%, Sigma-Aldrich) were also used as received. Acetone (≥99.9%, Sigma-Aldrich), acetonitrile (MeCN, 99.8%, Sigma-Aldrich), ethanol (EtOH, Sigma-Aldrich, 99%), and ultrapure water (with a resistivity of 18.5 MΩ cm prepared by a Milli-Q laboratory water purification system (Millipore Pty Ltd, North Ryde, NSW, Australia) were used for rinsing the microdisk electrode after polishing. High-purity oxygen gas (O2, >99.5%) and high-purity nitrogen gas (N2, 99.99%) were purchased from BOC gases (North Ryde, NSW, Australia). Aqueous solutions of 0.5 M sulfuric acid (H2SO4, 95–98 wt%, Ajax Finechem, WA, Australia) for activating electrodes were prepared in ultrapure water.
000, Sigma-Aldrich Pty Ltd, NSW, Australia), tetra-N-butylammonium perchlorate (TBAP, >99.0%, Sigma-Aldrich) and ferrocene (Fc, 98%, Sigma-Aldrich) were also used as received. Acetone (≥99.9%, Sigma-Aldrich), acetonitrile (MeCN, 99.8%, Sigma-Aldrich), ethanol (EtOH, Sigma-Aldrich, 99%), and ultrapure water (with a resistivity of 18.5 MΩ cm prepared by a Milli-Q laboratory water purification system (Millipore Pty Ltd, North Ryde, NSW, Australia) were used for rinsing the microdisk electrode after polishing. High-purity oxygen gas (O2, >99.5%) and high-purity nitrogen gas (N2, 99.99%) were purchased from BOC gases (North Ryde, NSW, Australia). Aqueous solutions of 0.5 M sulfuric acid (H2SO4, 95–98 wt%, Ajax Finechem, WA, Australia) for activating electrodes were prepared in ultrapure water.
2.2 Preparation of gel polymer electrolytes
For the platinum microdisk electrode experiments, mixtures of PMMA–[C2mim][NTf2] (10–50% mPMMA/mTot.) were prepared using acetone as a carrier solvent, following the procedure detailed in our previous work.19 30 μL of neat RTIL or PMMA–RTIL mixture (in acetone, see explanation below) was employed, giving an estimated electrolyte thickness above the electrode of ca. 1.5 mm. This was the minimum volume required to ensure good connection of the working electrode with the Ag wire counter/reference electrode at all PMMA doping concentrations. For the Pt microarray thin-film electrodes (MATFEs) the 50% mPMMA/mTot. mixture was prepared in the same way. 5 μL of neat [C2mim][NTf2] or 50% mPMMA/mTot. GPE (in acetone, see below) was dropcast to cover the three electrodes (working, counter and reference). Thicknesses of ca. 1 mm (for neat [C2mim][NTf2]) and ca. 0.5 mm (for 50% mPMMA/mTot. GPE) was estimated based on the volume and spread of the droplet. However, it is noted that the thickness is likely to vary over the layer due to meniscus formation. Note: acetone was added to the 50% mPMMA/mTot. mixture in a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GPE
1 GPE![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone (i.e. 20% acetone) in order to be able to dropcast the GPE by pipetting for both the microelectrode and TFE experiments.
acetone (i.e. 20% acetone) in order to be able to dropcast the GPE by pipetting for both the microelectrode and TFE experiments.
2.3 Electrochemical experiments
All electrochemical experiments were performed using a PGSTAT101 potentiostat (Eco-Chemie, Netherlands) interfaced to a PC with NOVA 1.11.2 software. All experiments were carried out inside a custom-made aluminium Faraday cage to reduce ambient electromagnetic interferences, and at temperatures of 294 ± 1 K. A step potential of 2.5 mV and a scan rate of 10 mV s−1 was used. Chronoamperometric transients on the microdisk electrode employed a sampling time of 0.01 s. Long-term chronoamperometry (LTCA) measurements were conducted with a sampling interval time of 2.5 s.The platinum microdisk electrode (radius = 7.44 μm) was kindly made and donated by the group of Professor Richard Compton, University of Oxford, UK. It was polished on soft lapping pads (Buehler, Illinois) in a Figure-8 motion, using alumina powder of decreasing size (3, 1 and 0.5 μm). A micropipette tip (Eppendorf, Australia) was fit at the top of the working electrode to hold the electrolyte (30 μL of neat RTIL or PMMA–RTIL mixture). The electrode was housed in a glass T-cell with a silver wire as a combined reference/counter electrode. The electrolyte was left under a N2 environment overnight to allow any O2 and other absorbed gases to be purged, and for any acetone to volatilize before the electrochemical measurements were commenced. After the introduction of O2 gas, cyclic voltammetry (CV) was conducted at 5-minute intervals to ensure that the gas was fully saturated and that the CVs were stable. Ca. 20 minutes was sufficient to saturate 30 μL of neat [C2mim][NTf2]. However, more than 1 hour was required for the 50% mPMMA/mTot. mixture, probably due to the slower diffusion of O2 in the viscous mixture. After experiments, the microdisk electrode was soaked and washed with acetone (to remove the GPE), re-polished, then rinsed with ethanol and acetone before subsequent experiments.
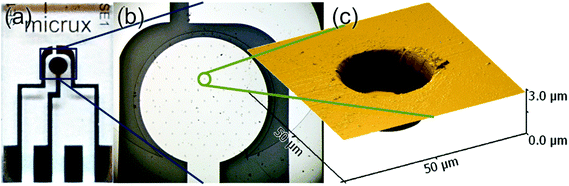
Platinum microarray thin-film electrodes (MATFEs) (MicruX Technologies, Oviedo, Spain; ED-mSE-10-Pt) were electrochemically activated by cycling for 30 cycles in 0.5 M H2SO4 between −0.75 V and 1.25 V. The MATFE has all three Pt electrodes (working, reference and counter) fabricated by thin-film technology and contained within a small area on the glass substrate. The working electrode array consists of 90 recessed Pt disk electrodes in a hexagonal arrangement, 10 μm in diameter with 100 μm between adjacent microholes (see a photo of the device in Fig. 1a, an optical image of the microholes in Fig. 1b and depth profile in Fig. 1c). According to the manufacturer, a layer of SU-8 resin (3.0 ± 0.5 μm thick) is used to define the array. Depth profiles (from atomic force microscopy experiments) from more than five different MATFEs confirmed this thickness, with values between 2.6 and 3.4 μm observed. The thickness was consistent over the whole array for an individual device. 5 μL of either the neat RTIL or 50% mPMMA/mTot. mixture (plus acetone carrier solvent) was used to cover the working, counter and reference electrodes, before the device was inserted using a rubber bung into a modified glass cell, as described previously.20 It was flushed with N2 for a sufficiently long time (ca. 1–2 hours in the neat RTIL and overnight in the 50% mPMMA/mTot. mixture) to remove oxygen and to allow the remaining acetone to volatilize, until stable baselines were obtained. Aluminium wires were soldered onto the electrode connections to allow easy attachment to the potentiostat.
2.4 Gas mixing experiments
Oxygen gas was diluted with nitrogen gas using a gas mixing system detailed in our previous work,20 based on the ratios of flow rates in the two digital flow meters. Two O2 concentration ranges were employed in this work, termed “low concentration” (1–20 vol% O2 for CV and 0.1–20 vol% O2 for LTCA) and “high concentration” (10–100 vol% O2 for CV and 1.1–100 vol% O2 for LTCA). For experiments within the “low concentration” range, the N2 flow rate was fixed at 180 sccm, and the O2 flow rate varied. For the “high concentration” range, the N2 flow rate was fixed at 1000 sccm, while varying the O2 flow rate. For LTCA, the initial response was allowed to stabilize (under N2) for ca. 30 min before commencing with the introduction of O2 gas. Adjusting of the flow rates was automated using a computer software controller for the LTCA experiments since the duration of the measurements was ca. 14 and up to 35 hours.3. Results and discussion
The aim of this work is to investigate the electroanalytical behavior of O2 in a gel polymer electrolyte (GPE) on a commercially available MATFE, as a simple, robust, inexpensive, miniaturized platform for oxygen sensing. The RTIL [C2mim][NTf2] was chosen as the solvent as it mixes well with PMMA, and the behavior of O2 in the mixture has been well characterized in our previous work.19 The electroanalytical behavior on the MATFE in the neat RTIL and the 50% mPMMA/mTot. gel polymer electrolyte (GPE) will be investigated. However, in order to obtain information about the physical properties (e.g. diffusion coefficient and solubility) of oxygen in the GPE PMMA–RTIL mixtures, the reduction of oxygen will first be studied on a conventional microdisk electrode in PMMA–RTIL mixtures, where the two parameters can be easily resolved from theoretical modeling of the data.213.1 Diffusion coefficient and solubility values in PMMA–[C2mim][NTf2] mixtures
Fig. 2a shows linear sweep voltammetry (LSV) for the reduction of 100 vol% O2 on a Pt microdisk electrode (diameter 14.88 μm) with various percentages of PMMA mixed with the RTIL. As was observed in our previous work with a working Pt thin film electrode (TFE, 1 mm diameter),19 the current decreases as the amount of PMMA in the mixture is increased. This is expected due to the higher viscosity of the mixture leading to slower diffusion coefficients of O2. The shape of the voltammammetry (where a true steady-state plateau is not obtained) is quite similar to that reported by Huang et al.13 in various ionic liquids on a Pt microdisk electrode at similar scan rates (50 mV s−1, lower scan rates were not investigated). Due to the nature of the Ag wire reference electrode, some potential shifting (of up to a few hundred millivolts) was observed during the course of measurements; however, the shape of the voltammetry was ultimately used to determine the end potential of the linear sweep and to determine a suitable biasing potential for the chronomaperometry experiments).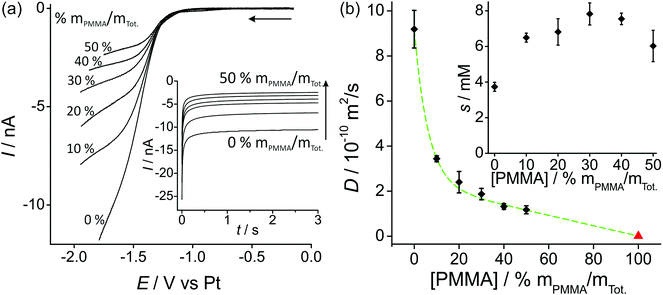 | ||
| Fig. 2 (a) Linear sweep voltammetry (10 mV s−1) for 100 vol% O2 in PMMA–[C2mim][NTf2] mixtures at 0–50% mPMMA/mTot., on a platinum microdisk electrode (radius 7.44 μm). The inset shows the corresponding chronoamperometric transients. (b) Plot of diffusion coefficient (D) of O2vs. [PMMA] (the red triangle for pure PMMA, i.e. 100% mPMMA/mTot. is taken from the literature22). The inset shows oxygen solubilities s vs. [PMMA]. D and s were obtained by fitting chronoamperometric transients to the Shoup and Szabo equation.21 | ||
In order to try to obtain diffusion coefficients and solubilities of oxygen in the various RTIL–PMMA mixtures, potential step chronoamperometry (PSCA) was carried for 100 vol% O2 out at each PMMA doping concentration in the RTIL. The inset to Fig. 2a shows the experimental transients obtained from PSCA where the potential was stepped from 0 V to a chosen potential (on the slanted plateau where oxygen reduction occurs), and monitoring the current over time. The transients were then fitted to the Shoup and Szabo expression:21
| I = −4nFDcrdf(τ) | (1) |
| f(τ) = 0.7854 + 0.8863τ−1/2 + 0.2146e−0.7823τ−1/2 | (2) |
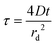 | (3) |
| [PMMA]/% mGPE/mTot. | N | I ss/nA | D/10−10 m2 s−1 | s/mM |
|---|---|---|---|---|
| 0 | 3 | −10.3 ± 0.4 | 9.2 ± 0.8 | 3.7 ± 0.3 |
| 10 | 4 | −6.8 ± 0.1 | 3.4 ± 0.1 | 6.5 ± 0.3 |
| 20 | 5 | −5.2 ± 0.1 | 2.5 ± 0.4 | 6.5 ± 0.3 |
| 30 | 5 | −4.6 ± 0.9 | 1.9 ± 0.3 | 7.8 ± 0.6 |
| 40 | 3 | −3.4 ± 0.3 | 1.4 ± 0.1 | 7.6 ± 0.4 |
| 50 | 5 | −2.3 ± 0.2 | 1.2 ± 0.2 | 6.0 ± 0.9 |
| 100 | 0.00698![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22 |
Fig. 2b shows a plot of the diffusion coefficients, D, (main figure) and solubilities, s, (inset figure) of oxygen in the RTIL, as a function of increasing concentrations of PMMA. The diffusion coefficient decreases significantly when 10% PMMA is added to the RTIL, and gets systematically smaller as the % of PMMA increases. The triangle on the figure also shows the literature value for 100% PMMA. Attempts were made to fit the data using a range of curves/models (e.g. linear, exponential, polynomial) but the best fit (shown as the dashed line) appears to be the Shah model, where D = 2.39 × 10−10 − 2.38 × 10−12[PMMA] + 6.73 × 10−10 × 0.849[PMMA]. D has units of m2 s−1 and [PMMA] has units of % mPMMA/mTot., with R2 = 0.9985. In this empirical model, an exponential and linear characteristic are both present, as shown in the dashed line in the figure.
The solubility of O2 (inset to Fig. 2b) appears to almost double from the neat RTIL to 10% PMMA doping (3.7 mM in the neat RTIL compared to 6.6 mM in the 10% mixture), but remains relatively constant (within experimental error) as the % of PMMA is increased further. This suggests a slightly stronger affinity of oxygen towards PMMA/RTIL mixtures, or an increase in gas permeability compared to the neat RTIL. The higher solubility of O2 in the GPE (50% mPMMA/mTot.) is advantageous for sensing purposes, however this is overcome by the much slower diffusion coefficient in the GPE compared to the neat RTIL, resulting in lower overall currents. The information on D and solubility of O2 in the mixtures will be used to calculate expected currents on the microarray thin-film electrode (MATFE) in the next section.
3.2 Analytical utility for oxygen reduction on a MATFE
In order to investigate the feasibility of employing a commercially available microarray thin film electrode (MATFE) for oxygen gas sensing, with the gel-polymer electrolyte (GPE) for robust sensing, both cyclic voltammetry (CV) and long-term chronoamperometry (LTCA) was carried out in the neat RTIL and the 50% mPMMA/mTot. GPE. Other PMMA doping concentrations were not studied since they are not sufficiently gellified to provide a robust sensing device.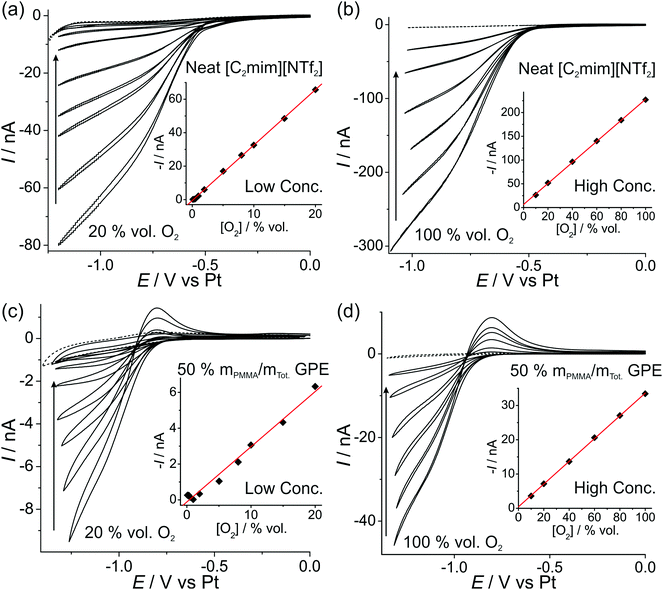 | ||
| Fig. 3 CV of the O2/O2˙− redox couple at (a, c) “low concentrations” of 20, 15, 10, 8, 5, 2, 1 vol% O2, and (b, d) “high concentrations” of 100, 80, 60, 40, 20, 10 vol% O2 for (a, b) neat [C2mim][NTf2] and (c, d) PMMA–[C2mim][NTf2] mixture at 50% mPMMA/mTot. at a scan rate of 10 mV s−1. The dotted lines are the CVs in the absence of oxygen. The insets are corresponding plots of background corrected current (obtained at a fixed potential, see Table 2) vs. vol% O2, and the line of best-fit. | ||
| Electrolyte | [O2] range/vol% O2 | Potential/V | Equation of calibration graph (where I/A and [O2]/vol%) | R 2 | LOD/vol% O2 | |
|---|---|---|---|---|---|---|
| CV | Neat [C2mim][NTf2] | 1–20 | −1.05 | −I = 3.31 × 10−9 [O2] − 5.3 × 10−10 | 0.9995 | 0.5 |
| 10–100 | −0.90 | −I = 2.21 × 10−9 [O2] + 6.5 × 10−9 | 0.9997 | 2.2 | ||
| 50% mPMMA/mTot. GPE | 1–20 | −1.15 | −I = 3.13 × 10−10 [O2] − 1.8 × 10−10 | 0.9874 | 2.6 | |
| 10–100 | −1.20 | −I = 3.32 × 10−10 [O2] + 4.4 × 10−10 | 0.9998 | 1.8 | ||
| LTCA | Order | |||||
| Neat [C2mim][NTf2] | 0.1–20 | Descending | −I = 3.06 × 10−10 [O2] + 4.2 × 10−10 | 0.9976 | 5.8 | |
| 0.1–20 | Ascending | −I = 3.03 × 10−10 [O2] + 3.3 × 10−10 | 0.9989 | 4.0 | ||
| 1.1–100 | Ascending | −I = 2.67 × 10−9 [O2] + 1.4 × 10−8 | 0.9721 | 21 | ||
| 50% mPMMA/mTot. GPE | 0.1–20 | Descending | −I = 3.18 × 10−10 [O2] + 6.6 × 10−11 | 0.9989 | 0.8 | |
| 0.1–20 | Ascending | −I = 3.11 × 10−10 [O2] + 6.6 × 10−11 | 0.9991 | 0.8 | ||
| 1.1–100 | Ascending | −I = 3.20 × 10−9 [O2] − 2.1 × 10−10 | 0.9959 | 1.7 | ||
| 1.1–100 | Descending | −I = 3.92 × 10−9 [O2] − 1.1 × 10−9 | 0.9986 | 1.0 | ||
The difference in the shape of the reverse sweep of the CV (oxidation of superoxide) in Fig. 3 is most likely due to the significantly lower diffusion coefficient of superoxide in the highly viscous 50% mPMMA/mTot. GPE compared to the neat RTIL, resulting in a peak-shaped oxidation in Fig. 3c and d (GPE), but a steady-state oxidation in Fig. 3a and d (neat RTIL). This effect has been previously reported for the oxygen/superoxide redox couple in the RTIL hexyltriethylammonium bis(trifluoromethylsulfonyl)imide ([N6,2,2,2][NTf2]) – where a 30× discrepancy in diffusion coefficients of oxygen and superoxide resulted in a voltammogram exhibiting both steady-state and transient (peak-shaped) behaviour on the same cycle.12
Using the fitted values for D and solubility of O2 obtained for the neat RTIL and 50% mPMMA/mTot. GPE (section 3.1), the expected currents for a recessed disk array electrode is given by the following equation:23,24
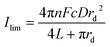 | (4) |
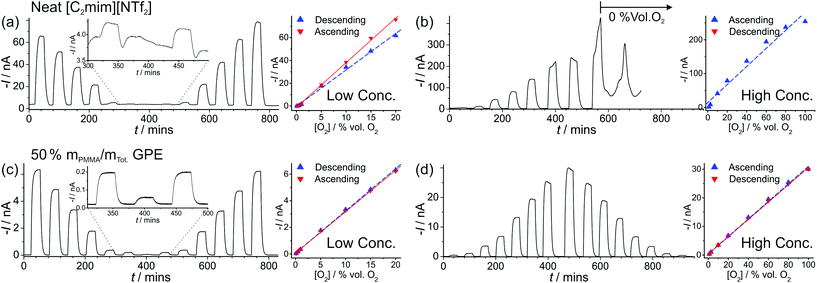 | ||
| Fig. 4 Long-term chronoamperometry (LTCA) at different O2 gas concentrations in (a, b) neat [C2mim][NTf2] and (c, d) 50% mPMMA/mTot. PMMA–[C2mim][NTf2] mixture. The gas flow was alternated between 100 vol% N2 and varying O2 concentrations: “low concentration” (a, c) 20, 15, 10, 5, 1, 0.5, 0.1, 0.5, 1, 5, 10, 15, 20 vol% and “high concentration” (b) 1.1, 2.7, 10, 20, 40, 60, 80, 100 vol% and (d) 1.1, 2.7, 10, 20, 40, 60, 80, 100, 80, 60, 40, 20, 10, 2.7, 1.1 vol% O2. Background subtracted current vs. concentration plots are shown on the right, along with the lines of best fit from the “descending” and “ascending” data sets. The equations of the line of best-fit, R2 value, and LODs are given in Table 2. | ||
For the high concentration range in Fig. 4b and d, the current response appears to be relatively stable at the starting concentrations (from 1.1–20 vol% O2). However, at higher concentrations (above 40 vol% O2), the current response rapidly deteriorates in the neat RTIL (Fig. 4b). This is likely due to the shift in the potential of the pseudo-reference electrode during the course of the LTCA experiment, and proved to be a severe problem in the neat RTIL. Even when N2 was added in (at ca. 570 minutes), a stable baseline could not obtained, and with the appearance of a large current spike at 660 min, despite no oxygen being present. In the GPE, signs of instability were also observed above 60 vol% O2, where the current drops after reaching a peak, instead of maintaining the expected steady-state. However, the potential shifting that was present in the neat RTIL was insignificant in the 50% mPMMA/mTot. GPE, and stable and reproducible responses were observed on several repeat experiments. This is probably due to the slower migration of counter electrode products towards the RE in the polymer matrix, or the lower overall currents in the GPE (compared to neat RTIL), generating less superoxide.
The limits of detection (LODs) at the low concentration range in the neat RTIL (Table 2) were much higher from LTCA (5.8 and 4.0 vol% O2) compared to CV (0.5 vol% O2). This is probably due to the accumulation of superoxide in the μL volume of electrolyte during LTCA biasing. At the higher concentration range, the LOD in the neat RTIL is substantially poorer (21 vol% O2) due to the visibly curved calibration plot (Fig. 4b, R2 = 0.9721) as a result of the degradation of the LTCA response. This is likely to be the result of instability of the pseudo-reference electrode, or accumulation of superoxide inhibiting the kinetics of the oxygen reduction reaction. However, for the 50% mPMMA/mTot. GPE, LODs obtained at the high concentration range from CV (1.8 vol% O2) and LTCA (1.7 vol% O2) experiments are comparable, and are actually better at the low concentration range using LTCA (0.8 vol% O2). Despite there not being a significant difference in LODs for the GPE obtained from LTCA (0.8 vol% O2) compared to the neat RTIL from CV (0.5 vol% O2) at the low concentration range, the O2 current responses are clearly more straight forward to extract from the LTCA data compared to the CV data – where the lack of a current plateau required the current to be extracted at an arbitrarily chosen potential where O2 reduction occurs (see Table 2). Therefore, it can be concluded that LTCA is the more reliable method, especially for the sensing of lower concentrations (e.g. ≤0.5 vol% O2) where the CV signal-to-background response is poor. Based on the LTCA transients in Fig. 4, a 90% response time, t90, of ca. 10 min is estimated in the neat RTIL and ca. 7 min in the 50% mPMMA/mTot. GPE. This is relatively long due to the moderate thickness of the electrolyte layers, and is expected to be smaller if thinner layers are employed. This is the focus of our future work.
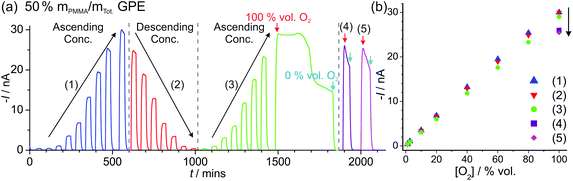
Fig. 5a shows LTCA for an extended period of time (ca. 2100 min) for different concentrations of O2 in the 50% mPMMA/mTot. GPE on a MATFE, and the corresponding plots of current vs. O2 concentration (Fig. 5b). Both the initial ascending and descending plots from 1.1–100 vol% O2 give very similar currents, as was observed in Fig. 4d. However, on the second ascending concentration set, the currents are slightly smaller (ca. 5–10%) suggesting a reduction in the sensitivity over time. When the 100 vol% O2 was reached (at ca. 1480 min), the sensor was tested under extreme conditions by exposing to 100% for ca. 350 min. As can be seen in Fig. 5a, after ca. 150 min, the current response rapidly deteriorates to around half of the expected current value over prolonged exposure to 100% O2. After this, N2 was then added to observe the return of a stable baseline, followed by two more additions of 100 vol% O2 at ca. 1880 min and 2000 min. The current responses are lower than that observed for 100% O2 in the earlier part of the LTCA transient (see (4) and (5) in Fig. 5b). For these two additions, the current reached a peak but then fell sharply, suggesting that the MATFE is no longer behaving optimally. This could suggest that the surface has become passivated, possibly due to the large build-up of superoxide at the working electrode or other passivating species at the counter electrode that have migrated towards the working or reference electrodes. As a result, continually biasing in the presence of high O2 concentrations (e.g. 60 vol% O2 and above), even in the 50% mPMMA/mTot. GPE, is not recommended for the long-term use of these devices.
Although this type of sensor could be regarded as ‘disposable’ once the surface has been fouled (e.g. exposed to 100% O2), it was actually found that reliable and reproducible current responses could be obtained on the same device if the GPE was rinsed off with acetone and the MATFE surface was re-activated in sulphuric acid. (Note: acetonitrile is not recommended for removal of the GPE for this as the SU-8 layer on the MATFE becomes compromised.) This suggests that even after exposure to high oxygen concentrations, the electrode can be reused provided the rinsing and reactivation steps are followed. However, for the majority of health-and-safety applications, concentrations in the 16–25% range are typically monitored (close to the concentration in air), so these devices have the potential to be easily and cheaply employed for long-term oxygen monitoring for these purposes. The use of a non-volatile RTIL as a gelled electrolyte also means these sensors could be employed in a wide range of conditions where typical membrane-based Clark-electrodes do not perform, such as at high temperatures and pressures, and under shaking, agitation and tilting of the sensor device.
4. Conclusions
The performance of a low-cost commercially-available MATFE was investigated for its response to different concentrations of oxygen at short timescales (CV) and long timescales (LTCA) in a neat RTIL and a RTIL gellified with PMMA. Although the current responses are lower in the gellified RTIL, they are much more stable, reproducible and less prone to shifts in the reference electrode potential. LTCA appears to be the most reliable technique to measure lower concentrations of O2 (less than 1 vol%) compared to CV (where currents were difficult to determine due to the slanted nature of the voltammetry). However, CV is the better technique at higher O2 concentrations (above 60 vol%) since it does not involve the continuous build-up of superoxide (as with LTCA). Overall the results look very promising for employing the MATFE for O2 sensing, particularly when using the 50% mPMMA/mTot. GPE. The variation in thicknesses of the SU-8 layer on the MATFE (3.0 ± 0.5 μm) could pose a problem if employed for oxygen sensing on a bulk scale. However, if this is taken into account (e.g. by calibrating with a gas standard), then it appears that these low-cost MATFE could be easily and cheaply employed in the field for long-term oxygen monitoring.Acknowledgements
DSS thanks the Australian Research Council for a Discovery Early Career Researcher Award (DECRA: DE120101456). The authors acknowledge the use of the instruments of the Scanning Probe Microscopy facility of the Nanochemistry Research Institute/Department of Chemistry at Curtin University, funded by ARC LIEF grant number LE130100121.References
- J. R. Stetter and J. Li, Chem. Rev., 2008, 108, 352–366 CrossRef CAS PubMed.
- L. Xiong and R. G. Compton, Int. J. Electrochem. Sci., 2014, 9, 7152–7181 CAS.
- M. C. Buzzeo, C. Hardacre and R. G. Compton, Anal. Chem., 2004, 76, 4583–4588 CrossRef CAS PubMed.
- M. C. Buzzeo, R. G. Evans and R. G. Compton, ChemPhysChem, 2004, 5, 1106–1120 CrossRef CAS PubMed.
- M. J. Earle and K. R. Seddon, Pure Appl. Chem., 2000, 72, 1391–1398 CrossRef CAS.
- D. S. Silvester and R. G. Compton, Z. Physiol. Chem., 2006, 220, 1247–1274 CrossRef CAS.
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS PubMed.
- A. Rehman and X. Zeng, RSC Adv., 2015, 5, 58371–58392 RSC.
- E. I. Rogers, A. M. O'Mahony, L. Aldous and R. G. Compton, ECS Trans., 2010, 33, 473–502 CrossRef CAS.
- D. S. Silvester, Analyst, 2011, 136, 4871–4882 RSC.
- D. S. Silvester and L. Aldous, in Electrochemical Strategies in Detection Science, ed. D. W. M. Arrigan, RSC, Cambridge, UK, 2016 Search PubMed.
- M. C. Buzzeo, O. V. Klymenko, J. D. Wadhawan, C. Hardacre, K. R. Seddon and R. G. Compton, J. Phys. Chem. A, 2003, 107, 8872–8878 CrossRef CAS.
- X.-J. Huang, E. I. Rogers, C. Hardacre and R. G. Compton, J. Phys. Chem. B, 2009, 113, 8953–8959 CrossRef CAS PubMed.
- P. Li, E. O. Barnes, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2015, 119, 2716–2726 CAS.
- P. Li and R. G. Compton, Electroanalysis, 2015, 27, 1550–1555 CrossRef CAS.
- E. I. Rogers, X.-J. Huang, E. J. F. Dickinson, C. Hardacre and R. G. Compton, J. Phys. Chem. C, 2009, 113, 17811–17823 CAS.
- R. G. Compton and C. E. Banks, Understanding Voltammetry, World Scientific, Singapore, 2007 Search PubMed.
- X.-J. Huang, L. Aldous, A. M. O'Mahony, F. J. del Campo and R. G. Compton, Anal. Chem., 2010, 82, 5238–5245 CrossRef CAS PubMed.
- J. Lee, G. Du Plessis, D. W. M. Arrigan and D. S. Silvester, Anal. Methods, 2015, 7, 7327–7335 RSC.
- J. Lee, K. Murugappan, D. W. M. Arrigan and D. S. Silvester, Electrochim. Acta, 2013, 101, 158–168 CrossRef CAS.
- D. Shoup and A. Szabo, J. Electroanal. Chem., 1982, 140, 237–245 CrossRef CAS.
- V. L. Vyazovkin, V. V. Korolev, V. M. Syutkin and V. A. Tolkatchev, React. Kinet. Catal. Lett., 2002, 77, 293–299 CrossRef CAS.
- D. W. M. Arrigan, Analyst, 2004, 129, 1157–1165 RSC.
- A. M. Bond, D. Luscombe, K. B. Oldham and C. G. Zoski, J. Electroanal. Chem., 1988, 249, 1–14 CrossRef CAS.
- T. J. Davies and R. G. Compton, J. Electroanal. Chem., 2005, 585, 63–82 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |