A sensitivity metric and software to guide the analysis of soft films measured by a quartz crystal microbalance

Abstract

This article introduces a set of mathematical and computational tools for use with a quartz crystal microbalance (QCM) to aid in experimental planning and data interpretation. The optimisation tools are based on a metric we term the total parameter matrix sensitivity (TPM-sensitivity). TPM-sensitivity is defined mathematically as the Jacobian determinant of a QCM's responses (e.g., frequency change or dissipation/bandwidth change for a given harmonic) with respect to changes in the physical properties of a soft film and surrounding solution (e.g., density or viscosity). Large TPM-sensitivity values denote conditions where the sensor responses are not only large but also allow the selected unknown physical properties to be mathematically decoupled. In some cases, the viscoelastic properties of an adlayer can be determined using only frequency responses. We validated this method using experimentally obtained data of an ageing adlayer of the enzyme bilirubin oxidase from Myrothecium verrucaria. Fits to these measurements produced more realistic film parameters when responses, including frequency-only combinations, were selected to maximise TPM sensitivity. We provide documented MATLAB code with a graphical user interface to enable other QCM users to employ this analysis. The current software can be applied to any single, homogeneous adlayer that obeys a Kelvin–Voigt viscoelastic model and sits under a semi-infinite Newtonian fluid. Only initial estimates of the film values are required, with the analysis providing guidance and predictions, allowing users to create testable hypothesis and determine the physical changes on the surface rather than have pre-existing values for them.

---

Introduction

The quartz crystal microbalance (QCM) is an analytical instrument that uses a resonating sensor to acoustically probe the volume near its surface, typically including the adsorbed film and a portion of the bulk medium. The QCM technique was first used in the gas phase as a simple mass sensor in the 1950s and then in the liquid phase in the 1980s, thus expanding the number of available applications to include biotechnological and, in particular, biosensor applications.^1–3 The QCM measures changes in the resonance frequency of a shear oscillation for a piezoelectric material. For thin, rigid, uniform films in the gas or liquid phase an increase in areal mass density (mass per unit area) is directly proportional to a drop in resonance frequency (Δf) and is sensitive to mass changes in the range of 1 ng cm⁻².^2,4,5 This relationship is formalised in the Sauerbrey equation.³

Many QCM systems are capable of measuring multiple overtone responses in rapid succession; these overtones are limited to odd numbers as only these can be electronically induced.⁴ Some modern QCM systems are also capable of quantifying the physical influence of a non-rigid, viscoelastic adlayer on a sensor's oscillation. Currently there are three measurements that can quantify the damping effect of a soft adlayer: energy dissipation, resonance bandwidth and motional resistance. These measurements in conjunction with the frequency response are typically reported as values relative to an unloaded sensor.

Dissipation is defined as the loss of energy per oscillation divided by the total amount of energy stored by the crystal. It is measured by recording how rapidly the response of the freely oscillating sensor decays. Q-Sense's quartz crystal microbalances with dissipation monitoring (QCM-D) are based on this method.⁶ A typical ringdown will be 99% complete in about 0.5 ms for a 5 MHz sensor operating in water. The ringdown time will be faster for surfaces with soft adlayers. A faster decay equates to a higher dissipation value.⁷ This change in dissipation (Δd) relates to how readily an adlayer elastically deforms when the crystal shears (its elastic modulus) and how much the films resists deformation (its viscosity). Due to this measure of film softness, in addition to real-time, non-destructive testing in situ, the QCM(-D) has been used to investigate the interactions of proteins,^8–15 vesicles^16–18 and cells^19–23 with surfaces, in addition to antibody²⁴ and virus²⁵ interactions on modified surfaces, thus allowing the determination of morphological changes during these interactions. Investigations into non-biological systems including polymers,²⁶ polymer brushes,^27,28 (electro)polymerisation,^29,30 and label-free detection of small molecules³¹ has also yielded insight into the interactions between surfaces and soft materials. General limitations of the Sauerbrey equation³² and non-intuitive responses from various materials have also been highlighted,²⁶ with work being done to create more accurate models to capture these behaviours. Examples include models to determine viscoelastic properties of homogeneous³³ and laterally inhomogeneous³⁴ films, accounting for rocking motion of particles,³⁵ roughness effects³⁶ and variability of the sensitivity of the sensor,^37,38 with others providing detailed analysis of specific films.⁸

Resonance bandwidth is a parameter which is derived from electrical impedance analysis of the quartz resonator.³⁹ It is equal to the product of dissipation and frequency, and so the methods developed in this paper can be readily applied instruments that measuring bandwidth rather than dissipation, such as MicroVacuum's QCM-I and KSV's QCM-Z500.⁴

Motional resistance is a parameter derived from an electromechanical equivalent circuit, and used in Inficon's RQCM and SRS's QCM200.⁴⁰ It is closely related to dissipation and provides similar insights into a film's viscoelastic properties.⁴¹ Unlike dissipation, which periodically stops the crystal oscillation, motional resistance can be continually measured for a given resonance frequency. However, motional resistance is not strictly proportional to the rate of energy loss and is more readily affected by calibration problems.⁴⁰ The analysis presented here focuses on the dissipation measurement rather than those of motional resistance.

Applying QCM analyses to viscoelastic films is still problematic because of the difficulty in interpreting of the resonator response generated by the interaction between the resonating sensor, the soft adlayer and any viscous fluid surrounding it. ‘Soft’ films on a QCM-D are often defined as having a Δd value above an arbitrary threshold such as 1 ppm. Once Δd is deemed significant, changes to the resonant frequency can no longer be consider equivalent to changes in adsorbed mass and mathematical models are required to quantify the changes to the adlayer on the surrounding fluid. As shown later, the dissipation response to changes in viscosity and shear for soft layers is non-linear, frequently non-monotonic, and dependent on measurement frequency.

The relationship between Δd and an adlayer's properties is also often non-intuitive. For example, one might expect an increasing Δd response to be associated with a film that is becoming less elastic (i.e., a decreasing shear modulus). However, at certain points the opposite is true, with a decrease in the shear modulus yielding a decrease in the Δd response (see Theory). Other combinations of shear and viscosity changes can yield no dissipation response and so remain undetected with others yielding responses in which the shear and viscosity changes are mathematically inseparable. This is further complicated by these areas of responses being specific for each film and having no easily generalisable rule.

This paper introduces a metric called the total parameter matrix sensitivity (TPM-sensitivity) to aid in extracting materials parameters from QCM data from soft films. The TPM-sensitivity value is calculated as the Jacobian determinant of the QCM-D's frequency and dissipation responses with respect to changes in the physical properties of the film and surrounding bulk fluid. Maps of TPM-sensitivity show areas where combinations of QCM responses will give the greatest responses as well as which combinations of measurements will result in the physical parameters being individually mathematically separable. This can be used to pre-test experimental conditions so that the QCM-D can be optimised to detect changes in specified physical parameters.

We have implemented the TPM-sensitivity calculation in MATLAB and packaged it with other functions to model QCM-D responses. The software outputs when a combination of physical parameters produces a Sauerbrey-type response and where the QCM-D response depends on the viscoelastic properties of the film. This also allows for experimental planning and ‘pretesting’ of experimental conditions to guide a user's selection of harmonics. Pre-planning which responses to record can also improve the time resolution of the experiment without sacrificing measurement precision. The pre-planning also aids in equipment selection: we present an experimentally validated example in which no dissipation responses are required to determine film viscosity and shear modulus, suggesting that a QCM-D is not always required for soft adlayer analysis.

Our overall aim here to provide a general and extensible analysis tool to aid others to continue to use this technique in ever more complex systems and further the techniques development. Other software is already available for fitting experimental results to a model, for example Q-Sense has developed QTools which is capable of calculating the parameter values based upon QCM-D data. Our functions, in contrast, simulate a response specific to a user's requirements and so have a predictive element and can be used as an experimental planning and response visualisation tool. This makes use of complimentary modelling software such as QTools or Dfind more straightforward as it allows for visualisation of the broad mathematical framework to which the software is working. This should allow users to more easily choose between multiple solutions offered by secondary modelling software and so calculate comparable parameter values in addition to being able to generate testable hypotheses.

Theory

The model presented here regards the quartz crystal as a harmonic oscillator fully covered by a single acoustically homogeneous viscoelastic film, which is turn is submerged beneath a semi-infinite bulk fluid (Fig. 1). The adlayer is modelled as a Kelvin–Voigt material and as such is regarded here as having a purely viscous damper and purely elastic spring in parallel. The TPM-sensitivity metric does not require the use of this viscoelastic model, but implements it because the theoretical QCM-D responses for such a system have previously been derived by Voinova et al. and Rodahl and Kasemo.^42,43 The Kelvin–Voigt model is comprehensive enough to account for the viscoelastic responses of an absorbed film and is more applicable to viscoelastic materials which conserve their shape and do not flow, in contrast to the Maxwell model, which is usually applied to more liquid-like materials.⁴⁴ The ‘no-slip’ boundary condition where the shear stress and displacement is continuous across the quartz–film interface is presumed within this model.⁴³

Fig. 1 A schematic of the model system: a single, uniform viscoelastic adlayer on a quartz crystal immersed in a semi-infinite Newtonian fluid. The components are labeled with the seven physical parameters that fully define the system. Quartz crystal: f₀ – fundamental frequency of the oscillator (Hz). Film: μ_film – shear modulus (Pa s), η_film – viscosity (Pa), ρ_film – density (kg m⁻³), h_film – height (m). Bulk fluid: η_bulk – viscosity (Pa s) and ρ_bulk – density (kg m⁻³).

The equations from Voinova and coworkers were implemented in MATLAB and shown to generate shear and viscosity response surface plots matching those presented in the paper (Fig. S1, ESI†).⁴³ These equations were used to create the frequency and dissipation response surfaces shown in Fig. 2A and B of a hypothetical soft 5 nm adlayer. Changes in the viscosity or shear modulus of the film can be represented as a line connecting two points on the surfaces. Changes in the height of the surfaces equate to changes in the frequency and dissipation responses. In this way an anticipated change in the films properties can be related to experimentally observable responses of Δf and Δd relative to an unloaded sensor under the same fluid. Note that the dissipation initially rises then falls for low viscosity films with a decreasing shear modulus, illustrating the non-intuitive nature of this response.

Fig. 2 Surface and contour plots showing the modelled (A) frequency response and (B) dissipation response to water-immersed adlayers with varying viscosities and shear moduli (both shown on logarithmic scales). Panel (C) presents a plot of TPM-sensitivity for this film. An increase in response is represented as an increase in colour saturation. Red and blue arrows represent gradients of the frequency and dissipation responses, respectively, with respect to these two materials parameters. At point O (η_film = 1.0 mPa s, μ_film = 0.25 MPa), the two vectors are nearly orthogonal, resulting in a high TPM-sensitivity for this system. At point P (η_film = 2.5 mPa s, μ_film = 0.10 MPa) the frequency and dissipation vectors are nearly parallel, resulting in a TPM-sensitivity close to zero. The third case, in which the vectors are antiparallel, is not shown but would also lead to a zero sensitivity. Fixed model parameters: h_film = 5 nm, ρ_film = 1.45 × 10³ kg m⁻³, ρ_bulk = 1.0 × 10³ kg m⁻³, η_bulk = 0.89 mPa s, f₀ = 4.95 MHz, N = 7. Sensitivity weightings (see text): σ_Δf = 0.053 Hz, σ_Δd = 0.021 ppm. QCM-D responses are shown with respect to the unloaded sensor in the same bulk fluid.

The mathematics of TPM-sensitivity account for how readily changes to physical parameters can be resolved by changes in the QCM-D's response. There are situations where it is impossible to mathematically decouple changes in a film's physical parameters based on measured QCM-D responses. Fig. 2 provides an example of this by presenting the response surfaces for a hypothetical protein adlayer. Although this example illustrates TPM-sensitivity with two parameters to make it easier to visualise, the method is applicable to multidimensional analysis. The z value of any point on Fig. 2A or B shows the frequency and dissipation shifts respectively upon loading an adlayer with the shear and viscosity values indicated, these responses being relative to an unloaded sensor under the bulk fluid. Two films which differ only in their viscosity and shear moduli values are labelled as O and P for orthogonal and parallel, respectively. The blue arrows show the direction of the greatest change in frequency with changes in the film's viscosity and shear modulus (i.e., its frequency gradient). The red arrows show the same for the dissipation response. The ability to mathematically decouple changes in the film's physical parameters is greatest when the angle between the slopes is 90° and decreases to zero when this angle goes to 0° or 180°. In the case with two unknown physical parameters, this leads to three limiting cases where the response vectors are orthogonal, parallel or antiparallel.

In the case of parallel response vectors, both Δf and Δd decrease significantly as the adlayer's viscosity increases but are barely affected by changes in shear modulus. Thus, the system would be completely unable to resolve these two film parameters and would have a TPM-sensitivity near zero. The antiparallel case, not present in the system in Fig. 2, could occur if the dissipation-response vector pointed in the opposite direction to the frequency-response vector; again, this system would have no sensitivity to the shear modulus and would have a TPM-sensitivity of zero. In the case of orthogonal response vectors, Δf responds primarily to changes in the adlayer's shear modulus and Δd responds primarily to changes to its viscosity. This leads to a high TPM-sensitivity, indicating that these two film parameters can be readily and independently determined from these QCM-D measurements. The TPM-sensitivity is also scaled by the product of the vectors’ magnitudes, meaning that a magnitude of zero for either vector will result in a sensitivity of zero; this is effectively the case for very stiff or viscous films.

In the two cases shown in Fig. 2 and discussed above, Δf or Δd is shown as being related to changes in a single physical parameter. It is unusual for each physical parameter to be linked to a single QCM-D response and not required to gain a high TPM-sensitivity score. More commonly, the sensor's responses are linked to the film and bulk parameters in mathematically complicated ways. However, the principle still holds: how precisely the physical parameters can be deconvoluted from the sensor's responses depends on the magnitude and orthogonality of the response vectors to each other.

Mathematically, the frequency and dissipation response vector is formalised as the gradient of the response with respect to the film parameters. TPM-sensitivity is equal to the magnitude of the cross product of these two gradients, which is equal to the magnitude of the determinant of the matrix made up of the gradient vectors (eqn (1)).

where the del operator, ∇, gives the gradient with respect to the shear modulus and the viscosity, and [small mu, Greek, circumflex]_film and [small eta, Greek, circumflex]_film are unit vectors along the axes for the film's shear modulus and viscosity, respectively, N is the harmonic number, and θ is the angle between the two response vectors. These equations assume that the film's density and thickness remain constant, as do the surrounding fluid's density and viscosity. If the gradients are being determined based on the logarithm of the film's viscosity and shear modulus, as they are in Fig. 2, then each partial derivative must be divided by that parameter's value (Section S2†). A sample response curve that considers the gradients with respect to linear changes in viscosity and shear modulus is presented in the Fig. S2.†

Beyond mathematical limitations, system noise (random error) affects the ability to resolve changes to the system's physical parameters. This is accounted for by dividing each gradient vector by a weighting that represents the level of random error in that measurement. In the models shown, frequency measurements were estimated to have a standard deviation of ±0.053 Hz and dissipation measurements ±2.1 × 10⁻² ppm for all harmonics. In practice, this varies slightly for each harmonic and can be determined by analysing the noise in a baseline response. These averaged errors before and after adlayer formation were the same to two significant figures. Putting in separate error estimates for each harmonic or small variations in the error estimates sometimes resulted in a reordering of the top TPM-sensitivity scores.

TPM-sensitivity is essentially the magnitude of the Jacobian determinant of the sensor's responses to changes in the system's physical properties (Section S3†). Therefore, it can be generalised to any number of unknown physical parameters. As in the two-parameter case, a scaling is applied to parameters evaluated on a log scale, and instrumental weightings are applied to each gradient vector. Although these are shown as pairs of responses for given harmonics, this is not a requirement. The number of measurements must equal the number of film parameters being determined. With the exception of fundamental frequency, the MATLAB routine (Section S4†) also allows for between two and six of the variables (namely, the film's height, density, shear and viscosity, and the bulk fluid's density and viscosity) to vary over independent ranges. TPM-sensitivity will generally decrease as the number of variables is increased. As more variables are added, it becomes increasingly likely that some of the gradient vectors will be nearly parallel or anti-parallel to others, thus reducing sensitivity.

The TPM-sensitivity metric can be optimised for a set of physical properties. Every combination of harmonic number, frequency and dissipation can be run to determine the combination that maximises TPM-sensitivity. We have implemented this in MATLAB as the ‘combo’ function (Section S4.3†).

Results and discussion

We first demonstrate the application of TPM-sensitivity and some key findings based on a hypothetical protein layer (Fig. 3 and 4), before validating these findings by analysis of experimentally obtained QCM-D data from a real protein adlayer (Section S5 and Fig. S3†). The top two rows of Fig. 3 show the effect of harmonic number on the frequency and dissipation responses for this hypothetical protein in bulk water at 25 °C. The film properties are based on those determined for an adlayer formed from ∼64 kDa globular protein molecules.⁴⁵ The range of viscosity and shear modulus values are typical of those from a dense protein layer formed at an interface.^46–48

Fig. 3 The modelled frequency (top row, red), dissipation (middle row, blue) and TPM-sensitivity (bottom row, green) responses for a 5 nm adlayer and for harmonics 3 (left), 7 (middle) and 13 (right). Each sensitivity response is derived from the frequency and dissipation pair above it. Fixed model parameters: h_film = 5 nm, ρ_film = 1.45 × 10³ kg m⁻³, ρ_bulk = 1.0 × 10³ kg m⁻³η_bulk = 0.89 mPa s, f₀ = 4.95 × 10⁶ Hz. Sensitivity weightings (see text): σ_Δf = 0.053 Hz, σ_Δd = 0.021 ppm.

Fig. 4 TPM-sensitivity surfaces for four combinations of QCM-D responses shown on identical viscosity, shear and sensitivity scales. (A) TPM-sensitivity surface for a pair of responses from a single harmonic (Δf₇ and Δd₇). The labelled points correspond to the viscosity and shear modulus values used to determine the combination of responses that maximised the TPM-sensitivity at that point. (B) Plot showing the optimum response combination for η_film = 31 mPa s and μ_film = 0.31 MPa (Δf₁₃ and Δd₃). (C) Plot showing the optimum response combination for η_film = 3.1 mPa s and μ_film = 3.1 MPa (Δf₁₃ and Δd₁₃). (D) Plot showing the optimum response combination for η_film = 3.1 mPa s, μ_film = 0.31 MPa (Δf₅ and Δf₁₃). Model parameters same as Fig. 3.

A large proportion of the frequency response surfaces (Fig. 3, top row) is flat, indicative of a Sauerbrey response, affected only by the adlayer's areal mass density (i.e., thickness multiplied by density). The magnitude of the response increases with harmonic number. (The output in Q-Sense software scales to the frequency response by dividing by harmonic number.) The inflection point at constant viscosity shifts to higher shear moduli with increasing harmonic number.

At the low viscosity and shear modulus corner of each frequency response surface is a ‘missing mass’ region, where the frequency response is lower than predicted by the Sauerbrey equation.³² This region does not necessarily overlap with where the dissipation response is highest, as noted in the Introduction and Theory. At higher harmonics, the missing mass effect encompasses a greater range of shear and viscosity values than at lower harmonics. On the dissipation surfaces (Fig. 3, middle row), in contrast, there is little effect of harmonic number on the response. So while the general shape of the frequency and dissipation surfaces are similar for each harmonic, the magnitude and position change.

The relative differences in individual response surfaces determines the shape of the TPM-sensitivity surface (Fig. 3, bottom row) and shifts the position of maximum TPM-sensitivity. Therefore, the ability to use QCM data to resolve a system's properties depends on the choice of responses used to in the fitting.

While Fig. 3 shows TPM-sensitivity plots that are calculated from the pairs of Δf and Δd responses for a single harmonic, other combinations of Δf and Δd responses from mixed harmonic values can provide a much higher overall TPM-sensitivity to changes in an adlayer's properties, particularly when the analysis can be guided by an initial estimate of some the film's unknown properties. This is illustrated in Fig. 4: Fig. 4A shows the same TPM-sensitivity data as the plot from the bottom centre of Fig. 3, formed from the Δf₇ and Δd₇ responses, but with the vertical range increased five times. Fig. 4B–D show three TPM-sensitivity plots optimised for the values for the shear modulus and viscosity at labelled grid points, and have TPM-sensitivity values that are approximately a half, one and two orders of magnitude higher than that of the Δf₇ and Δd₇ combination (values in Table S1†).

This increase of the TPM-sensitivity shows that less intuitive selections of harmonics, frequencies and dissipations can yield greater sensitivity towards the parameters under investigation. Also the selection generated for Fig. 4D is significant because it shows that combinations of only frequencies are capable of measuring viscoelastic changes and, in some cases, may be superior in this detection than combinations involving dissipation measurements. This could allow QCMs that do not measure dissipation, bandwidth or motional resistance to be used for viscoelastic monitoring, provided they can measure frequency changes at more than one harmonic.

Guided by an analysis such as this, QCM-D data acquisition can be pre-optimised to monitor changes in the viscoelastic properties of the films absorbed onto its surface. In some cases where recording of multiple harmonics would be carried out, pre-selection of the most sensitive harmonic combinations would also lead to an increased time resolution.

To validate these insights on a real rather than theoretical system, a 64 kDa globular protein, bilirubin oxidase from Myrothecium verrucaria (MvBOx), was adsorbed from a concentrated solution onto a silica-coated QCM-D sensor and allowed to age under flowing buffer (experimental details and complete QCM-D output in Section S5†). Following this, secondary fitting software (QTools) was used to fit a Voigt model to this data to determine the shear and viscosity values of the adlayer. Without use of the TPM-sensitivity metric, a user would intuitively use all recorded harmonics for fitting, thinking that more data would produce a more representative quantification of the underlying physical system.‡ In contrast, we use the TPM-sensitivity to select two optimised harmonic sets to fit to using the same dataset. Three of the protein film's properties were estimated (η_film = 3.2 mPa s, μ_film = 316 kPa, ρ_film = 1.45 × 10³ kg m⁻³) in order to generate the highest-scoring combination of harmonics that excluded the fundamental (Δd₃ Δf₅ Δf₁₃, TPM-sensitivity = 4.1 × 10¹⁶) and the highest-scoring combination that only included frequency responses (Δf₃ Δf₇ Δf₁₃, TPM-sensitivity = 4.0 × 10¹⁶). Values for η_film, μ_film and h_film for each time point were determined by fitting either all the responses (3 ≤ N ≤ 13)‡ or the two optimised subsets using QTools (noise-weighted χ² minimisation). Fig. 5 shows the fitting determined shear and viscosity values of the protein film from the experimental data. A comparison of the real and modelled responses for all QCM-D responses based on the fitted film parameters is given in the ESI.†

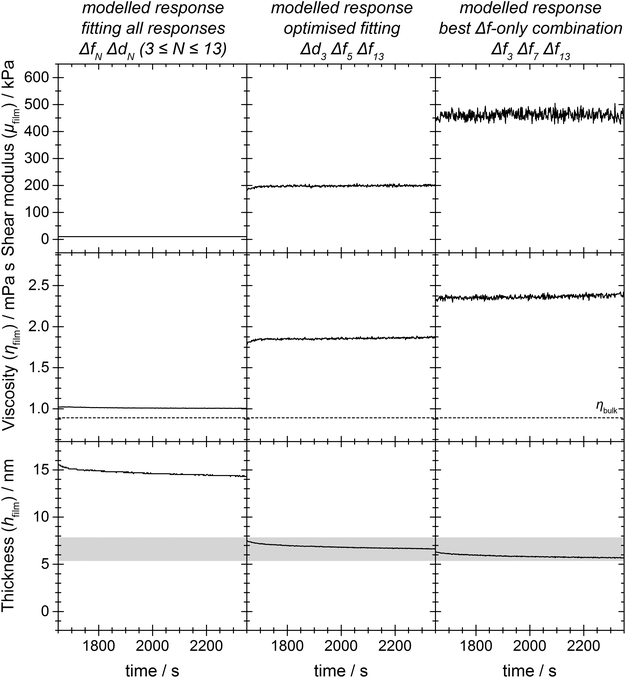Fig. 5 Fits to shear modulus, viscosity and thickness for a real protein layer on a silica-coated QCM-D sensor. From left to right: best fit using all responses from odd harmonics 3–13; TPM-sensitivity optimised selection of harmonics (Δd₃ Δf₅ Δf₁₃); TPM-sensitivity optimised selection using frequency responses only (Δf₃ Δf₇ Δf₁₃). The grey box denotes the thickness range determined by independent measurements on a dual polarisation interferometer.⁴⁵ Conditions: MvBOx concentration 14 mg ml⁻¹, volume of MvBOx addition 25 μl, pump flow rate 0.1 ml min⁻¹, cell temperature 25 °C. Protein injection at 1475 s with adsorption starting at 1536 s. Model parameters same as Fig. 3.

Only fits to the two optimised responses result in values and trends in film thickness that match those observed previously by combining QCM-D with dual polarisation interferometry,⁴⁵ namely a film that starts around 5–8 nm thick and thins with time. In contrast the ‘all responses’ fit to thickness is comparatively flat, about three times thicker than a protein monolayer and fluctuates between two solutions with similar chi-squared values because additional degrees of freedom are allowed in the fitting (i.e., the solution is overdetermined). Similarly, the viscosity and shear modulus values for the ‘all responses’ fit produces unrealistic results: a film viscosity just above that of water and dropping (rather than rising) with time, and a shear modulus about an order of magnitude lower than typical values for similar globular proteins.^46–48

None of the fits exactly match/regenerate the experimental data (Section S7†), including the fit to all responses N ≥ 3. However, both the selections optimised for high TPM-sensitivity have the same ordering of the overtones as the experimental data, with the ‘Δf only’ combination giving the best fit to the clustering observed in the Δf responses.

The optimised ‘Δf only’ response set is noteworthy because it produced the correct trends in the fits to the physical parameters, only deviating by about 2.5× in shear modulus. The results show the first example of where a QCM, without the dissipation or bandwidth measurement capability, can quantify viscoelastic changes, and in this experimental example even provides a more representative assessment of the film ripening process compared to the unguided fit of QCM-D measurements.

Selection of the most appropriate responses to fit to also helps bypass a common problem where the fit oscillates between two solutions with similar goodness-of-fit values but markedly different material properties. This can be avoided by having some foreknowledge of the limits of the physical properties of the system under investigation. For the illustration above, QTools had no limits set and a very wide range of values from which to seed the starting points in order to simulate a user starting with limited-to-zero prior knowledge of the adlayer's properties. Fitting based on responses that give the highest TPM-sensitivity value consistently produces more realistic values for materials properties than an ‘all harmonics’ fit, even if the initial estimates of film properties are off by two orders of magnitude (Fig. S8†). In this way, the TPM-sensitivity metric will be especially valuable in guiding measurements by novice users or on unknown soft films. For more experienced users this information can act as a guide to indicate parameter combinations that are especially difficult to deconvolute and where complementary measurement techniques may be required.

Conclusion

We have provided a new sensitivity metric, built into a MATLAB analysis package, that can be used by a QCM-D user to guide experimental measurements and data analysis. In the regions where the Sauerbrey assumption breaks down, it can indicate which responses are best for detecting viscoelastic changes and, potentially, to increase the time resolution of experiments by only recording mathematically important harmonics. This work described the surprising ability to use only frequency responses to quantify viscoelastic changes in a soft adlayer, something previously thought to be limited to the instruments that measure dissipation, bandwidth or motional resistance. Moreover, this work illustrates the importance of disregarding specific QCM-D responses to provide a valid fit to physical properties. Currently the response for up to six unknown system properties can be determined for a single Kelvin–Voigt adlayer, but the method can be applied to multiple layers and other linear viscoelastic models, though numerical (rather than analytical) methods may be required.

Abbreviations

Δd	Dissipation shift relative to unloaded resonator in fluid
f 0	Fundamental frequency
Δf	Frequency shift of resonator relative to unloaded resonator in fluid
h film	Film height
N	Harmonic number
QCM	Quartz crystal microbalance
QCM-D	Quartz crystal microbalance with dissipation monitoring
TPM-sensitivity	Total parameter matrix sensitivity
η bulk	Bulk (fluid) viscosity
η film	Film viscosity
μ film	Film shear modulus
ρ bulk	Bulk (fluid) density
ρ film	Film density

Acknowledgements

The authors acknowledge the UK's Engineering and Physical Sciences Research Council (EPSRC) (EP/G00434X/2) and the University of Manchester's School of Materials’ EPSRC-funded Doctoral Training Account for their support of the authors’ research, and to Prof. W. W. Sampson and Mr M. W. Sampson for enlightening mathematical discussions. In accordance with guidelines from the EPSRC, the protein adsorption data used to validate the TPM-sensitivity method and derivatives of the complex response function (‘beta function’) with respect to film and bulk parameters are openly available from The University of Manchester eScholar Data Repository at http://dx.doi.org/10.15127/1.280285 (research data) and http://dx.doi.org/10.15127/1.280338 (Mathematica notebook and associated PDF rendering). The computer code associated with this paper is available from GitHub: http://dx.doi.org/10.5281/zenodo.49578 (click on ‘Supplement to:’ then ‘Releases’ for updated versions).

Notes and references

1. A. Janshoff, H. Galla and C. Steinem, Angew. Chem., Int. Ed., 2000, 39, 4004–4032.
2. K. K. Kanazawa and J. G. Gordon, Anal. Chim. Acta, 1985, 175, 99–105.
3. G. Sauerbrey, Z. Phys., 1959, 155, 206–222.
4. D. Johannsmann, The Quartz Crystal Microbalance in Soft Matter Research, Springer, Clausthal-Zellerfeld, 2015.
5. V. Tsionsky and E. Gileadi, Langmuir, 1994, 10, 2830–2835.
6. M. Rodahl, F. Hook, A. Krozer, P. Brzezinski and B. Kasemo, Rev. Sci. Instrum., 1995, 66, 3924–3930.
7. M. Rodahl and B. Kasemo, Rev. Sci. Instrum., 1996, 67, 3238–3241.
8. R. Fogel and J. L. Limson, Enzyme Microb. Technol., 2011, 49, 146–152.
9. L. Jiang, J. Qian, X. Yang, Y. Yan, Q. Liu, K. Wang and K. Wang, Anal. Chim. Acta, 2014, 806, 128–135.
10. J. Jin, F. Huang, Y. Hu, W. Jiang, X. Ji, H. Liang and J. Yin, Colloids Surf., B, 2014, 123, 892–899.
11. C. G. Marxer, M. C. Coen and L. Schlapbach, J. Colloid Interface Sci., 2003, 261, 291–298.
12. S. M. S. Schoenwaelder, F. Bally, L. Heinke, C. Azucena, O. D. Bulut, S. Heissler, F. Kirschhoefer, T. P. Gebauer, A. T. Neffe, A. Lendlein, G. Brenner-Weiss, J. Lahann, A. Welle, J. Overhage and C. Woell, Biomacromolecules, 2014, 15, 2398–2406.
13. K. Singh and C. F. Blanford, ChemCatChem, 2014, 6, 921–929.
14. K. Singh, T. McArdle, P. R. Sullivan and C. F. Blanford, Energy Environ. Sci., 2013, 6, 2460–2464.
15. M. Xi and B. Zhang, Chin. J. Chem., 2015, 33, 253–260.
16. N.-Y. Lu, K. Yang, J.-L. Li, B. Yuan and Y.-Q. Ma, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 1918–1925.
17. R. Richter, A. Mukhopadhyay and A. Brisson, Biophys. J., 2003, 85, 3035–3047.
18. K. F. Wang, R. Nagarajan and T. A. Camesano, Colloids Surf., B, 2014, 116, 472–481.
19. C. Fredriksson, S. Kihlman, M. Rodahl and B. Kasemo, Langmuir, 1998, 14, 248–251.
20. C. Modin, A. Stranne, M. Foss, M. Duch, J. Justesen, J. Chevallier, L. Andersen, A. Hemmersam, F. Pedersen and F. Besenbacher, Biomaterials, 2006, 27, 1346–1354.
21. P. J. Molino, Z. Yue, B. Zhang, A. Tibbens, X. Liu, R. M. I. Kapsa, M. J. Higgins and G. G. Wallace, Adv. Mater. Interfaces, 2014, 1 , 1300122.
22. L. Nowacki, J. Follet, M. Vayssade, P. Vigneron, L. Rotellini, F. Cambay, C. Egles and C. Rossi, Biosens. Bioelectron., 2015, 64, 469–476.
23. M. Tagaya, T. Ikoma, N. Hanagata and J. Tanaka, Mater. Express, 2012, 2, 1–22.
24. M. Bianco, A. Aloisi, V. Arima, M. Capello, S. Ferri-Borgogno, F. Novelli, S. Leporatti and R. Rinaldi, Biosens. Bioelectron., 2013, 42, 646–652.
25. R. Wang and Y. Li, Biosens. Bioelectron., 2013, 42, 148–155.
26. G. Duner, E. Thormann and A. Dedinaite, J. Colloid Interface Sci., 2013, 408, 229–234.
27. L. Fu, X. Chen, J. He, C. Xiong and H. Ma, Langmuir, 2008, 24, 6100–6106.
28. M. Koenig, T. Kasputis, D. Schmidt, K. B. Rodenhausen, K.-J. Eichhorn, A. K. Pannier, M. Schubert, M. Stamm and P. Uhlmann, Anal. Bioanal. Chem., 2014, 406, 7233–7242.
29. M. Fabretto, M. Mueller, C. Hall, P. Murphy, R. D. Short and H. J. Griesser, Polymer, 2010, 51, 1737–1743.
30. A. F. Frau, N. C. Estillore, T. M. Fulghum and R. C. Advincula, ACS Appl. Mater. Interfaces, 2010, 2, 3726–3737.
31. N. L. Torad, M. Hu, Y. Kamachi, K. Takai, M. Imura, M. Naito and Y. Yamauchi, Chem. Commun., 2013, 49, 2521–2523.
32. M. V. Voinova, M. Jonson and B. Kasemo, Biosens. Bioelectron., 2002, 17, 835–841.
33. F. Hook, B. Kasemo, T. Nylander, C. Fant, K. Sott and H. Elwing, Anal. Chem., 2001, 73, 5796–5804.
34. D. Johannsmann, I. Reviakine, E. Rojas and M. Gallego, Anal. Chem., 2008, 80, 8891–8899.
35. D. Johannsmann, I. Reviakine and R. P. Richter, Anal. Chem., 2009, 81, 8167–8176.
36. L. Daikhin, E. Gileadi, G. Katz, V. Tsionsky, M. Urbakh and D. Zagidulin, Anal. Chem., 2002, 74, 554–561.
37. M. Edvardsson, M. Rodahl and F. Hook, Analyst, 2006, 131, 822–828.
38. J. F. Rosenbaum, Bulk Acoustic Wave Theory and Devices, Artech House, London, 1st edn, 1988.
39. R. Beck, U. Pittermann and K. Weil, Phys. Chem. Chem. Phys., 1988, 92, 1363–1368.
40. D. Johannsmann, in Piezoelectric Sensors, ed. C. Steinem and A. Janshoff, Springer, Berlin, 2007, vol. 5, pp. 49–109.
41. Stanford research systems, http://www.thinksrs.com/downloads/PDFs/ApplicationNotes/QCMTheoryapp.pdf, (accessed Jan 14, 2016).
42. M. Rodahl and B. Kasemo, Sens. Actuators, A, 1996, 54, 448–456.
43. M. Voinova, M. Rodahl, M. Jonson and B. Kasemo, Phys. Scr., 1999, 59, 391–396.
44. J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, Chichester, 3rd edn, 1980.
45. T. McArdle, T. P. McNamara, F. Fei, K. Singh and C. F. Blanford, ACS Appl. Mater. Interfaces, 2015, 7, 25270–25280.
46. M. Bos and T. van Vliet, Adv. Colloid Interface Sci., 2001, 91, 437–471.
47. D. Graham and M. Phillips, J. Colloid Interface Sci., 1980, 76, 240–250.
48. M. M. Ouberai, K. Xu and M. E. Welland, Biomaterials, 2014, 35, 6157–6163.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental materials and methods; QCM-D responses from MvBOx adlayer; sample plots showing TPM-sensitivity based on QCM-D responses to linear changes in shear modulus and viscosity; additional equations for calculating TPM-sensitivity; TPM-sensitivity analysis based on incorrect initial estimates of film properties; quantitative comparison between quality of fit and QCM-D responses used in fitting; description of MATLAB functions used for modelling and optimisation. See DOI: 10.1039/c6an00143b

‡ The fundamental harmonic was excluded from all fitting and modelling because of its sensitivity to mounting effects and consequent anomalous Δf and Δd responses.⁴⁴

---