Combining random forest and 2D correlation analysis to identify serum spectral signatures for neuro-oncology†
Benjamin R.
Smith
ab,
Katherine M.
Ashton
c,
Andrew
Brodbelt
d,
Timothy
Dawson
c,
Michael D.
Jenkinson
d,
Neil T.
Hunt
e,
David S.
Palmer
*a and
Matthew J.
Baker
*b
aWestCHEM, Department of Pure and Applied Chemistry, University of Strathclyde, Thomas Graham Building, 295 Cathedral Street, Glasgow, Scotland G1 1XL, UK. E-mail: david.palmer@strath.ac.uk
bWestCHEM, Department of Pure and Applied Chemistry, University of Strathclyde, Technology and Innovation Centre, 99 George Street, Glasgow G1 1RD, UK. E-mail: matthew.baker@strath.ac.uk
cNeuropathology, Lancashire Teaching Hospitals NHS Trust, Royal Preston Hospital, Sharoe Green Lane, Fulwood, Preston, PR2 9HT, UK
dNeurosurgery, The Walton Centre NHS Foundation Trust, Lower Lane, Fazakerley, Liverpool, L9 7LJ, UK
eSUPA, Department of Physics, University of Strathclyde, 107 Rottenrow East, Glasgow, G4 0NG, UK
First published on 19th January 2016
Abstract
Fourier transform infrared (FTIR) spectroscopy has long been established as an analytical technique for the measurement of vibrational modes of molecular systems. More recently, FTIR has been used for the analysis of biofluids with the aim of becoming a tool to aid diagnosis. For the clinician, this represents a convenient, fast, non-subjective option for the study of biofluids and the diagnosis of disease states. The patient also benefits from this method, as the procedure for the collection of serum is much less invasive and stressful than traditional biopsy. This is especially true of patients in whom brain cancer is suspected. A brain biopsy is very unpleasant for the patient, potentially dangerous and can occasionally be inconclusive. We therefore present a method for the diagnosis of brain cancer from serum samples using FTIR and machine learning techniques. The scope of the study involved 433 patients from whom were collected 9 spectra each in the range 600–4000 cm−1. To begin the development of the novel method, various pre-processing steps were investigated and ranked in terms of final accuracy of the diagnosis. Random forest machine learning was utilised as a classifier to separate patients into cancer or non-cancer categories based upon the intensities of wavenumbers present in their spectra. Generalised 2D correlational analysis was then employed to further augment the machine learning, and also to establish spectral features important for the distinction between cancer and non-cancer serum samples. Using these methods, sensitivities of up to 92.8% and specificities of up to 91.5% were possible. Furthermore, ratiometrics were also investigated in order to establish any correlations present in the dataset. We show a rapid, computationally light, accurate, statistically robust methodology for the identification of spectral features present in differing disease states. With current advances in IR technology, such as the development of rapid discrete frequency collection, this approach is of importance to enable future clinical translation and enables IR to achieve its potential.
1 Introduction
Cancer is a leading cause of death and ill health across the modern world. Approximately 14 million new cases and 8.2 million deaths attributed to cancer occurred in 2012.1 It is important that we have methods to quickly and easily diagnose types of cancer, to ensure the best treatment is provided for patients. Among all types of cancer, brain tumours stand out as a particular challenge to treat effectively. This category of cancer is one of the few which have a higher mortality than incidence rate. For example, in the UK in 2006–2010 brain cancer had an incidence of 18% among young cancer sufferers, but accounted for 34% of mortality.2 Despite the relatively high incidence of brain cancer in general, its causes are not fully understood, though some have been identified.3 Malignant gliomas cause on average a 20-year reduction in life expectancy4 and among those, high grade Glioblastoma Multiforme (GBM) represents a particularly bleak outcome with just 6% of adults surviving more than 5 years after diagnosis.5 There are two main classes of brain tumour, namely primary and secondary brain tumours. The distinction between these two is the location in the body from which the cancer originated. Primary tumours (e.g. GBM) originate from within the central nervous system (CNS), with gliomas originating from the tissue which surrounds and supports the neurons in the brain, i.e. glial cells.6 Secondary (metastatic) tumours originate from elsewhere in the body, and are transported to the brain. In the UK, around 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 people are diagnosed annually with brain cancer,7 of which about 67% are secondary tumours.8 Of these secondary tumours, the breakdown of origins is as follows: lung (50%), breast (15–25%), skin (melanoma) (5–20%) and all others (5–30%).9 By identifying the organ of origin, treatment efficiency and patient survival can be increased, but the primary location is unknown in around 15% of metastatic cases.
000 people are diagnosed annually with brain cancer,7 of which about 67% are secondary tumours.8 Of these secondary tumours, the breakdown of origins is as follows: lung (50%), breast (15–25%), skin (melanoma) (5–20%) and all others (5–30%).9 By identifying the organ of origin, treatment efficiency and patient survival can be increased, but the primary location is unknown in around 15% of metastatic cases.
Current diagnostic methods are time consuming, expensive and require highly skilled practitioners to interpret them. In the case of brain and CNS cancers, the test usually consists of an MRI or CT scan in the first instance.10 These types of complex results can be subjective in their conclusions. (The CT scan itself has disputed health risks.11,12) In some cases, these tests prove to be inconclusive, and warrant further investigation. Upon such an occurrence a biopsy of the suspected tumour is indicated. A biopsy of brain tissue represents an invasive and stressful procedure for patients, again needing highly skilled surgical and pathological expertise. Even when a biopsy is taken, there can be discrepancies in the interpretation of results between medics. Bruner et al. found that of 500 biopsy cases, 214 (42.8%) had a degree of disagreement between original and review diagnoses.13 In England in the period 2006–2010, 54% of cancer cases were diagnosed following a routine or urgent GP referral, either as part of the “two week wait” system or otherwise.14 The two-week wait system is an urgent referral (less than two weeks of waiting time for a consultation) of a patient to a specialist, should cancer be suspected by a GP. However, 23% of cancer cases in England during this time period were diagnosed after presenting as an emergency.14 Concentrating on brain and CNS cancers, the National Cancer Intelligence Network (NCIN) statistics show that more than half (58%) of brain and CNS cancers are diagnosed through presentation at emergency facilities, with the “two week wait” system only accounting for 1% of the total.15 In these later diagnoses, prognosis is much poorer for all types of cancer. As well as having on average a later secondary care diagnosis, brain tumours are very difficult to identify in primary care and a high index of suspicion is required. A survey carried out on behalf of The Brain Tumour Charity (UK) found that 38% of people living with a brain tumour had visited their GP more than 5 times before being diagnosed.16 Overall, the current system for the detection and diagnosis of brain tumours in general is not satisfactory. A reliable, fast and simple method to screen for these types of cancer would reduce time before diagnosis and therefore increase survival rates, as many therapies are more effective when started early.
IR spectroscopy has previously been investigated as a cancer diagnosis tool. Haka et al. showed the merit of human tissue spectroscopy in distinguishing breast tumours from normal tissue.17 Laboratory based proof of principle studies have shown the ability of serum spectroscopy to diagnose cancerous disease states, such as those reviewed by Kondepati et al.18 Pichardo et al. were also able to use spectroscopy together with machine learning to detect breast cancer.19 Most of these investigations in the literature focus on very specific types of cancerous diseases states, or require tissue samples from suspected tumours to aid in diagnosis. A broader approach based on IR spectroscopy of serum samples could be an ideal solution. Serum can be acquired from blood samples in a much less invasive procedure. Backhaus and Mueller et al. demonstrated a method to successfully detect breast cancer using serum samples and IR spectroscopy. The sensitivity and specificity achieved were 98% and 95% respectively.20 Gajjar et al. used FTIR of serum and plasma samples to distinguish ovarian and endometrial cancer patients from control patients.21 They used various feature extraction methods to obtain very promising results from a small pilot study. Ovarian cancer was detectable with 95% correct classification.
Our previous research has shown the ability of combined FTIR and machine learning to identify differing levels of cytokine and angiogenesis factors in patients with glioma.22 The Bioplex study provided sensitivities and specificities as high as 88% and 81% respectively. Furthermore, sensitivities and specificities of 87.5% and 100% were achieved when combining ATR-FTIR with Support Vector Machines (SVM). A similar approach was employed to distinguish differing grades of glioma (high-grade and low-grade) from non-cancer.6 Sensitivity and specificity were 93.75% and 96.53% respectively.
We now build on our previous diagnostic research6,22–25 with a larger dataset, a different approach to machine learning and the technique of generalised 2D correlational analysis. Some studies have used “black box” machine learning.22,26 While this can give good predictions, it does not give full insight into the actual features being used for classification, which in turn does not aid clinical translation. In order to translate novel technologies to the clinic, further information is required to identify spectral peaks that provide diagnostic information. In addition, identifying relevant features will enable future rapid collection protocols via techniques such as Quantum Cascade Laser IR spectroscopy.27,28 Focusing on the salient information of a spectral dataset also provides enhanced diagnostic accuracy due to the removal of extraneous information that is clouding the diagnosis based upon biological variance. Dorling and Baker29 describe the utility of serum spectroscopy in the clinic, in order to achieve this we have to provide rapid, accurate and information-rich analysis to correctly describe the difference in disease state molecular species.
IR spectroscopy of biological materials is not straightforward. Serum itself is a very complex mixture of various components. In addition to the chemical complexity of serum, optimum sample preparation techniques and their effect on the spectrum are not known. The group has therefore established guidelines by means of a dilution study coupled with a comparison of ATR-FTIR and High Throughput (HT)-FTIR.30 It was found that 3-fold dilution was optimal for HT-FTIR in terms of scores in a spectral quality test. ATR-FTIR although slower than HT-FTIR, proved to be the best when investigating discernible features. Also previously established by the group was the optimum drying time of 8 minutes.6
Generalised 2D correlation spectroscopy is a data analysis method developed by Noda,31 as distinct from ultrafast 2D-IR spectroscopy, which measures vibrational couplings in an analogous way to 2D-NMR.32 Noda's generalised method allows external perturbations (temperature, concentration, pH etc.) to be used to obtain information about the effect of external influences on spectra, and does so by offering two main types of correlation which are synchronous and asynchronous. Synchronous spectra represent coinciding changes in different spectral regions. The synchronous spectrum is symmetrical, and contains peaks (called autopeaks) along the diagonal. The strength of the highlighted areas along this line represent the band strength of the IR regions. Peaks off the diagonal (called cross-peaks) show correlation between underlying 1D spectral peaks. If the sign is positive (blue in this work), then both 1D peaks are changing in the same direction, either increasing or decreasing in intensity. Negative signs (red) show that the 1D spectral peaks are moving in opposite directions in terms of intensity. Asynchronous spectra represent sequential changes in the 1D spectra due to the perturbation. When a cross-peak is of a positive sign, then a peak from the first spectrum is changing before a band from the second spectrum, and vice versa. A feature of these asynchronous spectra is that they contain no autopeaks, and are anti-symmetric with respect to the diagonal.
The type of machine learning used in this work (Random Forest) is interpretable, and results in a better understanding of the relative importance of distinguishing features. Furthermore, we combine this method with 2D correlational analysis. The novel combination of these usually disparate methods allows for both the building of an accurate classifier, and the characterisation of spectral features important for diagnosis.
2 Materials and methods
2.1 Spectral collection
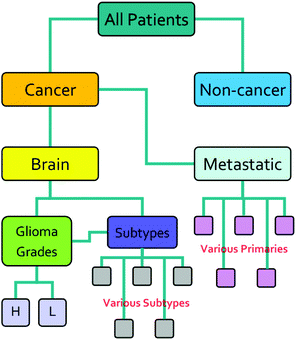
The research described in this paper was performed with full ethical approval (Walton Research Bank BTNW/WRTB 13_01/BTNW Application #1108). The dataset consists of IR data from serum samples of 433 patients with differing brain cancer diagnoses taken at the Royal Preston Hospital, in conjunction with Brain Tumour North West. The entire dataset comprises 9 spectra for each patient. These 9 spectra were generated from 3 IR passes of 3 separate sample preparations. Each sample of 1 μL, was allowed to dry for 8 minutes before spectra were collected. Data was gathered using an Agilent Cary-600 Series FTIR spectrometer with a PIKE Technologies MIRacle™ single-reflection ATR utilising a diamond crystal plate. Spectra were subject to Agilent Resolutions ATR correction. Spectra were obtained in the range 600–4000 cm−1, with a resolution of 1.926 cm−1. All samples had been frozen before spectral collection, and defrosted immediately prior to the measurement. Fig. 1 shows the organisation of the dataset, while Table 1 shows the number of patients per disease category.| Disease state | Number of patients |
|---|---|
| Cancer | 311 |
| Non-cancer | 122 |
| Primary brain cancer | 134 |
| Metastatic brain cancer | 177 |
| High grade glioma | 64 |
| Low grade glioma | 23 |
2.2 Pre-processing
All pre-processing was undertaken using Matlab.33 All spectra were vector normalised, and optionally a first or second derivative taken using 5 smoothing points (Savitzky–Golay method). During the pre-processing phase, any spectra displaying gross spectral error were discarded. These erroneous spectra amounted to 2 whole patients (18 spectra) and 7 other spectra, for a total of 25 spectra being removed. One of the patients for which all spectra were erroneous was from the Metastatic Brain Cancer group, and the other from the Low Grade Glioma group. For the analysis this left 309, 176 and 22 patients in the Cancer, Metastatic and Low Grade Glioma groups respectively. Other types of pre-processing were tried; (raw data and first derivative, both with or without normalisation) and the normalised second derivative with 5 smoothing points was found to be the best in terms of statistical results and clarity of Random Forest Gini importance peaks. (See section 2.5 for explanation of Gini importance.) The data was split into two sections after the removal of the CO2 region. The regions considered were 900–1800 cm−1 and 2400–4000 cm−1. See Fig. 2 for an overview of the spectra during pre-processing. Fig. S1 in the ESI† shows averaged cancer and non-cancer spectra together with standard deviations for each.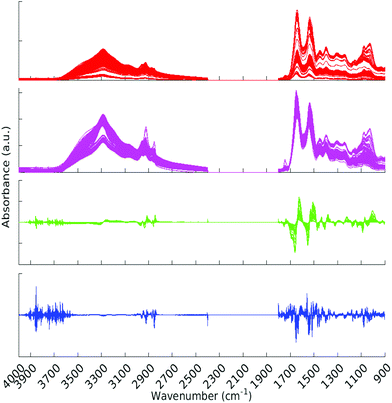 | ||
| Fig. 2 All spectra with various pre-processing. Red – raw data, magenta – normalised spectra, green – normalised first derivative and blue – normalised second derivative. | ||
2.3 Ratios
Ratios of ranges of wavenumbers were taken from the raw spectral data, after removal of erroneous spectra. These were calculated using a simple sum of intensities of the relevant regions of the spectra. Ratios such as these have been previously shown to be important in diagnosis of various diseases from IR spectra. Choice of wavenumber ranges was steered by previous literature, as well as wavenumber ranges found to be important to our machine learning classification. Ratios in the range 1030–1080 relating to glycogen and phosphate vibrations, are thought34 to be useful in distinguishing malignant and non-malignant disease states. Ratios 3160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3170 and 3190
3170 and 3190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3200 were found by Bassan et al.35 to be leading discriminatory metrics in malignant breast cancer detection. The ratio listed as “Navarro” was investigated in order to obtain protein
3200 were found by Bassan et al.35 to be leading discriminatory metrics in malignant breast cancer detection. The ratio listed as “Navarro” was investigated in order to obtain protein![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid ratios for the spectra as suggested by Navarro et al.36 Another protein
lipid ratios for the spectra as suggested by Navarro et al.36 Another protein![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid ratio was also investigated, this was established by Baker et al.37 as a protocol. Furthermore, we consider ratios BRS1-4 which were chosen from regions important for the classification of cancer/non-cancer which became apparent from preliminary RF models (Table 2).
lipid ratio was also investigated, this was established by Baker et al.37 as a protocol. Furthermore, we consider ratios BRS1-4 which were chosen from regions important for the classification of cancer/non-cancer which became apparent from preliminary RF models (Table 2).
| Ratio ID | Wavenumbers | Regions |
|---|---|---|
a [∑(1380–1420) + ∑(1480–1580) + ∑(1600–1680)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [∑(1430–1470) + ∑(1720–1760) + ∑(2830–3000)]. [∑(1430–1470) + ∑(1720–1760) + ∑(2830–3000)].
|
||
1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1050 1050 |
1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1050 1050 |
Carb. |
1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 1080 |
1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 1080 |
Carb.–phos. |
1050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 1080 |
1050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 1080 |
Phos. |
3160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3170 3170 |
3160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3170 3170 |
Alcohols |
3190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3200 3200 |
3190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3200 3200 |
O–H–O |
| Navarro | ∑(1650–1700)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑(1730–1800) ∑(1730–1800) |
Protein![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid lipid |
| Baker | manya | Protein![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid lipid |
| BRS 1 | ∑(1600–1680)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑(1500–1580) ∑(1500–1580) |
AmideI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AmideII AmideII |
| BRS 2 | ∑(1220–1280)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑(1380–1420) ∑(1380–1420) |
Phos.A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) COO− COO− |
| BRS 3 | ∑(1000–1050)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑(1430–1470) ∑(1430–1470) |
Carb.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2 CH2 |
| BRS 4 | ∑(1000–1050)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑(2830–3000) ∑(2830–3000) |
Carb.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2,CH3 CH2,CH3 |
2.4 Random forest
The main method employed for classification in this study was Random Forest (RF),38 as implemented in R. The specific package used was random forest, by Liaw and Wiener.39 This is a machine learning method used to find features associated with input classes. From the training set, RF builds a “forest” of regression trees using the CART (Classification and Regression Trees) algorithm. There are three possible training parameters for random forest: ntree – the number of trees in the Forest; mtry – the number of different descriptors tried at each split; and nodesize – the minimum node size below which leaves are not further subdivided. In our work, the number of trees generated per classification was 500. The variable ‘mtry’ was one third of the number of descriptors and ‘nodesize’ was 5. These are the default settings for the package, and have proved to be optimal in our previous studies using random forest.40–42 Training![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test set split was 80
test set split was 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, respectively. 5-Fold cross validation of the training set was also carried out.
20, respectively. 5-Fold cross validation of the training set was also carried out.
The random forest machine learning method (MLM) was chosen for this work for several reasons. Firstly, RF is easily scalable when compared to other MLM. This means that the same (or very similar) parameters can be used in the future with larger datasets. Secondly, RF has easily interpreted results when used with the Gini impurity metric (see section 2.5 for an explanation of the Gini metric). This meant that important distinguishing wavenumbers were clearly defined, and their relative importance was readily established. Third, RF is known for being able to robustly handle outliers in the input space. This property potentially allows classification of spectra without heavy pre-processing, whereas other MLM may require it. Finally, RF deals well with missing values from input classes. This was especially important to our work, as the wavenumber range 1800–2400 cm−1 was removed.
For the interpretation of the RF outcome, two main groups of results were considered. Firstly, a selection of statistical metrics were generated to give an in-depth analysis of the accuracy and reliability of each classification. These were based upon true positive (TP), true negative (TN), false positive (FP) and false negative (FN) predictions as well as “real”(actual number of positives and negatives in the dataset) positives (P) and negatives (N). The abbreviation MCC stands for Matthews Correlation Coefficient.
| Number of positives (P) = TP + FN | (1) |
| Number of negatives (N) = TN + FP | (2) |
 | (3) |
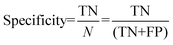 | (4) |
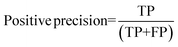 | (5) |
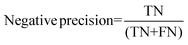 | (6) |
 | (7) |
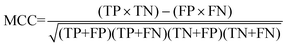 | (8) |
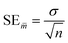 | (9) |
In the statistical results tables below, TS and CV represent results for the test set and cross-validation respectively. The tolerances shown for each result are their standard errors, generated according to eqn (9), where SE![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) is the standard error of the mean (of the 96 iterations), σ is the standard deviation and n is the number of samples.
is the standard error of the mean (of the 96 iterations), σ is the standard deviation and n is the number of samples.
2.5 Random forest feature importance
Spectral feature importance results were obtained using the combined mean decrease in Gini coefficient, with respect to wavenumbers. This allowed an easily-interpreted result to be found, and wavenumber ranges important to the classification were ascertained. The Gini impurity of a node is dependent on the probability of each possible outcome. For a single node τ in the RF classification, the Gini impurity is found by eqn (10) below, where g(τ) is the impurity of node τ, n is the total number of spectra at the node while nA and nB are the number of spectra belonging to class A or B respectively; i.e. cancer or non-cancer.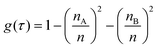 | (10) |
Every time a node is split on a predictor (wavenumber), the Gini impurity for the two child nodes is less than the parent node. This is because the dataset is gradually being sorted into predicted classes, and becoming more homogeneous with respect to the proportion of classes A or B. When node τ is split, resulting in two child nodes υ and ϕ, the change in Gini (Δg) is found by eqn (11) where nυ and nϕ are the number of spectra in nodes υ and ϕ respectively. The value of Δg is larger when a greater change in impurity occurs after the split, thus allowing for the decrease in Gini to be used as a measure of importance of a certain wavenumber.
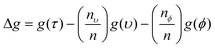 | (11) |
The overall Gini importance (G) of a particular spectral feature θ is found by the sum across all nodes of each tree ψ, and across all trees in forest ω (eqn (12)).
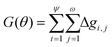 | (12) |
These values are then averaged for the 96 independent classifications, to arrive at the Mean Decrease (Gini) used in the figures presented in the Results and discussion section.
2.6 Generalised 2D correlational analysis
2D correlation plots were generated with the program 2DShige,43 and visualised in Matlab. Utilising the method developed by Noda,31 generalised 2D correlation plots can be produced from separate 1D IR spectra which highlight changes in these spectra due to some perturbation (in this case, the perturbation was the diagnosis of cancer or not). According to Noda's rules44 the synchronous spectra can (qualitatively) show whether spectral intensities at two different areas of the spectrum are changing in the same direction, i.e. whether intensities are increasing or decreasing simultaneously. If a cross-peak has a positive sign, the intensities are both changing in the same direction, and in opposite directions for a negative cross-peak. The asynchronous correlations on the other hand show the sequential order of changes in intensity. Both synchronous and asynchronous 2D plots were produced of normalised, first and second derivatives, both 900–1800 cm−1 and 2400–4000 cm−1 sections of the spectrum.3 Results and discussion
3.1 Random forest results
Results were obtained by combining the findings of 96 independent RF models, and the statistics and important wavenumber regions noted. 96 was found to be an adequate number of iterations through average convergence of test runs, the plot of which can be found in the ESI† of this article. The sections of the spectrum between 900–1800 cm−1 and 2400–4000 cm−1 were utilised. These sections were used in RF both separately and together. Presented here are results using normalised, first and second derivative spectra, as described in the pre-processing section. All results are in terms of a binary cancer/non-cancer classification.| Metric | 900–1800 cm−1 | 2400–4000 cm−1 | Both |
|---|---|---|---|
| Sensitivity TS | 0.901 ± 0.013 | 0.875 ± 0.014 | 0.900 ± 0.012 |
| Sensitivity CV | 0.899 ± 0.006 | 0.872 ± 0.007 | 0.897 ± 0.006 |
| Specificity TS | 0.785 ± 0.028 | 0.764 ± 0.030 | 0.812 ± 0.027 |
| Specificity CV | 0.768 ± 0.014 | 0.733 ± 0.016 | 0.786 ± 0.014 |
| Prediction accuracy TS | 0.869 ± 0.003 | 0.846 ± 0.003 | 0.877 ± 0.003 |
| Prediction accuracy CV | 0.863 ± 0.001 | 0.836 ± 0.001 | 0.868 ± 0.001 |
| Positive precision TS | 0.918 ± 0.012 | 0.916 ± 0.012 | 0.930 ± 0.011 |
| Positive precision CV | 0.912 ± 0.006 | 0.905 ± 0.006 | 0.922 ± 0.006 |
| Negative precision TS | 0.746 ± 0.029 | 0.677 ± 0.032 | 0.746 ± 0.029 |
| Negative precision CV | 0.739 ± 0.015 | 0.661 ± 0.016 | 0.729 ± 0.015 |
| Matthews correl. coeff. TS | 0.674 ± 0.007 | 0.615 ± 0.007 | 0.693 ± 0.007 |
| Matthews correl. coeff. CV | 0.659 ± 0.003 | 0.585 ± 0.003 | 0.667 ± 0.003 |
| Metric | 900–1800 cm−1 | 2400–4000 cm−1 | Both |
|---|---|---|---|
| Sensitivity TS | 0.918 ± 0.011 | 0.897 ± 0.013 | 0.912 ± 0.012 |
| Sensitivity CV | 0.918 ± 0.006 | 0.887 ± 0.007 | 0.912 ± 0.006 |
| Specificity TS | 0.883 ± 0.022 | 0.820 ± 0.027 | 0.875 ± 0.023 |
| Specificity CV | 0.839 ± 0.013 | 0.793 ± 0.015 | 0.853 ± 0.013 |
| Prediction accuracy TS | 0.909 ± 0.003 | 0.877 ± 0.003 | 0.902 ± 0.003 |
| Prediction accuracy CV | 0.897 ± 0.001 | 0.863 ± 0.001 | 0.897 ± 0.001 |
| Positive precision TS | 0.957 ± 0.008 | 0.937 ± 0.010 | 0.957 ± 0.008 |
| Positive precision CV | 0.941 ± 0.005 | 0.928 ± 0.005 | 0.948 ± 0.005 |
| Negative precision TS | 0.795 ± 0.027 | 0.730 ± 0.030 | 0.769 ± 0.028 |
| Negative precision CV | 0.785 ± 0.014 | 0.698 ± 0.015 | 0.768 ± 0.014 |
| Matthews correl. coeff. TS | 0.776 ± 0.007 | 0.691 ± 0.008 | 0.755 ± 0.008 |
| Matthews correl. coeff. CV | 0.742 ± 0.002 | 0.653 ± 0.003 | 0.740 ± 0.003 |
| Metric | 900–1800 cm−1 | 2400–4000 cm−1 | Both |
|---|---|---|---|
| Sensitivity TS | 0.928 ± 0.011 | 0.825 ± 0.015 | 0.923 ± 0.011 |
| Sensitivity CV | 0.929 ± 0.005 | 0.823 ± 0.008 | 0.922 ± 0.006 |
| Specificity TS | 0.915 ± 0.019 | 0.766 ± 0.035 | 0.914 ± 0.018 |
| Specificity CV | 0.888 ± 0.011 | 0.730 ± 0.018 | 0.892 ± 0.011 |
| Prediction accuracy TS | 0.924 ± 0.002 | 0.813 ± 0.03 | 0.921 ± 0.002 |
| Prediction accuracy CV | 0.918 ± 0.001 | 0.805 ± 0.001 | 0.914 ± 0.001 |
| Positive precision TS | 0.970 ± 0.007 | 0.937 ± 0.010 | 0.970 ± 0.007 |
| Positive precision CV | 0.960 ± 0.004 | 0.929 ± 0.005 | 0.963 ± 0.004 |
| Negative precision TS | 0.812 ± 0.026 | 0.511 ± 0.034 | 0.804 ± 0.026 |
| Negative precision CV | 0.813 ± 0.013 | 0.491 ± 0.017 | 0.792 ± 0.014 |
| Matthews correl. coeff. TS | 0.811 ± 0.006 | 0.513 ± 0.008 | 0.805 ± 0.006 |
| Matthews correl. coeff. CV | 0.795 ± 0.002 | 0.481 ± 0.003 | 0.784 ± 0.002 |
The normalised second derivative gave the best overall accuracy according to the statistical metrics which are presented in the tables below. The first derivative results achieved a performance between normalised spectra and second derivative in terms of classification accuracy. The 2400–4000 cm−1 section of the spectrum did not perform as well as the 900–1800 cm−1 section, nor did it add any accuracy when these two sections were combined together.
3.2 Spectral features
Table 6 gives an overview of the identified wavenumber ranges in order of importance, together with their regions in the IR spectrum for second derivative data. The column “∑Gini” in the table is a summation of the (average over 96 RF classifications) mean decrease in Gini for each wavenumber within a given range. The most prominent ranges in terms of RF importance are the carbohydrate region at 997–1003 cm−1, the phosphate region at 1290–1294 cm−1 and the lipid region at 1462–1464 cm−1. These areas of importance are closely followed by other carbohydrate and protein modes.| Wavenumber range | ∑Gini | Tentative assignment |
|---|---|---|
| 997–1003 cm−1 | 131.8 | Carbohydrate |
| 1290–1294 cm−1 | 93.1 | Phosphate |
| 1462–1464 cm−1 | 78.7 | Lipid CH2 |
| 1527–1533 cm−1 | 71.9 | Amide II |
| 1028–1034 cm−1 | 59.8 | Carbohydrate |
| 1387–1390 cm−1 | 46.7 | Protein COO− |
| 1194–1198 cm−1 | 41.9 | |
| 1373–1377 cm−1 | 39.9 | Protein COO− |
| 1080–1082 cm−1 | 31.4 | Phosphate |
| 1280–1282 cm−1 | 28.6 | |
| 1093–1095 cm−1 | 24.0 |
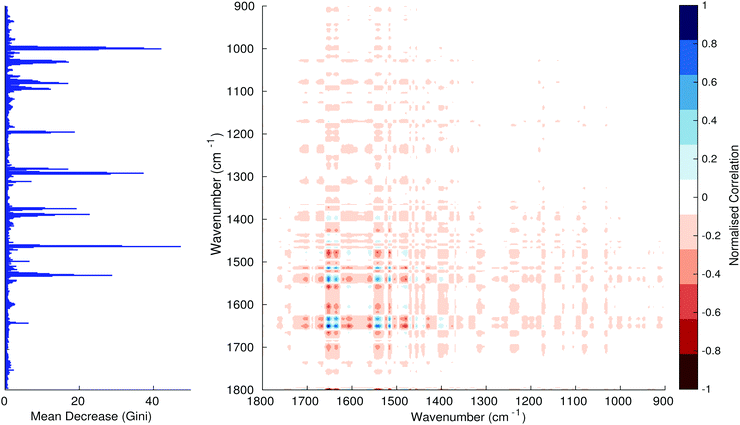
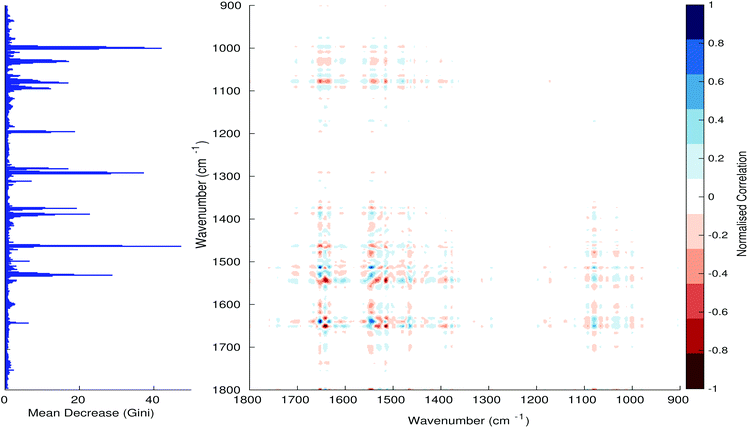
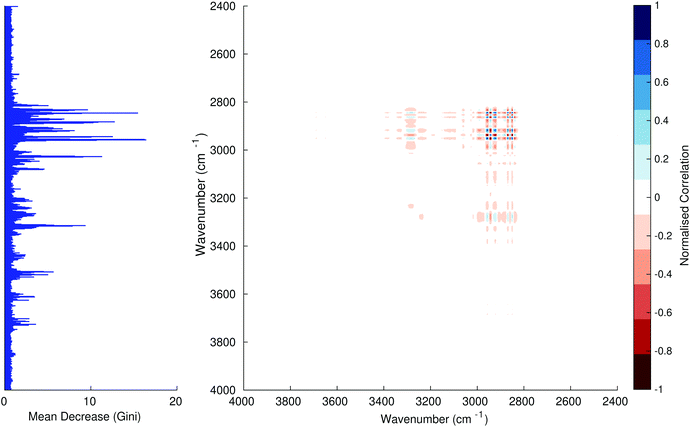
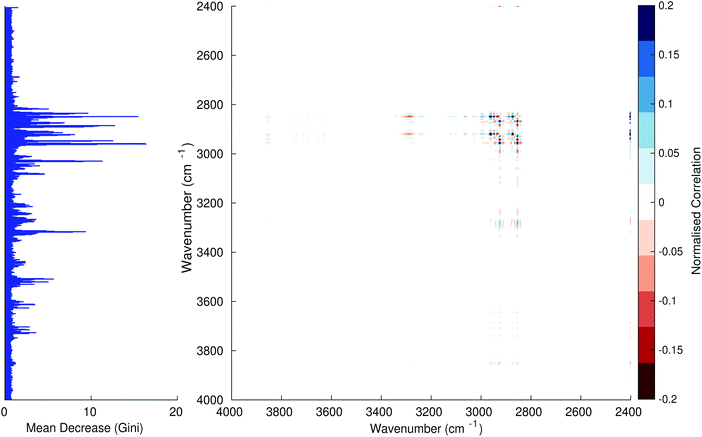
Fig. 3–6 show the mean decrease in Gini coefficient for all wavenumbers in a range, alongside generalised 2D correlation plots for the same data. In the 2D correlation plots, cancer spectra are on the horizontal axis, and non-cancer spectra are on the vertical. Data for the generalised 2D correlational analysis were obtained by averaging subsections of intensities in the dataset. In the figures showing the 2D correlation of the second derivative spectra, the averages were as follows: Fig. 3: synchronous spectrum of the average of all cancer spectra in the range 900–1800 cm−1vs. all non-cancer spectra in the same range. Fig. 4–6 use the same pattern of average intensities of cancer and non-cancer spectra in the same wavenumber range, for both synchronous and asynchronous 2D plots. In the ESI, Fig. S4–S11† show similar plots for normalised and first derivative data. Fig. S12–S14† show average cancer and non-cancer spectra plotted together with Gini importance for normalised, first and second derivative spectra.
Usually when these 2D plots are generated, an incremental variable is used for the perturbation between the two sides of the correlation (e.g. temperature, pressure etc.). In the case of this work, the perturbation is whether the patient has cancer or a normal diagnosis. It should also be borne in mind that the two in-putted comparison spectra were averages of the whole class; i.e. cancer and non-cancer. However, some information can still be gleaned from Noda's method in this scenario. The synchronous spectrum shows whether two wavenumber ranges increase or decrease in intensity in the same or opposite directions. This is as normal for a synchronous generalised 2D correlation plot. The asynchronous spectrum is more subtle in its interpretation with a correlation such as this. Noda's rules44 show whether an intensity change occurs before or after another, with an incremental increase of some outside perturbation. There is no such incremental increase of a perturbation in this work, only a binary cancer/non-cancer descriptor. Therefore, the asynchronous plots serve as extra clarification to further highlight differences in the averaged spectra, without the influence of auto peaks. This therefore can provide a better means to identify major regions of the spectra which are responsible for the cancer/non-cancer distinction.
In Fig. 3 & 4, it can be seen that the peaks at around 1640 and 1530 cm−1 show a strong correlation with each other. Only the peak centred around 1530 cm−1 appears as a strong spike in the RF classification. However, these two peaks are themselves correlated to other wavenumber ranges which are heavily featured in the RF study. In Fig. 5 & 6, a similar situation can be seen with the two cross-peaks around the 2850 and 2930 cm−1 areas. This time however, both of these peaks also show strong peaks in the mean decrease in Gini.
The coupling together of the RF importance charts and the 2D correlations is helpful for further clarification of where the differences in the spectra lie, and whether these are reproduced in both studies. Another helpful piece of information from this is whether the major features of the RF importance charts match up to areas of major difference in intensities at certain wavenumbers. This allows further characterisation of the RF results, and gives clues as to whether minor or major differences in spectra are responsible for the greatest discrimination. Overall, the RF and 2D correlations are showing the same features via very different analyses, providing us further confidence due to the use of orthogonal techniques.
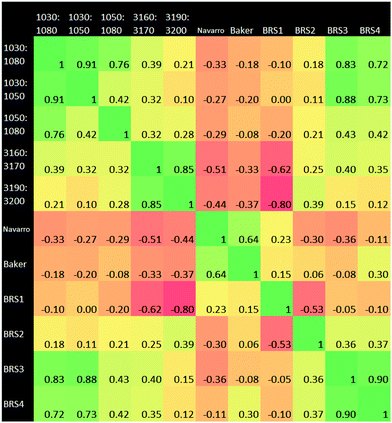
3.3 Ratiometrics
A Pearson correlation study was carried out on the ratios identified in the Materials and methods section. Of particular interest from this correlational analysis of wavenumber ratios is the strong anti-correlation between BRS1 and 3190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3200 cm−1. This may suggest a linked ratio apparent in our dataset, which spans a wide range from the Amide regions to the hydrogen bonding region. Ratio pairs from wavenumber ranges located near to each other on the spectrum generally had a strong positive correlation, for example those at 1030
3200 cm−1. This may suggest a linked ratio apparent in our dataset, which spans a wide range from the Amide regions to the hydrogen bonding region. Ratio pairs from wavenumber ranges located near to each other on the spectrum generally had a strong positive correlation, for example those at 1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1050 cm−1 and 1050
1050 cm−1 and 1050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 cm−1. An anti-correlation is noted the pair 3160
1080 cm−1. An anti-correlation is noted the pair 3160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3170 cm−1 and BRS1. BRS3 and BRS4 also exhibit a strong correlation; both ratios being a carbohydrate
3170 cm−1 and BRS1. BRS3 and BRS4 also exhibit a strong correlation; both ratios being a carbohydrate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lipid type at different wavenumber ranges. The result of 0.00 for 1030
lipid type at different wavenumber ranges. The result of 0.00 for 1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1050 cm−1vs. BRS1 is interesting, as this suggests that the ratio of intensities of AmideI
1050 cm−1vs. BRS1 is interesting, as this suggests that the ratio of intensities of AmideI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AmideII and those of the carbohydrate region vary completely independently of one another. The adjacent carbohydrate ratios of 1030
AmideII and those of the carbohydrate region vary completely independently of one another. The adjacent carbohydrate ratios of 1030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 cm−1 and 1050
1080 cm−1 and 1050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1080 cm−1 also show a very low correlation with the AmideI
1080 cm−1 also show a very low correlation with the AmideI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AmideII ratio.
AmideII ratio.
It was found that the 900–1800 cm−1 range of the spectral data produced the greatest accuracy for RF. The higher end of the spectrum from 2400–4000 cm−1 performed adequately alone, but did not add to the accuracy of the classification when used alongside 900–1800 cm−1. This suggests a correlation between the upper and lower ends of the spectrum, as evidenced also in the ratio correlation graphic (Fig. 7). The lower end therefore represents a better option, as the calculation is less expensive than using the full range. In the work leading up to these results, the first derivative spectra were found to be intermediate between raw data and the second derivative in terms of statistical results and clarity of important wavenumbers. The results of the generalised 2D correlational analysis proved to be useful as a comparison to the RF results. It allowed for better visualisation of the differences in spectra and tallied well (as expected) with the importance charts. Our method works well for the binary classification of cancer/non-cancer, the next step would be to develop further the classification of disease states within the cancer subset.
4 Conclusions
Significant differences in IR spectra of differing disease states were observed in this study, and we have proven that our approach has potential in the area of cancer diagnosis. We have employed and thoroughly tested the random forest technique and its associated Gini feature importance, and proven it to be effective in classifying cancer and non-cancer states. Noda's generalised 2D IR approach has proven to be a useful adjunct in verifying the importance results from RF. A robust pre-processing regimen was also developed in the course of this work; it was found that the normalised second derivative of the spectral data was most effective in our RF classification. Investigation of various spectral ratios was also carried out. While not immediately useful in RF classification, some new relationships between ratios were found which may prove interesting in further studies.This research has shown a rapid, computationally light, accurate, statistically robust methodology for the identification of spectral features that define a dataset. The identification of these features is in line with Occam's razor and supports accurate diagnostics by focusing upon salient information as opposed to including information from biological variance within the diagnosis. With current advances in IR technology, such as the development of rapid discrete frequency collection, this approach is of importance to enable future clinical translation and enables IR to achieve its potential.
Acknowledgements
MJB would like to thank EPSRC, Dstl, Rosemere Cancer Foundation, Brain Tumour North West, and the Sydney Driscoll Neuroscience Foundation for funding. DSP and BRS are grateful for use of the EPSRC funded ARCHIE- WeSt High Performance Computer (http://www.archie-west.ac.uk, EPSRC Grant No. EP/K000586/1). DSP thanks the University of Strathclyde for support through its Strategic Appointment and Investment Scheme. BRS thanks the University of Strathclyde for funding.References
- W. H. Organization, et al., World cancer report, 2014, WHO Report, Geneva: WHO, 2014 Search PubMed.
- ONS, Cancer Statistics Registrations, England, http://www.ons.gov.uk/ons/rel/vsob1/cancer-statistics-registrations-england-series-mb1-/no-41-2010/cancer-statistics-registrations-england-series-mb1--no-41-2010-statistical-bulletin.html, 2010, Accessed: 23-09-2015 Search PubMed.
- M. Wrensch, Y. Minn, T. Chew, M. Bondy and M. S. Berger, Neuro-oncology, 2002, 4, 278–299 Search PubMed.
- N. Burnet, S. Jefferies, R. Benson, D. Hunt and F. Treasure, Br. J. Cancer, 2005, 92, 241–245 CAS.
- C. R. UK, Statistics and outlook for brain tumours, http://www.cancerresearchuk.org/about-cancer/type/brain-tumour/treatment/statistics-and-outlook-for-brain-tumours, 2015, Accessed: 23-09-2015 Search PubMed.
- J. R. Hands, K. M. Dorling, P. Abel, K. M. Ashton, A. Brodbelt, C. Davis, T. Dawson, M. D. Jenkinson, R. W. Lea and C. Walker, et al. , J. Biophotonics, 2014, 7, 189–199 CrossRef CAS PubMed.
- B. R. Trust, About Brain Tumours, http://www.brt.org.uk/brain-tumours, 2014, Accessed: 23-09-2015 Search PubMed.
- C. R. UK, Primary and Secondary Brain Tumours, http://www.cancerresearchuk.org/about-cancer/type/brain-tumour/about/primary-and-secondary-brain-tumours, 2015, Accessed: 23-09-2015 Search PubMed.
- R. Soffietti, A. Ducati and R. Rudà, Handb. Clin. Neurol., 2012, 105, 747–755 CAS.
- NICE, Suspected cancer: recognition and referral, http://www.nice.org.uk/guidance/NG12/chapter/1-recommendations#brain-and-central-nervous-system-cancers, 2015, Accessed: 23-09-2015 Search PubMed.
- D. J. Brenner and E. J. Hall, N. Engl. J. Med., 2007, 357, 2277–2284 CrossRef CAS PubMed.
- M. S. Pearce, J. A. Salotti, M. P. Little, K. McHugh, C. Lee, K. P. Kim, N. L. Howe, C. M. Ronckers, P. Rajaraman and A. W. Craft, et al. , Lancet, 2012, 380, 499–505 CrossRef.
- J. M. Bruner, L. Inouye, G. N. Fuller and L. A. Langford, Cancer, 1997, 79, 796–803 CrossRef CAS PubMed.
- N. C. I. Network, routes to diagnosis, http://www.ncin.org.uk/publications/routes_to_diagnosis, 2010, Accessed: 23-09-2015 Search PubMed.
- N. C. I. Network, data briefings/routes to diagnosis, http://www.ncin.org.uk/publications/data_briefings/routes_to_diagnosis, 2010, Accessed: 23-09-2015 Search PubMed.
- M. H. via The Brain Tumour Charity, Finding a better way?, http://www.thebraintumourcharity.org/Resources/SDBTT/news/documents/the-brain-tumour-charity-report-on-improving-quality-of-life-final-report-dec2013.pdf, 2013, Accessed: 23-09-2015 Search PubMed.
- A. S. Haka, K. E. Shafer-Peltier, M. Fitzmaurice, J. Crowe, R. R. Dasari and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12371–12376 CrossRef CAS PubMed.
- V. R. Kondepati, H. M. Heise and J. Backhaus, Anal. Bioanal. Chem., 2008, 390, 125–139 CrossRef CAS PubMed.
- J. Pichardo-Molina, C. Frausto-Reyes, O. Barbosa-García, R. Huerta-Franco, J. González-Trujillo, C. Ramírez-Alvarado, G. Gutiérrez-Juárez and C. Medina-Gutiérrez, Laser. Med. Sci., 2007, 22, 229–236 CrossRef CAS PubMed.
- J. Backhaus, R. Mueller, N. Formanski, N. Szlama, H.-G. Meerpohl, M. Eidt and P. Bugert, Vib. Spectrosc., 2010, 52, 173–177 CrossRef CAS.
- K. Gajjar, J. Trevisan, G. Owens, P. J. Keating, N. J. Wood, H. F. Stringfellow, P. L. Martin-Hirsch and F. L. Martin, Analyst, 2013, 138, 3917–3926 RSC.
- J. R. Hands, P. Abel, K. Ashton, T. Dawson, C. Davis, R. W. Lea, A. J. McIntosh and M. J. Baker, Anal. Bioanal. Chem., 2013, 405, 7347–7355 CrossRef CAS PubMed.
- M. J. Baker, C. Clarke, D. Démoulin, J. Nicholson, F. M. Lyng, H. J. Byrne, C. A. Hart, M. D. Brown, N. W. Clarke and P. Gardner, Analyst, 2010, 135, 887–894 RSC.
- M. J. Baker, E. Gazi, M. D. Brown, J. H. Shanks, P. Gardner and N. W. Clarke, Br. J. Cancer, 2008, 99, 1859–1866 CrossRef CAS PubMed.
- E. Gazi, M. Baker, J. Dwyer, N. P. Lockyer, P. Gardner, J. H. Shanks, R. S. Reeve, C. A. Hart, N. W. Clarke and M. D. Brown, Eur. Urol., 2006, 50, 750–761 CrossRef PubMed.
- L. Li, H. Tang, Z. Wu, J. Gong, M. Gruidl, J. Zou, M. Tockman and R. A. Clark, Artificial Intelligence in Med., 2004, 32, 71–83 CrossRef PubMed.
- M. R. Kole, R. K. Reddy, M. V. Schulmerich, M. K. Gelber and R. Bhargava, Anal. Chem., 2012, 84, 10366–10372 CrossRef CAS PubMed.
- B. Bird and M. J. Baker, Trends Biotechnol., 2015, 33, 557–558 CrossRef CAS PubMed.
- K. M. Dorling and M. J. Baker, Appl. Environ. Microbiol., 2013, 74, 3868–3876 Search PubMed.
- L. Lovergne, G. Clemens, V. Untereiner, R. A. Lukaszweski, G. D. Sockalingum and M. J. Baker, Anal. Methods, 2015, 7, 7140–7149 RSC.
- I. Noda, Appl. Spectrosc., 1993, 47, 1329–1336 CrossRef CAS.
- N. T. Hunt, Chem. Soc. Rev., 2009, 38, 1837–1848 RSC.
- MATLAB, version 8.5.0 (R2015a), The MathWorks Inc., Natick, Massachusetts, 2015 Search PubMed.
- E. Gazi, J. Dwyer, P. Gardner, A. Ghanbari-Siahkali, A. Wade, J. Miyan, N. P. Lockyer, J. C. Vickerman, N. W. Clarke and J. H. Shanks, et al. , J. Pathol., 2003, 201, 99–108 CrossRef CAS PubMed.
- P. Bassan, J. Mellor, J. Shapiro, K. J. Williams, M. P. Lisanti and P. Gardner, Anal. Chem., 2014, 86, 1648–1653 CrossRef CAS PubMed.
- S. Navarro, D. Borchman and E. Bicknell-Brown, Anal. Biochem., 1984, 136, 382–389 CrossRef CAS PubMed.
- M. J. Baker, J. Trevisan, P. Bassan, R. Bhargava, H. J. Butler, K. M. Dorling, P. R. Fielden, S. W. Fogarty, N. J. Fullwood and K. A. Heys, et al. , Nat. Protoc., 2014, 9, 1771–1791 CrossRef CAS PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- A. Liaw and M. Wiener, R News, 2002, 2, 18–22 Search PubMed.
- D. S. Palmer, N. M. O'Boyle, R. C. Glen and J. B. O. Mitchell, J. Chem. Inf. Model., 2007, 47, 150–158 CrossRef CAS PubMed.
- L. D. Hughes, D. S. Palmer, F. Nigsch and J. B. Mitchell, J. Chem. Inf. Model., 2008, 48, 220–232 CrossRef CAS PubMed.
- D. S. Palmer, M. Mišin, M. V. Fedorov and A. Llinas, Mol. Pharm., 2015, 12, 3420–3432 CrossRef CAS PubMed.
- S. Morita, 2Dshige, Kwansei-Gakuin University, 2004 Search PubMed.
- I. Noda, J. Mol. Struct., 2006, 799, 41–47 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5an02452h |
| This journal is © The Royal Society of Chemistry 2016 |