Deformability measurement of red blood cells using a microfluidic channel array and an air cavity in a driving syringe with high throughput and precise detection of subpopulations†
Yang Jun
Kang
a,
Young-Ran
Ha
b and
Sang-Joon
Lee
*c
aDepartment of Mechanical Engineering, Chosun University, Gwangju, Republic of Korea
bDivision of Integrative Biosciences and Biotechnology, Pohang University of Science and Technology (POSTECH), Pohang, Republic of Korea
cDepartment of Mechanical Engineering, Pohang University of Science and Technology (POSTECH), Pohang, Republic of Korea. E-mail: sjlee@postech.ac.kr; Fax: +82-54-279-3199
First published on 30th November 2015
Abstract
Red blood cell (RBC) deformability has been considered a potential biomarker for monitoring pathological disorders. High throughput and detection of subpopulations in RBCs are essential in the measurement of RBC deformability. In this paper, we propose a new method to measure RBC deformability by evaluating temporal variations in the average velocity of blood flow and image intensity of successively clogged RBCs in the microfluidic channel array for specific time durations. In addition, to effectively detect differences in subpopulations of RBCs, an air compliance effect is employed by adding an air cavity into a disposable syringe. The syringe was equally filled with a blood sample (Vblood = 0.3 mL, hematocrit = 50%) and air (Vair = 0.3 mL). Owing to the air compliance effect, blood flow in the microfluidic device behaved transiently depending on the fluidic resistance in the microfluidic device. Based on the transient behaviors of blood flows, the deformability of RBCs is quantified by evaluating three representative parameters, namely, minimum value of the average velocity of blood flow, clogging index, and delivered blood volume. The proposed method was applied to measure the deformability of blood samples consisting of homogeneous RBCs fixed with four different concentrations of glutaraldehyde solution (0%–0.23%). The proposed method was also employed to evaluate the deformability of blood samples partially mixed with normal RBCs and hardened RBCs. Thereafter, the deformability of RBCs infected by human malaria parasite Plasmodium falciparum was measured. As a result, the three parameters significantly varied, depending on the degree of deformability. In addition, the deformability measurement of blood samples was successfully completed in a short time (∼10 min). Therefore, the proposed method has significant potential in deformability measurement of blood samples containing hematological diseases with high throughput and precise detection of subpopulations in RBCs.
Introduction
Approximately 80% of the overall pressure decrease in systemic circulation occurs in microcirculation, including the arteriolar and capillary networks, where oxygen, nutrients, and waste are exchanged.1 Blood flow2–4 in microcirculation is significantly dependent on the geometric features of blood vessels5 and biophysical properties of blood,6,7 including viscosity,8–12 viscoelasticity,13–15 hematocrit,16,17 deformability,18–22 aggregation,23,24 and erythrocyte sedimentation rate (ESR).25–27 Large variation in blood flow or rheological properties is related to hematological diseases or circulatory disorders, including hypertension,28,29 sickle cell anemia,30 and diabetes.31Among the biophysical properties of blood, RBC deformability is considered a potential biomarker for monitoring variations in pathological conditions.32–34 Deformability of red blood cells (RBCs) has been significantly influenced by several factors, including cytoplasmic viscosity, surface area to cell volume ratio, membrane skeleton and integral proteins.35 RBCs have high deformability, so they can easily pass through capillary networks, whose diameter is smaller than that of the RBCs. However, hematological diseases significantly decrease RBC deformability. Low RBC deformability hinders or occludes blood flow in capillary networks, which ultimately leads to organ failure. For example, malaria parasites cause structural and mechanical modifications to the host RBC. These changes lead to low RBC deformability and increase adherence to endothelial cells, which contribute to blockage of the capillary vessels of vital organs.36,37 According to a previous study, subpopulations in RBCs significantly contribute to pathological symptoms.38 Thus, it is important to effectively detect subpopulations in RBCs. In addition, high throughput is required to test large numbers of RBCs in the blood sample, especially within a short time.
Several experimental techniques have been proposed to measure RBC deformability by addressing certain requirements. The existing techniques can be classified into two categories, namely, the bulk-cell approach and single-cell approach.39 Bulk-cell approaches, including conventional membrane filtration40,41 and slit-flow ektacytometry,42–44 are capable of detecting RBC deformability with high throughput. However, these approaches have technical limitations in discriminating minor differences in subpopulations of RBCs. That is, because the average effect of the blood sample is quantifiably measured by the bulk-cell approach, it would be difficult to evaluate the effect of individual RBCs or subpopulations in RBCs. Thus, microfluidic-based filtration methods38,45–50 have been proposed to classify small differences in subpopulations by counting either the number of channels clogged by the RBCs or calculating the volume of RBCs trapped in the microfluidic filtration channels. In contrast, various single-cell approaches have been proposed to measure the deformability of individual RBCs by monitoring cell obstruction,51 membrane fluctuation,52 cell stretching,18,53 electric impedance,21,54,55 electric deformation,19 cell velocity,56,57 transient time,58 membrane tension,59–61 and lateral migration.62 This single-cell approach is considered an effective tool for monitoring the deformability of individual RBCs. However, this approach still has some technical limitations in clinical applications because of the extremely low throughput, and strict operation protocol including manipulation of RBCs and precise control of blood flow with the bulk-sized experimental setup.
Thus, in this paper, a new and effective measurement technique is proposed to quantify RBC deformability by evaluating the hemodynamic variations through a microfluidic channel array. A unique microfluidic platform consisting of a disposable syringe equally filled with air and blood sample and a microfluidic device with a parallel microfluidic channel array is proposed to provide high throughput and subpopulation detection of RBCs.
When RBCs gradually clog in the microfluidic channel array, the population of RBCs in the upper chamber of the microfluidic channel array becomes dense. However, the population of RBCs is rarely distributed behind the microfluidic channel. The clogging of RBCs in the microfluidic channel array tends to increase hemodynamic resistance. Owing to the air cavity within the disposable syringe, blood flow in the microfluidic device shows transient behaviour depending on the hemodynamic resistance. Thus, based on the transient behaviour of blood flow, the deformability of RBCs is evaluated by monitoring the velocity field of blood flow and the image intensity within a specific region of interest (ROI) as a function of time.
Compared with conventional deformability measurement techniques, the proposed method has distinctive advantages. First, the proposed method can evaluate the deformability of blood cells using the bulk-cell approach, which provides high throughput. Second, the proposed method can detect small differences in subpopulations of blood cells, with good sensitivity. Third, the proposed method can obtain quantitative information on the temporal variations in hemodynamic properties, including the velocity field of blood flow and image intensity showing the population of RBCs during successive clogging of RBCs in the microfluidic channel array. Therefore, the deformability measurement of blood samples (∼0.3 mL) with high hematocrit (∼50%) can be completed within a short time period (∼10 min).
The performance of the proposed method is quantitatively evaluated by varying several parameters, including the air cavity of the disposable syringe and the minimum gap of the microfluidic channel array, to optimize the method. In addition, blood samples with high hematocrit ranging from 40% to 50% are tested to evaluate the effect of hematocrit on the measurement of RBC deformability. Thereafter, the proposed method is applied to quantify the deformability of homogeneous RBCs fixed with chemical solution to test its performance and usefulness. In addition, blood samples mixed with various ratios of normal blood cells and hardened blood cells are tested to comparatively evaluate the deformability of subpopulations of RBCs. Finally, as a clinical application, the proposed method is successfully applied to quantify the deformability of Plasmodium falciparum-infected RBCs.
Measurement of RBC deformability using hemodynamic variations
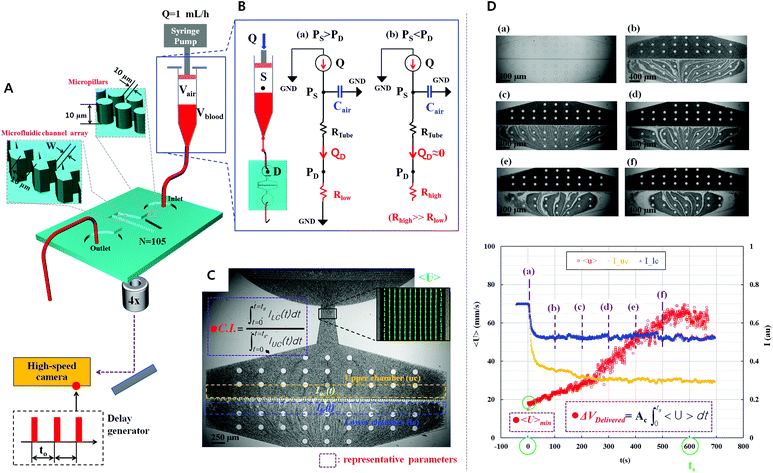
A simple but effective method of measuring the deformability of blood cells is proposed. The proposed method monitors the temporal variations in the average velocity of blood flow and an integral of image intensity of successively clogged RBCs in the microfluidic channel array for specific time durations. Using a microfluidic platform consisting of a microfluidic channel array and disposable syringe equally filled with blood sample and air, the proposed method can measure the deformability of blood cells with high throughout and precisely detect small differences in subpopulations of blood cells.The experimental setup is composed of a syringe pump for operating a disposable syringe, a disposable microfluidic device with two filtration channels (i.e., micropillars and microfluidic channel array), and an image acquisition system including a microscope and high-speed camera. As shown in Fig. 1A, the microfluidic device is designed to have one inlet, micropillars (gap = 10 μm, depth = 10 μm) for avoiding debris or large cells, microfluidic channel array (N = 105) with symmetric zigzag shape (minimum gap = W, maximum gap = 10 μm, and depth = 10 μm), and one outlet. In the upper and lower chambers, several pillars with circular shape (diameter = 100 μm) are only designed to avoid partially clogged channels due to the contact problem when bonding with the microfluidic device on the glass substrate. The air compliance effect is employed by adding an air cavity into the disposable syringe to improve the identification of subpopulations of RBCs. The disposable syringe is filled with equal amounts of blood sample (Vblood = 0.3 mL) and air (Vair = 0.3 mL). When the syringe is aligned in the vertical direction, the blood sample and air are separated into the lower and upper layers, respectively, because of their density difference. The flow rate of the blood sample in the syringe pump is fixed at 1 mL h−1 (i.e., Q = 1 mL h−1). After sufficiently compressing the air cavity to a specific volume, the blood sample in the syringe is delivered into the microfluidic device depending on the pressure difference (i.e., ΔP = PS − PD) between the syringe (PS) and microfluidic device (PD). Both pressures (PS, PD) are changed depending on several parameters including air compliance (Cair), fluidic resistance in tube (RTube), and fluidic resistance in the microfluidic device (R). To estimate blood flow in the microfluidic device (QD), a simple fluidic circuit model is constructed as shown in Fig. 1B. Firstly, if the RBCs are sufficiently deformable, most RBCs pass through the microfluidic channel array without the occurrence of clogging. The fluidic resistance in the microfluidic device remains at a low value (i.e., R = Rlow). The pressure in the syringe (PS) is greater than that in the microfluidic device (PD). Using the fluidic circuit model as represented in Fig. 1B-(a), flow rate conservation in the syringe (S) and microfluidic device (D) provides a mathematical relationship as eqn (1) and (2):
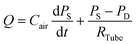 | (1) |
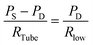 | (2) |
Using eqn (1) and (2), the flow rate (QD) in the microfluidic device is simply derived as the first order differential eqn (3):
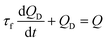 | (3) |
In eqn (3), the time constant (τf) is expressed as τf = (RTube + Rlow)Cair. According to eqn (3), the flow rate (QD) in the microfluidic device is transiently changed depending on the air compliance and overall fluidic resistance. After a certain time, the flow rate in the microfluidic device constantly remained as QD = Q. On the other hand, if the RBCs are less deformable, then successive clogging occurs in the microfluidic channel array, which leads to the increase in pressure inside the microfluidic channel array. As shown in Fig. 1B-(b), the fluidic resistance in the microfluidic device is increased to a high value (i.e., R = Rhigh). Because the pressure in the syringe (PS) is less than that in the microfluidic device (PD) (i.e., PS < PD), the blood sample in the syringe pump cannot be supplied into the microfluidic device. Thus, blood flow in the microfluidic device stops (i.e., QD ≈ 0). The pressure in the syringe (PS) is continuously increased as per eqn (4):
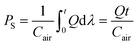 | (4) |
After some time elapses, PS is greater than PD. Immediately, the blood sample in the syringe tends to supply into the microfluidic device. Thus, according to eqn (3) and (4), the air compliance in the syringe is capable of controlling the transient flow rate of blood in the microfluidic device passively.
The velocity field and image intensity of blood flow in the specific ROI are measured to quantify hemodynamic variations resulting from successive clogging of RBCs in the microfluidic channel array. As shown in Fig. 1C and Movie-1 (ESI†), the velocity field of blood flow in the straight channel upstream of the microfluidic channel array is uniformly distributed along the width of the rectangular channel with a high aspect ratio (width = 250 μm, depth = 10 μm). Using the velocity field information, the average velocity of blood flow (<U>) is mathematically expressed and calculated in eqn (5) as follows:
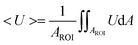 | (5) |
In eqn (5), U and AROI represent the velocity field of blood flow and ROI-area, respectively. The population of RBCs is densely distributed in the upper chamber of the microfluidic channel array because of consecutive clogging. However, the population of RBCs is rarely distributed behind the microfluidic channel array. The upper chamber (uc) and lower chamber (lc) with the same window size around the microfluidic channel array are carefully selected to quantify the spatial distribution of RBCs. By applying the digital image processing technique to microscopy images consecutively captured by the high-speed camera for 10 min, the image intensities for the upper chamber (Iuc) and lower chamber (Ilc) are calculated at intervals of 0.5 s. Assuming that the clogging of RBCs in the microfluidic channel array is strongly related to the deformability of blood cells, C.I. is proposed as a new effective parameter of deformability. Given that the image intensity of the lower chamber is greater than that of the upper chamber (i.e., Ilc > Iuc), the value of C.I., which is conveniently assumed as a function of Ilc/Iuc (i.e., C.I. = F[Ilc/Iuc]), is at least greater than 1. In addition, the C.I. can be expressed as an integral of image intensity for a specific time duration because clogging of RBCs in the microfluidic channel array occurs continuously for a specific time period. Therefore, the C.I. is mathematically formulated and calculated as,
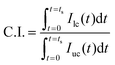 | (6) |
In eqn (6), ts represents the specific time duration of measurement. When RBCs are less deformable, C.I. tends to increase.
As a preliminary test, two consecutive microscopy images of the normal blood sample (Hct = 50%) are sequentially captured using the high-speed camera at intervals of 0.5 s for a time period of 700 s. As shown in Fig. 1D and Movie-2 (ESI†), the RBCs are consecutively clogged in the microfluidic channel array with respect to time (t) ([a] t = 0 s, [b] t = 100 s, [c] t = 200 s, [d] t = 300 s, [e] t = 400 s, and [f] t = 500 s). RBCs are stacked in the upper chamber of the microfluidic channel array because of successive clogging of blood cells with the increase in time. In other words, the population of blood cells in the upper chamber of the microfluidic channel array is greater than that behind the microfluidic channel array. By conducting digital image processing and time-resolved micro-PIV technique, two image intensities of the upper chamber (Iuc) and lower chamber (Ilc) and the average velocity of blood flow (<U>) are obtained with respect to time. The image intensity of the upper chamber is lower than that of the lower chamber because of successive clogging of blood cells. Although the syringe pump is controlled at a constant flow rate of 1 mL h−1, the average velocity tends to increase linearly for 600 s, which results from the air compliance effect in the disposable syringe. Thereafter, the average velocity of blood flow remains constant. Thus, the specific time duration of measurement is set to 600 s (ts = 600 s). Three parameters, namely, minimum value of the average velocity of blood flow (<U>min), blood volume delivered (ΔVDelivered), and C.I., are used as representative parameters of deformability. The blood volume delivered is derived from the temporal variation in the average velocity of blood flow (<U>) as eqn (7):
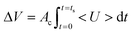 | (7) |
In eqn (7), Ac means cross-sectional area of the microfluidic channel.
Materials and methods
Fabrication of the microfluidic device and experimental procedure
The microfluidic device has one inlet port, micropillars, microfluidic channel array with a symmetric zigzag shape, and one outlet port. The depth of the microfluidic channel is fixed at 10 μm. First, a silicon molder is prepared using the typical micro-electro-mechanical system (MEMS) technique. Thereafter, polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning, Midland, MI, USA) is poured into the silicon molder placed on a Petri dish. Air bubbles dissolved in PDMS are completely removed using a vacuum pump. After curing PDMS in an oven at 80 °C for 1 h, the PDMS block is peeled off from the silicon molder. The inlet and outlet ports of the PDMS block are punched using a biopsy punch (O.D. = 0.75 mm). After treating the PDMS block and a glass slide with oxygen plasma, the microfluidic device is fabricated by bonding the PDMS block to the slide glass. The microfluidic device is placed on an optical microscope (Nikon, Tokyo, Japan) with 4× objective lens (NA = 0.1). To remove air and avoid the adhesion of RBCs in the microfluidic device, a disposable syringe (1 mL; BD Biosciences, Singapore) is filled with 1% bovine serum albumin (BSA) solution. The 1% BSA solution is prepared by adding 10 mg of BSA to 1 ml of PBS. The disposable syringe is connected to the inlet port with a polyethylene tube (I.D. = 250 μm, length = 300 mm). In addition, a polyethylene tube (I.D. = 250 μm, length = 100 mm) is connected to the outlet port to remove blood from the outlet port. After connecting the disposable syringe to the syringe pump (neMESYS, cetoni GmbH, Korbußen, Germany), the 1% BSA solution is delivered into the microfluidic device for 5 min. Air bubbles dissolved in the microfluidic device are then completely removed. After filling the disposable syringe with the blood sample (Vblood = 0.3 mL) and air (Vair = 0.3 mL), the syringe filled with BSA solution is replaced by the syringe filled with blood and air. After connecting the disposable syringe to the syringe pump, the flow rate is controlled at 1 mL h−1. All experiments are conducted at room temperature (25 °C).Time-resolved micro-PIV and image intensity measurement
The high-speed camera (FASTCAM SA 1.1, Photron, San Diego, CA, USA) is employed to effectively monitor the temporal variation in the velocity field of blood flow passing through the microfluidic channel. In addition, for the specific measurement time of 10 min, the high-speed camera is synchronized by using a digital delay pulse generator (Model 555, BNC, San Rafael, CA, USA) to capture images consecutively at intervals of 0.5 s. The camera has a resolution of 1280 × 1024 pixels, which corresponds to a spatial resolution of 10 μm per pixel. In a specific ROI (50 × 40 pixels) in the straight microfluidic channel upstream of the microfluidic channel array, velocity fields of blood flow are measured by using a time-resolved digital micro-PIV (particle image velocimetry) technique.63 The interrogation window size is 8 × 8 pixels, and window overlap is 50%. The obtained velocity vectors are validated with a median filter. Using the measured velocity information and eqn (5), the average velocity of blood flow (<U>) in the ROI is calculated as a function of time. Two specific ROIs (890 × 30 pixels) are carefully selected along the microfluidic channel array to evaluate the temporal variation in image intensity resulting from consecutive clogging of RBCs. The average pixel value in each ROI is estimated using commercial software (Matlab, Mathworks, Natick, MA, USA). The temporal variation in the average pixel value is quantitatively evaluated for the upper and lower chambers. Thereafter, the C.I. is calculated using eqn (6).Sample preparation of human blood
The human blood sample tested in this study is provided by a blood bank (Daegu–Gyeongbuk Blood Bank, Gyeongbuk, South Korea). The hematocrit of blood samples is adjusted to 40% or 50% by carefully adjusting the RBCs and 1× PBS solution (pH 7.4; Bio Solution, Seoul, South Korea). The membrane of RBCs is chemically fixed by maintaining RBCs in 1× PBS solution containing concentrations of glutaraldehyde (GA) solution (Junsei Chemical Co., Tokyo, Japan) ranging from 0.08% to 0.23% for 10 min to induce various levels of RBC deformability. Subsequently, the hematocrit of the hardened blood sample is set to 40% or 50%.P. falciparum (isolate 3D7) is maintained in human RBCs (blood type O+), RPMI 1640 (buffered with 25 mM HEPES and 25 mM NaHCO3), 10 μg mL−1 gentamycin, and 370 μM hypoxanthine under a gas mixture (5% CO2, 5% O2, and 90% N2) inside an incubator maintained at a temperature of 37 °C, for about 12 days. The parasite P. falciparum is diluted using the culture medium containing normal RBCs to prepare blood samples with 5% hematocrit and maintain the parasitemia level within the range of 0.8%–1.2%. The hematocrit of the P. falciparum-infected blood cells is set to 40% by adjusting the 1× PBS solution.
A thin blood smear is fixed with 99% methanol for 5 min. After fixing the slide, the slide is dried for 1–2 min. A diluted Giemsa stain solution (Merck, Darmstadt, Germany) is prepared prior to staining. The slide is immersed in the freshly prepared Giemsa stain solution for 25 min, rinsed with tap water, and dried. The stained malaria parasites are examined using a microscope (Zeiss, Jena, Germany) with a 100× oil immersion objective lens.
Results and discussion
Experimental evaluation of the parameters for optimal performance
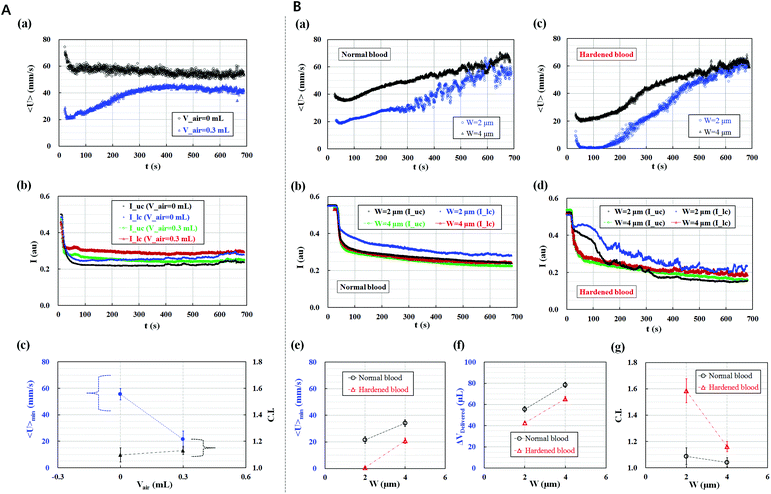
The effect of two parameters, namely, the air cavity in the disposable syringe (Vair) and minimum gap (W) in the microfluidic channel array, on the performance of the proposed method was quantitatively evaluated.The normal blood sample (Hct = 50%) was delivered into the microfluidic device using a syringe pump at a constant flow rate of 1 mL h−1, with and without an air cavity (Vair = 0–0.3 mL), to evaluate the air compliance effect on the effective deformability measurement of RBCs. Using the high-speed camera attached to the microscope, microscopy images were consecutively acquired to determine the temporal variations in the average velocity of blood flow (<U>) and image intensity of the blood sample in the upper and lower chambers. As shown in Fig. 2A-(a), when the disposable syringe was only filled with the normal blood sample (Vblood = 0.3 mL), the average velocity of blood flow remained constant for 700 s. However, when the syringe was equally filled with the normal blood sample (Vblood = 0.3 mL) and air (Vair = 0.3 mL), the average velocity of blood flow exhibited transient behavior for 400 s because of the air compliance effect.64 Thereafter, the average velocity of blood flow remained constant. This experimental result indicated that the average velocity of blood flow was strongly dependent on air compliance. Thus, the variation in the average velocity of blood could be used to monitor the variation in pressure in the microfluidic channel array effectively, under the effect of air compliance in the syringe. In addition, temporal variations in image intensity in the upper chamber (Iuc) and lower chamber (Ilc) were quantitatively evaluated by conducting digital image processing. The result is shown in Fig. 2A-(b). When the blood sample was delivered under the air compliance effect, the image intensity in each chamber increased. In other words, air compliance influenced the blood volume delivered into each chamber, which led to variations in image intensity. Thus, the air compliance effect was quantitatively compared using two parameters, namely, the minimum value of the average velocity of blood flow (<U>min) and C.I. As shown in Fig. 2A-(c), air compliance resulted in the decrease in the minimum value of the average velocity of blood flow. However, air compliance exerted a negligible effect on the C.I. In this study, all experiments were conducted after the disposable syringe was equally filled with the blood sample (Vblood = 0.3 mL) and air (Vair = 0.3 mL).
The effect of the minimum gap (W) in the microfluidic channel array was tested for the normal blood sample and hardened blood sample under identical sample delivery conditions of a constant flow rate of 1 mL h−1, blood volume of Vblood = 0.3 mL, and air cavity of Vair = 0.3 mL. The normal blood sample and hardened blood sample with 50% hematocrit were prepared by carefully adding 1× PBS solution into normal RBCs and hardened RBCs fixed with 0.15% GA solution. For normal blood samples, temporal variations in the average velocity of blood flow and image intensity in the upper and lower chambers were obtained with respect to the minimum gap (W) [(a) W = 2 μm, (b) W = 4 μm], respectively. As shown in Fig. 2B-(a) and (b), the minimum gap (W) significantly influenced the average velocity of blood flow and image intensity. The average velocity of blood flow notably decreased at the minimum gap of 2 μm, which led to the decrease in the minimum value of the average velocity of blood flow and blood volume delivered into the microfluidic device during a specific time duration (ts = 600 s).
In contrast, for the chemically fixed blood samples shown in Fig. 2B-(c) and (d), the average velocity of blood flow also significantly decreased at the minimum gap of 2 μm. Although the flow rate of blood was fixed at 1 mL h−1, blood flow stopped in the case of the minimum gap of 2 μm for the initial time of 100 s. Thereafter, the average velocity of blood flow gradually increased. In addition, the small minimum gap of 2 μm led to an increase in the image intensity in the lower chamber because of consecutive clogging of RBCs in the microfluidic channel array. Using the temporal variations in the average velocity of blood flow and image intensity in the two chambers with respect to the minimum channel gap, three parameters, namely, the minimum value of the average velocity of blood flow (<U>min), blood volume delivered (ΔVDelivered), and C.I., were estimated for the normal blood sample and hardened blood sample. As shown in Fig. 2C-(e)–(g), the hardened blood sample had lower minimum average velocity and blood volume delivered and a higher C.I. compared with the normal blood sample. Given that the minimum gap of 2 μm induced distinctive differences in the three parameters, the minimum gap of the microfluidic channel array was set to 2 μm for effective deformability measurement of blood samples.
Deformability measurement of human blood
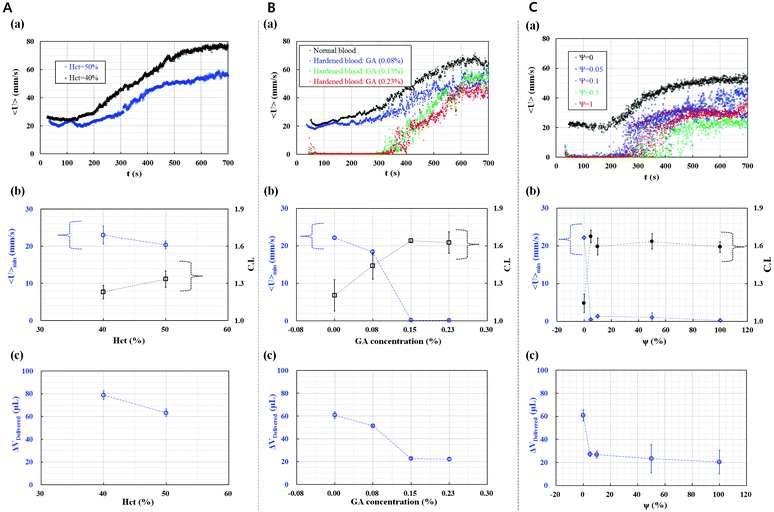
With the fixed air cavity of 0.3 mL in the disposable syringe and minimum gap of 2 μm in the microfluidic channel array, the performance of the proposed method was evaluated using human blood samples with different deformabilities.Two blood samples with hematocrit ranging from 40% to 50% were prepared by carefully adding normal RBCs into 1× PBS solution to evaluate the effect of hematocrit on the deformability of blood cells. As shown in Fig. 3A-(a), temporal variations in the average velocity of blood flow of the blood sample with 50% hematocrit were lower than those with 40% hematocrit. This finding implied that hematocrit increased blood viscosity,11 which contributed to the increase in hemodynamic resistance. Therefore, the average velocity of blood flow distinctively decreased at a higher level of hematocrit. Using temporal variations in the average velocity of blood flow and image intensity in the upper and lower chambers, the three parameters (<U>min, C.I., and ΔVDelivered) were quantitatively evaluated for two levels of hematocrit ranging from 40% to 50%. As shown in Fig. 3A-(b) and (c), C.I. slightly increased at a higher value of hematocrit (50%). However, no noticeable difference was observed with respect to hematocrit (i.e., p > 0.05). The minimum values of average velocity (<U>min) and blood volume delivered (ΔVDelivered) significantly decreased at a higher value of hematocrit (i.e., p < 0.05). Considering the previous result that the deformability of blood cells increased with respect to hematocrit,13,65 the three parameters, which are influenced by hematocrit, could be effectively used to monitor the variation in the deformability of blood samples. Furthermore, blood hematocrit should be constant to measure the deformability of blood cells accurately.
The membrane of normal RBCs was chemically fixed by immersing normal RBCs in GA solution to evaluate the deformability of human blood samples with different levels of RBC deformability. Four different concentrations of GA solution (C) [(a) C = 0, (b) C = 0.08%, (c) C = 0.15%, and (d) C = 0.23%] were prepared to obtain blood samples with different deformability levels. After normal RBCs and hardened RBCs were fixed by applying different concentrations of GA solution, the hematocrit of each blood sample was adjusted to 50% by adding hardened RBCs into 1× PBS solution. The RBCs hardened by the same concentration of GA solution were used to ensure the homogeneity of each blood sample. Fig. 3B-(a) shows the temporal variations in the average velocity of blood flow with respect to the concentration of GA solution. The blood sample with RBCs fixed with a low concentration of GA solution (0%–0.08%) had a relatively higher average velocity than that fixed with a high concentration of GA solution (0.15%–0.23%). In other words, the blood sample with RBCs fixed with a high concentration of GA solution had a low value of RBC deformability. Thus, RBCs could not easily pass through the microfluidic channel array, thereby increasing pressure in the microfluidic channel array. Thus, the average velocity of the blood sample was approximately 0 for a certain time period (∼300 s). However, the air cavity decreased continually because of the positive displacement of the syringe pump. When pressure in the syringe was greater than that in the microfluidic channel array, the average velocity gradually increased. As shown in Fig. 3B-(b), <U>min and C.I. were obtained with varying concentrations of GA solution. The minimum value of the average velocity of blood flow (<U>min) decreased, depending on the concentration of GA solution. However, the C.I. was larger for a higher concentration of GA solution. In addition, the blood sample fixed with a higher concentration of GA solution of greater than 0.15% had constant values of <U>min and C.I. This finding indicated that the proposed method demonstrated a technical difficulty in discriminating the two blood samples fixed with 0.15% and 0.23% GA solution. Given that the deformability of blood cells decreased at a higher concentration of GA solution, lower <U>min represented low deformability of the blood sample. In addition, a higher C.I. denoted that the blood sample was less deformable. From the temporal variations in average velocity, blood volume delivered (ΔVDelivered) into the microfluidic device was determined with respect to the concentration of GA solution. As shown in Fig. 3B-(c), the blood volume delivered into the microfluidic device decreased at the higher concentration of GA solution, which caused a decrease in the deformability of blood cells. The blood sample with low deformability demonstrated higher hemodynamic resistance. The minimum values of the average velocity of blood flow and blood volume delivered decreased. Therefore, the blood volume delivered into the microfluidic device could be used to classify the deformability of blood cells.
In addition, the proposed method was applied to measure the deformability of blood samples, which were partially mixed by normal RBCs and hardened RBCs, to quantitatively identify small differences in subpopulations of blood cells. Normal RBCs were fixed using 0.15% GA solution. The hematocrit of the hardened blood sample was carefully adjusted by adding the hardened RBCs into 1× PBS solution. The hematocrit of normal blood was adjusted by immersing normal RBCs in 1× PBS solution. Thereafter, five blood samples with different mixing ratio (ψ) [(a) ψ = 0, (b) ψ = 5%, (c) ψ = 10%, (d) ψ = 50%, and (e) ψ = 100%] were prepared by mixing the normal blood sample and hardened blood sample. The mixing ratio (ψ) is defined as the ratio of the volume of hardened blood (Vhard) to the summation of normal blood (Vnorm) and hardened blood [i.e., ψ = Vhard/(Vnorm + Vhard)]. In this study, ψ = 0 indicated that the blood sample was only composed of normal RBCs. In addition, ψ = 100% indicated that the blood sample was purely composed of RBCs fixed with 0.15% GA solution. Fig. 3C-(a) exhibited temporal variation in the average velocity of blood flow with respect to the mixing ratio (ψ). Except for the case of normal blood (ψ = 0), four blood samples with different mixing ratios had approximately 0 average velocity for a certain amount of time. Thereafter, the average velocity gradually increased. The blood sample with 5% mixing ratio (ψ = 5%) demonstrated similar behavior to the blood sample that was purely composed of hardened RBCs (ψ = 100%). On the other hand, to monitor the dynamic behaviors of RBCs (ψ = 5%) which pass through the microfluidic channel array, a high-magnification movie was captured by using an inverted optical microscope (Zeiss, Germany) equipped with 67× objective lens and a high-speed camera (see Movie-3, ESI†). As shown in the movie, several RBCs were sequentially clogged and stacked in front of the microfluidic channel arrays within a short period of time. However, after a little while, they passed through most of the channels with the help of highly developed pressure. The dynamic behaviors of RBCs in the microfluidic channel were well associated with the general trend of average velocity of blood flow (<U>) as shown in Fig. 3C-(a).
The minimum values of average velocity (<U>min) and C.I. were obtained by varying the mixing ratios (ψ) to quantitatively evaluate the deformability of blood samples. As shown in Fig. 3C-(b), <U>min of the normal blood sample was approximately 20 mm s−1. However, <U>min of the blood sample that was partially composed of hardened RBCs significantly decreased to approximately 2 mm s−1. The minimum value of the average velocity of blood flow (<U>min) was constant for mixing ratios ranging from 5% to 100%. In addition, the C.I. of the blood sample with hardened RBCs significantly increased, compared with that of the normal blood sample (ψ = 0). The C.I. remained constant in the extensive range of mixing ratios from ψ = 5% to ψ = 100%. Furthermore, the blood volume delivered into the microfluidic device was estimated with respect to the mixing ratio. As shown in Fig. 3C-(c), the delivered volume (ΔVDelivered) of the blood sample including the hardened RBCs notably decreased, compared with that of the normal blood sample. The variation in the blood volume delivered (ΔVDelivered) was similar to that of <U>min with respect to the mixing ratio. These results indicated that the proposed method could discriminate minor differences in deformability induced by subpopulations of blood samples.
Deformability measurement of malaria-infected blood samples
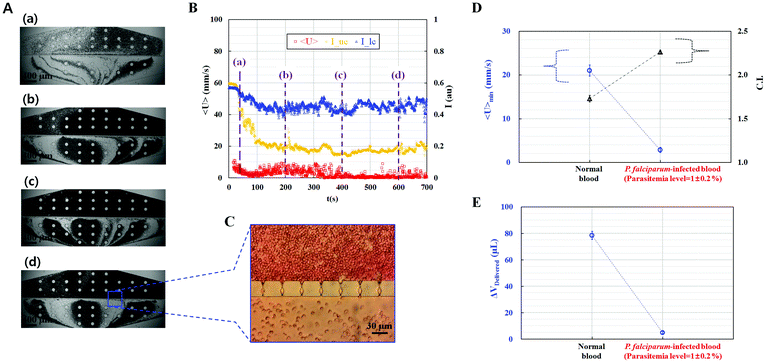
Malaria parasites induce morphological alterations in individual RBCs, which cause stiffening of the RBC membrane. Reduced RBC deformability results in the interruption of blood flow in microcirculation.51 In our previous study, we showed that ESR and viscosity are significantly related to the parasitemia level.25 However, classifying malaria-infected blood using ESR was difficult, especially when the parasitemia level was less than 10%. Instead of the ESR, the proposed method is suggested to evaluate the detection level of parasitemia effectively.For the clinical application of the proposed method, malaria-infected blood samples were prepared using human malaria (P. falciparum). The hematocrit of each blood sample was adjusted to 40% by carefully adding malaria-infected RBCs into 1× PBS solution.
P. falciparum-infected blood samples with different parasitemia levels ranging from 0.8% to 1.2% were prepared to validate the performance of the proposed method. Fig. 4A and Movie-4 (ESI†) show consecutive microscopy images of P. falciparum-infected blood samples captured at different time (t) [(a) t = 40 s, (b) t = 200 s, (c) t = 400 s, and (d) t = 600 s]. With the increase in the lapse of time, clogging of RBCs in the microfluidic channel array successively increased, which resulted in the increase in the RBC population in the upper chamber and decrease in the RBC population in the lower chamber. The average velocity <U> and image intensities (Iuc and Ilc) were obtained with respect to time to quantify the clogging behavior of the malaria-infected blood samples. As shown in Fig. 4B, the image intensity of the upper channel (Iuc) significantly decreased to approximately 0.2 because of consecutive clogging of RBCs in the microfluidic channel array. However, the image intensity of the lower chamber (Ilc) slightly decreased to approximately 0.45. In addition, the average velocity of the P. falciparum-infected blood sample significantly decreased to less than 2 mm s−1. After the experiment, images of the two chambers were captured by using a charge-coupled device camera. As shown in Fig. 4C, RBCs were stacked in the upper chamber of the microfluidic channel array because every channel of the microfluidic channel array was blocked. However, behind the microfluidic channel array, RBCs were rarely distributed. Using the information on the temporal variations in the average velocity (<U>) and image intensities (Iuc and Ilc) for each chamber, the minimum values of the average velocity of blood flow (<U>min) and C.I. were obtained for the normal blood sample and the P. falciparum-infected blood sample. As shown in Fig. 4D, the malaria-infected blood sample had a smaller <U>min and larger C.I. compared with the normal blood sample. As shown in Fig. 4E, the blood volume delivered of the malaria-infected blood sample was smaller than that of the normal blood sample. Based on a previous study,66 the low deformability of malaria-infected RBCs is influenced by their morphological changes.
From these experimental results, we believe that the human malaria parasite P. falciparum severely reduces RBC deformability, which hinders microcirculatory blood flow in vital organs. Furthermore, the proposed method could measure RBC deformability of blood samples using the three parameters <U>min, C.I., and ΔVDelivered, with high throughput and quantitative identification of subpopulations in RBCs.
Conclusion
In this paper, we propose an effective measurement method to measure RBC deformability by evaluating the temporal variations in the velocity field and image intensity of blood flow in a specific ROI because of successive clogging of RBCs in the microfluidic channel array. A microfluidic platform composed of a microfluidic device with multiple microfluidic channel arrays and an air cavity in a disposable syringe was used to accomplish this goal. RBC deformability was quantitatively evaluated using three parameters, namely, the minimum value of the average velocity of blood flow, blood volume delivered, and C.I.First, the effect of the three factors, namely, air cavity in the disposable syringe, minimum gap in the microfluidic channel array, and blood hematocrit, was quantitatively evaluated. RBC deformability was effectively measured at an air cavity of 0.3 mL and minimum gap of 2 μm. RBC deformability was also influenced by the hematocrit level of the blood sample.
Second, the performance of the proposed method was evaluated for human blood samples with homogeneous hardened RBCs. Normal RBCs were chemically fixed using four different concentrations of GA solution (0%–0.23%) to prepare various blood samples with different deformabilities. Compared with the normal blood sample, the blood sample with RBCs fixed with a higher concentration of GA solution had smaller values of average velocity and blood volume delivered, but a higher C.I. In other words, in the blood sample with less deformable RBCs, the minimum values of the average velocity of blood flow and blood volume delivered decreased, but the minimum value of the C.I. increased.
Third, the proposed method was applied to measure the deformability of blood samples, which were partially mixed with normal RBCs and hardened RBCs, to evaluate the quantitative identification of subpopulations of blood cells. The minimum values of the average velocity of blood flow (<U>min) and blood volume delivered in the microfluidic device (ΔVDelivered) were maintained at lower value, but the clogging index (C.I.) was remained at higher value, with the increase in the mixing ratio from 5% to 100%. Thus, the proposed method could detect minor differences in RBC deformability in subpopulations of blood samples.
Finally, as a clinical application, the deformability of RBCs infected by human malaria parasite P. falciparum, was quantitatively evaluated. Compared with normal RBCs, the three representative parameters of the P. falciparum-infected blood sample with a parasitemia level of 1% exhibited significant differences. In other words, the human malaria parasite (P. falciparum) severely reduces deformability. These experimental results indicated that the proposed method could effectively measure RBC deformability of blood samples using three parameters, namely, the minimum value of the average velocity of blood flow, C.I., and blood volume delivered into the microfluidic device, with high throughput and precise identification of subpopulations of blood cells. Furthermore, the deformability measurement of the blood samples (∼0.3 mL) with a high hematocrit level (∼50%) was completed within a short time period (∼10 min). In the near future, the proposed method may be used to quantitatively evaluate the deformability of various blood samples collected from patients with hematological diseases.
Acknowledgements
This work was supported by the National Research Foundation of Korea grant funded by the Korean Government (MSIP) (no. 2008-0061991). In addition, this study was supported by a research fund from Chosun University in 2014.References
- A. S. Popel and P. C. Johnson, Annu. Rev. Fluid Mech., 2005, 37, 43–69 CrossRef PubMed.
- A. M. Forsyth, J. Wan, P. D. Owrutsky, M. Abkarian and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10986–10991 CrossRef CAS PubMed.
- D. A. Fedosov, H. Lei, B. Caswell, S. Suresh and G. E. Karniadakis, PLoS Comput. Biol., 2011, 7, e1002270 CAS.
- A. M. Forsyth, J. Wan, W. D. Ristenpart and H. A. Stone, Microvasc. Res., 2010, 80, 37–43 CrossRef CAS PubMed.
- S. R. F. Whittaker and F. R. Winton, J. Physiol., 1933, 78, 339–369 CrossRef CAS.
- O. K. Baskurt, M. Boynard, G. C. Cokelet, P. Connes, B. M. Cooke, S. Forconi, F. Liao, M. R. Hardeman, F. Jung, H. J. Meiselman, G. Nash, N. Nemeth, B. Neu, B. Sandhagen, S. Shin, G. Thurston and J. L. Wautier, Clin. Hemorheol. Microcirc., 2009, 42, 75–97 Search PubMed.
- G. Tomaiuolo, Biomicrofluidics, 2014, 8, 051501 CrossRef PubMed.
- D. A. Fedosov, W. Pan, B. Caswell, G. Gompper and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11772–11777 CrossRef CAS PubMed.
- Y. J. Kang, E. Yeom and S.-J. Lee, Anal. Chem., 2013, 85, 10503–10511 CrossRef CAS PubMed.
- Y. J. Kang, E. Yeom and S.-J. Lee, Biomicrofluidics, 2013, 7, 054111 CrossRef PubMed.
- Y. J. Kang, J. Ryu and S.-J. Lee, Biomicrofluidics, 2013, 7, 044106 CrossRef PubMed.
- Y. J. Kang and S. Yang, Microfluid. Nanofluid., 2013, 14, 657–668 CrossRef CAS.
- Y. J. Kang and S.-J. Lee, Biomicrofluidics, 2013, 7, 054122 CrossRef PubMed.
- L. Campo-Deano, R. P. A. Dullens, D. G. A. L. Aarts, F. T. Pinho and M. S. N. Oliveira, Biomicrofluidics, 2013, 7, 034102 CrossRef PubMed.
- M. Brust, C. Schaefer, R. Doerr, L. Pan, M. Garcia, P. E. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS PubMed.
- G. A. M. Pop, L. L. A. Sisschops, B. Iliev, P. C. Struijk, J. G. v. d. Heven and C. W. E. Hoedemaekers, Biosens. Bioelectron., 2013, 41, 595–601 CrossRef CAS PubMed.
- M. Kim, A. Kim, S. Kim and S. Yang, Biosens. Bioelectron., 2012, 35, 416–420 CrossRef CAS PubMed.
- S. Cha, T. Shin, S. S. Lee, W. Shim, G. Lee, S. J. Lee, Y. Kim and J. M. Kim, Anal. Chem., 2012, 84, 10471–10477 CrossRef CAS PubMed.
- I. Doh, W. C. Lee, Y.-H. Cho, A. P. Pisano and F. A. Kuypers, Appl. Phys. Lett., 2012, 100, 173702 CrossRef PubMed.
- J. P. Beech, S. H. Holm, K. Adolfssona and J. O. Tegenfeldt, Lab Chip, 2012, 12, 1048–1051 RSC.
- Y. Zheng, E. S. Baghini, A. Azad, C. Wang and Y. Sun, Lab Chip, 2012, 12, 2560–2567 RSC.
- S. Chien, Annu. Rev. Physiol., 1987, 49, 177–192 CrossRef CAS PubMed.
- M. Brust, O. Aouane, M. Thie′baud, D. Flormann, C. Verdier, L. Kaestner, M. W. Laschke, H. Selmi, A. Benyoussef, T. Podgorski, G. Coupier, C. Misbah and C. Wagner, Sci. Rep., 2014, 4, 4348 CAS.
- J. M. Sherwood, J. Dusting, E. Kaliviotis and S. Balabani, Biomicrofluidics, 2012, 6, 024119 CrossRef CAS PubMed.
- Y. J. Kang, Y.-R. Ha and S.-J. Lee, Biomicrofluidics, 2014, 8, 044114 CrossRef PubMed.
- T. L. Fabry, Blood, 1987, 70, 1572–1576 CAS.
- C.-H. Cha, C.-J. Park, Y. J. Cha, H. K. Kim, D. H. Kim, Honghoon, J. H. Bae, J.-S. Jung, S. Jang, H.-S. Chi, D. S. Lee and H.-I. Cho, Am. J. Clin. Pathol., 2009, 131, 189–194 CrossRef PubMed.
- K. Ariyoshi, T. Maruyama, K. Odashiro, K. Askashi, T. Fujino and N. Uyesaka, Circ. J., 2010, 74, 129–136 CrossRef PubMed.
- A. Chabanel, D. Schachter and S. Chien, Hypertension, 1987, 10, 603–607 CrossRef CAS PubMed.
- G. A. Barabino, M. O. Platt and D. K. Kaul, Annu. Rev. Biomed. Eng., 2010, 12, 345–367 CrossRef CAS PubMed.
- C. Irace, C. Carallo, F. Scavelli, M. S. D. Franceschi, T. Esposito and A. Gnasso, Diabetes Care, 2014, 37, 488–492 CrossRef CAS PubMed.
- X. Li, W. Chen, Z. Li, L. Li, H. Gu and J. Fu, Trends Biotechnol., 2014, 32, 586–594 CrossRef CAS PubMed.
- D. D. Carlo, JALA, 2012, 17, 32–42 Search PubMed.
- Z. T. F. Yu, K. M. A. Yong and J. Fu, Small, 2014, 10, 1687–1703 CrossRef CAS PubMed.
- J. P. Shelby, J. White, K. Ganesan, P. K. Rathod and D. T. Chiu, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14618–14622 CrossRef CAS PubMed.
- D. A. Fedosov, B. Caswell, S. Suresh and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 35–39 CrossRef CAS PubMed.
- T. Wu and J. J. Feng, Biomicrofluidics, 2013, 7, 044115 CrossRef PubMed.
- M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Lab Chip, 2008, 8, 1062–1070 RSC.
- Y. Zheng, J. Nguyen, Y. Wei and Y. Sun, Lab Chip, 2013, 13, 2464–2483 RSC.
- J. Stuart, J. Clin. Pathol., 1985, 38, 965–977 CrossRef CAS PubMed.
- H. L. Reid, A. J. Barnes, P. J. Lock, J. A. Dormandy and T. L. Dormandy, J. Clin. Pathol., 1976, 29, 855–858 CrossRef CAS PubMed.
- O. K. Baskurt, M. R. Hardeman, M. Uyuklu, P. Ulker, M. Cengiz, N. Nemeth, S. Shin, T. Alexy and H. J. Meiselman, Biorheology, 2009, 46, 251–264 Search PubMed.
- S. Shin, Y. Ku, M.-S. Park and J.-S. Suh, Cytometry, Part B, 2005, 65, 6–13 CrossRef PubMed.
- W. Groner, N. Mohandas and M. Bessis, Clin. Chem., 1980, 26, 1435–1442 CAS.
- Y.-C. Chen, G.-Y. Chen, Y.-C. Lin and G.-J. Wang, Microfluid. Nanofluid., 2010, 9, 585–591 CrossRef CAS.
- H. M. Wyss, D. L. Blair, J. F. Morris, H. A. Stone and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061402 CrossRef PubMed.
- S. C. Gifford, M. G. Frank, J. Derganc, C. Gabel, R. H. Austin, T. Yoshida and M. W. Bitensky, Biophys. J., 2003, 84, 623–633 CrossRef CAS PubMed.
- P. Preira, V. Grandne, J.-M. Forel, S. Gabriele, M. Camaraa and O. Theodoly, Lab Chip, 2013, 13, 161–170 RSC.
- W. Beattie, X. Qin, L. Wang and H. Ma, Lab Chip, 2014, 14, 2657–2665 RSC.
- M.-E. Myrand-Lapierre, X. Deng, R. R. Ang, K. Matthews, A. T. Santoso and H. Ma, Lab Chip, 2015, 15, 159–167 RSC.
- J. P. Shelby, J. White, K. Ganesan, P. K. Rathod and D. T. Chiu, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14618–14522 CrossRef CAS PubMed.
- Y. Park, M. Diez-Silva, G. Popescu, G. Lykotrafitis, W. Choi and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13730–13735 CrossRef CAS PubMed.
- D. R. Gossett, H. T. K. Tse, S. A. Lee, Y. Ying, A. G. Lindgren, O. O. Yang, J. Rao, A. T. Clark and D. D. Carlo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7630–7635 CrossRef CAS PubMed.
- E. Du, S. Ha, M. Diez-Silva, M. Dao, S. Suresh and A. P. Chandrakasan, Lab Chip, 2013, 13, 3903–3909 RSC.
- S.-B. Huang, Y. Zhaob, D. Chen, H.-C. Lee, Y. Luo, T.-K. Chiu, J. Wang, J. Chen and M.-H. Wu, Sens. Actuators, B, 2014, 190, 928–936 CrossRef CAS.
- H. Bow, I. V. Pivkin, M. Diez-Silva, S. J. Goldfless, M. Dao, J. C. Niles, S. Sureshb and J. Han, Lab Chip, 2011, 11, 1065–1073 RSC.
- S. Huang, A. Undisz, M. Diez-Silva, H. Bow, M. Dao and J. Han, Integr. Biol., 2013, 5, 414–422 RSC.
- A. Adamo, A. Sharei, L. Adamo, B. Lee, S. Mao and K. F. Jensen, Anal. Chem., 2012, 84, 6438–6443 CrossRef CAS PubMed.
- L. M. Lee and A. P. Liu, Lab Chip, 2015, 15, 264–273 RSC.
- Q. Guo, S. Park and H. Ma, Lab Chip, 2012, 12, 2687–2695 RSC.
- Q. Guo, S. P. Duffy, K. Matthews, A. T. Santoso, M. D. Scott and H. Ma, J. Biomech., 2014, 47, 1767–1776 CrossRef PubMed.
- H. W. Hou, A. A. S. Bhagat, A. G. L. Chong, P. Mao, K. S. W. Tan, J. Han and C. T. Lim, Lab Chip, 2010, 10, 2605–2613 RSC.
- E. Yeom, Y. J. Kang and S.-J. Lee, Biomicrofluidics, 2014, 8, 034110 CrossRef PubMed.
- Y. J. Kang and S. Yang, Lab Chip, 2012, 12, 1881–1889 RSC.
- J. A. Long, A. Undar, K. B. Manning and S. Deutsch, ASAIO J., 2005, 51, 563–566 CrossRef PubMed.
- S. Jayavanth, K. Jagadeesan and M. Singh, Clin. Hemorheol. Microcirc., 2004, 31, 257–266 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5an01988e |
| This journal is © The Royal Society of Chemistry 2016 |