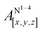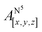Open Access Article
Open Access ArticleExploring template-bound dinuclear copper porphyrin nanorings by EPR spectroscopy†
Sabine
Richert
 a,
Jonathan
Cremers
b,
Harry L.
Anderson
a,
Jonathan
Cremers
b,
Harry L.
Anderson
 b and
Christiane R.
Timmel
*a
b and
Christiane R.
Timmel
*a
aCentre for Advanced Electron Spin Resonance (CAESR), University of Oxford, South Parks Road, Oxford, OX1 3QR, UK. E-mail: christiane.timmel@chem.ox.ac.uk
bChemistry Research Laboratory, University of Oxford, Mansfield Road, Oxford, OX1 3TA, UK
First published on 2nd August 2016
Abstract
Electron paramagnetic resonance (EPR) spectroscopy has been used to study the molecular geometry as well as metal–ligand interactions in ten-membered porphyrin nanorings (c-P10Cu2) containing two copper and eight zinc centers. The presence of copper in the structures allows intramolecular interactions, including dipolar interactions between electron spins and hyperfine interactions to be quantified. Results obtained for c-P10Cu2 samples bound to two molecular templates with four or five binding sites, respectively, are compared to those obtained for a sample of the porphyrin ring in the absence of any templates. It is shown that the observed lower binding affinity of the nitrogen ligand to copper as compared to zinc has a strong impact on the geometries of the respective template-bound c-P10Cu2 structures. The interaction between the central copper atom and nitrogen ligands is weak, but pulsed EPR hyperfine techniques such as ENDOR and HYSCORE are very sensitive to this interaction. Upon binding of a nitrogen ligand to copper, the hyperfine couplings of the in-plane nitrogen atoms of the porphyrin core are reduced by about 3 MHz. In addition, the copper hyperfine couplings as well as the g-factors are altered, as detected by continuous wave EPR. DFT calculations of the hyperfine coupling tensors support the assignment of the measured couplings to the nuclei within the structure and reproduce the experimentally observed trends. Finally, Double Electron Electron Resonance (DEER) is used to measure the distances between the copper centers in a range between 2.5 and 5 nm, revealing the preferred geometries of the template-bound nanorings.
1 Introduction
Recent advances in supramolecular chemistry have paved the way for efficient synthetic routes to complex structures on the nanometer scale. In many cases porphyrin units are used as building blocks.1 One of these synthetic approaches which has proven particularly powerful for the synthesis of cyclic porphyrin assemblies2,3 is Vernier templating.4,5 In this context, molecular templates containing nitrogen ligands in a star-shaped geometric arrangement are employed. Since these ligands have a high affinity for the central metal of the porphyrin units of a chain-like porphyrin precursor molecule, the template imposes a cyclic geometric arrangement onto the precursor which can then be transformed into the product in a final synthetic step involving ring-closure. The success of this approach crucially depends on the nature of the intermolecular metal–ligand interactions. To develop and improve synthetic strategies, precise knowledge of the relevant intermolecular interactions is of paramount importance.Techniques that have been used so far for the characterization of such interactions include nuclear magnetic resonance (NMR), UV-vis spectroscopy and small angle X-ray scattering (SAXS). Using these methods, metal–ligand binding constants could, for example, be obtained for a series of linear zinc–porphyrin oligomers.6–10 For structural characterization, X-ray diffraction is most frequently employed, but the technique has the disadvantage of requiring the availability of single crystals. Further, in the solid state the investigated compounds might adopt a different conformation to that in solution where most experiments are performed and larger structures cannot be crystallized easily. Similarly, NMR measurements can become difficult to analyze for larger complexes and the presence of any paramagnetic metals can adversely affect the use of NMR for characterization.
For the study of large systems containing paramagnetic centers (such as copper), EPR is frequently the technique of choice. Local changes in the electronic or nuclear environment of the paramagnetic centers, which occur upon interaction with any ligand, can be probed sensitively.11,12 Furthermore, EPR is also suitable for carrying out distance measurements between paramagnetic centres in the nanometer range13,14 and can thus give precise information about molecular structure. Since the measurements can be carried out in frozen solution, no crystallization of the structures is necessary. In addition, information about the flexibility of any investigated structures can be obtained in form of distance distributions.15,16 Finally, EPR benefits from a much higher sensitivity than NMR, so that smaller sample volumes and concentrations are required.
In this study, a ten-membered porphyrin nanoring containing two copper centers and eight zinc centers (c-P10Cu2)17 is investigated in detail by a variety of EPR techniques. The ring is studied either in isolation or in the presence of molecular templates providing either four (T4) or five (T5) potential binding sites for the central metal of the porphyrin units to form the structures proposed in Fig. 1, and henceforth referred to as c-P10Cu2, c-P10Cu2·(T4)2, and c-P10Cu2·(T5)2.
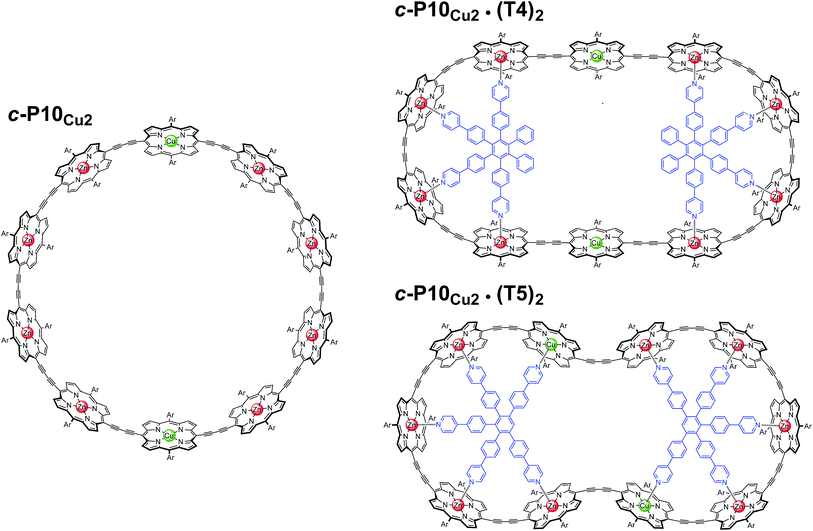 | ||
| Fig. 1 Chemical structures of c-P10Cu2, c-P10Cu2·(T4)2, and c-P10Cu2·(T5)2 (Ar = 3,5-di-tert-butylphenyl). | ||
The synthesis of the c-P10Zn10 nanoring was reported previously.18,19 Since the precursor to c-P10Cu2 is a linear pentamer containing one copper porphyrin as the central unit, the two copper porphyrin units in the ten-membered ring will necessarily be sitting opposite each other, separated by four zinc porphyrin units on either side. The positions of the copper centers in the free ring are therefore well defined. However, in the template-bound structures, three conceivable locations of the copper centers with respect to the structure imposed by the templates result in three different inter-copper distances, as illustrated in Fig. 2. The geometries and resulting distances for the different conformations indicated in the figure have been inferred from the distances obtained by molecular modeling of a c-P10Zn10·(T5)2 structure as explained in more detail in the ESI.†
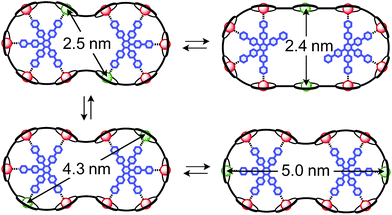 | ||
| Fig. 2 Possible conformations of c-P10Cu2·(T5)2 leading to different distances between the two copper centers. | ||
In this study, we determine the relative populations of these different conformations and elucidate the factors that control the preferred location of the copper units in the template-bound structures. The weaker binding of copper to axial pyridine ligands explains the observed populations of conformers.
2 Results and discussion
Unless otherwise stated, all EPR measurements were performed on 0.2 mM samples in deuterated toluene. Details on the sample preparation and experimental conditions are given in the ESI.† The template-bound structures were prepared by adding an excess of template to a solution of c-P10Cu2 so that two molecular templates are bound per c-P10Cu2 nanoring as schematically illustrated in Fig. 1. The binding of the templates was verified by UV-vis spectroscopy. Typical UV-vis spectra confirming the binding of the molecular templates T4 and T5 to c-P10Cu2 are shown in Fig. S2 to S5 in the ESI.†2.1 Continuous wave EPR
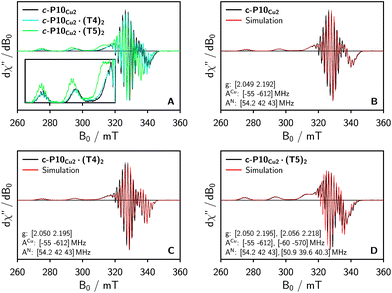
To characterize the electronic and nuclear environment around the copper centers in the c-P10Cu2 structures, continuous wave (cw) EPR spectroscopy was employed at X-band (9.5 GHz). The spectra obtained for the different c-P10Cu2 samples in frozen solution are shown in Fig. 3A; details of the experimental parameters and data processing are given in the ESI.†The spectrum of c-P10Cu2 without template (Fig. 3A, black line) essentially coincides with the spectrum of a typical copper porphyrin monomer as reported in the literature20,21 and shown for a copper porphyrin monomer (P1Cu) with the same side groups as present in c-P10Cu2 in the ESI† of this paper (Fig. S20): the interaction of the unpaired electron of copper with its nuclear spin of 3/2 results in four lines, two of which are clearly resolved at the low-field side of the spectrum (out-of-plane or z orientation). In the porphyrin plane (xy), the interaction of the unpaired electron spin with the four nitrogen atoms with I = 1 leads to additional (only partially resolved) hyperfine structure. The pronounced g- and A-tensor anisotropy results in a fairly broad, axially symmetric, spectrum.
The strong resemblance of the spectrum of c-P10Cu2 to that of a typical copper porphyrin monomer is not surprising since the two copper atoms in the structure are too far apart (cf.Fig. 2) for dipolar interactions between the electron spins to cause any visible changes to the EPR spectrum.
Also the spectrum of c-P10Cu2·(T4)2 strongly resembles that of a typical copper porphyrin monomer as can be seen from Fig. 3A (blue line). The g-values and hyperfine couplings of c-P10Cu2 and c-P10Cu2·(T4)2 are indistinguishable, based on a simple visual inspection of the spectra, indicating that the local nuclear and electronic structure at the copper centers is very similar in both cases.
However, compared to c-P10Cu2 and c-P10Cu2·(T4)2, the EPR spectrum of c-P10Cu2·(T5)2 is clearly different (cf. green spectrum in Fig. 3A). Most obvious is the increase in the g-values, in particular g‖, shifting the whole spectrum to lower fields. Additionally, the copper hyperfine couplings are altered with respect to c-P10Cu2 and c-P10Cu2·(T4)2, as exemplified by the reduced splitting between the two outmost copper transitions which are resolved at the low-field side of the spectrum.
Since it is likely that the observed changes in the spectrum of c-P10Cu2·(T5)2 arise from an interaction of the copper with the pyridine nitrogen of the fifth template leg, 14N pulsed electron nuclear double resonance (ENDOR) experiments were carried out to gain further information on the metal–ligand interaction by measurement of the nitrogen hyperfine couplings.
2.2 ENDOR
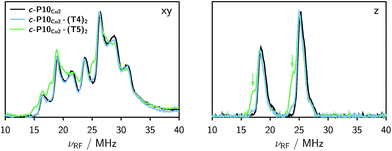
The Davies 14N ENDOR spectra of c-P10Cu2 with and without templates are shown in Fig. 4 for two different field positions corresponding to the xy and z orientations, respectively. A field-swept EPR spectrum showing the exact positions at which the ENDOR spectra were taken is shown in the ESI† (Fig. S6). Again, it is observed that the spectra of c-P10Cu2 (black) and c-P10Cu2·(T4)2 (blue) are almost identical, but clearly different from the spectrum of c-P10Cu2·(T5)2 (green). Most crucially the ENDOR spectra of c-P10Cu2·(T5)2 contain an additional minor contribution of a species with slightly reduced nitrogen hyperfine couplings (highlighted by arrows in the spectra for the z-orientation in Fig. 4).2.3 DFT calculations
Interpretation of the observed trends was aided by density functional theory (DFT) calculations allowing also the assignment of the experimentally determined hyperfine couplings. Additionally, the orientations of the hyperfine and g-tensors within the molecular frame were obtained which are needed for a precise numerical simulation of the experimental data. The structures of a copper porphyrin monomer (P1Cu) and a copper porphyrin monomer with a pyridine ligand bound to copper (P1Cu·py) were first optimized in Turbomole V6.122,23 under C2 symmetry constraint using DFT/B3LYP in combination with the TZVP basis set,24 RI-approximation25 and an empirical dispersion correction to the energies.26,27The hyperfine and nuclear quadrupole interaction tensors and their orientation were then calculated for the optimized structures using the program package ORCA V3.0.28 DFT calculations with the B3LYP functional were performed using the EPR II basis set29 for H, C, and N and the Wachters basis30 on copper. This combination of functional and basis sets was chosen since it was shown to yield computational results that are reasonably close to the corresponding experimental values in a series of very detailed theoretical investigations on hyperfine coupling parameters for comparable copper compounds with and without axial ligands.31–33 Although the B3LYP functional is known to overestimate the nitrogen couplings,31 the trends and relative variations in the individual values are informative since the computational error on these properties seems to be fairly systematic. For the copper hyperfine couplings DFT/B3LYP was shown to perform well,32 however the A⊥ value is generally predicted to be much smaller than experimentally observed even if relativistic and spin–orbit contributions are accounted for. The error on the calculated g-values is normally large, but trends can safely be predicted.
Table 1 shows the calculated hyperfine coupling constants for the four nitrogens in the porphyrin plane (N1–4) and, in the case of P1Cu·py, also for the pyridine nitrogen (N5). Here, x, y and z refer to the tensor components along the A-tensor axes of the respective nuclei in P1Cu and P1Cu·py, whose orientation is graphically depicted within the molecular frame of the copper porphyrin in the ESI† (Fig. S23 and S24).
Several observations can be made from the calculated nitrogen hyperfine couplings. First of all, it is noted that the hyperfine coupling constants of the pyridine nitrogen itself are very small and therefore do not contribute to the experimental 14N Davies ENDOR spectra shown above. Furthermore, it is observed that the in-plane nitrogen couplings are reduced by about 3 MHz in all directions upon binding of the pyridine ligand. This reduction in the in-plane hyperfine couplings explains the additional peaks observed in the ENDOR spectra of c-P10Cu2·(T5)2: the experimentally observed spectrum seems to be a linear combination of two spectra resulting from copper porphyrin units in the presence and absence of an axial pyridine ligand in their proximity, respectively.
Quadrupolar couplings for all nitrogen nuclei as well as the corresponding tensor orientations were also calculated and are shown in the ESI† (Table S2). Furthermore, upon binding of a pyridine ligand to the central copper atom of the porphyrin unit, DFT predicts an increase in g-values by a factor of 1.003 for g⊥ and 1.007 for g‖ and a decrease in the out-of-plane copper hyperfine coupling, A‖, by a factor of 1.05, which is in very close agreement with the parameter changes observed experimentally between P1Cu and P1Cu·py shown in the ESI† (Fig. S15 and S18–S21, Table S1) where relative values of 1.003, 1.010 and 1.07 were obtained for the increase in g⊥ and g‖ and the decrease in A‖, respectively.‡
2.4 Spectral simulations
Based on the results from DFT, in combination with the observations from ENDOR and cw EPR, it can thus be concluded that two species with different nitrogen and copper hyperfine couplings and different g-values contribute to the spectra of c-P10Cu2·(T5)2 (and to a lesser extent also to those of c-P10Cu2·(T4)2). As a consequence, the respective ENDOR and cw-EPR spectra were simulated as a linear combination of two contributions. The hyperfine, nuclear quadrupole, and g-values were taken from simulations of the ‘pure’ spectra of P1Cu and P1Cu·py shown in the ESI† (Fig. S18, S19, S21 and Table S1) and only the relative weights of the contributions were adapted to fit the spectra of the template-bound c-P10Cu2 structures. The numerical simulations of the spectra were carried out using the MATLAB34 package EasySpin.35 A reasonable agreement was obtained in all cases and the corresponding simulations for the three c-P10Cu2 samples are shown in Fig. 3B–D and the ESI† (Fig. S7–S9).From the simulations of the ENDOR spectra shown in Fig. S8 and S9 in the ESI,† a quantification of the additional contribution to the spectra of the template-bound structures, arising from an interaction between copper and the pyridine ligand of the template, can be attempted. Although the error on the values is difficult to determine, a reasonable estimate of the relative contributions of template bound vs. unbound copper units can be obtained. The best fits to the experimental ENDOR spectra as shown in the ESI† were obtained for relative contributions of bound copper of ≈5% for c-P10Cu2·(T4)2 and ≈30% for c-P10Cu2·(T5)2.
2.5 HYSCORE
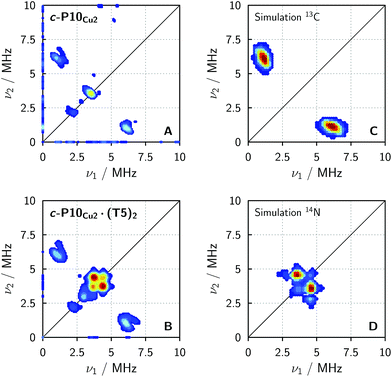
In order to confirm the presence of the small coupling between the copper ion and the pyridine nitrogen of the template predicted by DFT, X-band HYSCORE36 measurements were performed on c-P10Cu2 and c-P10Cu2·(T5)2 in toluene at 15 K.§ All experimental parameters and details on the data treatment are given in the ESI.†Fig. 5 shows the (+/+) quadrant of the experimental HYSCORE spectra of c-P10Cu2 (top left, A) and c-P10Cu2·(T5)2 (bottom left, B). No relevant signals were observed in the (−/+) quadrant. Strong 1H signals were detected on the diagonal close to 14 MHz in both spectra but are not shown for clarity. No other signals bigger than 10 MHz were observed. A comparison of the spectra of the two samples reveals that all signals observed for c-P10Cu2, are also present in the spectrum of c-P10Cu2·(T5)2. However, in addition, two prominent cross peaks at (4.4, 3.8) and (3.8, 4.4) MHz are detected in the latter spectrum, which could be indicative for weak coupling to a nitrogen ligand.
To confirm the assignment of the cross peaks at (4.4, 3.8) and (3.8, 4.4) MHz in the spectrum of c-P10Cu2·(T5)2 and to identify the nature of the cross peaks at (1, 6) and (6, 1) MHz observed in both samples, numerical simulations were performed using EasySpin. To simulate the expected HYSCORE spectrum for the coupling of copper to the template we used the hyperfine and nuclear quadrupole couplings obtained from DFT calculations for the pyridine nitrogen of P1Cu·py (A[x y z] = [−1.15 −1.14 −0.29] MHz, Q[x y z] = [0.80 1.30 −2.10] MHz). The simulation is shown in Fig. 5 (bottom right, D) and reproduces the observed experimental features convincingly. The cross peaks at (4.4, 3.8) and (3.8, 4.4) MHz can thus be assigned to the double-quantum peaks arising from the coupling of copper to the 14N nucleus of an axial pyridine ligand in c-P10Cu2·(T5)2.
To explain the rather intense cross peaks at (1, 6) and (6, 1) MHz, further simulations were carried out. Since the magnitude of the coupling corresponding to those cross peaks was most indicative of nearby 13C nuclei, DFT calculations were carried out for the 13C isotopes of all carbon atoms present in P1Cu·py. A total of 16 carbon atoms exhibit (almost equally large) couplings to copper with an average DFT hyperfine interaction of A = [4.0 5.0 7.2] MHz. Thence, although the 13C natural abundance is low, approximately 16% of all copper porphyrin units exhibit 13C couplings which contribute to the HYSCORE spectrum, resulting in the observed intense cross peaks. The simulations were carried out taking averaged values from DFT, representative for the 16 contributing 13C nuclei (A = [4.0 5.0 7.2] MHz) and are shown in Fig. 5 (top right, C).
2.6 DEER
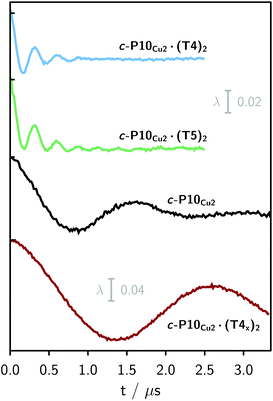
Finally, four-pulse double electron–electron resonance (DEER)37 measurements at 15 K were carried out at Q-band frequencies to obtain information about the geometry of the compounds and the location of the Cu-centers with respect to the structure imposed by the template in the template-bound structures (cf.Fig. 2). DEER spectroscopy may also provide information on the flexibility of the compounds as demonstrated previously for nitroxide-labeled porphyrin-based molecular wires38 and Cu porphyrin model systems.39 In this study the dipolar interaction between the two copper centers allows the determination of accurate distances without the need to attach any spin-labels to the structures. In the experiment, the pump pulse position was chosen to coincide with the maximum of the field swept EPR spectrum, and a detection pulse frequency offset of +100 MHz was applied. All further experimental details can be found in the ESI.†The top three traces in Fig. 6 show the background-corrected experimental DEER data obtained for the three c-P10 structures in Fig. 1 under identical experimental conditions. The corresponding raw data are shown in the ESI† (Fig. S12). Clear dipolar modulations can be discerned in all traces, pointing towards Cu⋯Cu separations of roughly 2.5 nm in the template-bound structures and 4.3 nm in c-P10Cu2. Since the modulations are well defined in all cases, it can be concluded that the distance distributions are rather narrow and the structures consequently fairly rigid.
The differences in the traces between c-P10Cu2·(T4)2 and c-P10Cu2·(T5)2 might arise from a larger contribution of longer Cu⋯Cu distances in the latter sample. It can, however, clearly be seen that, in both cases, the shortest of the three possible Cu⋯Cu distances (cf.Fig. 2) dominates the appearance of the dipolar evolution time trace.
As the copper samples exhibit a strongly axial symmetry of the g-tensor, and pump and observer pulses were chosen to excite spins in the g⊥ part of the spectrum, inter-spin distances may be obtained from the traces using Tikhonov regularization39,40 as implemented in DeerAnalysis.41 Previous analysis on Cu⋯Cu systems has shown that, under these conditions, the Pake pattern will always contain a contribution from the perpendicular component of the dipolar coupling and therefore extraction of a distance distribution using Tikhonov regularization will always yield a distance peak at the true inter-copper distance although other peaks may also be present in the distance distribution at shorter distances. In the Tikhonov analysis of the data presented here, the distance distributions yielded only one major peak at the distance expected from molecular modeling, indicating that the effects of orientation selection42–46 are negligible. In addition, data were obtained in different positions of the g⊥ component of the spectrum and resulted in identical distances and distance distributions (cf. Fig. S13 in the ESI†).
The distance distributions obtained from this model-free analysis of the experimental data are shown for all samples in Fig. 7.¶ The best fit to the experimental data corresponding to these distributions is shown in the ESI† in Fig. S11.
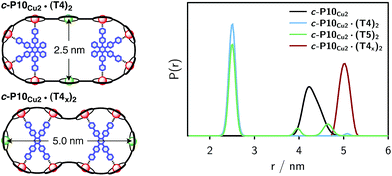 | ||
| Fig. 7 Distance distributions for the investigated samples obtained using Tikhonov regularization as implemented in DeerAnalysis after correction for g-factor differences. | ||
For c-P10Cu2 a distribution centered at 4.28 nm is obtained. Available crystal structures47 and DFT calculations performed for a porphyrin dimer, suggest a Zn⋯Zn distance of 1.35 nm resulting in a diameter of 4.3 nm for a perfectly circular 10-membered porphyrin ring. The experimentally obtained distance is in excellent agreement with this expected diameter, which confirms that the ring without template is fairly shape persistent in solution. The distance distribution of c-P10Cu2 is, however, broader (σr ∼ 0.2 nm) compared to those of the template-bound structures, indicating a slightly larger flexibility of the free c-P10Cu2 ring.
The distance distributions for the template-bound structures both show a major contribution of a well-defined short distance of 2.50 nm with a width of σr = 0.08 nm. This observed distance clearly corresponds to the shortest ones indicated in Fig. 2 (top). X-ray crystallography of a template-bound six-membered Zn–porphyrin nanoring,48 showed a radius of 1.22 nm measured between the Zn ions. Imposing this geometric constraint on the template-bound structures proposed in Fig. 2 (top), results in a predicted Cu⋯Cu distance (approx. 2.50 nm) in excellent agreement with the experimentally determined value.
For c-P10Cu2·(T4)2, the distance of 2.50 nm seems to be the major contribution with a relative importance of >98%. On the contrary, in the sample of c-P10Cu2·(T5)2, longer distances also appear to contribute. The contribution of the shortest distance is reduced to roughly 80%, and two additional peaks at 4.0 and 4.6 nm with relative contributions of 5% and 15% are obtained as a result from the analysis. These longer distances which, for reasons outlined below, should not be over-interpreted, seem somewhat shorter than the ones expected from a structural model of the complex as shown in Fig. 2. The discrepancy could arise from bending of the structure as proposed in the literature49 which would considerably shorten the longer distances. Twisting by large angles, however, appears unlikely, given that the shortest of the observed distances is in very good agreement with the expected value for a ‘planar’ structure and would be significantly shortened by any twisting of the structure. With respect to c-P10Cu2·(T4)2 there is no experimental evidence for either twisting or bending of the structure, given that a minor contribution to the distance distribution at a distance of roughly 5 nm is observed which is in excellent agreement with the expected value for a ‘planar’ structure.
It is important here to note that only the shortest distance in the template-bound structures and its distribution can be determined with high precision. The errors on any additional longer distances and their distributions are expected to be large, due to their small relative contribution to the time evolution and the limited length of the DEER trace. Furthermore, the presented analysis is dependent on the background correction used. In this respect it is not possible to reliably analyze the observed differences between c-P10Cu2·(T4)2 and c-P10Cu2·(T5)2 in more detail. It can be stated safely, however, that a larger percentage of longer distances contributes to the DEER signal in the case of c-P10Cu2·(T5)2, as compared to c-P10Cu2·(T4)2, leading to the observed ‘uplift’ in the evolution of the DEER trace of c-P10Cu2·(T5)2 at early times (<0.7 µs).
As only the shortest possible Cu⋯Cu distance is observed experimentally for c-P10Cu2·(T4)2, we can conclude that the binding affinity of the pyridine ligands of the template legs to the central metal of the porphyrin units is considerably smaller for copper than it is for zinc. As a consequence, and due to the geometry of the T4 template, the conformation corresponding to the shortest of the three possible Cu⋯Cu separation distances is largely preferred. This result suggests that it should be possible to influence the preferred location of the copper porphyrin units by modification of the template geometry. To test this hypothesis, we conducted DEER measurements on a molecular complex between c-P10Cu2 and a different, ‘X-shaped’, isomer of T4, referred to as T4x and introduced in Fig. 7. If the geometry of the rings is indeed determined by preferential binding of the template legs to Zn, the two Cu centers in the complex-bound structure should now be separated by the longest of the three possible distances.
The DEER trace and the corresponding distance distribution for c-P10Cu2·(T4x) obtained from Tikhonov regularization are shown Fig. 6 and 7, respectively. A well-defined modulation of the DEER trace is observed for this sample corresponding to a mean distance of 5.0 nm, confirming that the Cu sites are now separated by the largest possible Cu⋯Cu distance. No contributions of shorter distances are discernible. The result clearly shows that the preferred location of the copper porphyrin units is indeed governed by the differences in binding strength between zinc and copper to axial nitrogen ligands and opens up the possibility to control specific distances and thus geometries in supramolecular complexes at a molecular level.
3 Conclusions
EPR is very sensitive to small changes in the local environment of the probed paramagnetic centers so that even weak metal–ligand interactions can be selectively detected and characterized, as has been demonstrated in previous studies involving transition metals compounds containing cobalt or copper.11,50In this study, the copper centers in a ten-membered porphyrin nanoring were shown to interact with axial nitrogen ligands of molecular templates. Upon binding of the ligand, the hyperfine coupling constants of the in-plane nitrogen atoms of the copper porphyrin units are reduced by about 3 MHz (∼5%) as detected by Davies 14N ENDOR and confirmed by DFT calculations. The coupling of the copper electron spin to the 14N nucleus of the pyridine ligand is much smaller and could only be observed using HYSCORE.
Results from cw EPR spectroscopy revealed that, upon binding of the pyridine ligand, the g-values and copper hyperfine couplings are also altered. The increase in g-values and decrease in A‖ of copper were confirmed by DFT. The in-plane hyperfine coupling of copper, A⊥, is difficult to determine experimentally due to the strong overlap of features in the cw EPR spectra in the relevant region. In addition, the agreement of the experimental values for A⊥ with DFT calculations is rather poor, so that no conclusions on the trend regarding the changes in A⊥ upon ligand binding could be obtained. Recently, a new method for the determination of copper hyperfine coupling constants involving ultra-wideband excitation with frequency-swept chirp pulses has been developed51 which could be used to provide this additional information and is expected to find many useful applications in this context in the near future.
DEER measurements on the c-P10Cu2 samples showed that the shortest of the three possible Cu⋯Cu distances dominates in the template-bound structures c-P10Cu2·(T4)2 and c-P10Cu2·(T5)2, a direct consequence of the fact that zinc has a higher affinity of binding an axial pyridine ligand than copper. The geometry of c-P10Cu2·(T4)2 can therefore be determined: the eight legs of the two templates in c-P10Cu2·(T4)2 will preferentially bind to zinc, leaving the central positions, corresponding to the shortest distance, for the copper porphyrin units. Since all template legs are bound to zinc, virtually no interaction of pyridine ligands with copper could be detected in either the cw EPR or ENDOR spectra of c-P10Cu2·(T4)2.
In view of the structure of c-P10Cu2·(T5)2, the question of where the fifth template leg is pointing arises. DEER experiments showed that the shortest possible Cu⋯Cu distance is still by far the main contribution, indicating that the copper porphyrin units are preferentially sitting in the center of the structure. Due to the higher binding affinity of pyridine to zinc, it can be assumed that four of the five pyridine legs are bound to zinc. The fifth leg might now either point in the direction of the copper porphyrin unit, or extend towards the center of the structure.
Some speculation on the geometry of c-P10Cu2·(T5)2 may be attempted based on the semi-quantitative findings from DEER and ENDOR. Analysis of the ENDOR spectra (z-orientation), indicates that approximately 30% of all copper centers are bound to pyridine. Bearing in mind the uncertainty in the interpretation of the longer distances (and especially their distributions) due to the limited length of the DEER trace, the contribution of the short 2.5 nm distance obtained from DeerAnalysis amounts to at least 80% in c-P10Cu2·(T5)2. Longer distances correspond to complexes in which copper is sitting in one of the outer positions, where it is most likely bound to a pyridine leg. Thus, the contribution of longer distances accounts for most of the intensity of the second peak observed in ENDOR. The discrepancy found between the DEER and ENDOR percentages is hardly surprising given the large uncertainty in the determination of either quantity, although it might be speculated that in some cases the copper atoms sitting in the center of the structure are bound to the fifth template leg which could account for this difference. In most (if not all) cases, however, it appears that the fifth template leg does not bind to copper, but extends towards the center of the structure.
The difference in metal–ligand binding strength between copper and zinc was shown to have a dominant impact on the geometry of the binuclear copper porphyrin structures formed upon template addition. To further support this finding, additional experiments on a complex between c-P10Cu2 and a different, X-shaped, isomer of T4 were carried out. As predicted from the geometric shape of the template and the ligand binding arguments above, only the largest Cu⋯Cu distance of 5.0 nm was observed in contrast to a distance of 2.5 nm obtained for T4. This distance is indicative of a ‘planar’ structure, confirming once more that no significant twisting or bending of the complexes seems to occur.
For the c-P10Cu2 ring without template, a Cu⋯Cu separation of 4.3 nm was found experimentally, which is in very good agreement with expectations from molecular modeling and shows that the ring is fairly shape-persistent in solution. As expected and confirmed on inspection of the DEER distance distributions, the flexibility of the ring without template is larger as compared to the template-bound structures.
Acknowledgements
We thank the EPSRC (EPL011972/1) and the ERC (grant 320969) for support. The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out this work.References
- I. Beletskaya, V. S. Tyurin, A. Y. Tsivadze, R. Guilard and C. Stern, Chem. Rev., 2009, 109, 1659–1713 CrossRef CAS PubMed.
- M. Hoffmann, C. J. Wilson, B. Odell and H. L. Anderson, Angew. Chem., Int. Ed., 2007, 46, 3122–3125 CrossRef CAS PubMed.
- M. C. O'Sullivan, J. K. Sprafke, D. V. Kondratuk, C. Rinfray, T. D. W. Claridge, A. Saywell, M. O. Blunt, J. N. O'Shea, P. H. Beton, M. Malfois and H. L. Anderson, Nature, 2011, 469, 72–75 CrossRef PubMed.
- T. R. Kelly, R. L. Xie, C. Kreabel Weinreb and T. Bregant, Tetrahedron Lett., 1998, 39, 3675–3678 CrossRef CAS.
- C. A. Hunter and S. Tomas, J. Am. Chem. Soc., 2006, 128, 8975–8979 CrossRef CAS PubMed.
- R. J. Abraham, P. Leighton and J. K. M. Sanders, J. Am. Chem. Soc., 1985, 107, 3472–3478 CrossRef CAS.
- I. Tabushi, S. Kugimiya, M. G. Kinnaird and T. Sasaki, J. Am. Chem. Soc., 1985, 4192–4199 CrossRef CAS.
- H. L. Anderson, Inorg. Chem., 1994, 33, 972–981 CrossRef CAS.
- P. N. Taylor and H. L. Anderson, J. Am. Chem. Soc., 1999, 121, 11538–11545 CrossRef CAS.
- H. J. Hogben, J. K. Sprafke, M. Hoffmann, M. Pawlicki and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 20962–20969 CrossRef CAS PubMed.
- S. Van Doorslaer, D. M. Murphy and I. A. Fallis, Res. Chem. Intermed., 2007, 33, 807–823 CrossRef CAS.
- S. Van Doorslaer, I. Caretti, I. A. Fallis and D. M. Murphy, Coord. Chem. Rev., 2009, 253, 2116–2130 CrossRef CAS.
- G. Jeschke, ChemPhysChem, 2002, 3, 927–932 CrossRef CAS PubMed.
- Z. Yang, D. Kise and S. Saxena, J. Phys. Chem. B, 2010, 114, 6165–6174 CrossRef CAS PubMed.
- G. Jeschke, A. Koch, U. Jonas and A. Godt, J. Magn. Reson., 2002, 155, 72–82 CrossRef CAS PubMed.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- J. Cremers, S. Richert, D. V. Kondratuk, T. D. W. Claridge, C. R. Timmel and H. L. Anderson, Chem. Sci., 2016, 7 10.1039/C6SC01809B.
- D. V. Kondratuk, L. M. A. Perdigão, A. M. S. Esmail, J. N. O'Shea, P. H. Beton and H. L. Anderson, Nat. Chem., 2015, 7, 317–322 CrossRef CAS PubMed.
- S. Liu, D. V. Kondratuk, S. A. L. Rousseaux, G. Gil-Ramírez, M. C. O'Sullivan, J. Cremers, T. D. W. Claridge and H. L. Anderson, Angew. Chem., Int. Ed., 2015, 54, 5355–5359 CrossRef CAS PubMed.
- S. P. Greiner, D. L. Rowlands and R. W. Kreilick, J. Phys. Chem., 1992, 96, 9132–9139 CrossRef CAS.
- C. Finazzo, C. Calle, S. Stoll, S. Van Doorslaer and A. Schweiger, Phys. Chem. Chem. Phys., 2006, 8, 1942–1953 RSC.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- TURBOMOLE V6.1 2009, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, 1989–2007, since 2007; available from http://www.turbomole.com Search PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- V. Barone, Recent Advances in Density Functional Methods, Part I, World Scientific, Singapore, 1996 Search PubMed.
- A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036 CrossRef CAS.
- F. Neese, J. Phys. Chem. A, 2001, 105, 4290–4299 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2003, 118, 3939–3948 CrossRef CAS.
- F. Neese, Magn. Reson. Chem., 2004, 42, S187–S198 CrossRef CAS PubMed.
- MATLAB, version 7.11.0 (R2010b), The MathWorks Inc., Natick, Massachusetts, 2010 Search PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- P. Höfer, A. Grupp, H. Nebenführ and M. Mehring, Chem. Phys. Lett., 1986, 132, 279–282 CrossRef.
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340 CrossRef CAS PubMed.
- J. E. Lovett, M. Hoffmann, A. Cnossen, A. T. J. Shutter, H. J. Hogben, J. E. Warren, S. I. Pascu, C. W. M. Kay, C. R. Timmel and H. L. Anderson, J. Am. Chem. Soc., 2009, 131, 13852–13859 CrossRef CAS PubMed.
- A. M. Bowen, M. W. Jones, J. E. Lovett, T. G. Gaule, M. J. McPherson, J. R. Dilworth, C. R. Timmel and J. R. Harmer, Phys. Chem. Chem. Phys., 2016, 18, 5981–5994 RSC.
- A. M. Bowen, C. E. Tait, C. R. Timmel and J. R. Harmer, Structural Information from Spin-Labels and Intrinsic Paramagnetic Centres in the Biosciences, Springer, Berlin, Heidelberg, 2013, vol. 152, ch. 7, pp. 283–327 Search PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- Z. Yang, J. Becker and S. Saxena, J. Magn. Reson., 2007, 188, 337–343 CrossRef CAS PubMed.
- J. E. Lovett, A. M. Bowen, C. R. Timmel, M. W. Jones, J. R. Dilworth, D. Caprotti, S. G. Bell, L. L. Wong and J. Harmer, Phys. Chem. Chem. Phys., 2009, 11, 6840–6848 RSC.
- B. E. Bode, J. Plackmeyer, T. F. Prisner and O. Schiemann, J. Phys. Chem. A, 2008, 112, 5064–5073 CrossRef CAS PubMed.
- A. Marko, D. Margraf, H. Yu, Y. Mu, G. Stock and T. Prisner, J. Chem. Phys., 2009, 130, 064102 CrossRef CAS PubMed.
- D. Abdullin, G. Hagelueken, R. I. Hunter, G. M. Smith and O. Schiemann, Mol. Phys., 2015, 113, 544–560 CrossRef CAS.
- P. N. Taylor, J. Huuskonen, G. Rumbles, R. T. Aplin, E. Williams and H. L. Anderson, Chem. Commun., 1998, 909–910 RSC.
- J. K. Sprafke, D. V. Kondratuk, M. Wykes, A. L. Thompson, M. Hoffmann, R. Drevinskas, W.-H. Chen, C. K. Yong, J. Kärnbratt, J. E. Bullock, M. Malfois, M. R. Wasielewski, B. Albinsson, L. M. Herz, D. Zigmantas, D. Beljonne and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 17262–17273 CrossRef CAS PubMed.
- J. Q. Gong, P. Parkinson, D. V. Kondratuk, G. Gil-Ramírez, H. L. Anderson and L. M. Herz, J. Phys. Chem. C, 2015, 119, 6414–6420 CAS.
- I. Caretti, E. Carter, I. A. Fallis, D. M. Murphy and S. Van Doorslaer, Phys. Chem. Chem. Phys., 2011, 13, 20427–20434 RSC.
- T. F. Segawa, A. Doll, S. Pribitzer and G. Jeschke, J. Chem. Phys., 2015, 143, 044201 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Description of the experimental conditions and parameters applied; supplementary data sets and simulations; visualization of the calculated hyperfine and nuclear quadrupole tensors. See DOI: 10.1039/c6sc01810f |
| ‡ In agreement with other literature results,32,33 the in-plane copper hyperfine coupling, A⊥, is predicted to be much smaller by DFT than experimentally observed. It changes sign in the calculations between P1Cu and P1Cu·py and predictions of a trend in A⊥ based on the DFT results would therefore be difficult and shall not be attempted here. |
| § Experiments were performed in protonated toluene as the use of deuterated toluene as a solvent resulted in deuterium modulations which completely dominated the ESEEM time traces and considerably complicated the detection of any nitrogen couplings. |
| ¶ The distance distributions obtained from DeerAnalysis were corrected for g-factor differences prior to analysis. A g-factor of 2.05 was assumed for the copper compounds (excitation on xy), whereas DeerAnalysis uses the free electron g-factor for calculations of the distances. It should further be noted at this point that in all oligomers 30% of the copper porphyrin's spin density is spread onto the four in-plane nitrogens (Cu⋯N bond length 0.2 nm) which will contribute a minor component to the width of all distance distributions but should not affect the mean distance. |
| This journal is © The Royal Society of Chemistry 2016 |