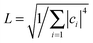Nuclear quantum tunnelling and carrier delocalization effects to bridge the gap between hopping and bandlike behaviors in organic semiconductors†
Yuqian
Jiang
ab,
Xinxin
Zhong
c,
Wen
Shi
a,
Qian
Peng
d,
Hua
Geng
d,
Yi
Zhao
*e and
Zhigang
Shuai
*ae
aMOE Key Laboratory of Organic Optoelectronics and Molecular Engineering, Department of Chemistry, Tsinghua University, Beijing 100084, China. E-mail: zgshuai@tsinghua.edu.cn
bNational Center for Nanoscience and Technology, Beijing 100190, China
cHubei Collaborative Innovation Center for Advanced Organic, Chemical Materials, and College of Chemistry and Chemical Engineering, Hubei University, Wuhan 430062, China
dInstitute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China
eCollaborative Innovation Center of Chemistry for Energy Materials, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China. E-mail: yizhao@xmu.edu.cn
First published on 8th October 2015
Abstract
The experimental carrier mobility value of organic semiconductors has been increasing rapidly in recent years to well exceed the theoretical limit based on the hopping model calculated using the semi-classical Marcus theory, calling for better understanding and evaluation of carrier mobility. On the other hand, bandlike transport behavior has been observed for some ultra-pure and closely-packed organic single crystals. In this work, we identify the roles of quantum nuclear tunnelling and the charge delocalization effects, leading to a comprehensive computational approach to assess the carrier mobility of organic semiconductors. We present the first-principles evaluated mobility results for some representative organic transport materials at four levels ranging from semiclassical hopping to quantum nuclear enabled hopping and to quantum wavepacket diffusion, and eventually to complete bandlike descriptions. We provide a comprehensive tool to assess the carrier mobility in organic semiconductors based on such improved understanding.
Conceptual insightsThe mechanism of charge transport in organic semiconductors has been a controversial issue in recent years. In this work, we apply four transport mechanisms covering fully localized Marcus theory, tunnelling enabled hopping, wavepacket diffusion, and the fully delocalized bandlike model, to identify the nuclear tunnelling effect, the charge coherence effect, and the charge delocalization effect in the transport process. Our research shows that the charge transport in organic crystals with high mobility tends to occur through nuclear-tunnelling-assisted hopping or wavepacket diffusion rather than being a fully localized or delocalized mechanism. The nuclear tunnelling effect can play a significant role in facilitating the charge transport process. Moreover, when the carrier delocalization effect is relatively strong, charge carrier transport will also be accelerated. |
Remarkable progress has been achieved in the last few decades in understanding and improving the carrier mobility of organic semiconductors (OSCs) after intensive investigations on new materials, processes, and devices. Systems with hole mobility higher than 10 cm2 V−1 s−1 have been discovered such as pentacene,1 rubrene,2 thienoacene derivatives3 and systems with electron mobility larger than 6 cm2 V−1 s−1 such as naphthalene diimide derivatives4 and perylene diimide derivatives5 have also been produced. Bandlike behavior is usually applied to explain such high mobility OSCs, much as in inorganic semiconductors,6 for example, band-like temperature-dependent mobility has been reported in pentacene,7 rubrene,8N,N′-bis(n-C3F7CH2)-(1,7 and 1,6)-dicyanoperylene-3,4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9,10- bis(dicarboximide)s (PDIF-CN2)5 and 6,13-bis (triisopropylsilylethynyl)-pentacene (TIPS-P).9 On the other hand, the well localized hopping process described by the semiclassical Marcus theory has gained tremendous popularity due to both conceptual clarity and success in molecular design.10 Such a model is appropriate when the intermolecular transfer integrals are much smaller than the charge reorganization energy and the elementary charge transfer (CT) rate is described as
9,10- bis(dicarboximide)s (PDIF-CN2)5 and 6,13-bis (triisopropylsilylethynyl)-pentacene (TIPS-P).9 On the other hand, the well localized hopping process described by the semiclassical Marcus theory has gained tremendous popularity due to both conceptual clarity and success in molecular design.10 Such a model is appropriate when the intermolecular transfer integrals are much smaller than the charge reorganization energy and the elementary charge transfer (CT) rate is described as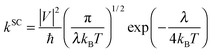 | (1) |
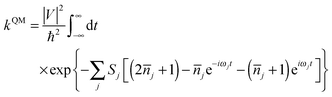 | (2) |
![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) j = 1/[exp(ℏωj/kBT) − 1] is the occupation number for the j-th vibrational mode with frequency ωj and Sj is the Huang–Rhys factor relating to the j-th mode, which represents the local electron–phonon coupling. In the limits of strong coupling
j = 1/[exp(ℏωj/kBT) − 1] is the occupation number for the j-th vibrational mode with frequency ωj and Sj is the Huang–Rhys factor relating to the j-th mode, which represents the local electron–phonon coupling. In the limits of strong coupling  , the short-time approximation exp(iωt) = 1 + iωt + (iωt)2/2, and high temperature ℏωj/kBT ≪ 1,
, the short-time approximation exp(iωt) = 1 + iωt + (iωt)2/2, and high temperature ℏωj/kBT ≪ 1, ![[n with combining overline]](https://www.rsc.org/images/entities/i_char_006e_0305.gif) j ≈ kBT/ℏωj, eqn (2) goes back to eqn (1) with
j ≈ kBT/ℏωj, eqn (2) goes back to eqn (1) with 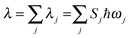 .
.
It is noted that even though eqn (1) can correctly identify the essential molecular parameters, the calculated mobility values are often underestimated compared to experiments. For example, for pentacene, Marcus theory led to a theoretical hole mobility ranging from 6 to 15 cm2 V−1 s−1,12 while recent experimental single crystal FET mobilities1 reached 15–40 cm2 V−1 s−1, calling for better theoretical descriptions, since, in principle the theoretical value should be considered as an upper limit. The increasing FET mobility trend is due to the improvement in material processes and device fabrication. It is generally believed that the active transport parts of an OFET are just a few molecular layers adjacent to the dielectrics. Due to the gate electric field, impurities or defects within these layers could be easily swept out, making the FET mobility in general higher than the bulk materials where the mobility is usually dominated by disorder, impurities or defects, as described by the phenomenological model proposed by Bässler.13
Our previous efforts of incorporating the quantum nuclear effect that was absent in the semiclassical Marcus theory have led to several novel findings, namely: (i) a few fold enhancement in mobility values due to the effective lowering of the barrier through quantum fluctuation;11 (ii) mobility decreases with temperature even for localized charge, which provided a more natural explanation for the paradoxical observations by Sakanoue and Sirringhaus that the optical signature of the carriers in TIPS-pentacene showed a localized charge, but the mobility decreased with temperature, behaving as delocalized “bandlike”;14 (iii) a negative isotope effect instead of null in semiclassical Marcus theory,15 which had been unclear for decades.16 Most interestingly, such a localized charge nuclear tunnelling model was adopted to clarify the long-standing disputes over the mechanism of electrical conduction in doped conjugated polymers: nuclear tunnelling assisted polaron hopping was claimed to be a universal description for all of the conducting polymers by Asadi et al.17
However, Marcus theory or the quantum nuclear tunnelling model, which has assumed strong electron localization and weak electron coherence, might not be applicable to recently discovered high mobility materials with an indication of bandlike behavior. And in most cases, the transport mechanism is situated in between the localized and the delocalized ends. Mixed quantum/classical dynamics (MQCD) and full quantum dynamics (FQD) methods have been proposed to investigate charge transport. MQCD methods are more efficient but treat nuclear motion by classical dynamics, as represented by the dynamic disorder-limited transport theory18 based on the Su–Schrieffer–Heeger-type model parameterized with the aid of first-principles calculation. In contrast, FQD methods can consider the nuclear quantum effect, such as nonperturbative hierarchically coupled equations of motion19 and the non-Markovian stochastic Schrödinger equation.20 However, most of them are limited to systems with only tens of sites due to numerical convergence problems and computer memory limitations. Thus, FQD methods are rarely applied to study real OSCs. Zhao et al. have recently proposed a more efficient FQD method based on the stochastic Schrödinger equation, namely the time-dependent wavepacket diffusion (TDWPD) approach to study charge transport properties. The TDWPD method can deal with hundreds or even thousands of orbitals/sites efficiently and the nuclear quantum effect is considered through the harmonic oscillator model. For the sake of benchmarking, it shows good agreement21 with the path integral method and the nonperturbative hierarchically coupled equations of motion19 for small-sized symmetric systems where the latter can be applied. TDWPD has been proven to be both effective and efficient despite the difficulty in reproducing the Boltzmann distribution for asymmetric systems.22 This method is introduced in the Method part in this paper.
As far as complete delocalized bandlike transport is concerned, we have shown previously that the deformation potential theory coupled with the Boltzmann equation can provide a reasonably quantitative description.23 It was found that the intrinsic bandlike mobility is dominated by scattering with the longitudinal acoustic phonons, while the optical phonons and the transverse acoustic phonon processes can be ignored at room temperature.24
Carrier (electron or hole) transport in real materials should fall in the range of the above four regimes. In order to better predict the carrier mobility, we present a systematic study on five typical high mobility OSCs employing all four models and compare with the available experimental results. These are pentacene, rubrene, dinaphtho-thieno-thiophene (DNTT), dianthra-thieno-thiophene (DATT), and PDIF-CN2, of which the first four are typical p-type materials and the latter is a typical n-type material (Fig. 1). All possess a layered structure. For simplicity, we investigate only the two-dimensional (2D) transport properties and extend to 3D through spatial averaging by ignoring the interlayer transport.
 | ||
| Fig. 1 The molecular structures of the high-mobility OSCs studied in this work: (a) pentacene, (b) rubrene, (c) DNTT, (d) DATT, and (e) PDIF-CN2. | ||
The crystallographic parameters of the corresponding crystals are listed in Table 1. The charge reorganization energies and the intermolecular electronic couplings for the five crystals are presented in Table 2. The directions of the corresponding charge transfer are drawn in Fig. 2.
| meV | Pentacene | Rubrene | DATT | DNTT | PDIF-CN2 |
|---|---|---|---|---|---|
| V1 | 32.6 | 83.0 | 66.8 | 67.2 | 95.2 |
| V2 | 47.0 | 14.1 | 38.4 | 86.1 | 0.1 |
| V3 | 77.1 | 1.2 | 84.8 | 20.5 | 65.0 |
| V4 | 29.9 | 0.1 | 2.2 | 2.5 | |
| V5 | 3.4 | 0.2 | 0.3 | ||
| λ | 91 | 151 | 86 | 131 | 277 |
 | ||
| Fig. 2 The most important hopping paths in the five crystals: (a) pentacene, (b) rubrene, (c) DNTT, (d) DATT, and (e) PDIF-CN2. | ||
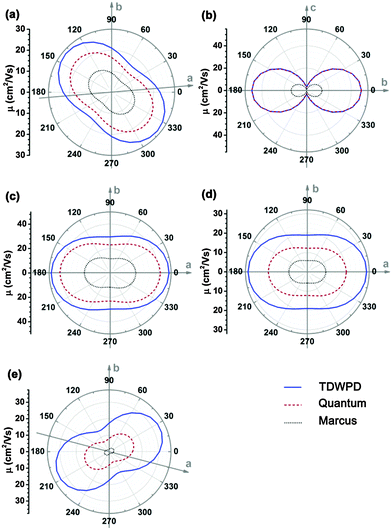
We first investigate the angular dependences of the mobility using the Marcus hopping model, the quantum nuclear tunnelling model, and the TDWPD method, which have been plotted in Fig. 3. The theoretical results show that the three random walk simulation based methods present very similar anisotropic behaviors. Among the five organic crystals, rubrene possesses the strongest anisotropic transport properties (μb ∼ 15μa), which is due to the much larger electronic coupling along the b direction (V1) than the others. On the other hand, pentacene, DATT and DNTT have the weakest anisotropic properties where μa < 2μb. The strong anisotropy in rubrene and the weak anisotropy in DNTT match well with experiments,3c,29 indicating the reliability of the random walk simulation.
For better understanding the transport mechanism, we then calculate the average mobilities by the four methods mentioned previously as listed in Table 3. For comparing with experiment, the averaged 3D mobilities are also presented. The bandlike mobility calculated with DP theory coupled with the Boltzmann transport equation represents the full delocalization, which usually gives much larger mobility values. The results for pentacene,6c DATT6b and DNTT6b are quoted from references, while the others are calculated according to the methodology presented in ref. 23 and the calculation details are shown in the ESI.† It should be noted that only acoustic phonon scattering is included in DP theory and optical phonons are excluded. Xi et al.24 used the Wannier-interpolation method to calculate the band mobility in 2D carbon materials considering both acoustic and optical phonons, and they found that the main scattering mechanism is because of acoustic phonons, while the optical phonons play some role only at high temperatures or at low electron energies. Therefore, it is feasible to apply DP theory for studying the band transport behavior. The mobilities resulting from the four methods show that the DP mobility (μDP) is the largest for all the systems. In particular, for rubrene, DATT, DNTT and PDIF-CN2, their DP mobilities are one order of magnitude larger than the other theoretical mobilities as well as experimental results. Therefore, the rationality of describing the charge transport in organic systems by a bandlike model should be questioned, and further theoretical and experimental studies are needed. As we have explained before,14 the so-called bandlike decreasing temperature behavior could arise from the nuclear tunnelling effect for a localized state, instead of a delocalization effect.
| μ (cm2 V−1 s−1) | Marcus | Quantum | TDWPD | DP | Exp. |
|---|---|---|---|---|---|
| Pentacene | a: 9.4 | a: 16.9 | a: 21.8 | a: 58.0 | 15–401 |
| b: 9.3 | b: 16.7 | b: 21.1 | b: 44.06c | ||
| AVG: 6.7 | AVG: 11.8 | AVG: 15.1 | |||
| Rubrene | b: 13.8 | b: 48.9 | b: 49.0 | b: 242.6 | 15–172a |
| c: 0.8 | c: 2.8 | c: 3.2 | c: 72.7 | ||
| AVG: 4.9 | AVG: 17.2 | AVG: 17.4 | |||
| DATT | a: 21.2 | a: 41.3 | a: 48.3 | a: 322.6 | 1610c |
| b: 11.6 | b: 23.0 | b: 29.6 | b: 19.16b | ||
| AVG: 10.6 | AVG: 21.1 | AVG: 25.2 | |||
| DNTT | a: 9.5 | a: 20.2 | a: 30.7 | a: 137.7 | 6.8–7 |
| b: 5.8 | b: 12.2 | b: 19.0 | b: 76.46b | 53c | |
| AVG: 5.1 | AVG: 10.7 | AVG: 16.3 | |||
| PDIF-CN2 | a: 2.3 | a: 12.1 | a: 25.9 | a: 132.8 | 1–630 |
| b: 1.5 | b: 8.0 | b: 17.4 | b: 91.2 | ||
| AVG: 1.4 | AVG: 7.5 | AVG: 16.1 |
The sequence of mobility values resulting from the other three methods for each system is: μTDWPD > μQuantum > μMarcus. It is natural that both the nuclear quantum effect and electron coherence can facilitate carrier transport. Upon comparing experimental results, Marcus theory underestimates the mobility for all the systems, even though the molecular parameters themselves are useful for molecular design, as stressed by Brédas et al. who evaluated the molecular parameters which were pertinent to material design.10 In contrast, both the quantum model and the TDWPD method with the nuclear tunnelling effect seem to be able to give reasonable results compared to experiments, illustrating the significance of the nuclear tunnelling effect in charge transport.
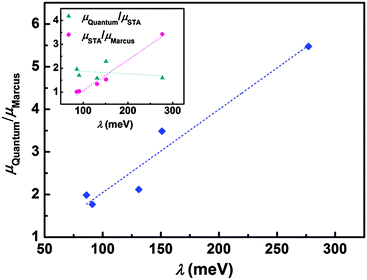
The step beyond Marcus theory is an extension to consider the nuclear quantum effect. Here, we simply regard the ratio of quantum mobility and the Marcus mobility (μQuantum/μMarcus) as representing the nuclear quantum effect, and we find that the nuclear quantum effect is directly determined by the charge reorganization energy, as seen in Fig. 4. As the reorganization energy increases, the scattering of intramolecular nuclear vibrations on electrons is strengthened, leading to smaller mobility. However, the nuclear quantum effect can linearly increase with reorganization energy. The results show that the nuclear tunnelling can at least double the Marcus mobility, so that the nuclear tunnelling effect cannot be neglected during the charge transport process for organic semiconductors.
As mentioned before eqn (1) can be derived from eqn (2) with two approximations, namely the short-time approximation (STA) and the high temperature assumption (HTA). These two lead to the classical limit. We now consider the mobility values using the quantum CT rate with only STA, to investigate the inhibitions of STA and HTA on the nuclear tunnelling effect, which reads
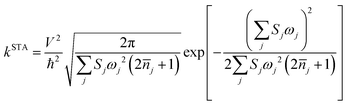 | (3) |
The TDWPD method can consider both the electronic coherence with delocalization effects and the quantum nature of nuclear motion through the harmonic oscillator model. It is seen from Table 3 that the mobility obtained by TDWPD is always larger than that obtained from the quantum nuclear tunnelling model. The electronic coherence length can be measured by the non-diagonal component 〈cicj〉.31 For the sake of simplicity, here we consider only the real part of the fluctuation in the correlation function. In fact, it is found that the particle dynamics caused by the neglect of imaginary fluctuation has been proved to be small.21 Charge population propagation on the initial site can qualitatively measure the coherence motion of the charge carrier which is given in Fig. S1 (ESI†). It is found that the charge populations of all systems start to decay with oscillation behavior within a period of 1000 a.u. (24 fs), which describes the coherent motion of charge. However, beyond that point, the quasi-thermal-equilibrium of diffusion can be obtained (Fig. S2, ESI†), and the population oscillating behavior disappears, indicating that the electronic coherence is lost. Therefore, we attribute the larger mobility achieved by the TDWPD model than the nuclear tunnelling model to the electronic delocalization effect rather than electronic coherence.
The electronic delocalization for the five systems at 24 fs is illustrated in Fig. 5. It is found that rubrene possesses the shortest delocalization length among all systems, even though its reorganization energy and transfer integral are similar to those in DNTT. The delocalization length of the latter is more than twice as long as that of rubrene. This is due to the strong anisotropy for V in the rubrene crystal, as seen from Table 2. The 1D-like behavior leads to relatively small charge delocalization. Thus, the mobility values from the quantum hopping model and the TDWPD method are very close to each other. However, for the other four systems, the charge delocalization effect is seen to be significant. It is also noted that the computed mobility values from a complete delocalized bandlike model as simulated with DP theory are well overestimated compared with experiments, demonstrating the inappropriateness of the bandlike picture for OSCs.
To summarize, we adopt four methods from hopping to bandlike mechanisms to investigate the intrinsic charge transport properties of several organic semiconductors with high mobility. In general, the semiclassical Marcus theory underestimates the mobility due to the neglect of the nuclear quantum effect, while the bandlike deformation potential theory always overestimates the mobility because of the neglect of the charge localization effect, especially for rubrene, DATT, DNTT and PDIF-CN2. Both the quantum nuclear tunnelling model and the TDWPD method can give appropriate descriptions for these high mobility organic materials, implying that polaron transport assisted by nuclear tunnelling is universal for organic materials including conducting polymers. Upon comparing μQuantum with μMarcus, we find that larger reorganization energy will lead to a stronger nuclear tunnelling effect, so that μQuantum/μMarcus becomes larger. The TDWPD method contains both electronic coherence and delocalization effects in addition to the quantum nuclear effect. TDWPD calculations demonstrate that the electronic coherence is not significant in the determination of charge transport mobility, while electronic delocalization plays an important role, and the delocalization effect can facilitate transport. When the electronic delocalization effect is relatively strong, the wavepacket description with the nuclear tunnelling effect is more appropriate, for example, in pentacene, DATT, DNTT and PDIF-CN2. While for systems with weak electronic delocalization like rubrene, a simple nuclear tunnelling enabled hopping model is sufficient.
Methods
The method of random walk simulation based on Marcus theory was summarized in ref. 10d. And the nuclear tunnelling method was presented in ref. 11 and 14. And the bandlike DP methodology and computational details are given in ESI,† Fig. S2. The TDWPD method is relatively new, so we give a brief introduction here. After an electron is injected into a molecule in the organic crystal, it hops or coherently moves to another. Its CT process is determined by the intermolecular transfer integral and the thermal vibration of molecules which is taken into account by allowing the site energy εii and the transfer integral εij to fluctuate in time. The corresponding Hamiltonian can be expressed as | (4) |
To obtain the memory effect of site energy fluctuation, we need the spectral density function of the electron–phonon interaction which can be written as 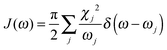 . Here the electron–phonon interaction strength of the j-th normal mode is χj = ΔQjωj2. The δ function is evaluated using the Lorentz distribution
. Here the electron–phonon interaction strength of the j-th normal mode is χj = ΔQjωj2. The δ function is evaluated using the Lorentz distribution  . Once J(ω) is known, the site energy fluctuation can be achieved using
. Once J(ω) is known, the site energy fluctuation can be achieved using  . Here, G(ω) = J(ω)
. Here, G(ω) = J(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(βTω/2)/π is the modified spectral density function at a special temperature T (β = 1/kBT) to make it satisfy the detailed balance principle. Δω = ωmax/N, where ωmax is the upper cutoff frequency, and ωn = nΔω. ϕn is the independent random phase which is uniformly distributed over the interval [0, 2π].
coth(βTω/2)/π is the modified spectral density function at a special temperature T (β = 1/kBT) to make it satisfy the detailed balance principle. Δω = ωmax/N, where ωmax is the upper cutoff frequency, and ωn = nΔω. ϕn is the independent random phase which is uniformly distributed over the interval [0, 2π].
To describe the electronic dynamics, the time-dependent Schrödinger equation is solved using the Chebyshev polynomial expansion technique.33 Once the wave function of a system  is known, the time-dependent electronic properties can be easily obtained. The diffusion coefficient D can be calculated as
is known, the time-dependent electronic properties can be easily obtained. The diffusion coefficient D can be calculated as  , where
, where  will grow linearly with time t after some time, and d represents the number of dimensions. The origin is defined as 〈R2(0)〉 = 0, and charge is completely localized on site a. ri is the distance from site i to site a, and ρii(t) = 〈ci*(t)ci(t)〉 is the charge population on site i, which is averaged over 400 independent trajectories here.
will grow linearly with time t after some time, and d represents the number of dimensions. The origin is defined as 〈R2(0)〉 = 0, and charge is completely localized on site a. ri is the distance from site i to site a, and ρii(t) = 〈ci*(t)ci(t)〉 is the charge population on site i, which is averaged over 400 independent trajectories here.
In eqn (1), (2) or (4), the intermolecular transfer integral V between molecules m and n is calculated using the site-energy corrected coupling method34 which can be expressed as  , where em = 〈ϕm|H|ϕm〉, V0mn = 〈ϕm|H|ϕn〉 and Omn = 〈ϕm|O|ϕn〉. ϕm(n) is the frontier molecular orbital of an isolated molecule m (n) in the dimer. For hole (electron) transport, the HOMO (LUMO) should be plugged in. H and O are the dimer Hamiltonian and the overlap matrix, respectively.
, where em = 〈ϕm|H|ϕm〉, V0mn = 〈ϕm|H|ϕn〉 and Omn = 〈ϕm|O|ϕn〉. ϕm(n) is the frontier molecular orbital of an isolated molecule m (n) in the dimer. For hole (electron) transport, the HOMO (LUMO) should be plugged in. H and O are the dimer Hamiltonian and the overlap matrix, respectively.
For Marcus and nuclear tunnelling models, the charge mobility can be obtained by assuming a diffusion process by virtue of the Einstein formula μ = eD/kBT after achieving the CT rate from one molecule to each neighbour. The diffusion constant D is simulated by a random walk by kinetic Monte Carlo simulation. The charge hops between nearest-neighbouring molecules with a probability  for the α-th pathway, and the simulation time is incremented by
for the α-th pathway, and the simulation time is incremented by 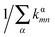 .35 The diffusion coefficient can also be obtained from
.35 The diffusion coefficient can also be obtained from  averaging over 8000 trajectories. We repeat 100 times, and the average mobility is evaluated as
averaging over 8000 trajectories. We repeat 100 times, and the average mobility is evaluated as 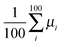 .
.
The reorganization energy and the electronic coupling necessary for Marcus theory, the quantum nuclear tunnelling model and the TDWPD method are determined by quantum chemical first-principles calculations. Density functional theory (DFT) is adopted as implemented in the Gaussian 09 package.36 The neutral and charged geometries of all systems are optimized using the B3LYP functional37 and the 6-31G(d) basis set, and vibrational frequencies are calculated at the same level. With the help of the DUSHIN program,38 the corresponding Huang–Rhys factor and the reorganization energy of each vibrational mode entered in eqn (2) are obtained under the displaced harmonic oscillator approximation. Then, the spectral density function needed in the TDWPD method can be derived. For the intermolecular transfer integral V for all the neighboring molecular pairs, the PW91PW91 functional39 plus a 6-31G(d) basis set is employed. All mobility calculations are carried out at 300 K. The cluster size used for TDWPD calculations for all the systems is 41 × 41.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21290191, 21303213, 91333202) and the Ministry of Science and Technology of China through the 973 program (Grant No. 2013CB933503).Notes and references
- O. D. Jurchescu, M. Popinciuc, B. J. van Wees and T. T. M. Palstra, Adv. Mater., 2007, 19, 688 CrossRef CAS PubMed
.
-
(a) W. Xie, K. A. McGarry, F. Liu, Y. Wu, P. P. Ruden, C. J. Douglas and C. D. Frisbie, J. Phys. Chem. C, 2013, 117, 11522 CrossRef CAS
; (b) R. Zeis, C. Besnard, T. Siegrist, C. Schlockermann, X. Chi and C. Kloc, Chem. Mater., 2005, 18, 244 CrossRef
; (c) V. Podzorov, E. Menard, A. Borissov, V. Kiryukhin, J. A. Rogers and M. E. Gershenson, Phys. Rev. Lett., 2004, 93, 086602 CrossRef CAS
.
-
(a) H. Ebata, T. Izawa, E. Miyazaki, K. Takimiya, M. Ikeda, H. Kuwabara and T. Yui, J. Am. Chem. Soc., 2007, 129, 15732 CrossRef CAS PubMed
; (b) K. Niimi, S. Shinamura, I. Osaka, E. Miyazaki and K. Takimiya, J. Am. Chem. Soc., 2011, 133, 8732 CrossRef CAS PubMed
; (c) W. Xie, K. Willa, Y. Wu, R. Häusermann, K. Takimiya, B. Batlogg and C. D. Frisbie, Adv. Mater., 2013, 25, 3478 CrossRef CAS PubMed
; (d) M. J. Kang, I. Doi, H. Mori, E. Miyazaki, K. Takimiya, M. Ikeda and H. Kuwabara, Adv. Mater., 2011, 23, 1222 CrossRef CAS PubMed
; (e) K. Takimiya, S. Shinamura, I. Osaka and E. Miyazaki, Adv. Mater., 2011, 23, 4347 CrossRef CAS PubMed
.
- T. He, M. Stolte and F. Würthner, Adv. Mater., 2013, 25, 6951 CrossRef CAS PubMed
.
- N. A. Minder, S. Ono, Z. Chen, A. Facchetti and A. F. Morpurgo, Adv. Mater., 2012, 24, 503 CrossRef CAS PubMed
.
-
(a) L. Tang, M. Long, D. Wang and Z. Shuai, Sci. China, Ser. B: Chem., 2009, 52, 1646 CrossRef CAS
; (b) J. Xi, M. Long, L. Tang, D. Wang and Z. Shuai, Nanoscale, 2012, 4, 4348 RSC
; (c) H. Kobayashi, N. Kobayashi, S. Hosoi, N. Koshitani, D. Murakami, R. Shirasawa, Y. Kudo, D. Hobara, Y. Tokita and M. Itabashi, J. Chem. Phys., 2013, 139, 014707 CrossRef PubMed
.
- O. Ostroverkhova, D. G. Cooke, S. Shcherbyna, R. F. Egerton, F. A. Hegmann, R. R. Tykwinski and J. E. Anthony, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035204 CrossRef
.
- V. Podzorov, E. Menard, J. A. Rogers and M. E. Gershenson, Phys. Rev. Lett., 2005, 95, 226601 CrossRef CAS
.
- T. Sakanoue and H. Sirringhaus, Nat. Mater., 2010, 9, 736 CrossRef CAS PubMed
.
-
(a) J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804 CrossRef PubMed
; (b) J. Cornil, D. Beljonne, J. P. Calbert and J. L. Brédas, Adv. Mater., 2001, 13, 1053 CrossRef CAS
; (c) V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926 CrossRef CAS PubMed
; (d) A. N. Sokolov, S. Atahan-Evrenk, R. Mondal, H. B. Akkerman, R. S. Sánchez-Carrera, S. Granados-Focil, J. Schrier, S. C. Mannsfeld, A. P. Zoombelt and Z. Bao, Nat. Commun., 2011, 2, 437 CrossRef PubMed
; (e) L. J. Wang, G. Nan, X. D. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423 RSC
.
-
(a) G. Nan, X. Yang, L. Wang, Z. Shuai and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115203 CrossRef
; (b) Z. Shuai, H. Geng, W. Xu, Y. Liao and J.-M. André, Chem. Soc. Rev., 2014, 43, 2662–2679 RSC
.
- W. Q. Deng and W. A. Goddard III, J. Phys. Chem. B, 2004, 108, 8614 CrossRef CAS
.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15 CrossRef PubMed
.
- H. Geng, Q. Peng, L. Wang, H. Li, Y. Liao, Z. Ma and Z. Shuai, Adv. Mater., 2012, 24, 3568 CrossRef CAS PubMed
.
-
(a) Y. Jiang, H. Geng, W. Shi, Q. Peng, X. Zheng and Z. Shuai, J. Phys. Chem. Lett., 2014, 5, 2267 CrossRef CAS PubMed
; (b) Y. Jiang, Q. Peng, H. Geng, H. Ma and Z. Shuai, Phys. Chem. Chem. Phys., 2015, 17, 3273 RSC
.
-
(a) R. W. Munn, J. R. Nicholson, W. Siebrand and D. F. Williams, J. Chem. Phys., 1970, 52, 6442 CrossRef CAS PubMed
; (b) R. W. Munn and W. Siebrand, J. Chem. Phys., 1970, 52, 6391 CrossRef CAS PubMed
.
- K. Asadi, A. J. Kronemeijer, T. Cramer, L. Jan Anton Koster, P. W. M. Blom and D. M. de Leeuw, Nat. Commun., 2013, 4, 1710 CrossRef PubMed
.
- A. Troisi and G. Orlandi, Phys. Rev. Lett., 2006, 96, 086601 CrossRef
.
- D. Wang, L. Chen, R. Zheng, L. Wang and Q. Shi, J. Chem. Phys., 2010, 132, 081101 CrossRef PubMed
.
- X. Zhong and Y. Zhao, J. Chem. Phys., 2013, 138, 014111 CrossRef PubMed
.
- X. Zhong and Y. Zhao, J. Chem. Phys., 2011, 135, 134110 CrossRef PubMed
.
- W. Zhang, X. Zhong and Y. Zhao, J. Phys. Chem. A, 2012, 116, 11075 CrossRef CAS PubMed
.
- W. Shi, J. Chen, J. Xi, D. Wang and Z. Shuai, Chem. Mater., 2014, 26, 2669–2677 CrossRef CAS
.
- J. Xi, D. Wang, Y. Yi and Z. Shuai, J. Chem. Phys., 2014, 141, 034704 CrossRef PubMed
.
- C. C. Mattheus, A. B. Dros, J. Baas, A. Meetsma, J. L. de Boer and T. T. M. Palstra, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 939 CAS
.
- O. D. Jurchescu, A. Meetsma and T. T. Palstra, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 330 Search PubMed
.
- T. Yamamoto and K. Takimiya, J. Am. Chem. Soc., 2007, 129, 2224 CrossRef CAS PubMed
.
- B. A. Jones, M. J. Ahrens, M.-H. Yoon, A. Facchetti, T. J. Marks and M. R. Wasielewski, Angew. Chem., Int. Ed., 2004, 43, 6363 CrossRef CAS PubMed
.
-
(a) V. C. Sundar, J. Zaumseil, V. Podzorov, E. Menard, R. L. Willett, T. Someya, M. E. Gershenson and J. A. Rogers, Science, 2004, 303, 1644–1646 CrossRef CAS PubMed
; (b) M.-M. Ling, C. Reese, A. L. Briseno and Z. Bao, Synth. Met., 2007, 157, 257 CrossRef CAS PubMed
.
- S. Molinari, H. Alves, Z. Chen, A. Facchetti and A. F. Morpurgo, J. Am. Chem. Soc., 2009, 131, 2462 CrossRef PubMed
.
- Y. Zhao, J. Theor. Comput. Chem., 2008, 7, 869 CrossRef CAS
.
-
(a) L. Wang, Q. Li, Z. Shuai, L. Chen and Q. Shi, Phys. Chem. Chem. Phys., 2010, 12, 3309–3314 RSC
; (b) Z. Shuai, L.-J. Wang and Q.-K. Li, Adv. Mater., 2011, 23, 1145–1153 CrossRef CAS PubMed
.
-
(a) H. Talezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967 CrossRef CAS PubMed
; (b) C. Leforestier, R. H. Bisseling, C. Cerjan, M. D. Feit, R. Friesner, A. Guldberg, A. Hammerich, G. Jolicard, W. Karrlein, H. D. Meyer, N. Lipkin, O. Roncero and R. Kosloff, J. Comp. Physiol., 1991, 94, 59–80 CrossRef
.
- E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J.-L. Brédas, J. Am. Chem. Soc., 2006, 128, 9882 CrossRef CAS PubMed
.
- W. M. Young and E. W. Elcock, Proc. Phys. Soc., 1966, 89, 735 CrossRef
.
-
M. J. Frisch, et al., Revision D.01 ed., Gaussian Inc., Wallingford CT, 2009 Search PubMed
.
-
(a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed
; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS
.
- J. R. Reimers, J. Chem. Phys., 2001, 115, 9103 CrossRef CAS PubMed
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: TDWPD and deformation potential theory calculation details. See DOI: 10.1039/c5nh00054h |
| This journal is © The Royal Society of Chemistry 2016 |