Synthesis and magnetic characterisation of Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) and their oxygen-excess derivatives, Fe_1−xMg_xSb₂O_4+y

Abstract

Three new materials of composition Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) with the tetragonal schafarzikite structure have been synthesised. Magnetic susceptibility measurements suggest that Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50) are canted antiferromagnets whilst Fe_0.25Mg_0.75Sb₂O₄ is paramagnetic. The magnetic ordering temperatures decrease as the Mg²⁺ concentration increases. The materials form oxygen-excess phases when heated in oxygen-rich atmospheres at temperatures of ∼350 °C. ⁵⁷Fe Mössbauer spectroscopy shows that the oxidation process involves the oxidation of Fe²⁺ to Fe³⁺. Powder neutron diffraction confirms the location of the excess oxygen within the structural channels and reveals a change in magnetic order at low temperatures from A-type (magnetic moments along 〈100〉) for Fe_1−xMg_xSb₂O₄ to C-type (magnetic moments along [001]) for the oxidised materials. The change is attributed to a weakening of the antiferromagnetic exchange interactions between edge-linked FeO₆ octahedra for the Fe³⁺-containing materials.

---

Introduction

The compound FeSb₂O₄ occurs naturally as the mineral schafarzikite and is isostructural with the tetragonal form of Pb₃O₄.¹ Its structure,² shown in Fig. 1, consists of chains of edge-linked FeO₆ octahedra along the c-axis; the chains are linked by trigonal pyramidal Sb³⁺ cations which are bonded to three oxide ions and possess lone pairs of electrons (E) directed into the empty channels that exist between the chains of FeO₆ octahedra. If the lone pairs are regarded as ligands, they provide pseudo-tetrahedral SbO₃E geometry for the Sb³⁺ ions. The Fe–Fe distance within the chains (2.96 Å) is shorter than the nearest Fe–Fe distance perpendicular to the chains (6.07 Å) and provides some one-dimensional character to FeSb₂O₄. The material undergoes an antiferromagnetic transition around 45 K.^3,4 A variety of structurally-related MSb₂O₄ (M = Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, Cu²⁺, Zn²⁺, Mg²⁺) have been reported.^5–9

Fig. 1 The structure of FeSb₂O₄ projected (a) along [001] showing channels between chains of FeO₆ octahedra and (b) along [110]. Fe ions are white within blue octahedra; O ions are shown as red spheres and Sb ions as green spheres.

One unsuccessful attempt to substitute on the Sb site has been reported,¹⁰ but we subsequently demonstrated that this is possible by successfully synthesising and characterising materials with composition FeSb_2−xPb_xO₄.¹¹ We have also prepared new phases that contain mixed magnetic cations on the M site and determined their magnetic properties.¹² Two principal types of antiferromagnetic order are observed for magnetic MSb₂O₄ compounds: A-type and C-type¹³ with the magnetic moments aligned as shown in Fig. 2. Only a small energy difference separates these types of order, and subtle changes to the existing magnetic exchange interactions can change the magnetic ground state. Low temperature powder neutron diffraction (PND) experiments, for example, revealed that the A-type magnetic ground state found for both FeSb₂O₄ and MnSb₂O₄ is gradually converted to C-type with increasing Co²⁺ substitution in the series with compositions Fe_1−xCo_xSb₂O₄ and Mn_1−xCo_xSb₂O₄.¹² In addition, the A-type order in FeSb₂O₄ can also be converted to C-type by partial oxidation of Fe²⁺ to Fe³⁺ which occurs in FeSb_2−xPb_xO₄.¹¹ Of particular interest is the ferromagnetic ground state observed below ∼7.4 K in the isostructural CuAs₂O₄,¹⁴ where both intrachain and interchain magnetic exchange interactions are ferromagnetic. The synthesis and low temperature behaviour of highly conducting ferromagnetic materials of this type would be extremely interesting and a better understanding, initially, of how to create strong intrachain ferromagnetism would be beneficial. Although FeSb_2−xPb_xO₄ has chain ferromagnetism,¹¹ it is not clear to what extent this relates to the formation of Fe³⁺ since the large Pb²⁺ ion causes significant structural changes. Indeed, the Fe³⁺-containing material FePbBiO₄ has A-type magnetic order.¹⁵

Fig. 2 The common types of magnetic order observed for magnetic MSb₂O₄ phases: (a) A-type, (b) C-type.

The ⁵⁷Fe Mössbauer spectrum of FeSb₂O₄ at ca. 4.2 K is unusual, being the result of combined magnetic hyperfine and electric quadrupole interactions of comparable strength;^16,17 combining this spectral information with data recorded above T_N has been used to determine the splitting of the ⁵T_2g ground state of Fe²⁺ caused by its distorted octahedral environment.¹⁸ We reinvestigated the Mössbauer spectra recorded from FeSb₂O₄ and reported on how, in FeSb_2−xPb_xO₄, the anisotropic magnetic interactions give rise to situations in which weakly coupled Fe²⁺ ions appear to coexist in a non-magnetic state alongside Fe³⁺ ions in a magnetically ordered state.¹⁹

We report here an investigation of the nature of the transition from A- to C-type magnetic order by exploring materials in which the overall magnetic exchange is weakened by the substitution of non-magnetic Mg²⁺ ions on the Fe sites to form Fe_1−xMg_xSb₂O₄; in particular, we explored whether this caused a change in the magnetic order. A particularly interesting feature of Fe²⁺-containing materials is their ability to undergo partial oxidation associated with the accommodation of additional oxide ions within the channels and bonded to Sb ions²⁰ (see Fig. 1). In this report, we highlight topotactic oxidation of this type for the new Fe_1−xMg_xSb₂O₄ compounds. We report on the low-temperature magnetic properties of the oxidised phases Fe_1−xMg_xSb₂O_4+y revealed by magnetic susceptibility measurements, ⁵⁷Fe Mössbauer spectroscopy and PND to determine whether oxidation of this type also causes a change in magnetic order, as was observed for FeSb_2−xPb_xO₄.¹¹ This is important to determine the extent to which the presence of Fe³⁺ influences the magnetic order, since the framework structure suffers little change compared with the substitution of Pb²⁺ ions on the Sb³⁺ sites previously reported.¹¹

Experimental details

All Fe_1−xMg_xSb₂O₄ samples were prepared by heating stoichiometric amounts of Fe₂O₃, MgO, Sb₂O₃ and Sb metal in alumina crucibles contained within evacuated sealed silica tubes. Samples were heated (700 °C for x = 0, 650 °C for all other samples) two or three times with intermediate grinding to obtain single phase products. Oxygen insertion to form materials of the type Fe_1−xMg_xSb₂O_4+y was studied by heating samples in oxygen in a Netzsch STA 449 F1 Jupiter thermogravimetric analyser; larger samples were obtained by heating Fe_1−xMg_xSb₂O₄ in air at 400 °C for 10 min.

Powder X-ray diffraction (PXD) data were collected on a Bruker D8 diffractometer in transmission mode using Cu-K_α1 radiation selected using a primary beam germanium monochromator. PND data were collected on the high resolution D2B diffractometer at ILL, Grenoble, France. PXD data from the samples examined were used to calibrate the neutron wavelength and 1.5923 Å was adopted for all work reported here. Rietveld refinement of PXD and PND data used the General Structure Analysis System (GSAS)²¹ in conjunction with the Graphical User Interface, EXPGUI.²² Magnetic refinements for reduced and oxidised materials used Fe²⁺ and Fe³⁺ magnetic form factors, respectively. Magnetic susceptibility data were measured with a MPMS Quantum Design XL instrument (applied field 500 Oe) for samples during warming after both field cooled (FC) and zero field cooled (ZFC) cooling to 5 K. Scanning electron microscope (SEM) images were recorded from unpolished sintered pellets using a JEOL 6060 microscope and an acceleration voltage of 20 kV. ⁵⁷Fe Mössbauer spectra were recorded in constant acceleration mode using a ca. 25 mCi ⁵⁷Co source and a liquid helium closed-cycle cryorefrigerator. All the spectra were computer fitted with those recorded from Mg_0.50Fe_0.50Sb₂O₄ and Mg_0.25Fe_0.75Sb₂O₄ at 16 K being fitted using the method of Kundig.²³ All the chemical isomer shift data are quoted relative to metallic iron at room temperature.

Results and discussion

Structural characterisation of Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75)

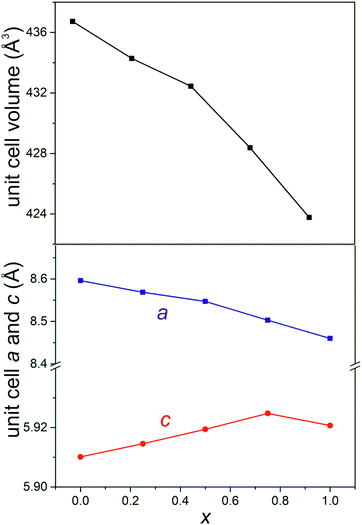
SEM images showed that materials of composition Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) had acicular crystals (Fig. 3) and energy-dispersive X-ray spectroscopy confirmed the cation ratios to be as expected for the desired compositions. FeSb₂O₄ and MgSb₂O₄ showed more uniform crystal shapes.

Fig. 3 SEM image recorded from Fe_0.75Mg_0.25Sb₂O₄.

PXD showed that materials with composition Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) were single phase with the tetragonal schafarzikite structure but with anisotropic broadening of some diffraction peaks consistent with the needle-like morphology revealed by SEM with the unique axis being along [001]. The parameters from the Rietveld refinement of the PXD data recorded from the Fe_1−xMg_xSb₂O₄ materials at 300 K are collected in Table 1 and the refinement plot for Fe_0.50Mg_0.50Sb₂O₄ is shown in Fig. 4. In Table 1, O1 corresponds to the apical site and O2 is equatorial. The fractional coordinates reported in Table 1 are close to those expected for a situation in which increasing amounts of magnesium substitute for iron on the octahedral sites. As expected from the crystal morphologies observed from SEM, preferred orientation was not apparent for FeSb₂O₄ and MgSb₂O₄; however, for the mixed iron–magnesium phases, a significant preferred orientation correction was necessary and was modelled using the March–Dollase correction in GSAS.²¹ Although the displacement parameters for Sb and O1 are normally anisotropic for this structure, the PXD data were insensitive to this and a common isotropic displacement parameter was adopted for all ions. The variations of unit cell parameters and volume with composition in Fe_1−xMg_xSb₂O₄ are shown in Fig. 5. The results show that increasing magnesium content causes the unit cell volume to decrease in accordance with the smaller ionic radius of 6-coordinate Mg²⁺ (0.72 Å) compared with Fe²⁺ (0.78 Å).²⁴Fig. 5 demonstrates that the overall contraction relates to a decrease in the a and b unit cell parameters, whereas c shows less change but actually increases as Mg is substituted for Fe in FeSb₂O₄. At first sight, this seems unusual since both apical and equatorial Fe(Mg)–O bond distances decrease similarly: for x = 0 and x = 1, for example, both decrease by ∼2.5%. We attribute this slight expansion in c to the unfavourable increase in Fe(Mg)−Fe(Mg) repulsions across the common edge of adjacent octahedra that would result if the decrease in bond lengths caused a simple contraction in c. Instead, the octahedra accommodate the shortened equatorial bonds by reducing the O2–Fe(Mg)–O2 bond angle, where the two O2 atoms form a common edge between two adjacent octahedra. In this way, the c parameter, and hence the dependent cation repulsions along the chains, are maintained. For example, the angles are 90.5° and 87.9° for x = 0 and x = 1, respectively.

Table 1 Structural data from PXD. Space group P4₂/mbc: Fe 4d (0,0.5,0.25); Sb 8h (x,y,0); O1 8g (x,0.5 + x,0.25); O2 8h (x,y,0)

		FeSb2O4	Fe0.75Mg0.25Sb2O4	Fe0.50Mg0.50Sb2O4	Fe0.25Mg0.75Sb2O4	MgSb2O4
a (Å)		8.59621(7)	8.5689(1)	8.5472(2)	8.5031(1)	8.4602(1)
c (Å)		5.91014(5)	5.91455(7)	5.91942(9)	5.92477(7)	5.92069(9)
Volume (Å^3)		436.729(9)	434.28(2)	432.44(2)	428.38(2)	423.77(2)
Sb	x	0.1763(2)	0.1773(3)	0.1765(3)	0.1762(3)	0.1753(3)
	y	0.1660(2)	0.1654(3)	0.1656(3)	0.1648(3)	0.1648(3)
O1	x	0.6793(9)	0.686(1)	0.682(1)	0.678(1)	0.680(1)
	y	0.1793(9)	0.186(1)	0.182(1)	0.178(1)	0.180(1)
O2	x	0.100(1)	0.093(6)	0.100(2)	0.101(2)	0.100(2)
	y	0.644(1)	0.632(2)	0.628(2)	0.633(2)	0.635(2)
U iso (Å^2)		0.0199(4)	0.0121(7)	0.0126(6)	0.0076(6)	0.0095(6)
Fe/Mg occupancy		—	0.73(1)/0.27(1)	0.57(1)/0.43(1)	0.29(1)/0.71(1)	—
χ ^2		2.763	1.490	1.292	1.884	1.963
R wp		0.047	0.049	0.048	0.064	0.077
R F ^2		0.041	0.078	0.063	0.052	0.060

---

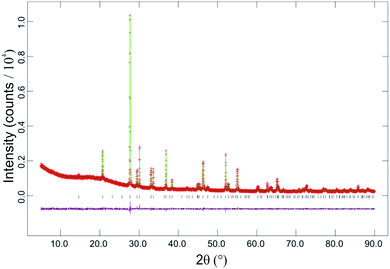Fig. 4 Plots for Rietveld structure refinement against PXD data recorded at 300 K from Fe_0.50Mg_0.50Sb₂O₄. Observed data are red crosses, calculated green line and difference plot is magenta.

Fig. 5 Variation of unit cell volume and parameters with increasing magnesium content in Fe_1−xMg_xSb₂O₄ derived from Rietveld refinement of the PXD data. (The estimated standard deviations are smaller than the symbols on the graph.)

Oxygen uptake in Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75)

The materials of composition Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) were found to incorporate oxygen into the empty channels on low temperature oxidation in oxygen or air, in similar fashion to that which we recently reported for other schafarzikite-related materials.²⁰ Thermogravimetric analysis of samples containing both Fe and Mg under flowing oxygen is shown in Fig. 6. The compounds showed topotactic uptake of oxygen in the approximate temperature range 300–500 °C before further oxidation at higher temperatures resulted in decomposition to form Sb₂O₄, MgSb₂O₆ and FeSbO₄. The properties of the materials formed at the low temperature plateaus were determined from samples prepared by heating the Fe_1−xMg_xSb₂O₄ phases at 400 °C for 10 min. under flowing oxygen. PXD confirmed the products to have retained the schafarzikite-related structure (Fig. 7) and that Fe_0.25Mg_0.75Sb₂O_4+y, for which the value of y is smallest (see Fig. 6), is most crystalline (smallest peak widths) and gave the smallest shifts in peak positions consistent with the sample having the lowest oxygen uptake. In contrast, the iron-rich materials Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50) gave samples which showed greater shifts in peak position and a lower degree of crystallinity. Rietveld refinement of the PXD data showed the materials to consist of two (or possibly more) schafarzikite-related phases whose unit cell sizes suggested that the phases had different levels of oxygen absorption. One phase was always closely related to the initial, unoxidised material, and suggested that for these low temperature oxidations, kinetic factors limited the potential to oxidise the centres of large particles. Attempts to produce single phase materials of composition Fe_1−xMg_xSb₂O_4+y by varying the heating conditions were unsuccessful. The observed increase in mass following heating of Fe_1−xMg_xSb₂O₄ at 400 °C for 10 min. exceeded that expected from simple oxidation of Fe²⁺ to Fe³⁺ (Table 2). It is seen, for example, that for x = 0.25 a mass increase of 2.3(1)% occurred which corresponds to a final oxygen content of 4.51(3), whereas oxidation of all Fe²⁺ to Fe³⁺ would provide a value of only 4.375. The amount of oxygen absorbed decreases as x increases, i.e. as the Fe²⁺ concentration decreases. This has previously been discussed in detail²⁰ and the enhanced oxygen uptake occurs because of the simultaneous oxidation of both Fe²⁺ to Fe³⁺ and Sb³⁺ to Sb⁵⁺.

Fig. 6 Thermogravimetric analysis of Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) in oxygen.

Fig. 7 PXD patterns recorded from oxidised samples, Fe_1−xMg_xSb₂O_4+y (x = 0.25, 0.50, 0.75).

Table 2 Absorbed oxygen content, y, in Fe_1−xMg_xSb₂O_4+y, after heating in oxygen to 400 °C and holding for 10 min

x	Mass increase (%)	y	Expected y for 100% oxidation of Fe^2+ to Fe^3+
0.25	2.3(1)	0.51(3)	0.375
0.50	1.8(1)	0.40(2)	0.25
0.75	0.98(7)	0.21(1)	0.125

---

Magnetic properties of Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75)

The magnetic susceptibility measurements recorded between 5 and 300 K for Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) are compared with FeSb₂O₄ (x = 0) in Fig. 8. The latter compound shows an antiferromagnetic transition at ∼45 K as previously reported.^3,4 The magnetic order has previously been reported to be complex with predominantly A-type order but with a minor C-type contribution;³ however, for the sample prepared in this study a significant ferromagnetic contribution is seen, which suggests a canted ground state. For x = 0.25 and 0.50, a low temperature divergence of FC and ZFC data at low temperatures is also indicative of canted antiferromagnetic order, whereas the magnesium-rich Fe_0.25Mg_0.75Sb₂O₄ appears paramagnetic. The inverse susceptibility data (Fig. 8) all obeyed the Curie–Weiss law and the Weiss constants, effective magnetic moments and magnetic ordering temperatures (T_N) are collated in Table 3. The values of T_N correspond to the low temperature maximum in the ZFC data (x = 0.25) and the onset of significant divergence between ZFC and FC data (x = 0.50). The negative Weiss constants are indicative of predominantly antiferromagnetic exchange and the canted configuration for x ≤ 0.50 is similar to that observed in FeSb_2−xPb_xO₄.¹¹ The effective magnetic moments determined for all four materials are seen to be significantly larger than the spin-only value for high-spin Fe²⁺ ions, 4.9 μ_B. However, they are similar to those expected for octahedral Fe²⁺ ions, where the ⁵T_2g ground state results in a significant orbital contribution to the moment, and agree well, for example, with the range reported for Fe²⁺ substituted into MgO: 5.5–5.7 μ_B.²⁵ It should be noted that the coordination around Fe is distorted in the compounds under investigation, so that comparisons can only be approximate. The magnetic ordering temperatures decrease with increasing magnesium content, consistent with the Fe²⁺–Fe²⁺ magnetic exchange interactions being weakened by the presence of non-magnetic Mg²⁺ ions. The change in the Weiss constant also reflects the weakening of magnetic exchange as x increases but |θ| is always significantly larger than the ordering temperatures. This has previously been observed in related materials¹² and is commonly observed for antiferromagnetic order when the mean field of each magnetic sublattice is not solely determined by the other sublattice.

Fig. 8 Variation of magnetic susceptibility (χ) with temperature for Fe_1−xMg_xSb₂O₄: (a) x = 0, (b) x = 0.25, (c) x = 0.50, (d) x = 0.75. FC and ZFC data are represented by open red squares and solid blue squares, respectively. Insets show plots of 1/χ versus T fitted to the Curie–Weiss law; linear fits are marked in black.

Table 3 Magnetic parameters obtained from SQUID magnetometry data for Fe_1−xMg_xSb₂O₄

x	θ/K	μ eff per Fe/μB	T N/K
0.0	−131(2)	6.3(1)	45(5)
0.25	−92(2)	5.9(1)	45(5)
0.50	−60(2)	5.8(1)	20(2)
0.75	−25(1)	5.5(1)	—

---

In order to explore the nature of the magnetic order in Fe_1−xMg_xSb₂O₄, PND data were collected at 300 and 4 K for Fe_0.5Mg_0.5Sb₂O₄. The observed and calculated profiles for 300 K data are shown in Fig. 9(a) and, at first sight, the data collected at 4 K (Fig. 9(b)) appeared similar; the figure shows only the low angle range since we are primarily concerned with the effects of magnetic order. However, it is seen (Fig. 9(b)) that refinement using a single nuclear phase consistent with the 300 K structure produced anomalies at low angle which suggested magnetic order. The scattering is, in fact, fitted well (Fig. 9(c)) by including an A-type magnetic phase shown in Fig. 2(a). The refined magnetic moment of 2.9(1) μ_B is significantly lower than the spin-only value of 4 μ_B; although covalence reduces the moment, the large orbital contribution will increase it. For example, in LiFePO₄, the Fe²⁺ moment is reported to be 4.15(3) μ_B from PND.²⁶ The reduction in magnetic moment therefore suggests incomplete magnetic order, presumably resulting from the weaker overall exchange caused by the Mg substitution. In fact, the moment suggests approximately 20–30% paramagnetic Fe²⁺ ions and it may be relevant that a random arrangement of Fe and Mg would result in 25% of Fe²⁺ ions having Mg²⁺ for both its nearest neighbours which may result in the disappearance of magnetic order for this site.

Fig. 9 PND data from Fe_0.50Mg_0.50Sb₂O₄ collected at 300 and 4 K. (a) 300 K; (b) 4 K fitted to nuclear scattering only; (c) 4 K fitted to nuclear and magnetic scattering. Observed data are red crosses, calculated green line and difference plot is magenta.

⁵⁷Fe Mössbauer spectra were recorded at 300 and 16 K for samples with x = 0.25, 0.50, 0.75. Spectral parameters for original and oxidised samples of composition Fe_1−xMg_xSb₂O₄ (x = 0.50, 0.75) at 16 K are contained in Table 4, those from Fe_0.75Mg_0.25Sb₂O₄ at 300 and 16 K are collected in Table 5.

Table 4 ⁵⁷Fe Mossbauer parameters recorded at 16 K from Fe_1−xMg_xSb₂O₄ and Fe_1−xMg_xSb₂O_4+y (x = 0.50, 0.75)

	δ ± 0.02 (mm s^−1)	Δ ± 0.02 (mm s^−1)	B hf ± 0.5 (T)	θ (°)	ψ (°)	η	Area ± 3%
a η is the asymmetry parameter for the electric field gradient at the nucleus; θ and ψ are the polar and azimuthal angles that specify the direction of the magnetic field with respect to the coordinates of the electric field gradient.
Fe0.50Mg0.50Sb2O4	1.26	2.70	12.1	38.7	0	0.25	22
	1.23	2.94					78
Fe0.50Mg0.50Sb2O4+y	0.46	1.46					20
	0.52	−0.06	46.7				16
	0.56	−0.12	42.4				64
Fe0.25Mg0.75Sb2O4	1.21	2.89					100
Fe0.25Mg0.75Sb2O4+y	1.21	2.80					31
	0.41	0.46					69

---

Table 5 ⁵⁷Fe Mossbauer parameters recorded from Fe_0.75Mg_0.25Sb₂O₄

T	δ ± 0.02 (mm s^−1)	Δ or e^2qQ/2 ± 0.02 (mm s^−1)	B hf ± 0.5 (T)	θ (°)	ψ (°)	η	Area ± 3%
a η is the asymmetry parameter for the electric field gradient at the nucleus; θ and ψ are the polar and azimuthal angles that specify the direction of the magnetic field with respect to the coordinates of the electric field gradient.
300 K	1.08	2.09
16 K	1.24	2.85	17.0	63	0	0.25	35
	1.24	2.85	13.7	54	0	0.25	38
	1.36	2.85	5.0	0.1	0	0.25	27

---

The ⁵⁷Fe Mossbauer spectrum recorded from Fe_0.25Mg_0.75Sb₂O₄ at 16 K (Fig. 10) shows a quadrupole split absorption characteristic of paramagnetic Fe²⁺. The absence of magnetic hyperfine interaction at 16 K contrasts with the spectra recorded¹⁹ from FeSb₂O₄ and suggests that the high concentration of Mg²⁺ on the cation sites along the c-axis precludes significant magnetic interactions between the Fe²⁺ ions because of their increased separation. The result is consistent with magnetisation data which showed no magnetic transition between 5 and 300 K (see above).

Fig. 10 ⁵⁷Fe Mössbauer spectra recorded from materials of composition Fe_1−xMg_xSb₂O₄ at 16 K.

For x = 0.5, the ⁵⁷Fe Mossbauer spectrum recorded at 16 K (Fig. 10 and Table 4) showed a major quadrupole split absorption corresponding to paramagnetic Fe²⁺ ions and a minor area component corresponding to magnetically ordered Fe²⁺ ions which was best fitted according to the method of Kundig.²³ The material thus shows mixed magnetic phases. Magnetisation measurements indicated a transition to a magnetically ordered state at 20 K (see above and Table 3) but the transition is not clearly defined. Clearly this sample is mainly paramagnetic at 16 K, and ordering probably occurs over a substantial temperature range caused by the statistical distribution of Fe²⁺ and Mg²⁺ cations. It should be recalled that the PND data suggest some disorder even at 4 K in this material.

For x = 0.25, the ⁵⁷Fe Mössbauer data at 16 K (Fig. 10 and Table 5) were significantly different from the spectra recorded from compositions with lower iron contents. The spectrum was also best fitted according to the method of Kundig²³ and was composed of a broad-lined magnetically split pattern similar to that recorded¹⁹ from FeSb₂O₄ at 30 K and reflecting similar combined magnetic hyperfine and electric quadrupole interactions of comparable strength. The result is consistent with magnetisation measurements which indicated magnetic ordering at ca. 45 K (see above, Table 3) and demonstrates that the higher iron content facilitates such magnetic order. Interestingly, the magnetic component in the spectrum was best fitted to three sextets. The parameters of the component with the largest magnetic hyperfine field are very similar to those recorded from FeSb₂O₄ at 30 K.¹⁹ The chemical isomer shift and quadrupole interaction of the component with magnetic hyperfine field B_hf = 13.7 T are also similar to those of FeSb₂O₄, and the smaller magnetic hyperfine field probably reflects the effect of magnesium weakening the magnetic interactions. The parameters of the third component (B_hf = 5 T) are very different, and also indicate weaker magnetic interactions. The spectrum recorded at 300 K (Fig. 11 and Table 5) showed a quadrupole split absorption characteristic of paramagnetic Fe²⁺, similar to that recorded from FeSb₂O₄ at 300 K.¹⁹

Fig. 11 ⁵⁷Fe Mössbauer spectra recorded from Fe_0.75Mg_0.25Sb₂O₄ and Fe_0.75Mg_0.25Sb₂O_4+y at 300 K.

Magnetic properties of Fe_1−xMg_xSb₂O_4+y (x = 0.25, 0.50, 0.75)

PXD data from the oxidised samples revealed that each comprised a mixture of closely related phases with similar structure. It was assumed that the samples were inhomogeneous with respect to the distribution of the excess oxygen, y. Magnetic susceptibility data for the samples with x = 0.25, 0.50 and 0.75 are given in Fig. 12, which shows plots of susceptibility, χ, versus T and 1/χ versus T. Relevant magnetic data deduced from the plots are presented in Table 6. As for the original samples, magnetic transitions are observed for x = 0.25 and 0.50 but not for x = 0.75. For x = 0.25, the transition is clearly to an antiferromagnetic ground state but for x = 0.50, the appearance is similar to a simple ferromagnetic transition but with a very low resultant moment. It seemed likely that this transition actually resulted in a canted antiferromagnet which was subsequently confirmed using PND (see later). Whereas the data for x = 0.25 and 0.50 conform to the Curie–Weiss law, the sample with lowest Fe concentration (x = 0.75) showed slight curvature in the 1/χ–T plot. This probably reflects a small diamagnetic effect and the susceptibility could be modelled well using a modified Curie–Weiss equation that includes a temperature-independent component, α (χ = C/(T − θ) + α); the χ–T fit obtained is included in Fig. 12(c). Table 6 shows that all the magnetic moments are slightly higher than that expected for Fe³⁺ (spin-only moment 5.9 μ_B) even though no orbital contribution is expected for octahedral Fe³⁺ ions. The decrease in θ as x increases (Table 6) reflects the weakening of magnetic exchange energy as the Mg content increases. It is also interesting that the Weiss constants (θ) in Table 6, although confirming overall antiferromagnetic exchange above the ordering temperature, are significantly lower than those for the samples prior to oxidation (Table 3). This was thought likely to indicate the occurrence of different magnetic order compared with the unoxidised materials. The low temperature magnetic order was therefore examined for one sample (x = 0.50) using PND data collected at 4 K even though PXD data suggested that the samples contained some degree of inhomogeneity.

Fig. 12 Variation of magnetic susceptibility (χ) with temperature for Fe_1−xMg_xSb₂O_4+y: (a) x = 0.25, (b) x = 0.50, (c) x = 0.75. FC and ZFC data are shown using open red squares and solid blue squares, respectively. Insets to (a) and (b) show plots of 1/χ versus T fitted to the Curie–Weiss law; the inset to (c) shows χ versus T fitted to the Curie–Weiss law including a small temperature-independent component.

Table 6 Magnetic parameters obtained from SQUID magnetometry data for Fe_1−xMg_xSb₂O_4+y

x	θ/K	μ eff per Fe/μB	T N/K
0.25	−69(2)	6.4(1)	56(5)
0.50	−37(2)	6.7(1)	29(4)
0.75	−29(2)	6.4(2)	—

---

Structure refinements against neutron data were, in fact, found to be satisfactory using a single phase, and fits were certainly very good in the low angle region used for magnetic structure evaluation. Refinements for the x = 0.50 sample at 300 and 4 K are shown in Fig. 13 and refined structural parameters are given in Table 7. For both data sets the Mg/Fe site occupancy remained as was weighed out within experimental error and was therefore constrained at this value. The Sb and O1 displacement parameters were strongly anisotropic, as is usually observed in this structure, and were refined accordingly. To improve the precision in the interstitial oxygen (O3) occupancy, the O3 and O2 isotropic displacement parameters were constrained to be equal. It is seen that the 300 K data can be fitted satisfactorily to a single phase as is shown for the low angle region in Fig. 13(a). The excess oxygen was located within the channels in sites previously reported²⁰ and the refined O3 position is in excellent agreement with that reported for FeSb_1.25Pb_0.75O_4.24, for which x = 0.540(5), y = 0.417(3), z = 0.254(7). Changes in the Mg/Fe coordination environment caused by oxidation were deduced from Mg/Fe−O bond distances and angles in Fe_0.50Mg_0.50Sb₂O₄ and Fe_0.50Mg_0.50Sb₂O_4+y (from PND data at 300 K), which are given in Table 8. Reduction in the bond distances can be attributed to the smaller Fe³⁺ ionic radius (compared with Fe²⁺)²⁴ and the apical bond to O1 undergoes a larger contraction (3.1%) than the equatorial bond to O2 (1.4%). The O2−Mg/Fe−O2 angle where the two O2 atoms form a common edge is reduced from 88.9° to 86.6° by oxidation which is caused by stretching of the octahedra in the chains and relates to an increase in c from 5.9228(1) Å to 5.9577(2) Å. This increase is caused by the enhanced cation repulsions along the chains after oxidation.²⁰

Fig. 13 PND data from Fe_0.50Mg_0.50Sb₂O_4+y collected at 300 and 4 K. (a) 300 K; (b) 4 K fitted to nuclear scattering only; (c) 4 K fitted to nuclear and magnetic scattering. Observed data are red crosses, calculated green line and difference plot is magenta.

Table 7 Results of Rietveld refinement against PND data at 300 K and 4 K (data in italics) for Fe_0.50Mg_0.50Sb₂O_4+y. Space group P4₂/mbc: Mg/Fe 4d, Sb 8h, O1 8g, O2 8h, O3 16i

Atom	x	y	z	Site occupancy	100 × Uiso/Å^2
a = 8.3895(4) (8.3766(4)) Å; c = 5.9577(2) (5.9459(2)) Å. Magnetic moment at 4 K: 2.24(5) μB. χ^2 = 3.99 (6.10); Rwp = 0.049 (0.055); RF^2 = 0.044 (0.049).a Anisotropic displacement parameters × 100/Å^2.
Mg/Fe	0	0.5	0.25	0.5/0.5	1.64(7)
	0	0.5	0.25	0.5/0.5	1.04(6)
Sb	0.1648(6)	0.1596(6)	0	1.0
	0.1642(5)	0.1587(5)	0	1.0
O1	0.6758(3)	0.1758(3)	0.25	1.0
	0.6742(3)	0.1742(3)	0.25	1.0
O2	0.1027(4)	0.6320(5)	0	1.0	2.29(8)
	0.1017(4)	0.6315(4)	0	1.0	1.63(7)
O3	0.551(3)	0.415(3)	0.245(4)	0.098(4)	2.29(8)
	0.558(2)	0.420(2)	0.251(3)	0.107(3)	1.63(7)

---

Atom	U 11	U 22	U 33	U 12	U 13	U 23
Sb	1.9(3)	4.0(3)	1.7(2)	0.2(2)	0	0
	1.8(2)	3.3(3)	0.5(1)	0.2(1)	0	0
O1	5.3(2)	5.3(2)	1.1(1)	−3.1(2)	−0.8(2)	0.8(2)
	3.6(1)	3.6(1)	0.5(1)	−2.0(2)	−0.4(1)	0.4(1)

---

Table 8 Bond distances (Å) and angles (°) around Mg/Fe in Fe_0.50Mg_0.50Sb₂O₄ and Fe_0.50Mg_0.50Sb₂O_4+y at 300 K

	Fe0.50Mg0.50Sb2O4	Fe0.50Mg0.50Sb2O4+y
Mg/Fe–O1	2.151(1) [×2]	2.085(4) [×2]
Mg/Fe–O2	2.075(1) [×4]	2.046(3) [×4]
O1–Mg/Fe–O2	83.58(4); 96.42(4)	85.1(1); 94.9(1)
O2–Mg/Fe–O2	88.93(6); 92.50(6)	86.6(2); 94.3(2)

---

At 4 K, fitting using a non-magnetic phase shows additional peaks (Fig. 13(b)), but these are seen to be very different from those observed for the unoxidised material, Fig. 9(b). The peak at ∼11° is, in fact, characteristic of C-type magnetic order, Fig. 2(b), in which the moments are aligned along [001] with ferromagnetic order within a given chain. Including the corresponding magnetic unit cell resulted in the satisfactory fit shown in Fig. 13(c). In accordance with the mass increase on oxidation (Table 2), it was assumed that most Fe²⁺ had oxidised to Fe³⁺ and the Fe³⁺ magnetic form factor was adopted for the refinement. The magnetic moment per Fe³⁺ ion was determined to be 2.24(5) μ_B. The small peak seen at ∼19° corresponds to magnetic scattering from a very small (<1% by weight) contamination from Fe₃O₄, which is difficult to avoid in the synthesis of Fe-containing schafarzikite phases. The O3 site occupancies for the 300 and 4 K data agree well, not only with each other (indicating the compositions Mg_0.50Fe_0.50Sb₂O_4.39(2) and Mg_0.50Fe_0.50Sb₂O_4.43(1), respectively), but also with thermogravimetric data (Mg_0.50Fe_0.50Sb₂O_4.40(2)).

The magnetic structure is of interest for two main reasons:

• The magnetic ground state changes from A- to C-type on oxidation. The ferromagnetic ordering in the chains can be attributed to a reduction in the direct Fe–Fe antiferromagnetic exchange that results from the d-orbital contraction in Fe³⁺ and the increase in Fe–Fe separation along c.

• The moment is substantially lower than that expected for Fe³⁺ and is even lower than that found for the unoxidised sample (2.9(1) μ_B per Fe²⁺ ion) as discussed above. This reduction is indicative of ∼40–50% of the Fe³⁺ ions being magnetically disordered and paramagnetic. This aspect will be considered further during discussion of the results from Mössbauer spectroscopy.

The presence of C-type magnetic order in Fe_0.50Mg_0.50Sb₂O_4+y is consistent with the change in magnetic order observed in FeSb_2−xPb_xO₄ where oxidation results from the substitution of Pb²⁺ for Sb³⁺, and may explain the higher magnetic moments calculated from the susceptibility data. High moments were also reported for some materials containing mixed transition metal ions (Mn/Co and Fe/Co) in this structure and this was attributed to the occurrence of small clusters of cations for which ferromagnetic order was retained above the long-range magnetic ordering temperature.¹² In the present study, C-type order provides ferromagnetic order within each individual chain of octahedra, so small groups of Fe³⁺ cations would be expected to experience strong ferromagnetic exchange; the general disorder caused by the substitution of Mg²⁺ ions would weaken the antiferromagnetic exchange between the chains so some ferromagnetic clusters could exist to high temperatures and result in the slightly high magnetic moments determined from the susceptibility data for the oxidised samples, Table 6.

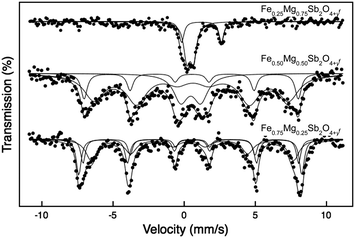
The ⁵⁷Fe Mössbauer spectra recorded from Fe_1−xMg_xSb₂O_4+y at 16 K are shown in Fig. 14. The spectrum for x = 0.75 shows two quadrupole split absorptions with chemical isomer shifts characteristic of Fe²⁺ and Fe³⁺ (Table 4). The result shows that ca. 69% of the Fe²⁺ in Fe_0.25Mg_0.75Sb₂O₄ is oxidised to Fe³⁺ – presumably the remaining Fe²⁺ could be oxidised under different heating conditions. It is important to note that oxidation of Sb³⁺ to Sb⁵⁺ has been shown to occur²⁰ simultaneously during such oxidations so that the oxygen content of the sample (y) is not directly related to the Fe²⁺ : Fe³⁺ ratio. The absence of magnetic hyperfine splitting illustrates the effective blocking by Mg²⁺ of magnetic interactions between Fe³⁺/Fe²⁺ ions for this composition.

Fig. 14 ⁵⁷Fe Mössbauer spectra recorded at 16 K from materials of composition Fe_1−xMg_xSb₂O_4+y.

The ⁵⁷Fe Mössbauer spectrum recorded at 16 K Fe_0.50Mg_0.50Sb₂O_4+y (Fig. 14 and Table 4) is composed of broad lines which are best fitted to a doublet and two sextets. The chemical isomer shifts of all components are characteristic of Fe³⁺ and indicate complete oxidation, in contrast to the data from Fe_0.25Mg_0.75Sb₂O_4+y. It appears that the x = 0.50 material, with a higher iron content, has ca. 80% of the Fe³⁺ being magnetically ordered at 16 K. The different hyperfine fields for the magnetically ordered species relate to the local Fe/Mg distribution and will be discussed in detail in a subsequent publication. The presence of a significant amount of paramagnetic Fe³⁺ ions is therefore deduced from both PND and Mössbauer data, although the reduced magnetic moment from the PND data is suggestive of a higher percentage that does not contribute to the primary C-type order included in the refinement.

The spectrum recorded from Fe_0.75Mg_0.25Sb₂O_4+y at 300 K (Fig. 11 and Table 9) was best fitted to two quadrupole split absorptions whilst that recorded at 16 K (Fig. 14 and Table 9) was best fitted to three sextets. The chemical isomer shifts of all components are characteristic of Fe³⁺ and reflect the ease of oxidation of Fe²⁺ to Fe³⁺ in the Fe_1−xMg_xSb₂O₄ series. As for the x = 0.50 compound, the presence of Fe³⁺ species with different local environments, both structural and magnetic, can be related to the different local Fe/Mg distributions that are possible around a given Fe³⁺ ion.

Table 9 ⁵⁷Fe Mossbauer parameters recorded from Fe_0.75Mg_0.25Sb₂O_4+y

Temperature (K)	δ ± 0.02 (mm s^−1)	Δ or e^2qQ/2 ± 0.02 (mm s^−1)	B hf ± 0.5 (T)	Area ± 3%
300	0.38	0.97		33
	0.35	0.57		67
16	0.48	−0.12	48.6	34
	0.53	−0.14	46.9	23
	0.45	0.26	43.8	43

---

Conclusions

Three new phases of composition Fe_1−xMg_xSb₂O₄ (x = 0.25, 0.50, 0.75) have been synthesised and shown to adopt the schafarzikite structure. The materials with x = 0.25 and 0.50 are canted antiferromagnets with A-type magnetic order below T_N, whereas for x = 0.75 paramagnetic behaviour occurs. The materials readily absorb oxygen between ca. 300 and 500 °C to an extent which exceeds that corresponding only to the simple oxidation of the Fe²⁺ ions. Although the oxidised materials are not strictly single phase, because of inhomogeneity of the excess oxygen concentration, their magnetic properties have been reliably determined using PND and magnetic susceptibility data. Importantly, the oxidised materials with x = 0.25 and x = 0.50 also undergo a magnetic ordering transition at low temperature but now the ground state is C-type. This confirms that for Sb-containing materials, the oxidation of Fe²⁺ to Fe³⁺ induces the presence of ferromagnetic order on the chains of octahedra (C-type order). The interpretation of the detailed features of the Mössbauer spectra recorded from magnetically ordered materials created by substitution of magnesium ions into the parent material FeSb₂O₄ are complex because of different local configurations of cations relating to the Fe/Mg statistical distribution.

Acknowledgements

We thank the Engineering and Science Research Council for financial support of this research (EPSRC EP/L014114/1) and also acknowledge financial support from Spanish MINECO (Project MAT 2015-64110-C2-1-P). We are grateful to EPSRC, EU and ILL for the provision of PND facilities and to Dr Emma Suard for assistance in collecting the PND data. The X-ray diffractometers, TG analyser and magnetometer used in this research were obtained through Birmingham Science City: Creating and Characterising Next Generation Advanced Materials (West Midlands Centre for Advanced Materials Project 1), with support from Advantage West Midlands (AWM) and part funded by the European Regional Development Fund (ERDF). The Advanced Materials Facility is part of the Centre for Chemical and Materials Analysis in the School of Chemistry at the University of Birmingham. Data associated with the results shown in this paper are accessible from the University of Birmingham Archive: http://epapers.bham.ac.uk/2985/.

References

1. J. R. Gavarri and D. Weigel, J. Solid State Chem., 1975, 13, 252.
2. R. Fischer and F. Pertlik, Tschermaks Mineral. Petrogr. Mitt., 1975, 22, 236.
3. J. A. Gonzalo, D. E. Cox and G. Shirane, Phys. Rev., 1966, 147, 415.
4. R. Chater, J. R. Gavarri and A. W. Hewat, J. Solid State Chem., 1985, 60, 78.
5. E. Koyama, I. Nakai and K. Nagashima, Nippon Kagaku Kaishi, 1979, 6, 793.
6. J. R. Gavarri, G. Calvarin and B. Chardon, J. Solid State Chem., 1983, 47, 132.
7. H. T. Witteveen, Solid State Commun., 1971, 9, 1971.
8. S. Ståhl, Ark. Kemi, Mineral. Geol., 1943, 17B, 1.
9. M. T. Atanasova, A. M. Strydom, C. J. H. Schutte, L. C. Prinsloo and W. W. Focke, J. Mater. Sci., 2014, 49, 3497.
10. M. Abakumov, M. G. Rozova, E. V. Antipov, J. Hadermann, G. Van Tendeloo, M. Lobanov, M. Greenblatt, M. Croft, E. V. Tsiper, A. Llobet, K. A. Lokshin and Y. Zhao, Chem. Mater., 2005, 17, 1123.
11. M. J. Whitaker, R. D. Bayliss, F. J. Berry and C. Greaves, J. Mater. Chem., 2011, 21, 14523.
12. J. Cumby, B. P. de Laune and C. Greaves, J. Mater. Chem. C, 2016, 4, 201.
13. E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545.
14. K. Caslin, R. K. Kremer, F. S. Ravazi, A. Shulz, A. Muñoz, F. Pertlik, J. Liu, M.-H. Whangbo and J. M. Law, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014412.
15. B. P. de Laune, F. J. Berry, J. F. Marco, S. L. Horswell and C. Greaves, J. Mater. Chem. C, 2016, 4, 5320.
16. F. Varret, P. Imbert, A. Gerard and F. Hartmann-Boutron, Solid State Commun., 1968, 6, 889.
17. G. Pettit and M. R. Meder, Hyperfine Interact., 1978, 5, 323.
18. M. Eibschutz and U. Ganiel, Solid State Commun., 1968, 6, 775.
19. R. D. Bayliss, F. J. Berry, B. P. de Laune, C. Greaves, O. Helgason, J. F. Marco, M. F. Thomas, L. Vergara and M. J. Whitaker, J. Phys.: Condens. Matter, 2012, 24, 276001.
20. P. de Laune, G. J. Rees, M. J. Whitaker, H.-Y. Hah, C. E. Johnson, J. A. Johnson, D. E. Brown, M. G. Tucker, T. C. Hansen, F. J. Berry, J. V. Hanna and C. Greaves, Inorg. Chem., 2017, 56, 594.
21. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR 86-748, 2004.
22. H. Toby, J. Appl. Crystallogr., 2001, 34, 210.
23. W. Kundig, Nucl. Instrum. Methods, 1967, 48, 219.
24. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
25. M. Valigi, F. Pepe and M. Schiavello, J. Chem. Soc., Faraday Trans., 1975, 71, 1631.
26. G. Rousse, J. Rodriguez-Carvajal, S. Patoux and C. Masquelier, Chem. Mater., 2003, 15, 4082.

---