Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Green-blue light-emitting platinum(II) complexes of cyclometallated 4,6-difluoro-1,3-dipyridylbenzenes showing mesophase organisation†
Valery N.
Kozhevnikov
 *a,
Bertrand
Donnio
*bc,
Benoît
Heinrich
b,
J. A. Gareth
Williams
d and
Duncan W.
Bruce
*e
*a,
Bertrand
Donnio
*bc,
Benoît
Heinrich
b,
J. A. Gareth
Williams
d and
Duncan W.
Bruce
*e
aSchool of Life Sciences, Northumbria University, Newcastle-Upon-Tyne, NE1 8ST, UK. E-mail: valery.kozhevnikov@northumbria.ac.uk
bInstitut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), UMR 7504, CNRS-Université de Strasbourg, 23 rue du Loess, BP43, 67034 Strasbourg cedex 2, France. E-mail: bertrand.donnio@ipcms.unistra.fr
cComplex Assemblies of Soft Matter Laboratory (COMPASS), UMI 3254, CNRS-Solvay-University of Pennsylvania, CRTB, 350 George Patterson Boulevard, Bristol, PA 19007, USA
dDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK
eDepartment of Chemistry, University of York, Heslington, YORK. YO10 5DD, UK. E-mail: duncan.bruce@york.ac.uk
First published on 16th September 2015
Abstract
Blue-green light-emitting phosphorescent PtII complexes of 1,3-bis(2-pyridyl)benzene are reported that incorporate hexadecyl-containing fragments in the 5-position of the pyridine rings. Along with the more classical half disc-shaped hexacatenar molecule with six pendant alkoxy chains, which shows an R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m mesophase, the simpler complex functionalised by just two alkoxy chains, one at each pyridyl 5-position, was also found to be mesomorphic. The luminescence of pure films obtained from these complexes is orange-red, dominated by the excimer-like emission, and is independent of the thermal history of the film. The mesophases of the complexes are three-dimensional and columnar in nature – all are based on a two-dimensional hexagonal arrangement extended into the third dimension.
m mesophase, the simpler complex functionalised by just two alkoxy chains, one at each pyridyl 5-position, was also found to be mesomorphic. The luminescence of pure films obtained from these complexes is orange-red, dominated by the excimer-like emission, and is independent of the thermal history of the film. The mesophases of the complexes are three-dimensional and columnar in nature – all are based on a two-dimensional hexagonal arrangement extended into the third dimension.
Introduction
Phosphorescent complexes of PtII and IrIII underpin modern developments in OLED technology, providing the possibility to convert both singlet and triplet excitons into light on a useable timescale (μs) and therefore improving the efficiency of the device.1 The field has undergone huge developments over the past decade and numerous metal complexes have been synthesised. More recently, multifunctional materials were successfully developed aiming for simultaneous optimisation of not only emissive but also charge-transport and other properties.2 The morphology of the thin-films is a very important characteristic for OLED device function; for example, microcrystalline morphologies lead to undesirable grain boundaries and so most OLED devices employ amorphous thin films. Self-organising materials such as liquid crystals provide for films that can be organised and ordered over long length scales and which can, therefore, contribute to improved charge-transport or induce effects such as polarised emission.3 Early results based on liquid-crystalline organic molecules have been quite promising.4 It is, therefore, of great relevance to combine the concepts of phosphorescent OLEDs with the intrinsic self-organising nature and self-healing feature of liquid crystals.To be able to achieve this, it is necessary to design metal complexes that are both highly luminescent as well as liquid crystalline. The logical concept would be to take the best-performing complexes, for example cyclometallated IrIII or PtII complexes, and induce liquid crystallinity by designing suitably anisotropic derivatives.5 Square-planar, cyclometallated PtII complexes are easier targets for this purpose due to their planar geometry, and many such materials have already been reported. For example PtII complexes formed by bidentate ligands such as phenylpyridines,6 phenylpyrimidines7 and related pyridylpyrazolates8 were modified successfully to induce mesomorphism while remaining highly luminescent. In our recent studies, liquid crystallinity was induced in PtII complexes of 1,3-bis(2-pyridyl)benzene (dpybH)9 by incorporating six terminal, aliphatic chains in order to create a ‘half-disc’ geometry. Although very interesting photophysical effects related to the liquid-crystalline properties of the material were observed, the complexes showed only moderate luminescence quantum efficiencies of the order of ϕ = 0.2. Moreover, the emission was limited to the yellow region of the spectrum, which is of little importance for OLED applications where the primary colours blue, green and red are of prime interest. Here we report on a new, highly luminescent, mesomorphic PtII complex emitting in the blue-green region, as well as the unexpected finding that much simpler molecules – containing just two terminal aliphatic chains – also show mesophase behaviour.
Results
Synthesis
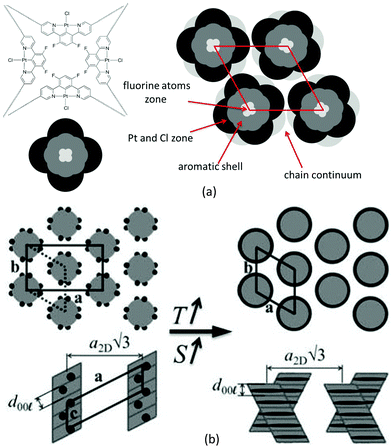
The syntheses of the ligands and their corresponding PtII complexes are depicted in Scheme 1. The highly versatile synthon 4,6-difluoro-1,3-bis(5-hydroxypyrid-2-yl)benzene, 3, was designed specifically: (i) to bind PtII ions through N^C^N cyclometallation and (ii) to allow the incorporation of a wide range of lipophilic fragments on both sides through the available hydroxy functions. The diboronic acid derivative 1 was reacted with 2-bromo-5-methoxypyridine using a Suzuki–Miyaura protocol. The resulting dimethoxy derivative 2 was first demethylated using boron tribromide to give the corresponding dihydroxy derivative, 3, and then either alkylated by 1-bromohexadecane to give ligand 4 or reacted with 3,4,5-tri(hexadecyloxy)benzoic acid to give ligand 6. Cycloplatination of 4 was achieved upon reaction with potassium tetrachloroplatinate(II) in acetic acid under reflux to give the final complexes, 5 in 87% yield. In the synthesis of 7, cis-[PtCl2(NCPh)2] was used instead of potassium tetrachloroplatinate and gave the target complex in 46% yield. Neither ligand, 4 and 6, was found to be mesomorphic. In the case of 4, as a simple bent-core material it would not be expected to be mesomorphic with only three rings, whereas with 6 the whole rigid core is rather short (especially given the bent-core nature of the compound) for a mesophase to be seen with six terminal chains.Thermal behaviour of complexes 5 and 7
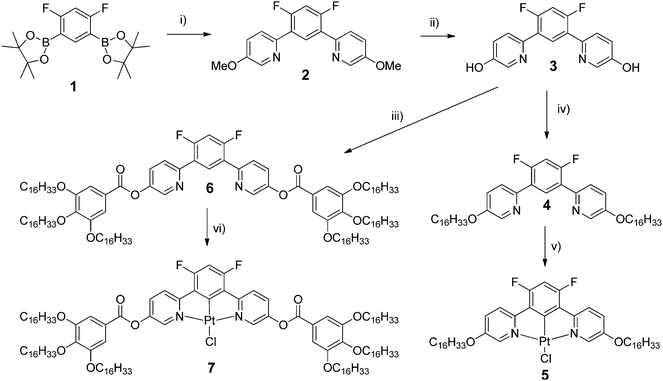
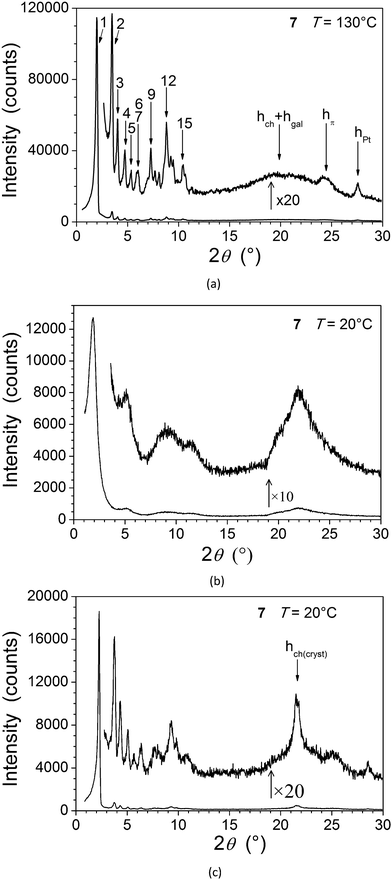
The thermal behaviour of both types of metal complexes (Table 1) and the nature of their supramolecular self-organisation were investigated by differential scanning calorimetry (DSC), polarised optical microscopy (POM) and small-angle X-ray scattering (SAXS). All the data indicate the formation of mesophases for the two complexes in contrast to the precursor ligands 4 and 6. The hexacatenar complex 7 is a pasty solid as obtained and at room temperature, which crystallises partially between 80 and 120 °C on heating, and eventually melts into a single mesophase at around 120 °C (Fig. S1, ESI† and Table 1). The mesophase is maintained up to the isotropisation temperature of around 145 °C, and is recovered on cooling, persisting down to room temperature where partial crystallisation occurs. It is believed that the pasty solid at room temperature is, therefore, a fluid material that has only crystallised partially. No characteristic optical texture was observed, but the presence of fluid and birefringent domains was indicative of mesophase formation in this temperature range (Fig. 1a). A SAXS pattern of 7 recorded at room temperature and obtained on cooling largely confirms these interpretations and, in particular, shows that the frozen state preserves a segregated molecular organisation similar to that in the fluid mesophase (Fig. 2a and c). The appearance of a characteristic broadened reflection hch(cryst) between 4.10 and 4.15 Å provide evidence that the solidification process consists in the crystallisation of the aliphatic domains according to the rotator phase-like lateral arrangements.10,11 On the other hand, the general profile of the overall reflections and scattering signals approximately fits the diffuse signals, which compose the pattern in the pristine state (see Fig. 2b). Hence the molecular organisation is likely the same from the beginning, except that it limits to small correlation volumes before the first heating in a fluid state.| Compound | Phase sequence | T onset/°C | ΔH/kJ mol−1 |
|---|---|---|---|
a Cr: crystalline phase; Iso: isotropic liquid; all mesophases (M1, M2 and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) are 3D in nature (see text). The temperatures are given for the onset transitions obtained during the first heating run; (heating rate = 5 °C min−1).
b Transition not detected by DSC (see text).
c Complex thermal events occurred before this transition (see ESI). m) are 3D in nature (see text). The temperatures are given for the onset transitions obtained during the first heating run; (heating rate = 5 °C min−1).
b Transition not detected by DSC (see text).
c Complex thermal events occurred before this transition (see ESI).
|
|||
| 5 | Cr → M1 | 105 | 163 |
| M1 → M2b | 160b | — | |
| M2 → Iso | 261 | 94 | |
| 7 | Crc → R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
121.5 | 36 |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → Iso m → Iso |
144.5 | 16 | |
 | ||
| Fig. 1 Optical textures of the mesophase of (a) complex 7 at 140 °C and (b) complex 5 at 260 °C on cooling from the isotropic liquid. | ||
On cooling complex 5 from the isotropic liquid, large and fluid birefringent conical domains with striations develop readily over the whole area (Fig. 1b), indicative of a mesomorphic state albeit an ordered one. The DSC trace (Fig. S2, ESI†) shows two close peaks at the isotropic-to-mesophase transition on cooling yet careful microscopy with slow cooling has not succeeded in identifying the extra transition. The texture that forms is characteristic of a Colh mesophase with some focal conic and spherulitic features, but there is no obvious transition to the more ordered mesophase. The temperature range of this extra phase is too small to allow characterisation by X-ray diffraction. It is most likely that this additional phase also has hexagonal symmetry and it may be a true Colh phase preceding the lower-temperature phase, but as it cannot be characterised separately, no definitive assignment is offered and it is not noted in Table 1.
On further cooling, no visible change in the optical texture was detected down to room temperature and the complex crystallised below 40 °C. Consistently the SAXS pattern at room temperature (Fig. 5c) is constituted of overlapping reflections in the small, intermediate and wide-angle range without detectable scattering signal from partial structural disorder, which indicates a true crystalline phase. DSC analysis revealed that complex 5, crystalline at room temperature, exhibits two main, reversible, first-order thermal transitions at 110 and 263 °C (Fig. S2, ESI† and Table 1). The first is associated with melting into a mesophase, whereas above 263 °C, the compound is in its isotropic state. Note that while the temperatures of 5 are high, which can often be the case with metallomesogens, SAXS patterns were also recorded at room temperature on cooling from the mesophases, and reheated again to find the same results.
The structure of the mesophases of both complexes was confirmed by SAXS analysis, which shows wide-angle scattering reflections due to lateral distances between the molten chains (hch) and between various molecular fragments (see below), in addition to several sharp, small-angle reflections associated with long-range correlations (Fig. 2 and 5, Tables S1–S3, ESI†).
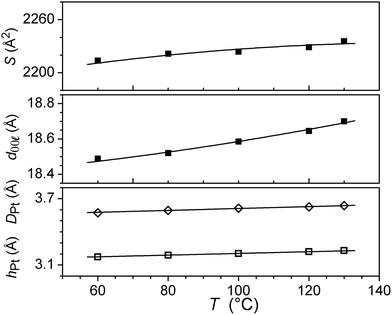
The wide-angle region of SAXS patterns of 7, recorded above 120 °C on heating and down to about 60 °C on cooling, contains reflections arising from periodic distances between various molecular fragments labelled as hch, hgal, hπ, and hPt (Fig. 2, Table 2), besides numerous sharp, small-angle reflections of a large lattice correlated over long length scales. Twelve of these reflections can be indexed in a two-dimensional sub-lattice of hexagonal symmetry arising from the aggregation of columns formed from stacks of complexes (hk in Table 2). However, this series of sharp peaks also includes four additional reflections associated with periodicity along the columns and crossed reflections. With their inclusion, all reflections can now be indexed within orthogonal sub-cell with a height of 18.7 Å at 130 °C (hkl in Table 2). All parameters of the sub-cell, as well as distances from scattering maxima, show only a very small increase with temperature (Fig. 3).
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m mesophase of 7 (at 130 °C)
m mesophase of 7 (at 130 °C)
| No. | 2θmeasa (°) | d meas (Å) | I(ξ)c | hk | hkl | 2θcalcf (°) | d calc (Å) |
|---|---|---|---|---|---|---|---|
| a Measured Bragg angles (θ). b Measured spacings (d). c Intensity (VS: very strong, S: strong, M: medium, W: weak, VW: very weak) and width (ξ: correlation length from Scherrer formula; no indication: sharp). d Miller indices in the columnar hexagonal sub-lattice (see text); hch and hgal correspond to the maximum of the undifferentiated diffuse scattering due to lateral distances between molten aliphatic tails (hch) and between gallate fragments (hgal), respectively, hπ is attributed to the stacking of the metal chelate, and hPt to the superposition of Pt-containing zones. e Miller indices in the three-dimensional rhombohedral lattice (see text). f Calculated Bragg angles (θ). g Calculated and spacings (d). | |||||||
| 1 | 2.00 | 44.2 | VS | 10 | 110 | 2.01 | 44.00 |
| 2 | 3.47 | 25.45 | S | 11 | 300 | 3.47 | 25.40 |
| 3 | 4.00 | 22.06 | M | 20 | 220 | 4.01 | 22.00 |
| 4 | 4.71 | 18.74 | M | × | 003 | 4.72 | 18.70 |
| 5 | 5.29 | 16.69 | W | 21 | 410 | 5.31 | 16.63 |
| 6 | 5.86 | 15.07 | W | × | 303 | 5.86 | 15.06 |
| 7 | 6.00 | 14.71 | W | 30 | 330 | 6.02 | 14.67 |
| 8 | 6.94 | 12.73 | VW | 22 | 600 | 6.95 | 12.70 |
| 9 | 7.26 | 12.17 | M | 31 | 520 | 7.24 | 12.20 |
| 10 | 7.69 | 11.49 | W | × | 333 | 7.65 | 11.54 |
| 11 | 8.06 | 10.96 | W | 40 | 440 | 8.03 | 11.00 |
| 12 | 8.79 | 10.05 | M | 32 | 710 | 8.75 | 10.09 |
| 13 | 9.23 | 9.57 | W | 41 | 630 | 9.20 | 9.60 |
| 14 | 9.46 | 9.34 | W | × | 006 | 9.45 | 9.35 |
| 15 | 10.44 | 8.47 | W | 33 | 900 | 10.44 | 8.47 |
| 16 | 10.65 | 8.30 | VW | 42 | 820 | 10.63 | 8.32 |
| 20 | 4.4 | S(10) | h ch + hgal | ||||
| 24.4 | 3.64 | M(60) | h π | ||||
| 27.6 | 3.23 | M(200) | h Pt | ||||
| 2D hexagonal sub-lattice parameters (a2D, b2D, γ2D) and area (S): a2D = b2D = 50.8 (07) Å, γ2D = 120°, S = a2Db2Dsinγ2D = 2236 Å2. | |||||||
| Lattice parameters of the rhombohedral cell (a, b, c, α, β, γ): a = b = 88.0(00) Å, c = 56.1(000) Å, α = β = 90°, γ = 120°. | |||||||
V
mol = 3559 ± 180 Å3, Vcell = 376![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å3, Z = 106 ± 5, Zcol = 3. 000 Å3, Z = 106 ± 5, Zcol = 3. |
|||||||
The development of such a large and long range-correlated, three-dimensional structure with sharp interfaces leading to numerous reflections is unusual for systems incorporating such a large volume fraction of molten aliphatic chains (f ≈ 79% here).‡ While this might be a consequence of particularly cohesive interactions between π-stacked complexes, the multi-segregated structure is also likely to be of significance. There is indeed potential incompatibility between the types of self-assembly of the metal chelate and gallate fragments: face-to-face stacking with typical spacing of 3.3–3.6 Å for the former, and packing of small fragments (gallate) with a typical lateral distance of 4.5–5 Å for the latter if it is assumed that it librates freely. The gallate fragments can, therefore, potentially segregate sterically from the metal chelate moiety with a liquid lateral packing characterised by a scattering signal, hgal, coincident with that of the molten chains, hch.
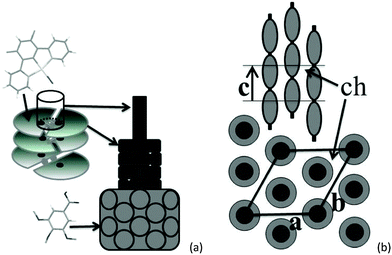
The self organisation of these hexacatenar complexes gives rise to two scattering signals with slightly different periodicities. Thus, the signal with the smaller periodicity (3.2 Å) is attributed to the superposition of Pt-containing zones (hPt), consistent with the patterns observed for the di-alkoxy derivative 5 (below). The broader, dissymmetric signal at 3.6 Å is attributed to the stacking of the metal chelate moiety (hπ); the slightly increased periodicity and the shape might be explained by the lateral shift and the distortions due to the connection to the bulky gallate fragments. The column segment height, hπ, thus corresponds to the periodicity of the stacking in the columns and the ratio of its volume to the molecular volume (Vmol) gives the number of molecular equivalents per columnar section (NCol), which is a meaningful quantity in this case as a stacking period is observed clearly. Vmol is readily evaluated from reference structures and dilatometric data (Table 2), by assuming partial molecular volume additivity; the value of NCol turns out to be equal to 2.0. The way in which these two molecules assemble can be clarified with the intensity modulation in the reflection series that depends mainly on the location of the zones of high electron density that contain Pt.12 The high intensity of the first-order reflections and the steep decrease in intensity in the series at low-angle are consistent with an increase in electronic density in the central region of columns; both complexes thus assemble with facing Pt-containing zones (Fig. 4a). Although the gallate regions intercalate between the metal chelate core and the aliphatic periphery, the surface of columns enveloped by a shell of radiating tails would not be sufficient for the space requirement of all chains (less than 90% of the overall minimum interface area according to the calculation method detailed in ref. 13). To compensate for this crowded aliphatic periphery, not all of the chains will adopt an average all-trans conformation and will fold back to cover the remaining part of the periphery, creating a non-uniform profile of chains around the columns. The periodic distribution of such so-called disruption zones along and between columns is the origin of the three-dimensional structure. That there is a three-dimensional arrangement would then suggest that these areas might approach one another in order to fill space effectively and that these interactions are correlated through the structure over rather long length scales.
Such behaviour has been encountered recently in columnar phases of fused porphyrins13 and of semiperfluorinated co-dendrimers.14 with crowded aliphatic peripheries. Contrarily to these previous systems, which showed monoclinic phases, the hexagonal sub-lattice symmetry is preserved in this case, which requires the interlocking of three disrupted columns with different shifts along their axis (Fig. 4b). In this packing model, the periodicity of the disruption zones in the columns is 56 Å, leading to a three-dimensional, rhombohedral cell; the highest possible and most likely space group is thus R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.15
m.15
For 5, the presence in the X-ray diffraction patterns of wide-angle reflections arising from the lateral distance between molten chains (hch) and between metallic fragments (hPt, DPt, see below), in addition to several sharp, small-angle reflections, are indicative of a mesomorphic material correlated over long length scales (Fig. 5). Whilst not detected by DSC and microscopy, a reversible transition is evident at 160 °C from the X-ray measurements and the two mesophases (Table 1) are referred to as M1 (lower-temperature phase) and M2 (higher-temperature phase). In both cases, the numerous sharp small-angle reflections (ca. 10, Table 3) accord perfectly with a two-dimensional sub-lattice of hexagonal symmetry, formed by the aggregation of the complexes stacks into columns. In the crystal structure of the analogous square-planar complex devoid of aliphatic side-chains,16 the flat metal complex arrange head-to-tail into stacks, located at the nodes of a rectangular sub-lattice of an overall P21/c cell. The stacked metal chelates are separated by 3.35 Å and tilted by 36° out-of the sub-lattice plane.
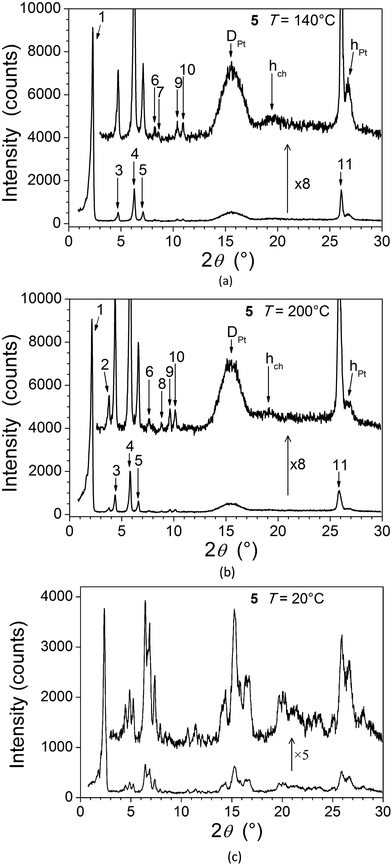 | ||
| Fig. 5 SAXS diffractograms of 5: (a) at 140 °C (M1); (b) at 200 °C (M2); (c) in the crystalline phase, at room temperature, on cooling from the mesophase. | ||
| Low-temperature, 3D monoclinic phase (M1) of 5 (at 140 °C) | |||||||
|---|---|---|---|---|---|---|---|
| No. | 2θmeasa (°) | d meas (Å) | I(ξ)c | hk | hkl | 2θcalcf (°) | d calc (Å) |
| a Measured Bragg angles (θ) and spacings (d). b Measured Bragg angles (θ) and spacings (d). c Intensity (VS: very strong, S: strong, M: medium, W: weak, VW: very weak) and width (ξ: correlation length from Scherrer formula; no indication: sharp). d Miller indices in the columnar hexagonal sub-lattice (see text); hch corresponds to the maximum of the diffuse scattering due to lateral distances between molten aliphatic tails (hch), hPt to the superposition of Pt-containing zones, and DPt to lateral distances between Pt centres in the sub-lattice plane, respectively. e Miller indices in the three-dimensional hexagonal lattice (see text). f Calculated Bragg angles (θ). g Calculated spacings (d). | |||||||
| 1 | 2.35 | 37.5 | VS | 10 | 200/110 | 2.36 | 37.41 |
| 3 | 4.71 | 18.76 | M | 20 | 400/220 | 4.72 | 18.71 |
| 4 | 6.26 | 14.11 | S | 21 | 510/420/130 | 6.25 | 14.14 |
| 5 | 7.12 | 12.41 | M | 30 | 600/330 | 7.08 | 12.47 |
| 6 | 8.14 | 10.85 | W | 22 | 620/040 | 8.18 | 10.80 |
| 7 | 8.48 | 10.42 | VW | 31 | 710/530/240 | 8.51 | 10.38 |
| 9 | 10.36 | 8.53 | W | 32 | 820/730/150 | 10.30 | 8.58 |
| 10 | 10.85 | 8.15 | W | 41 | 910/640/350 | 10.83 | 8.16 |
| 11 | 26.09 | 3.41 | S | × | 002 | 26.09 | 3.41 |
| 15.6 | 5.7 | S(30) | D Pt | ||||
| 19.5 | 4.5 | M(20) | h ch | ||||
| 26.7 | 3.34 | M(80) | h Pt | ||||
| 2D hexagonal sub-lattice parameters (a2D, b2D, γ2D) and area (S): a2D = b2D = 43.2 (00) Å, γ2D = 120°, S = a2Db2Dsinγ2D = 1616 Å2. | |||||||
| Lattice parameters of the monoclinic cell (a, b, c, α, β, γ): | |||||||
| (i) α = γ = 90°, β = 117.6°, a = 84.4(28) Å, b = 43.2 (00) Å, c = 7.69(58) Å; | |||||||
| (ii) β = γ = 90°, α = 117.6°, a = 74.8(20), b = 48.7(47) Å, c = 7.69(58) Å. | |||||||
V
cell, Z: cell volume and number of molecules per cell: Vmol = 1344 ± 67 Å3, Vcell = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å3, Z = 18.4 ± 1.0. 000 Å3, Z = 18.4 ± 1.0. |
|||||||
| High-temperature, 3D hexagonal phase (M2) of 5 (at 200 °C) | |||||||
|---|---|---|---|---|---|---|---|
| No. | 2θmeasa (°) | d meas (Å) | I(ξ)c | hk | hkl | 2θcalcf (°) | d calc (Å) |
| 1 | 2.18 | 40.5 | VS | 10 | 100 | 2.19 | 40.32 |
| 2 | 3.79 | 23.32 | M | 11 | 110 | 3.79 | 23.28 |
| 3 | 4.38 | 20.17 | S | 20 | 200 | 4.38 | 20.16 |
| 4 | 5.78 | 15.28 | S | 21 | 210 | 5.79 | 15.24 |
| 5 | 6.55 | 13.49 | M | 30 | 300 | 6.57 | 13.44 |
| 6 | 7.58 | 11.65 | W | 22 | 220 | 7.59 | 11.64 |
| 7 | 7.85 | 11.25 | VW | 31 | 310 | 7.90 | 11.18 |
| 8 | 8.83 | 10.01 | W | 40 | 400 | 8.76 | 10.08 |
| 9 | 9.63 | 9.18 | W | 32 | 320 | 9.55 | 9.25 |
| 10 | 10.04 | 8.80 | W | 41 | 410 | 10.04 | 8.80 |
| 11 | 25.86 | 3.44 | S | × | 001 | 25.86 | 3.44 |
| 15.4 | 5.7 | S(30) | D Pt | ||||
| 19 | 4.6 | M(20) | h ch | ||||
| 26.7 | 3.33 | M(80) | h Pt | ||||
| 2D hexagonal sub-lattice parameters (a2D, b2D, γ2D) and area (S): a2D = b2D = 46.5(57) Å, γ2D = 120°, S = a2Db2Dsin γ2D = 1877 Å2. | |||||||
| Lattice parameters of the hexagonal cell (a, b, c, α, β, γ): a = b = 46.5(57) Å, c = 3.44(23) Å, α = β = 90°, γ = 120°. | |||||||
| V cell = 6460 Å3; Vmol = 1399 ± 70 Å3; Z = 4.6 ± 0.3. | |||||||
Contrary to the normal situation with a Colh mesophase, the respective positions of individual complexes within and between columns in these systems remain correlated over long length scales, as shown by the additional sharp reflection in the wide-angle region (Fig. 5, hPt). Both mesophases are thus three-dimensional, the transition taking place by a subtle distortion of the lattice, i.e. with a lattice periodicity along the columns, c, of two or one complexes, respectively, for the low- and high-temperature phases. The fact that the DSC trace shows that the transition is evidently second-order suggests strongly that the symmetry of the two phases should be different.
The long length scale correlation within the metal chelate stacks leads to correlations between areas of high electronic density that contain Pt and result in specific wide-angle reflections. The spacing of these zones along stacks leads to the intense hPt scattering and explains the proximity with the reflection from the structural periodicity from the 2D sub-lattice. The stacking period hPt then also reflects the stacking of the chelate, which explains its positional coincidence with the sharp, wide-angle reflection. A further broad and intense signal (DPt) is attributed to lateral distances between Pt centres in and between the sub-lattice planes.17 The complete resolution of the structure involves knowing the α and β parameters, which cannot be determined directly in the absence of crossed reflections (hkl). However the transition to M2 is associated with an increase of 13% in the columnar area, whilst the unmodified wide-angle scatterings and reflection exclude any significant change in aggregation (Fig. 6). As a consequence, the columns are elongated in M1, which could be explained by out-of-plane tilting of the metal-containing core in a manner analogous to that found in the single crystal structure. This might then imply that the cores were untilted in M2. The three-dimensional structure of the latter would then be assigned as a hexagonal cell with a unique column per lattice (P6/mm).15,18 The tilt angle in M1 would imply that the symmetry is necessarily reduced to monoclinic, with two columns per lattice.19 The change in symmetry would then be consistent with a second-order transition.
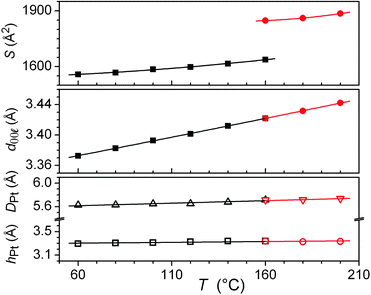 | ||
| Fig. 6 Variations as a function of temperature in the low- and high-temperature phases (black squares and red circles, respectively) of 5 of the columnar sub-lattice area (top), the spacing of the (00l, l = 2 for M1 and l = 1 for M2, see text and Table 3) reflection (middle) and the scattering maxima DPt (open triangles) and hPt (open squares) (bottom). Lines are guides for the eyes. | ||
The average number of stacks aggregated in columns can be deduced from the ratio of cell volume Vcell and molecular volume Vmol. The latter volume leads to aggregation numbers of between four and five stacks in both mesophases. Considering the nature and shape of the complex, it is postulated that aggregation very likely occurs to form a tetrameric arrangement as indicated in Fig. 7. The Pt atoms are found at the edge of columns, which is in agreement with the intensity variation in the small-angle reflections. Indeed, the relatively weak first- and second-order and the strong fourth- and fifth-order reflections reveal an increase in electronic density at the edge of columns.17 A schematic view of the molecular organisation in both mesophases is represented in Fig. 7.
Luminescence properties
Both complexes 5 and 7 are highly photoluminescent in solution at room temperature as well as in solid-state films. In dilute dichloromethane solution, the emission of 5 appears green whilst that of complex 7 is blue-green, this visual observation being reflected quantitatively in the respective emission maxima, blue-shifted by about 20 nm for 7 compared to 5 (Table 4, Fig. S4 and S5 in ESI†). The spectra display pronounced vibrational structure, quite typical of cyclometallated platinum(II) complexes with arylpyridine ligands, in which the emissive state has mixed 3[dPt/πAr → π*py] character.20 The triplet nature of the emissive excited state is evident from the long lifetimes of the luminescence, in excess of 1 μs (Table 4).| Complex | Absorption λmax/nm (ε/M−1 cm−1) | Emission λmax/nm monomer [excimer] | τ 0 /ns degassed (aerated) | Φ lum | k SQ /M−1 s−1 |
|---|---|---|---|---|---|
| a τ 0 is the lifetime at infinite dilution and kSQ the self-quenching rate constant, obtained, respectively, from the y-intercept and gradient of the best-fit line through a plot of 1/τ versus concentration. b Φ lum is the luminescence quantum yield in degassed solution, measured using [Pt(dpyb)Cl] as a secondary standard for which Φlum = 0.60 under the same conditions. | |||||
| 5 | 239 (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900), 267 (58 900), 267 (58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900), 295sh (23 900), 295sh (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100), 343 (15 100), 343 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), 360 (12 800), 360 (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400) 400) |
497, 532, 567 [662] | 9700 (875) | 0.54 | 1.8 × 109 |
| 7 | 288 (47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500), 341 (14 500), 341 (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700), 368 (11 700), 368 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
479, 513, 545 [670] | 7900 (1200) | 0.72 | 0.67 × 109 |
The difference in emission energy between the two complexes can be understood in terms of the more strongly electron-donating nature of the alkoxy groups directly appended at the pyridyl 5-positions in 5 compared to the ester groups in the equivalent positions of 7. Substituents at this position are expected to affect not only the LUMO (based predominantly on the pyridyl rings, according to TD-DFT studies) but also the HOMO (based on the central aryl ring and metal), owing to the conjugation through the pyridyl ring to the aryl ring.21 In the present instance, the electron-donating alkoxy groups evidently have a greater destabilising influence on the HOMO than LUMO leading to a lower excited state energy (the corresponding complex of 1,3-bis(2-pyridyl)-4,6-difluorobenzene emits at 472 nm under the same conditions22).
At higher concentrations, the emission from the isolated molecules is accompanied by a broad, structureless band in the red region of the spectrum, centred around 680 nm in each case, and attributed to the formation of excimers. This is a well-established observation for many platinum(II) complexes of dipyridylbenzene ligands.23 The luminescence lifetime of the monomer emission decreases with concentration, reflecting the fact that excimer formation depletes the monomeric excited state. The self-quenching constants (Table 4) are, however, significantly different for the two complexes, that measured for 5 being larger by a factor of approximately three compared to 7. This could reflect the more planar nature of 5 in solution, which lacks the pendant aryl rings at the pyridyl 5-positions of 7 that will be able to rotate around the interannular bond and perhaps somewhat hinder the face-to-face interactions required for excimer formation. Perhaps more simply, greater steric hindrance is anticipated from the presence of six aliphatic chains in 7 compared to only two in 5.
In contrast to the solutions, the neat films of both complexes display bright orange-red luminescence, with an unstructured profile centred around 670 nm for 5 (Fig. 8), marginally red-shifted to 680 nm for 7, and very similar to the excimer emission in solution. No monomer emission is observed for 7 and only a trace for 5 (weak bands between 500 and 550 nm). The red emission may be attributed either to excimer formation or to ground-state interactions, and is reminiscent of that seen in neat films of the parent complex under irradiation or when electrically driven in an OLED.24 Given that the X-ray diffraction studies indicate face-to-face separations of the order of 3.2 to 3.5 Å and show distinct Pt⋯Pt correlations, ground-state aggregates having stabilised excited states compared to the isolated molecules are plausible.25 The luminescence lifetime for the red emission in the films was found to be 1.8 ± 0.3 μs under ambient conditions, indicative of triplet character to the excited state.
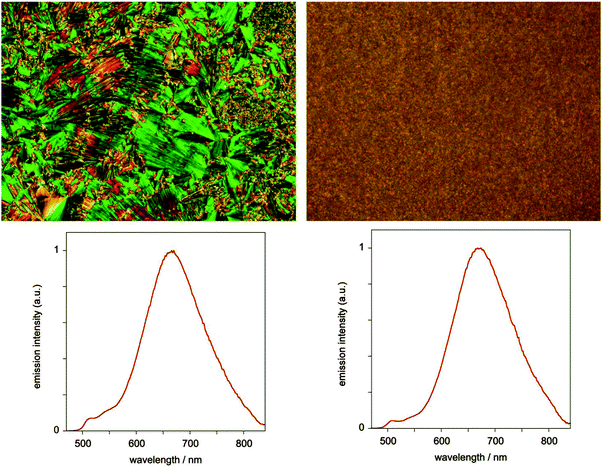 | ||
| Fig. 8 Photomicrographs and corresponding emission spectra (λex = 405 nm) for the neat film of complex 5 in LC (left) and isotropic (right) phases. | ||
We found no dependence of the luminescent properties of the films on the thermal history of the samples. Those obtained by fast cooling from the liquid-crystalline phase are nearly identical to the samples obtained by fast cooling from isotropic liquid, despite the different appearance of the films under polarised microscopy (Fig. 8).
Discussion
As the study of liquid crystals has advanced, as structural techniques have become more widely available and as the chemists' imaginations have been given broader remits within which to work, so the range of available materials has increased markedly. With this increase, there has been an accompanying increase in the number of ways in which compounds have been found to organise to form liquid crystal phases (note that there was no systematic literature on bent-core mesogens twenty years ago) and so the former certainties of mesophase classification have largely gone. What has replaced these certainties has been something of a free-for-all to label ‘new’ phases in ever increasingly complex (and potentially unsystematic, if internally consistent) ways.Back in 1987, Leadbetter26 offered a classification in which he distinguished (for smectics) between what we now call ‘true’ liquid crystal phases based on a one-dimensional density wave (SmA, SmC) or on weakly coupled, ordered layers (SmB, SmF and SmI), and disordered crystals (crystal smectic B, E, G, H, J, K as well as the cubic phases). The distinction was made as follows “when a structure has long-range order of the molecular positions in three dimensions it is a crystal, despite the presence of various other kinds of disorder”. He went on to say that “structures having less than this degree of positional order, but retaining some aspects of order above that possessed by an isotropic liquid, are properly called liquid crystals”. In applying the same tests to the columnar phases of disc-like molecules (still relatively new in 1987 and with little systematic work) he concluded that as the columns were not in register along their axes then they were not three-dimensional and so were liquid crystals.
Such clear statements are helpful in understanding how phases might be classified, but what we might add to this is the useful idea of a mesophase which, taken from its translation, means ‘between phases’. Thus, the crystal smectic phases would not be regarded as crystalline if a single-crystal structure was sought as for all the presence of three-dimensional order, there is far too much disorder to obtain high-quality data about precise atomic positions. Thus, while accepting that these are not liquid crystals, they are truly mesophases.
The phases considered here are then also truly mesophases, but should not be considered as liquid crystalline in nature. Thus for both materials and in all three phases, there is a well-developed, two-dimensional, hexagonal net with the addition of long-range correlations in the columnar direction. For the mesophase in 7, it has been possible to index the phase precisely as the rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. However, it should be noted that such an assignment is not trivial and is a result of detailed consideration of the X-ray data. Similarly for 5, the lower-temperature phase can be indexed into a monoclinic space group, while the higher-temperature phase can be more precisely defined as existing in a P6/mm lattice.
m. However, it should be noted that such an assignment is not trivial and is a result of detailed consideration of the X-ray data. Similarly for 5, the lower-temperature phase can be indexed into a monoclinic space group, while the higher-temperature phase can be more precisely defined as existing in a P6/mm lattice.
There is then the question of how these mesophases should be labelled. There exists some systematic classification of smectic-like mesophases that are not liquid crystalline (see above), but this has not been extended to mesophases that might be thought of as ‘columnar-like’. We do not wish unilaterally to introduce a new nomenclature and so we stick with the two space groups and the broad monoclinic descriptor used in the discussion.
Strictly then from their potential as ‘multifunctional’ materials, these complexes would not qualify in the absence of liquid crystal properties for the complexes. However, the broader question of application would not see this as a barrier, for if the use of hexa(alkylthio)triphenylenes as fast photoconductors is recalled,27 these materials showed their optimum properties in a highly ordered (helical) columnar phase, which would not classify as a liquid crystal. Thus occasionally it is important to see past the simple label and evaluate materials for what they are rather than what they are not.
Experimental
Materials and methods
All commercially available reagents were used as received. TLC was carried out on silica gel Si 60-F254. Column chromatography was carried out on silica gel Si 60, mesh size 0.040–0.063 mm (Merck, Darmstadt, Germany). Nuclear magnetic resonance spectra were recorded on a Jeol JNM-EX 270 FT NMR system or Bruker 400 MHz and referenced to TMS or residual solvent resonances. UV-Vis and Infrared spectra were obtained by using a Shimadzu UV-2401 PC and Shimadzu IR Prestige-21 spectrometers, respectively. UV-Vis spectra were obtained using a Shimadzu UV-2401 PC instrument. Microanalyses were performed at the Department of Chemistry, University of York using Exeter Analytical Inc. CE 440 instrument. Luminescence spectra were recorded with a Jobin Yvon Fluoromax-2 spectrofluorimeter, and lifetimes were measured by time-correlated single photon counting following excitation at 405 nm with a laser diode. The phase transition temperatures were determined using Mettler Toledo DSC-822e differential scanning calorimeter with a heating and cooling rate of 10 °C min−1 (the apparatus was calibrated with indium, 156.6 °C). Texture observations were made using Olympus BX50 polarizing microscope in conjunction with a Linkam LTS350 hot stage and Linkam TMS92 control unit. SAXS patterns were obtained with a linear monochromatic Cu Kα1 beam (λ = 1.5405 Å) obtained using a sealed-tube generator (600 W) equipped with a bent quartz monochromator. Patterns were recorded with a curved Inel CPS 120 counter gas-filled detector linked to a data acquisition computer; periodicities up to 70 Å can be measured, and the sample temperature controlled to within ±0.01 °C from 20 to 200 °C. Alternatively, patterns were recorded on an image plate; periodicities up to 120 Å can be measured (scanned by STORM 820 from Molecular Dynamics with 50 mm resolution). In all cases, the crude powder was filled in Lindemann capillaries of 1 mm diameter and 10 μm wall thickness and exposure times were varied from 1 to 24 h.4,6-Difluoro-1,3-di(5-methoxy-2-pyridyl)benzene 2
A mixture of 2-bromo-5-methoxypyridine (1 g, 5.3 mmol), 4,6-difluorobenzene-1,3-diboronic acid dipinacol ester 1 (811 mg, 2.2 mmol), K3PO4 (1.40 g, 6.6 mmol) and dry DMF (50 cm3) was outgassed by bubbling argon through the mixture for 10 minutes. [Pd(PPh3)4] (152 mg, 0.132 mmol) was added and the mixture was degassed for additional 15 minutes. The reaction mixture was then stirred at 100 °C for 14 hours under argon atmosphere. The solvent was removed under reduced pressure and the product is purified by column chromatography (silica gel, ethyl acetate). Yield 550 mg, 45%. δH (270 MHz; CDCl3; solvent): 3.89 (6H, s), 6.98 (1H, t, J = 10.7 Hz), 7.26 (2H, dd, J = 8.7, 2.3 Hz), 7.70 (2H, d, J = 8.6 Hz), 8.40 (2H, d, J = 2.6 Hz), 8.49 (1H, t, J = 9.1 Hz). Elemental analysis calcd for C18H14F2N2O2: C 65.85, H 4.30, N 8.53; found C 65.16, H 4.32, N 8.43.4,6-Difluoro-1,3-di(5-hydroxy-2-pyridyl)benzene 3
4,6-Difluoro-1,3-di(5-methoxy-2-pyridyl)benzene 2 (660 mg, 2 mmol) was dissolved in dichloromethane (50 cm3) and cooled to 0 °C. BBr3 (6 cm3, 1 M in dichloromethane, 6 mol equiv.) was then added at 0 °C, and the reaction mixture was stirred at room temperature for 2 d. The reaction was quenched by slow addition of methanol (10 cm3) and all volatiles were removed under reduced pressure. The residue was dissolved in methanol (5 cm3) and heated under reflux for 15 min. Water was added and the pH adjusted to 7–8 with saturated solution of NaHCO3. The precipitated solid was filtered off, washed with water and crystallised from acetone/water (1/5) mixture. Yield 318 mg, 53%. δH (270 MHz; DMSO-d6; solvent): 7.25 (2H, dd, J = 8.6, 2.1 Hz), 7.35 (1H, t, J = 10.7 Hz), 7.63 (2H, d, J = 8.6 Hz), 8.25 (2H, d, J = 2.1 Hz), 8.48 (1H, t, J = 9.1 Hz), 10.15 br, s (2H).4,6-Difluoro-1,3-di(5-n-hexadecyloxy-2-pyridyl)benzene 4
A mixture of 4,6-difluoro-1,3-di(5-hydroxy-2-pyridyl)benzene 3 (150 mg, 0.5 mmol, 1 mol eq.), potassium carbonate (414 mg, 3 mmol, 6 eq.) and bromohexadecane (457 mg, 1.5 mmol, 3 mol eq.) in DMF (10 cm3) was stirred at 105 °C for 14 hours. Water (30 cm3) was added, the precipitated solid was filtered off, washed with water (10 cm3), methanol (5 cm3) and crystallised from acetone. Yield 275 mg, 74%. δH (400 MHz; CDCl3; solvent): 0.87 (6H, t, J = 7.3), 1.15–1.40 (48H, m), 1.47 (4H, q, J = 7.8 Hz), 1.81 (4H, q, J = 7.2 Hz), 4.04 (4H, t, J = 6.5 Hz), 6.98 (1H, t, J = 10.7 Hz), 7.25 (2H, dd, J = 9.0, 2.8 Hz), 7.68 (2H, d, J = 9.0 Hz), 8.39 (2H, d, J = 2.8 Hz), 8.49 (1H, t, J = 9.2 Hz). Elemental analysis calculated for C48H74F2N2O2: C 76.96, H 9.96, N 3.74; found C 76.41, H 9.94, N 3.73.Complex 5
A mixture of the ligand (150 mg, 0.2 mmol), K2[PtCl4] (83 mg, 0.2 mmol) and acetic acid was (30 cm3) heated under reflux for 24 h. Precipitated solid was filtered off, washed on filter with acetone (20 cm3), dissolved in chloroform (20 cm3) and filtered. Acetone (30 cm3) was added to the filtrate, and a precipitated solid was filtered off to give the desired product. Yield 170 mg, 87%. δH (400 MHz; CDCl3; solvent): 0.87 (6H, t, J = 7.3 Hz), 1.15–1.40 (48H, m), 1.47 (4H, q, J = 7.8 Hz), 1.81 (4H, q, J = 7.2 Hz), 4.06 (4H, t, J = 6.5 Hz), 6.61 (1H, t, J = 11.2 Hz), 7.42 (2H, dd, J = 9.0, 2.8 Hz), 7.74 (2H, d, J = 9.0 Hz), 9.00 (2H, d, J = 2.8 Hz). Elemental analysis calculated for C48H73ClF2N2O2Pt: C 58.91, H 7.52, N 2.86; found C 58.92, H 7.46, N 2.82.Ligand 6
A mixture of diphenol 3 (172 mg, 0.573 mmol), 3,4,5-tri(hexadecyloxy)benzoic acid (970 mg, 1.15 mmol), 4-(N,N-dimethylamino)pyridine (0.6 mmol) and DCC (472 mg, 2.3 mmol) in dichloromethane (100 cm3) was stirred at room temperature under argon atmosphere for 2 days. The mixture was filtered and the filtrate was evaporated to dryness. The product was purified by column chromatography (silica gel, chloroform/ethyl acetate, 15/1). Yield 620 mg, 55%. δH (270 MHz; CDCl3; solvent): 0.80 (18H, m), 1.2 (144H, m), 1.4 (12H, m), 1.69 (4H, q, J = 7.2 Hz), 1.76 (8H, q, J = 7.2 Hz), 4.00 (12H, m), 6.98 (1H, t, J = 11.2 Hz), 7.36 (4H,s), 7.61 (2H, dd, J = 8.9, 2.8 Hz), 7.81 (2H, d, J = 8.9 Hz), 8.57 (2H, d, J = 2.8 Hz), 8.63 (1H, t, J = 9.6 Hz).Complex 7
A mixture of the ligand (230 mg, 0.118 mmol) and acetic acid (100 mL) was degassed by bubbling Ar through the mixture for 10 min. cis-[PtCl2(NCPh)2] (56 mg, 0.118 mmol) was added and the reaction mixture was heated under reflux for 5 d. The solvent was removed under reduced pressure. The product was purified by column chromatography (silica gel, DCM). Yield 118 mg (46%). δH (270 MHz; CDCl3; solvent): 0.81 (18H, m), 1.2 (144H, m), 1.4 (12H, m), 1.8 (12H, m), 4.05 (12H, m), 6.72 (1H, t, J = 11.2 Hz), 7.31 (4H,s), 7.92 (4H, m), 9.21 (2H, d, J = 2.8 Hz). Elemental analysis calculated for C126H209ClF2N2O10Pt: C 69.40, H 9.66, N 1.28; found C 69.59, H 9.74, N 1.35.Acknowledgements
We thank EPSRC, the EU and CNRS for support of this work.References
- J. Kalinowski, V. Fattori, M. Cocchi and J. A. G. Williams, Coord. Chem. Rev., 2011, 255, 2401 CrossRef CAS PubMed; Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley-VCH, Weinheim, 2008 CrossRef; M. A. Baldo, D. F. O'Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151 CrossRef.
- W.-Y. Wong and C.-L. Ho, J. Mater. Chem., 2009, 19, 4457 RSC; K. M.-C. Wong, M. M.-Y. Chan and V. W.-W. Yam, Adv. Mater., 2014, 26, 5558 CrossRef CAS PubMed.
- S.-H. Liu, M.-S. Lin, L.-Y. Chen, Y.-H. Hong, C.-H. Tsai, C.-C. Wu, A. Poloek, Y. Chi, C.-A. Chen, S. H. Chen and H.-F. Hsu, Org. Electron., 2011, 12, 15 CrossRef CAS PubMed; T. Sato, H. Awano, H. Katagiri, Y.-J. Pu, T. Takahashi and K. Yonetake, Eur. J. Inorg. Chem., 2013, 2212 CrossRef PubMed.
- M. O'Neill and S. M. Kelly, Adv. Mater., 2011, 23, 566 CrossRef CAS PubMed; A. Liedtke, M. O'Neill, A. Wertmöller, S. P. Kitney and S. M. Kelly, Chem. Mater., 2008, 20, 3579 CrossRef.
- A. Santoro, A. M. Prokhorov, V. N. Kozhevnikov, A. C. Whitwood, B. Donnio, J. A. G. Williams and D. W. Bruce, J. Am. Chem. Soc., 2011, 133, 5248 CrossRef CAS PubMed.
- S. W. Thomas III, S. Yagi and T. M. Swager, J. Mater. Chem., 2005, 15, 2829 RSC; K. Venkatesan, P. H. J. Kouwer, S. Yagi, P. Mueller and T. M. Swager, J. Mater. Chem., 2008, 18, 400 RSC; A. Santoro, A. C. Whitwood, J. A. G. Williams, V. N. Kozhevnikov and D. W. Bruce, Chem. Mater., 2009, 21, 3871 CrossRef CAS; Y. Wang, Y. Liu, J. Luo, H. Qi, X. Li, M. Nin, M. Liu, D. Shi, W. Zhu and Y. Cao, Dalton Trans., 2011, 40, 5046 RSC; M. Spencer, A. Santoro, G. R. Freeman, A. Diez, P. R. Murray, J. Torroba, A. C. Whitwood, L. J. Yellowlees, J. A. G. Williams and D. W. Bruce, Dalton Trans., 2012, 41, 14244 RSC.
- C. Damm, G. Israel, T. Hegmann and C. Tschierske, J. Mater. Chem., 2006, 16, 1808 RSC.
- C. T. Liao, H. H. Chen, H. F. Hsu, A. Poloek, H. H. Yeh, Y. Chi, K. W. Wang, C. H. Lai, G. H. Lee, C. W. Shih and P. T. Chou, Chem. – Eur. J., 2011, 17, 546 CrossRef CAS PubMed.
- V. N. Kozhevnikov, B. Donnio and D. W. Bruce, Angew. Chem., Int. Ed., 2008, 47, 6286 CrossRef CAS PubMed.
- I. Bury, B. Heinrich, C. Bourgogne, G. H. Mehl, D. Guillon and B. Donnio, New J. Chem., 2012, 36, 452–468 RSC.
- E. B. Sirota, H. E. King Jr., D. M. Singer and H. H. Shao, J. Chem. Phys., 1993, 98, 5809–5824 CrossRef CAS PubMed.
- B. Alameddine, O. F. Aebischer, B. Heinrich, D. Guillon, B. Donnio and T. A. Jenny, Supramol. Chem., 2013, 26, 125 CrossRef PubMed.
- D. Mysliwiec, B. Donnio, P. J. Chmielewski, B. Heinrich and M. Stepien, J. Am. Chem. Soc., 2012, 134, 4822 CrossRef CAS PubMed.
- I. Bury, B. Heinrich, C. Bourgogne, G. H. Mehl, D. Guillon and B. Donnio, New J. Chem., 2012, 36, 452 RSC.
- M. Prehm, G. Ungar and C. Tschierske, J. Am. Chem. Soc., 2011, 133, 4906 CrossRef CAS PubMed.
- Structure from the Cambridge Structural Database, CSD number: IYURAW.
- C. Dominguez, B. Heinrich, B. Donnio, S. Coco and P. Espinet, Chem. – Eur. J., 2013, 19, 5988 CrossRef CAS PubMed; A. B. Miguel-Coello, M. Bardají, S. Coco, B. Donnio, B. Heinrich and P. Espinet, Inorg. Chem., 2014, 53, 10893 CrossRef PubMed.
- F. Liu, M. Prehm, X. Zeng, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2011, 50, 10599 CrossRef CAS PubMed.
- M. Stepien, B. Donnio and J. L. Sessler, Chem. – Eur. J., 2007, 13, 6853 CrossRef CAS PubMed; B. Zhao, B. Liu, R. Q. Png, K. Zhang, K. A. Lim, J. Luo, J. Shao, P. K. H. Ho, C. Chi and J. Wu, Chem. Mater., 2010, 22, 435 CrossRef; V. Percec, H.-J. Sun, P. Leowanawat, M. Peterca, R. Graf, H. W. Spiess, X. Zeng, G. Ungar and P. A. Heiney, J. Am. Chem. Soc., 2013, 135, 4129 CrossRef PubMed.
- J. Brooks, Y. Babayan, S. Lamansky, P. I. Djurovich, I. Tsyba, R. Bau and M. E. Thompson, Inorg. Chem., 2002, 41, 3055 CrossRef CAS PubMed.
- W. Sotoyama, T. Satoh, H. Sato, A. Matsuura and N. Sawatari, J. Phys. Chem. A, 2005, 109, 9760 CrossRef CAS PubMed; D. L. Rochester, S. Develay, S. Záliš and J. A. G. Williams, Dalton Trans., 2009, 1728 RSC; G. S.-M. Tong and C.-M. Che, Chem. – Eur. J., 2009, 15, 7225 CrossRef PubMed.
- M. Cocchi, J. Kalinowski, V. Fattori, J. A. G. Williams and L. Murphy, Appl. Phys. Lett., 2009, 94, 073309 CrossRef CAS PubMed; A. F. Rausch, L. Murphy, J. A. G. Williams and H. Yersin, Inorg. Chem., 2012, 51, 312 CrossRef PubMed.
- M. Cocchi, J. Kalinowski, L. Murphy and J. A. G. Williams, Org. Electron., 2010, 11, 388 CrossRef CAS PubMed; E. Rossi, L. Murphy, P. L. Brothwood, A. Colombo, C. Dragonetti, D. Roberto, R. Ugo, M. Cocchi and J. A. G. Williams, J. Mater. Chem., 2011, 21, 15501 RSC.
- M. Cocchi, D. Virgili, V. Fattori, J. A. G. Williams and J. Kalinowski, Appl. Phys. Lett., 2007, 90, 023506 CrossRef PubMed.
- J. Kalinowski, M. Cocchi, L. Murphy, J. A. G. Williams and V. Fattori, Chem. Phys., 2010, 378, 47 CrossRef CAS PubMed.
- A. J. Leadbetter, in Thermotropic Liquid Crystals, ed. G. W. Gray, Wiley, Chichester, 1987 Search PubMed.
- D. Adam, P. Schuhmacher, J. Simmerer, L. Häussling, K. Siemensmeyer, K. H. Etzbach, H. Ringsdorf and D. Haarer, Nature, 1994, 371, 141 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5tc02077h |
| ‡ Obtained from the ratio Vch/Vmol, where Vch is the volume of the chains, and Vmol, the molecular volume (Vmol = Vch + Vcore). Vch and Vcore were calculated from dilatometry of reference compounds. |
| This journal is © The Royal Society of Chemistry 2015 |