Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Artificial opal photonic crystals and inverse opal structures – fundamentals and applications from optics to energy storage
Eileen
Armstrong
a and
Colm
O'Dwyer
*ab
aDepartment of Chemistry, University College Cork, Cork, Ireland. E-mail: c.odwyer@ucc.ie; Fax: +353 (0)21 4274097; Tel: +353 (0)21 4902732
bTyndall National Institute, Lee Maltings, Cork, Ireland
First published on 20th May 2015
Abstract
Photonic crystals (PhCs) influence the propagation of light by their periodic variation in dielectric contrast or refractive index. This review outlines the attractive optical qualities inherent to most PhCs namely the presence of full or partial photonic band gaps and the possibilities they present towards the inhibition of spontaneous emission and the localization of light. Colloidal self-assembly of polymer or silica spheres is one of the most favoured and low cost methods for the formation of PhCs as artificial opals. The state of the art in growth methods currently used for colloidal self-assembly are discussed and the use of these structures for the formation of inverse opal architectures is then presented. Inverse opal structures with their porous and interconnected architecture span several technological arenas – optics and optoelectronics, energy storage, communications, sensor and biological applications. This review presents several of these applications and an accessible overview of the physics of photonic crystal optics that may be useful for opal and inverse opal researchers in general, with a particular emphasis on the recent use of these three-dimensional porous structures in electrochemical energy storage technology. Progress towards all-optical integrated circuits may lie with the concepts of the photonic crystal, but the unique optical and structural properties of these materials and the convergence of PhC and energy storage disciplines may facilitate further developments and non-destructive optical analysis capabilities for (electro)chemical processes that occur within a wide variety of materials in energy storage research.
I Introduction
The continuous and ever increasing drive for miniaturization and higher speed information systems has led to the now widespread idea of using photons instead of electrons as the information carrier. While photons hold many advantages over electrons the manipulation and control of light presents some difficulties. Efforts to achieve all-optical integrated circuits have led to a growing interest in the fabrication and use of photonic crystals (PhCs); PhCs have a periodic variation in dielectric function that affects the propagation of photons much like the periodic potential in semiconductors affects the flow of electrons. The use of PhCs for the manipulation of light stems from the early ideas of Yablonovitch and John that a three-dimensional (3D) periodic array could, by the presence of an electromagnetic band gap, control the radiative properties of materials, and so limit spontaneous emission.1,2 This concept was initially presented by Yablonovitch in the late 1980s.1 John followed with the idea that periodic structures could affect photon localization by a random refractive index variation.2 These two discoveries and the subsequent growth in PhC research for information management systems has led to an increasing awareness of the potential applications of PhCs within other technologies. For example, most recently PhCs have gained significant consideration as Li-ion battery electrodes due to their ability to incorporate electrolytes and reduce diffusion limitations. Examination of material permittivity and electrical conductivity variation, electrochemical processes, electrochromic and resonant optical amplification of emission processes, among many other dynamically variable processes and changes to ordered porous electrodes, have received limited optical analysis. In many cases this is due to a perceived limitation in the long range order for structured porous materials that is much less stringent in (electro)chemical electrodes for satisfactory operation, compared to a high quality PBG material.3 The substantial number of structural and optical advantages possessed by PhC's, make them ideally suited to many functional regimes that benefit from a porous, continuously interconnected, and in most cases, an optically significant material.4,5In this focused review, the attractive optical characteristics of PhCs are discussed and the fabrication techniques available for the formation of PhCs through colloidal self-assembly routes are reviewed, focusing on recent developments beyond recent reviews. The application of these artificial opal PhCs as templates for the formation of inverse opal (IO) PhCs is then outlined with an emphasis on the application and future development of these materials to a number of functional device fields from optoelectronics, to (bio)sensors, and from thermophotovoltaics to the emerging application of programmable structured 3D materials in energy storage research fields.
II Optical characteristics of photonic crystals
A. Photonic band gap in a 3D photonic crystal
In this section, the primary physics of PhCs are summarised so that researchers investigating PhCs primarily as templates and active electrode materials for example, may have a condensed form for analysis of optical transmission or reflection data, useful for their investigations. PhC's exist throughout the natural world,6 from opal gemstones7 and beetles,8 to bird feathers,9–11 and butterfly wings,12–14 and the common characteristic between all is their iridescent colour. This directional-dependent colour (colour that changes depending on angle of observation), does not arise from any absorption or pigmentation alone but is instead caused by the interaction of light with the periodic or random architecture of these materials' natural design, as shown in Fig. 1. PhCs are often most easily explained as an analogue to semiconductor materials. In a semiconductor, an electron passing through an ordered atomic lattice experiences a periodic potential, this interaction produces a band of energies over which electrons are forbidden to propagate in any direction. Much like a semiconductor affects the flow of electrons, a photonic crystal (PhC) affects the flow of photons. As a consequence of the differing dielectric media and the subsequent refractive index contrast within the crystal, light is scattered and/or diffracted from the different surfaces, producing a band of forbidden frequencies where interference of the scattered waves is destructive in all directions. Light cannot propagate within this region and the greater the refractive index contrast, the wider this photonic band gap (PBG) becomes. A full PBG is a characteristic only observed in PhCs where the propagation of light is prohibited in all directions. An incomplete PBG or pseudogap, sometimes referred to as a stop-band, is one that prohibits light from propagating in only some directions. The refractive index contrast and the lattice topology affects the existence of a full PBG but the wavelength range affected is determined by the length scale or lattice parameter of the crystal. The presence of the PBG and the potential ability to tune its position to suit specific frequencies is perhaps the most attractive quality of PhCs. | ||
| Fig. 1 Natural photonic crystals: (a) the blue iridescence and SEM image of the 1D structure of the Morpho butterfly.14 Adapted with permission from ref. 14. Copyright 2004 The Royal Society. (b) Multi-coloured peacock feather (Image by Wikimedia Commons/CC BY-SA 3.0) and TEM image of transverse cross section of the 2D structure of the blue area of a wing.11 Adapted with permission from ref. 11. Copyright 2002 Sci. press. (c) Natural opal gemstone and SEM image of the silica sphere structure within.15 Adapted with permission from ref. 15. Copyright 2008 Mineralogical Society of America. (d) Wing of the male Sasakia Charonda butterfly and SEM image of the 3D structure of the white iridescent area.12 Adapted with permission from ref. 12. Copyright 2010 The Japan Institute of Metals and Materials. (e) Schematic representation of 1D, 2D and 3D PhC structures, with different colours representative of different dielectric constants, indicating periodicity in one, two or three directions. Adapted from ref. 18. Copyright 2008 Princeton University Press. | ||
The origin of this PBG is explored here in order to concisely describe the optical characteristics inherent in a PhC through its design. While PhCs can be classified as one-dimensional (1D), two-dimensional (2D) or three-dimensional (3D), with periodicity in one, two or three directions respectively (as outlined in the schematic in Fig. 1(e)), for ease of description the properties of a 1D PhC is examined first. The optical phenomena of greatest interest, that is, the PBG or stop-band, the subsequent inhibition of spontaneous emission, and the possibility of localized modes are transferable to all dimensional systems.
A number of comprehensive reviews,16,17 and text books18,19 are available for a more in depth approach to the underlying optics of PhC behaviour but all discussions on the propagation of light in a PhC and determination of the PBG, must invariably begin with Maxwells equations, the four equations governing all macroscopic electromagnetism.
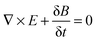 | (1) |
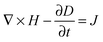 | (2) |
| ∇·B = 0 | (3) |
| ∇·D = ρ | (4) |
| D = ε0εE | (5) |
| B = μ0μH | (6) |
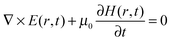 | (7) |
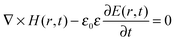 | (8) |
| ∇·H(r,t) = 0 | (9) |
| ∇·εE(r,t) = 0 | (10) |
| E(r,t) = E(r)e−iωt | (11) |
| H(r,t) = H(r)e−iωt | (12) |
| ∇ × E(r) − iωμ0H(r) = 0 | (13) |
| ∇ × H(r) + iωε0εrE(r) = 0 | (14) |
Looking solely at the magnetic field for mathematical convenience18 (the electric field can be derived similarly), these two equations can be decoupled to formulate an equation entirely in H(r). Dividing eqn (14) by εr, obtaining the curl of the equation, and then substituting for ∇ × E(r) using eqn (13), gives a master wave equation describing the propagation of the magnetic field (H(r)) of a photon:
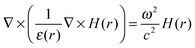 | (15) |
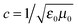 , ω is the frequency and εr is the macroscopic dielectric function of the material. This equation is in the form of an eigenvalue problem with eigenvector H(r), eigenvalue ω2/c2 and eigen-operator
, ω is the frequency and εr is the macroscopic dielectric function of the material. This equation is in the form of an eigenvalue problem with eigenvector H(r), eigenvalue ω2/c2 and eigen-operator 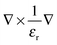 . This operator, is known as the Hermitan operator and has real and positive eigenvalues, much like the Hamiltonian operator of quantum mechanics and this allows us to view photonic crystals in solid-state physics terms and to assume some of the same properties, such as orthogonality and that all eigenfrequencies are real. However, it is important here to apply the transversality constraint; the two divergence equations ∇·H(r) = 0 and ∇·εE(r) = 0 must be taken into consideration, and with this constraint, the master equation for a material ε(r) can be solved to produce the mode H(r) and the corresponding frequencies.
. This operator, is known as the Hermitan operator and has real and positive eigenvalues, much like the Hamiltonian operator of quantum mechanics and this allows us to view photonic crystals in solid-state physics terms and to assume some of the same properties, such as orthogonality and that all eigenfrequencies are real. However, it is important here to apply the transversality constraint; the two divergence equations ∇·H(r) = 0 and ∇·εE(r) = 0 must be taken into consideration, and with this constraint, the master equation for a material ε(r) can be solved to produce the mode H(r) and the corresponding frequencies.
As mentioned above, a photonic crystal is a material whose dielectric function varies periodically, therefore:
| ε(r) = ε(r + R) | (16) |
| H(r) = hk(r)eikr | (17) |
| hk(r) = hk(r + R) | (18) |
Solving the master equation can be done by a number of computational methods, but the most commonly used approach is known as the plane-wave expansion method which involves the expansion of the magnetic and dielectric constant on the basis of a plane wave. The master equation eqn (15), after some vector operations, can be reduced to a matrix, whose eigenvalues, a series of functions in the form ωn(k) with n = 1, 2, … form the photonic bands. This band structure shows all the frequencies in which the optical modes are allowed for a given wave vector k. A photonic band gap (PBG) is a range of ω for which there are no propagating eigensolutions for any k, though there are above and below.
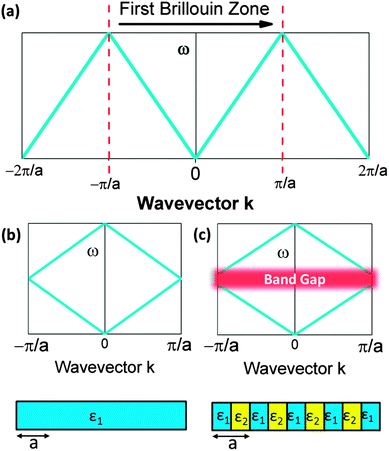
For every lattice vector (R) in real space, there is a lattice vector (G) in reciprocal space for which the dispersion relation is determined and periodicity in real space results in periodicity in the dispersion relation. Two states with wavevectors differing by 2π/a represent the same state exactly, which means eigensolutions for the wavevector k need only be computed within the primitive cell of the reciprocal lattice. This can be conventionally realized as the first Brillouin zone (BZ). This constitutes a ‘folding back’ of the dispersion relation into the first BZ which is schematically represented in Fig. 2, analogous to the formation of an electronic band structure. The dispersion relation defines the relationship between angular frequency ω of the photon and its wavevector 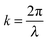 and in free space amounts to a linear dependence with the slope equal to the speed of light c, or in some cases, the group velocity of the wavepacket.
and in free space amounts to a linear dependence with the slope equal to the speed of light c, or in some cases, the group velocity of the wavepacket.
| ω = ck | (19) |
For a one dimensional, homogeneous material with a uniform dielectric function, the band structure or dispersion relation, is simply:
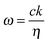 | (20) |
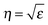 . Forward propagation results in a straight line as does backward propagation. This is shown schematically in Fig. 2(a) and (b). However for a periodic material, as in Fig. 2(c), the periodic dielectric function causes forward moving waves to be partially reflected at every interface. For frequencies that fulfill what's known as the Bragg condition, which is similar to x-ray diffraction theory but for optical wavelengths, interference of the forward and backward waves creates a standing wave at the edge of the BZ. Due to the splitting of the ±π/a planewaves into cos(πx/a) and sin(πx/a) standing waves by the different effective refractive indices and the subsequent difference in photon energies, a gap in the dispersion relation opens up – the photonic band gap (Fig. 2(c)). Maxwell's equations are scale invariant meaning there is no fundamental length scale for PhCs, such as the Bohr radius in atomic physics. Therefore, similar structures of different sizes behave similarly, if the lattice constant of a PhC is scaled by a factor s (its mode profile and frequency are re-scaled versions of the old mode profile) i.e. the solution to the master equation at one length scale provides the information for all length scales. For this reason the eigenfrequencies are usually given in a unit normalized to the lattice constant, ω = a/λ and since a/λ = ω/(2πc/a) the energy is often expressed in these units, as per the dispersion relations shown in Fig. 3, which highlights the PBG variation due to refractive index contrast; the larger the contrast the wider the gap.
. Forward propagation results in a straight line as does backward propagation. This is shown schematically in Fig. 2(a) and (b). However for a periodic material, as in Fig. 2(c), the periodic dielectric function causes forward moving waves to be partially reflected at every interface. For frequencies that fulfill what's known as the Bragg condition, which is similar to x-ray diffraction theory but for optical wavelengths, interference of the forward and backward waves creates a standing wave at the edge of the BZ. Due to the splitting of the ±π/a planewaves into cos(πx/a) and sin(πx/a) standing waves by the different effective refractive indices and the subsequent difference in photon energies, a gap in the dispersion relation opens up – the photonic band gap (Fig. 2(c)). Maxwell's equations are scale invariant meaning there is no fundamental length scale for PhCs, such as the Bohr radius in atomic physics. Therefore, similar structures of different sizes behave similarly, if the lattice constant of a PhC is scaled by a factor s (its mode profile and frequency are re-scaled versions of the old mode profile) i.e. the solution to the master equation at one length scale provides the information for all length scales. For this reason the eigenfrequencies are usually given in a unit normalized to the lattice constant, ω = a/λ and since a/λ = ω/(2πc/a) the energy is often expressed in these units, as per the dispersion relations shown in Fig. 3, which highlights the PBG variation due to refractive index contrast; the larger the contrast the wider the gap.
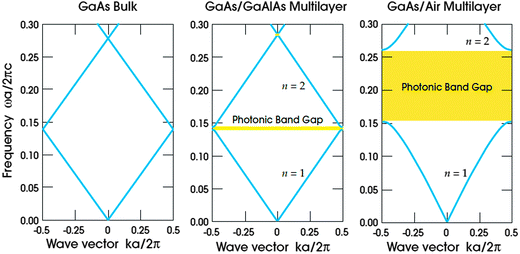 | ||
| Fig. 3 The photonic band dependence on refractive index contrast computed for three different multilayer films with layers of width 0.5a, in (a) the dielectric constant is the same for every layer ω = 13 in (b) layers alternate between a material of dielectric constant 13 and 12 and (d) shows the wider PBG for the larger contrast with alternating layers of dielectric constant 13 and 1.18 Reproduced from ref. 18. Copyright 2008 Princeton University Press. | ||
This PBG and the ability to manipulate it through material choice is the central driving force for the fabrication of PhCs because with it comes a litany of extremely useful optical phenomena. The initial theories from Yablonovitch and John mentioned above still represent two of the most interesting and attractive qualities of PhCs. Spontaneous emission of excited atoms is a fundamental problem faced by many optoelectronic devices, causing energy loss, speed limitations and noise.20,21 Spontaneous emission and the rate at which an atom decays is related to the number of allowed electromagnetic states available for an emitted photon, the PBG represents a region of forbidden modes, therefore the density of states (DOS) is zero inside the gap. This suppression of the density of states is what gives PBGs the potential to inhibit spontaneous emission.22 At the edge of the PBG the DOS suddenly increases and this enhanced DOS subsequently enhances emission, which if controlled could also be useful for certain devices. The ability to tune the position and width of the PBG or stopband and in turn manage spontaneous emission is extremely promising for a number of applications, including LEDs and low threshold lasers. The localization and the guiding of light through the introduction of defects is highly beneficial for the formation of waveguides and optical cavities. Point or line defects can be introduced to a PhC and introduce a state within the gap with a localized wavefunction, light that propagates with a frequency within the bandgap of the crystal will be confined within this mode since it is forbidden to propagate outside the defect. This is very beneficial for the manipulation of light around bends (see Fig. 4), obstacles, and for exotic optical effects such as cloaking when meta-material PhCs are used,23–25 minimising losses compared with dielectric waveguides.26
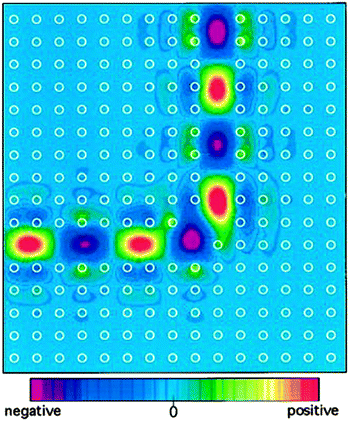 | ||
| Fig. 4 A mode completely confined and guided smoothly around the sharp bend with 2D photonic crystal of dielectric rods in air, the white circles indicate the position of the rods.26 Reproduced from ref. 26. Copyright 1996 American Physical Society. | ||
A modification to Snell's law for refraction of light between media of dissimilar refractive index, and Bragg's law for optical diffraction can be derived to describe the wavelength-dependent ‘structural colour’ observable in colloidal opals or photonic crystals. As outlined in Fig. 5, the opal film is modelled as a multilayer of two media with different refractive indices (in this case two, but it may vary depending on the complexity of the structure, porosity, phase homogeneity etc.). In the present case, one of these indices (η1) is typically vacuum, air or a liquid, the other (η2) that of the material. In the case of constructive interference of diffracted photons, Bragg's law is
mλm = 2ηeffd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ2 ϕ2 | (21) |
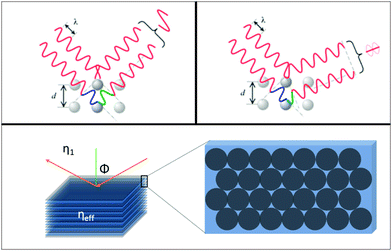 | ||
| Fig. 5 Schematic outlining the interaction of light with the periodic material with an effective refractive index, and the light scattered by the sphere planes. | ||
The corresponding Snell's law criterion for the light incident at an angle ϕ1 can be written as
η1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1 = η2 ϕ1 = η2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ2 ϕ2 | (22) |
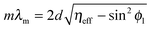 | (23) |
Since the layer or slab in a well-defined opal is periodic, Fabry–Pérot resonances are observable at energies lower than the PBG provided the effective refractive index is well-defined and constitutes a homogeneous thin layer with effective refractive index ηeff. For ordered, simple thin film opals (but typically not for single monolayer opals as they are typically weaker and broader than diffraction contributions), ηeff and the number of layers can be estimated from the periodicity of the Fabry–Pérot resonances in optical reflection or transmission spectra. The number of layers, or the opal film thickness, is distinct from the optical thickness obtained from the spectral separation of the Fabry–Pérot fringes, which also includes the effective index. To estimate film thickness (at least for a simple 3D ordered opal of identical spheres), the fringes will appear in reflectance or transmission spectra at
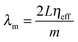 | (24) |
B. 2D opals and ordered structures – planar dielectric grating diffraction
2D diffraction can also be used in assessing monolayer, or 2D PhC structures. The planar grating equation can be used in calculating the theoretical dispersion of incident light diffracted from a 2D artificial opal.27,28 There are a number of discrete angles (β) for a given groove spacing (d) where constructive interference occurs between diffracted light,| λ = d[sin(α) + sin(β + x)] | (25) |
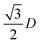 where D is the sphere diameter, α is the angle of incidence, β the angle of diffraction, and x is a free constant commonly used in data fitting, and is likely associated with the discrepancy in diffraction energy caused by the spherical particles/grooves. In the case of 2D opals, the discrepancy between ideal fit and the measured diffraction maxima are associated with variations in the periodic order of the 2D opal. This effect, experimentally, can arise from non-close packed structures with a fixed diameter of spheres, and include a constant or spatially variant spacing between spheres within domains of the ordered PhC. Additionally, solutions or solvents may shrink or swell certain polymeric forms of spheres within a 2D PhC (and also 3D systems) that affects the angular diffraction response as a dielectric grating. Readers are referred to several classic papers on planar diffraction gratings for in depth analysis of the optics of such systems, such as in Gaylord and Moharam29 for example.
where D is the sphere diameter, α is the angle of incidence, β the angle of diffraction, and x is a free constant commonly used in data fitting, and is likely associated with the discrepancy in diffraction energy caused by the spherical particles/grooves. In the case of 2D opals, the discrepancy between ideal fit and the measured diffraction maxima are associated with variations in the periodic order of the 2D opal. This effect, experimentally, can arise from non-close packed structures with a fixed diameter of spheres, and include a constant or spatially variant spacing between spheres within domains of the ordered PhC. Additionally, solutions or solvents may shrink or swell certain polymeric forms of spheres within a 2D PhC (and also 3D systems) that affects the angular diffraction response as a dielectric grating. Readers are referred to several classic papers on planar diffraction gratings for in depth analysis of the optics of such systems, such as in Gaylord and Moharam29 for example.
The position of the bandgap is determined by the lattice constant and the spectra PBG width by the effective refractive index contrast and filling factor. If materials of sufficiently high refractive index contrast are used in conjunction with materials with low absorption in the desired spectral range, then light with energies located inside the PBG will be reflected from the PhC without absorption, which makes PBG materials highly suited to optical filter applications. The light that is reflected or diffracted by a PhC follows Braggs law and so can be used in determining the reciprocal lattice of a given structure. This facilitates probing of the optical characteristics of a given PhC by angle resolved light reflection and transmission experiments, which is a useful characteristic when designing and synthesising PhCs for a particular application.
PhCs can be designed and formed by several methods, including sophisticated and expensive lithography techniques, both holographic30 and mask31 methods. However, one of the more popular approaches is the formation of artificial opals through the self-assembly of colloidal spheres of either silica or different polymers.16,32 This route has the benefit of low cost and aside from limitations due to natural imperfections that in some cases can lead to a certain degree of disorder, these approaches still offer amenable and useful properties for a host of real and theoretical applications in a number of technologies. However, perhaps the most significant application of artificial opals is in fact as templates for the formation of 3D PhCs in the form of inverse opals (IOs). Inverse opals are three dimensionally ordered macroporous materials formed through the infiltration of an artificial opal with a material precursor and then removal of the spheres. Provided a material of sufficiently high refractive index is used, IOs offer the possibility of achieving a complete PBG. The ability to control the structure and symmetry of 3D PhCs through template design has ensured a substantial and continuously growing interest in methods of artificial opal growth by colloidal self-assembly.
III Colloidal self-assembly
A. Using capillary and/or external forces
As discussed above, the working range of a photonic crystal is dependent on the spatial periodicity of the refractive index. For this reason, periodicity needs to be on the order of a few hundred nanometers to 1 μm in order to operate in the visible or near-infrared region of the electromagnetic spectrum. The lattice constant of the photonic crystal must be comparable to the wavelength of light. It is important to note that for self-assembly to occur, a balance must be made between the colloidal forces, the forces induced by colloidal phenomena and any external forces acting on the system, all of which can be either attractive driving forces or repulsive forces that can oppose coagulation of the spheres.Various methods have been developed for the assembly of monodisperse spheres into ordered or semi-ordered lattices. The type of methods available are often discussed in terms of the various phenomena or forces used or manipulated in order to influence their assembly; gravitational or inertial forces, surface tension or capillary forces, or electric or magnetic fields. Certain methods can also involve some form of spatial confinement to further direct the self-assembly process. The predominant assembly routes are discussed in summary here with several reviews16,17,19,32–35 available discussing the various methods and their effectiveness in further detail.
Among the oldest and simplest method of assembly is sedimentation.36,37 Colloidal particles in solution will settle under gravity to produce thick, ordered structures, the thickness of which can be controlled by controlling the concentration of the sphere mixture. For this to occur naturally, with no external force applied, the density of the particles must be sufficiently higher than that of the dispersion medium. The movement of the spheres under gravity creates a diffusive force in the opposite direction due to the concentration gradient caused by the particle descent under gravity. For large particles, the effect of gravity will overtake the effect of diffusion, and the opposite is true of very small particles. Depending on the size of the spheres, this process of allowing the colloids to settle under gravitational forces can take from between several days to several months. For this reason, it is unsuited for large scale production and so other, more controllable and faster routes are more commonly used.
Sphere assembly/deposition by sedimentation has since been adapted by the application of external forces, for example, the sedimentation of spheres under centrifugal or inertial force. The use of centrifugation, produces thick deposits of unsupported spheres, applicable to almost all sizes of spheres provided the density difference between them and the dispersant is sufficient and the centrifuge speed is strong enough.38–41 This method, however, becomes more difficult for samples or applications requiring the use of a substrate.
Manipulation of inertial forces through spin-coating42–45 can produce polycrystalline deposits over large areas. However, with this technique the best results seem to occur for those involving some kind of localized restraint to ensure close packing of the spheres, such as what Jiang et al. demonstrated, whereby large, wafer scale 3D colloidal crystals were formed using silica spheres inside a polymer matrix, and then selective removal of the spheres or polymer produced either colloidal crystals or macroporous polymers, respectively;42 this is shown in Fig. 6(a–c). They further developed the technique by producing non-close packed, two dimensional monolayer colloidal crystal–polymer nanocomposites through spin coating with a gradual increase in spin speed.
 | ||
| Fig. 6 (a) Wafer-scale non close packed monolayer colloidal crystal made by spin-coating on a 4-in. sample illuminated with white light. (b) High magnification SEM image of the typical top surface of the sample in (a) and (c) is a cross sectional SEM image showing a monolayer colloidal crystal polymer nanocomposite made by spin-coating.43 Reprinted with permission from ref. 43 Copyright 2006 AIP Publishing LLC. Contact angle measurement of (d) water (α = 26.9°) and (e) DMF (α ≈ 0 or immeasurable) and the comparison of wettability with 300 μL (50 mg mL−1) of (f) silica spheres in water and (g) silica spheres in DMF solution droplets on piranha cleaned 2 inch Si substrates. SEM images after-spin-coating at the same speed of silica spheres (h) in water and (i) in DMF.46 Adapted with permission from ref. 46. Copyright 2014 American Chemical Society. | ||
Spin coating requires significant optimization and balance in terms of material concentration, particle size and spin speed, and has a tendency to produce patchy deposits which is why Jiang et al. advises priming the silicon substrate with 3-acryloxypropyl trichlorosilane to reduce patch formation using net charged species.43 Arcos et al. investigated the local and large scale order for spin coated colloids, showing thickness and symmetry to be controllable by solvent choice and spin speed.44
More recently as shown by Fig. 6(d–i), the addition of the organic solvent N,N-dimethylformamide (DMF) (Fig. 6(e), (g) and (i)) has been suggested as a means of producing enhanced uniformity and coverage for spin-coating silica sphere monolayers compared with spheres suspended in water (Fig. 6(e), (g) and (h)).46 This further highlights the importance of the dispersal solvent properties, such as surface tension, evaporation rate and subsequent wettability, in achieving large scale coverage of uniform sphere structures by spin coating. However, the polycrystalline nature of most spin coated structures produced to date could make them more suited as templates for the production of monolayer porous materials with very low crack densities, as opposed to photonic applications directly.44
The application of a magnetic or an electric field, in directing sedimentation has proved useful for the formation of highly ordered structures, at much faster rates than those methods relying on gravity alone. The surface charge of the colloidal particles and the pH of the entire solution can be controlled for enhancing or slowing sedimentation of the spheres under the external force. A magnetic field can be modulated spatially in time and in magnitude and so can provide a versatile driving force for colloidal self-assembly.
Li et al. has investigated several methods of magnetic self-assembly, taking advantage of the dipole–dipole interactions between magnetic particles for the assembly of 1-dimensional chain-like sphere assemblies (Fig. 7(a and b)),47 and using a ferrofluid for the magnetic assembly of non-magnetic particles (PS spheres) into 1D chains under a weak external magnetic field and into 3D structures with the application of a strong magnetic field (Fig. 7(c–e)).48 Li also highlighted an improvement in the effect an externally applied magnetic field can have on the packing and order of the non-magnetic sphere assembly when sustained over for a period of time, shown by the reflectance spectra in Fig. 7(e). Asher et al. assembled superparamagnetic non-close packed photonic crystals using highly charged superparamagnetic polystyrene–iron oxide composite colloidal particles, fabricated by the emulsion polymerization of styrene in the presence of ∼10 nm iron oxide particles. The application of an inhomogeneous magnetic field to an aqueous assembly of these particles produced particle attraction towards the maximum of the local magnetic field gradient, compressing the already partially assembled colloidal arrays along the magnetic field gradient.
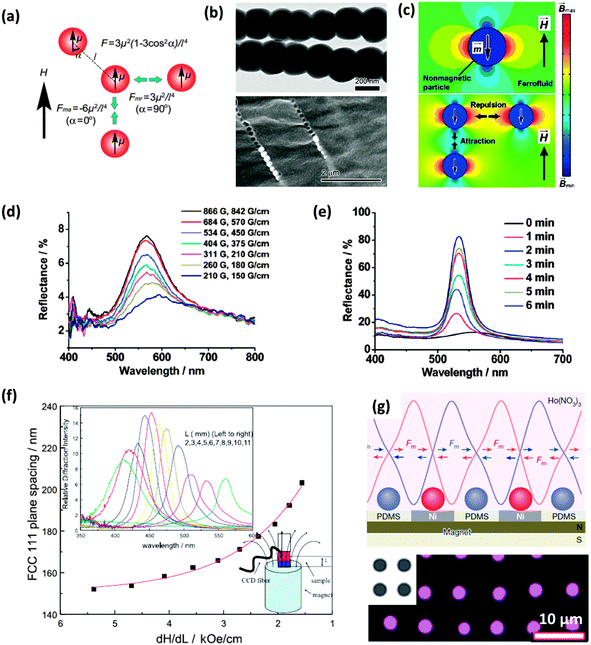 | ||
| Fig. 7 (a) Schematic illustration of the dipole–dipole interactions between two identical magnetic particles in an external magnetic field.49 Reproduced with permission from ref. 49. Copyright 2011 Royal Society of Chemistry. (b) TEM and SEM images of Fe3O4@SiO2 particle chains fixed in a polymer matrix.47 (c) Magnetic field distribution around a non-magnetic particle with a dipole moment in the direction opposite to the applied magnetic field (top) and the dependence of the interparticle dipole–dipole force on particle configuration (bottom), the colour bar indicates magnetic field strength.47 Adapted with permission from ref. 47. Copyright 2012 American Chemical Society. The reflectance spectra for a 1 mm thick PS film in ferrofluid solution for external magnetic fields with varying strength (d) and for a fixed magnetic field (2530 G) over time (e).48 Adapted with permission from ref. 48. Copyright 2010 American Chemical Society. (f) Influence of the average magnetic field gradient, dH/dL on the lattice constant of a thick CCA composed of 134 nm superparamagnetic particles.50 Reproduced with permission from ref. 50. Copyright 2001 Wiley-VCH. (g) In-plane forces attracting paramagnetic particles (red) onto the nickel grids embedded in a layer of poly(dimethyl siloxane) (PDMS) placed on a permanent magnet of typical strength 0.442 (top) and (bottom) magnetic particles (purple) assembled on the nickel grids (grey).51 Reproduced with permission from ref. 51. Copyright 2016 Nature Publishing Group. | ||
The lattice constant, as a balance between the magnetic packing forces and the interparticle electrostatic repulsive forces, was a minimum at the locus of the magnetic field gradient maximum. An increase in the magnetic field and magnetic field gradient saw a decrease in the lattice constant of the packing structure, shifting the diffraction wavelength of the assembled structure to lower wavelengths (Fig. 7(f)). Magnetic assembly has also been used for the assembly of colloidal particles into patterned structures as shown in Fig. 7(g). Patterning of colloidal spheres by different methods will be discussed in more detail later. The necessity of using ferro- or paramagnetic materials, or the doping of latex particles with superparamagnetic nanoparticles47–50 can make magnetic-field-induced self-assembly seem less applicable than the use of, for example, an electric field52–58 to direct sphere aggregation.
Electrophoretic deposition is a process where conductive electrodes are suspended in parallel in a solution of charged colloidal particles and the manipulation of the electric field induces sedimentation on the oppositely charged electrode by the process of electrophoresis. Control parameters include substrate choice and conditioning, sphere functionalization and solution pH. This has been demonstrated for silica spheres, whereby Holgado et al. established electrophoretic deposition of silica particles as a method for controlling sedimentation velocity, thereby overcoming the sedimentation complications that arise for sphere sizes that are too small or too large.53 Rogach et al. further developed the method and showed its suitability for the formation of 3D ordered polystyrene sphere deposits, which underlined the high level of quality and increased assembly time that was achievable through electrophoretic deposition.54 Despite the fact that this method allows for the production of thick opals deposits, little investigation has been conducted into the influence of different experimental parameters on the nature of the deposits formed. For example, the influence of substrate used, time and voltage dependences and the degree of control that can be achieved over opal ordering remain relatively open issues.
The development of vertical deposition via evaporation induced self-assembly compelled by capillary interactions is one of the most frequently used methods for sphere assembly and has been shown to produce better quality films than those achieved through simple sedimentation. The development of this technique began with the early work of Dimitrov and Nagayama which outlined a process of convective assembly for the growth of homogeneous monolayers of PS spheres on planar substrates by controlling the position of the leading edge of a meniscus on a substrate vertically removed from a solution of colloidal spheres.59 This process and the forces involved are outlined in the schematic in Fig. 8(a). The factors governing the order, thickness and rate of formation of the film are quantified, from humidity and temperature to volume fraction.
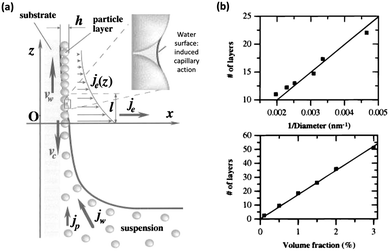 | ||
| Fig. 8 (a) Schematic of the particle and water fluxes at the liquid–air contact line, in the vicinity of monolayer particle arrays growing on a substrate plate that is being withdrawn from a suspension with an inset highlighting the liquid bridge between two neighbouring particles. Here, vw is the substrate withdrawal rate, vc is the array growth rate, jw is the water influx, jp is the respective particle influx, je is the water evaporation flux, and h is the thickness of the array.59 Reproduced with permission from ref. 59. Copyright 1996 American Chemical Society. (b) Number of layers vs. the inverse of the particle diameter, for samples grown from a 1% volume fraction solution (top) and the number of layers vs. the particle volume fraction (bottom) for 298.6 nm spheres grown by the Colvin method.60 Reproduced with permission from ref. 60. Copyright 1999 American Chemical Society. | ||
The vertical deposition technique more directly refers to the method outlined by the Colvin group where a substrate is settled vertically in a solution of spheres forming a meniscus which is then swept vertically along the substrate as the solution evaporates, requiring no substrate removal. This action forces the colloidal particles to self-assemble on the substrate as the meniscus advances with evaporation, resulting in the formation of high-quality multi-layer films of close-packed silica spheres, with thicknesses up to 50 μm.60 Jiang and colleagues applied the quantitative model developed by Dimitrov and Nagayama for the relationship between volume fraction and sphere diameter with the number of colloidal layers assembled by their stationary method. This vertical deposition technique, often referred to as the Colvin method, has since become a favoured technique for sphere assembly, due in most part to its simplicity and thickness control (see Fig. 8(b)), it is however somewhat limited by the time needed for solution evaporation and is highly sensitive to substrate and environmental conditions, such as evaporation rate.
Both of these methods are conceptually similar to the layer-by-layer scooping technique,61 or the Langmuir–Blodgett technique,62,63 however with vertical dip-coating the film forms out of solution directly onto the substrate and by Langmuir–Blodgett the spheres, latex or silica, are first arranged at the air–water interface or the surface of a non-miscible solvent. The arranged spheres are then transferred to the substrate by a moving barrier exerting a compaction force on the particles. Repeated cycles of Langmuir–Blodgett can produce 3D structures but the transfer of the ordered layers from the liquid interface to the substrate can cause disruptions that limit the structural order. Langmuir–Blodgett is therefore best suited to large-area monolayer formation but can provide a high degree of control for synthesising layered structures.
Since Nagayama's early investigations into the use of dip-coating for the formation of well-ordered sphere assemblies, dip-coating has been substantially investigated and varied in order to optimize the process.28,64–73 Several methods have been investigated towards improving the order of dip-coated colloidal crystals, for example, Khunsin et al. investigated the effect of perturbative noise-like acoustic waves on colloidal crystal growth during dip-coating (Fig. 9(a)). The authors studied the overall changes in colloidal ordering as a function of the mean vibration magnitude67,74 and observed an improvement in overall opal order when continuously displacing the meniscus, as shown in Fig. 9(b and c).47,57 They determined an optimum level of acoustic vibrations for increasing the effective crystallization time in the solution meniscus, leading to a less stressed lattice with no change in generic symmetry.
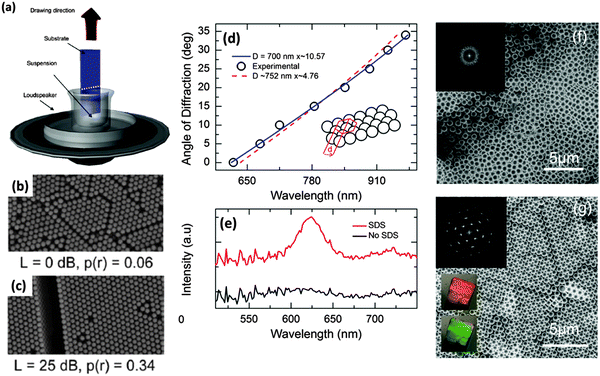 | ||
| Fig. 9 (a) Schematic representation of the deposition process for a colloidal crystal from an aqueous suspension of PMMA spheres with acoustic vibrations with the white noise spectrum applied from below while the substrate was vertically drawn out of the suspension by a stepper motor and (b and c) SEM images of samples crystallized at noise levels L with calculated regularity measures p(r) illustrating the higher degree of order for noise assisted crystallization.67 (d) SEM image and corresponding FFTs showing a 2D photonic glass monolayer (without SDS) and (e) a 2D monolayer photonic crystal (with SDS). (f) The dispersion of the diffraction maximum of SDS-assisted 2D opals from angle resolved reflectance measurements compared with the theoretical dispersion and the schematic representation of the grating groove d, and (g) light scattering normal to the surface (i.e. angle of diffraction = 0°) for light incident at 60°.28 Adapted with permission from ref. 67 and 28. Copyright 2012 and 2014 Wiley VCH. | ||
One of the limiting factors of both vertical deposition and dip coating is the settling of the colloidal solution over time. In particular, for larger sized particles, the long periods of time often required for achieving well-ordered opals through controlled withdrawal or evaporation of the dispersant liquid is problematic. Therefore, one of the major benefits of the noise agitation not initially highlighted by these works is quite simply the interruption it provides in the settling of the suspended spheres. Dip-coating as a whole provides a lot of potential for industry application with, for example, its suitability to a process-line-type production scenario. It also provides the desired controllability over sample assembly needed for industry application through the variety of controllable and adaptable parameters available, for example, the withdrawal rate, the concentration of spheres and the evaporation rate, providing several routes towards perfecting and idealizing sample formation standards. Armstrong et al.28 recently showed that fast-rate dip coating facilitates the formation of an ordered 2D monolayer colloidal crystal of polymer (PMMA) spheres on a gold substrate when a surfactant such as SDS is mixed into the sphere solution prior to dipping (Fig. 9(d–g)). That work also demonstrated that a reduction in the concentration of both spheres and SDS by 50% improves the deposition at a slow (common) withdrawal rate as evidenced by grating-like optical diffraction from angle-resolved light scattering measurements. Higher quality 2D colloidal crystals of polymer spheres can be formed on gold substrates with the addition of SDS surfactant, when dip-coating at fast or slow rates, provided concentrations are controlled (in this case lowered) at slower rates, overcoming the hydrophobicity issues of some metallic substrates. This method compliments self-assembly protocols that allow tetragonal or other geometric arrangements within opal films that offer unique or well-defined optical properties.75
Several of the techniques or effective forces already discussed have been further adapted or exploited by the addition of some type of spatial confinement. For example, Kim et al. demonstrated a method whereby regular convective assembly was modified by the addition of another glass substrate in front of the glass substrate attached to the dipping apparatus, with a inter-substrate gap of ∼100 μm.76 A small amount of colloidal suspension was then inserted into this gap with a capillary force strong enough to keep the suspension inside the gap. Raising the back glass substrate at a specific rate while applying hot air to the meniscus edge caused the water in the colloidal suspension to evaporate, assembling the spheres into ordered structures and fixing them to the back substrate. The meniscus thinning rate could be modulated by controlling the lift up rate of the substrate and the method was shown to be successful for the formation of both mono- and multi-layered structures as well as binary colloidal crystals (discussed in detail later).76 A similar method produced two dimensional monolayers of PMMA spheres self-assembled from a colloidal solution dragged between two plates; the top plate was dragged at a constant velocity in the direction opposite to monolayer growth. The spheres were directed towards the contact line of the solution meniscus by evaporation induced convective assembly, much like the vertical deposition and dip-coating techniques discussed previously. However, this method allowed for smaller amounts of colloidal solution, producing monolayer particle arrays covering large areas provided that the particle concentration, sliding speed of the top substrate and wettability of the bottom substrate were optimized.77
B. Binary colloidal crystals
First observed in nature in the Brazillian opal,78 binary colloidal crystals (bCCs) consisting of spheres of two sizes, large (L) and small (S) particles, can offer a rich variety of crystal structures compared with the colloidal crystals discussed so far. The type of patterns and symmetries formed are generally characterized by the stoichiometry LSN, where L represents the large spheres, S the small spheres, and N represents the number ratio of small to large spheres. These complicated structures however, have seen limited use to date due to the difficulties in formation and characterisation they present compared with their single sphere-size counterpart. The first laboratory example was created using charge-stabilized latex particles dispersed in water by Hachisu and Yoshimura, who connected the type of structures formed with the size ratio of the particles, the number ratio, and particle concentration.79 Yoshimura and Hachisu also pointed out the similarity of these structures to the structure of several metal alloys. The potential therefore, of bCCs, formed with polymer and/or silica spheres, lies not only in their photonic characteristics but in their exploitation as ideal models for the atomic arrangements80,81 of certain metal compounds,62,63 as well as lithographic templates for complex micro- and nano-structures and surface patterning.82,83 Synthesis routes initially relied on sedimentation under gravity which (as with ordinary colloidal crystals) is extremely time consuming making it a less viable route for large scale production.Over the last decade however several layer-by-layer84,86–88 and co-deposition techniques82,89–93 have been designed for the formation of both ordered and disordered bCCs. Van Blaaderen and co-workers reported the fabrication of bCCs through vertical deposition, where a 2D hexagonal close packed crystal of large silica spheres was grown first at the slow rate of ∼1 to 2 mm a day on a glass substrate. The small particles, of either silica or polystyrene, were then deposited onto the large-particle template by the same method. These steps were successively repeated to create 3D structures of alternating layers of large and small spheres, and structures with stoichiometries of LS, LS2, or LS3 were grown by this method by varying the size ratios and volume fractions (see Fig. 10(a and b)). Kitaev and Ozin presented an accelerated vertical deposition technique where low pressure was applied to accelerate the rate of ethanol evaporation from a solution of both large and small negatively charged spheres at low concentrations, producing monolayer bCCs. In this case the smaller spheres were organized within the interstitial sites between the hexagonally ordered larger spheres. The number of small spheres between the larger was shown to vary with small sphere sizes and concentration85 as seen in the SEM images in Fig. 10(c).
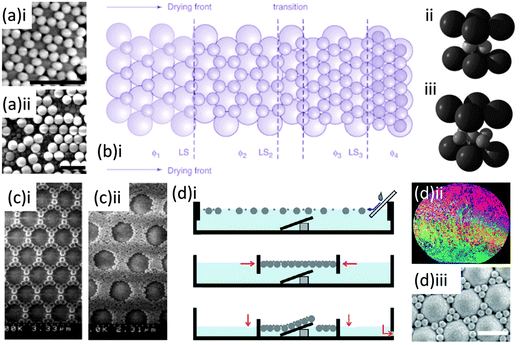 | ||
Fig. 10 SEM image of binary structure grown by a layer-by-layer technique showing (a)i a layer of smaller spheres on a 2D layer of larger 203 nm silica spheres in a LS3 stoichiometry and (a)ii an incomplete third layer of larger spheres to illustrate over-layer formation and a schematic representation (b)i of the process of assembly for the smaller spheres onto the larger 2D structure as a function of volume fraction φ and diagrams for the unit cells of the (b)ii LS2 and b(iii) LS3 arrangements.84 Adapted with permission from ref. 84. Copyright 2002 AAAS. (c) SEM images of the variation in binary stoichiometry for different volume fractions φ and sizes ds of small spheres (i) φ = 3.1 × 10−4ds = 290 nm (ii) φ = 5.6 × 10−4ds = 145 nm deposited by the accelerated vertical deposition.85 Adapted with permission from ref. 85. Copyright 2003 Wiley-VCH. (d)i Schematic representation outlining the formation of binary structures using the water air interface and compression forces (d)ii wafer surface after liquid lowering and the monolayer formed from 1063 nm and 225 nm sphere solution with size ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 transferred from the water air interface and dried (d)iii SEM image of the top surface.82 Adapted with permission from ref. 82. Copyright 2011 Wiley VCH. 6 transferred from the water air interface and dried (d)iii SEM image of the top surface.82 Adapted with permission from ref. 82. Copyright 2011 Wiley VCH. | ||
Both step wise spin coating86 forming LS2 and LS3 stoichiometries, and confined-convective assembly87 forming structures of LS2, LS3 as well as the more complicated LS4 and LS5 stoichiometries have been presented as faster routes for the assembly of bCCs. Kim et al. suggested that confined convective assembly can be used to produce ordered binary structures for a size ratio ≤0.58 with anything above leading to the formation of only random configurations. If the diameter of the smaller spheres is too large, filling the interstices between the larger particles in the already assembled monolayer with the required periodicity will not be possible, therefore ordering is disrupted.87 Smaller spheres have also been assembled on an already formed monolayer of larger spheres by electrophoretic deposition, producing several stoichiometries (e.g. LS, LS2, LS4 and LS8) controlled by the size and the volume fraction of the small spheres used.88 It is important to note in this case that the monolayer of larger spheres is deposited through ordinary capillary interactions caused by solution evaporation, and therefore already in place to provide a template for the electric field induced assembly, designating this method as a layer-by-layer technique for 2D crystal formation and limiting the speed of the technique. Wang et al. described a vertical lifting co-assembly technique90,94 for the formation of 3D bCCs. More recently, monolayer assembly using interactions at the water–air interface has become one of the more widely studied techniques for bCC assembly due in part to its adaptability to almost any substrate. Shen et al., first assembled the binary structure at the water–air interface in the presence of a surfactant (SDS) and then transferred it to the desired substrate, thus preparing monolayer bCCs over large areas in a short time.89 A colloidal mixture in ethanol was drop cast onto hydrophilic glass surrounded by DI water, spreading out rapidly across the slide and on to the surface of the water where the floating spheres then assembled into ordered 2D arrays on the surface with the help of added SDS which reduced overall surface tension. The glass slide reduces the spreading speed of the suspension enough so as to allow time for an ordered monolayer to self-assemble.
This approach prompted several other studies into the formation of bCCs using the water–air interface; Vogel et al. explored the assembling of bCCs using a Langmuir trough attempting to establish more control over the composition for a large range of size and number ratios. As shown in Fig. 10(d), a floating 2D binary crystal monolayer was compressed by the Langmuir trough and, as the water sub-phase was pumped out, transferred to the substrate which was submerged at an angle just below the water–air surface.82 Dai et al. described another method where the binary colloidal solution with added ethanol was dispersed into a liquid film on the chosen substrate. Solvent evaporation caused convective flow of the spheres towards the water–air interface and assembly into ordered binary arrays under de-wetting and capillary effects, provided that the size difference between the large and small spheres was sufficient. On the basis of this type of assembly Dai et al. established a phase diagram, in Fig. 11 as a function of volume ratio for the formation of monolayer bCCs offering an effective way for predicting the resulting pattern stoichiometries provided that the size and volume ratios for the spheres well dispersed on a water–air interface is known.92
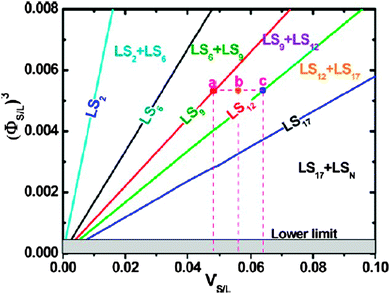 | ||
| Fig. 11 Phase diagram of monolayer bCCs, or (ΦS/L)3, as a function of VS/L for different monolayer LSN bCCs. Each plot corresponds to the denoted single-phase line. The areas between two adjacent straight lines correspond to the denoted two-phase regions. Shadow area corresponds to a ΦS/L smaller than the lower limit (or 0.077). The points a, b, and c indicate the LS9, LS9 LS12 hybrid, and LS12 bCCs, respectively. Reproduced with permission from ref. 92. Copyright 2012 American Chemical Society. | ||
Very recently, a technique for the growth of bCCs within microfluidic devices has been presented by Harrison and co-workers.93 A mixed colloidal dispersion was injected into a dispersion reservoir and pulled along a microfluidic channel fabricated via soft lithography in PDMS. Evaporation occurred though the evaporation reservoir at the other end and triggered self-assembly. For silica particles the suspension was repeatedly mixed via a periodic chip rotator thereby counteracting the hydrodynamically amplified sedimentation and producing well-ordered bCCs.93
As discussed above, a binary colloidal crystal structure is primarily determined by the size ratio of large (L) to small (S) colloidal spheres, as well as the relative content of both spheres. The number and variety of assembly routes for bCCs developed so far are relatively few compared with ordinary colloidal crystals and the bulk of these generally refer to the formation of monolayer or 2D structures only, though some layer-by layer techniques can deliver 3D structures. Several routes suffer from lengthy time requirements, premature sedimentation of the larger particles and poor control over larger dimensions. Further development into a cost effective and fast single step method for controllable fabrication of bCCs is therefore needed, because 3D binary structures still hold great possibilities and are ideally suited as a complex template architecture for inverse opal fabrication, their untapped potential, both optically and structurally, could be of specific use to future optoelectronics94,95 or as templates for reduced refractive index materials for tandem solar cells or enhance light extraction efficiency coatings for light emitting devices, to name a few.
C. Patterned substrates and constrained PhC assembly
As already discussed, most of these assembly routes utilize the naturally occurring gravitational or capillary forces incurred by colloidal particles, which can have different effects on colloidal assembly, being in most cases advantageous for thickness control, ordering, and domain size definition of the colloidal arrays. However, capillary interactions usually lead to the formation of close-packed colloidal crystals with the hexagonal or FCC (111) lattice plane almost always parallel to the substrate surface, thereby limiting the crystal orientation and type of packing. As the optical characteristics of the PhC, specifically the position and wavelength range of the PBG are affected by lattice structure and symmetry as well as filling fraction, the ability to design and direct lattice orientation is of interest for PhC investigations and application. For example, non-close packed spheres allow higher filling fractions96 useful in creating wider PBG materials and have shown a lot of potential in the fabrication of nano-hole arrays97 and microwells.97,98 As already mentioned earlier, control over defect positioning and density is also paramount when designing PhC structures for use in optoelectronic devices that require both long-range order and precise pattern registrations. Solid surface patterning through the use of colloidal sphere masks has also received a lot of attention for the formation of structures at sub-micrometer- and nano-scales. This nanosphere lithography (NSL) could be improved if the assembly of the spheres could be controlled more precisely. With these rewards in mind, several routes towards directing colloidal growth have been investigated through the use of topographically99–103 or chemically104,105 patterned substrates, the use of electric or magnetic field manipulation or a combination of both.51,106,107 Chongjun Jin et al. also demonstrated that a colloidal crystallization approach on templated surfaces can facilitate large area, crack and stacking fault defect free formation of (100)-oriented FCC ordered opal photonic crystals.99Complex aggregates (polygonal and polyhedral clusters) of polymer spheres were assembled by Xia et al., by using a 2D array of holes patterned into photoresist and then removing the resist.103 Van Blaaderen and colleagues demonstrated the templated assembly of silica particles by vertical deposition on silicon substrates patterned using a combination of electron-beam lithography and reactive ion etching. They determined that for many cases, symmetry tends to alter for a single layer but revert to its favoured hexagonal ordering for subsequent layers.101 Silica spheres have been patterned into particle wires by coupling solvent chemistry and regions of hydrophilic silanol groups formed using self-assembled monolayers (SAMs) of octadecyltrichlorosilane (OTS) modified by UV irradiation, as shown in Fig. 12(a–c).105 Recently, Qian et al. investigated the relationship between voltage and particle-to-hole size ratio when electrophoretically depositing on hole patterned substrates. They determined that for smaller hole sizes, a larger electric field was required for sphere deposition to occur. For example, no deposition occurred for an applied voltage of 5 V cm−1 but particle deposition began in the larger 5 μm hole at 10 V cm−1, however, an electric field of 15 V cm−1 was needed for spheres to assemble in the smaller 2 μm hole (see Fig. 12(d)). The discovery of a voltage threshold for each size hole is useful for more precise control of sphere deposition through adjustments of pattern hole size and voltage. With the inclusion of a positively charged surface by application of poly-L-lysine, further anchoring of the negatively charged PS spheres within the pattern was encouraged. Qian and co-workers created a variety of assembly patterns, including dimers, trimers and higher order assemblies with different separations, see Fig. 12(e).107
 | ||
| Fig. 12 (a) Schematic of the process for the fabrication of a particle wire using a patterned SAM and liquid bridge and SEM images of the wire structures formed for spheres in (b) an aqueous solution and (c) ethanol solution.105 Adapted with permission from ref. 105. Copyright 2003 American Chemical Society. (d) SEM images showing the effect of pattern hole size with respect to voltage applied. Four different hole sizes of 5 μm, 2 μm, 1 μm, and 500 nm were patterned onto an electrode. At 5 V cm−1, no deposition was seen in any of the holes. With increasing voltage, depositions into subsequently smaller sized holes were observed. (e) SEM image of PS dimer structures constructed by EPD onto a two hole array pattern, with increased separation, showing the controlled spacing of the PS beads. Adapted with permission from ref. 107. Copyright 2014 American Chemical Society. | ||
As has been shown, methods for artificial opal assembly abound, and while photonic crystals themselves offer unique opportunities still, their popularity is perhaps derived more as a result of the simplicity and diversity they provide as templates for the formation of three-dimensional porous structures, more specifically inverse opals (IO). Inverse opals are created by the infiltration of synthetic opals with a material of high refractive index and subsequent removal of the spheres to produce a structure of periodic voids (air) surrounded by a continuously interconnected material, and this creates a large refractive index contrast that has the potential to produce a full PBG. Not only however, are these structures used for the formation of optically significant inverse opal materials, but they present a simple and ideal route for the formation of both ordered and disordered three-dimensionally porous structures beneficial to several areas of research, and recent advancements are reviewed in the next section.
IV Inverse opals: formation and emerging technological applications
IO's are a close packed array of spherical voids, formed by infiltration of the artificial opal with a material of high refractive index and the removal of the spheres by chemical etching or calcination. There are a variety of methods that are capable of producing programmable porosity from a range of gel, liquid,108 gas109 and solid phase starting or precursor materials, such as evaporation induced self-assembly (EISA),110 glancing or oblique angle deposition (GLAD/OAD),111–114 hybrid organic–inorganic mesoscale templating,115 controlled phase demixing of block co-polymers116 and many others. These materials can be hierarchically rough, or porous on many length scales and may be ordered38,117 or disordered.118 Here, we address the inverse opal morphology and physical properties that lend themselves to new technological research uses and applications.In general, IO formation can be summarized in three steps: (1) opal template formation by one of the techniques outlined previously, (2) material infiltration and some method of conversion, for example, by hydrolysis or other means, and (3) inversion by the removal of the spheres. This last step may occur in tandem with the second step, for example, the crystallization and/or chemical conversion of solution based precursors infilled into the template may occur during the sphere removal step in some preparation methods. As discussed above, most opal templates are formed using silica, PS or PMMA spheres. Silica spheres offer high temperature stability but require removal by wet chemical etching in non-aqueous HF or NH4F, polymer spheres are removed more easily by solvent removal, plasma treatment, or calcination at temperatures above the glass transition temperature of the sphere material. The type of spheres used should reflect the choice of infilled material and the method of synthesis, given that these can vary between three general approaches: (a) impregnation with liquid precursor or sol–gel,58,119 (b) gas-phase depositions such as chemical vapour deposition (CVD)120,121 and atomic layer deposition (ALD)122,123 that take place at extremely high temperatures unsuitable for polymer templates, and (c) electrochemical deposition whereby the chosen material is precipitated out of an electrolyte and gradually nucleates and grows within the template interstitials. There are many reviews and book chapters that highlight the methods and details of the inverse opal infiltration procedures and materials chemistry.19,120,124 More recent investigations have shown that evaporative deposition, or co-assembly, of polymeric spheres with a silicate sol–gel precursor solution and subsequent removal of the colloidal template allows the formation of the opal and inverse opal material in a single step.125
Both the choice of network material and the method of synthesis are dependent on the desired application. A material with a sufficiently high refractive index, ideally higher than 2.8 and an optimal filling fraction can produce a full PBG in the near infrared and visible range, provided the material exhibits minimal absorption along the desired wavelength range. There are however, abundant applications that do not require a complete PBG but still benefit from the porosity, topology and symmetry of the IO structure and the optical characteristics maintained therein. Therefore, the technologies presently under investigation for functional enhancement by IO inclusion are wide-ranging and include for example, photochemistry and catalysis,123,126 high pressure liquid chromatography,127 solid-state dye and polymer lasers, as well as sensors, waveguides, optical switches128 and light emitting devices.129 One of the more promising arenas of application, increasingly gaining attention is in energy storage and generation, such as thermophotovoltaic (TPV) systems, dye sensitized solar cells (DSSCs) and Li-ion batteries (LIBs).
A. Inverted opals for optoelectronics and telecommunications
As discussed above, the optical characteristics of photonic crystals make them ideally suited to several light relevant applications. Through the introduction of defects that locally disrupt the periodicity, allowed states can be created within the band-gap, thereby producing light localization close to the defect, ideal for trapping and guiding light. The use of light as opposed to electrons for the transfer of information has become increasingly more prevalent with the collective aim of developing all-optical integrated circuits. The existence of the PBG or stop bands and the resultant reflection of certain wavelengths, as well as the localization properties and possibilities for suppressed or heightened spontaneous emission, coupled with the ability to control these characteristics through material choice and design bestow inverse opals with significant application potential. They have thus far been investigated for a number of optical devices, including waveguides,26,130 LEDs,129,131 filters,132 optical switches128 as well as sensors both chemical and biological.133The first important step in photonic crystal applications within communications was the synthesis of a Si IO with a full PBG (see Fig. 13) within the frequency range relevant for telecommunications ∼1.3–1.5 μm and above the absorption edge of Si, therefore limiting absorptive losses. Si was grown by CVD within a template of silica spheres, using disilane (Si2H6) gas as the precursor.134
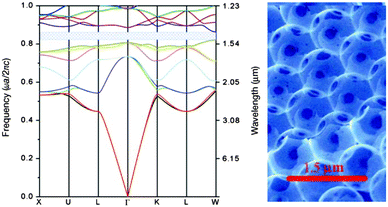 | ||
| Fig. 13 Band structure of silicon inverse opal with an 88% infiltration of Si, the full PBG is shown by the crosshatched region, with a gap to mid gap ratio of 5.1% and SEM image of the (111) face of the silicon IO. Adapted with permission from ref. 134. Copyright 2000 Nature Publishing Group. | ||
In a 2013 work, Feng Jin et al. demonstrated the lasing and amplified spontaneous emission of a resonant cavity fabricated by sandwiching a tert-butyl rhodamine B doped PMMA film between two polymer IOs that acted as feedback mirrors. The polymer IOs were formed as shown in Fig. 14(a) by the infiltration of a PS sphere template with a photopolymerizable resin and polymerized by exposure to UV light. When the gain medium was sandwiched between two IO structures as in Fig. 14(b), the overlap of the photonic stop band of the polymeric IOs with the photoluminescence band of the dye molecules in the sandwiched layer produced single mode lasing emission135 (see Fig. 14(c) and (d)).
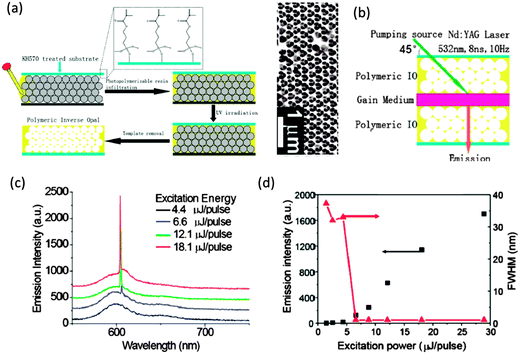 | ||
| Fig. 14 (a) Schematic illustration of the construction process of the polymeric IOs and an SEM image of the resulting IO formed with 256 nm PS spheres. (b) Schematic outline of the fabricated lasing structure. (c) Emission spectra of the resonating cavity with photonic stop band at the wavelength of 610 nm under different excitation energy with spectra offset for clarity. (d) Dependence of the FWHM and integrated emission intensity on the excitation energy in the resonating cavity with 610 nm photonic stop band. Adapted with permission from ref. 135. Copyright 2013 American Chemical Society. | ||
The epitaxial growth of group III–V semiconductor materials in 3D IO nanostructures using selective area epitaxy through a 3D artificial opal template has been demonstrated by Nelson et al., specifically, the formation of GaAs IOs (shown in Fig. 15(a) and (b)) for optical applications.131 A 3D PhC LED was then fabricated by incorporating a passivation layer of InGaAs between Si doped and C doped GaAs IO cladding layers during growth through the PhC template, thereby creating a LED heterostructure within the 3D PhC structure, shown schematically in Fig. 15(c). This PhC LED displayed electrically driven emission at increasing drive currents (see Fig. 15(d)).
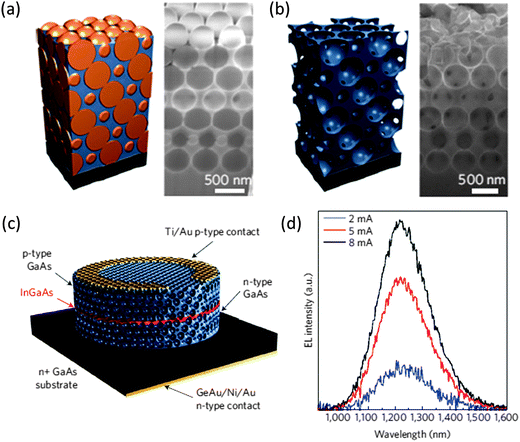 | ||
| Fig. 15 Schematic and SEM image of (a) a GaAs filled PhC template and (b) an inverted GaAs structure after template removal. (c) Schematic of a GaAs 3D photonic crystal LED fabricated by containing an InGaAs light-emitting layer (red) with a GaAs 3D PhC (blue). The complete structure was then lithographically patterned into a cylindrical mesa with a Au ring electrode on the surface and (d) the electroluminescence spectra from the 3D PhC LED with emission not modified by the 3D photonic structure and showing the intensity to be linearly dependent on drive current.131 Reproduced with permission from ref. 131. Copyright 2011 Nature Publishing Company. | ||
Photonic crystals have also been investigated as a route towards considerably enhancing the emission of up-conversion materials, where the deposition of these materials on the surface of 3D PhCs benefits from enhanced coupling of light to the emissive crystals.136–138 Up conversion materials are materials capable of converting two or more low-energy incident photons i.e. light in the infrared into one higher energy emitted photon i.e. visible light. These materials (typically doped with lanthanides) have received significant attention for their potential application in LEDs, lasers, solar cells and within the fields of sensing and biological labelling.139 Unfortunately however, these materials tend to suffer from poor emission intensities. Photonic crystals have unique optical properties that could enhance the emission intensity. For example, Jiayan Liao and colleagues presented enhanced emission for up conversion materials deposited on a opal covered with metal nanoparticles (Ag).138 Based on coupling the photonic band gap effects of the artificial opal and the surface plasmons in the Ag nanoparticles, emission from the up conversion materials (NaYF4:Yb3+,Er3+ nanoparticles) was enhanced by more than a factor of 10 for incident light at wavelengths that overlapped with the PBG of the opal–Ag hybrid. Niu et al. demonstrated more than a 30 fold enhancement in luminescent emission when coupling fluoride up conversion nanoparticles with a 3D opal PhC.137 Wenbin Niu and colleagues attribute this improvement to the enhanced absorption and extraction provided by the 3D opal. These results illustrate the potential application of PhC structures with up conversion materials, in particular, in optoelectronic device design, solar cell technology and sensing.
B. Inverted opals for sensor applications
The reflection of light at particular wavelengths and the dependence of these wavelengths on the refractive index contrast of the PhC make IOs extremely useful in sensor applications. Simply altering the refractive index contrast by replacing or altering one of the materials (usually air) with a material of different refractive index will produce a shift in the PBG or stopband of the IO structure. Hydrogel IOs in particular have been presented as pH,140,141 humidity,142 glucose143 and gas sensors.144 For example, amine-functionalized hydrogel IOs have been described for use in CO2 gas sensing, formed through infiltration of a silica opal with dimethyl aminopropyl methacrylamide (DMAPMA) precursor which was then photopolymerized (Fig. 16).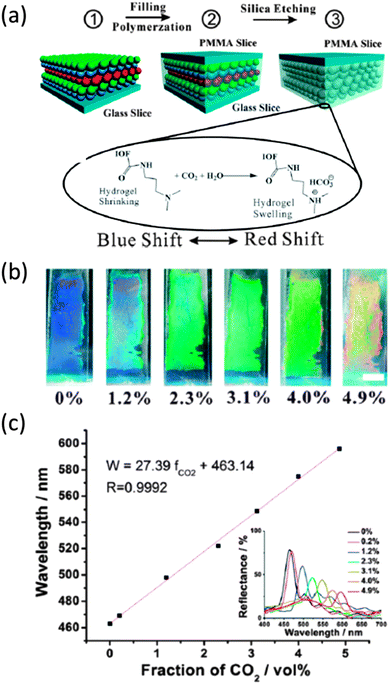 | ||
| Fig. 16 (a) Schematic illustration for the fabrication of the CO2 sensitive inverse opal film and the sensing mechanism of the inverse opal film (IOF) for CO2 gas sensing. (b) The induced colour change of the CO2 sensitive inverse opal film in pure water after being bubbled with 1 mL CO2–N2 mixtures from 0 to 4.9 vol%. Scale bar: 0.5 cm. (c) Plot of the diffraction maxima of the photonic film versus fractions of CO2 in 1 mL CO2–N2 mixtures. Inset in panel (c): the reflectance spectra of the photonic film corresponding to the fractions in (b).145 Reproduced with permission from ref. 145. Copyright 2013 The Royal Society of Chemistry. | ||
The resultant IO structure once the spheres are removed when immersed in pure water, exhibited a significant redshift in diffraction peak when CO2 gas was injected into the water, as shown in Fig. 16(c). A quantifiable relationship was observed between the colour diffraction from the PhC and CO2 concentration over the whole concentration range. Bubbling CO2 gas through the hydrogel functionalized with amino groups produced ion pairs more hydrophilic than the non-ionic amino groups and a Donnan potential that forces the hydrogel to swell, sensitivity to CO2 is developed by the increase of the fixed charge in the polymer network and a corresponding shift in the diffraction of light from the IO. These hydrogel IO structures were shown by Wei Hong and colleagues as capable of detecting CO2 from environmental gas samples.145
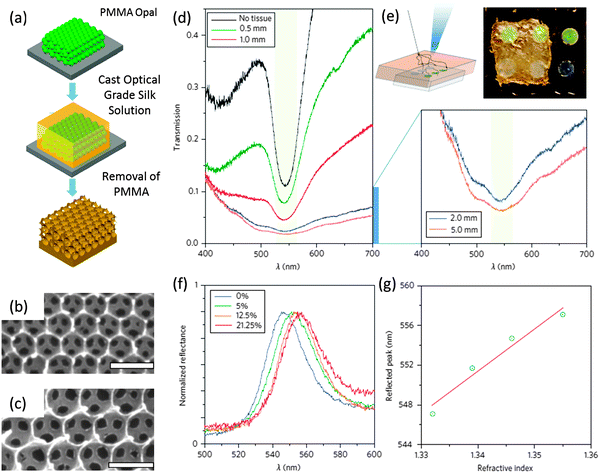
IO sensors also hold a lot of possibilities for use in biological applications.146,147 Biocompatible silk inverse opals formed as schematically outlined in Fig. 17(a) from a purified natural protein, silk fibroin, were fabricated by Sunghwan Kim et al. By examining the optical response from their silk IOs (Fig. 17(b) and (c)) under tissue (chicken breast) of between 2 and 5 mm, Sunghwan Kim and colleagues confirm the ability to still detect the photonic stop-band even under a high scattering environment (see Fig. 17(d) and (e)). The biocompatibility and the degradable, implantable nature of silk IOs present a number of possible applications within biological environments, in particular once the photonic response can still be detected, under living tissue. They also highlight the potential these structures have with regard to colorimetric sensing, by applying different glucose concentrations to affect refractive index changes within the structure causing a shift in the stop band position, as shown in Fig. 17(f) and (g).146 The tunability of the stop band coupled with their low cost and ease of synthesis make IOs and PhCs in general133,148 applicable to both sensing and switching applications. They present a number of possibilities for functional sensing devices for both gas144,145,149 and solvent146,150 detection, provided that material characteristics and design parameters can be tuned for fabrication within specific devices. However, one of their greatest application possibilities could be in bridging the medicinal and technical worlds, especially as research into the combination of biomaterials and PhC architectures continues. Photonic material architectures show potential within sensing applications but throughout biological applications, including drug delivery151 and as scaffolds for tissue regeneration.152,153
 | ||
| Fig. 17 (a) Schematic diagram of the process of formation for the silk fibroin IO structure and SEM images of IO structures formed with pore sizes (b) 240 nm and (c) 300 nm. (d) Transmission spectra for the silk IO lattice 300 nm when placed under tissue (chicken) slices of different thicknesses highlight pseudogap behaviour. (e) An image of the silk IO under one layer of tissue (0.5 mm thick) with a cover glass inserted between the tissue and the IO to avoid swelling and magnified transmission spectra to emphasize the transmission dip in thick tissue. (f) Glucose refractive index sensing for a silk IO with lattice constant 240 nm, showing reflectance spectra for different concentrations of glucose (0%, 5%, 12.5% and 21.25%). (g) Plot of wavelength of reflectance peaks as a function of refractive index.146 Adapted with permission from ref. 146. Copyright 2012 Nature Publishing Group. | ||
C. Inverted opals for thermophotovoltaics and dye-sensitized solar cells
Metallic IOs are not normally favoured for optical applications due to their high absorbance in the visible range, but are showing increasing potential for modifying thermal emission as a result of the periodic modulation in the IO structure.154 One of the most limiting components in thermophotovoltaic (TPV) systems for example, is the narrow band thermal emitter, which emits radiation in a narrowed range of energies towards the photovoltaic (PV) cell which then converts it to electricity. Therefore, the range of energies emitted must be comparable to the electronic band gap energy of the PV cell in order to minimize losses and enhance efficiencies. Thermal emission is directly related to absorption and so at the energies within the photonic bad gap, where the density of states is zero and absorption is low, thermal emission is limited. There is a difficulty however in finding a material that can withstand the high operating temperatures required for these devices. While the 3D PhC has the ability to provide enhanced optical responses over 1 and 2D structures, there is still considerable attention given to 2D PhCs for application in TPV structures. The use of TPV systems as a method of recycling the heat produced in many industrial or combustion processes could be a viable route for achieving portable energy, accessible in remote locations.155In particular, tungsten IOs have the potential to become the leading candidate for selective emitters due to the high melting temperature of tungsten allowing thermal emission over a broad range, however, the thermal stability of tungsten IOs is low.157,158 One route towards improving this is the implementation of oxide passivation layers as a method of preventing surface diffusion and thereby maintaining structural integrity. This was presented by Arpin et al., in 2011, by the application of protective coatings of alumina or hafnia to the surface of tungsten IOs using atomic layer deposition, shown in Fig. 18. This method allowed the production of IOs with thermal stability (for at least 12 hours) of up to 1000 °C with the alumina coating and up to 1400 °C for the hafnia coated IOs.156
 | ||
| Fig. 18 (a) Schematic outline of formation of the tungsten IOs on tungsten foils by electrodeposited inside the 3D silica sphere template and the tungsten inverse opals are then coated with HfO2 or Al2O3 by ALD to impart thermal stability and SEM images (b) showing complete structural degradation after heating a tungsten inverse opal (not protected) to 1000 °C for 30 min in forming gas and of (c) Al2O3 coated and (d) HfO2 coated tungsten IOs after heating to 1000 °C for 12 h.156 Adapted with permission from ref. 156. Copyright 2011 American Chemical Society. | ||
There is presently a growing interest in the use of PhCs for solar energy harvesting in DSSCs whereby the porosity of the IO structure allows for better electrolyte infiltration and improvements in the photo-collection efficiency though enhanced electron transport. Traditionally, DSSCs consist of a number of stacked layers, including, a glass slide, a transparent conducting oxide, a photoanode of semiconductor oxide particulates (frequently disordered TiO2 nanoparticles) along with dyes, electrolyte and the counter electrode. During operation, electrons from the dye are injected due to photoexcitation into the TiO2 nanoparticles. It is the magnitude of the electron flux in the injection/transport process as well as the recombination processes that occur between the photoexcited electrons and the redox ions in the electrolyte that determines the efficiency of the DSSC. Replacing the nanoparticle materials with 3D IOs has shown a lot of promise in improving electron transport characteristics, due to better electrolyte infiltration and shorter electron diffusion distances.159 However, some issues have arisen due to a relatively lower specific area compared with the conventional nanoparticle method leading to lower levels of dye absorption.160
Some progress on improving this has been shown by the formation of mesoporous TiO2 IO structures160 and by Park et al. by combining the nanoparticles approach and the 3D IO layout.161 Through the hydrothermal growth of TiO2 1D nanorods on the surface of the TiO2 IO structure, outlined in the SEM images of Fig. 19(a–c), the effective surface area was increases up to a maximum of 4× the surface area of a bare IO. This along with a slight improvement in scattering response in visible light and improved dye absorption (Fig. 19(d)), led to improvements in several of the DSSC properties over the bare IO structure, including the short circuit current and the photocurrent (see Fig. 19(e)).161 The growth of nanorods on the surface of the IO structure could be of benefit to other IO applications as well, increasing the surface area while maintaining the connection to the overall IO base.
 | ||
| Fig. 19 SEM images of (a) the TiO2 IO structure with an inset showing the TiO2 IO coated with the TiO2 nanoparticle seeds for nanorod growth (b) the nanorod-coated TiO2 IO structure. (c) Magnified SEM image of the nanorods on the surface of the IO structure. (d) Dye-adsorption density versus growth time of the nanorods illustrating the increase in absorption with increase in surface area (e) J–V curves of DSSCs comprising bare IO and nanorod IO electrodes.161 Adapted with permission from ref. 161. Copyright 2014 The Royal Society of Chemistry. | ||
However, the IO structure has also been applied to other aspects of the solar cell make-up both for DSSCs and for Si solar cells, with promising results. For example, carbon IOs have been investigated as a possible counter electrode material for DSSCs.162 Si IOs have shown promise as back reflectors for Si solar cells.163 Their inclusion was shown to improve absorption of near-IR wavelengths and give a 10% enhancement to short circuit current with no degradation in the open-circuit voltage. Mihi et al. has also presented a technique for transferring preformed 3D Si PhCs onto different substrates including independently processed porous DSSCs of nanocrystalline TiO2 and ZnO nanowire electrodes, see Fig. 20(a)–(d).164 The performance of a device with and without the IO back-reflector were compared (Fig. 20(e)) and the power efficiency for both devices with the IO structure i.e. either on TiO2 or ZnO nanowires, was much better than that of the structure without, as shown by the external quantum efficiency plot in Fig. 20(e)II, indicating the higher photocurrent for the IO-containing device. The ability to transfer Si IOs to DSSCs without disruption to structural integrity, could be adopted for other device types, that would benefit from the full or partial PBG provided by these Si IOs.164 As mentioned above, the initial attraction for IO incorporation in DSSCs stems from a need to improve electron transport, which IOs with their porous interconnected architecture allow through better electrolyte infiltration and a three dimensional connected network.
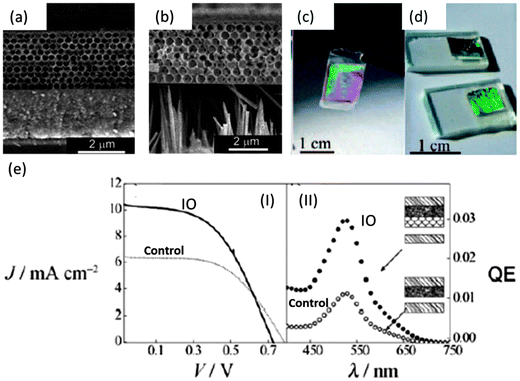 | ||
| Fig. 20 SEM images of 500 nm diameter silicon IO PhC on (a) a 5 mm thick nanocrystalline TiO2 layer and (b) on a substrate covered with 10 mm long ZnO nanowires (150–200 nm diameter) and photographs of (c) a preformed film peeled from the original substrate (d) silicon IOs on dye sensitized ZnO nanowire electrodes after calcination at 500 °C for 2 h and (e) current–voltage curve (AM 1.5 illumination 112 mW cm−2; active area 0.25 cm2) and (e)II quantum efficiency (monochromator slit opening 1.5 mm) for control and IO coupled DSSCs. The values for the reference cell are Jsc = 6.3 mA cm−2, Voc = 0.78 V, h = 2.33%, FF = 0.52. The values for the PhC coupled cell are Jsc = 10.26 mA cm−2, Voc = 0.73 V, h = 3.2%, FF = 0.48. QE = quantum efficiency. Adapted with permission from ref. 164. Copyright 2011 Wiley-VCH. | ||
This advantage can also be considered for the adaption of IO structures for Li-ion battery electrodes, and for low-cost perovskite-based solar cell technologies. They provide options for low-κ dielectrics critical to the future success of the semiconductor industry, but the vast majority of potential applications have yet to be explored, particularly involving IOs where a significant reduction in defect density and greater long range order is needed in IO production. The ability to alter the chemistry of the films, to incorporate or tether species from luminescent nanocrystals to living cells into the porous matrix of these materials offers a host of potential sensing and biomedical applications. In addition, the unique optical properties of IOs can also be exploited to explore other synergistic effects that are not possible without the phenomenological attributes of an optically active host structure, as opposed to an optically active host material.
D. Inverted opals for electrochemical energy storage
Li-ion batteries power most of our portable electronics by virtue of their high energy and power density. It is well known however, that due to the brittle and disordered nature of the active electrode material presently used in most commercial Li-ion batteries and the subsequent need for conductive additives and/or binders to ensure good electrical contact, current batteries often suffer performance limitations, with electrical disconnections and poor ion and electron diffusion. There remains therefore, an ever-increasing need for a charge storage technology capable of providing the high performance and fast charging, needed to sustain our rapidly advancing, high-powered portable electronics industry as well as placate our need for cleaner energies, from electric vehicles to solar and wind storage, all, while maintaining stable and safe capacity retentions during operation. For this reason, a lot of consideration is currently given to the development of materials and architectures for the formation and optimization of electrodes in high-performance, rechargeable Li-ion and emerging alternative batteries.165,166 In particular, the open but continuously interconnected material design of IO electrode architectures167 has been shown to promote stable, and more efficient electronic and ionic conduction during Li insertion and removal, substantially improving both power and rate capabilities.168,169The first investigation of inverted opal electrode design was completed on sol–gel vanadium pentoxide (V2O5) in its ambigel form (Fig. 21), a cathode material with high surface area and high porosity.170 Xerogels, aerogels and ambigels are nanostructured materials formed from the drying of wet gel precursors; a different level of drying creates a different level of porosity and surface area. Ambigels are low density materials with a level of porosity and surface area between that of a xerogel (moderately low surface area and porosity) and aerogel (high porosity and high surface area obtained under supercritical drying conditions). This was formed by centrifuging 5 μL of IPA diluted vanadyl alkoxide into the sphere template, aging for 24 hours and removal of the spheres in toluene. Solvent exchange was performed in cyclohexane to produce the aerogel-like material.
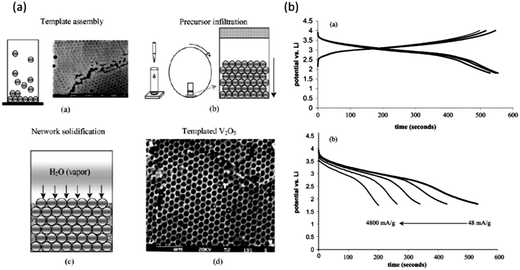 | ||
| Fig. 21 (a) Process for fabricating the hierarchical V2O5 IO electrode, vanadium alkoxide precursor was infiltrated into a PS template, the precursor was exposed to water vapor for hydrolysis and condensation and sphere removal produced a V2O5 ambigel IO (b) galvanostatic characteristics for the hierarchical V2O5 electrode: (a) discharge–charge behavior at 48 mA g−1 for three cycles; (b) discharge curves for a series of currents varying from 48 to 4800 mA g−1. Reproduced with permission from ref. 170. Copyright The Royal Society of Chemistry 2002. | ||
Sakamoto and Dunn discovered in this 2002 study that the inverted structure with pores of ∼800 nm, combined with the mesoporosity of the ambigel on the scale of 10 to 30 nm, led to higher capacities at higher discharge rates, which they attributed to improved mass transport and better electrolyte infiltration. The inverted opal architecture should potentially reduce the tortuosity and resulting polarization caused by mass transport through the active material compared with other conventional electrode designs. Vanadium pentoxide IOs have been studied several times following this but have generally concentrated more heavily on electrochromic behaviour rather than Li-ion battery cycling.171,172 However, since the initial investigation using V2O5 ambigel, several studies have since investigated the potential benefits of the inverse opal design on battery performance, for a host of other materials and material composites both for anode and cathode materials as well as the current collector and separator.
E. IO cathodes
The effects of the IO macroporosity have also been investigated for LiCoO2, the cathode material currently used in most commercial LIBs. A PMMA sphere template was infiltrated with a mixture of lithium acetate and cobalt acetate and heated to form the desired phase of LiCoO2. In order to improve the porosity, grain control agents such as poly(ethylene glycol) or platinum modifiers were added to the salt precursors. These IO structures however, showed poor cycling ability and at high temperature the phase transformation of the LiCoO2 resulted in significant grain growth that led to disruptive shrinkage in the material pores.173 Due to the scarcity of cobalt, its high cost and poor cycle life, LiCoO2 is not considered as the most ideal cathode material for our growing future energy needs. One example being considered as a potential replacement is LiFePO4, a low cost material with a low toxicity and high thermal stability with a high theoretical specific capacity, it suffers however from poor electrical conductivity in some forms giving a lower but very stable specific capacity. The IO architecture has been investigated as a route to overcoming this issue by increasing the interface between the electrode and electrolyte.174–176The investigations into LiFePO4 materials for battery applications have usually involved brittle, disordered particles, therefore an interconnected porous material could greatly decrease the diffusion distances the ions must travel, increase the surface area in contact with electrolyte and thus improve conductivity and overall performance. Doherty et al. investigated the performance of LiFePO4 IOs of different pore sizes and calcination temperatures and found templates made with spheres of 240 nm, the largest used in the study, were found to have consistently higher discharge capacities than samples made with smaller diameter templates. Templates of PMMA spheres were infilled by drop-casting with precursor solution formed using iron nitrate nonahydrate (Fe(NO3)3·9H2O), lithium acetate (CH3COOLi), and phosphoric acid. Some decomposition was observed in the IO structure during the necessary crystallization process by calcination at high temperatures, and it was suggested that templates of very small sphere sizes are unlikely to produce uniform, undamaged IO structures. Discharge capacities close to the theoretical capacity of 170 mA h g−1 were observed at low discharge rates for samples calcined at temperatures between 500–800 °C. At higher discharge rates it was the higher temperature calcined samples that performed best, i.e. the crystalline materials. Significantly less polarization was seen for samples prepared at 800 °C than those at 500 °C, indicating an improved conductivity due to the increased sintering of grain boundaries. The benefit of the IO structure was outlined as the most ideal method for controlling pore size and while increased surface area did not produce the best results here the increased performance for the larger template diameters was attributed to better electrolyte soakage.174
In a similar IO based approach, improved conductivity and shorter diffusion distances were achieved by combining the IO architecture with a conductive coating, FeF3 IO electrodes coated with the conducting polymer PEDOT. A PS template was first infiltrated with a solution of FeF3·3H2O in water and methanol with vacuum filtration to remove any residual solution. After the spheres were removed in toluene the conducting polymer PEDOT was then coated onto the surface of the FeF3 IO electrodes by the in situ polymerization of EDOT. The complete electrode had the benefit of increased conductivity from the PEDOT and the short diffusion distances of the porous FeF3 structure. This combination produced a reported capacity of 210 mA h g−1 at a current density of 20 mA g−1 and high power capability of 120 mA h g−1 at a current density of 1 A g−1 at room temperature, with good cycling stability, all attributed to the enhanced ionic and electronic transport in the porous, conducting-polymer coated cathode.177
F. IO anodes
Due to its low cost, chemical stability and high electrical conductivity, carbon is presently the leading candidate as the anode material of LIBs and graphitic carbon is currently used in commercial LIB anodes. While carbon benefits from a high electrical conductivity, its performance at high discharge is limited by poor ionic conductivity. The IO structure has proven attractive as a possible architecture to improve overall carbon performance due in most part to its attractive mass transport capabilities and easier electrolyte infiltration. The first forays into the synthesis of carbon IOs concentrated mainly on optical capabilities,178 however since then, C IOs have shown a lot of potential as a solution to rate limitations in LIBs.179 The rate capability of a LIB is affected by a number of factors including charge-transfer reactions at the surface of the electrodes and the solid state diffusion of Li ions within the electrodes. The IO structure can potentially improve both of these through their increased surface areas, and macroporosity, shortening diffusion lengths. Significant improvement over non-templated carbon was reported by Lee et al. for hard C IOs synthesised using a PMMA sphere template and resorcinol-formaldehyde (RF) polymer precursor.179 Their potential as anode materials has been further emphasised by recent investigations into further improving their battery performance through surface modification.180Kang et al. investigated the battery performance of C IOs (Fig. 22(a)) formed by the infiltration of a PS template with a phloroglucinol/formaldehyde (PF) resol precursor and compared this with the performance of both mesoporous C IO (Fig. 22(b)) and C IO coated with amino-groups (Fig. 22(c)).180 The amino-groups were grafted on to the C IOs by dispersion of C IO material in deionized water, and the addition of 8.3 mmol of p-phenylenediamine and 8.3 mmol of sodium nitrate, 10 mL hydrochloric acid was subsequently added dropwise and the complete mixture was stirred for 4 h at room temperature. Mesoporous IOs were fabricated by adding a block copolymer Pluronic F127 to the PF-resol for infiltration of the PS template. Large irreversible specific capacities were presented for all the C IOs and attributed to the formation of a solid electrolyte interphase (SEI) layer on the IO material. The amino-coated C, with an initial capacity of 359 mA h g−1, showed very little improvement over the ordinary C IO material, however the first specific capacity for the mesoporous material is reported, for a specific current of 100 mA g−1, as 432 mA h g−1 compared to the 350 mA h g−1 of the ordinary IO (see Fig. 22(d)) and to the ∼372 mA h g−1 of commercial graphite.
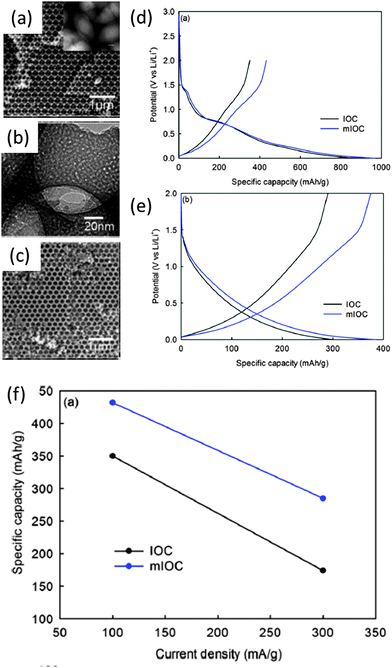 | ||
| Fig. 22 SEM images of the (a) IO C (b) mesoporous IO C (c) amino group coated IO C and the discharge–charge profiles for the IO C and mesoporous coated IO C for the (d) first and (e) the tenth cycle and (f) the variation in specific capacity with an increase in specific current illustrating a greater decrease for the IO C compared with the mesoporous structure. Adapted with permission from ref. 180. Copyright 2013 American Chemical Society. | ||
After 10 cycles the reversible specific capacity of the mesoporous C IO material was 375 mA h g−1 compared with the 290 mA h g−1 of the ordinary IO structure (Fig. 22(e)) and the decrease in this capacity with increasing cycle number was less for the mesoporous IO structures. This was attributed to an easier ion transport channel and shorter solid-state diffusion lengths in the mesoporous IO material. In general, such statements are deemed applicable to these inverse opal structures, but are rarely assessed definitively. In this study, as in many others, an increase in the specific current from 100 to 300 mA g−1 was observed, whereas the decrease in capacity of the C IO was larger than that of the mesoporous structure (see Fig. 22(f)) and this was attributed to the faster Li-ion intake of the material and/or faster diffusion within the material due to the access afforded by the mesopores.180
Reductions in the characteristic dimensions of the active material in an electrode are more effective in improving battery cycling rates than increases in ion diffusivity D, because the characteristic time constant t for diffusion is proportional to the square of the diffusion length L (t ∼ L2/D). For IO electrodes, however, quantitative investigation of this remains open. For example, control over the IO wall thickness to unequivocally determine the rate limitations caused by solid state diffusion are not defined in all studies, and the inherent dynamic changes in dielectric constant (increase in electrode impedance) and concomitant reduction in pore volume due to lithiation, are not typically accounted for when broad statements on ambipolar conductivity enhancements are made. While IO electrodes and porous or nanoscale material in general offer greater surface area (at the expense of reduced gravimetric energy density), the ability to template these structures on a range of substrates is likely to be very beneficial in non-planar designs of battery electrodes.
Both dense walled and porous walled germanium IOs have also been investigated for the anode of lithium ion batteries.181 Formed by chemical vapour deposition onto silica sphere templates, the resultant structures more closely resembled their template counterpart more so than the more familiar IO open-network structures. However, coulombic efficiencies of over 90% after the first cycle were reported for these germanium IOs, both for the dense and porous walled IO material, which is presented as much higher than those of other germanium anodes, such as nanowires or thin film electrodes. An enhanced rate performance was also shown at high current rates for the porous walled IO and the higher capacity of ∼10% attributed to the increase in surface area and the increase in Li-ion flux at the electrode electrolyte interface. The walls of the porous IO structure were shown through SEM and TEM to swell significantly during lithiation but no pulverization was seen which was accredited to the facile strain relaxation allowed by the free space available in the IO pores.
Several other materials have been investigated for IO anodes, including TiO2182 and NiO183 and in general, both cathode and anode IO materials have shown promising potential in enhancing the transport kinetics in the batteries, but have displayed only moderate improvements in rate performance and cycling stability. The macroporosity of the active material improves ion transport but does little to improve electron transport, the IO structure does not extend to the current collecting substrate or material. This has been suggested as the main reason for poor rate performance. For this reason in recent years, concentration has moved towards applying the IO structure to the current collector in order to improve electron transport, but there remains many open questions on the role of phase and dielectric constant changes during reversible lithiation on the resistivity of the material, including any physical material disconnections caused by volumetric swelling and contraction during discharging and charging. The use of plastically deformable IO structures that internally house active materials may be one method to accommodate the physical deformation, while maintaining a defined 3D interconnected electrical conductivity. The active material can then be applied to the IO structure as nanoparticles or thin films thereby allowing the dimensionality and connectivity of the IO network to extend to the active electrode as well. Essentially the use of a 3D IO structure as a support material allows the formation of nanocomposite active materials with improved conductivity or stability. These investigations have produced some of the most promising results towards achieving high power and high energy density batteries.165 Lastly, for cathodes, the response to high rate performance has been assessed to some degree.
Approximatively 360 W is required to charge a 1 W h cell phone battery in 10 s (at a 360 C charging rate – the C-rate being the inverse time in hours to full charge or discharge). Even at the highest charge rate tested thus far for these materials (∼1150 C), corresponding to a time of ∼3 s to fully discharge the capacity, the material achieves about 80% of its theoretical capacity. Such discharge rates are 2–3 orders of magnitude larger than those used in today's lithium ion batteries.184
For conventional lithium ion batteries, typical volumetric energy and power densities are ∼60 mW h cm−3 and 100 mW cm−3. It is possible to achieve higher power density, up to 1000 mW cm−3, by using porous battery electrodes that reduce ion diffusion through the active anode and cathode materials, as well as designs that reduce ion diffusion time in the electrolyte and decrease electrical resistance in the electrodes.185 There is limited research that quantifies electrical resistance changes in porous battery electrodes and even less information on the direct influence of phase change and structural changes that are related to the capacity and rate capability as a function of cycle life for cathode–anode pairs using IO structures. Lastly, a note on the types of materials that have been tested in some form of ordered porous network for Li-ion batteries specifically. The preceding discussion has largely detailed the state of the art and some of the important aspects, but several other materials and systems are also important. A recent book chapter186 succinctly details many of the studies in which inverse opals have been used, and methods for making a wide variety of oxide and other materials and compositions. Critically, the majority of Li-ion systems use standard perchlorate or hexafluorophosphate and related electrolytes, and are arranged in half-cells, where only one material is investigated. Also, no full cell assembly based on non-planar designs of materials with such potential benefits have been examined.
G. IO current collector and separator
A recent advance in the use of IOs and structured porous material in energy storage has been the development of structured metallic current collectors and 3D porous separators used to store electrolyte between the cathode and anode in a lithium-ion battery. In principle, by ensuring a 3D conductive matrix onto which a thin active material is uniformly coated, very high charge rates are possible if the thickness approaches the solid state diffusion limit of the material, reducing polarization resistance, and increasing the rate of charge without adversely affecting the conductivity of the electrode. The third physical ‘layer’ that is critical for battery function is the separator – a porous material membrane that can be fashioned from a range of polymers or from glass fibre, whose function is to electrically isolate the anode from the cathode while simultaneously allowing ionic conduction with ideally no ionic conductivity impedance. Since the function of a separator is facilitated by a type of porosity, 3D structured materials and inverse opals have, just very recently, been synthesized as battery separators, as well as current collectors, and cathode or anode materials.Zhang et al. reported superior rate performance in bicontinuous electrodes formed using a Ni IO support for the active material, synthesised by electrodeposition into a PS sphere template (of either 1.8 μm or 466 nm diameter), with a current of ∼2 mA cm−2 using a commercial electroplating solution (Techni Nickel S, Technic Corp), as outlined in Fig. 23(a).
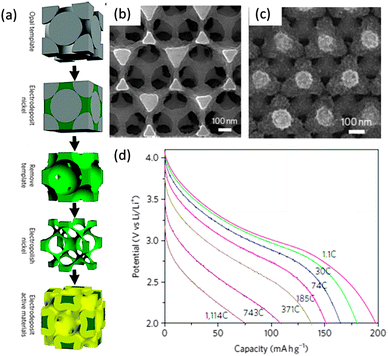 | ||
| Fig. 23 (a) Schematic for the formation of the bicontinuous electrode fabrication process, the yellow indicates the electrolytically active MnO2 and the green is the Ni current collector and SEM images for (b) the polished Ni IO and (c) the lithiated MnO2–Ni composite electrode. (d) Ultrafast discharge of the lithiated MnO2 material, at C-rates ranging from 1.1 to 1114 C.187 Adapted with permission from ref. 187. Copyright 2011 Nature Publishing Group. | ||
The Ni IO was electropolished before infilling with the active material in order to increase the overall porosity to ∼94%, see Fig. 23(b). The active cathode material MnO2 was then electrodeposited on to the Ni framework and lithiated in a molten salt solution of LiNO3 and LiOH. This three-dimensional bicontinuous lithiated MnO2 cathode (Fig. 23(c)) with a thickness of ∼30 nm was shown to retain 76% of its capacity when discharged at 185 C, and 38% when discharged at 1114 C, as shown in Fig. 23(d). The authors reported that the use of smaller sized spheres at the templating stage resulted in a greater energy density for a given thickness of active material, due to the increase in surface area of the smaller pored system.187
Large volume changes (up to 400%) can occur with silicon anodes during lithium insertion and extraction which leads to electrode pulverization and a loss of electric contact between the active material and the current collector (see schematic Fig. 24(a)). In order to alleviate this, Zhang and colleagues also investigated the use of a Ni IO current collector (Fig. 24(b)) with a thin film of silicon material. A PS sphere template was formed on a tungsten foil by vertical deposition, infiltrated with Ni by electrodeposition and the spheres then removed in tetrahydrofuran. The resultant Ni IO (Fig. 24(d)) was then electro-polished to increase pore size as before and a thin film of silicon deposited by CVD from dislane. This produced a bi-continuous anode of thin layer silicon on a porous 3D Ni metal scaffold (Fig. 24(c and e)) that showed improved cycling behaviour compared to a thick layer of silicon deposited on a planar Ni foil.
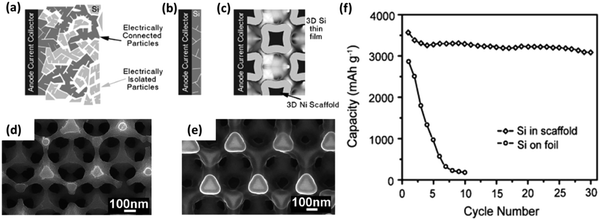 | ||
| Fig. 24 (a) Illustration of the loss of electric contact in a thick silicon film on a current collector foil during cycling. (b) Silicon thin film showing good contact to Ni substrate. (c) Bicontinuous bulk anode consisting of a silicon thin film on a 3D porous Ni scaffold. SEM image of (d) the Ni scaffold and (e) silicon coated Ni after CVD. (f) Capacity retention comparison of a 3D silicon anode and a foil supported silicon anode at a 0.05 C rate.188 Adapted with permission from ref. 188. Copyright 2012 American Chemical Society. | ||
After 10 cycles only 10% capacity remained for the flat film on the Ni foil, which was attributed to pulverization of the silicon material and loss of electrical contact. The spherical pores of the 3D Ni provided a nanoscale reaction space for the silicon to lithium alloying/dealloying and limited the electrical disconnections due to volume changes responsible for the capacity fading in the flat film sample. Therefore the 3D structured electrode presented much higher specific capacity overall and much higher capacity retention, as shown by Fig. 24(f).
Recently, Ni–Si composite electrodes have been fabricated by the electrodeposition of a silicon layer on to a Ni IO scaffold.189,190 In one such study, the battery performance of the Si-on-Ni IO structure was compared to a Si-on-Ni nanocable array of equal active material mass. The Si on Ni IO material did exhibit higher volumetric capacities and better rate capabilities than the nanocable array, however, both suffered capacity fading common with Si anodes, which they attributed in this case to the formation of an SEI layer on the silicon surface. Silicon film thickness was varied for a number of samples and a decrease in capacity retention was seen for silicon thickness of ∼50 nm. Li insertion increases the thickness of the silicon material, causing the porosity of the IO to decrease which is believed to lower electrolyte infiltration and contact thereby lowering capacity values. Therefore IO performance can be optimized through silicon film thickness and IO pore size.190
One of the disadvantages of thin film active materials atop conductive IOs is that volume expansion on lithium insertion can still be problematic, causing the material to delaminate from the IO current collector. Some success in alleviating this problem was seen by integrating IO C with geometrically entrapped active nanoparticles, in this case SnO2 as is schematically shown in Fig. 25.191 The macroporous nature of the C IO allows easy access for the Li ions and the geometrical constrains of the elastic C IO can better accommodate the volume changes in the active nanoparticles on lithium insertion and removal, reducing tendencies to self-aggregate and/or delaminate from the conductive IO. As the technology advances, fundamental questions may benefit from in situ or optical probing of phase and material changes during charging and discharging, and this is amenable from ordered porous structures that behave as inverse opal photonic crystals (as least while periodic long range order and index contrast is maintained). However, full cells that have all porous architectures can be brittle, and the adaption of interpenetrating polymer networks (using Li-ion conducting polymers) may provide a possible solution to an all porous cathode–anode pairing in a full cell, and inspiration may come from Li–polymer batteries in this regard.
 | ||
| Fig. 25 Schematic illustration showing the preparation of the C IO electrode with entrapped SnO2 nanoparticles.191 Reproduced with permission from ref. 191. Copyright 2013 Nature Publishing Group. | ||
In Li-ion and other batteries that require liquid electrolytes, this will need to be stored in a separator, and advances in engineering the structure of the separator has become a topic of importance.
Most research into the utilization of the IO architecture within LIBs has concentrated on the active components. Recently however, Hwan Kim et al. presented a study looking at the formation and potential benefits of an IO separator.192 The separator membrane takes its place between anode and cathode, and in most current LIBs is made of porous (randomly distributed) polyolefin materials. It is incumbent for high battery performance that fast and uniform ionic flow can occur through the electrolyte soaked separator. In this work by Kim and colleagues, an IO separator was formed by combining the template assembly and infiltration into a single step. In a polyethylene terephthalate (PET) nonwoven substrate, vertical deposition was used to assemble silica spheres in the presence of a UV cross-linked ethoxylated trimethylolpropane triacrylate (ETPTA) polymer matrix. The ETPTP monomer formed between the assembled spheres and was cured under UV irradiation for 15 s with the help of a photoinitiator. The silica spheres were then removed in hydrofluroric acid which resulted in a thin and flexible IO separator with a thickness of ∼20 μm, see Fig. 26(a). The ideal SiO2–ETPTA composition for the formation of a well ordered well packed IO structure by this method was reported as 74/26 (v/v), composition ratios above and below this produced non close-packed randomly dispersed spheres and poorly ordered aggregated assemblies, respectively. In a LiCoO2 cathode/graphite anode cell, the OCV profile for the ordered IO separator is comparable to that of a polypropylene/polyethelene/polypropylene (PP/PE/PP) commercial separator. The behaviour of the disordered structures is less comparable, with sharp decreases in OCV profiles attributed to leakage currents.
 | ||
Fig. 26 (a) Schematic representation of IO separator manufactured via the simple one-pot EISA of SiO2 nanoparticles in the presence of a UV-curable ETPTA monomer inside a PET nonwoven substrate, followed by UV-cross-linking and selective removal of the SiO2 nanoparticle superlattices and the cycling performance of cells, where the cells were assembled with high-mass-loading electrodes (cathode/anode = 25.0/11.5 mg cm−2) and IO separator (SiO2/ETPTA = 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 (v/v)) or PP/PE/PP separator. The cells were cycled between 3.0 and 4.2 V at a charge–discharge current density of 1.0 C/1.0 C. (b) Variation in the charge–discharge profiles with cycling. (c) Capacity retention as a function of the cycle number.192 Reproduced with permission from ref. 192. Copyright 2014 American Chemical Society. 26 (v/v)) or PP/PE/PP separator. The cells were cycled between 3.0 and 4.2 V at a charge–discharge current density of 1.0 C/1.0 C. (b) Variation in the charge–discharge profiles with cycling. (c) Capacity retention as a function of the cycle number.192 Reproduced with permission from ref. 192. Copyright 2014 American Chemical Society. | ||
The flexibility of this IO material while little different from current separator materials could be of interest within other applications, the seamless nano-scaffold structure is not disrupted when wound around a stainless steel rod with a diameter of 1.5 mm. The mechanical stability of the IO structure is maintained even after frequent bending deformation. This is however dependent on the non-woven substrate material. This IO separator has been shown to greatly improve ion transport under harsh conditions such as high mass loading, fast charging/discharging and highly polar liquid electrolyte compared with an example of a commercial separator, as shown in Fig. 26(b) and (c). The Ragone plot, describes the relationship between energy and power density, and the use of IO separator saw an increase in energy density compared with commercial PP/PE/PP separator for high power densities, i.e. a change in the Ragone plot was seen for a change in separator. While only the first step, the high wettability and 3D ordered macroporous interconnected nature of the IO separator presented by Hwan Kim et al. could lead to expanded thinking within battery performance optimization and material investigations. The higher ion conductivity of this IO separator appears very promising.192
Today's energy needs require a storage technology with the energy density of a battery and a power density of a supercapacitor. Supercapacitors store charge differently to batteries, by accessing charge compensation mechanisms at the electrical double layer at the surface–electrolyte interface. Usually, limited or no intercalation, alloying or other phase change processes occur as they do in Li-ion batteries, yet capacitance may be accessed in Li-ion containing electrolytes as well as aqueous electrolytes. In 2013 Pikul et al.,193 presented a microbattery design, schematically depicted in Fig. 27(a), consisting of 3D bicontinuous interdigitated microelectrodes formed from thin layers of nickel–tin, for the anode, and lithiated manganese oxide, for the cathode, electrodeposited onto interdigitated highly porous Ni scaffolds, shown in Fig. 27(b). The Ni scaffolds were fabricated through electro-deposition on PS opal templates assembled on glass with gold sputter coated into interdigitated rectangular templates on the glass. The top down view of the interdigitated electrodes are shown in Fig. 27(c). The rate capabilities for this type of microbattery were examined to determine what possibilities the IO structure provided in terms of the energy and power densities (see Fig. 27(d)).
 | ||
| Fig. 27 (a) Schematic illustrating the microbattery design. (b) Cross-section SEM image of the interdigitated electrodes spanning two periods with insets of the magnified Ni scaffold coated with nickel–tin on the left and lithiated manganese oxide electrode on the right. (c) A top-down SEM image of the interdigitated electrodes. (d) Discharge profiles for different rates. (e) Capacity of the microbattery for the first 15 cycles at the noted C rate, normalized to the energy at 0.5 C. The secondary y axis indicates the percentage of capacity retained in the given cycle when compared with the previous cycle (calculated for low C rate cycles only).193 Reproduced with permission from ref. 193. Copyright 2013 Nature Publishing Group. | ||
Higher power densities up to 7.4 mW cm−2 μm−1, without sacrificing energy density, were reported. After four high rate cycles the microbattery cell retains 92% of its energy and 64% after 15 high rate cycles, see Fig. 27(d). This is attributed to a reduction in ion diffusion lengths through the active electrode material, the time for ion diffusion in electrolyte, and electrical resistances across the entire microbattery. This meets or exceeds the high power densities of the best supercapacitors with comparable energy density, 2000× greater and 2× greater than the power density and energy density, respectively, of other 3D microbatteries. This first example of a full battery system of IO electrodes highlights the full extent of the possibilities IOs bring to battery and energy research and design. The shorter diffusion distances, the increase in surface area and electrolyte infiltration and less stringent requirements for conductive additives ensure IO electrodes a place in future energy storage developments, and as engineered porous materials that provide an optical signature for material and phase changes in order to understand the influence of charging rate, material swelling, dielectric constant changes, conductivity variations and reduction in ordered porosity in cases where this is perceived to be a benefit, can be assessed.
V Adapting photonic crystal properties to electrochemical energy storage
This section will summarise in a generally amenable manner, the approaches from PBG materials optics to electrochemical energy storage that involves inverse opal electrodes. In particular we will focus on Li-ion batteries (and applicable to any cation insertion that causes a crystal structure and volume change in the host material) and to some extent, electrochromic materials. Pseudocapacitive electrochemical energy storage (EES) systems165 are not explored as there is formally little change in the active materials – the IO structure in such cases provides a greater surface area but does not undergo changes that fundamentally alter the definition of the PBG and optical diffraction from periodic arrangements of dielectric contrast caused by (electro)chemical interactions, mechanical deformation, or applied voltage.A. Optical probing of IO battery materials
Optical probes or photonic spectroscopies that can interrogate not only physical properties, but basic phenomena as well as correlating separate characteristics (optical–electrochemical, optical–thermal, magnetic–chemical as pertinent examples etc.) are becoming increasingly useful as the versatility of experimental designs improves. Incorporating opals in 2D or 3D form has been established as a useful method for improving internal quantum efficiencies of semiconductor optoelectronics, using a periodicity designed to reflect operational wavelengths and improve the directionality of emission.194 Photonic crystals can also aid in redirecting unwanted radiation from semiconductor materials,195 or indeed enhance radiative recombination or photoluminescence from some materials through resonant cavity enhancement methods akin to Fabry–Pérot resonators via enhanced coupling to emissive states,196 using the internal ordered porous structure as an effective medium. More recently, porous photonic crystal scaffolds have been integrated into the photoactive layer of an opaque perovskite solar cell in order to increase not only the efficiency, but the response to a broader band of incident radiation. This is made possible by facilitating tunable color absorption across the visible spectrum mediated by the photonic crystal architecture in the absorber layer and the index contrast.197 These examples highlight the usefulness of photonic and diffractive optics in device oriented research, and there are many more besides, such as graded refractive index antireflection coatings,198,199 enhanced light extraction efficiency200–202 by narrowing and focusing of the output light cone203 from LEDs, lasers, and photon management in solar cells204 and other absorption and emission-based devices etc.In the area of electrochemical energy storage, the knowledge of photonic crystals and inverse opals may also play an important multidisciplinary role, while providing new scientific opportunities. As outlined in previous sections, the functional porous material architecture of inverse opals has proven to provide a new gamut of energy storage, capacitor and Li-ion battery materials with enhanced characteristics. New classes of materials research and electrode technology development are crucial for advances in energy storage and lithium (ion) and emerging alternative electrochemical energy storage technologies. For exciting and important advances in electrochemical energy storage (EES) and battery science for consumer electronics and technology of the future, the marriage of optical physics and materials electrochemistry may address and mitigate current issues and provide new ideas for advancement.
For high performance, Li-ion materials the inverse opal structures may provide a colour-coded state of charge and depth of discharge determination, while fundamentally describing the processes that occur in any new materials non-destructively, once arranged into a photonic architecture. Such innovation exploits these new materials' abilities to retain charge capacity by controlling composition and structure, while optics may probe material order and coupled electrical and optical response during charge–discharge. In parallel, the electro-photonic circuitry provided by the 3D porous structure,3 and the chemical, electrical and optical changes caused by the energy storage mechanism (capacitance, alloying, or intercalation)205,206 could essentially be probed using diffraction-based spectroscopy so that the state of charge and discharge can be determined in operando. The type of EES mechanism could also be identified for new materials under a range of electrochemical parameters, and so a powerful method of examining the response of the material to operation is in principle possible via coupled electrical, electrochemical and visible-to-near infrared spectroscopies and photonic bandgap mapping. Thus, fashioning any important or electrochemically active material into an inverse opal structure, may give a colour-coded ‘chameleon’ battery strip where the type of process, the voltage, remaining capacity, cycle health and state of charge or discharge may be distinguishable by examining its spectral or diffractive response, i.e. its colour. Table 1 below shows a brief overview of some of the salient features and phenomena that occur in many battery and related electrochemical energy storage cells,207–210 and the state of the art in their characterization. Many of these effects are common to many materials on several length scales when tested in half or full cell configurations. The table is not exhaustive, but highlights how relatively simple methods paired with detailed examination of the optical response of inverse opals or ordered, periodic structures,211,212 can provide a means of in situ examination of many of these processes.
| Mechanism/material change | Standard method | Optical probe | Techniques |
|---|---|---|---|
| Intercalation, insertion, alloying reactions during discharge and charge | Electron microscopy, X-ray diffraction, energy dispersive spectroscopies (EELS, EDX, XRF, XPS etc.) | 2D diffraction (Bragg, grating) | Angle resolved reflectance, transmission (UV-vis-NIR) |
| 3D photonic band gap (PBG) and resonances from variations in stacking | |||
| Photonic band gap modification: phase change; refractive index change; porous periodicity (volumetric swelling of active material) and material order change etc. | |||
| Capacitive charge storage mechanism | Electrochemical quartz microbalance | Index contrast stability of 2D diffraction or 3D stop bands when no phase changes occur (surface redox capacitance). | Angle resolved reflectance, transmission |
| Cyclic voltammetry | For new materials, the nature (insertion or capacitive) assessed optically | UV-vis absorption, interrogation of photo-enhanced charge transfer | |
| Electrochromism | Optical transmission and voltage biasing | Optical conductivity variation – linking optical transmission to cation insertion effects on materials structure, order, periodicity and associated PBG change | Electrochemical optical transmission, reflectance for structural colour monitoring |
| Deconvolution of material electrochromism under optical excitation versus electrochemically induced colour changes from variation in periodicity, pore volume, material dielectric constant etc. | UV-vis spectroscopy for material electrochromism | ||
| State of charge, depth of discharge | Materials: electron microscopy, X-ray diffraction, energy dispersive spectroscopies (EELS, EDX, XRF, XPS etc.) | Mapping the crystallinity variation to the lithiation state | Electrochemical optical transmission, reflectance |
| Cell: electrochemical methods | Correlation between photonic band gap (3D) or energy, bandwidth and intensity of 2D Bragg diffraction (2D) to discharge (cathode) or charge (anode) voltage | ||
| Crystal-amorphous transitions | Materials: electron microscopy, X-ray diffraction, energy dispersive spectroscopies (EELS, EDX, XRF, XPS etc.) | Materials whose capacity retention is inherently linked to a contribution from material disorder. Does (de)lithiation cause homogenous or heterogeneous amorphization and material contraction (pore volume increase) during charging (as a cathode), or material swelling (pore volume, periodicity alteration) during discharging (cathode). | Electrochemical optical transmission, reflectance (in situ) 2D diffraction or 3D stop band variation |
| Differential capacity analyses, electrochemical methods | Amorphization via homogenous processes – bandwidth consistency in angle-resolved optical transmission – equal pore volume reduction (material swelling) and vice versa during electrochemical processes | ||
| Material longevity and structural integrity in the cell | XRD, electron diffraction methods (convergent beam electron diffraction), GIXRD of thin films, cross-section post-mortem microscopy | Stress–strain development during large volume changes during cycling | Electrochemical optical transmission, reflectance |
| Mapping of material changes – indicator of electroactive materials or areal consistency in adhesion to the current collector. | Opto-electrochemical Raman scattering | ||
Controlling the flow of light at sub-wavelength scales provides access to functionalities such as negative refractive index, optical transformations, cloaking, and metamaterials. Phenomena associated with diffraction can limit the control of light, particularly when so many variables of the material, arrangement and dielectric environment change during electrochemical cycling of an inverse opal material in a battery or supercapacitor. In the near future, probing photon transport and collimation that is enhanced by transverse Anderson localization may be useful and necessary in active battery materials that behave or respond to anisotropic cation insertion and removal. Modification of the material geometry caused by the state of charge or depth of discharge to material order and physical parameters may in principle allow a specific structural disorder whose mechanism is captured to some degree by examination of disorder-induced transverse localization. With increasing disorder during discharge for example, one may observe the crossover from cascaded guided resonances directly into transverse localization, and capture this as a direct function of the complex material changes that occur when intercalation or alloying occurs.
Developments in new materials, electrode architecture165 comprising electro-photonic materials, and methods for bespoke assembly onto mouldable, flexible or other atypically shaped surface (non-planar batteries) may also provide opportunities that can be exploited for coupling with other thin film energy generating technologies such as thermoelectrics, flexible electronics, solar cells as colour-coded indicators of the electrical, optical or electrochemical process, for use with electronic displays, touch screens and lightweight portable electronics.
An ordered porous 3D material architecture has proven already to provide definable short electron and ion transport lengths in the active material169 and electrolyte (yielding high-power density) while maintaining a high volume of active material.187,188 Charge rates up to 1000 C (∼4 s) for lithium-ion chemistries are possible, allowing full charging in minutes or seconds. Thus, for battery electrodes, changes it the material phase and index contrast in the inverse opal will occur rapidly, and allow an instantaneous state of charge indicator in cases where structural changes are caused (intercalation, amorphization, alloying etc.) or the relative contributions to the total stored charge caused by capacitive storage, where changes to the dielectric constant, crystallinity and phase are not caused by insertion reactions. As outlined in Table 1, the analysis of pseudo stop-bands in 3D inverse opals through light scattering, diffraction from 2D inverse opals of active materials, or indeed the transition from order-mediated light scattering to effects (such as Anderson localization among others) caused by the development of disorder, can be developed as a diagnostic analytical monitor of the behaviour of electrochemical or battery materials under a range of conditions in situ, to be a direct colour-coded battery capacity health check. There are limited methods, all post-mortem, that can assess the electrochemical health or state of an active battery material and none can correlate this assessment to the physical characteristics of many materials processes that occur in the complex materials electrochemistry of EES.
Crucially, porous materials that exhibit both function and new routes to process interrogation, can provide a new gamut of optically active power check charge storage or electrochemical modules integration-capable with other thin film technologies. These applied scientific advances may be feasible by adapting the physics of photonic crystals to materials science and electrochemistry for promising battery and energy storage materials, and as a new series of electro-optic probes utilizing photonic materials circuitry to interrogate material response to reversible charge storage mechanisms.
VI Conclusions and outlook
In summary, the growth of PhCs by colloidal assembly routes has been presented with particular emphasis on directing and improving lattice arrangements through adaptations of long established methods, for example, using acoustic vibrations,67 confinement77 or patterned substrates.102 Assembly is essentially a balance of colloidal and external forces. Polymer spheres in particular are well suited to surface functionalization, offering further scope to manipulate their assembly behaviour. Through particle growth or resizing, and other factors such as untried sphere–solvent, sphere–solvent–substrate couplings there remains room for further improvement and development. Assembly is still limited somewhat by the time requirements necessary for much of the growth methods discussed and uncontrolled defect registrations remain continuously problematic for ordered self-assembly particularly on functional substrates. Lithographic methods can provide more specific defect placement but these routes are expensive and prove more difficult in the fabrication of layered or 3D structures. It is therefore likely that colloidal assembly will maintain its favour and encourage continuous examination and adaptation given its low cost and versatility.The intent of this review was to highlight the wide ranging uses of PhC structures, specifically IOs. These structures have already been shown as highly advantageous within a number of fields, and they will no doubt play an important role in bridging optical and electrical functions, and further the development and progress towards achieving all-optical information management and/or optoelectronic device design. The flexibility of IOs to span various applications is remarkable, whether within sensing, lasing, or energy storage to name a few. The complete scope of possible applications for these structurally advantageous and optically useful materials has no doubt still to be discovered. Given the availability of different material precursors and various synthesis routes, the scientific and technological potential of IO's are very attractive (particularly within the biological and energy sciences where defects are not major issues for function such as for photonics, but contribute to surface area, as one example).
There is also an untapped potential for applications that do not specifically exploit the unique optical properties of these materials but instead rely solely on the structural advantages they provide as nanostructured networks of active material. The development of non-destructive device and material diagnostic methods through the exploitation of the optical characteristics of these IO materials could lead to increased understanding of the chemical and interfacial processes happening during device function. In particular the unique diffractive optics of these materials and the ability to gain information from diffraction signatures on the lattice structure and integrity of a given IO could provide information on the nature of the network material and its ability to withstand certain stresses such as the intercalation of Li or other ions. Therefore, if the photonic abilities of these materials were coupled with their other operational capabilities and advantages, a new route towards material testing and design may emerge.
In the near future, promising and useful applications will no doubt concentrate on the optical and energy related potential of these materials. Their scalability is particularly attractive, allowing designs and modelling on large scales to be directly translated to the nanoscale (synthesis routes allowing). However, before any real-world application of the self-assembly approach to the fabrication and design of these materials can prosper certain issues still need to be addressed, for example, that of overall stability, both thermal and mechanical stability in particular. This is perhaps where the coupling of patterning techniques and chemical functionalization with self-assembly methods could prove successful. Defect density remains a limiting factor in many self-assembly approaches, particularly on broader device scales and for those applications requiring very precise defect positioning. While the full scale optical and optical-dependent application of these materials requires some further optimization, the structural advantages they supply towards templating three-dimensional macroporous functional devices is extremely relevant and applicable even now. The central limiting factor with regard to this is simply what precursors are available and compatible. Artificial opal structures can however present vulnerability with respect to irreversible structural changes related to environment and certain application processes. This is particularly limiting for structural dependent applications, making their reusability low and potentially increasing costs. Therefore, investigations into material design coupled with the addition of optical diagnostic methods particularly for those areas presently neglecting the optical significance IOs present could lead to a deeper understanding, allowing these materials to reach their full and exciting potential.
Acknowledgements
E. Armstrong acknowledges the support of the Irish Research Council under award RS/2010/2920. Support from Science Foundation Ireland under grant no. 07/BK/1232a-STTF11 is also acknowledged. We thank Dr Hugh Geaney for critical reading of the manuscript and for useful comments and suggestions.References
- E. Yablonovitch, Phys. Rev. Lett., 1987, 58, 2059–2062 CrossRef CAS.
- S. John, Phys. Rev. Lett., 1987, 58, 2486–2489 CrossRef CAS.
- A. Stein, Nat. Nanotechnol., 2011, 6, 262–263 CrossRef CAS PubMed.
- C. I. Aguirre, E. Reguera and A. Stein, Adv. Funct. Mater., 2010, 20, 2565–2578 CrossRef CAS.
- J. F. Galisteo-Lopez, F. Lopez-Tejeira, S. Rubio, C. Lopez and J. Sanchez-Dehesa, Appl. Phys. Lett., 2003, 82, 4068–4070 CrossRef CAS.
- S. Kinoshita and S. Yoshioka, ChemPhysChem, 2005, 6, 1442–1459 CrossRef CAS PubMed.
- J. V. Sanders, Nature, 1964, 204, 1151–1153 CrossRef.
- F. Liu, H. Yin, B. Dong, Y. Qing, L. Zhao, S. Meyer, X. Liu, J. Zi and B. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 012901 CrossRef.
- J. Zi, X. Yu, Y. Li, X. Hu, C. Xu, X. Wang, X. Liu and R. Fu, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 12576–12578 CrossRef CAS PubMed.
- H. Yin, L. Shi, J. Sha, Y. Li, Y. Qin, B. Dong, S. Meyer, X. Liu, L. Zhao and J. Zi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 051916 CrossRef.
- S. Yoshioka and S. Kinoshita, Forma, 2002, 17, 169–181 Search PubMed.
- J. Matêjkovà-Plskova, D. Jancik, M. Maslan, S. Shiojiri and M. Shiojiri, Mater. Trans., 2010, 51, 202–208 CrossRef.
- J. Matêjkovà-Plskova, S. Shiojiri and M. Shiojiri, J. Microsc., 2009, 236, 88–93 CrossRef PubMed.
- S. Yoshioka and S. Kinoshita, Wavelength—selective and anisotropic light—diffusing scale on the wing of the Morpho butterfly, 2004 Search PubMed.
- E. Gaillou, E. Fritsch, B. Aguilar-Reyes, B. Rondeau, J. Post, A. Barreau and M. Ostroumov, Am. Mineral., 2008, 93, 1865–1873 CrossRef CAS.
- G. von Freymann, V. Kitaev, B. V. Lotsch and G. A. Ozin, Chem. Soc. Rev., 2013, 42, 2528–2554 RSC.
- J. D. Joannopoulos, P. R. Villeneuve and S. Fan, Nature, 1997, 386, 143–149 CrossRef CAS.
- J. D. Joannopoulos, S. G. Johnson, J. N. Winn and R. D. Meade, Photonic Crystals Molding the Flow of Light, Princeton University Press, Princeton, NJ, 2008 Search PubMed.
- G. A. Ozin, A. C. Arsenault and L. Cademartiri, Nanochemistry: A Chemical Approach to Nanomaterials, Royal Society of Chemistry, 2009 Search PubMed.
- W. Mesfin and J. Sajeev, J. Opt. B: Quantum Semiclassical Opt., 2003, 5, R43 CrossRef.
- J.-f. Liu and X.-h. Wang, Front. Phys. China, 2010, 5, 245–259 CrossRef.
- A. Koenderink, L. Bechger, H. Schriemer, A. Lagendijk and W. Vos, Phys. Rev. Lett., 2002, 88, 143903 CrossRef.
- S. O’Brien, D. McPeake, S. A. Ramakrishna and J. B. Pendry, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 241101 CrossRef.
- M. L. Povinelli, S. G. Johnson, J. D. Joannopoulos and J. B. Pendry, Appl. Phys. Lett., 2003, 82, 1069–1071 CrossRef CAS.
- D. R. Smith, J. B. Pendry and M. C. K. Wiltshire, Science, 2004, 305, 788–792 CrossRef CAS PubMed.
- A. Mekis, J. Chen, I. Kurland, S. Fan, P. Villeneuve and J. Joannopoulos, Phys. Rev. Lett., 1996, 77, 3787–3790 CrossRef CAS.
- S. G. Romanov, M. Bardosova, I. M. Povey, M. E. Pemble and C. M. Sotomayor Torres, Appl. Phys. Lett., 2008, 92, 191106 CrossRef.
- E. Armstrong, W. Khunsin, M. Osiak, M. Blömker, C. M. S. Torres and C. O’Dwyer, Small, 2014, 10, 1895–1901 CrossRef CAS PubMed.
- T. K. Gaylord and M. G. Moharam, Appl. Phys. B: Photophys. Laser Chem., 1982, 28, 1–14 CrossRef.
- M. Campbell, D. N. Sharp, M. T. Harrison, R. G. Denning and A. J. Turberfield, Nature, 2000, 404, 53–56 CrossRef CAS PubMed.
- D. Shir, E. C. Nelson, Y. C. Chen, A. Brzezinski, H. Liao, P. V. Braun, P. Wiltzius, K. H. A. Bogart and J. A. Rogers, Appl. Phys. Lett., 2009, 94, 011101 CrossRef.
- J. F. Galisteo-López, M. Ibisate, R. Sapienza, L. S. Froufe-Pérez, Á. Blanco and C. López, Adv. Mater., 2011, 23, 30–69 CrossRef PubMed.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS PubMed.
- J. Zhang, Y. Li, X. Zhang and B. Yang, Adv. Mater., 2010, 22, 4249–4269 CrossRef CAS PubMed.
- Z. Li, J. Wang and Y. Song, Particuology, 2011, 9, 559–565 CrossRef CAS.
- Y. A. Vlasov, V. N. Astratov, A. V. Baryshev, A. A. Kaplyanskii, O. Z. Karimov and M. F. Limonov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 5784–5793 CrossRef CAS.
- K. E. Davis, W. B. Russel and W. J. Glantschnig, J. Chem. Soc., Faraday Trans., 1991, 87, 411–424 RSC.
- B. T. Holland, C. F. Blanford and A. Stein, Science, 1998, 281, 538–540 CrossRef CAS.
- G. I. N. Waterhouse and M. R. Waterland, Polyhedron, 2007, 26, 356–368 CrossRef CAS.
- O. D. Velev and A. M. Lenhoff, Curr. Opin. Colloid Interface Sci., 2000, 5, 56–63 CrossRef CAS.
- Y. Suzuki, T. Sawada and K. Tamura, J. Cryst. Growth, 2011, 318, 780–783 CrossRef CAS.
- P. Jiang and M. J. McFarland, J. Am. Chem. Soc., 2004, 126, 13778–13786 CrossRef CAS PubMed.
- P. Jiang, T. Prasad, M. J. McFarland and V. L. Colvin, Appl. Phys. Lett., 2006, 89, 011908 CrossRef.
- C. Arcos, K. Kumar, W. González-Viñas, R. Sirera, K. M. Poduska and A. Yethiraj, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 050402 CrossRef.
- M. Pichumani, P. Bagheri, K. M. Poduska, W. Gonzalez-Vinas and A. Yethiraj, Soft Matter, 2013, 9, 3220–3229 RSC.
- J.-Y. Choi, T. L. Alford and C. B. Honsberg, Langmuir, 2014, 30, 5732–5738 CrossRef CAS PubMed.
- L. He, M. Wang, J. Ge and Y. Yin, Acc. Chem. Res., 2012, 45, 1431–1440 CrossRef CAS PubMed.
- L. He, Y. Hu, H. Kim, J. Ge, S. Kwon and Y. Yin, Nano Lett., 2010, 10, 4708–4714 CrossRef CAS PubMed.
- J. Ge, L. He, Y. Hu and Y. Yin, Nanoscale, 2011, 3, 177–183 RSC.
- X. Xu, G. Friedman, K. D. Humfeld, S. A. Majetich and S. A. Asher, Adv. Mater., 2001, 13, 1681–1684 CrossRef CAS.
- A. F. Demirors, P. P. Pillai, B. Kowalczyk and B. A. Grzybowski, Nature, 2013, 503, 99–103 CrossRef PubMed.
- M. Böhmer, Langmuir, 1996, 12, 5747–5750 CrossRef.
- M. Holgado, F. García-Santamaría, A. Blanco, M. Ibisate, A. Cintas, H. Míguez, C. J. Serna, C. Molpeceres, J. Requena, A. Mifsud, F. Meseguer and C. López, Langmuir, 1999, 15, 4701–4704 CrossRef CAS.
- A. L. Rogach, N. A. Kotov, D. S. Koktysh, J. W. Ostrander and G. A. Ragoisha, Chem. Mater., 2000, 12, 2721–2726 CrossRef CAS.
- S.-R. Yeh, M. Seul and B. I. Shraiman, Nature, 1997, 386, 57–59 CrossRef CAS.
- M. Trau, D. A. Saville and I. A. Aksay, Langmuir, 1997, 13, 6375–6381 CrossRef CAS.
- D. C. Prieve, P. J. Sides and C. L. Wirth, Curr. Opin. Colloid Interface Sci., 2010, 15, 160–174 CrossRef CAS.
- E. Armstrong, M. Osiak, H. Geaney, C. Glynn and C. O’Dwyer, CrystEngComm, 2014, 16, 10804–10815 RSC.
- A. S. Dimitrov and K. Nagayama, Langmuir, 1996, 12, 1303–1311 CrossRef CAS.
- P. Jiang, J. F. Bertone, K. S. Hwang and V. L. Colvin, Chem. Mater., 1999, 11, 2132–2140 CrossRef CAS.
- J. R. Oh, J. H. Moon, S. Yoon, C. R. Park and Y. R. Do, J. Mater. Chem., 2011, 21, 14167–14172 RSC.
- M. Bardosova, P. Hodge, L. Pach, M. E. Pemble, V. Smatko, R. H. Tredgold and D. Whitehead, Thin Solid Films, 2003, 437, 276–279 CrossRef CAS.
- B. van Duffel, R. H. A. Ras, F. C. De Schryver and R. A. Schoonheydt, J. Mater. Chem., 2001, 11, 3333–3336 RSC.
- M. Ghosh, F. Q. Fan and K. J. Stebe, Langmuir, 2007, 23, 2180–2183 CrossRef CAS PubMed.
- Y. N. Fu, Z. G. Jin, Z. F. Liu, Y. Liu and W. Li, Mater. Lett., 2008, 62, 4286–4289 CrossRef CAS.
- C. Hsueh, C. L. Moraila Martínez, F. Doumenc, M. A. Rodríguez-Valverde and B. Guerrier, Chem. Eng. Process, 2013, 68, 64–68 CrossRef CAS.
- W. Khunsin, A. Amann, G. Kocher-Oberlehner, S. G. Romanov, S. Pullteap, H. C. Seat, E. P. O’Reilly, R. Zentel and C. M. S. Torres, Adv. Funct. Mater., 2012, 22, 1812–1821 CrossRef CAS.
- Y. Wang, L. Chen, H. Yang, Q. Guo, W. Zhou and M. Tao, Mater. Sci., 2010, 28, 467–478 CAS.
- Z. Z. Gu, A. Fujishima and O. Sato, Chem. Mater., 2002, 14, 760–765 CrossRef CAS.
- G. Berteloot, A. Daerr, F. Lequeux and L. Limat, Chem. Eng. Process., 2013, 68, 69–73 CrossRef CAS.
- Z. Liu, J. Ya, Y. Xin, J. Ma and C. Zhou, J. Cryst. Growth, 2006, 297, 223–227 CrossRef CAS.
- S. Takeda and P. Wiltzius, Chem. Mater., 2006, 18, 5643–5645 CrossRef CAS.
- C. Deleuze, B. Sarrat, F. Ehrenfeld, S. Perquis, C. Derail and L. Billon, Phys. Chem. Chem. Phys., 2011, 13, 10681–10689 RSC.
- W. Khunsin, G. Kocher, S. G. Romanov and C. M. S. Torres, Adv. Funct. Mater., 2008, 18, 2471–2479 CrossRef CAS.
- C. Jin, Z.-Y. Li, M. A. McLachlan, D. W. McComb, R. M. D. L. Rue and N. P. Johnson, J. Appl. Phys., 2006, 99, 116109 CrossRef.
- M. H. Kim, S. H. Im and O. O. Park, Adv. Funct. Mater., 2005, 15, 1329–1335 CrossRef CAS.
- S. Kim, H. D. Choi, I. D. Kim, J. C. Lee, B. K. Rhee, J. A. Lim and J. M. Hong, J. Colloid Interface Sci., 2012, 368, 9–13 CrossRef CAS PubMed.
- J. V. Sanders and M. J. Murray, Nature, 1978, 275, 201–203 CrossRef CAS.
- S. Hachisu and S. Yoshimura, Nature, 1980, 283, 188–189 CrossRef CAS.
- M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240 CrossRef CAS PubMed.
- E. C. M. Vermolen, A. Kuijk, L. C. Filion, M. Hermes, J. H. J. Thijssen, M. Dijkstra and A. van Blaaderen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16063–16067 CrossRef CAS PubMed.
- N. Vogel, L. de Viguerie, U. Jonas, C. K. Weiss and K. Landfester, Adv. Funct. Mater., 2011, 21, 3064–3073 CrossRef CAS.
- G. Singh, H. J. Griesser, K. Bremmell and P. Kingshott, Adv. Funct. Mater., 2011, 21, 540–546 CrossRef CAS.
- K. P. Velikov, C. G. Christova, R. P. A. Dullens and A. van Blaaderen, Science, 2002, 296, 106–109 CrossRef CAS PubMed.
- V. Kitaev and G. A. Ozin, Adv. Mater., 2003, 15, 75–78 CrossRef CAS.
- D. Wang and H. Möhwald, Adv. Mater., 2004, 16, 244–247 CrossRef CAS.
- M. H. Kim, S. H. Im and O. O. Park, Adv. Mater., 2005, 17, 2501–2505 CrossRef CAS.
- X. Huang, J. Zhou, M. Fu, B. Li, Y. Wang, Q. Zhao, Z. Yang, Q. Xie and L. Li, Langmuir, 2007, 23, 8695–8698 CrossRef CAS PubMed.
- J. Yu, Q. Yan and D. Shen, ACS Appl. Mater. Interfaces, 2010, 2, 1922–1926 CAS.
- J. Wang, S. Ahl, Q. Li, M. Kreiter, T. Neumann, K. Burkert, W. Knoll and U. Jonas, J. Mater. Chem., 2008, 18, 981–988 RSC.
- R. Mukhopadhyay, O. Al-Hanbali, S. Pillai, A. G. Hemmersam, R. L. Meyer, A. C. Hunter, K. J. Rutt, F. Besenbacher, S. M. Moghimi and P. Kingshott, J. Am. Chem. Soc., 2007, 129, 13390–13391 CrossRef CAS PubMed.
- Z. Dai, Y. Li, G. Duan, L. Jia and W. Cai, ACS Nano, 2012, 6, 6706–6716 CrossRef CAS PubMed.
- A. Malekpourkoupaei, L. W. Kostiuk and D. J. Harrison, Chem. Mater., 2013, 25, 3808–3815 CrossRef CAS.
- J. Wang, Q. Li, W. Knoll and U. Jonas, J. Am. Chem. Soc., 2006, 128, 15606–15607 CrossRef CAS PubMed.
- Y. Wan, Z. Cai, L. Xia, L. Wang, Y. Li, Q. Li and X. S. Zhao, Mater. Lett., 2009, 63, 2078–2081 CrossRef CAS.
- R. Fenollosa and F. Meseguer, Adv. Mater., 2003, 15, 1282–1285 CrossRef CAS.
- P. Jiang, Angew. Chem., Int. Ed., 2004, 43, 5625–5628 CrossRef CAS PubMed.
- Z. Ren, X. Li, J. Zhang, W. Li, X. Zhang and B. Yang, Langmuir, 2007, 23, 8272–8276 CrossRef CAS PubMed.
- C. Jin, M. A. McLachlan, D. W. McComb, R. M. De La Rue and N. P. Johnson, Nano Lett., 2005, 5, 2646–2650 CrossRef CAS PubMed.
- J. Zhang, A. Alsayed, K. H. Lin, S. Sanyal, F. Zhang, W.-J. Pao, V. S. K. Balagurusamy, P. A. Heiney and A. G. Yodh, Appl. Phys. Lett., 2002, 81, 3176–3178 CrossRef CAS.
- J. P. Hoogenboom, C. Rétif, E. de Bres, M. van de Boer, A. K. van Langen-Suurling, J. Romijn and A. van Blaaderen, Nano Lett., 2004, 4, 205–208 CrossRef CAS.
- N. V. Dziomkina and G. J. Vancso, Soft Matter, 2005, 1, 265–279 RSC.
- Y. Yin, Y. Lu, B. Gates and Y. Xia, J. Am. Chem. Soc., 2001, 123, 8718–8729 CrossRef CAS.
- Y. Masuda, T. Itoh and K. Koumoto, Langmuir, 2005, 21, 4478–4481 CrossRef CAS.
- Y. Masuda, K. Tomimoto and K. Koumoto, Langmuir, 2003, 19, 5179–5183 CrossRef CAS.
- R. C. Hayward, D. A. Saville and I. A. Aksay, Nature, 2000, 404, 56–59 CrossRef CAS PubMed.
- F. Qian, A. Pascall, M. Bora, T. Y.-J. Han, S. Guo, S. Ly, M. A. Worsley, J. D. Kuntz and T. Y. Olson, Langmuir, 2015, 31, 3563–3568 CrossRef CAS PubMed.
- M. Ojha, W. N. Gill, J. L. Plawsky and W. Cho, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2006, 24, 1109–1116 CrossRef CAS.
- Y. Yang, Y. Lu, M. Lu, J. Huang, R. Haddad, G. Xomeritakis, N. Liu, A. P. Malanoski, D. Sturmayr, H. Fan, D. Y. Sasaki, R. A. Assink, J. A. Shelnutt, F. van Swol, G. P. Lopez, A. R. Burns and C. J. Brinker, J. Am. Chem. Soc., 2003, 125, 1269–1277 CrossRef CAS PubMed.
- C. J. Brinker, Y. Lu, A. Sellinger and H. Fan, Adv. Mater., 1999, 11, 579–585 CrossRef CAS.
- K. Robbie and M. J. Brett, J. Vac. Sci. Technol., A, 1997, 15, 1460 CAS.
- K. Robbie, M. J. Brett and A. Lakhtakia, Nature, 1996, 384, 616 CrossRef CAS.
- A. G. Mark, J. G. Gibbs, T.-C. Lee and P. Fischer, Nat. Mater., 2013, 12, 802–807 CrossRef CAS PubMed.
- M. M. Hawkeye and M. J. Brett, J. Vac. Sci. Technol., A, 2007, 25, 1317–1335 CAS.
- A. Carretero-Genevrier, G. L. Drisko, D. Grosso, C. Boissiere and C. Sanchez, Nanoscale, 2014, 6, 14025–14043 RSC.
- C. Park, J. Yoon and E. L. Thomas, Polymer, 2003, 44, 6725–6760 CrossRef CAS.
- Y. Lu, H. Fan, A. Stump, T. L. Ward, T. Rieker and C. J. Brinker, Nature, 1999, 398, 223 CrossRef CAS.
- S. V. Nitta, V. Pisupatti, A. Jain, P. C. Wayner, W. N. Gill and J. L. Plawskya, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1999, 17, 205–212 CrossRef CAS.
- E. Armstrong, W. Khunsin, C. M. Sotomayor Torres, M. Osiak and C. O’Dwyer, ECS Trans., 2014, 58, 7–14 CrossRef.
- F. Meseguer, A. Blanco, H. Míguez, F. García-Santamaría, M. Ibisate and C. López, Colloids Surf., A, 2002, 202, 281–290 CrossRef CAS.
- A. Esmanski and G. A. Ozin, Adv. Funct. Mater., 2009, 19, 1999–2010 CrossRef CAS.
- A. Rugge, J. S. Becker, R. G. Gordon and S. H. Tolbert, Nano Lett., 2003, 3, 1293–1297 CrossRef CAS.
- V. O. Williams, E. J. DeMarco, M. J. Katz, J. A. Libera, S. C. Riha, D. W. Kim, J. R. Avila, A. B. F. Martinson, J. W. Elam, M. J. Pellin, O. K. Farha and J. T. Hupp, ACS Appl. Mater. Interfaces, 2014, 6, 12290–12294 CAS.
- J. C. Lytle and A. Stein, in Annual Review of Nano Research, ed. G. Cao and C. J. Brinker, World Scientific Publishing Co. Pte. Ltd., 2006, vol. 1, pp. 1–80 Search PubMed.
- L. Mishchenko, B. Hatton and J. Aizenberg, Small, 2012, 8, 1904–1911 CrossRef CAS PubMed.
- G. Collins, M. Blömker, M. Osiak, J. D. Holmes, M. Bredol and C. O’Dwyer, Chem. Mater., 2013, 25, 4312–4320 CrossRef CAS.
- Z.-Y. Yuan and B.-L. Su, J. Mater. Chem., 2006, 16, 663–677 RSC.
- Y. Liu, F. Qin, Z.-Y. Wei, Q.-B. Meng, D.-Z. Zhang and Z.-Y. Li, Appl. Phys. Lett., 2009, 95, 131116 CrossRef.
- C. Geng, T. Wei, X. Wang, D. Shen, Z. Hao and Q. Yan, Small, 2014, 10, 1668–1686 CrossRef CAS PubMed.
- L. Lu, J. D. Joannopoulos and M. Soljačić, Phys. Rev. Lett., 2012, 108, 243901 CrossRef.
- E. C. Nelson, N. L. Dias, K. P. Bassett, S. N. Dunham, V. Verma, M. Miyake, P. Wiltzius, J. A. Rogers, J. J. Coleman, X. Li and P. V. Braun, Nat. Mater., 2011, 10, 676–681 CrossRef CAS PubMed.
- A. C. Arsenault, D. P. Puzzo, I. Manners and G. A. Ozin, Nat. Photonics, 2007, 1, 468–472 CrossRef CAS.
- C. Fenzl, T. Hirsch and O. S. Wolfbeis, Angew. Chem., Int. Ed., 2014, 53, 3318–3335 CrossRef CAS PubMed.
- A. Blanco, E. Chomski, S. Grabtchak, M. Ibisate, S. John, S. W. Leonard, C. Lopez, F. Meseguer, H. Miguez, J. P. Mondia, G. A. Ozin, O. Toader and H. M. van Driel, Nature, 2000, 405, 437–440 CrossRef CAS PubMed.
- F. Jin, L.-T. Shi, M.-L. Zheng, X.-Z. Dong, S. Chen, Z.-S. Zhao and X.-M. Duan, J. Phys. Chem. C, 2013, 117, 9463–9468 CAS.
- J. Liao, Z. Yang, H. Wu, D. Yan, J. Qiu, Z. Song, Y. Yang, D. Zhou and Z. Yin, J. Mater. Chem. C, 2013, 1, 6541–6546 RSC.
- W. Niu, L. T. Su, R. Chen, H. Chen, Y. Wang, A. Palaniappan, H. Sun and A. I. Yoong Tok, Nanoscale, 2014, 6, 817–824 RSC.
- J. Liao, Z. Yang, S. Lai, B. Shao, J. Li, J. Qiu, Z. Song and Y. Yang, J. Phys. Chem. C, 2014, 118, 17992–17999 CAS.
- J. Zhou, Q. Liu, W. Feng, Y. Sun and F. Li, Chem. Rev., 2015, 115, 395–465 CrossRef CAS PubMed.
- Y. J. Lee and P. V. Braun, Adv. Mater., 2003, 15, 563–566 CrossRef CAS.
- F. Xue, Z. Meng, F. Qi, M. Xue, F. Wang, W. Chen and Z. Yan, Analyst, 2014, 139, 6192–6196 RSC.
- R. A. Barry and P. Wiltzius, Langmuir, 2005, 22, 1369–1374 CrossRef PubMed.
- D. Nakayama, Y. Takeoka, M. Watanabe and K. Kataoka, Angew. Chem., Int. Ed., 2003, 42, 4197–4200 CrossRef CAS PubMed.
- R. Pernice, G. Adamo, S. Stivala, A. Parisi, A. C. Busacca, D. Spigolon, M. A. Sabatino, L. D?Acquisto and C. Dispenza, Opt. Mater. Express, 2013, 3, 1820–1833 CrossRef.
- W. Hong, Y. Chen, X. Feng, Y. Yan, X. Hu, B. Zhao, F. Zhang, D. Zhang, Z. Xu and Y. Lai, Chem. Commun., 2013, 49, 8229–8231 RSC.
- S. Kim, A. N. Mitropoulos, J. D. Spitzberg, H. Tao, D. L. Kaplan and F. G. Omenetto, Nat. Photonics, 2012, 6, 818–823 CrossRef CAS.
- L. D. Bonifacio, D. P. Puzzo, S. Breslav, B. M. Willey, A. McGeer and G. A. Ozin, Adv. Mater., 2010, 22, 1351–1354 CrossRef CAS PubMed.
- H. Wang and K.-Q. Zhang, Sensors, 2013, 13, 4192–4213 CrossRef CAS PubMed.
- Y. Zhang, J. Qiu, M. Gao, P. Li, L. Gao, L. Heng, B. Z. Tang and L. Jiang, J. Mater. Chem. C, 2014, 2, 8865–8872 RSC.
- C. F. Blanford, R. C. Schroden, M. Al-Daous and A. Stein, Adv. Mater., 2001, 13, 26–29 CrossRef CAS.
- M. Sharma, G. I. N. Waterhouse, S. W. C. Loader, S. Garg and D. Svirskis, Int. J. Pharm., 2013, 443, 163–168 CrossRef CAS PubMed.
- C. F. C. João, J. M. Vasconcelos, J. C. Silva and J. P. Borges, Tissue Eng., Part B, 2013, 20, 437–454 CrossRef PubMed.
- Y. S. Zhang, S.-W. Choi and Y. Xia, Soft Matter, 2013, 9, 9747–9754 RSC.
- V. Rinnerbauer, S. Ndao, Y. X. Yeng, W. R. Chan, J. J. Senkevich, J. D. Joannopoulos, M. Soljacic and I. Celanovic, Energy Environ. Sci., 2012, 5, 8815–8823 CAS.
- K. Arpin, PhD thesis, University of Illinois at Urbana-Champaign, 2013.
- K. A. Arpin, M. D. Losego and P. V. Braun, Chem. Mater., 2011, 23, 4783–4788 CrossRef CAS.
- N. R. Denny, S. E. Han, D. J. Norris and A. Stein, Chem. Mater., 2007, 19, 4563–4569 CrossRef CAS.
- S. Han, A. Stein and D. Norris, Phys. Rev. Lett., 2007, 99, 053906 CrossRef CAS.
- K. Cheng-Yu and L. Shih-Yuan, Nanotechnology, 2008, 19, 095705 CrossRef PubMed.
- C.-Y. Cho and J. H. Moon, Langmuir, 2012, 28, 9372–9377 CrossRef CAS PubMed.
- Y. Park, J. W. Lee, S.-J. Ha and J. H. Moon, Nanoscale, 2014, 6, 3105–3109 RSC.
- D.-Y. Kang, Y. Lee, C.-Y. Cho and J. H. Moon, Langmuir, 2012, 28, 7033–7038 CrossRef CAS PubMed.
- L. T. Varghese, Y. Xuan, B. Niu, L. Fan, P. Bermel and M. Qi, Adv. Opt. Mater., 2013, 1, 692–698 CrossRef.
- A. Mihi, C. Zhang and P. V. Braun, Angew. Chem., Int. Ed., 2011, 50, 5712–5715 CrossRef CAS PubMed.
- M. Osiak, H. Geaney, E. Armstrong and C. O’Dwyer, J. Mater. Chem. A, 2014, 2, 9433–9460 CAS.
- J. W. Long, B. Dunn, D. R. Rolison and H. S. White, Chem. Rev., 2004, 104, 4463–4492 CrossRef CAS.
- J. C. Lytle, J. M. Wallace, M. B. Sassin, A. J. Barrow, J. W. Long, J. L. Dysart, C. H. Renninger, M. P. Saunders, N. L. Brandell and D. R. Rolison, Energy Environ. Sci., 2011, 4, 1913–1925 CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2009, 22, 587–603 CrossRef.
- A. Vu, Y. Q. Qian and A. Stein, Adv. Energy Mater., 2012, 2, 1056–1085 CrossRef CAS.
- J. S. Sakamoto and B. Dunn, J. Mater. Chem., 2002, 12, 2859–2861 RSC.
- Z. Tong, J. Hao, K. Zhang, J. Zhao, B.-L. Su and Y. Li, J. Mater. Chem. C, 2014, 2, 3651–3658 RSC.
- L. Li, U. Steiner and S. Mahajan, J. Mater. Chem., 2010, 20, 7131–7134 RSC.
- N. S. Ergang, J. C. Lytle, H. Yan and A. Stein, J. Electrochem. Soc., 2005, 152, A1989–A1995 CrossRef CAS.
- C. M. Doherty, R. A. Caruso, B. M. Smarsly and C. J. Drummond, Chem. Mater., 2009, 21, 2895–2903 CrossRef CAS.
- J. Lu, Z. Tang, Z. Zhang and W. Shen, Mater. Res. Bull., 2005, 40, 2039–2046 CrossRef CAS.
- J. Lu, Z. Tang, Z. Zhang and W. Shen, J. Electrochem. Soc., 2005, 152, A1441–A1444 CrossRef CAS.
- D. L. Ma, Z. Y. Cao, H. G. Wang, X. L. Huang, L. M. Wang and X. B. Zhang, Energy Environ. Sci., 2012, 5, 8538–8542 CAS.
- A. A. Zakhidov, R. H. Baughman, Z. Iqbal, C. Cui, I. Khayrullin, S. O. Dantas, J. Marti and V. G. Ralchenko, Science, 1998, 282, 897–901 CrossRef CAS.
- K. T. Lee, J. C. Lytle, N. S. Ergang, S. M. Oh and A. Stein, Adv. Funct. Mater., 2005, 15, 547–556 CrossRef CAS.
- D.-Y. Kang, S.-O. Kim, Y. J. Chae, J. K. Lee and J. H. Moon, Langmuir, 2013, 29, 1192–1198 CrossRef CAS PubMed.
- T. Song, Y. Jeon, M. Samal, H. Han, H. Park, J. Ha, D. K. Yi, J.-M. Choi, H. Chang, Y.-M. Choi and U. Paik, Energy Environ. Sci., 2012, 5, 9028–9033 CAS.
- L. Kavan, M. Zukalová, M. Kalbáč and M. Graetzel, J. Electrochem. Soc., 2004, 151, A1301–A1307 CrossRef CAS.
- M.-S. Wu and Y.-P. Lin, Electrochim. Acta, 2011, 56, 2068–2073 CrossRef CAS.
- H.-G. Jung, M. W. Jang, J. Hassoun, Y.-K. Sun and B. Scrosati, Nat. Commun., 2011, 2, 516 CrossRef PubMed.
- J. W. Long, B. Dunn, D. R. Rolison and H. S. White, Chem. Rev., 2004, 104, 4463–4492 CrossRef CAS.
- J. C. Lytle, in Nanotechnology for Lithium-Ion Batteries, ed. Y. Abu-Lebdeh and I. Davidson, Springer Science+Business Media, LLC, 2013 Search PubMed.
- H. Zhang, X. Yu and P. V. Braun, Nat. Nanotechnol., 2011, 6, 277–281 CrossRef CAS PubMed.
- H. Zhang and P. V. Braun, Nano Lett., 2012, 12, 2778–2783 CrossRef CAS PubMed.
- D. Y. Kim, J. Suk, D. W. Kim, Y. Kang, S. H. Im, Y. Yang and O. O. Park, J. Mater. Chem. A, 2014, 2, 6396–6401 CAS.
- H. Liu, H.-M. Cho, Y. S. Meng and Q. Li, ACS Appl. Mater. Interfaces, 2014, 6, 9842–9849 CAS.
- X. Huang, J. Chen, Z. Lu, H. Yu, Q. Yan and H. H. Hng, Sci. Rep., 2013, 3, 2317 Search PubMed.
- J.-H. Kim, J.-H. Kim, K.-H. Choi, H. K. Yu, J. H. Kim, J. S. Lee and S.-Y. Lee, Nano Lett., 2014, 14, 4438–4448 CrossRef CAS PubMed.
- J. H. Pikul, H. G. Zhang, J. Cho, P. V. Braun and W. P. King, Nat. Commun., 2013, 4, 1732–1736 CrossRef PubMed.
- C. H. Ho, D. H. Lien, Y. H. Hsiao, M. S. Tsai, D. Chang, K. Y. Lai, C. C. Sun and J. H. He, Appl. Phys. Lett., 2013, 103, 161104 CrossRef.
- A. Z. Khokhar, R. M. D. L. Rue and N. P. Johnson, IET Circuits, Devices & Systems, 2007, 1, 210 Search PubMed.
- P. Lodahl, A. F. v. Driel, I. S. Nikolaev, A. Irman, O. Karin, D. Vanmaekelbergh and W. L. Vos, Nature, 2004, 430, 654–657 CrossRef CAS PubMed.
- W. Zhang, M. Anaya, G. Lozano, M. E. Calvo, M. B. Johnston, H. Míguez and H. J. Snaith, Nano Lett., 2015, 15, 1698–1702 CrossRef CAS PubMed.
- C. O’Dwyer and C. M. S. Torres, Front. Phys., 2013, 1, 18 Search PubMed.
- M. Osiak, W. Khunsin, E. Armstrong, T. Kennedy, C. M. S. Torres, K. M. Ryan and C. O’Dwyer, Nanotechnology, 2013, 24, 065401 CrossRef CAS PubMed.
- C. O’Dwyer, M. Szachowicz, G. Visimberga, V. Lavayen, S. B. Newcomb and C. M. S. Torres, Nat. Nanotechnol., 2009, 4, 239–244 CrossRef PubMed.
- J. K. Kim, S. Chhajed, M. F. Schubert, E. F. Schubert, A. J. Fischer and M. H. Crawford, Adv. Mater., 2008, 20, 801–804 CrossRef CAS.
- P. H. Fu, G. J. Lin, H. P. Wang, K. Y. Lai and J. H. He, Nano Energy, 2014, 8, 78–83 CrossRef CAS.
- Y. H. Hsiao, C. Y. Chen, L. C. Huang, G. J. Lin, D. H. Lien, J. J. Huang and J. H. He, Nanoscale, 2014, 6, 2624–2628 RSC.
- H. P. Wang, D. H. Lien, M. L. Tsai, C. A. Lin, H. C. Chang, K. Y. Lai and J. H. He, J. Mater. Chem. C, 2014, 2, 3144–3171 RSC.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269–281 CrossRef CAS.
- J. W. Fergus, J. Power Sources, 2010, 195, 939–954 CrossRef CAS.
- W. McSweeney, H. Geaney and C. O’Dwyer, Nano Res., 2015, 8, 1395–1442 CrossRef CAS.
- B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430 CrossRef CAS.
- D. R. Rolison, R. W. Long, J. C. Lytle, A. E. Fischer, C. P. Rhodes, T. M. McEvoy, M. E. Bourga and A. M. Lubers, Chem. Soc. Rev., 2009, 38, 226–252 RSC.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4302 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |