Unexpected origin of magnetism in monoclinic Nb₁₂O₂₉ from first-principles calculations

Abstract

Nb₁₂O₂₉ is a 4d transition metal oxide that occurs in two forms with different symmetries, monoclinic (m) and orthorhombic (o). The monoclinic form has unusual magnetic properties; below a temperature of 12 K, it exhibits both metallic conductivity and antiferromagnetic ordering. Here, first-principles density-functional theory calculations are used to study the structure, relative stability and electronic properties of Nb₁₂O₂₉. The optimized crystal structures are in good agreement with experimental observations and total energy calculations show similar stability of the two phases, while a magnetic electronic state is slightly favoured for m-Nb₁₂O₂₉. The unusual magnetism of the monoclinic phase originates from a Stoner instability that can be attributed to the Nb atoms with valence states close to Nb⁵⁺, i.e., the atoms with an electronic configuration of ∼d⁰. This is in clear contradiction to current models in which the magnetism is attributed to the presence of localized Nb⁴⁺ ions with a formal d¹ configuration. Our study demonstrates that in complex structures, magnetic properties are best not inferred from ionic models, but require a full quantum mechanical calculation over the whole unit cell.

---

I. Introduction

Nb₁₂O₂₉ has been of interest due to its unique phase relationships, interesting crystal structures, and above all, unusual magnetic properties.^1–10 It has two crystallographic forms at ambient temperature; one is monoclinic (m-) and the other orthorhombic (o-). Both Nb₁₂O₂₉ forms have similar short range (local) crystal structures, consisting of perovskite-like 4 × 3 blocks of corner-sharing NbO₆ octahedra that share edges with other blocks to fill space. The difference between the two forms is the long-range ordering of the blocks,^1–3,5 which is schematically shown in Fig. 1. The chemical representation of the 12 NbO₆ octahedra in the building blocks (there are 6 pairs of symmetrically equivalent octahedra per block) can be written in both the m- and o-forms as Nb₂⁴⁺Nb₁₀⁵⁺O₂₉²⁻ in the commonly used ionic model.^4–7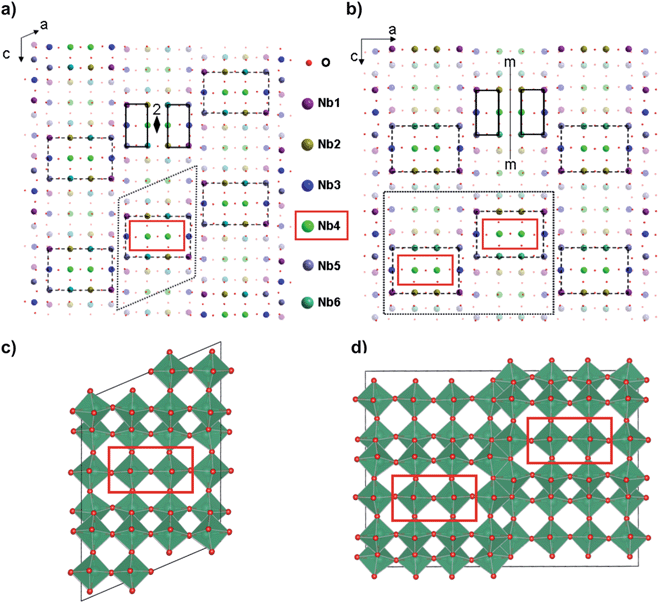

Fig. 1 Schematic crystal structures of the monoclinic-Nb₁₂O₂₉ (a and c) and orthorhombic-Nb₁₂O₂₉ (b and d) phases, both shown in [010] projection. Atoms are depicted using collared spheres as indicated in the figure. Atoms at y = 1/2 are plotted half-transparent. Both structures contain similar blocks of 3 × 4 NbO₆ octahedra, outlined by rectangular dashed lines. The monoclinic (m-) phase is a consequence of the ‘staircase’ stacking of the blocks, while the orthorhombic (o-) phase is a consequence of ‘zigzag’ stacking of the blocks. The resulting unit cells are indicated with dotted lines. The 12 NbO₆ octahedra in the 3 × 4 blocks consist of 6 pairs of symmetry-equivalent octahedra; the pairs of octahedra are related by 2-fold symmetry in the monoclinic phase and mirror symmetry in the orthorhombic phase. The Nb4 atoms are at the centre of the 3 × 4 blocks and are indicated with red rectangles. Only the Nb4 atoms in the monoclinic phase satisfy the criterion for the Stoner mechanism (Table 2).

As an early 4d transition metal oxide, it is unusual that Nb₁₂O₂₉ is experimentally found to display Curie–Weiss behaviour of the magnetic susceptibility in both forms. The o-form does not order magnetically, while the m-form does, with a Neel temperature of 12 K,^3–9 despite the fact that both forms have very similar local structures.^1–3 Experimental measurements also show that m-Nb₁₂O₂₉ is a metallic conductor.^3–7 Therefore, m-Nb₁₂O₂₉ can be classified as only one of a handful of transition metal oxides, such as CaRuO₃ (ref. 11) and Na_0.7CoO₂ (ref. 12–14), that are metallic conductors and yet show antiferromagnetic Curie–Weiss-like behaviour of the magnetic susceptibility.^5,15

Many efforts have been made to understand the origin of magnetism of the m-form of Nb₁₂O₂₉.^3–9 In the currently accepted ionic picture, the magnetic ordering in m-Nb₁₂O₂₉ has been attributed to the ordering of distinct d¹ (s = 1/2) Nb⁴⁺ ions in the perovskite blocks, as Nb⁴⁺ formally has one unpaired d-electron, and the other Nb ions present are Nb⁵⁺, with the non-magnetic electronic configuration d⁰. Why the m-phase magnetically orders at 12 K, while the o-phase shows similar magnetic susceptibility and yet does not magnetically order, remains one of the interesting puzzles of Nb₁₂O₂₉. Though the long range arrangements of the blocks in the o-form has been credited as frustrating the magnetic ordering in that phase,⁶ this would be surprising since magnetic ordering is normally expected to be mainly determined by the local magnetic interactions. Due to limitations of the experimental characterization that arise from distinguishing the complex structures, the weak magnetism, and the intergrowths of the two forms during materials synthesis, theoretical approaches, especially those based on parameter-free first-principles techniques, can be helpful to elucidate the electronic properties. Until now, however, the only theoretical work in this system is by Llundell, Alemany and Canadell, who discussed the dual localized/delocalized nature of the Nb 4d electrons using the tight-binding extended Hückel method.¹⁶ In the present study, first principles electronic structure calculations are used to determine the electronically most stable crystal structure and the electronic properties of m-Nb₁₂O₂₉. The calculations show that the magnetism of the m-phase originates from the Stoner instability of the electronic structure of the Nb atoms that have valencies closer to Nb⁵⁺, which is in contrast with present beliefs. The information obtained here is not only helpful for understanding the structural, electrical transport and magnetic properties of the niobium oxides and related phases, but also has implications for understanding the magnetic properties of other 4d or 5d transition metal compounds and their surfaces, such as those demonstrated recently for the origin of magnetism on the clean and oxygen covered (110) surfaces of nonmagnetic bulk RuO₂.¹⁷

II. Details of computational techniques

In the present work, the first-principles Vienna Ab initio Simulation Program (VASP)^18,19 employing the density functional theory (DFT) within the Projector-Augmented Wave (PAW) method was used.^20,21 Both the Generalized Gradient Approximation (GGA) and the Local Density Approximation (LDA) were employed for the exchange and correlation energy terms.^22,23 In our calculations, we employ the potential Nb_sv which contains the Nb 4p semicore electron (4s² 4p⁶ 5s² 4d⁵).

The cut-off energy of the wave functions was 500.0 eV. The cut-off energy of the augmentation wave functions was 650.0 eV. The electronic wave functions were sampled on a 2 × 16 × 2 grid with 36 irreducible k-points and a 1 × 16 × 2 grid with 16 irreducible k-points in the Brillouin zone (BZ) of the m- or o-Nb₁₂O₂₉ form, using the Monkhorst and Pack method.²⁴ The magnetism of the m-phase was calculated for different types of magnetic ordering. The Wigner–Seitz radii were set to 1.4 Å for O and 1.0 Å for Nb. Tests of k-mesh density and cut-off energies showed a good convergence (well within 1 meV per atom).

III. Results and discussions

III.A Crystal structure and chemical bonding in Nb₁₂O₂₉

Table 1 lists the results of the structural optimizations for the m- and o-Nb₁₂O₂₉ phases using DFT-GGA and DFT-LDA, with comparisons to the experimental observations. The lattice parameters from the GGA calculations are slightly larger than the experimental values, while the lattice parameters from the LDA calculations are slightly smaller than the experimental values, within 1.2%. Such results are not unusual for calculations using the DFT approximation. In the remainder of this paper we focus on the DFT-GGA results, as they are considered to be more accurate for electronic properties.

Table 1 Calculated results (lattice parameters, energy relative to the non-magnetic (NM) o-phase) for Nb₁₂O₂₉ using the DFT methods in comparison with experimental values. The AFM ordering is along the (100) orientation with the FM domain in one unit-cell anti-ferromagnetic to the neighbouring cell in a 2a × b × c supercell (see text). (a) Crystal structure, formation energy and magnetic moment of m-Nb₁₂O₂₉, space group A2/m (nr. 12). (b) Crystal structure and formation energy of o-Nb₁₂O₂₉, space group Amma (nr. 62)

	GGA	LDA	Exp.
(a)
a (Å)	15.9011	15.5955	15.66 (ref. 2)
			15.6920 (ref. 9)
b (Å)	3.8362	3.7907	3.832 (ref. 2)
			3.8303 (ref. 9)
c (Å)	20.9743	20.6548	20.72 (ref. 2)
			20.7171 (ref. 9)
β (°)	113.12	113.12	112.93 (ref. 2)
			113.11 (ref. 9)
V (Å^3 per f.u.)	588.33	561.51	572.57 (ref. 2)
			572.64 (ref. 9)
ΔE (eV per f.u.)	0.025 (NM)		Co-existence of o- and m-phases
	0.010 (FM)
	0.012 (AF)
M (μB per uc)	0.82		0.84 (ref. 4 and 5)
(b)
a (Å)	29.2428	28.6550	28.90 (ref. 1)
			28.8901 (ref. 3)
b (Å)	3.8355	3.7991	3.835 (ref. 1)
			3.8320 (ref. 3)
c (Å)	20.9766	20.6041	20.72 (ref. 1)
			20.7400 (ref. 3)
V (Å^3 per f.u.)	588.19	560.77	574.11 (ref. 1)
			574.02 (ref. 3)
ΔE (eV per f.u.)	0.0

---

Accurate total energy calculations find that the lowest energy solution for the o-form of Nb₁₂O₂₉ is not magnetically ordered (NM, non-magnetic). For the m-phase, there is an anti-ferromagnetic (AFM) ordering along the (100) direction with the magnetic domain in one unit cell anti-ferromagnetic to that of the neighbouring unit cell, within a 2a × b × c supercell. All solutions found for the m-form (non-magnetic, NM, ferromagnetic, FM, and antiferromagnetic, AF) have slightly higher energies than those for the o-form, but the two polymorphs are nearly degenerate in energy from the electronic perspective (energy differences are less than 1 meV per atom). This is consistent with the experimental results, which show that it is difficult to prepare samples with only one form present. With respect to the energy of the o-phase, the nonmagnetic (NM) solution is the least favourable for m-Nb₁₂O₂₉, with an excess energy of 25 meV per formula-unit (f.u.) compared to the o-form. The ferromagnetic (FM) and antiferromagnetic (AF) solutions for the m-form are slightly more favourable, with energies of 10 meV per f.u. and 12 meV per f.u in excess of that of the o-form. Thus for the m-phase, within the present computational accuracy, the ferromagnetic solution has almost the same energy as the antiferromagnetic solution. The calculated magnetic moment for the m-phase is about 1.65 μ_B per unit cell (uc), in good agreement with the experimental values of 1.64–1.80 μ_B per unit cell.^5–7,15 Antiferromagnetic input parameters for the m-form confining the system to one chemical unit cell result in non-magnetic or ferromagnetic solutions; the antiferromagnetically ordered m-phase is predicted to have a magnetic supercell with a doubled a-axis. To date, magnetic supercell reflections have not been observed experimentally by neutron diffraction in m-Nb₁₂O₂₉ due to the weakness of the expected magnetic scattering.

All the Nb ions in Nb₁₂O₂₉ have six O neighbours in distorted octahedral coordination. The valency of Nb ion is determined from the calculated Nb_i–O_j distances using Brown's bond valence approach:^25,26

V_i = ∑v_ij = ∑exp[(R_ij − R₀)/A₀)], (1)

where A₀ = 0.37 is a universal parameter and R₀ = 1.91 Å is a scaling bond-length obtained for the structure optimization of rutile NbO₂. The crystal structure and coordination of atoms have been discussed in detail in the literature.^1–3,5 The local bonding of typical Nb atoms in the NbO₆ octahedrons is depicted in Fig. S1† and all Nb–O bond lengths are listed in Table S1.† Magnetic Nb atoms in the m-phase have a short Nb–O bond with bond length smaller or equal to 1.80 Å (see Table S1 in ESI†). The Nb6–O bond lengths in o-Nb₁₂O₂₉ are quite similar to that of the Nb4–O bond in the m-phase. However, as shown in Fig. S1,† the distortion of the Nb6 octahedron in the o-phase, with the smallest O–Nb–O angle at about 74°, is significantly larger than the distortion of the Nb4 octahedra in the m-phase (the smallest O–Nb–O angle is about 82°). Furthermore, the smallest O–Nb–O angle for Nb1 in the m-phase is also about 74° (Fig. S1†).

Using these values, the calculated total valence of the 6 unique Nb ions in Nb₁₂O₂₉ is +28.98, closely matching the expected value of +29. As shown in Table 2 (the indexing of the Nb atoms (Nb1…Nb6) is shown in Fig. 1), the calculated valencies of the individual Nb ions range from +4.68 to +4.92; they do not extend down to values of +4. It is also possible to obtain information about the Nb ion charge directly from the electronic distributions within the spheres of the atoms. This charge counting is convenient, but we note that all the valence electrons in Nb₁₂O₂₉, due to their band-like character, belong to the whole crystal and are not actually localized at individual ions. That this is the case can be seen in Fig. 2 and 3, where the Nb 4d states are shown to form bands with widths of 2 to 4 eV, with the details discussed in the next section. If the electron states were localized on the ions, then the band widths would be much narrower. We also note that there is no unique definition of the size of atoms in solids – the number of electrons integrated in the sphere of an atom strongly depends on the sphere size. However, here we are interested only in the relative number of 4d electrons in the Nb spheres. We find that the number of electrons occupying Nb 4d states ranges from 1.13 to 1.22 within the Wigner–Seitz spheres of Nb (R_W–S = 1.0 Å).

Table 2 Calculated Nb bond-valences (V in valence units, V.U.), number of 4d electrons on the Nb atoms, and local magnetic moments (M in Bohr magnetons, μ_B, per Nb). The indexing of the Nb atoms in the crystal structures (Nb1…Nb6) is shown in Fig. 1. The Nb4 atom, which satisfies the criterion for Stoner magnetism (eqn (2) in the text) is printed in bold

	x/a, y/b, z/c	V (V.U.)	Q 4d (e)	M Nb (μB)
o-Nb 12 O 29
Nb1	0.0507, 0.0, 0.0362	4.77	1.22	0
Nb2	0.0505, 0.0, 0.6687	4.82	1.23	0
Nb3	0.0484, 0.0, 0.8514	4.68	1.23	0
Nb4	0.1849, 0.0, 0.0336	4.88	1.18	0
Nb5	0.1845, 0.0, 0.6675	4.87	1.18	0
Nb6	0.1848, 0.0, 0.8508	4.92	1.13	0
m-Nb 12 O 29
Nb1	0.1019, 0.0, 0.0667	4.77	1.22	0.01
Nb2	0.3709, 0.0, 0.1445	4.87	1.18	0.05
Nb3	0.0968, 0.0, 0.8804	4.72	1.23	0.02
Nb4	0.3695, 0.0, 0.9613	4.90	1.14	0.10
Nb5	0.1005, 0.0, 0.6988	4.82	1.22	0.02
Nb6	0.3679, 0.0, 0.7774	4.88	1.18	0.06

---

Fig. 2 Total calculated density of states (tDOS) over a wide energy range for non-magnetic o-Nb₁₂O₂₉ (a), non-magnetic (b) and ferromagnetic (FM) (c) m-Nb₁₂O₂₉.

Fig. 3 Partial density of states (pDOS) near E_F for the Nb atoms in Nb₁₂O₂₉, as calculated for the o-phase (left), and the m-phase in the non-spin-polarized solution (center) and in the ferromagnetic solution (right). Only states close to the Fermi level (set at 0 eV) are shown.

The Nb4 ions in m-Nb₁₂O₂₉ are calculated to have the largest local magnetic moment (∼0.1 μ_B per atom). The isosurfaces of the spin-densities for the Nb atoms in the FM m-phase are shown in Fig. S2.† Significant magnetic moments (∼0.06 μ_B per atom) can also be found for the Nb2 and Nb6 ions. These are substantially lower than the moments expected for 1 localized unpaired electron at a particular site. Interestingly, all the moment-bearing Nb ions are calculated to also have the highest chemical valences (∼4.9) and correspondingly the smallest d electron orbital occupancies. This is in contrast to the expectation that the magnetism should originate from the Nb ions that are closest in formal valence to Nb⁴⁺. This shows the failure of the simple ionic model, i.e. Nb₂⁴⁺Nb₁₀⁵⁺O₂₉²⁻, to correctly describe the system. The results clearly point to an itinerant electron origin for the observed antiferromagnetism.

III.B Electronic and magnetic properties of the Nb₁₂O₂₉ phases

Fig. 2a shows the calculated total density of states (tDOS) for the o- (upper), and m- (middle and lower) forms of Nb₁₂O₂₉. Both non-magnetic (middle) and magnetic (lower) solutions are shown for m-Nb₁₂O₂₉. Fig. 2b compares the partial density of Nb 4d states in the Nb₁₂O₂₉ phases. The strong overall similarity between the tDOS curves of the o- and m-phases is apparent, corresponding to the strong relationship between the two structures. Considering the full energy range, a simple chemical model can describe the general features of the tDOS plots (Fig. 2a). At energies far below the Fermi Energy (E_F, 0 eV), a band with a bandwidth of about 3.3 eV (from about −20.8 eV to −17.5 eV) is composed of O 2s states. There is a gap of about 9.3 eV separating this O 2s sub-band from another sub-band (from about −8.2 eV to −2.3 eV) that is dominated by O 2p states with some admixture of Nb 4d states. The band at positive energies that begins just below E_F is dominated by Nb 4d states, separated by a gap of about 1.8 eV from the O 2p sub-band below it. This is by far the emptiest Nb 4d band. Distinct peaks in the total density of states are seen at E_F in both phases.

Detailed information about the electronic structures of the phases around E_F is presented in Fig. 3, which compares the partial DOS (pDOS) of the Nb 4d states for o- and m-Nb₁₂O₂₉ without spin polarization. There are significant differences in the shapes of the 4d pDOS curves for the different Nb sites. The pDOS for the Nb2, Nb4, and Nb6 atoms in m-Nb₁₂O₂₉ without spin-polarization have much higher peaks around E_F than the other atoms in this phase; the pDOS for Nb4 is especially distinct and high, and E_F is positioned exactly at this peak of the Nb4 pDOS. The resulting high density of electronic states at E_F results in a higher calculated energy for the non-magnetic solution of the m-phase. The difference is primarily that the peaks in the o-form near E_F are slightly split in energy. The result is that the Nb pDOS are not as sharply peaked in the o-form, with the highest pDOS calculated to be only slightly above E_F.

In the 1930s, Stoner investigated the relationship between the exchange interaction and kinetic contribution for a band structure and proposed the well-known Stoner criterion:^27–29

ID(E_F) ≥ 1 (2)

where D(E_F) is the density of states at the Fermi level. The Stoner parameter, which is a measure of the strength of the exchange correlation, is denoted I. The Stoner criterion has been successfully applied to predict the magnetism of different compounds.^17,30–32

The Nb4 atom in m-Nb₁₂O₂₉ has a large D(E_F) value of about 1.6 states per eV per atom while the D(E_F) values for rest of the Nb atoms, as well as all the Nb atoms in o-Nb₁₂O₂₉, are significantly smaller (0.8 states per eV per atom) (see Fig. 2). Unfortunately, there is no data on the Stoner parameter for Nb. If we use I = 0.9, the value for Fe,³¹ the Stoner criterion is satisfied for the Nb4 atom in m-Nb₁₂O₂₉, ID(E_F) ∼ 1.45, ≥1, whereas for the other Nb atoms ID(E_F) ∼ (0.2 to 0.7) < 1. This is in agreement with the local moment of the Nb4 atom in the m-phase as shown in Table 2. The Nb4 atoms are the Nb atoms located at the centre of the blocks of 3 × 4 NbO₆ octahedra, indicated with red rectangles in Fig. 1.

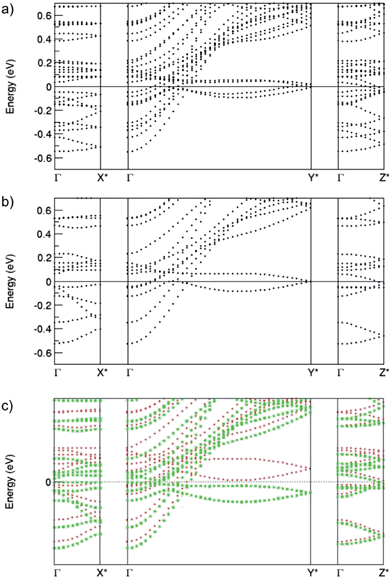
Fig. 4 also shows the dispersion curves of the non-spin-polarized Nb₁₂O₂₉ phases. The curves are very similar, except that the number of states for the o-phase is twice as high as the number of states for the m-phase due to the relationship of the unit cells (the cell volume of the orthorhombic phase is close to double that of the m-phase). A subtle difference can be found at k-point Y*: the states are degenerate for the m-phase, whereas in the o-phase they are split into two states, with the Fermi level in between. This explains the splitting of the pDOS peaks in Fig. 3b. Correspondingly, as shown in the dispersion curves of the magnetic m-phase in the spin-polarized calculations, the state at Y* splits into two due to spin-splitting, and correspondingly the density of states dominated by Nb 4d states at the Fermi level is strongly reduced.

Fig. 4 Dispersion curves of the band structure close to the Fermi level from the centre (Γ) to the axes X*, Y* and Z* in the Brillouin zone for (a) o-Nb₁₂O₂₉ (non-magnetic solution), (b) the non-magnetic solution for m-Nb₁₂O₂₉, and (c) the ferromagnetic (FM) solution for m-Nb₁₂O₂₉. The red dots represent the states for the majority (spin-up) electrons and green dots represent the minority (spin-down) electrons.

It is also of interest to analyse the anisotropy in charge carrier transport properties. Fig. 4 shows clearly a strong anisotropy of the energy-wavevector dispersion curves along the three axes. The bands show very small dispersion along a, taking the length ratios into account (b*/a* = 7.7, and c*/a* = 1.4, and b*/c* = 5.5). This indicates a strong anisotropy of effective masses for the charge carriers. The band just below the Fermi level along a* has a dispersion of about 0.08 eV, while some of the bands along c* show a dispersion of about 0.2 eV. These states are highly localized. Some of the bands along the b*-axis have dispersions larger than 1 eV, while four bands show small dispersions of only about 0.4 eV, reflecting a difference in the localization of the states in this direction, though they are substantially more delocalized than those along a* and c*. Eigen-character analysis reveals that the localized bands are dominated by Nb4 4d states for the m-phase and Nb6 4d states for the o-phase, corresponding to the sharp peaks in the pDOS around E_F for the non-magnetic o- and m-phases seen in Fig. 2.

IV. Conclusions

First-principles DFT calculations have been performed for the two forms of Nb₁₂O₂₉. The calculations showed only a small energy difference (∼0.01 eV per f.u.) between the monoclinic and the orthorhombic forms, with the o-phase slightly favoured. This is in agreement with experimental observations, as the o-form samples can be prepared with high purity, whereas the m-form is sometimes found intergrowing with the o-form. For the m-form, a spin-polarized solution is favoured over the non-magnetic solution. The calculated lattice parameters and magnetic moments are in good agreement with the available experimental data. The magnetism in the m-form originates from the high density of states of the itinerant 4d states of the atoms indexed as Nb4 atoms, fulfilling Stoner's magnetic instability criterion. Both electronic configurations and bond valence analysis showed that the spin-polarized Nb atoms (indexed Nb4 in the m-phase) are close to a valence state of 5+. This conclusion is in contrast to the current belief that the magnetism can be attributed to the Nb⁴⁺ ions when an ionic model is considered. Electronic band structure analysis predicts a strong anisotropy in the charge carrier mobility.

Acknowledgements

MvH acknowledges a VIDI grant from the Dutch Science Foundation NWO. JK was supported by the Austrian Science Fund (FWF) within the SFB ViCoM (Grant F 41).

References

1. R. Norin, Acta Chem. Scand., 1963, 17, 1391.
2. R. Norin, Acta Chem. Scand., 1966, 20, 871.
3. T. McQueen, Q. Xu, E. N. Andersen, H. W. Zandbergen and R. J. Cava, J. Solid State Chem., 2007, 180, 2864.
4. R. J. Cava, B. Batlogg, J. J. Krajewski, P. Gammel, H. F. Poulsen, W. F. Peck Jr and L. W. Rupp, Nature, 1991, 350, 598.
5. R. J. Cava, B. Batlogg, J. J. Krajewski, H. F. Poulsen, P. Gammel and W. F. Peck, Jr, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 6973.
6. E. N. Andersen, T. Klimczuk, V. I. Miller, H. W. Zandbergen and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 033413.
7. J.-G. Cheng, J.-S. Zhou, J. B. Goodenough, H. D. Zhou, C. R. Wiebe, T. Takami and T. Fujii, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134428.
8. J. E. L. Waldron, M. A. Green and D. A. Neumann, J. Am. Chem. Soc., 2001, 123, 5833.
9. J. E. L. Waldron, M. A. Green and D. A. Neumann, J. Phys. Chem. Solids, 2004, 65, 79.
10. T. Naka, T. Nakane, Y. Furukawa, Y. Takano, T. Adschiri and A. Matsushita, Phys. B, 2006, 378–380, 337.
11. J. M. Longo, P. M. Raccah and J. B. Goodenough, J. Appl. Phys., 1968, 39, 1327.
12. Y. Wang, N. S. Rogado, R. J. Cava and N. P. Ong, Nature, 2003, 423, 425.
13. I. Terasaki, Y. Susago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R12685.
14. Y. Ando, N. Miyamoto, K. Segawa, T. Kawata and I. Terasaki, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 10580.
15. C. H. Rüsher and M. Nygren, J. Phys.: Condens. Matter, 1991, 3, 3997.
16. M. Llunell, P. Alemany and E. Canadell, J. Solid State Chem., 2000, 149, 176.
17. E. Torun, C. M. Fang, G. A. De Wijs and R. A. De Groot, J. Phys. Chem. C, 2013, 117, 6353.
18. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
19. G. Kresse and J. Furthmueller, Comput. Mater. Sci., 1996, 6, 15.
20. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
21. G. J. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 54, 1758.
22. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
23. C. Amador, W. R. Lambrecht and B. Segall, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1870.
24. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
25. I. D. Brown, The Chemical Bond in Inorganic Chemistry. IUCr Monographs in Crystallography 12, Oxford Science Publications, OUP, 2002.
26. I. D. Brown, Chem. Rev., 2009, 109, 6858.
27. E. C. Stoner, Proc. R. Soc. London, Ser. A, 1936, 154, 656.
28. E. C. Stoner, Proc. R. Soc. London, Ser. A, 1938, 165, 372.
29. E. C. Stoner, Proc. R. Soc. London, Ser. A, 1939, 169, 339.
30. M. S. S. Brooks, Conduction electrons in magnetic metals, in Magnetism in Metals, ed. D. F. McMorrow, J. Jensen and H. M. Rønnow, Det Kongelige Danske Videnskabernes Selskab, Bianco Lunos Bogtrykkeri A/S, Denmark, 1997, p. 291.
31. K. Janicka, J. P. Veley and E. Y. Tsymbal, J. Appl. Phys., 2008, 103, 07B508.
32. C. M. Fang, R. S. Koster, W.-F. Li and M. A. Van Huis, RSC Adv., 2014, 4, 7885.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4tc02222j

---