Hydrogenation of silicene with tensile strains

Abstract

Hydrogenation of silicene has been shown to be an efficient way to open the band gap of silicene and manipulate its electronic properties for application in electronic devices. However, the reaction energy barrier of silicene hydrogenation is quite high, which prevents the occurrence of this chemical reaction. Using density functional theory calculations, we propose an alternative approach to reduce the energy barrier, thus facilitating hydrogenation of silicene. Our results demonstrate that biaxial strain and uniaxial tensile strain along the armchair direction can reduce the energy barrier of dissociative H₂ adsorption on silicene significantly, and the barrier decreases as the strains increase. However, the biaxial strain has a better effect on the energy barrier reduction. It is found that the barrier reduces from 1.71 to 0.24 eV when the biaxial strain reaches the critical value of about 12%, above which the structure of silicene after hydrogenation would be destroyed. In this way, the reaction time for the hydrogenation of silicene can be reduced significantly from 8.06 × 10¹⁶ to 1.68 × 10⁻⁸ s. The mechanism of the effect of tensile strains can be understood through analysing the density of states of the system and atomic charge transfer during hydrogenation.

---

Introduction

Silicene, a two-dimensional honeycomb network of silicon atoms, has attracted lots of interest since it was first predicted in 1994.^1–10 Though silicene is the silicon analogue of graphene, the energetically favourable conformation of silicene has been confirmed to be a low buckled honeycomb structure, because in silicon, the sp³ hybridization is more stable than the sp² hybridization, which is converse to that in graphene.¹¹ By investigating the band structure of this buckled structure, it is found that, like graphene, there are linear dispersions at the Dirac points K and K′ of the hexagonal Brillouin zone, indicating the semimetallic or zero band gap semiconducting character of silicene.^12–15 This structure has been confirmed by density functional theory (DFT) studies¹⁶ and phonon dispersion calculations.¹⁷ Several other works have also confirmed that silicene is a zero band gap semiconductor.^18–20 Recently, single layer sheets of silicene have been obtained via chemical exfoliation²¹ and also successfully fabricated on Ag substrates.^22–25 As silicon has similar chemical properties to carbon, and properties of graphene can be controlled by hybridisation,^26–28 external electric fields,^29,30 doping,^31,32 chirality³³ and strain,^34,35 it is desirable to manipulate the properties of silicene for its future potential applications.

With these expectations and methods, various breakthroughs on silicene have been reported. For example, it is found that the band gaps of silicene adsorbed with F, Cl, Br and I undergo a non-monotonic change as the periodic number of the halogen element increases.²⁰ Through functionalization of silicene, particularly hydrogenation, it is found that the properties of silicene can be tuned by the hydrogenation ratio. For example, half hydrogenated freestanding silicene generates an indirect band gap (about 0.84 eV) and becomes a ferromagnetic semiconductor based on the generalized gradient approximation (GGA) calculation.¹⁶ A similar magnetic transition is also found in the hydrogenation of silicene on a substrate.³⁶ Furthermore, in fully hydrogenated silicene (silicane), a 2 eV indirect band gap is found, causing the silicane to be an insulator based on the local density approximation (LDA) calculation.³⁷ Therefore, by applying a proper hydrogenation ratio, the band structure of silicene is tuneable, which can enable the system to be metallic, semiconducting or insulating.^16,19,38

However, according to the study of binding energy on low buckled silicene based on DFT–GGA calculations,³⁹ the energy barrier of hydrogen atom adsorption in silicene is too high compared to that of gaseous hydrogen molecules. This indicates that the dissociative adsorption of hydrogen on silicene would be difficult due to the passive surface of silicene. The dissociation possibility can be understood by the energy barrier, which is defined as the energy difference between the reactant and the highest energy state along the minimum energy reaction path (transition state, TS). With a high energy barrier, reactions cannot proceed effectively and may not even happen.^40,41 Recently, it was reported that strain can significantly modify the atomic structures, binding energies and mechanical and electronic properties of pure and hydrogenated graphene.^42–45 For the hydrogenation of graphene, the tensile strain has been found to effectively lower the out-plane diffusion of H atoms, which makes diffusion possible at room temperature.⁴² Furthermore, by applying strain to the graphene, the barrier of the dissociation of molecular hydrogen greatly decreases and the process of hydrogenation changes from endothermic to exothermic.⁴³ In addition, silicene can be converted to a semimetal by a tensile strain of 7% and turned into a conventional metal under a larger homogeneous strain.⁴⁴ Therefore, strain is expected to be an effective way to manipulate the electronic properties and the energy barrier for the hydrogenation of silicene.

In this work, in order to reduce the energy barrier of silicene hydrogenation, biaxial strain and uniaxial tensile strains along both zigzag and armchair directions are applied and the corresponding effects on hydrogenation are investigated through DFT calculations. The hydrogenation of silicene can be understood through the calculation of the reaction pathways under the strains. The mechanism of the energy barrier reduction induced by the tensile strains can be analysed through partial density of states (PDOS) and atomic charge transfer between H₂ and silicene. In addition, the effect of hydrogenation on the electronic properties of the silicene with strains is also discussed.

Simulation methodology

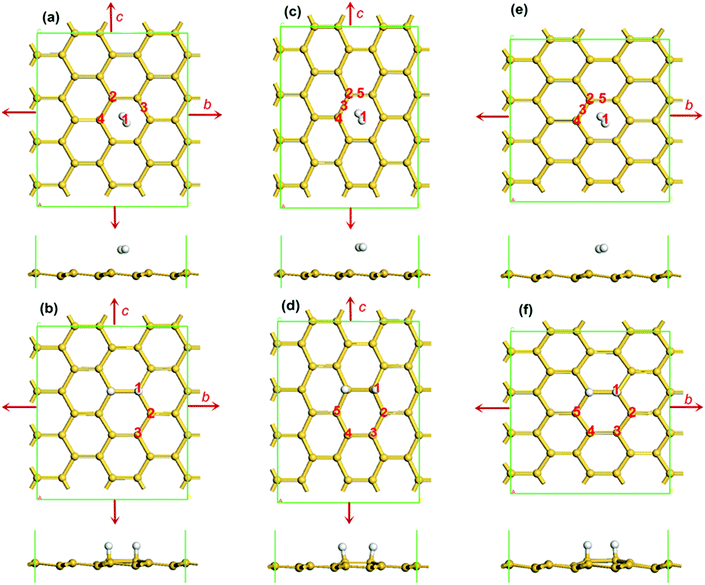
The spin-polarised DFT calculations were performed using the DMol³ module in the Materials Studio package. LDA with the Perdew and Wang functional was employed as the exchange–correlation functional. To consider the effect of the van der Waals interface, the OBS method for DFT-D correction was used. A double numerical plus polarization (DNP) was used as the basis set. The convergence tolerance of energy was taken as 10⁻⁵ Ha (1 Ha = 27.21 eV), with a maximum allowed force and displacement of 0.002 Ha and 0.005 Å respectively. Linear synchronous transit/quadratic synchronous transit (LST/QST)¹ and nudged elastic band (NEB)⁴⁶ tools in DMol³ were also employed to investigate the minimum energy pathway for dissociative adsorption of hydrogen on silicene. Three-dimensional periodic boundary conditions were used in the simulation. A 4 × 4 × 1 supercell was adopted for all the calculations with a vacuum width of 18 Å above the layer to minimize the interlayer interaction as presented in Fig. 1. The calculations were performed with a 6 × 6 × 1 K-point set, and all atoms were relaxed to their most stable geometry. To apply biaxial or uniaxial tensile strains to silicene, the lattice parameter of both b and c or only b or c was increased at different ratios, as indicated by the arrows in Fig. 1. Note that when we did the structure relaxation under a uniaxial tensile strain, the lattices along the direction of the applied tension strain and the direction normal to the silicene were fixed, while the lattice of the other direction was allowed to relax. For example along the zigzag direction as shown in Fig. 1(c), the lattice constants along c and the direction normal to the silicene surface were fixed, while the lattice constant along b was allowed to relax.

Fig. 1 The initial and final structures of a H₂ molecule on silicene before and after dissociative adsorption with biaxial strain [(a) and (b)], uniaxial strain along the zigzag [(c) and (d)] and along the armchair [(e) and (f)] directions. The possible positions for a H₂ molecule physically adsorbed on silicene or the possible positions of the second H atom when 2H atoms are chemically adsorbed on silicene are indicated by numbers. The direction of the tensile strain is denoted by arrows. The numbers in the top panel of the figure denote the different possible adsorption positions of the H₂ molecule, while the numbers in the bottom panel of the figure denote the different possible bonding positions of the second H atom.

For the adsorption of one H₂ molecule on silicene, the adsorption energy E_ad is defined as:

E_ad = E_H2+silicene − (E_silicene + E_H2) (1a)

where E_H2+silicene, E_silicene, and E_H2 denote the total energies of silicene with a H₂ molecule adsorbed, bare silicene, and a H₂ molecule respectively. After hydrogenation, the binding energy of H atoms on silicene E_Si–H can be determined as:

E_Si–H = E_2H+silicene − (E_silicene + 2E_H) (1b)

where subscripts 2H + silicene and H denote the silicene with 2H atoms chemically adsorbed and a free H atom respectively.

Results and discussion

Before hydrogenation, the H₂ molecule is weakly physically adsorbed on silicene. Under the biaxial tensile strain, silicene expands symmetrically and there are 4 possible adsorption positions for the H₂ molecule as indicated in Fig. 1(a): positions 2 and 4 on the top of a silicon atom in the higher or lower plane of the buckled structure, position 3 over the middle of a Si–Si bond and position 1 at the center of a Si ring. In order to determine the most stable structure, we calculated the energies of all four possible positions under different strains. Note that the strain limit for hydrogenated silicene was 12% under biaxial strain, 14% under uniaxial strain along the zigzag direction and 13% under uniaxial strain along the armchair direction; if the strain were further increased, the Si–Si bond of the two silicon atoms which are bonded with the hydrogen atoms or other Si–Si bonds would break, which should be avoided in applications. The results also agree with a reported result showing that the structure of buckled silicene is stable when the tensile strain is smaller than 14%.⁴⁷ Other work also confirms the stability of silicene under similar strains.⁴⁸ From phonon dispersions calculations,^49,50 it is also known that silicene is stable under strains smaller than 14%. The results in Table 1 show that under different biaxial tensile strains, the total energy and adsorption energy of a H₂ molecule on silicene at positions 2–4 are almost the same but those at position 1 are much lower, especially the adsorption energy. Thus, it is favourable for the H₂ molecule to adsorb at the hollow site of the Si ring regardless of the intensity of the strain. This is easy to understand because the silicene expands symmetrically under the biaxial tensile strain. This configuration is considered to be the reactant for the silicene hydrogenation reaction. Note that the distance between the H₂ molecule and the silicene layer D_H–Si at position 1 is always shorter than that in the other three positions at a given strain, due to the stronger adsorption energy.

Table 1 The total energy, adsorption energy, and the distance between the H₂ molecule and the silicene layer D_H–Si in all the possible structures before hydrogenation under different biaxial tensile strains. Total energy is shown relative to the energy of H₂ adsorption at position 1 of silicene without strain

Strain	Total energy (eV)				Adsorption energy (eV)				D H–Si (Å)
	1	2	3	4	1	2	3	4	1	2	3	4
0	0	0.09	0.08	0.08	−0.29	−0.20	−0.21	−0.21	2.49	3.04	3.06	2.98
5%	3.18	3.29	3.28	3.28	−0.30	−0.19	−0.20	−0.20	2.44	3.22	3.25	3.11
10%	10.86	10.96	10.94	10.96	−0.28	−0.18	−0.20	−0.18	2.34	3.18	3.10	3.10
12%	14.15	14.26	14.24	14.25	−0.55	−0.44	−0.46	−0.45	2.31	3.26	3.13	3.12

---

Silicene under uniaxial strains along both zigzag and armchair directions is studied in a similar way as shown in Fig. 1(c) and (e), respectively. Since the structure of silicene is not symmetric any more due to the lattice deformation under a uniaxial strain, there are more possible positions for hydrogen molecule adsorption, such as on the top of a silicon atom either on the upper (position 2) or lower layer (position 4), on the top of a Si–Si bond (there are two types of Si–Si bonds due to the deformation, thus two possible positions: positions 3 and 5) and at the hollow site of a Si ring (position 1). The results of system total energy and adsorption energy of a H₂ molecule on silicene under different uniaxial tensile strains along the zigzag and armchair directions are shown in Tables 2 and 3, respectively.

Table 2 The total energy, adsorption energy, and the distance between the H₂ molecule and the silicene layer D_H–Si in the five possible structures before hydrogenation under different uniaxial tensile strains along the zigzag direction. Total energy is shown relative to the energy of H₂ adsorption at position 1 of silicene without strain

Strain	Total energy (eV)					Adsorption energy (eV)					D H–Si (Å)
	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
0	0	0.09	0.08	0.08	0.08	−0.29	−0.20	−0.21	−0.21	−0.21	2.49	3.04	3.06	2.98	3.03
5%	1.72	1.80	1.84	1.80	1.80	−0.28	−0.20	−0.19	−0.20	−0.20	2.52	3.19	3.15	3.08	3.18
10%	4.35	4.45	4.44	4.45	4.45	−0.28	−0.18	−0.19	−0.19	−0.19	2.46	3.19	3.19	3.08	3.18
14%	7.57	7.66	7.64	7.64	7.64	−0.27	−0.18	−0.20	−0.20	−0.19	2.53	3.26	3.24	3.19	3.22

---

Table 3 The total energy, adsorption energy, and the distance between the H₂ molecule and the silicene layer D_H–Si in the five possible structures before hydrogenation under different uniaxial tensile strains along the armchair direction. Total energy is shown relative to the energy of H₂ adsorption at position 1 of silicene without strain

Strain	Total energy (eV)					Adsorption energy (eV)					D H–Si (Å)
	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
0	0	0.09	0.08	0.08	0.08	−0.29	−0.20	−0.21	−0.21	−0.21	2.49	3.04	3.06	2.98	3.03
5%	1.32	1.42	1.41	1.41	1.40	−0.29	−0.19	−0.20	−0.20	−0.20	2.52	3.14	3.13	3.08	3.08
10%	4.63	4.73	4.72	4.73	4.72	−0.29	−0.19	−0.19	−0.19	−0.20	2.40	3.23	3.19	3.12	3.14
13%	7.33	7.43	7.42	7.42	7.41	−0.29	−0.18	−0.19	−0.19	−0.20	2.36	3.32	3.18	3.15	3.15

---

It is shown that the structure with the hydrogen molecule at the hollow site (position 1) of a Si ring is the most stable structure that has the lowest total energy, shortest D_H–Si and the strongest binding energy under any strain. Although the symmetry of silicene is destroyed under uniaxial strain, the H₂ molecule still prefers to adsorb at the hollow site of a Si ring (position 1) regardless of the intensity of strain, which is similar to the result obtained under biaxial strain. In the subsequent dissociative adsorption of hydrogen, the possible positions under biaxial tensile strains for the two adsorbed hydrogen atoms are shown in Fig. 1(b). All the possible configurations are calculated and the corresponding results are listed in Table 4. It is found that under biaxial tensile strain, as shown in Fig. 1(b), the two H atoms bind with Si atoms in the form of covalent bonds, and there are three possible configurations. The structure with the ortho position of the two hydrogen atoms, i.e. the second H atom at position 1, has much the lowest energy and strongest binding energy under any strain. Therefore, the possible reaction pathways for dissociative adsorption of hydrogen on silicene, i.e. from the reactant structure with a H₂ molecule physically adsorbed at position 1 to the product structure with the second H atom binding at position 1, is calculated. Fig. 2 shows the minimum reaction pathway of a H₂ molecule's dissociative adsorption on silicene without strain as an example of how to determine the dissociative energy barrier and obtain other relevant information. The structures as shown in Fig. 1(a) and (b) are reactant and product, respectively. After LST/QST and NBE calculations, the energy minimum dissociative adsorption pathway is shown in Fig. 2. From this figure, the reaction energy barrier E_bar = E_TS − E_IS is 1.71 eV. Note that before the transition state, TS, the H₂ molecule adjusts its position over silicene and then the H₂ molecule is dissociated into two free H atoms with one of the H atoms binding with a Si atom nearby on the top layer while the other H atom remains free, as shown in the TS in Fig. 2. In addition, the Si atom that is going to bind with the free H atom has shifted upwards, but the two H atoms are still close to each other maintaining a strong interaction, which prevents the binding between the free H atom and the Si atom. In the final state, FS, the distance between the two H atoms increases, and thus the other free H atom also binds with the nearest Si atom as shown in Fig. 2. Therefore, this reaction can be separated into two steps: the H₂ molecule is first dissociated into two H atoms, and then one of them binds with a Si atom nearby while the other one is free; in the second step, the two H atoms adjust their positions and the other H atom also binds with its nearest Si atom. Although this reaction releases energy of about 0.21 eV in total (E_FS − E_IS), there is a high potential energy barrier of 1.71 eV for the first step. Consequently, the first step becomes a rate-limiting step because of the large amount of energy needed.

Table 4 The total energy and binding energy of all the possible structures after hydrogenation under biaxial tensile strain. The energy barrier and reaction energy of final structure 1 are listed. Total energy is shown relative to the energy of the structure with the second H atom adsorbed at position 1 of silicene without strain

Strain	Total energy (eV)			Binding energy (eV)			Energy barrier (eV)	Reaction energy (eV)
	1	2	3	1	2	3	1	1
0	0	0.55	0.12	−5.50	−4.94	−5.37	1.71	−0.21
5%	3.04	3.63	3.12	−5.65	−5.06	−5.57	1.49	−0.35
10%	10.20	10.55	10.34	−6.15	−5.80	−6.00	1.06	−0.74
12%	13.44	13.66	13.50	−6.46	−6.24	−6.40	0.24	−0.85

---

Fig. 2 The reaction pathway of the dissociative adsorption of a H₂ molecule on silicene without strain from the structure as shown in Fig. 1(a) to the structure as shown in Fig. 1(b). The energy of reactant IS is taken to be zero. IS, TS and FS denote initial structure, transition state, and final structure, respectively. E_bar is the energy barrier and E_R is the reaction energy, both expressed in eV.

It is reported that a reaction is difficult at room temperature if the reaction energy barrier is higher than 0.75 eV.⁴⁶ Due to the high energy barrier of 1.71 eV for this hydrogenation process, it is considered to be difficult for the reaction to proceed at room temperature; a high reaction temperature or other external energy source is required. Therefore, it is desirable to reduce the hydrogenation energy barrier. Applying tensile strain is an alternative way to alter the electronic distribution of silicene,⁴⁷ thus changing its chemical potential. As mentioned before, it has been proved that strain can modify the atomic structures and the electronic properties of silicene.⁴⁷ In addition, the barrier for the dissociation of molecular hydrogen on graphene has been greatly reduced by applying strain to graphene,⁴³ which is the current challenge for the hydrogenation of silicene. Therefore, tensile strain is considered here to investigate the possibility of reducing the hydrogenation energy barrier of silicene.

Using the same method, the dissociative adsorption of hydrogen on silicene under different biaxial tensile strains is calculated. The product with the second H atom at position 1 is considered, and the results are listed in Table 4. It is clearly shown that the energy barrier reduces when a biaxial tensile strain is present. The barrier decreases as the strain increases. When reaching the maximum possible strain of 12%, the barrier is at its minimum of 0.24 eV. Under uniaxial strains, there are five possible configurations for the product as shown in Fig. 1(d) and (f) where five possible binding positions for the second H atom are indicated. After geometry optimization, the results are shown in Tables 5 and 6, respectively. Similar to the case of biaxial strain, it is found that the hydrogenated silicene with two hydrogen atoms in structures 1, 3 and 5 in Fig. 1(d) and (f) have similar and lower total energy with stronger binding energy under both types of uniaxial strain, indicating that all three positions are possible after the H₂ molecule's dissociative adsorption. Therefore, all three reaction pathways from the structure in Fig. 1(c) to the structure in Fig. 1(d) with the second H atom at each of positions 1, 3 and 5, are considered. Similarly, the three reaction pathways from the structure in Fig. 1(e) to the structure in Fig. 1(f) with the second H atom at each of positions 1, 3 and 5 are considered. The results of the corresponding reaction energy barriers and reaction energies are listed in Tables 5 and 6, respectively. It is found that the energy barrier is always the lowest for the reaction in which the second H atom binds to position 1 under different uniaxial strains, which indicates that this reaction is preferred. Therefore, the pathway of dissociative adsorption of hydrogen on silicene under these two types of uniaxial tensile strains from the initial structure with the H₂ molecule adsorbed on the hollow site of a Si ring to the final structure with the second H atom at position 1 is calculated and discussed below.

Table 5 The total energy and binding energy of all the possible structures after hydrogenation under uniaxial tensile strain along the zigzag direction. The energy barrier and reaction energy to produce final structures 1, 3 and 5 are also listed. Total energy is shown relative to the energy of the structure with the second H atom adsorbed at position 1 of silicene without strain

Strain	Total energy (eV)					Binding energy (eV)					Energy barrier (eV)			Reaction energy (eV)
	1	2	3	4	5	1	2	3	4	5	1	3	5	1	3	5
0	0	0.55	0.12	0.57	0.19	−5.50	−4.94	−5.38	−4.92	−5.31	1.71	1.82	1.98	−0.21	−0.06	−0.24
5%	1.59	1.15	1.56	1.16	1.51	−5.62	5.18	−5.59	−5.19	−5.55	1.55	1.66	1.66	−0.29	−0.17	−0.32
10%	4.07	4.49	4.15	4.51	4.02	−5.78	−5.35	−5.70	−5.34	−5.82	1.40	1.41	1.48	−0.51	−0.36	−0.46
14%	6.61	7.25	7.02	7.22	7.02	−6.44	−5.80	−6.02	−5.83	−6.03	1.26	1.38	1.35	−0.70	−0.57	−0.60

---

Table 6 The total energy and binding energy of all the possible structures after hydrogenation under uniaxial tensile strain along the armchair direction. The energy barrier and reaction energy to produce final structures 1, 3 and 5 are also listed. Total energy is shown relative to the energy of the structure with the second H atom adsorbed at position 1 of silicene without strain

Strain	Total energy (eV)					Binding energy (eV)					Energy barrier (eV)			Reaction energy (eV)
	1	2	3	4	5	1	2	3	4	5	1	3	5	1	3	5
0	0	0.55	0.12	0.57	0.19	−5.50	−4.94	−5.38	−4.92	−5.31	1.71	1.82	1.98	−0.21	−0.06	−0.24
5%	1.20	1.84	1.38	1.83	1.30	−5.52	−4.97	−5.43	−4.98	−5.62	1.64	1.73	1.86	−0.22	−0.11	−0.28
10%	4.46	5.04	4.53	5.04	4.36	−5.66	−5.08	−5.59	−5.08	−5.76	1.38	1.52	1.67	−0.36	−0.28	−0.33
13%	7.01	7.60	7.10	7.43	6.93	−5.81	−5.23	−5.72	−5.38	−5.88	0.26	0.96	1.31	−0.49	0.40	−0.43

---

To better understand the effect of the tensile strain, the hydrogenation pathways of silicene under different strains are shown in Fig. 3. Fig. 3(a)–(c) represent the pathways under biaxial tensile strain along the energy minimum pathway to structure 1 in Fig. 1(b). Fig. 3(d)–(f) are for the cases under uniaxial tensile strain in the zigzag direction along the energy minimum pathway to structure 1 in Fig. 1(d) and Fig. 3(g)–(i) demonstrate the pathways under uniaxial tensile strain in the armchair direction along the energy minimum pathway to structure 1. As shown in the figure, the configurations before and after hydrogenation are constructed as expected under the strains. In the transition state (TS), the H₂ molecule is dissociated into two separate H atoms (except in Fig. 3(c) and (i) with molecular H₂). There are no covalent bonds yet between the two H atoms and silicene, except in Fig. 3(a), (g) and (h), where one of the H atoms binds with a Si atom in the upper layer of silicene similar to the case without strain in Fig. 2. This can be understood by analysing the bond length change of Si–Si and H–H bonds. It is known that the length of the Si–Si bond in silicene increases as the strain increases. Under a strain of 10%, the Si–Si bond can become weak enough to allow the formation of a Si–H bond over the silicene layer. On the other hand, when the binding of the Si–Si bonds in silicene becomes weaker under the strain, the interaction between the H atoms can become stronger, which is indicated by a shorter distance between the two H atoms D_H–H. It is found that D_H–H decreases when strain increases. This is also consistent with the general rule that the interaction in a molecule is stronger when the binding in a substrate becomes weaker.^29,48 The stronger H–H interaction prevents the covalent bond formation between H and Si atoms under the limit strain although the Si–Si bond is weak enough in this case. On the other hand, although the Si–Si bond is still strong in the case without strain, the H–H bond is at its weakest, which can also induce the formation of a Si–H bond at the transition state as shown in Fig. 2. Therefore, the Si–H bond at the transition state forms only when a balance is achieved between the interactions of Si–Si and H–H bonds. After the transition state, the distance between the two H atoms increases and the corresponding interaction decreases gradually, then the two H atoms bind with the corresponding Si atoms as shown in the FS in Fig. 3.

Fig. 3 The pathway of dissociative adsorption of a H₂ molecule on silicene with increasing biaxial tensile strain [(a)–(c)], uniaxial tensile strain along the zigzag direction [(d)–(f)] and along the armchair direction [(g)–(i)]. The transition state and energy minimum states 1 are represented by TS and 1 respectively. The energy of IS is set to be zero. FS is the final structure. The E_bar and E_R are the energy barrier and reaction energy respectively and their units are eV.

The corresponding energy barrier and reaction energy for a H₂ molecule's dissociative adsorption on silicene under different strains are also shown in Fig. 3. It is found that the energy barrier decreases with increasing strain for all three types of strain, while the corresponding reaction energy becomes more negative. Therefore, the H₂ molecule dissociates more easily under the strains, thus facilitating the hydrogenation of silicene. In order to better display the effects of strains on the hydrogenation of silicene, the energy barrier of a H₂ molecule's dissociative adsorption on silicene under different strains is shown in Fig. 4. It is clearly shown that both the biaxial and armchair direction strains can reduce the energy barrier of hydrogenation remarkably, but the energy barrier decreases the most efficiently under biaxial strain. Strain along the zigzag direction also has effects on the barrier but it is not very effective compared to the other two types of strain. When the strain is smaller than 8%, the two uniaxial strains have similar effects on the reduction of the energy barrier. If the strains are increased above 8%, the energy barrier of the system with the strain along the armchair direction becomes much lower than the other uniaxial strain and reaches the same low barrier as the system under biaxial strain. In other words, applying biaxial strain and uniaxial strain along the armchair direction to silicene can reduce the hydrogenation energy barrier more efficiently. When the strain increases to 12% or 13%, the energy barrier is reduced significantly from 1.71 eV to about 0.24 eV, which can facilitate hydrogenation of silicene significantly.

Fig. 4 Energy barrier of the dissociative adsorption of a H₂ molecule on silicene under increasing tensile strain. The black, red and blue lines stand for the results under biaxial tensile strain, uniaxial tensile strain along the armchair direction and uniaxial tensile strain along the zigzag direction, respectively.

To better understand the effect of energy barrier reduction on the reaction time, eqn (2) is used to predict the reaction time τ at room temperature,⁵¹

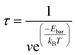where v is of the order of 10¹² Hz, k_B is the Boltzmann constant and T = 298.15 K. Without strain, τ = 8.06 × 10¹⁶ s, while with 12% biaxial strain τ = 1.68 × 10⁻⁸ s. As one can see, there is a huge difference on the reaction time between the cases with and without strain.

The mechanism of the effect of tensile strain on the energy barrier of silicene hydrogenation can be understood through analysing PDOS of the configuration at the TS under different strains as shown in Fig. 5. The bands of the s orbitals of the two H atoms and the p orbitals of the two corresponding Si atoms which bind with the two H atoms at the TS are provided. It is clear that the Si–H interaction band of the s orbital of H and the p orbital of Si near the Fermi level is significantly depressed under both biaxial strain and uniaxial tensile strain along the armchair direction as the strains increase. It is known that a weaker interaction near the Fermi level results in a lower energy barrier.⁵² This could also explain why strain along the zigzag direction cannot reduce the barrier obviously because the interaction near the Fermi level is depressed only slightly. In addition, comparing the PDOS under biaxial and uniaxial strain along the armchair direction, the interaction between Si and H atoms at the TS for the case of biaxial strain drops more obviously. Therefore, the energy barrier decreases as the strains increase and the effect of the biaxial strain is more obvious, which is consistent with the results in Fig. 3 and 4.

Fig. 5 The PDOS of the two H atoms and the two corresponding Si atoms at the TS without strain (a), under increasing biaxial tensile strain [(b)–(d)], under uniaxial tensile strain along the zigzag direction [(e)–(g)] and under uniaxial tensile strain along the armchair direction [(h)–(j)]. The black curves are the PDOS of the two silicon atoms and the blue curves indicate that of the two hydrogen atoms. The red dashed lines stand for the Fermi level.

The reduction of the energy barrier can also be understood through analysing the charge transfer between H atoms and silicene. Without strain, the atomic charges of one H atom and its corresponding Si atom in the reactant are −0.029 and 0.013e, respectively. After dissociative adsorption, the charges are −0.053 and 0.054e, respectively. It can be seen that the Si atoms are positively charged, while the H atoms are negatively charged. In other words, the electrons are transferred from Si to H atoms during hydrogenation. With all three types of strain, the charges of H and Si atoms in the reactant are almost the same as in the case of no strain, i.e. strain does not affect the interaction between H and Si much. This also agrees with the results in Tables 1–3, where the adsorption energy does not change much under strains. However, after dissociative adsorption, the atomic charges change remarkably. Under the maximum possible strains, the charge of the H atom decreases from −0.053e to about −0.073 (biaxial), −0.064e (armchair) and −0.057e (zigzag) and the corresponding Si atom is positively charged with about 0.07e (biaxial), 0.065e (armchair) and 0.057e (zigzag) charges. Therefore, more electrons are transferred from the Si atoms to the H atoms under the biaxial strain, which would lead to easier formation of Si–H bonds during hydrogenation and thus contribute to the reduction of the energy barrier.

It is known that hydrogenation of silicene is an efficient way to open and tune the band gap of silicene for its potential applications in electronic devices.^16,19,38 To understand the effect of the strain and hydrogenation on the electronic properties, the band structure of silicene before and after hydrogenation with different biaxial strains is calculated as an example because the biaxial strain has the best effect in reducing the hydrogenation energy barrier. The results without strain and under 12% biaxial strain are shown in Fig. 6. Note that the band structure was calculated using the CASTEP package using the HSE06 hybrid functional due to its more accurate band structure result. It can be seen from Fig. 6(a) that, similar to graphene, silicene is a zero band gap material and the physical adsorption of H₂ does not change the pattern of the band structure near the Dirac point. After dissociative adsorption of hydrogen, the band gap opens to ∼0.34 eV as shown in Fig. 6(b). This means that partial hydrogenation could also open the band gap of silicene due to the newly formed Si–H bonds. This is also consistent with the reported result that the band gap of silicene depends on the ratio of hydrogenation, where half hydrogenated silicene turns out to be a semiconductor with a band gap about of 0.84 eV (ref. 26) and fully hydrogenated silicene, named silicane, generates about a 2 eV band gap.³⁷Fig. 6(c) shows that with 12% biaxial strain, the band gap of silicene at the Dirac point does not open with π and π* bands contacting at the K-point under the biaxial strain, and that the Fermi level shifts downwards. Thus, the biaxial strain cannot open the band gap of silicene due to the remaining symmetry. This result is also consistent with a previous report.⁴⁴ However, silicene transits from a semimetal into a metal due to the presence of bands at the Fermi level, which is also consistent with the reported result that this semimetal–metal transition occurs when the biaxial strain is larger than 7%.⁴⁷ It can be understood because the buckled structure becomes flatter under greater strain, which changes the orientation of the Si–Si bonds. For hydrogenated silicene, at the Dirac point, the band gap is still open under the strain, but the gap decreases to ∼0.12 eV. In addition, the Fermi level shifts downwards, which also induces the semimetal–metal transition. Therefore, the application of tensile strain is an effective method for tuning the properties of silicene through hydrogenation. However, the stability of hydrogen on silicene should also be understood through investigating the hydrogen diffusion on silicene, similar to the reported works, where hydrogenation and diffusion on graphene^42,53 and on two-dimensional MoS₂ (ref. 54) have been reported. Due to the complexity of this work, such as considering the effects of strains, defects and the external electric field on hydrogen diffusion, we will show the corresponding results in another work.

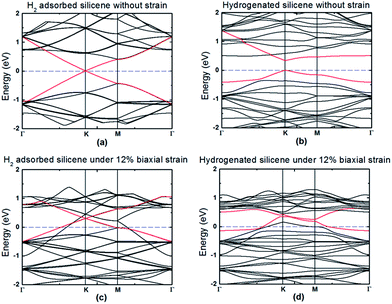Fig. 6 Band structures of pure and hydrogenated silicene without strain [(a) and (b)] and under 12% biaxial strain [(c) and (d)]. The red lines are the bands near the Dirac point.

Conclusion

The dissociative adsorption of a H₂ molecule on silicene with different tensile strains is investigated by DFT calculations. It is found that the energy barrier of dissociative adsorption of a H₂ molecule on silicene can be reduced significantly by applying biaxial tensile strain or uniaxial tensile strain along the armchair direction, while the biaxial strain has the better effect at reducing the energy barrier. The energy barrier also decreases under uniaxial strain along the zigzag direction, but the effect is not so obvious. Under 12% biaxial strain, the energy barrier drops from 1.71 eV to about 0.24 eV, which can greatly reduce the reaction time from 8.06 × 10¹⁶ s to 1.68 × 10⁻⁸ s. Thus, the hydrogenation of silicene can be facilitated efficiently under the strains. Therefore, we propose an alternative method for hydrogenation of silicene, which is essential to tune its electronic properties for application in electronic devices.

Acknowledgements

We acknowledge the financial support from the Chancellor's Research Fellowship Program of the University of Technology, Sydney. This research was also supported by the National Computational Infrastructure (NCI) through the merit allocation scheme and used NCI resources and facilities in Canberra, Australia.

Notes and references

1. K. Takeda and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14916.
2. G. G. Buzman-Verri and L. C. Lew Yan Voon, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075131.
3. B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109.
4. S. Q. Wang, Phys. Chem. Chem. Phys., 2011, 13, 11929.
5. C. C. Liu, W. X. Feng and Y. G. Yao, Phys. Rev. Lett., 2011, 107, 076802.
6. G. G. Buzman-Verri and L. C. Lew Yan Voon, J. Phys.: Condens. Matter, 2011, 23, 145502.
7. X. Q. Wang, H. D. Li and J. T. Wang, Phys. Chem. Chem. Phys., 2012, 14, 3031.
8. C. W. Zhang and S. S. Yan, J. Phys. Chem. C, 2012, 116, 4163.
9. M. Houssa, G. Pourtois, V. V. Afanasev and A. Stesmans, Appl. Phys. Lett., 2010, 97, 112106.
10. Y. C. Cheng, Z. Y. Zhu and U. Schwingenschlogl, Europhys. Lett., 2011, 95, 17005.
11. U. Rhlisberger, W. Andreoni and M. Parrinello, Phys. Rev. Lett., 1994, 72, 665.
12. H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
13. M. F. Cabrera, A. Munoz, W. Windl, A. A. Demkov and O. F. Sankey, Modell. Simul. Mater. Sci. Eng., 1999, 7, 929.
14. L. Chen, C.-C. Liu, B. Feng, X. He, P. Cheng, Z. Ding, S. Meng, Y. Yao and K. Wu, Phys. Rev. Lett., 2012, 109, 056804.
15. A. O. Hare, F. V. Kusmartsev and K. I. Kugel, Nano Lett., 2012, 12, 1045.
16. P. Zhang, X. D. Li, C. H. Hu, S. Q. Wu and Z. Z. Zhu, Phys. Lett. A, 2012, 376, 1230.
17. J. S. McEwen, P. Gaspard, F. Mittendorfer, T. Visart de Bocarmé and N. Kruse, Chem. Phys. Lett., 2008, 452, 133.
18. M. Houssa, E. Scalise, K. Sankaran, G. Pourtois, V. V. Afanasev and A. Stesmans, Appl. Phys. Lett., 2011, 98, 223107.
19. T. H. Osborn, A. A. Farajian, O. V. Pupysheva, R. S. Aga and L. C. Lew Yan Voon, Chem. Phys. Lett., 2011, 511, 101.
20. N. Gao, W. T. Zheng and Q. Jiang, Phys. Chem. Chem. Phys., 2012, 14, 257.
21. H. Nakano, T. Mitsuoka, M. Harada, K. Horibuchi, H. Nozaki, N. Takahashi, T. Nonaka, Y. Seno and H. Nakamura, Angew. Chem., Int. Ed., 2006, 118, 6451.
22. C. Leandri, G. Le Lay, B. Aufray, C. Girardeaux, J. Avila, M. E. Davila, M. C. Asensio, C. Ottaviani and A. Cricenti, Surf. Sci., 2005, 574, L9.
23. B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet and B. Aufray, Appl. Phys. Lett., 2010, 97, 223109.
24. B. Aufray, A. Vizzini, S. Oughaddou, H. Leandri, C. Ealet and G. Le Lay, Appl. Phys. Lett., 2010, 96, 183102.
25. G. Le Lay, B. Aufray, C. Landri, H. Oughaddou, J. P. Biberian, P. De Padova, M. E. Dvila, B. Ealet and A. Kara, Appl. Surf. Sci., 2009, 256, 524.
26. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610.
27. S. Ryu, M. Y. Han, J. Maultzsch, T. F. Heinz, P. Kim, M. L. Steigerwald and L. E. Brus, Nano Lett., 2008, 8, 4597.
28. Z. Q. Luo, T. Yu, K. J. Kim, Z. H. Ni, Y. M. You, S. Lim, Z. X. Shen, S. Z. Wang and J. Y. Lin, ACS Nano, 2009, 3, 1781.
29. Z. M. Ao, W. T. Zheng and Q. Jiang, Nanotechnology, 2008, 19, 275710.
30. Z. M. Ao and F. M. Peeters, Appl. Phys. Lett., 2010, 96, 253106.
31. T. B. Martins, R. H. Miwa, A. J. R. da Silva and A. Fazzio, Phys. Rev. Lett., 2007, 98, 196803.
32. Z. M. Ao, S. Li and Q. Jiang, Phys. Chem. Chem. Phys., 2009, 11, 1683.
33. M. I. Katsnelson, K. S. Novoselov and A. K. Geim, Nat. Phys., 2006, 2, 620.
34. G. Gui, J. Li and J. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075435.
35. L. Sun, Q. Li, H. Ren, H. Su, Q. W. Shi and J. Yang, J. Chem. Phys., 2008, 129, 074704.
36. F. B. Zheng and C. W. Zhang, Nanoscale Res. Lett., 2012, 7, 422.
37. L. C. Lew Yan Voon, E. Sandberg, R. S. Aga and A. A. Farajian, Appl. Phys. Lett., 2010, 97, 163114.
38. W. Wu, Z. M. Ao, T. Wang, C. Li and S. Li, Phys. Chem. Chem. Phys., 2014, 16, 16588.
39. A. Kara, H. Enriquez, A. P. Seitsonen, L. C. Lew Yan Voon, S. Vizzini, B. Aufray and H. Oughaddou, Surf. Sci. Rep., 2012, 67, 1.
40. P. R. Pereda and N. Takeuchi, J. Chem. Phys., 2013, 138, 194702.
41. N. Takeuchi and A. Selloni, J. Phys. Chem. B, 2005, 109, 11967.
42. M. Yang, A. Nurbawono, C. Zhang, R. Wu, Y. Feng and Ariando, AIP Adv., 2011, 1, 032109.
43. H. Mckay, D. J. Wales, S. J. Jenkins, J. A. Verges and P. L. de Andres, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075425.
44. R. Qin, C. H. Wang, W. Zhu and Y. Zhang, AIP Adv., 2012, 2, 022159.
45. C. Shang and Z. P. Liu, J. Am. Chem. Soc., 2011, 133, 9938.
46. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978.
47. G. Liu, M. S. Wu, C. Y. Ouyang and B. Xu, EPL, 2012, 99, 17010.
48. T. Aizawa, R. Souda, S. Otani, Y. Ishizawa and C. Oshima, Phys. Rev. Lett., 1990, 64, 768.
49. B. Wang, J. Wu, X. Gu, H. Yin, Y. Wei, R. Yang and M. Dresselhaus, Appl. Phys. Lett., 2014, 104, 081902.
50. C. Yang, Z. Yu, P. Lu, Y. Liu, H. Ye and T. Gao, Comput. Mater. Sci., 2014, 95, 420.
51. Q. G. Jiang, Z. M. Ao, S. Li and Z. Wen, RSC Adv., 2014, 4, 20290.
52. Z. M. Ao and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205406.
53. Z. M. Ao, A. D. Hernández-Nieves, F. M. Peeters and S. Li, Phys. Chem. Chem. Phys., 2012, 14, 1463.
54. Y. Cai, Z. Bai, H. Pan, Y. P. Feng, B. I. Yakobson and Y. W. W. Zhang, Nanoscale, 2014, 6, 1691.

---