Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Highly pseudocapacitive Nb-doped TiO2 high power anodes for lithium-ion batteries†
Mechthild
Lübke
ab,
Juhun
Shin
a,
Peter
Marchand
a,
Dan
Brett
c,
Paul
Shearing
c,
Zhaolin
Liu
b and
Jawwad A.
Darr
*a
aChristopher Ingold Laboratories, Department of Chemistry, University College London, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: j.a.darr@ucl.ac.uk
bInstitute of Materials Research and Engineering, Agency for Science, Technology and Research (A*STAR), 3 Research Link, Singapore 117602, Singapore
cDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK
First published on 1st October 2015
Abstract
Nb-doped TiO2 (anatase) nanoparticles were synthesized using a continuous hydrothermal flow synthesis reactor using a supercritical water flow as a reagent and crystallizing medium. The as-prepared nano-powders with ca. 25 at% Nb5+ (<6 nm diameter) were used as possible anodes for lithium-ion batteries without any further heat-treatment. Cyclic voltammetry and galvanostatic charge/discharge cycling tests were performed in the range of 1.2 to 3.0 V vs. Li/Li+. The Nb-doped TiO2 samples showed superior capacity retention at high current rates compared to the corresponding undoped nano-TiO2. The superior performance of the doped samples (at specific currents up to 15 A g−1) was attributed to higher electronic conductivity and a greater charge storage contribution from surface effects like pseudocapacitance (Faradaic processes) as well as Helmholtz double layer charge storage.
Introduction
Lithium-ion batteries are widely used as the main power source for portable electronics such as mobile phones and handheld devices. Developments in consumer electronics and the need to reduce CO2 emissions in cities have led to interest in the use of Li-ion batteries in electric vehicles.1 The typical design of a Li-ion battery consists of a Li-ion containing cathode (e.g. lithium iron phosphate), an anode (e.g. graphitic carbons), an organic electrolyte (containing Li-ion salt), and a separator to physically separate the two electrodes.2 The charge/discharge process refers to the reversible electrochemical process of ions moving between the positive and negative electrodes, which allows storage and release of charge in the form of electrical energy.Because of their high surface area to volume ratio, nanomaterials are of interest as Li-ion battery electrodes. The greater proportion of electrically charged species nearer to the surface (compared to bulk materials) can aid faster electronic/ion transfer processes. This can facilitate charge storage in electrodes via surface effects (i.e. not exclusively from Li-ion intercalation/insertion).3 For example, fast Faradaic reactions (pseudocapacitive effects) of Li-ions at the extensive surfaces can enhance charge storage at higher current rates.4 Additionally, a high surface area nanomaterial can behave like an electrochemical double layer capacitor, in which the charge is stored physically via a Helmholtz double layer. Hence, overall storage in nanomaterial electrodes, such as nano-TiO2 (ref. 4–8) and nano-Nb2O5,9–11 can be a combination of (i) battery-like Li-ion insertion/intercalation and (ii) supercapacitor-like charge arising from Faradaic redox reactions at the surface12 and Helmholtz double layer charge transfer.
Titanium dioxide is an ideal electrode material to replace graphite as the former is inexpensive, environmentally friendly and stable under a wide range of temperature and pH conditions. In comparison to TiO2, graphite suffers from low power density issues and requires a protective solid electrolyte interface layer to be formed.4–7,13–17 Moreover, TiO2 as an anode offers low irreversible capacity loss and has a structure that is stable under long term charge/discharge cycling across a range of C-rates, including very high rates. Although the theoretical capacity of TiO2 is relatively low compared to some other anode materials (theoretical capacities of Li-metal, Si, Sn, graphite and TiO2 are 3860, 4200, 993, 372, and 335 mA h g−1, respectively), TiO2 can offer better performance at higher power. Furthermore, alloy materials undergo very large volume expansions during lithiation and delithiation processes and, therefore, they can experience relatively high irreversible capacity losses due to changes in the electrode structure.2,18–20
Unmodified TiO2 (anatase) anodes possess low electronic conductivity due to a wide band gap (ca. 3.0 to 3.4 eV).21 However, it is possible to increase conductivity via introduction of dopants (such as Nb5+) into the structure.7,15,16,22 Recently, Fehse et al. showed that the partial density of states (PDOS) of Nb 4d and Ti 3d are similar, but the additional Nb 4d electron pushes the Fermi level from the top of the valence band for undoped TiO2 to the bottom of the conduction band for Nb-doped TiO2. The lowest Nb 4d empty states are not in the band gap, but overlap with Ti 3d empty states to form a band in the range of 0 to 2 eV. As the Fermi level is located within this band, Nb-doped anatase TiO2 exhibits metallic conductivity due to the delocalization of this additional Nb 4d electron.16
High power Nb2O5 based anodes have received much attention due to their ability to rapidly store charge from a combination of Li-ion intercalation/deintercalation and pseudocapacitive charge storage.10,11,23–25 DFT analysis has suggested that strong lithium-ion adsorption at the surface of NbOx (where x = 1.3, 1.6 or 2), contributes to the observed high rate performance. Therefore, in this case, the presence of local charge transfer at adsorption sites, drastically increases the energy density.9
In this work, the direct and continuous synthesis of undoped nano-TiO2 (anatase) and nanosized Nb-doped TiO2 (up to 25 at% dopant) is reported. The incorporation of Nb5+ in the structure improves the electrochemical performance (compared to undoped nano-TiO2) at higher charge/discharge rates. The results are described in terms of the impact of doping on electronic conductivity, Li-ion diffusion kinetics and charge storage properties (via diffusion controlled and surface effects) on timescales of a few minutes or a few seconds.
Experimental
Materials
TiBALD (Titanium(IV) bis(ammonium lactato)dihydroxide solution, 50% H2O, Sigma Aldrich, Steinheim, Germany), ammonium niobate(V) oxalate hydrate (>99.99%, Sigma Aldrich, Steinheim, Germany) and KOH (Fisher Scientific, Loughborough, UK) were used as aqueous precursors in D.I. water (10 MΩ).Synthesis
The nanoparticles were synthesized using a laboratory scale continuous hydrothermal flow synthesis (CHFS) reactor incorporating a confined jet mixer (CJM), the basic design of which is described elsewhere.26–28 The laboratory scale process is similar to the pilot plant CHFS process described elsewhere29,30 but on ca. 1/5 of the scale. In the lab scale process, three identical diaphragm pumps (Primeroyal K, Milton Roy, Pont-Saint-Pierre, France) were used to supply three feeds, which were pressurized to 24.1 MPa. Pump 1 supplied a feed of DI water at a flow rate of 80 mL min−1, which was then heated well above the critical point of water (Tc = 374 °C and Pc = 22.1 MPa) in flow using a 7 kW electrical water heater. Pump 2 supplied the metal salt (precursor 1) at a flow rate of 40 mL min−1 and pump 3 supplied either auxiliary reagents (precursor 2) or DI water at a flow rate of 40 mL min−1. The feeds from pumps 2 and 3 were combined in flow at room temperature in a dead volume tee-piece. This precursor mixture was then brought into contact (co-currently) with the flow of supercritical water in a CJM (patent application no. GB1008721).For the synthesis of undoped TiO2, 0.3 M TiBALD was used as metal salt precursor 1 and DI water was used in place of precursor 2. DI water from pump 1 was heated in flow to 400 °C and mixed with the combined precursor feed, resulting in a calculated reaction temperature of 305 °C inside the CJM.
For the synthesis of Nb-doped TiO2, 0.4 M TiBALD and 0.1 M ammonium niobate(V) oxalate hydrate were premixed at room temperature and then used as metal salt precursor 1. This mixture was then combined in flow with 0.3 M KOH (precursor 2) in the tee-piece (as part of the CHFS process). This combined precursor feed (metal salt + base) was mixed with the supercritical water flow (heated to 450 °C) to give a calculated mixing temperature of 335 °C in the CJM.
The residence time of both the undoped and doped nanomaterials that were formed in the mixer was ca. 5 s, before the start of the pipe-on-pipe cooler which is part of the CHFS process. The particle-laden flow was cooled to ∼40 °C, whereupon it passed through a back-pressure regulator (BPR) and was collected. More details of the synthesis method can be found in the ESI.†
The resulting nanoparticle-laden slurry was cleaned by allowing the solids to settle before washing with DI water and then freeze-dried (Virtis Genesis 35XL) by cooling to −60 °C, followed by slow heating under vacuum of <100 mTorr over a period of 24 h. The dried powders were used directly for preparation as electrode inks with no further processing.
Characterization
Powder X-ray diffraction (XRD) patterns of the samples were obtained on a STOE diffractometer using Mo-Kα radiation (λ = 0.71 Å) over the 2θ range of 7 to 40° with a step size of 0.5° and a step time of 30 s. X-ray photoelectron spectroscopy (XPS) measurements were collected using a Thermo Scientific™ K-alpha™ spectrometer using Al-Kα radiation and a 128-channel position sensitive detector. Survey scans were conducted at a pass energy of 150 eV and high resolution scans were conducted at a pass energy of 50 eV for Ti(2p), Nb(3d), O(1s) and C(1s). The XPS spectra were processed using CasaXPS™ software (version 2.3.16) and the binding energy scales were calibrated using the adventitious C 1s peak at 284.5 eV. Backgrounds were subtracted using the Shirley routine31 and peaks were fitted with an appropriate Gaussian/Lorentzian line shape. The relative concentrations of Ti and Nb within the sample were estimated by the measurement of the peak areas of Ti(2p) and Nb(3d) core lines and application of the appropriate relative sensitivity factors. Full details of this analysis can be found in the ESI.†The size and morphology of the crystallites were determined by transmission electron microscopy (TEM) using a Jeol JEM 2100 – LaB6 filament. The system was equipped with a Gatan Orius digital camera for digital image capturing. Samples were prepared by ultrasonically dispersing a few mg of the powder in ethanol (>99.5%, EMPLURA, Darmstadt, Germany) and pipetting drops of the dispersed sample onto a copper film grid (300 mesh – Agar Scientific, Stansted, UK). The average crystallite size (TEM) was determined by the average of at least 60 crystallites. Brunauer–Emmett–Teller (BET) surface area measurements were carried out using N2 in a micrometrics ASAP 2020 machine. Prior to analysis, the samples were degassed at 150 °C (12 h) under vacuum before measurements.
Electrochemical characterization
The freeze-dried nanomaterials were used as electrode active materials without any further processing or treatments. The slurry for the electrode was prepared with a content of 70 wt% active material, 20 wt% conductive agent (carbon black, Super P, Alfa Aesar, Heysham, UK) and 10 wt% polyvinylidene fluoride, PVDF, (PI-KEM, Staffordshire, UK). PVDF was dissolved in NMP (N-methyl-2-pyrrolidone, Sigma Aldrich, St Louis, USA) for at least 1 hour at room temperature, before adding the active material and conductive agent. The mixtures were milled and the slurry was cast on a copper foil (PI-KEM, Staffordshire, UK) and dried in an oven at 70 °C for 1 hour and then left overnight at room temperature. Electrodes with a diameter of 16 mm were punched out, pressed and finally dried overnight at 70 °C. The specific electrode mass loading for each electrode disc with a diameter of 16 mm was in the range of 1.0 to 1.5 mg cm−2. Electrochemical experiments were performed using a two-electrode 2032-type coin cell, which was assembled in an argon-filled glovebox with O2 and H2O limited below 50 ppm. The counter electrode was lithium metal foil (PI-KEM, Staffordshire, UK). The separator (glass microfiber filters, WHATMAN, Buckinghamshire, UK) was saturated with an organic electrolyte of LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 wt% ethylene carbonate/ethyl methyl carbonate (BASF, Ludwigshafen, Germany).
7 wt% ethylene carbonate/ethyl methyl carbonate (BASF, Ludwigshafen, Germany).
Electrochemical measurements were performed using a 48-channel Arbin Instrument (Caltest Instruments Ltd, Guildford, UK) at room temperature. The electrochemical performance was first investigated by cyclic voltammetry (CV) in the potential range of 1.2 to 2.5 V vs. Li/Li+ with a scan rate in the range of 0.05 mV s−1 to 1 mV s−1. The specific current rate test was performed between an applied current in the range 0.1 to 15 A g−1 in the potential range of 1.2 to 3 V vs. Li/Li+. The specific current and specific capacity were calculated based on the mass of the active material in each printed electrode and 1C corresponded to a theoretical specific capacity of 175 mA h g−1.
Electrochemical impedance spectroscopy (EIS) was performed by applying an AC (alternating current) potential (5 mV) across a frequency range of 10 mHz to 500 kHz to an electrochemical cell and then measuring the current response through the cell with a galvanostat/potentiostat (PGSTAT302, AUTOLAB, Metrohm). The cell was assembled with a Celgard 2400 separator soaked in 1 M LiPF6 in EC/DMC/DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) as the electrolyte with a lithium metal counter electrode for this measurement.
1, v/v) as the electrolyte with a lithium metal counter electrode for this measurement.
Results and discussion
Undoped TiO2 and Nb-doped TiO2 were obtained as white and blue powders, respectively (see Fig. 1a). The reaction yield in each case was >90%. The XRD data confirmed a good match to the pattern of phase pure anatase TiO2 (tetragonal, space group I41/amd, JCPDS 21-1272), see Fig. 1b. High-quality XRD data revealed very minor impurity peaks in the Nb-doped TiO2 sample at 2θ = 14.4 and 20.5°. The peak at 2θ = 14.4° might be attributed to the (100) peak of a very small amount of pseudohexagonal TT-Nb2O5 (JCPDS 28-317)10 although the other peak did not correspond to any possible Nb2O5 phase. Therefore, the two impurity peaks most likely corresponded to the (211) and (302) peaks of a very minor brookite phase (similar to JCPDS reference pattern 29-1360). Another indication for a brookite impurity was the slight shoulder of the first peak at ca. 13° which might be attributed to the (111) brookite peak. There was a small shift to lower 2θ values for the peaks of the Nb-doped TiO2 compared to the undoped counterpart at higher angles. This was due to lattice expansion, resulting from the substitution of larger Nb5+ (ionic radius = 0.64 Å) for Ti4+ (ionic radius = 0.61 Å) in the anatase structure (TiO6 octahedra). The calculated Scherrer crystallite sizes were ca. 4.3 and 5.0 nm for the undoped and Nb-doped TiO2, respectively, which were comparable to the sizes of previously reported TiO2 based materials made via CHFS.32–35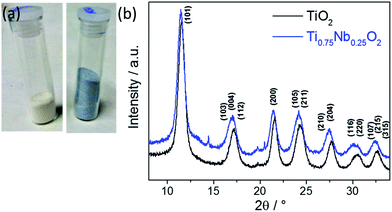 | ||
| Fig. 1 (a) Photograph of the pure (left) and doped (right) dried powder. (b) XRD patterns of pure (bottom, black) and Nb-doped anatase TiO2 (top, blue). | ||
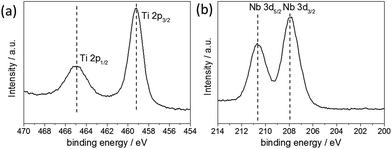
The valence state of the metal ions was determined by X-ray photoelectron spectroscopy (XPS) [see Fig. 2]. The Nb-3d level binding energies were 210.65 eV (Nb 3d5/2) and 207.91 eV (Nb 3d3/2) with a spin orbit splitting of 2.74 eV, which were assigned to the core levels of Nb5+. The Ti-2p level binding energies were 464.92 eV (Ti 2p1/2) and 459.15 eV (Ti 2p3/2) with a spin orbit splitting of 5.77 eV, which were assigned to the core levels of Ti4+. No additional Ti peaks were observed within the spectra, suggesting that Ti4+ was the only Ti species present. Semi-quantitative analysis of the peak areas of the Ti(2p) and Nb(3d) core lines, estimated the elemental composition at the surface to be 25 at% Nb relative to Ti. It is noted, however, that such analysis is relevant only for the surface of the sample and can be subject to errors arising from ineffective background subtraction and potential sample inhomogeneity.36 Corroboratory compositional analysis was therefore obtained by EDX measurements, giving values of 22.6 ± 1.9 at% Nb relative to Ti. These results corresponded well to the value estimated by XPS, as well as the precursor concentration used in the synthesis, suggesting that the Nb dopant was effectively and homogenously incorporated into the TiO2 structure.
TEM images revealed very small spherical particles with narrow size distribution for both undoped and Nb-doped titania (Fig. 3 for doped sample). The average crystallite size of undoped and Nb-doped TiO2 was 4.5 (±0.6) and 4.9 (±0.6) nm, respectively, which was in agreement with the trends of the BET surface area. The interlayer spacing of undoped and doped TiO2 was calculated from relevant TEM images and was found to be 0.34 (±0.02) and 0.34 (±0.01) nm, respectively, which is consistent with expectations for the (101) planes of tetragonal-phase anatase. STEM/EDX mapping confirmed a homogenous distribution of Ti and Nb atoms in the sample (Fig. 3c and d, respectively). The BET surface area of the undoped TiO2 was 288 m2 g−1 and for Nb-doped TiO2 was 239 m2 g−1.
 | ||
| Fig. 3 (a) and (b) HRTEM images of Ti0.75Nb0.25O2. EDX mappings of Ti0.75Nb0.25O2 showing the homogenous distribution of (c) Ti and (d) Nb atoms. | ||
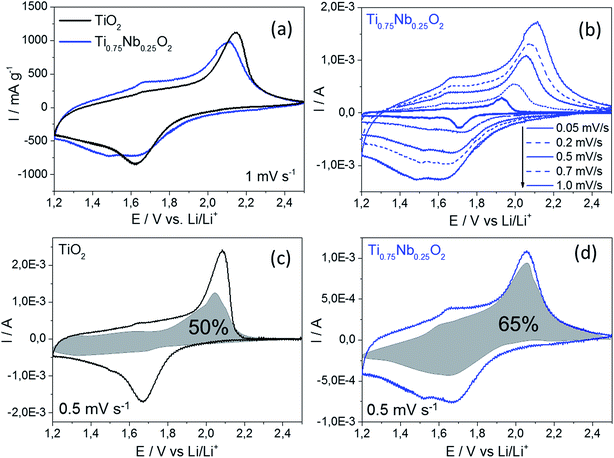
Cyclic voltammetry under different conditions was carried out to gain better understanding of the electrochemical performance of these two materials. The specific current response at an applied scan rate of 1 mV s−1 is presented in Fig. 4a. A decrease in peak height was observed with a doping of 25 at% Nb into TiO2 in the characteristic range where Ti3+/Ti4+ is active (1.6 and 2.2 V vs. Li/Li+, respectively). Interestingly, the peak potential of undoped titania exhibited a higher peak shift (difference between the lithiation and delithiation peaks) of 0.52 V compared to that of the Nb-doped material (peak shift 0.47 V). This gave an indirect indication of better Li-ion insertion kinetics for the Nb-doped TiO2,37,38 which could be a consequence of a slightly higher interlayer spacing expected for the Nb-doped sample (compared to the undoped TiO2). Two further peaks were observed for the Nb-doped TiO2 at 1.49 and 1.67 V vs. Li/Li+ for the lithiation and delithiation, respectively. These might be attributed to the reduction of Nb5+ and oxidation of Nb4+ back to Nb5+.11,23
A scan rate test was carried out to distinguish the charge stored via diffusion-controlled Li-ion insertion from surface effects (Fig. 4b). In general, the current in a scan rate experiment can be expressed by a power law (eqn (1)), where i is the current (A), a and b are arbitrary coefficients and v is the potential scan rate (V s−1).
| I = avb | (1) |
The coefficient b can be expected to vary in the range of 0.5 to 1.0, with a value of 0.5 being characteristic of a diffusion-limited process (charge storage via Li-ion insertion) and a value of 1.0 for a capacitive process (charge storage via surface capacitive effects). Therefore, to further quantify the different charge storage mechanisms, charge storage via Li-ion insertion and surface capacitive effects were separated out, using a method that has been described previously in the literature.5,10–12 At a fixed potential, the current response can be seen as a combination of the two aforementioned charge storage mechanisms. The surface capacitive effect (fast kinetics) can be expressed by k1v (b = 1.0), whereas the diffusion-controlled (Li-ion insertion) contribution can be expressed by 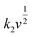 (b = 0.5) (eqn (2)).
(b = 0.5) (eqn (2)).
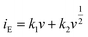 | (2) |
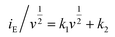 | (3) |
At a certain potential, the current value was measured for each scan rate. A plot of 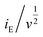 versus
versus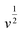 , allowed the calculation of k2 from the y-intercept and k1 from the slope of eqn (3). The slight shift of the Li-ion de-insertion peak for higher applied sweep rates was ignored and the potential value from a sweep rate of 0.5 mV s−1 was used as the standard de-insertion potential. Low scan rates (range of 0.05 to 1 mV s−1) were chosen as the peak shifted more at higher applied rates.5 The calculated k2 value was then used to quantify the amount of charge stored via surface capacitance at each potential. In this work, the current that resulted from capacitive effects at the surface was calculated at a scan rate of 0.5 mV s−1, which was then plotted against the overall measured current (as shown in Fig. 4c and d). The calculated current response arising from capacitive effects at the surface was then deduced (grey areas in Fig. 4c and d). It can be seen that the grey area in Fig. 4d was larger for the Nb-doped sample than that for the undoped sample (Fig. 4c), particularly in the range of 1.4 to 1.7 V vs. Li/Li+. This was due to the presence of the near surface Nb-dopant, as suggested previously.10,23,25,39–42 Thus, calculation of the areas as described above, enabled approximate quantification of the relative contributions from charge stored via capacitive (pseudocapacitance and Helmholtz double layer charge) and diffusion-limited processes (i.e. classical Li-ion insertion). Undoped TiO2 showed charge storage contributions via capacitance and conventional Li-ion insertion to be ca. 50% each (scan rate 0.5 mV s−1). In contrast, Nb-doped TiO2 showed charge storage contributions of ca. 65% via capacitance and 35% via diffusion-limited Li-ion insertion processes (scan rate 0.5 mV s−1). In comparison, Wang et al. previously made similar investigations on undoped titania at this scan rate, and found that capacitance accounted for ca. 55% of the capacity.5
, allowed the calculation of k2 from the y-intercept and k1 from the slope of eqn (3). The slight shift of the Li-ion de-insertion peak for higher applied sweep rates was ignored and the potential value from a sweep rate of 0.5 mV s−1 was used as the standard de-insertion potential. Low scan rates (range of 0.05 to 1 mV s−1) were chosen as the peak shifted more at higher applied rates.5 The calculated k2 value was then used to quantify the amount of charge stored via surface capacitance at each potential. In this work, the current that resulted from capacitive effects at the surface was calculated at a scan rate of 0.5 mV s−1, which was then plotted against the overall measured current (as shown in Fig. 4c and d). The calculated current response arising from capacitive effects at the surface was then deduced (grey areas in Fig. 4c and d). It can be seen that the grey area in Fig. 4d was larger for the Nb-doped sample than that for the undoped sample (Fig. 4c), particularly in the range of 1.4 to 1.7 V vs. Li/Li+. This was due to the presence of the near surface Nb-dopant, as suggested previously.10,23,25,39–42 Thus, calculation of the areas as described above, enabled approximate quantification of the relative contributions from charge stored via capacitive (pseudocapacitance and Helmholtz double layer charge) and diffusion-limited processes (i.e. classical Li-ion insertion). Undoped TiO2 showed charge storage contributions via capacitance and conventional Li-ion insertion to be ca. 50% each (scan rate 0.5 mV s−1). In contrast, Nb-doped TiO2 showed charge storage contributions of ca. 65% via capacitance and 35% via diffusion-limited Li-ion insertion processes (scan rate 0.5 mV s−1). In comparison, Wang et al. previously made similar investigations on undoped titania at this scan rate, and found that capacitance accounted for ca. 55% of the capacity.5
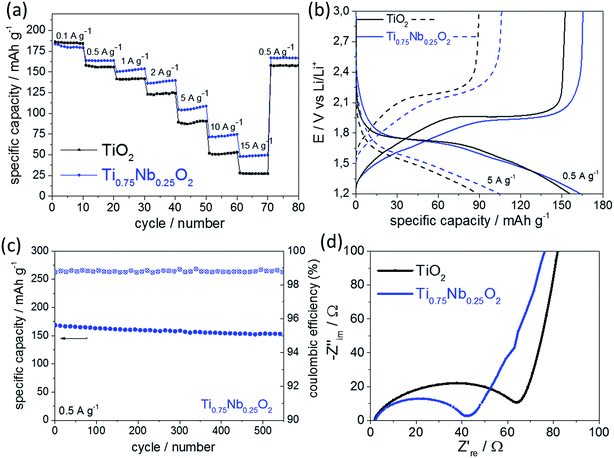
Overall, the charge storage behavior shown in Fig. 4c and 4d fitted well to the galvanostatic charge/discharge cycling results (Fig. 5a). Diffusion-limited charge storage processes are expected to decrease drastically when the electrode material is electrochemically cycled within seconds, as the main charge storage mechanism is due to the surface reactions/effects at these high rates. As shown in Fig. 5a, galvanostatic cycling tests at different specific current rates were performed in a wide current range from 0.1 to 15 A g−1 (considering 1C = 175 mA h g−1, this is equivalent to a nominal C-rate range of ca. 0.5C to 86C). It should be mentioned that the C-rate corresponds to the full theoretical charge/discharge within one hour for 1C, but this relates to the bulk de-lithiation charge storage mechanism, which is typical for a battery material. The materials presented herein showed significant charge storage via surface effects, which are more commonly associated with oxide supercapacitors. Therefore, the authors prefer to use the term “nominal C-rate” hereafter and will also name each measured time for charge/discharge at each rate.
At the lowest applied current rate, the undoped and Nb-doped TiO2 showed a specific capacity of 186 mA h g−1 and 180 mA h g−1, respectively (nominal C-rate ca. 0.5C, 6200 s per charge or discharge). At higher currents, the Nb-doped TiO2 showed superior rate retention when compared to its undoped counterpart; at a current rate of 5 A g−1 (nominal C-rate ca. 29C, 65 s per charge or discharge), the undoped and Nb-doped TiO2 showed a specific capacity of 88 mA h g−1 and 105 mA h g−1, respectively. At the highest applied current of 15 A g−1 (nominal C-rate ca. 86C, 10 s per charge or discharge), the undoped and doped nano-TiO2 samples showed a specific capacity of 27 and 48 mA h g−1, respectively.
The potential versus capacity plot suggested that the overpotential between lithiation and delithiation (current rate 5 A g−1) was higher for the undoped TiO2 compared to that for the Nb-doped TiO2 (Fig. 5b), which suggested higher electronic conductivity of the Nb-doped sample. As this can often be a limiting factor for high power electrode materials,43 it explains the better performance of the doped sample. Long-term galvanostatic charge/discharge cycling of the Nb-doped sample is presented in Fig. 5c (specific current rate 0.5 A g−1). The coulombic efficiency remained >98.7% and overall a specific capacity retention of ca. 91% (initial and final value 168 and 153 mA h g−1, respectively) was achieved after 540 cycles. Therefore, the as-prepared nano-sized Nb-doped TiO2 showed very high cycle stability at a modest current rate of 0.5 A g−1.
Electrochemical impedance spectroscopy (EIS) was performed in order to further investigate the improved performance of Nb-doped TiO2 at higher rates (Fig. 5d). The EIS results were similar for both samples and each curve was divided into a high frequency region (a semicircle) and a low frequency region (a straight line). The high-frequency intercept with the real axis, represents the ohmic resistance, which is related to the electrolyte and therefore, in the same range for both samples (as they were both measured under the same conditions). The semicircle at higher frequencies, gives some information about the electrode resistance (charge-transfer resistance). As shown in the Nyquist plot in Fig. 5d, the general trend was towards lower resistance for the doped sample (41 Ω) versus the undoped sample (62 Ω). This suggested higher electronic conductivity, which has been previously observed for Nb-doped titanium oxides.16,44,45
Interestingly, the results herein suggested that the BET surface area was not the most critical parameter for the high power performance. Although the BET surface area decreased with a higher Nb-dopant level, the overall stored charge increased. This has been observed previously with both Nb2O5 (ref. 10) and MnO2 (ref. 46) anode materials. Therefore, the combined effects of higher electronic conductivity, improved lithium-ion kinetics and higher capacity for charge storage via surface effects, benefitted the high power performance of nanosized Nb-doped TiO2 compared to the undoped material. As other transition metal oxides are known to show very promising high power performances due to Faradaic processes, future studies will investigate the effect of alternative dopants (e.g. Ru, Mn, Fe, Ni, etc.) in nano-TiO2 and other host systems.47
Conclusions
This work reports the direct and continuous synthesis of high surface area anatase undoped TiO2 and Nb-doped TiO2 nanoparticles. Doping 25 at% Nb5+ into the anatase TiO2 drastically improved the electrochemical performance at higher charge/discharge rates. The improved high power performance of the Nb-doped TiO2 was attributed to its higher electronic conductivity, higher lithium-ion diffusivity and increased charge stored via surface reactions/effects. Overall, the direct synthesis of high power doped/undoped anode nanomaterials has been demonstrated and the CHFS process holds potential for further materials development and even scale-up production in the future. The authors hope to develop these areas further and the results of such endeavors will be reported in due course.Acknowledgements
The EPSRC is thanked for funding the Centre for Doctoral Training in Molecular Modelling & Materials Science (UCL, UK) and A Star (Singapore) is thanked for supporting a studentship for ML. Mr Joe Nolan (UCL) is thanked for technical support. Dr Chris Tighe and Dr Rob Gruar are acknowledged for their contributions towards development of the lab scale CHFS process, which was used in this work. JAD, DB and PS thank EPSRC for support of the ELEVATE (ELEctrochemical Vehicle Advanced TEchnology) low carbon vehicles project (EP/M009394/1).References
- Z. Juda, J. KONES, 2011, 18, 165–171 Search PubMed.
- M. Winter and R. J. Brodd, Chem. Rev., 2004, 104, 4245–4270 CrossRef CAS.
- P. Simon, Y. Gogotsi and B. Dunn, Sci. Mag., 2014, 343, 1210–1211 CAS.
- K. Zhu, Q. Wang, J.-H. Kim, A. A. Pesaran and A. J. Frank, J. Phys. Chem. C, 2012, 116, 11895–11899 CAS.
- J. Wang, J. Polleux, J. Lim and B. Dunn, J. Phys. Chem. C, 2007, 111, 14925–14931 CAS.
- L. Wu, D. Buchholz, D. Bresser, L. Gomes Chagas and S. Passerini, J. Power Sources, 2014, 251, 379–385 CrossRef CAS PubMed.
- H. Usui, S. Yoshioka, K. Wasada, M. Shimizu and H. Sakaguchi, ACS Appl. Mater. Interfaces, 2015, 7, 6567–6573 CAS.
- M. Lübke, I. Johnson, N. M. Makwana, D. Brett, P. Shearing, Z. Liu and J. A. Darr, J. Power Sources, 2015, 294, 94–102 CrossRef PubMed.
- A. A. Lubimtsev, P. R. Kent, B. G. Sumpter and P. Ganesh, J. Mater. Chem. A, 2013, 1, 14951–14956 CAS.
- J. W. Kim, V. Augustyn and B. Dunn, Adv. Energy Mater., 2012, 2, 141–148 CrossRef CAS PubMed.
- V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P.-L. Taberna, S. H. Tolbert, H. D. Abruña, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518–522 CrossRef CAS PubMed.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 CAS.
- Y. S. Hu, L. Kienle, Y. G. Guo and J. Maier, Adv. Mater., 2006, 18, 1421–1426 CrossRef CAS PubMed.
- S. Hu, H. Wang, J. Cao, J. Liu, B. Fang, M. Zheng, G. Ji, F. Zhang and Z. Yang, Mater. Lett., 2008, 62, 2954–2956 CrossRef CAS PubMed.
- Y. Wang, B. M. Smarsly and I. Djerdj, Chem. Mater., 2010, 22, 6624–6631 CrossRef CAS.
- M. Fehse, S. Cavaliere, P. E. Lippens, I. Savych, A. Iadecola, L. Monconduit, D. J. Jones, J. Rozière, F. Fischer, C. Tessier and L. Stievano, J. Phys. Chem. C, 2013, 117, 13827–13835 CAS.
- J. Qiu, S. Li, E. Gray, H. Liu, Q.-F. Gu, C. Sun, C. Lai, H. Zhao and S. Zhang, J. Phys. Chem. C, 2014, 118, 8824–8830 CAS.
- S. Goriparti, E. Miele, F. de Angelis, E. Di Fabrizio, R. Proietti Zaccaria and C. Capiglia, J. Power Sources, 2014, 257, 421–443 CrossRef CAS PubMed.
- M. R. Palacin, Chem. Soc. Rev., 2009, 38, 2565–2575 RSC.
- W.-J. Zhang, J. Power Sources, 2011, 196, 13–24 CrossRef CAS PubMed.
- A. G. Dylla, G. Henkelman and K. J. Stevenson, Acc. Chem. Res., 2013, 46, 1104–1112 CrossRef CAS PubMed.
- J.-H. Jeong, D.-W. Jung, E. W. Shin and E.-S. Oh, J. Alloys Compd., 2014, 604, 226–232 CrossRef CAS PubMed.
- M. Wei, K. Wei, M. Ichihara and H. Zhou, Electrochem. Commun., 2008, 10, 980–983 CrossRef CAS PubMed.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J. M. Tarascon, Nature, 2000, 407, 496–499 CrossRef CAS PubMed.
- J. Come, V. Augustyn, J. W. Kim, P. Rozier, P.-L. Taberna, P. Gogotsi, J. W. Long, B. Dunn and P. Simon, J. Electrochem. Soc., 2014, 161, A718–A725 CrossRef CAS PubMed.
- J. A. Darr and M. Poliakoff, Chem. Rev., 1999, 99, 495–542 CrossRef CAS PubMed.
- R. I. Gruar, C. J. Tighe and J. A. Darr, Ind. Eng. Chem. Res., 2013, 52, 5270–5281 CrossRef CAS.
- M. Lübke, N. M. Makwana, R. Gruar, C. Tighe, D. Brett, P. Shearing, Z. Liu and J. A. Darr, J. Power Sources, 2015, 291, 102–107 CrossRef PubMed.
- M. Chen, C. Y. Ma, T. Mahmud, J. A. Darr and X. Z. Wang, J. Supercrit. Fluids, 2011, 59, 131–139 CrossRef CAS PubMed.
- C. J. Tighe, R. Q. Cabrera, R. I. Gruar and J. A. Darr, Ind. Eng. Chem. Res., 2013, 52, 5522–5528 CrossRef CAS.
- D. A. Shirley, Phys. Rev. B, 1972, 5(12), 4709–4714 CrossRef.
- Z. Zhang, S. Brown, J. B. Goodall, X. Weng, K. Thompson, K. Gong, S. Kellici, R. J. Clark, J. R. Evans and J. A. Darr, J. Alloys Compd., 2009, 476, 451–456 CrossRef CAS PubMed.
- X. Li, Y. Qiu, S. Wang, S. Lu, R. I. Gruar, X. Zhang, J. A. Darr and T. He, Phys. Chem. Chem. Phys., 2013, 15, 14729–14735 RSC.
- J. B. Goodall, S. Kellici, D. Illsley, R. Lines, J. C. Knowles and J. A. Darr, RSC Adv., 2014, 4, 31799–31809 RSC.
- Z. Zhang, J. B. Goodall, D. J. Morgan, S. Brown, R. J. Clark, J. C. Knowles, N. J. Mordan, J. R. Evans, A. F. Carley and M. Bowker, J. Eur. Ceram. Soc., 2009, 29, 2343–2353 CrossRef CAS PubMed.
- P. van der Heide, X-ray photoelectron spectroscopy: an introduction to principles and practices, John Wiley & Sons, 2011 Search PubMed.
- B. Hao, Y. Yan, X. Wang and G. Chen, ACS Appl. Mater. Interfaces, 2013, 5, 6285–6291 CAS.
- J. Wang, Y. Zhou, Y. Hu, R. O'Hayre and Z. Shao, J. Mater. Sci., 2013, 48, 2733–2742 CrossRef CAS.
- M. Wei, Z.-M. Qi, M. Ichihara and H. Zhou, Acta Mater., 2008, 56, 2488–2494 CrossRef CAS PubMed.
- H. Luo, M. Wei and K. Wei, Mater. Chem. Phys., 2010, 120, 6–9 CrossRef CAS PubMed.
- H. Wen, Z. Liu, J. Wang, Q. Yang, Y. Li and J. Yu, Appl. Surf. Sci., 2011, 257, 10084–10088 CrossRef CAS PubMed.
- A. le Viet, M. V. Reddy, R. Jose, B. V. R. Chowdari and S. Ramakrishna, Electrochim. Acta, 2011, 56, 1518–1528 CrossRef CAS PubMed.
- P. V. Braun, J. Cho, J. H. Pikul, W. P. King and H. Zhang, Curr. Opin. Solid State Mater. Sci., 2012, 16, 186–198 CrossRef CAS PubMed.
- B. Tian, H. Xiang, L. Zhang, Z. Li and H. Wang, Electrochim. Acta, 2010, 55, 5453–5458 CrossRef CAS PubMed.
- S. Lee, J. H. Noh, H. S. Han, D. K. Yim, D. H. Kim, J.-K. Lee, J. Y. Kim, H. S. Jung and K. S. Hong, J. Phys. Chem. C, 2009, 113, 6878–6882 CAS.
- O. Ghodbane, J.-L. Pascal and F. Favier, ACS Appl. Mater. Interfaces, 2009, 1, 1130–1139 CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ta07554h |
| This journal is © The Royal Society of Chemistry 2015 |