A comprehensive picture of the current rate dependence of the structural evolution of P2-Na_2/3Fe_2/3Mn_1/3O₂

Abstract

Cathodes that feature a layered structure are attractive reversible sodium hosts for ambient temperature sodium-ion batteries which may meet the demands for large-scale energy storage devices. However, crystallographic data on these electrodes are limited to equilibrium or quasi-equilibrium information. Here we report the current-dependent structural evolution of the P2-Na_2/3Fe_2/3Mn_1/3O₂ electrode during charge/discharge at different current rates. The structural evolution is highly dependent on the current rate used, e.g., there is significant disorder in the layered structure near the charged state at slower rates and following the cessation of high-current rate cycling. At moderate and high rates this disordered structure does not appear. In addition, at the slower rates the disordered structure persists during subsequent discharge. In all rates examined, we show the presence of an additional two-phase region that has not been observed before, where both phases maintain P6₃/mmc symmetry but with varying sodium contents. Notably, most of the charge at each current rate is transferred via P2 (P6₃/mmc) phases with varying sodium contents. This illustrates that the high-rate performance of these electrodes is in part due to the preservation of the P2 structure and the disordered phases appear predominantly at lower rates. Such current-dependent structural information is critical to understand how electrodes function in batteries which can be used to develop optimised charge/discharge routines and better materials.

---

Introduction

The Li-ion battery (LIB) has long been the most popular rechargeable battery system for high energy electronic applications, and LIBs are also now being used for electric vehicles.^1,2 Some predictions indicate that global Li sources may not satisfy the demands placed by LIB-use in digital electronics, electric vehicles, consumer gadgets, etc. beyond 2025. This estimate also takes into account LIB recycling.³ Furthermore, the geographical isolation and distribution of lithium resources may become a more sensitive political issue in the near future. Consequently, much of the attention has shifted towards the search for alternative storage systems. This is especially true for large grid supporting storage devices where smaller energy densities can be compensated by significantly lower manufacturing and maintenance costs and long cycle lives. One of the most intriguing alternatives to LIBs are Na-ion batteries (NIBs) because of their similar intercalation chemistry and abundance of the intercalation element, Na.^4,5 It is generally understood that NIBs may not reach the energy densities of LIBs because Na is more than 3 times heavier than Li and the operational voltage is lower. However, some of the cathode candidates, like layered oxides for NIBs, show very comparable electrochemical performance to the commercially available LIBs and such materials can be used to translate into a working full cell within a few years.⁶

Among the cathode candidates, layered oxides of the general formula NaM_TO₂ (M_T = Cr, Mn, Fe, Co, Ni, Cu and mixtures of 2–3 elements) have been extensively investigated because of their high reversible capacity, ease of synthesis, and tunable electrochemical characteristics.^7–12 The sodium deficient P2-phase and fully sodiated O3-phase, which are classified based on the oxygen layer stacking and the surrounding environment of sodium atoms, have been investigated and compared for their overall electrochemical performance. Generally, the P2-phase outperforms the O3-phase due to the series of phase transitions that the O3-phase undergoes during battery operation.¹³ However, recent work shows that the overall electrochemical performance is very similar for P2- and O3-phases of Na_2/3Fe_2/3Mn_1/3O₂,¹⁴ and in fact, the O3-phase does not suffer from serious structural degradation during the charge/discharge process at high current rates of C/2.5.¹⁵ The structural stability of the O3-Na_2/3Fe_2/3Mn_1/3O₂ phase during battery function is remarkable and as a consequence it exhibits highly reversible electrochemical performance. In addition, a series of phase transitions, potential-regions of simultaneous biphasic and solid solution mechanisms have been observed illustrating electrode structural evolution during the C/2.5 cycling procedure employed. However, the O3 structural motif appears to be preserved throughout the charge/discharge process at C/2.5 which in part gives rise to the performance of the electrode. Obviously, such a discovery combined with a literature comparison is a useful tool in designing an electrode with desired electrochemical performance characteristics.

For O3-Na_2/3Fe_2/3Mn_1/3O₂ a slower rate laboratory based XRD study at C/50-C/80 used Le Bail methods for in situ and Rietveld methods for ex situ data analysis, looking essentially at equilibrium structures.¹⁶ The authors first discharged the electrode to reach Na = 0.96 contrasting to the latter high-current rate work which first charged the electrode from the Na = 0.67 composition. For the slower rate experiments the phase transitions are shown to follow O′3 → O3 → P3 via a sequence of solid solution and biphasic regions, however, the O3 phase is described to be persistent in the structural data once formed even at C/80 (e.g. into the P3 region). Note, in the higher current¹⁵in situ experiments the major phase is the O3-phase throughout the charge/discharge cycling, with no evidence of the P3 phase. Interestingly both studies show similar evolution of the c lattice parameter and slab distance evolution (distance between adjacent transition metal layers) with slightly different Na content values for the onset of the maximum of slab distance.^15,16

A pertinent recent study on P2-Na_0.67[Fe_0.5−2yNi_yMn_0.5+y]O₂ (y = 0, 0.10, 0.15) showed that the optimal electrochemical performance was found for the y = 0.15 composition and weak and broad reflections were observed near the charged state.¹⁷ At C/20 the authors showed the evolution from P′2 → P2 → “Z” which they characterised as being different from the OP4 ^13,18 phase (a disordered phase). These transitions were reversible and featured different onset Na concentrations, as determined from electrochemical calculations, as a function of y. To fully characterise the “Z” phase the authors used pair distribution function analysis, but noted that it showed poor crystallinity making X-ray diffraction data poor for structural determination and that the composition of the electrode, e.g. with carbon black, would make it difficult to undertake pair-distribution function analysis. Previous work on the “Z” phase for P2-Na_0.62Fe_0.5Mn_0.5O₂ also struggled to index this phase.¹⁸ Therefore the authors used chemically desodiated samples, noting subtle differences between electrochemical and chemical sodium removal, and showed that at such low Na concentrations and hence large Na vacancy concentrations Fe³⁺ could populate the tetrahedral sites in the interlayer space, e.g. between the notionally transition metal layers. However, since this occurred throughout the range of compositions tested, the authors suggested that it was not Na vacancy driven. Note that this “Z” phase is still fairly disordered and requires a large supercell to model. This shows that the Jahn Teller distortion of Fe⁴⁺ is not the biggest contributor to the behaviour at high voltage but Fe migration and electrochemically avoiding the high voltage behaviour, e.g. by using a lower cutoff voltage, can boost capacity retention by ∼15%. Interestingly, O3-Na_xCrO₂ ¹⁹ and O3-Na_xFeO₂ ²⁰ have been shown to form a similar phase but do not show the reversibility that this P2 phase shows.

An ex situ study also considered the samples Na_xFe_xMn_1−xO₂ (1.0 ≤ x ≤ 0.5) and showed that below x = 0.65 composition (i.e., below Na_2/3Fe_2/3Mn_1/3O₂) there are combinations of phases, some of which can be modelled with two sets of P2 phases.²¹ The authors linked the broadening of 00l reflections to sodium vacancy groups or staged vacancy ordering.

In situ XRD studies on P2-Na_2/3Fe_2/3Mn_1/3O₂ and related P2-phases, such as Na_2/3Fe_1/2Mn_1/2O₂, at slow C-rates show the reversible transition upon charge from P2 to OP4 (a disordered phase) or the “Z” phase,^17,18 a two-phase reaction mechanism. The formation of the OP4-phase is a result of increasing oxide layer repulsion as the sodium content in the interlayer space is reduced. Upon discharge the P2-phase forms, after a solid solution region of the OP4-phase, and at lower voltages close to the completion of discharge a new distorted phase is also found.^13,22

Based on these studies, it is necessary to perform in situ structural characterisation at relatively high cycling rates to gain insight into the dependence of structural evolution at these rates, since structure is directly linked with battery performance. It is important to note that only a few techniques can probe batteries in situ in a non-destructive manner and of these a smaller number of techniques can do so with sufficient time-resolution to examine high rate cycling. To date only neutron powder and synchrotron X-ray powder diffraction (XRD) have satisfied this criterion. Ex situ or low-rate in situ diffraction methods show electrode structure at equilibrium or quasi-equilibrium conditions, they do not represent the electrode structure at moderate or high rates. In situ methods with sufficient time-resolution to capture data in short enough intervals with sufficient resolution and quality can be used for structural analysis at high current rates and some examples of this work can be found in ref. 23–30. For sodium-ion batteries at high-rates, non-destructive structural information essentially means in situ synchrotron X-ray diffraction for now. In principle, with sufficient resolution almost all structural parameters can be determined for the electrode in question.^15,31–33

Herein, we report the current-dependent in situ synchrotron XRD analysis of P2-phase Na_2/3Fe_2/3Mn_1/3O₂. We have focused our study on the influence of kinetics on the electrochemical performance and phase transitions of this cathode material by determining its structural evolution as a function of applied current rate.

Experimental

The synthesis of P2-Na_2/3Fe_2/3Mn_1/3O₂ was carried out using a slightly modified method compared to that found in the literature.¹⁴ A stoichiometric mixture of Na₂CO₃, Fe₂O₃, and Mn₂O₃ was ground in a planetary ball mill for 1 hour at 250 rpm with 12 mm diameter zirconia balls (1 : 20 active material : balls weight ratio) and pressed into pellets. Then, the pellets were fired at 1000 °C for 12 hours under 1 bar O₂ pressure followed by slow cooling.¹⁴

Electrode preparation was performed in an Ar-filled glove box in order to avoid any atmospheric moisture contamination. The electrode slurry was prepared by mixing an active material, super carbon C65, and polyvinylidene fluoride (PVdF) as a binder in the mass ratio of 80 : 10 : 10 in N-methyl-2-pyrrolidone (NMP) followed by vigorous stirring for 2 hours. The slurry was then cast onto an aluminum current collector sheet using a mini-coater. The laminate was immediately transferred into a vacuum oven and dried at 80 °C under constant vacuum for 12 hours.

Half coin cells with 3 mm diameter holes in the casing and 5 mm diameter holes in the stainless spacer were used for the construction of the coin cells for the in situ measurements. The coin cells contained Na metal (∼1 mm thickness), a glass fibre separator with 0.5 M NaPF₆ in ethylene carbonate and dimethyl carbonate (1 : 1 wt%) electrolyte solution. In situ synchrotron X-ray diffraction experiments were performed within 1–2 days after cell construction. Further details regarding coin cell construction and beamline setup can be found in ref. 31 and 32

In situ synchrotron XRD data were collected on the Powder Diffraction beamline³⁴ at the Australian Synchrotron with a wavelength (λ) of 0.68829(2) Å or 0.68863(2) Å, determined using the NIST 660a LaB₆ standard reference material. Data were collected continuously in 4.42 minute acquisitions on the coin cell in transmission geometry throughout the charge/discharge cycles.

Three sets of experiments were conducted on three coin cells. The first cell was charged to 4.2 V starting with a current of 0.2 mA and increasing this to 0.4 mA. The cell was then discharged to 1.5 V at 0.4 mA and increased to 0.8 mA near the end of discharge. These steps were used to ensure a cycle was complete within the particular allocated beamtime and corresponded to a variable C-rate (and current-rate) experiment, noting that the first part of charge using 0.2 mA corresponded to ∼C/16 (cell 1 with electrode loading of 2.8 mg). The second coin cell was charged to 4.2 V, discharged to 1.5 V and charged to 4.2 V using the same current of 0.8 mA corresponding to C/2.5 (cell 2 with electrode loading of 2.1 mg). Finally the third coin cell featured a lower mass loading of the electrode and was charged to 4.2 V, discharged to 1.5 V, charged to 4.2 V using 0.4 mA and then allowed to rest (cell 3 with electrode loading of 1 mg). Lower loading meant that the C-rate was highest for the third cell of 1C. Note, we refer to C as the time taken to complete a charge and discharge cycle in this case. The third cell also features a no current step after cycling to see the relaxation process (cell 3). Therefore, this combination of cells provides a comparison of the effect of variable current rates on the structural response of the electrode.

In each case, Rietveld refinements were carried out using the GSAS³⁵ software suite with the EXPGUI³⁶ software interface. The lattice, background, and profile terms were initially refined for the first dataset and then the atomic parameters were refined, specifically the oxygen position, all atomic displacement parameters (ADPs) and then the Na site occupancy factors (SOFs). Note that the ADPs were refined and fixed alternatively to the Na occupancies. For the sequential refinements the refinable parameters were the lattice, background, oxygen positional parameter and Na occupancies unless otherwise stated in the text. For these refinements reflections arising from the aluminum current collector and sodium anode were excluded as their positions did not overlap with many cathode reflections.

Results

The results will be presented in 3 sections where each section corresponds to the 3 different protocols used, e.g. each of the current rates applied. Each section is further subdivided into phase evolution, initial structural characterisation and full time-dependent structural characterisation. A final discussion provides an overview of the results.

Cell 1: phase evolution

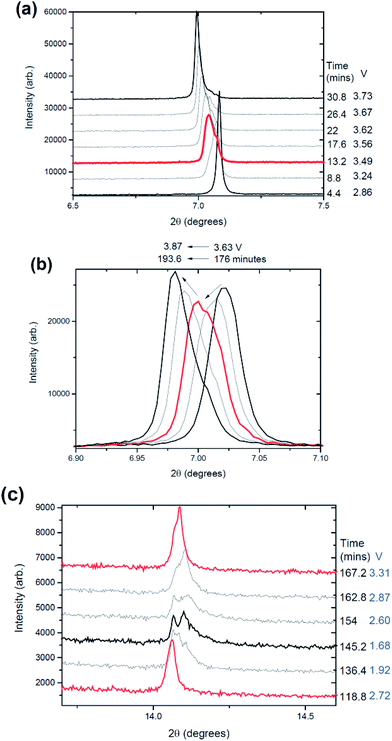
The phase evolution during most of the charge process appears to be wholly solid solution at first as shown in Fig. 1 for the 002, 004, 100, 101 and 103 reflections in the P2 setting.³⁷ The changes in the 2θ-value of the 002 and 004 or 00l reflections are in contrast to the changes in 100, 101 and 103 or h0l reflections during charge, e.g., as the 002 and 004 2θ-values decrease, the 100, 101 and 103 2θ-values increase as shown by the blue arrows in Fig. 1(a)–(c). This suggests an anisotropic evolution of the lattice parameters. Closer inspection of the charge processes shows a loss of reflection intensity for the 002, 004 and 100 reflections at approximately 35 minutes into charge as indicated by the black arrows in Fig. 1(a) and (b). A stacked plot of this region, Fig. 2, shows the presence of a two-phase reaction mechanism, with both phases containing very similar structural motifs. In other words, the two-phases appear to adopt the same structure with slightly different lattice parameters and presumably slightly different sodium contents, e.g. a sodium-rich and a sodium-poor phase. The sodium-rich P2 to sodium-poor P2 two-phase region has not been found in the literature before using either in situ or ex situ studies generally for Na_xFe_yMn_1−yO₂ or three transition metal-containing P2-type materials.^{13,14,22,37,38} The biphasic transitions found in the literature for the P2-Na_xFe_yMn_1−yO₂ phases are the transitions to the “OP4” or “Z” or “O2”⁹ phase near the charged state or to an orthorhombic P′2 phase at lower voltage (e.g.ref. 12, 13, 17, 22) but a hexagonal P2 to hexagonal P2 has not been found. Some preliminary indication of the two-phase behaviour was given for P2-Na_0.66[Li_0.22Ti_0.78]O₂.³⁹ The higher current rates used in these measurements may account for the presence of this two-phase region. What is noted in previous ex situ and in situ work on a related system is a solid solution reaction until 4.0 V where a two-phase reaction begins.²² The slight differences in the lattice parameters (reflection positions) observed in our study are likely to be interpreted as a solid solution mechanism in studies with insufficient angular resolution similar to our previous findings on the Na₃V₂O_2x(PO₄)₂F_3−2x system, where x = 0.8.^31,40 We term the phases “original P2” and “P2 new” respectively.

Fig. 1 Selected 2θ regions of in situ synchrotron XRD data highlighting the evolution of the (a) 002, (b) 004, 100, 101, and (c) 103 reflections in cell 1 by a colour scale and the potential profiles (right). The orange shaded box highlights the drastic reduction in reflection intensity during discharge in cell 1. The reflections marked with an * appear not to change at all during charge/discharge.

Fig. 2 (a) Snapshots via a stacked plot of the in situ data of the 002 reflection with the time shown on the right hand side and (b) focuses on this reflection during discharge. In (a) the red arrow shows the decrease in intensity around 35 minutes, the blue arrow the change in the 2θ position and the magenta arrow the decrease in intensity near the charged state. In (c) the 004, 100 and 101 reflections are shown, in (d) the 004 reflection region circled in (c) and in (e) the 100 reflection region circled in (c). In (d) the initial two-phase reaction around 35 minutes is evidenced, with the black arrow indicating the phase that disappears and the blue arrow showing the phase that appears and that undergoes a solid solution reaction. In (e) the two-phase reaction during discharge is shown with the appearance of the second phase, presumably “original P2”. The reflections marked with an * appear not to change at all during charge/discharge.

An interesting observation also appears around 3.96 V or ∼260 minutes into charge where the 002, 004, 100, 101 and 103 reflections not only start to stabilise (i.e., show minimal changes in their 2θ values) but also begin to dramatically decrease in measured intensity. No new reflections are apparent immediately but they begin to appear at 390 minutes which corresponds to the charged state at 4.2 V.

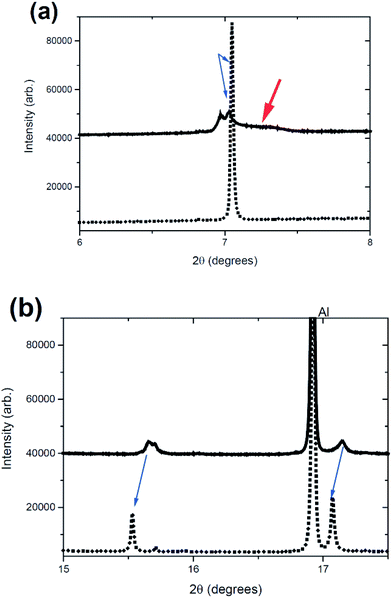
An odd feature is noted in the range 7 < 2θ < 7.5°, the red arrow in Fig. 2(b) and 3(a). It is a broad reflection that forms on discharge (from the charged state) and may indicate some superstructure contributions or more likely some disorder.^13,41 Disorder is the most likely explanation for the rapid decrease in intensity of certain reflections. Notably the reflection intensities decrease significantly for the 00l type reflections but the h00 and h0l reflections show a smaller decrease. The 00l reflections are associated with the stacking c axis of the layered structure. Furthermore at the end of charge, the amount of Na in the interlayer space is relatively low, and therefore, the layered structure may suffer from instabilities especially when O–O repulsion is large for the P2-phase. Therefore the disorder is likely to be correlated with a high level of stacking faults on the c stacking axis but a small amount of faults or “disorder” in the ab plane. If we compare the whole process against the literature,¹³ it appears that the broad reflections near the charged state are the OP4 phase or highly disordered P2 (with stacking faults). An alternative model is the so-called “Z” phase which using chemical desodiation methods on related systems has been found to show Fe³⁺ migration into the tetrahedral sites where sodium vacancies are located in the sodium-poor layers.^17,18,20

Fig. 3 Snapshots via a stacked plot of the in situ data of the (a) 002, (b) 100 and 102 reflections of the initial electrode (dotted line) and the charged/discharged electrode (solid line). The blue arrows indicate likely reflections that resemble the original P2 phase while the red arrow represents an interesting broad feature observed on discharge.

For most of the discharge process a two-phase reaction occurs that converts part of the electrode back to a phase very similar to the original cathode (original P2). The equivalent 002 reflection for the “P2 new” phase shows evidence of reflection position change (2θ-value) during discharge. In other words, “P2 new” undergoes a solid solution reaction while the two-phase reaction proceeds (to reform the “original P2” phase), e.g. similar to what is found in LiFePO₄ electrodes where both solid solution and two-phase reactions occur simultaneously.²⁴ At the discharged state there is co-existence of the “original P2”, “P2 new” and the OP4/“Z” or disordered phases (the OP4 and disordered phases are discussed below). Fig. 3 shows the first (2.8 V) and final pattern (1.5 V) collected in this experiment, i.e., electrode in the coin cell and the electrode after charge and discharge.

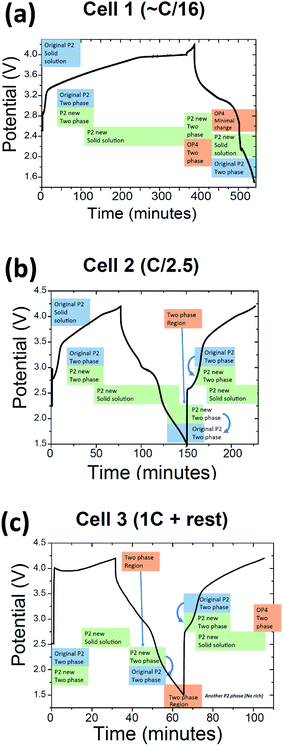
Fig. 4(a) summarises the phase evolution, essentially a solid solution of the “original P2” phase, then the two-phase reaction of what appears to be two P2 phases (“original P2” and “P2 new”) around 3.36 V, followed by a two phase reaction between the “P2 new” and OP4/“Z” phase extending from 3.96 V on charge to at least 3.45 V on discharge, followed by a reaction that generates the “original P2” phase for the remainder of discharge with some evidence of a solid solution reaction in the “P2 new” phase during the same discharge period. Note that slow current charge was initially used followed by a higher current charge/discharge and the capacity was 156 mA h g⁻¹ during charge and 146 mA h g⁻¹ during discharge. The slightly lower capacity during discharge arises from the high current rate used.

Fig. 4 The reaction mechanism evolution of the P2-Na_2/3Fe_2/3Mn_1/3O₂ cathode during (a) ∼C/16 and (b) C/2.5 charge and discharge and (c) during 1C charge and discharge followed by subsequent relaxation.

Cell 1: initial structural characterization

The initial OCV of the cell was 2.51 V and the cathode was fitted with the P2 model using the “O and P-type” definition of these layered phases as proposed by Delmas and co-workers.^37,42 The electrode crystal structure adopted P6₃/mmc symmetry and the refined lattice parameters were a = 2.95347(3) and c = 11.2414(1) Å. Crystallographic details can be found in Table 1 and the fit is shown in Fig. 5(a). The sodium occupancy (site occupancy factors or SOFs) and the atomic displacement parameters (ADPs) correlated to a certain extent and therefore were refined sequentially to obtain the model shown in Table 1.

Table 1 Refined crystallographic parameters for Na_0.597(8)Fe_2/3Mn_1/3O₂^a

Atom	Wyckoff	x	y	z	SOF	Isotropic ADP (×100/Å^2)
a Atomic displacement parameter (ADP), site occupancy factor (SOF). *Refined alternatively to SOFs and refined and fixed. # Constrained to be equal. Space group = P63/mmc, 23 refinement parameters, χ^2 = 3.64, Rp = 3.78%, wRp = 5.63%, a = 2.95347(3), c = 11.2414(1) Å.
Na(1)	2	0	0	0.25	0.179(5)	8.00*
Na(2)	2	1/3	2/3	0.75	0.418(8)	11.7*
Mn	2	0	0	0	1/3	13.6*^,#
Fe	2	0	0	0	2/3	13.6*^,#
O	4	1/3	2/3	0.1029(6)	1	20.4*

---

Fig. 5 Rietveld refined fit of the (a) Na_0.597(8)Fe_2/3Mn_1/3O₂ cell 1, (b) Na_0.637(10)Fe_2/3Mn_1/3O₂ cell 2, and (c) Na_0.637(10)Fe_2/3Mn_1/3O₂ cell 3 models to the initial in situ synchrotron XRD datasets. Data are shown as crosses, the calculated Rietveld model as a line through the data, and the difference between the data and the model as the line below the data. The vertical reflection markers are for models used and in (a) and (c) zoomed in sections are shown. For (c) the zoomed figure shows the presence of the 2^nd phase in this dataset. The feature at 2θ ∼ 10° is due to the carbon black used in the electrode material.^25,26 Note that the coloured 110 reflection features the textured Al 220 at the same 2θ location and this shows a mismatch in intensity for cells 2 and 3, see text for further details.

The refined sodium content is slightly lower than the expected sodium content of 2/3. Also note that extra reflections appear to be present in the diffraction patterns, denoted by the * in Fig. 5(a), but these do not evolve during charge/discharge as shown by the * in Fig. 1(a)–(c) and 2. The fitting statistics are likely to be influenced by these features.

Cell 1: evolution during battery function

As an initial approach to model the structural change of the electrode during the charge/discharge process, the P2 model defined above was used and the lattice parameter, sodium site occupancies and z positional parameter refined during a sequential refinement. The result is shown in Fig. 6(a).

Fig. 6 (a) A crude single phase picture of the evolution of the Na_0.597(8)Fe_2/3Mn_1/3O₂ electrode during charge/discharge. The volume (blue triangles), c (green diamonds) and a (purple triangles) lattice parameters, oxygen positional parameter (red circles), sodium SOF (black squares) and the potential profile. (b) The evolution of the Na_0.597(8)Fe_2/3Mn_1/3O₂ electrode during charge/discharge at ∼C/16. The volume (purple triangles), c (navy diamonds) and a (green triangles) lattice parameters, oxygen positional parameter (magenta triangles), Na site occupancies (red circles, black squares), total sodium content (blue triangles) and the potential profile. The transition between the “original P2” phase and the “P2 new” is the first shaded region, while the second shaded region represents the appearance of the OP4 phase. In the second shaded region only the “P2 new” phase is modelled. The black arrow indicates the approximate sodium content evolution if the formation of the OP4 phase is taken into account. Closer to discharge the “original P2” phase forms and its relative phase fraction is given by the red symbols in the upper most panel of the figure with the black symbols reflecting the “P2 new” phase fraction.

Using this crude single phase approximation, the c lattice parameter is shown to expand while the a lattice parameter contracts. Note, unlike the related O3 phase,¹⁵ the c lattice parameter does not expand and then decrease within the charge step. Interestingly the increase and subsequent decrease in the c lattice parameter during charge of layered cathodes are also observed in lithium-ion batteries via in situ neutron diffraction.^43,44 In order to “tune” the c lattice parameter behaviour in layered lithium-ion battery cathodes, the compositions of cathodes have to be adjusted. However, tuning the c lattice parameter from expansion followed by contraction during charge to solely expansion during charge can be undertaken by converting the initial polymorph of the electrode between O3 and P2 types in these sodium-ion battery cathodes under the electrochemical conditions used here. Thus, as expected polymorphic changes have a significant influence on lattice expansion/contraction and can be adjusted for the desired structure-electrochemistry outcome.

Further the c lattice parameter increases linearly until 280 minutes or 3.96 V at a rate of 7.04(9) × 10⁻⁴ Å min⁻¹ and then flattens out or decreases to the rate of increase to 2.6(7) × 10⁻⁵ Å min⁻¹ until the charged state (the rates of expansion are determined by linear fits to the data). This change in expansion occurs slightly before the reflection broadening. This reduction in the expansion of the c lattice parameter may instigate or lead to the observed disordered (OP4/“Z”) structure at the charged state. Speculatively, once the critical Na concentration is reached, the remaining Na concentration cannot support the layered structure as the O–O repulsion becomes too large, then stacking faults or Fe³⁺ migration and disorder begin to occur.

Notably the P2 phase is often considered superior in terms of electrochemical performance for the (in general the sodium transition-metal oxide) layered materials.^7,14 This observation might be related to the behaviour of the c lattice parameter, expanding and stabilising at the later stages of charge and thus showing comparably smaller volume fluctuations during charge relative to the O3-type phases.¹⁵ Comparatively the maximum and minimum values of the c lattice parameter in the O3-phase of the same composition investigated by in situ synchrotron XRD are ∼0.5 Å (ref. 15) while in the P2 case at this rate they are only ∼0.2 Å. In addition, the P2-phase has been considered not to undergo multiple phase transitions during the cycling while O3-phase does undergo multiple phase transitions.¹⁴ However, this may not be as general a statement as considered in previous work.^14,15 In any case, the number of phase transitions and smaller lattice expansion may result in better performance for the P2 phase compared to the O3-phase.

On charge the stabilisation of the c lattice parameter corresponds to the marked increase in the O positional parameter from z ∼ 0.1 to 0.14. Additionally, the Na(2) occupancy decreases virtually uniformly during charge, while the Na(1) occupancy is quite stable (<300 minutes or 3.97 V) until the last part of charge. Therefore, most of the charge in the initial stages of charge is likely to be carried by the Na(2) site; similar behaviour is seen in ex situ studies of Na_2/3Ni_1/3Mn_2/3O₂.⁴⁵ The Na(1) site increases in occupancy after ∼300 minutes or 3.97 V which is highly unusual and presumably characteristic of the growth of new phases in the cathode and the onset of another reaction mechanism as shown above. These new phases, e.g. OP4 or “Z”, are not modelled with the data and therefore the refined atomic parameters are significantly less reliable; however the lattice parameters, determined by reflection positions, of the modelled phases remain reliable.

The volume decreases with charge (Na removal) and increases on discharge. On the initial stages of discharge the c lattice and Na(1) occupancy (to an extent) decrease while the a lattice and Na(2) occupancy increase. However, all these parameters appear to stabilise (note that z stabilises at the start of discharge). The stable value is different from that of the original cathode, as expected since the cathode at this state would correspond to a different composition.

Now that the general trends are highlighted, below a more detailed structural evaluation is carried out, splitting the data into sections corresponding to the various phase transitions and other complexities in data analysis (Fig. 6(b)). The first 35 minutes or until 3.40 V a single phase electrode is used to model the evolution with the initial P2-phase defined in Table 1. Then a dataset is chosen in the middle of the “P2 new” phase or sodium-poor P2 phase at 225 minutes or 3.90 V and the structure is refined (lattice, sodium occupancies and oxygen positional parameter but ADPs kept to original values). This structure is then sequentially refined to the two phase region. Peak splitting is clearly observed in Fig. 2 and the similarity of such phases can be often overlooked with ex situ or lower resolution data.

The “P2 new” model was then refined to the charged state and during initial discharge to 406 minutes or 3.41 V on discharge. As noted in the single-phase approximation (Fig. 6(a)) the Na(1) content and total Na content increase around 300 minutes or 3.97 V and correspond to the dramatic decrease in the reflection intensities shown in Fig. 1(a)–(c) and 2. This is again accounted by the fact that the model does not take into account at these stages the OP4 or “Z” type phases. Thus, the structural model(s) do not appear to be modelling these data well. Taking a look at the data in this region (shaded section in Fig. 6(b)) shows the formation of broad reflections, in particular adjacent and at higher angles to the 001 reflection of the P2 phase (see Fig. 2(b)). This appears to correspond to the onset of a degradation in crystallinity possibly due to the formation of OP4 or “Z” type phases with their associated stacking faults or Fe³⁺ migration.^13,17,20 Note that the width of the reflection observed adjacent to the 001 reflection (Fig. 1(a)) may indicate multiple OP4-type phases or a structure with a large amount of stacking faults.

The OP4 phase reported for Na_xFe_1/2Mn_1/2O₂ (ref. 13) features lattice parameters of a = 2.874(2) Å and c = 20.29(1) Å with a Na content of 0.12 in the P6̄m2 setting. The lattice parameters of the OP4 phase within the Na_xFe_2/3Mn_1/3O₂ system are a ∼ 3.3 Å and c ∼ 21.88 Å, larger in both dimensions relative to the previously reported composition. Of importance is the broadness of the 004 reflection of the OP4 or “Z” phase, as shown in Fig. 7. The OP4 or “Z” type reflection is significantly broader than the P2 phases modelled (the initial model, Table 1, of the “original P2” and the “P2 new” phase). Note that the fit shown in Fig. 7 is almost immediately observed (with only the background and scale factors refining). It is obvious that the c lattice parameter of this OP4 phase or to model the disorder would have a wide range to cover the 7.05 ≲ 2θ ≲ 7.52° range that encompasses the broad 004 OP4 type reflection. Alternatively the “Z” phase could explain this behaviour, but in any case modelling atomic parameters, in the disordered OP4 or “Z” phase, is quite difficult, especially considering that the sample is inside a coin cell, rather than completely isolated as was demonstrated in a recent study (chemically desodiated sample).¹⁷ Further work is underway to investigate the disordered nature of this electrode at these states of charge.

Fig. 7 The initial fit of the “original P2”, the “P2 new” and the OP4-type phases to the reflection shown in Fig. 2(a) for the last dataset in the in situ experiment. The “original P2” phase fits the phase that reforms (see Fig. 2(a)) while the broad feature is associated with the OP4-type phase.

During discharge, the “P2 new” and the OP4/“Z” phases persist to the very last dataset collected in this experiment at the discharged state. Additionally from 410 minutes or 3.73 V on discharge the “original P2” phase begins to appear and grows rapidly from 495 minutes or below 2.85 V. The original phase was used to model this discharged phase and there were minimal changes in the lattice parameter (it could have been kept fixed). This highlights the reversible formation of the “original P2” phase; however it appears that a 3-phase coexistence exists at the discharged state. The ratio between “P2 new” and the “original P2” phase is 1 : 3, note that the disordered nature of the OP4/“Z” phase meant it was not modelled in this case, but future work is directed at characterising the disorder and faults.⁴¹

At the discharged state the “P2 new” phase loses most of the Na on the Na(2) site and shows predominant Na(1) site occupancy, the “original P2” phase that reforms has similar lattice parameters and so is likely to have the same Na distribution as the starting material. With this in mind, we kept the atomic parameters the same as the original phase for the reformed discharged version of it.

The anomalous increase in the Na(1) and total Na content during charge is likely associated with the formation of the OP4/“Z” phase and the charge being transferred via a two phase mechanism bringing the total sodium content in the electrode closer to the anticipated values. The black arrow in Fig. 6(b) indicates the overall sodium content trend that may be expected with such a transition. With further detailed modelling of the OP4/“Z”-type phases, the Na distribution and content near the charged state can be determined more accurately.

Cell 2: phase evolution

In this cell, a faster current rate is used and the charge/discharge/charge cycle is measured using in situ synchrotron XRD. Fig. 8(a)–(c) show the evolution of the 002, 004, 100, 101 and 103 reflections. There are clearly differences between the structural evolution observed at the higher rate, C/2.5, in cell 2 compared to the slower rate, ∼C/16, in cell 1. The first major difference is no evidence of the disordered phases (including OP4/“Z”) forming at the charged state. The second difference is a two-phase region near the discharged state (Fig. 8(c), expanded in Fig. 8(d)) and not throughout the entire discharge process as observed in cell 1 (Fig. 2(e)). The similarities between the two cells and their applied current rates include the trend in the evolution of the reflections, e.g. the 001 reflection moves to lower 2θ values during charge, and the two-phase region during the charge process which appears to be a sodium-rich and sodium-poor phase, e.g. “original P2” and “P2 new”. The latter is indicated by black arrows in Fig. 8(d) similar to Fig. 1(a).

Fig. 8 Selected 2θ regions of in situ synchrotron XRD data highlighting the evolution of the (a) 002, (b) 004, 100, 101, and (c) 103 reflections in cell 2 by a colour scale and the potential profiles (right). A zoomed in region near the discharged state of the 103 reflection is shown in (d). The reflections marked with an * appear not to change at all during charge/discharge.

Focusing on the two-phase region on initial charge observed in both cells, the data from cell 2 indicate that this process also occurs on 2^nd charge as shown in Fig. 9. This illustrates that the process occurs on subsequent cycles even at higher current rates and thus a process that is likely to occur on charge independent of the current rate used (see below for 1C).

Fig. 9 Snapshots via a stacked plot of the in situ data of the 002 reflection with the time and voltage shown. Figure (a) shows the first charge while (b) shows the 2^nd charge. In (c) the 004 reflection is shown at the discharged state.

It is interesting to note that no OP4/“Z” phase or evidence of disorder is seen near the charged state and on discharge at this higher current rate. An explanation for this may be that the depth of charge achieved at the higher rates is slightly lower than at slower rates. Comparing capacities in cell 2 the charge capacities are 149 and 148 mA h g⁻¹ relative to 156 mA h g⁻¹ for cell 1, while the discharge capacity is 144 mA h g⁻¹ compared to 146 mA h g⁻¹ for cell 1. The slightly lower capacity in combination with the higher current rates in the cell 2 electrode may place it in a state where the disordered structure does not form. Thus cycling these batteries at higher rates may prevent the formation of the OP4/“Z” or disordered phases and may preserve the structural integrity of the electrode. In other words, new phases are not nucleated and grown at the higher rates. In addition, a smaller capacity typically implies a lower amount of Na insertion/extraction, and the current rate used here may result in the electrode not reaching a sodium content that perpetuates the formation of the OP4/“Z” or disordered phases.

An interesting difference is observed in the discharged state, where a two-phase reaction is evident as shown in Fig. 9(c). The peak widths also show some increase. It is worthwhile to note that this two-phase region may be because the cell is discharged to 1.5 V. If the cut-off for the electrochemistry was set at 2 V, this reaction at the discharged state may not be observed. It is likely that this two-phase reaction forms the “original P2” phase (converting from “P2 new” to “original P2”) but since the structures are so similar it is hard to differentiate them. If the “original P2” phase forms then it undergoes a brief solid solution region before the transformation back to the “P2 new” phase. The sequence of the reaction mechanisms is described in Fig. 4(b).

Cell 2: structural characterization

The electrode crystal structure adopted P6₃/mmc symmetry and the refined lattice parameters were a = 2.95916(3) and c = 11.1489(1) Å which is slightly smaller in the stacking axis than for cell 1 discussed above (c = 11.2414(1) Å). Similar procedures to those described above were used. The crystallographic details can be found in Table 2 and the fit is shown in Fig. 5(b).

Table 2 Refined crystallographic parameters for Na_0.637(10)Fe_2/3Mn_1/3O₂^a

Atom	Wyckoff	x	y	z	SOF	Isotropic ADP (×100/Å^2)
a Atomic displacement parameter (ADP), site occupancy factor (SOF). *Refined alternatively to SOFs and refined and fixed. # Constrained to be equal. Space group = P63/mmc, 23 refinement parameters, χ^2 = 3.10, Rp = 4.75%, wRp = 8.73%, a = 2.95916(3), c = 11.1489(1) Å.
Na(1)	2	0	0	0.25	0.171(7)	3.55*
Na(2)	2	1/3	2/3	0.75	0.466(7)	1.84*
Mn	2	0	0	0	1/3	2.68*^,#
Fe	2	0	0	0	2/3	2.68*^,#
O	4	1/3	2/3	0.0914(5)	1	4.09*

---

It is interesting to note that the 110 reflection shows a distinct mismatch in intensity. There is a reflection marker at this location but there appears to be no intensity associated with this plane in the structure. However, in cell 1, there appears to be minimal intensity present in the 110 reflection (see Fig. 5(a)). Including another Na site above and below the Na(1) site⁴⁶ or placing Na along regions of weak positive Fourier electron density (Fig. S1 in the ESI†) does not improve the fit and the mismatch still exists. On closer inspection, the 110 reflection of the P2 phase lies directly underneath an intense 220 reflection of highly textured Al in this cell (and cell 3 below), but this Al reflection is absent in the data collected for cell 1. Thus by excluding the Al in cells 2 and 3 there is a large mismatch with the 110 reflection intensity. Unfortunately there is no confident method to model the textured Al reflections. Interestingly the lower cutoff Fourier intensities (Fig. S1† right) show a possible Na pathway for extraction/insertion.

Cell 2: evolution during battery function

The lattice parameters follow similar trends to cell 1, the a lattice parameter contracts on charge and expands on discharge (Fig. 10), likely to be associated with the changes in the oxidation state of Fe/Mn during charge and discharge. For charge the oxidation state increases, reducing the transition metal to oxygen bond length, contracting the octahedral layers and thus the a lattice parameter. While the c lattice expands on charge, as Na is removed, oxygens from adjacent layers repel each other causing an expansion of the cell. During discharge the c lattice parameter decreases.

Fig. 10 The evolution of the Na_0.637(10)Fe_2/3Mn_1/3O₂ electrode during charge/discharge. The c (navy triangles) and a (green diamonds) lattice parameters, oxygen positional parameter (magenta triangles), Na site occupancies (red circles, black squares), total sodium content (blue triangles) and the potential profile. The blue shaded regions represent two phase reactions occurring between the Na-rich and Na-poor phase and only a single phase is modelled in the figure and the arrows are described in the text.

Arguably the most powerful observations from such high quality data and detailed structural analysis are the atomic parameter evolution. Let us first consider the total sodium occupancy, Na(1) + Na(2). This decreases during charge as expected (red arrow in Fig. 10). The total sodium content increases during discharge but appears to go through a plateau type region (purple circle in Fig. 10) and this is correlated with a reduction in the oxygen position parameter. Additionally, at this plateau the Na(1) site appears to reach its maximum value and for the remainder of charge does not accept further sodium (equilibrates), and additional sodium is taken up by the Na(2) site. This is likely to be a critical factor why the Na(1) site shows lower Na occupancy than the Na(2) site. Earlier calculations and ex situ XRD work show similar trends.⁴⁵ Our initial speculation is that the dip in the oxygen positional parameter is a result of a Jahn–Teller influence which in turn slows the rate of sodium insertion into the crystal structure during discharge.

In the individual sodium sites, Na(1) and Na(2), the increase and decrease during discharge and charge respectively appear to follow similar trends, e.g. both increasing or decreasing rather than one site undergoing most of the process (with the exception of the region discussed above). The magnitude differs with the Na(1) site varying by 0.13 while the Na(2) site varies by 0.32. The Na(1) site does not drop below 0.13 while the Na(2) site does not drop below 0.17. Additionally the minimum total sodium content is 0.31 and this is seen on the charged state. This is slightly higher than the lowest Na content in cell 1 of ∼0.21 which complements the slightly lower capacity relative to cell 1.

Comparing the structure at the 2.86 V stage from the first in situ synchrotron XRD dataset to the 2^nd charge step at the same potential in cell 2 (ESI Table S1†), the sodium distribution between the sites is similar with a slight increase on the 2^nd charge. However, the largest difference appears to be the ∼0.6 Å increase in the lattice parameters on the 2^nd charge. The charged state features a composition of Na_0.326(12)Fe_2/3Mn_1/3O₂ (ESI Table S2†) with the largest decrease noted in the Na(2) site occupancy.

Cell 3: phase evolution

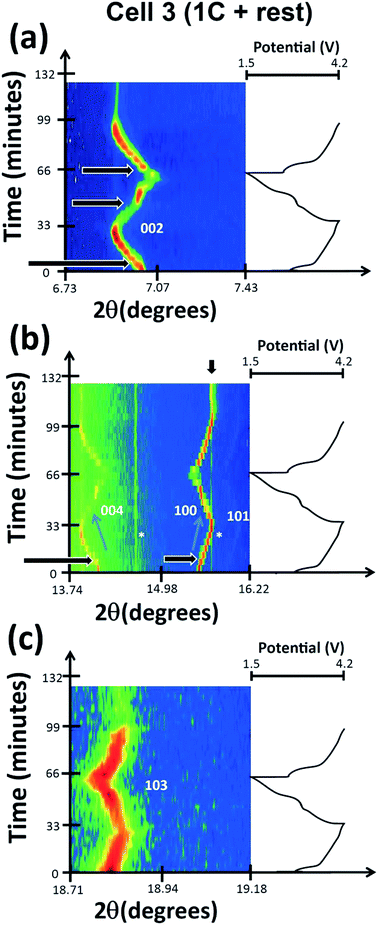
In this cell, two further factors were probed: first, cycling at an even higher rate, charge/discharge in 1 hour and second the influence of relaxing the cell or turning the current off. The current relaxation was chosen to occur at the charged state, as this was where disorder and the OP4/“Z” phase were observed in cell 1 but were not evident in cell 2 and at the 1^st charged state in cell 3 (see below). Unfortunately, a thinner electrode was used which does influence signal statistics, however the trends and analysis were still applicable.

Fig. 11(a)–(c) show the evolution of the 002, 004, 100, 101 and 103 reflections. On charge/discharge this cell resembles cell 2 and there is no evidence of the disordered or OP4/“Z” phase at the charged state. However, during the final proportion of 2^nd charge and subsequent relaxation step at the charged state there is a noticeable drop in reflection intensity, in particular for the 00l reflections (see Fig. 11(a)–(c) and 12), which are similar to that observed in cell 1 (slower rate charge). This suggests that the slower rates and cell relaxation at the charged state should result in the formation of disordered phases and/or the OP4/“Z” phase. Fig. 12 shows the 1^st charged state, 2^nd charged state and the relaxation process as a stacked plot. The loss in reflection intensity for the 002 reflection begins near the last stages of the 2^nd charge.

Fig. 11 Selected 2θ regions of in situ synchrotron XRD data highlighting the evolution of the (a) 002, (b) 004, 100, 101, and (c) 103 reflections in cell 3 by a colour scale and the potential profiles (right). The reflections marked with an * appear not to change at all during charge/discharge.

Fig. 12 Snapshots via a stacked plot of the in situ data of the 002 reflection with the time and voltage shown. Figure (a) shows the two-phase behavior during discharge while (b) shows a comparison of the charged states and the dramatic reduction of reflection intensity at the 2^nd charged state and during relaxation.

Every cell shows the two-phase region during charge (black arrows in Fig. 1, 8 and 11) and the same trend with respect to evolution during charge and discharge, e.g. 004 decreases in the 2θ position while 101 increases in the 2θ position during 1^st charge. Cell 2 and cell 3 (Fig. 11(a)–(c)) also show evidence of a two-phase reaction at the discharged state and as discussed above this could be the “P2 new” to “original P2” transition. Interestingly, cell 3 appears to show another two-phase region on discharge indicated by the arrow in Fig. 11(a) which could be a kinetic limitation of the electrode. Fig. 12 shows a stacked plot of this region illustrating the loss in reflection intensity of the 1^st phase, two-phase composition and growth of the 2^nd phase reflection intensity. This occurs very close to the onset of discharge and finishes before the inflexion point in potential during discharge. Fig. 4(c) shows the phase evolution of this cell.

Cell 3: structural characterization

The electrode crystal structure adopted P6₃/mmc symmetry and the refined lattice parameters were a = 2.94490(4) and c = 11.2263(2) Å where the stacking axis is in between the previous two cells (cell 2 with c = 11.1489(1) Å and cell 1 with c = 11.2414(1) Å). Crystallographic details can be found in Table 3 and the fit is shown in Fig. 5(c). A similar approach to the above is used in the refinements. Note that the 110 reflection again appears to show a poor fit to the collected data. This sample gives the highest sodium content of the electrodes analyzed; however, all cells average to ∼0.64. It is interesting to note that the second phase is already present in the original dataset due to the current rate employed, a rapid transition in this case.

Table 3 Refined crystallographic parameters for Na_0.681(16)Fe_2/3Mn_1/3O₂^a

Atom	Wyckoff	x	y	z	SOF	Isotropic ADP (×100/Å^2)
a Atomic displacement parameter (ADP), site occupancy factor (SOF). *Refined alternatively to SOFs and refined and fixed. # Constrained to be equal. Space group = P63/mmc, 25 refinement parameters, χ^2 = 1.66, Rp = 2.78%, wRp = 4.09%, a = 2.94490(4), c = 11.2263(2) Å.
Na(1)	2	0	0	0.25	0.267(10)	4.71*
Na(2)	2	1/3	2/3	0.75	0.414(12)	2.68*
Mn	2	0	0	0	1/3	3.87*^,#
Fe	2	0	0	0	2/3	3.87*^,#
O	4	1/3	2/3	0.0948(9)	1	7.30*

---

Cell 3: evolution during battery function

In this case a higher current was applied and on charge similar trends are observed in comparison with cell 2 (see Fig. 10 and 13), again noting that a single phase model was used. The red arrow indicates the drop in sodium content, with the charged state total sodium content of 0.43 corresponding to a smaller capacity at these rates (50 and 63 mA h g⁻¹ on charge and 54 mA h g⁻¹ on discharge). On discharge, again very similar behaviour to cell 2 is observed. In particular the sodium content increases and then stabilises, which corresponds to a significant change in the oxygen positional parameters (see the purple circle and arrows in Fig. 10 and 13). However, on closer inspection in both cases another parallel can be drawn. The apparent slowdown in the increase of sodium content and change in the oxygen positional parameter correspond to an obvious inflexion in the electrochemical curve (see the purple arrow in Fig. 13). Thus, the electrochemical curve appears to move from one region to another (between plateaus or between sloping regions) and this is correlated with the stabilisation in the sodium content of the P2 phase and change in the oxygen positional parameters. There appears to be a direct correlation between the structure and the electrochemical curve at this point. It also corresponds to the approximate end of the two-phase region found in this cell during discharge (Fig. 4(c)).

Fig. 13 The evolution of the Na_0.681(16)Fe_2/3Mn_1/3O₂ electrode during charge/discharge. The c (navy triangles) and a (green diamonds) lattice parameters, oxygen positional parameter (magenta triangles), Na site occupancies (red circles, black squares), total sodium content (blue triangles) and the potential profile. The arrows are described in the text.

In this cell, relaxation or the consequence of turning off the current with high current rate cycling was also examined. Relaxation was conducted at the charged state, since the charged state is often the least stable state in the electrode. Interestingly the lattice parameters maintain their value but the atomic parameters show some differences. The oxygen positional parameters change marginally, dropping and then increasing, to reach similar values to the charged state, while the total sodium content increases and then drops, to reach a higher value than at the charged state. This is reminiscent of discharge and may indicate an amount of self-discharge (or polarization/equilibration). Both Na sites increase from 0.23/0.24 to 0.43 and then drop down to 0.36. Therefore, these data indicate that some atomic relaxation occurs. Note, with XRD data, the results correspond to the average structure and atomic distribution but alternative in situ techniques that provide local information at high rates are at this point in time not available. However, if local sodium information could be probed at 1C then this would lead to further insight into the mechanisms reported here.

What is notable is the formation of the disordered or OP4/“Z” phase on the 2^nd charge/relaxation process as this implies that the OP4/“Z” phase forms due to the result of achieving equilibrium-like conditions. This supports the lower current rate results; the closer the electrode is to equilibrium-like conditions the more likely it will form the OP4/“Z” phase. For cell 3, it means that the OP4/“Z” phase can form when the overall electrode Na concentration > 0.33, as cell 3 does not drop below a sodium content of 0.36. Therefore, if sodium extraction is slow enough, the OP4/“Z” phase can form.

Discussion

Conventionally for the study of electrode crystal structures during battery charge or discharge or voltage-specific behaviour, the current is monitored and allowed to become stable – this is the equilibrium state. Typically ex situ and the majority of in situ measurements are performed with this or very similar conditions (low applied current). At a fast C-rate the equilibrium is clearly not attained,^15,27,47 and the Na distribution, volume change and phase transitions are likely to be at kinetically mediated states. Thus the electrode evolution described above can be dramatically different from that in equilibrium based studies. In essence, high rate performance is determined by the higher rate of structural changes and the typically lower amount of Na insertion/extraction, i.e. smaller capacity. If a phase formation process is composition or Na content dependent, then it may not appear at higher rates as the Na content may not reach the required concentration. This argument was expected to be illustrated for the OP4/“Z” phase at 1C cycling since the OP4/“Z” phase was expected to form below Na ∼ 0.33. However, the presence of OP4/“Z” at higher Na concentrations during high rate cycling/relaxation suggests that the bulk Na content is not necessarily the critical driver for this transformation.

Each electrode shows very similar initial composition or total Na content and distribution amongst the Na sites with the Na(2) site favoured. Considering the single phase model used in the sequential refinements (with the exception of cell 1 with the slowest rate) the Na(2) site shows the largest magnitude of sodium extraction of the two Na sites at every current rate. The trends in lattice evolution are similar during charge and discharge at each current rate but the rates of lattice expansion and contraction vary. Table 4 shows the lattice parameter rates of change at the current rates used in this study. The a and c lattice parameter rate of evolution increases by a factor of 2–3.5 from the C/2.5 to the 1C rate. This essentially shows a linear relationship between lattice expansion/contraction rates and the current rate, which is also found for some electrodes used in lithium-ion batteries.²⁵ The rates of expansion/contraction were determined using linear fits and the ∼C/16 cell had to be divided into two regions during charge and discharge. There is a ∼5 times increase in the rate of expansion/contraction of the lattice in the first region of charge from ∼C/16 to C/2.5. However, when the plateau in the lattice parameters is observed during charge (Fig. 6(a) and (b)) the expansion/contraction rate drops by at least an order of magnitude compared to C/2.5. A similar observation is made on discharge. Although not directly comparable due to the dramatic change in the lattice evolution between the slow and faster current rates, the lattice rate evolution increases with an overall increase in current.

Table 4 The rates of a and c lattice expansion and contraction during charge and discharge determined by performing linear fits on the sequentially determined Rietveld refined lattice parameters (Fig. 6(b)–(d))

Current rate used	Charge		Discharge		Charge
	a (Å)/min	c (Å)/min	a (Å)/min	c (Å)/min	a (Å)/min	c (Å)/min
∼C/16	−1.13(4) × 10^−4 to 3.96 V then −2.2(3) × 10^−5	7.04(9) × 10^−4 to 3.96 V then 2.6(7) × 10^−5	3.3(2) × 10^−4 to 3.34 V then 2.5(4) × 10^−5	−1.9(1) × 10^−3 to 3.34 V then −4.0(9) × 10^−5	—	—
C/2.5	−6.2(4) × 10^−4	3.6(1) × 10^−3	4.1(4) × 10^−4	−2.6(2) × 10^−3	−4.5(1) × 10^−4	2.8(1) × 10^−3
1C	−1.3(4) × 10^−3	7.7(3) × 10^−3	1.4(1) × 10^−3	−7.9(5) × 10^−3	−1.4(1) × 10^−3	7.8(7) × 10^−3

---

The C/2.5 and 1C rates show similar correlations of the oxygen positional parameter, total sodium content and the potential curve during discharge. The oxygen position reaches a minimum, the sodium content plateaus and a distinct feature is observed in the potential curve, see purple arrows in Fig. 10 and 13. Unfortunately, the three-phase mixture on discharge of cell 1 does not allow a good comparison to be made to cells 2 and 3.

Overall, there are marked differences in phase evolution between the cells 1–3 as shown by Fig. 4(a)–(c). However a new two-phase region on 1^st charge is noted in each case for the first time in these P2-type materials. The range appears to be dependent on the Na content, independent of the current rate used. With the single phase model during sequential refinements, the two-phase region appears between a total Na content of ∼0.640.56, 0.65–0.53 and 0.68–0.49 at the ∼C/16, C/2.5 and 1C rates respectively. This is very close to the original composition of the electrodes and suggests a subtle transition just below the synthesized composition and future work may look at compositions of Na_0.5Fe_2/3Mn_1/3O₂ to avoid this transition.

Another aspect that was considered was the formation of the P2′ phase adopting Cmcm orthorhombic space-group symmetry: however no evidence of this phase was found at the discharged states. The P2 model in P6₃/mmc fits the reflections and no new reflections indicative of the orthorhombic splitting are clearly present. Thus at the rates employed here it is possible that the Cmcm phase does not have sufficient time to nucleate and form, the P2 (P6₃/mmc) motif is retained.

Finally, let us consider the electrochemical capacity and the lowest sodium content observed at each rate. Cells cycled at ∼C/16, C/2.5 and 1C have charge/discharge capacities of 156/146, 149/144 and 50/54 mA h g⁻¹ respectively with the lowest sodium contents of ∼0.21, 0.31 and 0.43. The correlation between capacities and total sodium content is qualitatively as expected but note that each cell is different and future experiments will explore cycling a cell at different current rates to minimise differences between measurements. Most importantly the formation of the disordered phase at the higher rates and higher Na content show that this phase is stable even if total Na > 0.33. Cells were also tested offline in conventional cells at C/2.5 and 1C, noting that ∼C/16 was not tested as variable current rates were used during the in situ synchrotron XRD experiment (Fig. S2 in the ESI†). The capacities drop from approximately 120 mA h g⁻¹ to 60 mA h g⁻¹ after 30 cycles in conventional cells for both cases. The slightly higher observed capacities at 1C in conventional cells may be due to better contact in conventional cells compared to in situ cells.

Conclusions

The current-rate dependent behaviour of P2-Na_2/3Fe_2/3Mn_1/3O₂ electrodes shows dramatic differences when probed using time-resolved in situ synchrotron XRD. At every rate on charge a new two-phase region is found that converts a Na-rich P2 phase to a Na-poor P2 phase (termed P2 new): however, the space-group symmetry is preserved. The OP4 or disordered phase(s) forms in the charged state when cycled at ∼C/16 and when allowed to rest from the charged state after cycling at 1C. This phase(s) forms at low sodium contents between the layers and thus the presence of stacking faults is required to stabilise the electrode. In the case of ∼C/16 the disorder persists until discharge leaving a three-phase electrode in the discharged state. On discharge, at the 1C rate a new two-phase region is found, however, at this rate the P2 structure is maintained.

The maintenance of the P2 or the formation of the OP4/“Z” (disordered) structure is arguably the reason for the rate capability observed in these electrodes. Therefore, these non-equilibrium structural facts shed light on how electrodes actually behave in batteries with high-rate cycling. Using this information we can determine optimised routines for charging/discharging, i.e. are the OP4/“Z” or disordered phases beneficial or is it better to avoid them. In addition, new doping regimes can be trialled and compared to see if they influence the formation of these phases at various current rates. This approach can be used to design better electrodes and batteries.

Acknowledgements

We would like to thank undergraduate UNSW students Laura Jeffress, Damian Goonetilleke, Othman Al Bahri, Mackenzie Hagan and Emily Cheung for assistance during the in situ synchrotron XRD experiments. James C. Pramudita would like to thank UNSW/ANSTO for the PhD Scholarship. Neeraj Sharma would like to thank AINSE Ltd for providing support through the research fellowship scheme. Part of this research was undertaken on the Powder Diffraction beamline at the Australian Synchrotron, Victoria, Australia. CIC Energigune work was financially supported by Ministerio de Economía y Competitividad (Proyecto I+D. Retos 2013), reference number: ENE 2013-44330 R and FPDI-2013-17329, and the Gobierno Vasco/EuskoJaurlaritza (Etortek CICEnergigune 10, SAIOTEK-12 ENERGIBA and IT570-13).

Notes and references

1. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
2. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657.
3. T. C. Wanger, Conserv. Lett., 2011, 4, 202–206.
4. V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-Gonzalez and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901.
5. V. Palomares, M. Casas-Cabanas, E. Castillo-Martinez, M. H. Han and T. Rojo, Energy Environ. Sci., 2013, 6, 2312–2337.
6. M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958.
7. M. H. Han, E. Gonzalo, G. Singh and T. Rojo, Energy Environ. Sci., 2015, 8, 81–102.
8. Y. Li, Z. Yang, S. Xu, L. Mu, L. Gu, Y.-S. Hu, H. Li and L. Chen, Adv. Sci., 2015 DOI:10.1002/advs.201500031.
9. Y. H. Jung, A. S. Christiansen, R. E. Johnsen, P. Norby and D. K. Kim, Adv. Funct. Mater., 2015, 25, 3227–3237.
10. J. S. Thorne, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2014, 161, A2232–A2236.
11. P. Vassilaras, A. J. Toumar and G. Ceder, Electrochem. Commun., 2014, 38, 79–81.
12. W. K. Pang, S. Kalluri, V. K. Peterson, N. Sharma, J. Kimpton, B. Johannessen, H. K. Liu, S. X. Dou and Z. Guo, Chem. Mater., 2015, 27, 3150–3158.
13. N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, Nat. Mater., 2012, 11, 512–517.
14. E. Gonzalo, M. H. Han, J. M. Lopez del Amo, B. Acebedo, M. Casas-Cabanas and J. M. Rojo, J. Mater. Chem. A, 2014, 2, 18523–18530.
15. N. Sharma, E. Gonzalo, J. C. Pramudita, M. H. Han, H. E. A. Brand, J. N. Hart, W. K. Pang, Z. Guo and T. Rojo, Adv. Funct. Mater., 2015, 25, 4994–5005.
16. B. Mortemard de Boisse, J.-H. Cheng, D. Carlier, M. Guignard, C.-J. Pan, S. Bordere, D. Filimonov, C. Drathen, E. Suard, B. J. Hwang, A. Wattiaux and C. Delmas, J. Mater. Chem. A, 2015, 3, 10976–10989.
17. E. Talaie, V. Duffort, H. L. Smith, B. Fultz and L. F. Nazar, Energy Environ. Sci., 2015, 8, 2512–2523.
18. B. M. de Boisse, D. Carlier, M. Guignard, L. Bourgeois and C. Delmas, Inorg. Chem., 2014, 53, 11197–11205.
19. K. Kubota, I. Ikeuchi, T. Nakayama, C. Takei, N. Yabuuchi, H. Shiiba, M. Nakayama and S. Komaba, J. Phys. Chem. C, 2015, 119, 166–175.
20. N. Yabuuchi and S. Komaba, Sci. Technol. Adv. Mater., 2014, 15, 043501.
21. J. S. Thorne, R. A. Dunlap and M. N. Obrovac, J. Electrochem. Soc., 2013, 160, A361–A367.
22. G. Singh, J. M. Lopez del Amo, M. Galceran, S. Perez-Villar and T. Rojo, J. Mater. Chem. A, 2015, 3, 6954–6961.
23. N. Sharma, V. K. Peterson, M. M. Elcombe, M. Avdeev, A. J. Studer, N. Blagojevic, R. Yusoff and N. Kamarulzaman, J. Power Sources, 2010, 195, 8258–8266.
24. N. Sharma, X. Guo, G. Du, Z. Guo, J. Wang, Z. Wang and V. K. Peterson, J. Am. Chem. Soc., 2012, 134, 7867–7873.
25. N. Sharma and V. K. Peterson, Electrochim. Acta, 2013, 101, 79–85.
26. N. Sharma, D. Yu, Y. Zhu, Y. Wu and V. K. Peterson, Chem. Mater., 2013, 25, 754–760.
27. N. Sharma and M. Wagemaker, in Neutrons Applications in Materials for Energy, ed. V. K. Peterson and G. J. Kearley, Springer, Heidelberg, 2015, ch. 7, pp. 139–204.
28. H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, P. J. Chupas and C. P. Grey, Science, 2014, 344, 1252817.
29. Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, J. Am. Chem. Soc., 2013, 135, 5497–5500.
30. X. Zhang, M. van Hulzen, D. P. Singh, A. Brownrigg, J. P. Wright, N. H. van Dijk and M. Wagemaker, Nano Lett., 2014, 14, 2279–2285.
31. P. Serras, V. Palomares, T. Rojo, H. E. A. Brand and N. Sharma, J. Mater. Chem. A, 2014, 2, 7766–7779.
32. N. Sharma, P. Serras, V. Palomares, H. E. A. Brand, J. Alonso, P. Kubiak, M. L. Fdez-Gubieda and T. Rojo, Chem. Mater., 2014, 26, 3391–3402.
33. J. C. Pramudita, S. Schmid, T. Godfrey, T. Whittle, M. Alam, T. Hanley, H. E. A. Brand and N. Sharma, Phys. Chem. Chem. Phys., 2014, 15, 24178–24187.
34. K. S. Wallwork, B. J. Kennedy and D. Wang, AIP Conf. Proc., 2007, 879.
35. A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report LAUR 86-748, 1994.
36. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
37. R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74–80.
38. M. Guignard, D. Carlier, C. Didier, M. R. Suchomel, E. Elkaim, P. Bordet, R. Decourt, J. Darriet and C. Delmas, Chem. Mater., 2014, 26, 1538–1548.
39. Y. Wang, X. Yu, S. Xu, J. Bai, R. Xiao, Y.-S. Hu, H. Li, L. Chen and X. Huang, Nat. Commun., 2013, 4, 2365.
40. P. Serras, V. Palomares, J. Alonso, N. Sharma, J. M. Lopez del Amo, P. Kubiak, M. L. Fdez-Gubieda and T. Rojo, Chem. Mater., 2013, 25, 4917–4925.
41. J. Breger, M. Jiang, N. Dupre, Y. S. Meng, Y. Shao-Horn, G. Ceder and C. P. Grey, J. Solid State Chem., 2005, 178, 2575–2585.
42. C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85.
43. M. Alam, T. Hanley, W. K. Pang, V. K. Peterson and N. Sharma, Powder Diffr., 2014, 29, S35–S39.
44. O. Dolotko, A. Senyshyn, M. J. Muhlbauer, K. Nikolowski and H. Ehrenberg, J. Power Sources, 2014, 255, 197–203.
45. D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312.
46. T. Matsumura, N. Sonoyama and R. Kanno, Solid State Ionics, 2003, 161, 31–39.
47. N. Sharma, M. V. Reddy, G. Du, S. Adams, B. V. R. Chowdari, Z. Guo and V. K. Peterson, J. Phys. Chem. C, 2011, 115, 21473–21480.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic parameter tables and Fourier difference maps. See DOI: 10.1039/c5ta04976h

---