Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Why Ni is absent from the surface of La2NiO4+δ?
Ji
Wu
 a,
Stevin S.
Pramana
a,
Stephen J.
Skinner
a,
John A.
Kilner
ab and
Andrew P.
Horsfield
*a
a,
Stevin S.
Pramana
a,
Stephen J.
Skinner
a,
John A.
Kilner
ab and
Andrew P.
Horsfield
*a
aDepartment of Materials, Imperial College London, SW7 2AZ, London, UK. E-mail: a.horsfield@imperial.ac.uk; Tel: +44 (0)20 7594 6753
bHydrogen Production Division, International Institute for Carbon-Neutral Energy Research (I2CNER), Motooka 744, Nishi-Ku, Fukuoka 819-0395, Japan
First published on 16th October 2015
Abstract
La2NiO4+δ (LNO214) is a potential intermediate temperature solid oxide fuel cell (IT-SOFC) cathode material which belongs to the Ruddlesden–Popper (RP) structure series An+1BnO3n+1. There is interest in this material as it offers a way to avoid Sr segregation and associated degradation, as LNO214 can take in oxygen interstitials and become catalytically active without A-site doping. While the bulk ionic conduction mechanisms are well studied, its surface structure and chemistry are still a matter of debate. Recent experimental studies (both with and without dopants) reveal that it has a La-terminated surface and a highly Ni deficient surface layer. These results disagree with previous computer simulations, and undermine the conventional explanation for the oxygen reduction process at the surface. In this work we evaluate the thermodynamic stability of La2NiO4+δ at IT-SOFC operation temperatures. We find that the decomposition of La2NiO4+δ to produce La2O3 and higher order RP phases is indeed thermodynamically favourable. A hypothesis for the formation mechanism of the La-terminated and Ni deficient surface based on partial decomposition and surface passivation is proposed and evaluated.
1 Introduction
The Ruddlesden–Popper (RP) family material lanthanum nickelate, La2NiO4+δ (LNO214) (general formula An+1BnO3n+1), has attracted much interest in the past decade as a potential cathode material for intermediate temperature solid oxide fuel cells (IT-SOFC) operating at 600–800 °C.1–6 It has decent mixed ionic and electronic conductivities (55–65 S cm−1 overall at 500–750 °C)7 without the need for any A-site aliovalent doping due to the RP structure's ability to take in oxygen interstitials in the rock-salt-like AO layers.4 Compared to La1−xSrxCoO3−δ (LSC) and La0.6Sr0.4Fe0.2Co0.8O3−δ (LSCF), the LNO214 has lower total conductivity and oxygen self-diffusion coefficient at 500–750°C, but it also does not suffer from the Sr-segregation problem of the Sr-doped materials.7,8 The Sr-segregation severely damages the performance of LSC-based materials over time (typically 0.05% efficiency loss per hour).8,9 Therefore, LNO214 becomes a nice candidate for IT-SOFC cathodes considering long-term stability and cost-effectiveness. Both the bulk structure and oxygen ion diffusion mechanism in LNO214 are well understood with insights coming from computer simulations6 and experiments.4,5 However, the La2NiO4+δ surface structure and chemistry, which strongly affect surface oxygen exchange and limit the rate of overall oxygen ion migration, have not been explored in detail.There are only two sets of simulations of LNO214 surfaces performed so far10,11 to the best of the authors' knowledge. Read et al.10 suggested that LNO surfaces should terminate with Ni due to its lower surface energy. Zhou et al.11 studied the oxygen adsorption mechanism based on the La2NiO4 surface proposed in Read's work. However, the recent surface characterisation of similar RP structured materials, including La2NiO4+δ, La2−xSrxNiO4+δ (LSNO) and PrLaNiO4+δ (PLNO), has revealed that these surfaces terminate with purely A-site cations (La, Sr, and Pr);12–14 no Ni was found in the low energy ion scattering (LEIS) spectra of the surfaces within the detection limit. The Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La(Sr) ratio was also found to be far from stoichiometry down to a depth of about 7 nm.12 A similar absence of Ni and Ni
La(Sr) ratio was also found to be far from stoichiometry down to a depth of about 7 nm.12 A similar absence of Ni and Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La non-stoichiometry was obtained in LNO.14 These results suggest that the conventional oxygen reduction mechanism which requires oxygen atoms to adsorb onto surface Ni sites might not be possible.
La non-stoichiometry was obtained in LNO.14 These results suggest that the conventional oxygen reduction mechanism which requires oxygen atoms to adsorb onto surface Ni sites might not be possible.
In this study, we provide an explanation for the Ni absence on La2NiO4 surfaces by evaluating the thermodynamic stabilities of a set of related phases over a range of temperatures and oxygen partial pressures. The calculations are based on the existing experimental thermodynamic data for relevant materials.15,16 Based on our calculations, a hypothesis explaining the absence of Ni on LNO surfaces is proposed and discussed. We find that it is thermodynamically advantageous for La2NiO4 to form a combination of La2O3 (containing no Ni, and presumed to appear at the surface) and higher order RP phases (Lan+1NinO3n+1 where n = 2 or 3).
2 Method
The thermodynamic stability of LNO at any given temperature and oxygen partial pressure can be determined by considering the change in Gibbs free energy of its possible decomposition reactions. In this work, the following reactions are considered: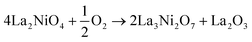 | (1) |
 | (2) |
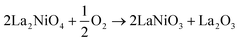 | (3) |
For ease of comparison, all reactions were normalised to consume half a mole of oxygen gas and produce one mole of La2O3.
The change in Gibbs free energy of the above reactions at different temperatures and oxygen partial pressures can be written as:
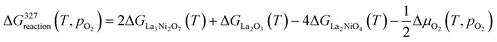 | (4) |
 | (5) |
 | (6) |
The standard molar Gibbs formation energy, ΔG0(T), of a compound phase can be expressed as:
ΔG0(T) = G(T) − HSER = a + bT + cT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(T) + ΣdnTn ln(T) + ΣdnTn | (7) |
| a (J mol−1) | b (J mol−1 K−1) | c (J mol−1 K−1) | d 2 (J mol−1 K−2) | d −1 (J K mol−1) | Ref. | |
|---|---|---|---|---|---|---|
| La2NiO4 | −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 095 095![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 507.6 507.6 |
1035.849 | −178.04 | −0.007089 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190 |
16 |
| La3Ni2O7 | −3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980.1 980.1 |
1781.990 | −301.86 | −0.01712 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580 580![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 |
| La4Ni3O10 | −4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431.3 431.3 |
2368.174 | −405.25 | −0.0326 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 |
| LaNiO3 | −1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967.7 967.7 |
696.185 | −118.12 | −0.0096 | 648![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
16 |
| La2O3 | −1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 835 835![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
674.72 | −118 | −0.008 | 620![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
17 |
The chemical potential of oxygen is given by18,19
 | (8) |
 | (9) |
 | (10) |
The constants A, B, C, D, E, F, G, and H are given in Table 2, and are obtained from the NIST chemical data handbook.19 The temperature coefficient t is 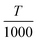 , where T is the temperature in Kelvin. The unit of
, where T is the temperature in Kelvin. The unit of 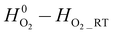 is kJ mol−1, where RT stands for room temperature (298.15 K), and the unit of
is kJ mol−1, where RT stands for room temperature (298.15 K), and the unit of  is J mol−1 K−1.
is J mol−1 K−1.
| Temperature (K) | 100–700 | 700–2000 | 2000–6000 |
|---|---|---|---|
| A (kJ mol−1 K−1) | 31.32234 | 30.03235 | 20.91111 |
| B (kJ mol−1 K−2) | −20.23531 | 8.772972 | 10.72071 |
| C (kJ mol−1 K−3) | 57.86644 | −3.988133 | −2.020498 |
| D (kJ mol−1 K−4) | −36.50624 | 0.788313 | 0.146449 |
| E (kJ K mol−1) | −0.007374 | −0.741599 | 9.245722 |
| F (kJ mol−1) | −8.903471 | −11.32468 | 5.337651 |
| G (kJ mol−1) | 246.7945 | 236.1663 | 237.6185 |
| H (kJ mol−1) | 0.0 | 0.0 | 0.0 |
The Gibbs free energy of selected decomposition reactions can now be calculated at various temperatures and oxygen partial pressures based on thermodynamic equations and associated constants given above.
It is important to note that the lanthanum nickelates are not stoichiometric when operating as a cathode under SOFC working conditions, where oxygen partial pressure is equal to or more than 0.2 bar. La2NiO4 is usually oxygen rich, while the higher order La3Ni2O7 and La4Ni3O10 are oxygen deficient. In this study, the thermodynamic equation constants of the compounds used are fitted as stoichiometric phases based on thermal measurements on real, non-stoichiometric phases.15–17 To provide a better prediction under experimental conditions, the error due to this difference should be estimated. For example, the Gibbs free energy of formation of the non-stoichiometric La2NiO4+δ is given as:
 | (11) |
 is the Gibbs free energy of formation of
is the Gibbs free energy of formation of  at temperature, T, and oxygen partial pressure, pO2. The chemical potential of
at temperature, T, and oxygen partial pressure, pO2. The chemical potential of  at this temperature and pressure is
at this temperature and pressure is  , while μLa, μNi and μO2 are the chemical potentials of reference elements La, Ni and oxygen gas at standard temperature and pressure.
, while μLa, μNi and μO2 are the chemical potentials of reference elements La, Ni and oxygen gas at standard temperature and pressure.
To determine the uncertainty in the experimental value, we need the stoichiometric Gibbs free energy of formation to compare with. The formation free energy of stoichiometric La2NiO4 is given by:
| ΔGLa2NiO4(T, pO2) = μLa2NiO4 − (2μLa + μNi + 2μO2) | (12) |
The difference between the experimental ΔGLa2NiO4+δ and ideal ΔGLa2NiO4 is then:
 | (13) |
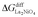 and
and  is equal to
is equal to  .
.
Similarly, for the higher order La3Ni2O7 and La4Ni3O10, there is:
 | (14) |
 | (15) |
 and
and  are defined in the same way as
are defined in the same way as 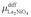 .
.
The differences in the chemical potential of respective LNO RP compounds can be estimated using their DFT calculated ground state energies, assuming a small free energy change due to entropy. The chemical potential of oxygen gas can be calculated using data from the NIST chemical database.19 The defect structures selected for DFT calculation are La2NiO4.25, La3Ni2O6.75 and La4Ni3O9.5. These non-stoichiometries are selected to represent extreme cases observed in experiments. The energy differences between these defect structures and their respective ideal structures are used to plot the Gibbs free energies of reaction when defect species are involved.
Taking the reaction between La2NiO4.25 and La3Ni2O7 as an example, for the overall reaction, we have:
| 4La2NiO4.25 → 2La3Ni2O7 + La2O3 | (16) |
Its Gibbs free energy of reaction will be:
 | (17) |
The other three defect reactions considered are:
 | (18) |
 | (19) |
 | (20) |
Free energy changes of these reactions are then plotted together with their respective ideal reactions.
All density functional theory calculations in this work have been performed using the CRYSTAL09 software package,20,21 based on the expansion of the crystalline orbitals as a linear combination of a local basis set consisting of atom-centered Gaussian orbitals. The basis sets used for Ni and O atoms are triple-valence all-electron basis sets. A Ni atom is described by a 28–411d(41) contraction (one s, four sp, -and two d shells). An O atom is described by an 8–411d(1) contraction (one s, three sp, and one d shells). The most diffuse sp(d) exponents are αNi = 0.6144(0.411) bohrs−2 and αO = 0.1843(0.6) bohrs−2.21 The La core electrons are described by using a pseudopotential, which is adapted from Dolg et al.'s quasirelativistic La pseudopotential.22 The La valence electron basis functions are 411p(411)d(311)f(11) contracted sets (three s, three p, three d and two f shells) with the most diffuse exponent being αLa = 0.15 bohrs−2 for each s, p, d and f shell.23 A ”ghost” atom is used to describe La vacancy by removing all but the two most diffuse contractions of each original La s, p, d and f shell. These basis sets ensure that we have an accurate description of electron density at the La vacancy site.
The B3LYP hybrid-exchange electron density functional,24 implemented in the CRYSTAL09 package, is used to approximate electron exchange and correlation. This hybrid functional is expected to give a reliable description of solid oxide systems such as the LNO-RP family oxides.23,25,26 Numerical integration of the exchange and correlation potentials and energy functional is performed on an atom-centered grid of points. The XXLGRID option implemented in CRYSTAL09 was used for all calculations, which consisted of a pruned grid consisting of 99 radial points and 5 subintervals with (146, 302, 590, 1454 and 590) angular points.21 The cutoff threshold parameters of direct summation of the Coulomb and exchange series are set to be 7, 7, 7, 7 and 14 as described in the CRYSTAL09 manual.21 A Pack–Monkhorst mesh with a shrinking factor of 8 was chosen for reciprocal space sampling of La2NiO4. For larger La3Ni2O7 and La4Ni3O10 systems, the shrinking factor used is 4. The structures selected as the initial input for DFT simulation are taken from Skinner's4 (La2NiO4) and Ling's27 (La3Ni2O7 and La4Ni3O10) neutron diffraction studies. The supercells used in the calculations are the respective minimum conventional crystallographic cells of La2NiO4 (28 atoms), La3Ni2O7 (24 atoms) and La4Ni3O10 (34 atoms). We computed the La vacancy migration barrier height using a (2 × 1 × 1) supercell of the conventional La2NiO4 lattice. This defective supercell contains 55 atoms. One of the La atoms is replaced by the La “ghost” atom mentioned above. Charge neutrality is maintained by promoting three Ni2+ atoms to Ni3+. The La vacancy migration energy is evaluated using the Distinguished Reaction Coordinate (DRC) method implemented in the CRYSTAL09 package. A full description of the DRC method and its robustness has been given by Rimola et al. and will not be detailed here.28
3 Results and discussion
3.1 Thermodynamic calculations
To study the thermodynamic feasibility of La2NiO4 decomposition, the Gibbs free energy of the reactions given in eqn (4) to (6) was calculated for temperatures in the range of 305 K to 1673 K, and oxygen partial pressure ranging from 1 × 10−25 bar to 1 bar. Plots of the results are given in Fig. 1–3.According to Fig. 1, the decomposition of La2NiO4 into higher order RP La–Ni–O materials is thermodynamically favourable up to about 1400 K at 0.2 bar oxygen partial pressure (atmospheric pressure of oxygen). La3Ni2O7 is the energetically favourable phase below 1000 K, while La4Ni3O10 will be more favourable above 1000 K. LaNiO3 is never the preferred phase over the entire temperature range considered. These results show that LNO would start to decompose when it is in contact with air even at room temperature. The decompositions will also take place at the designated IT-SOFC operation temperature (600–800 °C). We suspect that the decomposition products La2O3 and La3Ni2O7 will form a layered structure on top of the bulk La2NiO4. Taking the (001) surface as an example, there are two possible stacking orders, La3Ni2O7–La2O3–La2NiO4 and La2O3–La3Ni2O7–La2NiO4, with both being ordered from the surface to the bulk. The latter one is predicted to be the favourable stacking order. The first stacking order contains a large lattice mismatch between La2O3 and the two La–Ni–O RP phases, while the second one only contains one such large mismatch and one very small interfacial strain between the two La–Ni–O RP phases. The lattice mismatch between La3Ni2O7 and La2NiO4 is only about 1% at the (001) interface.4,27,29 This predicted stacking order is consistent with Druce et al.'s secondary ion mass spectrometry (SIMS) – low energy ion scattering (LEIS) depth profiling of polycrystalline La2NiO4. Druce's depth profile also showed a La enriched – Ni enriched – stoichiometric layered structure from the surface to the bulk of the crystal.14 The peak Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La ratio they observed in the Ni enriched region is about 2
La ratio they observed in the Ni enriched region is about 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, which agrees with the Ni
3, which agrees with the Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La ratio in our predicted sub-surface La3Ni2O7 layer.
La ratio in our predicted sub-surface La3Ni2O7 layer.
These predictions agree partly with a long-term decomposition experiment on La2NiO4+δ. In this experiment Gauquelin et al. heated La2NiO4+δ to 1273 K in flowing air for two weeks.30 The characterisation of the heated surface by transmission electron microscopy (TEM) revealed layers of La3Ni2O7 and La4Ni3O10 with thicknesses of about 700 nm. On the (100) surface, both La3Ni2O7 and La4Ni3O10 were found, but only La4Ni3O10 was present on the (001) surface. According to our calculations, La4Ni3O10 should be the most stable phase at 1273 K. The mixed layer of La4Ni3O10 and La3Ni2O7 may be due to incomplete conversion of La3Ni2O7 formed at a lower temperature during the heating process and the previous thermal history.
To form the transformed layers, La needs to move from the bulk to the surface. As there are different diffusion paths for La to the (001) and (100) surfaces we expect different La diffusion rates, and hence different growth rates for the transformed layers at these surfaces. One significant difference between our prediction and that of Gauquelin's experiment is that the other predicted product, La2O3, was not observed in the experiment.30 A surface layer only containing La2NiO4 and its higher order RP counterparts cannot give the La rich region observed by XPS12 and SIMS-LEIS depth profiling14 but rather the opposite (La deficient region30). Burriel et al. reported that the La and Sr rich surface layer is about 7 nm thick in the related La2−xSrxNiO4+δ phase. In Druce's more recent work,14 the La enriched layer is only about 1 nm thick in the depth profile of polycrystalline ceramic La2NiO4. Such a thin layer may be damaged by the destructive Focused Ion Beam (FIB) technique, which was used to cut a suitable lamellar cross-section at the surface for the TEM study in Gauquelin's experiment.
Despite the thermodynamically favoured decomposition process (about −100 kJ mol−1 for La2O3 production at room temperature), La2NiO4 is stable and does not transform into its higher order RP phases completely at room temperature. In the long-term decomposition experiment, only about 700 nm of the surface La2NiO4 was converted into La3Ni2O7 or La4Ni3O10 after two weeks.30 Therefore, there must be a very slow rate determining step or a surface passivation mechanism to prevent complete decomposition of La2NiO4. The three experimental studies mentioned earlier treated the samples differently (1273 K for two weeks (Gauquelin), 723 K for 72 hours (Burriel) and 1273 K for 12 hours (Druce)). A shorter heating time at a lower temperature gives a thinner transformed layer (only a few nanometers) than the high temperature, long-term heated sample (about 700 nm).12,14,30 Heating temperature and duration do have a significant impact on the amount of La2NiO4 transformed. The reactions that result in the formation of the surface oxide layer must therefore include at least one activation process. A strong candidate is the diffusion of La, a process that is necessary for the oxide formation, which will be activated. The diffusion barriers of several possible La diffusion paths are briefly evaluated in the next section. The large difference in the thickness of A-site enriched layers reported by Burriel and Druce, despite having similar thermal treatments, is believed to be mainly due to Sr segregation which only occurs in Burriel's Sr-doped La2−xSrxNiO4+δ. This would lead to a much thicker (7 nm compared to Druce's 1 nm) A-site (La + Sr) enriched region despite a similar thermal history. In addition, Burriel's sample is a single crystal while Druce tested a polycrystalline ceramic sample. The different natures of the samples should also affect the amount of decomposed La2NiO4.
Fig. 2 and 3 clearly show that oxygen partial pressure has a significant impact on the Gibbs free energy of these reactions. According to the graphs, the critical oxygen partial pressure required to allow decomposition varies with temperature. Therefore, the thickness of maximum decomposition layers formed at different temperatures after long heating times will vary with critical oxygen partial pressure. In a controlled low pO2 or high vacuum environment, this maximum transformation thickness can be measured to verify the hypothesis. If this proves to be true, controlling the oxygen partial pressure and the temperature might provide a way to suppress or reverse the decomposition when desired.
3.2 Density functional based calculations
To obtain a more complete picture of the decomposition thermodynamics, we used density functional theory simulations to check the effect of oxygen defects on the reactions as described in the Method section. Ideal experimental structures of the La–Ni–O compounds are fully relaxed and optimised first with antiferromagnetic ordering. The results are summarised in Table 3. The differences between the experimental structures and the calculated structures are small (less than 3%) in all three cases. Therefore, we believe the DFT simulations describe these Ruddlesden–Popper compounds well. Respective defective compounds are constructed by adding oxygen interstitials or vacancies to the relaxed ideal structures. The position of interstitials or vacancies is chosen according to the literature results.4,27 The defective compounds are then also relaxed and optimised for the evaluation of the Gibbs reaction energies' change due to the defects. The resulting Gibbs energies of the reaction for the different defect cases are plotted in Fig. 4 and 5.| Compound | a (Å) | b (Å) | c (Å) | Ref. | |
|---|---|---|---|---|---|
| La2NiO4 | Expt. | 5.459 | 5.464 | 12.685 | 4 |
| Calc. | 5.538(8) | 5.539(3) | 12.752(2) | ||
| Error | 1.47% | 1.39% | 0.52% | ||
| La3Ni2O7 | Expt. | 5.397 | 5.450 | 20.507 | 27 |
| Calc. | 5.435(0) | 5.586(1) | 20.868(3) | ||
| Error | 0.70% | 2.49% | 1.76% | ||
| La4Ni3O10 | Expt. | 5.413 | 5.462 | 27.960 | 27 |
| Calc. | 5.448(3) | 5.570(8) | 28.512(2) | ||
| Error | 0.65% | 1.99% | 1.97% |
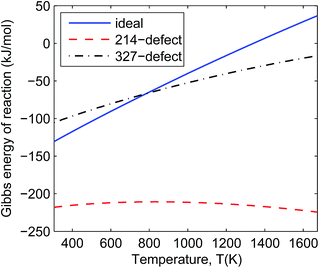
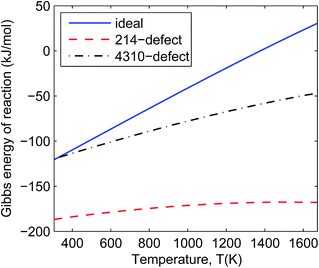
In Fig. 4 and 5 we can see that all the defective reactions still have negative reaction Gibbs energy in the IT-SOFC working temperature range (873–1073 K). The defective reactions seem to be always favourable even at temperatures beyond 1673 K according to the trend shown in Fig. 4 and 5. However, the assumption of small energy change due to entropy will not hold at temperatures much higher than 1673 K, so the estimated trends based on ground-state DFT calculations should only be used to predict reactions at lower temperature ranges. For the temperature range we are interested in (873–1073 K), these four reactions can give an idea of the order of magnitude of the decomposition Gibbs energies under experimental conditions since the involved phases are some of the extremely defective cases. It is noted that the 214-defect reactions are particularly favourable as shown in the figures (about 100 kJ mol−1 more favourable than ideal reactions). This suggests that a significant amount of energy is required to accommodate the oxygen interstitials in La2NiO4.25 at the ground state (DFT simulation condition). At the ground state (0 K), it is more difficult for the ideal lattice to take in an interstitial oxygen (like defective LNO214) than to lose an oxygen and form a vacancy (like defective LNO327 and LNO4310) due to the contraction of the lattice at a low temperature. This is one of the sources of errors when using DFT simulation to estimate the Gibbs energies of reaction for the defective reactions. At IT-SOFC working temperatures, the energy differences between the defective LNO214 reaction and the defective LNO327 (or LNO4310) reactions should be smaller. The actual Gibbs free energy of reaction will be affected by specific experimental conditions, including temperature, oxygen partial pressure, thermal histories and initial composition of the materials, but they will fall somewhere close to the calculated region where the Gibbs free energy of the decomposition reaction is less than zero. Therefore, the simple conclusion drawn from these estimations is that the decomposition will be favoured at IT-SOFC operation temperatures even for the extremely defective compositions.
As noted earlier, for the LNO214 structure to decompose, La atoms need to diffuse into the surface. As an activation process, this diffusion has an associated activation energy. We have computed the activation energy of two possible diffusion steps (shown in Fig. 6). We obtained a barrier height of 4.31 eV for the rocksalt path, and a height of 4.57 eV for the perovskite path. Although no experimental cation diffusion data for La2NiO4 are available, our calculated value for the perovskite layer (4.57 eV) is comparable to the La diffusion activation energy of 4.98 eV in LaCrO3.31 Compared to the oxygen diffusion activation energy (0.88 eV)5 in single crystal La2NiO4, the La diffusion activation energy is about five times as large. Assuming a simple Arrhenius relationship between the diffusion rate and the diffusion activation energy, we can estimate that the La diffusion rate is at least 3 orders of magnitudes smaller than the O diffusion rate. This might be part of the reason behind the limited decomposition. A more detailed study on the La diffusion during the decomposition reaction is being carried out, and the results will be presented in a future publication.
4 Conclusion
The decomposition of La2NiO4 into LaNiO3, La3Ni2O7 or La4Ni3O10 and La2O3 has been found to be thermodynamically favourable over the temperature range of 300 K to about 1373 K under 0.2 bar oxygen partial pressure, based on calculations using literature thermodynamic equation constants. The Gibbs free energy of reactions for La2NiO4 decomposition into LaNiO3, La3Ni2O7 or La4Ni3O10 and La2O3 are plotted over a range of temperature and oxygen partial pressure. It is then suggested that a partial decomposition of La2NiO4 takes place at the surface when exposed to air. Further estimation of the reaction energetics for defective reactions based on DFT also supports the hypothesis. The decomposition leads to a stacking of (La2O3)–(La3Ni2O7/La4Ni3O10)–(La2NiO4) (labelled from surface to bulk) depending on temperature. Such stacking could be responsible for the observed Ni-absence and Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La non-stoichiometry at La2NiO4 surfaces.12,14,30 This hypothesis agrees particularly well with Druce's depth profile of the near-surface composition of La2NiO4 measured by SIMS-LEIS.14 While the kinetics of the cation diffusion necessary for LNO214 decomposition are not known yet, the microstructures of the actual ceramic cathode in operation will play an important role. As pointed out by Kubicek et al., the grain boundaries and dislocations will act as short paths for fast cation diffusions, like Sr diffusion in La0.6Sr0.4CoO3−δ.32 The long term stability of La2NiO4 over 773–1023 K and its long-term performance as a cathode for IT-SOFCs are therefore uncertain. In addition, instead of an ideal La2NiO4 surface, the proposed oxidized La surface will quickly become the relevant surface for oxygen reduction and exchange under the IT-SOFC working environment. The oxygen reduction mechanism on such a surface requires investigation.
La non-stoichiometry at La2NiO4 surfaces.12,14,30 This hypothesis agrees particularly well with Druce's depth profile of the near-surface composition of La2NiO4 measured by SIMS-LEIS.14 While the kinetics of the cation diffusion necessary for LNO214 decomposition are not known yet, the microstructures of the actual ceramic cathode in operation will play an important role. As pointed out by Kubicek et al., the grain boundaries and dislocations will act as short paths for fast cation diffusions, like Sr diffusion in La0.6Sr0.4CoO3−δ.32 The long term stability of La2NiO4 over 773–1023 K and its long-term performance as a cathode for IT-SOFCs are therefore uncertain. In addition, instead of an ideal La2NiO4 surface, the proposed oxidized La surface will quickly become the relevant surface for oxygen reduction and exchange under the IT-SOFC working environment. The oxygen reduction mechanism on such a surface requires investigation.
Some questions remain unclear and cannot be answered with the hypothesis. Although thermodynamically favourable, the decomposition reactions studied were very slow as shown in experiments. The diffusion barrier of La is briefly evaluated and shows a quite high diffusion activation energy. The details of the decomposition reaction kinetics are being studied at the moment. These reaction kinetics will be critical to the evaluation of the long term stability of La2NiO4. Only a few particular decomposition reactions were considered in this study. Therefore, there might be other combinations of stable species. To find out the most stable combinations of phases, a density functional theory (DFT) based full phase diagram of the La–Ni–O system is planned.
Acknowledgements
The authors would like to thank the King Abdullah University of Science and Technology (KAUST) for funding this work through a KAUST-Imperial College Academic Excellence Alliance award. This work made use of the high performance computing facilities of Imperial College London and – via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202) – of the ARCHER UK National Supercomputing Service.References
- V. V. Kharton, A. P. Viskup, E. N. Naumovich and F. M. B. Marques, J. Mater. Chem., 1999, 9, 2623–2629 RSC.
- S. J. Skinner and J. A. Kilner, Solid State Ionics, 2000, 135, 709–712 CrossRef CAS.
- V. Kharton, A. P. Viskup, A. Kovalevsky, E. Naumovich and F. Marques, Solid State Ionics, 2001, 143, 337–353 CrossRef CAS.
- S. J. Skinner, Solid State Sci., 2003, 5, 419–426 CrossRef CAS.
- J. Bassat, P. Odier, A. Villesuzanne, C. Marin and M. Pouchard, Solid State Ionics, 2004, 167, 341–347 CrossRef CAS.
- A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266 RSC.
- J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
- E. Bucher and W. Sitte, Solid State Ionics, 2011, 192, 480–482 CrossRef CAS.
- H. Ding, A. V. Virkar, M. Liu and F. Liu, Phys. Chem. Chem. Phys., 2013, 15, 489–496 RSC.
- M. S. D. Read, M. S. Islam, G. W. Watson and F. E. Hancock, J. Mater. Chem., 2001, 11, 2597–2602 RSC.
- J. Zhou, G. Chen, K. Wu and Y. Cheng, J. Phys. Chem. C, 2013, 117, 12991–12999 CAS.
- M. Burriel, S. Wilkins, J. P. Hill, M. A. Muñoz Márquez, H. H. Brongersma, J. A. Kilner, M. P. Ryan and S. J. Skinner, Energy Environ. Sci., 2014, 7, 311 CAS.
- J. Druce, T. Ishihara and J. A. Kilner, Solid State Ionics, 2014, 262, 893–896 CrossRef CAS.
- J. Druce, H. Téllez, M. Burriel, M. D. Sharp, L. J. Fawcett, S. N. Cook, D. S. McPhail, T. Ishihara, H. H. Brongersma and J. A. Kilner, Energy Environ. Sci., 2014, 7, 3593–3599 CAS.
- M. Zinkevich and F. Aldinger, J. Alloys Compd., 2004, 375, 147–161 CrossRef CAS.
- M. Zinkevich, N. Solak, H. Nitsche, M. Ahrens and F. Aldinger, J. Alloys Compd., 2007, 438, 92–99 CrossRef CAS.
- A. N. Grundy, B. Hallstedt and L. J. Gauckler, J. Phase Equilib., 2001, 22, 105–113 CrossRef CAS.
- K. Johnston, M. Castell, A. Paxton and M. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 085415 CrossRef.
- P. Linstrom and W. Mallard, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, 2000 Search PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571–573 CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. Darco and M. Llunell, CRYSTAL09 Users' Manual, Universita di Torino, Torino, 2010 Search PubMed.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- D. Muñoz, N. Harrison and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 085115 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- J. Muscat, A. Wander and N. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
- G. Mallia and N. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165201 CrossRef.
- C. D. Ling, D. N. Argyriou, G. Wu and J. Neumeier, J. Solid State Chem., 2000, 152, 517–525 CrossRef CAS.
- A. Rimola, C. M. Zicovich-Wilson, R. Dovesi and P. Ugliengo, J. Chem. Theory Comput., 2010, 6, 1341–1350 CrossRef CAS.
- V. Voronin, I. Berger, V. Cherepanov, L. Gavrilova, A. Petrov, A. Ancharov, B. Tolochko and S. Nikitenko, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 470, 202–209 CrossRef CAS.
- N. Gauquelin, T. E. Weirich, M. Ceretti, W. Paulus and M. Schroeder, Monatsh. Chem., 2009, 140, 1095–1102 CrossRef CAS.
- T. Akashi, M. Nanko, T. Maruyama, Y. Shiraishi and J. Tanabe, J. Electrochem. Soc., 1998, 145, 2090 CrossRef CAS.
- M. Kubicek, G. M. Rupp, S. Huber, A. Penn, A. K. Opitz, J. Bernardi, M. Stöger-Pollach, H. Hutter and J. Fleig, Phys. Chem. Chem. Phys., 2014, 16, 2715–2726 RSC.
| This journal is © The Royal Society of Chemistry 2015 |