A global view of the phase transitions of SnO₂ in rechargeable batteries based on results of high throughput calculations

Abstract

Lithium, sodium and magnesium have attracted wide attention as potential ions for rechargeable batteries. The Materials Project database of high throughput first principles calculations is used to investigate the phase transitions of SnO₂ during ion intercalation and extraction. Various intermediate phases are predicted to be formed during the first intercalation, whereas in later cycles other intermediate phases are encountered. The volume expansions after intercalation and extraction are analyzed. We show that different lithium and sodium oxide products found in recent experiments are due to different oxygen chemical potentials.

---

Introduction

Lithium ion batteries are key components in current energy conversion and storage technologies because of their high energy density and long cycle life. However, the ever-growing need for high-capacity storage in applications ranging from portable electronic devices and electric vehicles to green energy requires new battery concepts. Recently, sodium^1–3 and magnesium⁴ ion batteries have attracted a lot of interest because of limited lithium reserves and the associated high costs. Alternative active anodes, such as SnO₂, are extensively investigated both experimentally and theoretically with respect to the intercalation, conversion, and alloying mechanisms.^5–13 In this context, SnO₂ possesses a low reaction potential and high theoretical capacity, being cheap and environmentally friendly.^11–16 Due to the relatively short history of SnO₂ based batteries, however, fundamental understanding of the reaction mechanism is missing. Experimentally, the reaction products can be investigated with respect to their short- and long-range atomic structures by X-ray, neutron, and electron diffraction, as well as by nuclear magnetic resonance and other methods.^9–13In situ observation of ion intercalation and extraction by transmission electron microscopy (TEM) has provided atomic scale insight into the reaction dynamics,^9,15–25 whereas theoretical transition barriers and the mechanical failure mechanism have been investigated by first principles calculations.^15–18 Yet, the understanding of the phase transitions in batteries based on SnO₂ is far from complete.

Using the Inorganic Crystal Structure Database,²⁶ the total energies and electronic structures of a large number of compounds have been determined by the Materials Project²⁷ and AFLOWLIB consortium²⁸ by high throughput schemes, making it possible to screen for specific properties²⁹ and new materials.^30,31 In this work, we demonstrate that the results of high throughput calculations can be used to construct phase diagrams by analyzing the relative thermodynamic stability of different phases using a free energy model.^27,32,33 This allows us to clarify the phase transitions of SnO₂ in Li/Na/Mg ion batteries and particularly to identify intermediate phases, which is key for understanding the battery processes.

Results and discussion

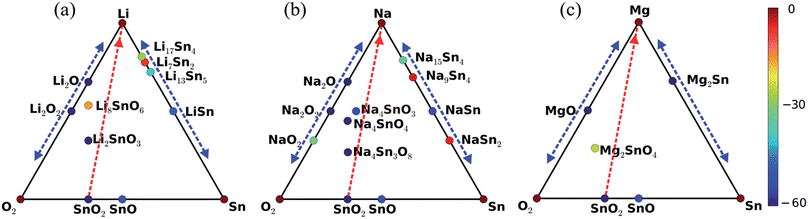
The high throughput data forming the basis of our investigation are taken from the Materials Project database and were obtained by density functional theory as implemented in the Vienna Ab initio Simulation Package,³⁴ using the generalized gradient approximation without and with the onsite Coulomb interaction.³⁵ The calculations took into account spin-polarization and employed an energy cutoff of 520 eV. The number of points in the k-mesh was set to 1000 divided by the number of atoms in the unit cell. The Gibbs free energy is defined as G(P, T) = U + PV − TS, where U, P, V, T, and S are the internal energy, pressure, volume, temperature, and entropy, respectively. In the alkali battery reactions, no gas phase reactants or products are involved and surfaces effects of the electrodes are not considered, so that P = 0 GPa and T = 0 K are valid approximations.^32,36–42 Therefore, G is given by the internal energy, which corresponds to the total energy of density functional theory.

We used the total energies E_i (per atom) of the involved elements as the reference to define the formation energy E = (E_tot − ∑N_iE_i)/∑N_i of a compound, where E_tot is the total energy of the compound and N_i is the amount of atoms in the compound. The structures of bulk lithium, sodium, and magnesium are shown in Fig. 1(a)–(c), respectively. It has been recently found that the reaction product after several cycles of lithiation and delithiation of β-Sn, SnS, and SnO₂ contains a mixture of β-Sn and α-Sn,³⁴ which are the two Sn polymorphs at ambient pressure. α-Sn (Fig. 1(d)) is stable at temperatures below 13.2 °C and β-Sn (Fig. 1(e)) at temperatures up to 232 °C. We note that cubic α-Sn is favored at small sizes.⁹ Sn nanostructures as a function of temperature and size have been investigated recently in ref. 38. The phase diagram of α-Sn, O, and Li/Na/Mg is shown in Fig. 2 including all stable compounds found in high throughput calculations.^27,28 The color indicates the formation energy per atom (E).

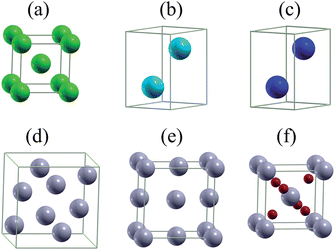Fig. 1 Unit cells of (a) Li, (b) Na, (c) Mg, (d) α-Sn, (e) β-Sn, and (f) SnO₂. Green, cyan, blue, gray, and red balls represent Li, Na, Mg, Sn, and O atoms.

Fig. 2 (a) Li, Sn, O₂, (b) Na, Sn, O₂, and (c) Mg, Sn, O₂ phase diagrams. Circles indicate stable compounds and the colors refer to the formation energy per atom (meV). The red arrow stands for the first intercalation, while the blue arrows represent the following intercalations/extractions.

It has been conjectured¹⁵ that the first step of the lithiation process is the insertion of Li⁺ into the SnO₂ lattice: SnO₂ + xLi⁺ + xe⁻ ↔ Li_xSnO₂. However, what is the detailed phase evolution? The first lithiation line in Fig. 2(a) shows that there exist two lithium tin oxides, Li₂SnO₃ and Li₈SnO₆, see Fig. 3(c) and (d), which have not been characterized experimentally so far. Li₂SnO₃ is obtained before Li₈SnO₆. Meanwhile, Sn and Li_xSn are formed by means of irreversible conversion of SnO₂ into Sn and lithium oxide: SnO₂ + 4Li⁺ + 4e⁻ → 2Li₂O + Sn. Finally, there is a reversible alloying reaction: Sn + xLi⁺ + xe⁻ ↔ Li_xSn. All encountered structures are shown in Fig. 3. For sodiation there exist three intermediate phases (Na₄Sn₃O₈, Na₄SnO₄, and Na₄SnO₃), see Fig. 4. Theoretically, all mentioned phases can form in Li/Na ion batteries, whereas experimentally it is challenging to identify them by conventional techniques, such as Raman spectroscopy and X-ray diffraction. However, identification can be achieved by in situ TEM, though the lithiation/sodiation front is tiny and the process is fast.^15–18

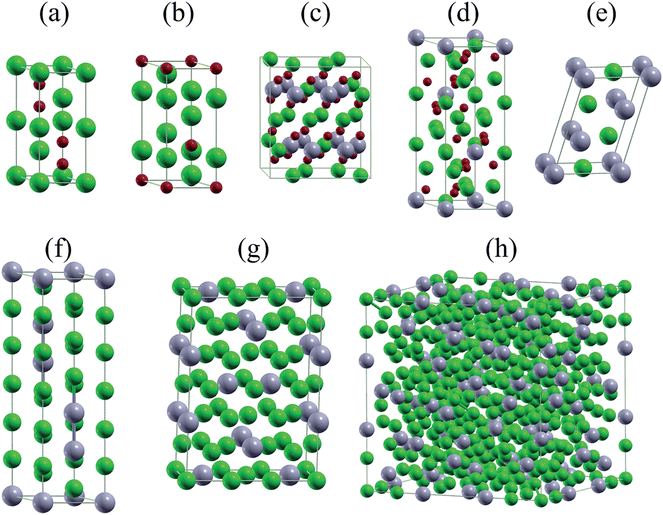Fig. 3 Unit cells of (a) Li₂O₂, (b) LiO₂, (c) Li₂SnO₃, (d) Li₈SnO₆, (e) LiSn, (f) Li₁₃Sn₅, (g) Li₇Sn₂, and (h) Li₁₇Sn₄. Green, gray, and red balls represent Li, Sn, and O atoms.

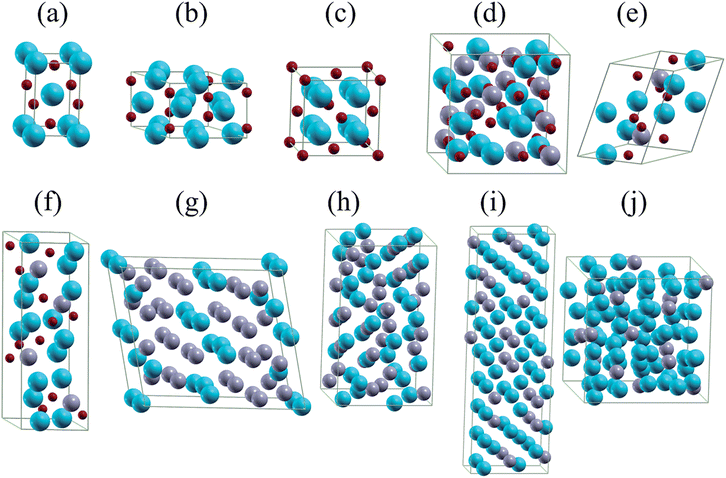Fig. 4 Unit cells of (a) NaO₂, (b) Na₂O₂, (c) Na₂O, (d) Na₄Sn₃O₈, (e) Na₄SnO₄, (f) Na₄SnO₃, (g) NaSn₂, (h) NaSn, (i) Na₉Sn₄, and (j) Na₁₅Sn₄. Cyan, gray, and red balls represent Na, Sn, and O atoms.

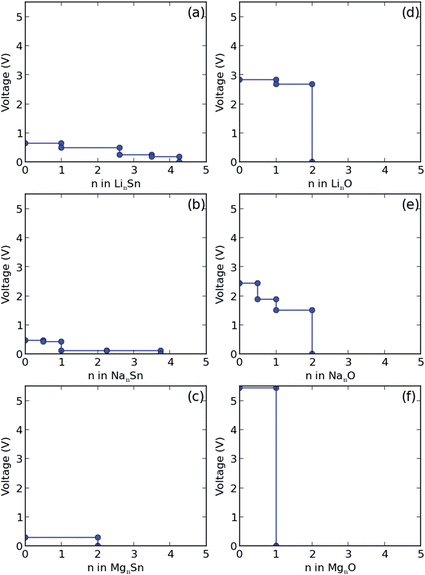
According to the phase diagram in Fig. 2(a), the final lithiation products are Li₂O and Li₁₇Sn₄. The voltage required for the initial lithiation from SnO₂ to Li₂SnO₃ ranges from 1.93 to 1.16 eV for different byproducts, see Table 1. The values are obtained as negative ratios of the change in G and the number of alkali atoms transferred.⁴³ It is known that Sn nanoparticles form during the first lithiation,¹⁵ while Li_xSn forms without Sn nanoparticles using LiCoO₂ as the cathode and a liquid-based electrolyte.¹⁸ The different lithiation products can be attributed to the different experimental setups. The voltage for the second lithiation from Li₂SnO₃ to Li₈SnO₆ is lower as compared to that for the initial lithiation. For lithiation to Li₂O, the voltage ranges from 0.82 to 1.12 eV. We found that the final product is Li₁₇Sn₄. During delithiation, Li₂O is assumed to be transformed into Li₂O₂ and Li₁₇Sn₄ into Sn. While a transformation from Li₁₇Sn₄ to Sn has already been reported,¹⁵ transformation from Li₂O to Li₂O₂ has not been observed yet. The absence of Li₂O₂ is explained by the fact that it will oxidize Li_xSn and Sn to transfer to Li₂O. Therefore, Li₂O is always present. The intermediate phases in later cycles (Li₇Sn₂, Li₁₃Sn₅, and LiSn) are different from those during the first lithiation. The voltage profile of Li_nSn shown in Fig. 5(a) is fully consistent with a previous report.⁴³ Moreover, the reversibility of the Li–Sn alloying process agrees with the cycling behavior observed in ref. 6 for SnO₂ anodes and the formation of Li₂O explains that experimentally the capacity of the battery is reduced after the first cycle.^6,8

Table 1 Voltage for different reaction paths for lithiation

Reaction	Voltage (eV)
4Li + 3SnO2 → 2Li2SnO3 + Sn	1.93
3Li + 3SnO2 → 2Li2SnO3 + LiSn	1.68
33Li + 15SnO2 → 10Li2SnO3 + Li13Sn5	1.39
11Li + 6SnO2 → 4Li2SnO3 + Li7Sn2	1.26
35Li + 12SnO2 → 8Li2SnO3 + Li17Sn4	1.16
4Li + 2Li2SnO3 → Li8SnO6 + Sn	1.36
3Li + 2Li2SnO3 → Li8SnO6 + LiSn	1.22
33Li + 10Li2SnO3 → 5Li8SnO6 + Li13Sn5	1.05
15Li + 4Li2SnO3 → 2Li8SnO6 + Li7Sn2	0.95
33Li + 8Li2SnO3 → 4Li8SnO6 + Li17Sn4	0.88
3Li + 5Li8SnO6 → 15Li2O2 + Li13Sn5	−16.06
3Li + 2Li8SnO6 → 6Li2O2 + Li7Sn2	−6.27
9Li + 4Li8SnO6 → 12Li2O2 + Li17Sn4	−4.12
5Li + Li8SnO6 → 6Li2O + LiSn	1.12
33Li + 5Li8SnO6 → 30Li2O + Li13Sn5	0.97
5Li + 2Li8SnO6 → 12Li2O + Li7Sn2	0.89
33Li + 4Li8SnO6 → 24Li2O + Li17Sn4	0.82

---

Fig. 5 Voltage profiles of (a) Li_nSn, (b) Na_nSn, (c) Mg_nSn, (d) Li_nO, (e) Na_nO, and (f) Mg_nO.

For the first sodiation we found the products Na₂O and Na₁₅Sn₄, as identified earlier.¹⁷ According to Fig. 2(b), there are three intermediate phases (Na₄Sn₃O₈, Na₄SnO₄, and Na₄SnO₃), which have not been observed so far, see the structures in Fig. 4. The voltage required for the first sodiation turns out to be lower than that for the first lithiation (Tables 1 and 2). The lower voltages indicate that sodiation is slower than lithiation, as found earlier for SnO₂,^16–18 which is supported by the higher transition barrier of Na as compared to that of Li. Fig. 2(b) shows that the desodiation products are Na₂O and Sn, as previously identified by TEM.¹⁷ There are Na₂O₂ as well as Na₉Sn₄, NaSn, and NaSn₂ intermediate phases and the voltage profile of Na_nSn in Fig. 5(b) is consistent with that reported in the literature.¹

Table 2 Voltage for different reaction paths for sodiation

Reaction	Voltage (eV)
4Na + 4SnO2 → Na4Sn3O8 + Sn	1.45
9Na + 8SnO2 → 2Na4Sn3O8 + NaSn2	1.34
5Na + 4SnO2 → Na4Sn3O8 + NaSn	1.25
25Na + 16SnO2 → 4Na4Sn3O8 + Na9Sn4	1.02
31Na + 16SnO2 → 4Na4Sn3O8 + Na15Sn4	0.85
4Na + Na4Sn3O8 → 2Na4SnO4 + Sn	0.65
9Na + 2Na4Sn3O8 → 4Na4SnO4 + NaSn2	0.63
5Na + Na4Sn3O8 → 2Na4SnO4 + NaSn	0.61
25Na + 4Na4Sn3O8 → 8Na4SnO4 + Na9Sn4	0.52
31Na + 4Na4Sn3O8 → 8Na4SnO4 + Na15Sn4	0.44
23Na + 4Na4SnO3 → 12Na2O + Na15Sn4	0.08
11Na + 4Na4SnO3 → 6Na2O2 + Na15Sn4	−1.47
5Na + 4Na4SnO3 → 6NaO2 + Na15Sn4	−5.50
17Na + 4Na4SnO3 → 12Na2O + Na9Sn4	0.08
5Na + 4Na4SnO3 → 6Na2O2 + Na9Sn4	−3.36
3Na + Na4SnO3 → 3Na2O + NaSn	0.05
5Na + 2Na4SnO3 → 6Na2O + NaSn2	−0.03
2Na + Na4SnO3 → 3Na2O + Sn	−0.15

---

Instead of Li₂O, Li–O₂ cell experiments found Li₂O₂ as the product by Fourier transform infrared spectroscopy and surface enhanced Raman spectroscopy.^44–46 Though there are reports about the formation of lithium superoxide (LiO₂) in the cell, LiO₂ is unstable and will disproportionate into Li₂O₂ and O₂.⁴⁶ Therefore, only Li₂O₂ and Li₂O appear in Fig. 3(a). According to the phase diagram in Fig. 2(b), there are three sodium oxide polymorphs (NaO₂, NaO, and Na₂O), for which the structures are displayed in Fig. 4(a)–(c). In situ TEM of sodiation of SnO₂ nanowires found Na₂O as the product,¹⁷ whereas crystalline sodium superoxide (NaO₂) was reported recently for a Na–O₂ cell.⁴⁷ The different alkali oxide products after intercalation can be attributed to the oxygen poor environment in the TEM experiments (high vacuum) and the oxygen rich environment in the Li/Na–O₂ cell. Voltage profiles of the Li–O₂ and Na–O₂ cells are shown in Fig. 5(d) and (e), respectively. The voltage for the formation of Li₂O₂ (2.8 eV) is consistent with the experimental value of 2.6 eV,^46,47 whereas that for the formation of NaO₂ (2.4 eV) exceeds the experimental value of 1.8 eV substantially.⁴⁷

Being an additional parameter of the ion battery performance, a large volume expansion indicates the high capacity of the anode but at the same time induces much damage. Since by ion intercalation into SnO₂ the volume will change, we studied the ratio V_products/V_SnO2, where V_products is the total volume of the products and V_SnO2 is that of SnO₂. We obtained values of 3.8/6.1 for Li/Na, which suggests a higher capacity for Na than for Li. For the extraction process, the result is 1.9/2.0 for Li/Na and thus more than 1, which indicates irreversibility for both Na and Li. The volume expansion after the first sodiation of a SnO₂ nanowire is 4.7,¹⁹ which is less than the theoretical value, and 2.6 after the first desodiation, which exceeds the theoretical value of 2.0. This discrepancy points to incomplete sodiation and desodiation in the experiment. Moreover, the volume expansion decreases for further sodiation and increases for further desodiation, which suggests the formation of intermediate structures that hinder the cycling and eventually result in failure of batteries. The formation of such structures also could be the origin of observed cracking.¹⁹ During a full cycle, the volume changes by a factor of 2.0 for Li and a larger factor of 3.0 for Na.

According to Fig. 2(c), there is only one intermediate phase for magnesiation (Mg₂SnO₄), see the structure in Fig. 6, and the products are MgO and Mg₂Sn. Because there are no other magnesium oxide phases, it is difficult to transform MgO, see the Mg_nO voltage profile in Fig. 5(f). By comparing Table 3 with Tables 1 and 2 we find that the voltage required for the first magnesiation is much higher than in the cases of lithiation and sodiation. The value of 5.5 eV is much higher than that found for lithiation and sodiation, which implies that SnO₂ is not a suitable anode for magnesium ion batteries. Only one magnesium tin alloy (Mg₂Sn) appears in Fig. 2(c). However, the Mg_nSn voltage is 0.3 eV and thus much lower than the values found for Li_nSn and Na_nSn. Therefore, it is expected that the products of demagnesiation are Sn and MgO. We obtained theoretical volume expansions of 3.1 and 2.0 for magnesiation and demagnesiation, respectively.

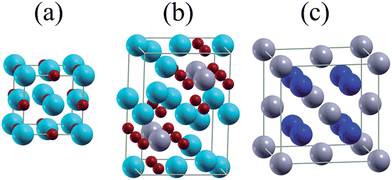Fig. 6 Unit cells of (a) MgO, (b) Mg₂SnO₄, and (c) Mg₂Sn. Blue, gray, and red balls represent Mg, Sn, and O atoms.

Table 3 Voltage for different reaction paths for magnesiation

Reaction	Voltage (eV)
2Mg + 2SnO2 → Mg2SnO4 + Sn	3.04
4Mg + 2SnO2 → Mg2SnO4 + Mg2Sn	1.66
2Mg + Mg2SnO4 → 4MgO + Sn	2.87
4Mg + Mg2SnO4 → 4MgO + Mg2Sn	1.58

---

While our present study focuses on the phase transitions in the SnO₂ electrode during alkali ion intercalation, typically also the interface between the electrolyte and the electrodes (both cathode and anode) plays an important role in the performance of batteries. For example, it has been demonstrated theoretically that the voltage depends on the surface charge density,^48,49 which can explain differences between experimental values and the voltages calculated for bulk electrodes. Important challenges for the first principles modeling in this area have been reviewed very recently in ref. 50.

Conclusions

Based on the results taken from the Materials Project database of high throughput first principles calculations, we have established the Sn, O, and Li/Na/Mg phase diagram for batteries based on SnO₂. For the first intercalation, we predict intermediate phases (Li₂SnO₃ and Li₈SnO₆ for lithiation, Na₄Sn₃O₈, Na₄SnO₄, and Na₄SnO₃ for sodiation, and Mg₂SnO₄ for magnesiation) which so far have not been verified experimentally. After full intercalation SnO₂ is transformed into tin alloys (Li₁₇Sn₄, Na₁₅Sn₄, and Mg₂Sn) and oxides (Li₂O, Na₂O, and MgO) and after full extraction the products are Sn and oxides (Li₂O₂, NaO₂, and MgO). The volume expansion after Li/Na/Mg intercalation is predicted as 3.8/6.1/3.1 and that after extraction as 1.9/2.1/2.0. Different oxide products found in recent experiments on Li/Na air batteries and in in situ TEM on nanowires are attributed to different oxygen chemical potentials in the two experiments. Comparison of different reaction paths allows us to predict that an applied voltage experimentally will have a crucial effect on the final products, which is an important insight because voltage dependent investigations are still strongly limited today. We have demonstrated that the results of high throughput calculations can be used for predicting the phase transitions in batteries and thus pave the way to provide instructions for the development of novel battery concepts.

Acknowledgements

Research reported in this publication was supported by the King Abdullah University of Science and Technology (KAUST).

References

1. V. L. Chevrier and G. Ceder, Challenges for Na-Ion Negative Electrodes, J. Electrochem. Soc., 2011, 158, A1011–A1014.
2. V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-Gonzalez and T. Rojo, Na-Ion Batteries, Recent Advances and Present Challenges to Become Low Cost Energy Storage Systems, Energy Environ. Sci., 2012, 5, 5884–5901.
3. N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research Development on Sodium-Ion Batteries, Chem. Rev., 2014, 114, 11636–11682.
4. H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Mg Rechargeable Batteries: an On-Going Challenge, Energy Environ. Sci., 2013, 6, 2265–2279.
5. J. Yang, M. Winter and J. O. Besenhard, Small Particle Size Multiphase Li-alloy Anodes for Lithium-ion-batteries, Solid State Ionics, 1996, 90, 281–287.
6. I. A. Courtney and J. R. Dahn, Electrochemical and In Situ X-ray Diffraction Studies of The Reaction of Lithium with Tin Oxide Composites, J. Electrochem. Soc., 1997, 144, 2045–2052.
7. Y. Idota, T. Kubota, A. Matsufuji, Y. Maekawa and T. Miyasaka, Tin-based Amorphous Oxide: A High-capacity Lithium-ion-storage Material, Science, 1997, 276, 1395–1397.
8. T. Brousse, R. Retoux, U. Herterich and D. M. Schleich, Thin-film Crystalline SnO₂-lithium Electrodes, J. Electrochem. Soc., 1998, 145, 1–4.
9. C. Kim, M. Noh, M. Choi, J. Cho and B. Park, Critical Size of a Nano SnO₂ Electrode for Li-secondary Battery, Chem. Mater., 2005, 17, 3297–3301.
10. Y. Wang, D. W. Su, C. Y. Wang and G. X. Wang, SnO₂@MWCNT Nanocomposite as a High Capacity Anode Material for Sodium-Ion Batteries, Electrochem. Commun., 2013, 29, 8–11.
11. D. W. Su, H. J. Ahn and G. X. Wang, SnO₂@Graphene Nanocomposites as Anode Materials for Na-ion Batteries with Superior Electrochemical Performance, Chem. Commun., 2013, 49, 3131–3133.
12. T. Xiao, Y. W. Tang, Z. Y. Jia and S. L. Feng, Synthesis of SnO₂/Mg₂SnO₄ Nanoparticles and Their Electrochemical Performance for Use in Li-ion Battery Electrodes, Electrochim. Acta, 2009, 54, 2396–2401.
13. Y. X. Wang, Y. G. Lim, M. S. Park, S. L. Chou, J. H. Kim and H. K. Liu, et al. Ultrafine SnO₂ Nanoparticle Loading onto Reduced Graphene Oxide as Anodes for Sodium-Ion Batteries with Superior Rate and Cycling Performances, J. Mater. Chem. A, 2014, 2, 529–534.
14. H. Zheng, J. B. Wang, J. Y. Huang, A. J. Cao and S. X. Mao, In Situ Visualization of Birth and Annihilation of Grain Boundaries in an Au Nanocrystal, Phys. Rev. Lett., 2012, 109, 225501.
15. A. M. Nie, L. Y. Gan, Y. C. Cheng, H. Asayesh-Ardakani, Q. Q. Li and C. Z. Dong, et al. Atomic-Scale Observation of Lithiation Reaction Front in Nanoscale SnO₂ Materials, ACS Nano, 2013, 7, 6203–6211.
16. J. Y. Huang, L. Zhong, C. M. Wang, J. P. Sullivan, W. Xu and L. Q. Zhang, et al. In Situ Observation of the Electrochemical Lithiation of a Single SnO₂ Nanowire Electrode, Science, 2010, 330, 1515–1520.
17. M. Gu, A. Kushima, Y. Y. Shao, J. G. Zhang, J. Liu and N. D. Browning, et al. Probing the Failure Mechanism of SnO₂ Nanowires for Sodium-Ion Batteries, Nano Lett., 2013, 13, 5203–5211.
18. C. M. Wang, W. Xu, J. Liu, J. G. Zhang, L. V. Saraf and B. W. Arey, et al. In Situ Transmission Electron Microscopy Observation of Microstructure and Phase Evolution in a SnO₂ Nanowire during Lithium Intercalation, Nano Lett., 2011, 11, 1874–1880.
19. M. Gu, Y. Li, X. L. Li, S. Y. Hu, X. W. Zhang and W. Xu, et al. In Situ TEM Study of Lithiation Behavior of Silicon Nanoparticles Attached to and Embedded in a Carbon Matrix, ACS Nano, 2012, 6, 8439–8447.
20. N. Liu, H. Wu, M. T. McDowell, Y. Yao, C. M. Wang and Y. Cui, A Yolk-Shell Design for Stabilized and Scalable Li-Ion Battery Alloy Anodes, Nano Lett., 2012, 12, 3315–3321.
21. X. H. Liu, Y. Liu, A. Kushima, S. L. Zhang, T. Zhu and J. Li, et al. In Situ TEM Experiments of Electrochemical Lithiation and Delithiation of Individual Nanostructures, Adv. Eng. Mater., 2012, 2, 722–741.
22. X. H. Liu, J. W. Wang, S. Huang, F. F. Fan, X. Huang and Y. Liu, et al. In Situ Atomic-Scale Imaging of Electrochemical Lithiation in Silicon, Nat. Nanotechnol., 2012, 7, 749–756.
23. X. H. Liu, J. W. Wang, Y. Liu, H. Zheng, A. Kushima and S. Huang, et al. In situ Transmission Electron Microscopy of Electrochemical Lithiation, Delithiation and Deformation of Individual Graphene Nanoribbons, Carbon, 2012, 50, 3836–3844.
24. X. H. Liu, L. Zhong, S. Huang, S. X. Mao, T. Zhu and J. Y. Huang, Size-Dependent Fracture of Silicon Nanoparticles during Lithiation, ACS Nano, 2012, 6, 1522–1531.
25. H. Yang, S. Huang, X. Huang, F. F. Fan, W. T. Liang and X. H. Liu, et al. Orientation-Dependent Interfacial Mobility Governs the Anisotropic Swelling in Lithiated Silicon Nanowires, Nano Lett., 2012, 12, 1953–1958.
26. G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, The Inorganic Crystal-Structure Database, J. Chem. Inf. Comput. Sci., 1983, 23, 66.
27. A. Jain, G. Hautier, C. J. Moore, S. P. Ong, C. C. Fischer and T. Mueller, et al. A High-Throughput Infrastructure For Density Functional Theory Calculations, Comput. Mater. Sci., 2011, 50, 2295–2310.
28. S. Curtarolo, W. Setyawan, S. D. Wang, J. K. Xue, K. S. Yang and R. H. Taylor, et al. AFLOWLIB.ORG: A Distributed Materials Properties Repository From High-Throughput Ab Initio Calculations, Comput. Mater. Sci., 2012, 58, 227–235.
29. S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, The High-Throughput Highway to Computational Materials Design, Nat. Mater., 2013, 12, 191–201.
30. A. N. Kolmogorov and S. Curtarolo, Prediction of Different Crystal Structure Phases in Metal Borides: A Lithium Monoboride Analog to MgB₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 180501.
31. A. N. Kolmogorov, S. Shah, E. R. Margine, A. F. Bialon, T. Hammerschmidt and R. Drautz, New Superconducting and Semiconducting Fe-B Compounds Predicted with an Ab Initio Evolutionary Search, Phys. Rev. Lett., 2010, 105, 217003.
32. S. P. Ong, L. Wang, B. Kang and G. Ceder, Li-Fe-P-O₂ Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20, 1798–1807.
33. S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Thermal Stabilities of Delithiated Olivine MPO₄ (M = Fe, Mn) Cathodes Investigated Using First Principles Calculations, Electrochem. Commun., 2010, 12, 427–430.
34. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. A. Jain, G. Hautier, S. P. Ong, C. Moore, C. C. Fischer and K. A. Persson, et al. Formation Enthalpies by Mixing GGA and GGA+U calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115.
36. K. Reuter and M. Scheffler, Composition, Structure, and Stability of RuO₂(110) as a Function of Oxygen Pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406.
37. K. Reuter and M. Scheffler, First-Principles Atomistic Thermodynamics for Oxidation Catalysis: Surface Phase Diagrams and Catalytically Interesting Regions, Phys. Rev. Lett., 2003, 90, 046103.
38. N. G. Hörmann, A. Gross and P. Kaghazchi, Semiconductor-Metal Transition Induced by Nanoscale Stabilization, Phys. Chem. Chem. Phys., 2015, 17, 5569–5573.
39. M. H. Hansen, L. A. Stern, L. G. Feng, J. Rossmeisl and X. L. Hu, Widely Available Active Sites on Ni₂P for Electrochemical Hydrogen Evolution – Insights from First Principles Calculations, Phys. Chem. Chem. Phys., 2015, 17, 10823–10829.
40. M. Nielsen, M. E. Bjorketun, M. H. Hansen and J. Rossmeisl, Towards First Principles Modeling of Electrochemical Electrode–Electrolyte Interfaces, Surf. Sci., 2015, 631, 2–7.
41. M. Garcia-Mota, A. Vojvodic, F. Abild-Pedersen and J. K. Norskov, Electronic Origin of the Surface Reactivity of Transition-Metal-Doped TiO₂(110), J. Phys. Chem. C, 2013, 117, 460–465.
42. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter and P. G. Moses, et al. Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99, 016105.
43. I. A. Courtney, J. S. Tse, O. Mao, J. Hafner and J. R. Dahn, Ab Initio Calculation of the Lithium–Tin Voltage Profile, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 15583–15588.
44. T. Zhang and H. S. Zhou, A Reversible Long-Life Lithium–Air Battery in Ambient Air, Nat. Commun., 2013, 4, 1817.
45. Z. Q. Peng, S. A. Freunberger, Y. H. Chen and P. G. Bruce, A Reversible and Higher-Rate Li-O₂ Battery, Science, 2012, 337, 563–566.
46. Z. Q. Peng, S. A. Freunberger, L. J. Hardwick, Y. H. Chen, V. Giordani and F. Barde, et al. Oxygen Reactions in a Non-Aqueous Li⁺ Electrolyte, Angew. Chem., Int. Ed., 2011, 50, 6351–6355.
47. P. Hartmann, C. L. Bender, M. Vracar, A. K. Durr, A. Garsuch and J. Janek, et al. A Rechargeable Room-Temperature Sodium Superoxide (NaO₂) Battery, Nat. Mater., 2013, 12, 228–232.
48. K. Leung and C. M. Tenney, Toward First Principles Prediction of Voltage Dependences of Electrolyte/Electrolyte Interfacial Processes in Lithium Ion Batteries, J. Phys. Chem. C, 2013, 117, 24224–24235.
49. K. Leung, Predicting the Voltage Dependence of Interfacial Electrochemical Processes at Lithium-Intercalated Graphite Edge Planes, Phys. Chem. Chem. Phys., 2015, 17, 1637–1643.
50. N. G. Hörmann, M. Jäckle, F. Gossenberger, T. Roman, K. Forster-Tonigold and M. Naderian, et al. Some Challenges in the First-Principles Modeling of Structures and Processes in Electrochemical Energy Storage and Transfer, J. Power Sources, 2015, 275, 531–538.

---