Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Perovskite La0.6Sr0.4Cr1−xCoxO3−δ solid solutions for solar-thermochemical fuel production: strategies to lower the operation temperature†
A. H.
Bork
,
M.
Kubicek
,
M.
Struzik
and
J. L. M.
Rupp
*
Electrochemical Materials, Department of Materials, ETH Zurich, Switzerland
First published on 18th June 2015
Abstract
Storing abundant solar energy in synthetic fuels is key to ensure a sustainable energy future by replacing fossil fuels and reducing global warming emissions. Practical implementation of the solar-to-fuel technology is predicated on finding new materials with higher efficiency and lower operation temperature than state-of-the-art materials. We use criteria aimed for designing such efficient solar-to-fuel conversion materials in the perovskite system. Based on thermodynamic considerations, the first perovskite solute–solution series, La0.6Sr0.4Cr1−xCoxO3−δ, is investigated to gain fundamental understanding on the role of B-site cationic doping in water and CO2 splitting to produce synthetic fuel. Notably, all of the novel material compositions operate in a strongly lowered temperature regime of 800–1200 °C compared to state-of-the-art binary oxides in the field. We found an optimum in doping for fuel production performance, namely La0.6Sr0.4Cr0.8Co0.2O3−δ, which viably splits both CO2 and H2O. Based on thermogravimetric analysis, we show that the highest performing perovskite splits 25 times more CO2 compared to the current state-of-the-art material, ceria, for two-step thermochemical cycling at 800–1200 °C. No adverse formation of carbonates in a CO2 atmosphere or cation segregation was observed in near and long range structural investigations, which highlight the durability and potential of these solid solutions. These new perovskite compositions enable lowering of the standard solar-to-fuel reactor temperature by 300 °C. The lowered operating temperature has tremendous implications for solar-synthesized fuels in a reactor in terms of lowered heat loss, increased efficiency, and reactor materials.
1. Introduction
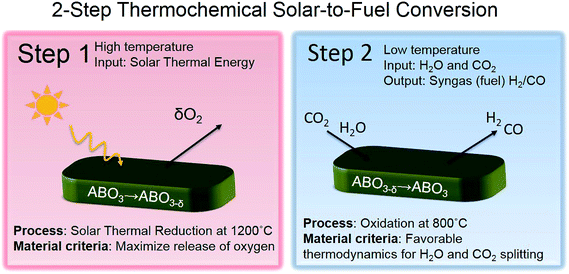
The efficient use of renewable resources and transition away from the dependence of fossil fuels is a global challenge of the 21st century. Energy storage and harvesting solutions beyond batteries and without restrictions on the storage capacity of materials are the key.1,2 Today's electrochemical and photochemical energy converters and electrolysis provide new promise to profit on renewable fuel production and storage in sizable-tanks with no volume restrictions. A critical element in the pursuit of this quest is the design of materials towards efficient splitting of water and carbon dioxide to obtain hydrogen and carbon monoxide, from which storable liquid fuels can be produced. For our society, solar-synthesized chemicals and fuels are an important storable energy resource contributing to global energy management strategies.3,4In solar-to-fuel conversion, a metal oxide (ceramic) is thermally reduced in the first step by concentrated solar power and then re-oxidized in the second step by splitting CO2 and H2O to syngas (CO and H2). The efficiency of the process depends on the effective oxygen stoichiometry variation of the metal oxide and its catalytic activity towards the educts. Earlier system studies of solar hydrogen production show that higher theoretical efficiencies can be achieved for two-step solar thermochemical hydrogen production compared to other techniques such as photoelectrolysis or photovoltaics with an electrolyser.5,6 A solar-driven thermochemical cycle is exemplified by a binary metal oxide in the following two-step thermochemical reactions, see Fig. 1:
 | (1) |
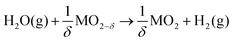 | (2a) |
 | (2b) |
Ceria shows promise for solar-driven thermochemical fuel production due to its stability at high temperature as well as desirable thermodynamic and kinetic characteristics.7 Additionally, it has the highest recorded efficiency for actual on-sun testing.8 Despite its promise, the potential to further increase the efficiency by varying the oxygen non-stoichiometry at lowered operation temperature is thermodynamically limited for ceria solid solutions. Various extrinsic trivalent dopants such as Gd, Y, Sm, Sr, and Ca in ceria have been tested to improve the solar-thermochemical fuel production, but with a minor effect on the solar-to-fuel efficiency;9 in terms of defect thermodynamics (Brouwer diagrams) this is to be expected, see Mogensen,10 Bishop,11 Wachsman12 and Rupp13,14 for details. In contrast, substitution of ceria solid solutions with smaller isovalent cations such as Zr4+ results in a remarkable increase of the defect association energy whereby the changed cerium coordination in the fluorite structure favors the formation of oxygen vacancies.15–17 Among all tested dopants, the ceria–zirconia solid solutions reveal the highest potential to increase the oxygen storage capacity.18 However, the very high operation temperature of 1500 °C needed for reduction is undesirable for reactor design, in terms of reactor material requirements and heat loss. The development of novel design principles for solar-to-fuel ceramics to operate at a lower temperature and manipulate the oxygen non-stoichiometry beyond classic binary oxides is an exciting scientific and technological goal.
As an alternative, one may consider perovskites with the ABO3−δ structure as a new material class for solar-to-fuel conversion. In contrast to ceria, where vacancies are intrinsically formed at high temperatures, perovskites reported in the literature rely on extrinsic acceptor doping.19,20 The temperature and pO2 dependent equilibrium shift between predominantly electronic (holes) and ionic (oxygen vacancies) p-type-defects is used as the operation principle in thermal cycling. Here, both cationic sites (A- and B-site) can be doped to manipulate the oxygen non-stoichiometry, electric conductivity, and kinetic and thermodynamic properties over a wider range compared to classic binary oxides.21–23 It is due to their unique structure–oxygen non-stoichiometry relationships that perovskites are high performing ceramic catalysts,24 memristors,25–27 or electrodes for metal air batteries,28 oxygen separation membranes29 and fuel cells.30–32 Hence, it is surprising that only recently first perovskites based on (La,Sr,Ca)MnO3−δ20,33,34 and their alumina solid solutions35,36 have been studied as potential solar-to-fuel conversion reactor materials. McDaniel et al. have shown LaAlO3 perovskites doped with Mn and Sr as promising materials for solar-to-fuel conversion due to an impressive 9 times higher H2 yield and 6 times greater CO yield compared to the state-of-the-art binary oxide ceria in the field.35 In another recent study, Demont et al. studied various classes of A- and B-site doped perovskites (ABO3−δ) with (A = La and Sr and B = Mn,Co, and Fe) as well as (Ba,Sr) (Co,Fe)O3−δ and their water splitting capabilities. In their comparison, (La,Sr)MnO3−δ showed the highest H2 yield among the tested perovskites with 190 and 160 μmol g−1 in the first and second thermochemical cycle, respectively. Generally, these perovskite compositions showed high reduction yields, i.e. high oxygen release, but low re-oxidation levels during the second step of the thermochemical cycling.37
Recent studies on perovskites highlight this material class as very promising for solar-to-fuel conversion, but also show a need to gain further understanding on the role of cationic doping and its implication on the fuel yields. Due to the numerous combinations of A- and B-site cationic dopants in the perovskite structure, it is imperative to have a design strategy when searching for new solar-to-fuel materials.
In this study, we screened the existing literature data for materials with a high degree of tunability towards efficient solar to fuel conversion. We synthesized transition metal ion B-site doped La0.6Sr0.4Cr1−xCoxO3−δ perovskite materials. The concept behind this composition is to introduce as much p-type (acceptor) doping with strontium at the A-site38 for higher maximum non-stoichiometry, while staying within the limits of Sr doping for a single phase perovskite.39 We fix the A-site concentration and vary the B-site concentration to tune the thermodynamic properties. First, the materials are synthesized and the structure is critically investigated by X-ray diffraction analysis, Raman spectroscopy, and electron microscopy to verify their chemical stability. Second, we assess the applicability of our design criteria by the analysis of the splitting properties and fuel yields. Finally, we describe how the newly selected material composition of La0.6Sr0.4Cr0.8Co0.2O3−δ produces the same amount of fuel at correspondingly 300 °C lowered operation temperatures as compared to the state-of-the-art material ceria.
2. Design criteria for solar-to-fuel conversion perovskite materials
To design a new perovskite material for solar-to-fuel conversion we use two criteria: one criterion for each step in the two-step thermochemical reaction in order to assess the suitability of the new material, see Fig. 1. For the first step, a material criterion is a high release of oxygen for the lowest temperature possible. In the second step, a material criterion is favorable thermodynamics for H2O and CO2 splitting. In the following, we show how B-site doping in the solid solutions of La0.60Sr0.40Cr1−xCoxO3−δ can be tuned to fulfill the two design criteria. We demonstrate this by the comparison of existing thermogravimetric data15,21,22 on (La,Sr)CrO3−δ and (La,Sr)CoO3−δ in the oxygen non-stoichiometry and Gibbs free energy of oxidation, Fig. 2. These thermodynamic characteristics are further compared to the ones of Zr-doped and pristine ceria, currently considered the state-of-the-art material for solar to fuel conversion.The oxygen release criteria
Fig. 2a shows the effect of different B-site cations of the perovskite compositions, La0.7Sr0.3CrO3−δ and La0.7Sr0.3CoO3−δ, in comparison to CeO2−δ, Ce0.95Zr0.05O2−δ and Ce0.80Zr0.20O2−δ on the evolution of oxygen non-stoichiometry, with respect to temperature at an exemplified oxygen partial pressure of 10−5 atm. The latter condition refers to a typical value of oxygen partial pressure during thermal reduction in a solar-to-fuel reactor.9,40,41 Up to reduction temperatures of 1300 °C, the perovskite La0.7Sr0.3CrO3−δ reveals an almost invariant oxygen non-stoichiometry on temperature. In contrast, substituting Co on the B-site to form La0.7Sr0.3CoO3−δ leads to a pronounced and increasing oxygen release, starting already at temperatures as low as 400 °C. Hence, the choice of the B-site cation, cobalt vs. chromium, implicates a remarkable difference in the oxygen non-stoichiometry i.e. δ = 0.16 at 700 °C. The state-of-the-art reduction temperature for pristine and zirconia–ceria solid solutions in solar-to-fuel operation is 1500 °C, for which an oxygen non-stoichiometry difference of up to δ = 0.04 is measurable with respect to doping. In the plot of pO2 and temperature range, La0.7Sr0.3CoO3−δ reveals a 4 time increase in oxygen non-stoichiometry when compared to state-of-the-art ceria-based materials at 10−5 atm. Consequently, the amount and temperature of release of oxygen for the perovskite can be varied to a greater extent than in commonly used ceria and zirconia-doped ceria materials.In Fig. 2b, the oxygen non-stoichiometry, δ, is plotted versus the oxygen partial pressure, pO2, at 1000 °C. All materials exhibit an increase in δ for decreasing pO2. We compare the equilibrium oxygen partial pressure at which the oxygen non-stoichiometry equals to δ = 0.1 for the different materials: exchange of the B-site cation from Co to Cr shifts the equilibrium pO2 from approximately 10−4 to 10−16 atm, respectively. Thus, the equilibrium oxygen partial pressure changes by more than 12 orders of magnitude. In comparison, partial substitution of ceria by zirconia enables only a limited variation of the equilibrium oxygen partial pressure of less than 3 orders of magnitude for the same value of non-stoichiometry.
In conclusion, the temperature and equilibrium oxygen partial pressure for oxygen release can be manipulated to a much larger extent by doping the B-site in (La,Sr)BO3−δ with chromium and cobalt in perovskites compared to state-of-the-art ceria. Moreover, we conclude that doping with cobalt is beneficial for tuning the maximum release capacity of oxygen for the first step in the thermochemical cycling.
The thermodynamic material criteria
In order to design suitable solar to fuel materials, the thermodynamic properties can be compared to determine the theoretical thermochemical conversion efficiency. However, in the literature, there is not a consistent set of assumptions defining the theoretical efficiency, since this depends on the reactor type and operation. Calculations of theoretical system efficiency result in 20% for inert gas sweeping operation9,20 while they were in excess of 30% for packed bed operation6 for the same material, i.e. ceria. Despite the difference in theoretical process efficiency, one can assert the thermodynamic suitability of new materials by using thermodynamic criteria. The criteria can be exemplified by considering the Gibbs free energy change for the water splitting reaction, eqn (2a)| Δgrxn = Δgoxd − ΔgH2O | (3) |
 | (4) |
In the following, we compare existing thermodynamic data to show that it is possible to tune the thermodynamic equilibrium of oxidation of the perovskites to a much larger extent compared to ceria. The Gibbs free energy change, Δgoxd, of the oxidation reaction of the perovskites, La0.8Sr0.2CrO3−δ and La0.8Sr0.2CoO3−δ, and the binary oxide ceria with respect to the water-gas shift reactions of H2 and CO oxidation and temperature is shown in Fig. 2c. The value of Δgoxd is more negative for La0.8Sr0.2CrO3−δ; viz. chromium on the B-site is thermodynamically more favorable for splitting of H2O and CO2 when compared to cobalt-doping for the second step of the thermochemical cycle, see eqn (2). In addition, we conclude that it is possible to shift the Gibbs free energy of oxidation for La0.8Sr0.2Cr1−xCoxO3−δ solid solutions with 150 kJ mole−1 by a different doping at 1000 °C. Here, state-of-the-art metal oxides such as ceria and its zirconia solid solutions would restrict the range of Δgoxd to approximately 60 kJ mole−1.
To this end, we use two main criteria to assess the suitability of the new perovskite composition for solar-to-fuel conversion. From the comparison of thermodynamic literature data on B-site doping with Co and Cr in (La,Sr)BO3−δ, Fig. 2, it is reasonable to conclude that: (a) higher Co contents are beneficial for increased oxygen release in the first reduction step and (b) higher Cr contents are beneficial for efficient water and CO2 splitting in the second step of the thermochemical cycle. Hence, there is a trade-off in Cr and Co doping between having a material that has a high possible oxygen non-stoichiometry and favorable thermodynamics for syngas production. By mixing Cr and Co, the two extremes on either side of the lines of water and CO2 splitting in Fig. 2c, one can shift the thermodynamic equilibrium of oxidation of the perovskite for efficient splitting relative to different reactor temperatures. Furthermore, this comparison demonstrates how perovskites can be optimized for different reactor temperatures to a higher extent compared to the state-of-the-art solar-to-fuel conversion material ceria. We have synthesized solid solution La0.6Sr0.4Cr1−xCoxO3−δ perovskite materials with x = 0.05, 0.10, 0.20, and 0.50 to test the predictions for mixing Cr and Co on the B-site and aim to find an optimum composition within this window of cobalt concentrations.
3. Results and discussion
Structural characterization of La0.6Sr0.4Cr1−xCoxO3−δ solid solutions as new solar-to-fuel perovskite material
To investigate the crystal structure and chemical stability of La0.60Sr0.40Cr1−xCoxO3−δ compounds with x = 0.05, 0.10, 0.20 and 0.50, we performed an XRD analysis of the as-synthesized powders and after four thermochemical cycles, shown in Fig. 3a. The XRD patterns are characteristic of the rhombohedral structure. No impurity phases are detectable, and there is no observable indication of phase changes between the as-synthesized and thermochemically cycled materials. Lattice parameters of the unit cell for all compositions before and after cycling were determined by full profile Rietveld refinement using an R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c rhombohedral model of the unit cell. An exemplified fit for La0.60Sr0.40Cr0.8Co0.2O3−δ is shown in Fig. 3b. The lattice parameters for all compositions studied are plotted in Fig. 3c. A clear linear trend between the unit cell volume is observed for increasing cobalt concentration in agreement with Vegard's law. As expected a decrease in the unit cell volume is observed for cobalt doping, since cobalt (Co3+/Co4+) has smaller ionic radii compared to chromium (Cr3+/Cr4+) in an octahedral coordination.43
c rhombohedral model of the unit cell. An exemplified fit for La0.60Sr0.40Cr0.8Co0.2O3−δ is shown in Fig. 3b. The lattice parameters for all compositions studied are plotted in Fig. 3c. A clear linear trend between the unit cell volume is observed for increasing cobalt concentration in agreement with Vegard's law. As expected a decrease in the unit cell volume is observed for cobalt doping, since cobalt (Co3+/Co4+) has smaller ionic radii compared to chromium (Cr3+/Cr4+) in an octahedral coordination.43
The XRD results are in agreement with the literature, since similar perovskite compositions display rhombohedral symmetry.44,45 The high purity phase compositions obtained through the successful Pechini process in this work are ascribed to the higher temperature and longer holding time used for the synthesis compared to similar compositions where impurity phases are observed.45,46
To clarify the cation–anion near order structure relationships, we performed Raman spectroscopy for the La0.60Sr0.40Cr1−xCoxO3−δ, Fig. 4. The spectra exhibit two distinctive features at ∼700 and ∼870 cm−1. The as-synthesized powder samples are treated at 1200 °C in air and are therefore in an oxidized state, while the thermochemically cycled powders are cooled in argon and will be in a more reduced state. The characteristics of the broad peak at ∼700 cm−1 for the reduced La0.60Sr0.40Cr1−xCoxO3−δ solid solutions are: (i) decreased intensity for increasing cobalt content and (ii) the peak position is shifted to lower wavenumbers for increasing cobalt content. In perovskites, this broad Raman peak signature is typically assigned to the local bending modes of oxygen in the vicinity of the B-site cation.45–47 In line with Gupta et al., we further assign this band to a mix of B2g and B3g Raman modes. The rhombohedral (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) structure is confirmed by the absence of Ag modes, since Jahn–Teller distortions are incompatible with this structure type.48 The high intensity peak at 870 cm−1 detected for the as-synthesized (oxidized) samples is attributed to impurity phase SrCrO4.46 However, this surface impurity phase is only present in some areas of the sample and it disappears after thermochemical cycling.
c) structure is confirmed by the absence of Ag modes, since Jahn–Teller distortions are incompatible with this structure type.48 The high intensity peak at 870 cm−1 detected for the as-synthesized (oxidized) samples is attributed to impurity phase SrCrO4.46 However, this surface impurity phase is only present in some areas of the sample and it disappears after thermochemical cycling.
In summary, the structural analysis shows full miscibility of Cr/Co on the B-site and all compositions can be characterized by the same rhombohedral model in both XRD and Raman spectroscopy. It can also be concluded that the materials have the same crystal structure before and after thermochemical cycling, hence displaying promise of long-term durability.
In order to study the microstructure and distribution of metal ions, scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDX) of the as-synthesized and thermochemically cycled La0.60Sr0.40Cr1−xCoxO3−δ compounds with x = 0.05, 0.10, 0.20 and 0.50 are performed, displayed in Fig. 5. Comparing Fig. 5a and b reveals a grain size of 0.5 to 3 μm, forming agglomerated particles of approximately 50–100 μm, which is the same for the compositions x = 0.05, 0.10, and 0.20 of the as-synthesized and cycled powders. However, further increase in cobalt doping to 50 mol% results in pronounced grain growth with an average grain size of 5–10 μm, Fig. 5c, which we ascribe to progressed Ostwald ripening. Ricardo et al. have shown that cobalt can be used as a sintering agent to accelerate grain boundary and volume diffusion.49 In accordance, we confirm the increased particle size and also lower number of grain facets of neighboring grains for the La0.60Sr0.40Cr00.50Co0.50O3−δ, Fig. 5c. We compare the microstructures of the as-synthesized and thermochemically cycled La0.6Sr0.4Cr0.8Co0.2O3−δ powders up to 1200 °C, Fig. 5b–d. The average grain size and particle shape remain unchanged after thermochemical cycling of the material.
Energy dispersive X-ray diffraction (EDX) was performed to analyse the homogeneity of distribution of all cations, Fig. 5e and f. The analysis shows a homogeneous distribution of the metal ions throughout both the as-synthesized and thermochemically cycled samples. Differences in concentrations of Sr and Co are related to morphological differences, see the ESI S1† for further details. In essence, the results from scanning electron micrographs and chemical analysis show that the grain size and distribution of chemical elements remain unchanged for the as-synthesized samples and those after four thermochemical cycles.
Novel La0.6Sr0.4Cr1−xCoxO3−δ perovskite compositions for thermochemical fuel production
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of CO2 and argon. By varying the dopant concentration from 0.05 to 0.50 mol% in La0.60Sr0.40Cr1−xCoxO3−δ, we vary the redox-properties of the material, Fig. 6a. Three clear trends are observed as a function of doping: first, an increase in mass loss (oxygen release) for increasing cobalt contents during the reduction step. Second, up to a cobalt dopant concentration of 20 mol% we observe a mass increase (incorporating oxygen by CO2 splitting) during the oxidation step equivalent to the mass loss in the reduction step. However, for a high cobalt content of 50 mol%, the material is re-oxidized to a lower extent. Third, we found an optimum in doping of 20 mol% of cobalt for La0.60Sr0.40Cr1−xCoxO3−δ (x = 0.2) in terms of fuel yield for the tested compositions. The trends observed in CO yield as a function of doping are in agreement with the design criteria and thermodynamic expectations; see Fig. 2. In Fig. 2a and b, it was shown that (La,Sr)BO3−δ perovskite solutions with Co on the B-site are easier reduced compared to those with Cr, in line with the experimental results for increased cobalt content. The lower re-oxidation extent observed for the high Co content (x = 0.50) is in line with the presented data in Fig. 2c where we showed that the thermodynamic driving force for CO2 splitting is lower for La0.8Sr0.2CoO3−δ compared to La0.8Sr0.2CrO3−δ.
1 mixture of CO2 and argon. By varying the dopant concentration from 0.05 to 0.50 mol% in La0.60Sr0.40Cr1−xCoxO3−δ, we vary the redox-properties of the material, Fig. 6a. Three clear trends are observed as a function of doping: first, an increase in mass loss (oxygen release) for increasing cobalt contents during the reduction step. Second, up to a cobalt dopant concentration of 20 mol% we observe a mass increase (incorporating oxygen by CO2 splitting) during the oxidation step equivalent to the mass loss in the reduction step. However, for a high cobalt content of 50 mol%, the material is re-oxidized to a lower extent. Third, we found an optimum in doping of 20 mol% of cobalt for La0.60Sr0.40Cr1−xCoxO3−δ (x = 0.2) in terms of fuel yield for the tested compositions. The trends observed in CO yield as a function of doping are in agreement with the design criteria and thermodynamic expectations; see Fig. 2. In Fig. 2a and b, it was shown that (La,Sr)BO3−δ perovskite solutions with Co on the B-site are easier reduced compared to those with Cr, in line with the experimental results for increased cobalt content. The lower re-oxidation extent observed for the high Co content (x = 0.50) is in line with the presented data in Fig. 2c where we showed that the thermodynamic driving force for CO2 splitting is lower for La0.8Sr0.2CoO3−δ compared to La0.8Sr0.2CrO3−δ.
The fuel production performance of the La0.6Sr0.4Cr0.8Co0.2O3−δ perovskite is benchmarked towards pristine ceria, currently considered the state-of-the-art material in the field of solar-to-fuel conversion, see Fig. 6b. The comparison at low temperature cycle conditions, between 800 °C (oxidation in CO2) and 1200 °C (reduction in argon), reveals that the mass changes associated with CO2 splitting (Δmgain = 0.25%) are 25 times higher than those in ceria (Δmgain = 0.01%) at the same operation conditions. We also compare the CO yield of the best performing perovskite operating at 800–1200 °C to that of pristine ceria operating between 1000 °C and 1500 °C. The latter high temperature cycles are commonly reported operating temperature conditions for ceria.8,9,50 During the oxidation of CeO2 operating at a high temperature, we observe an almost identical mass change of 0.27% compared to 0.25% for La0.6Sr0.4Cr0.8Co0.2O3−δ at a 300 °C lowered operation temperature. It should be noted that the profile of the mass change curve, Fig. 6b, indicates that CO production is slower for the perovskite. This either indicates that the kinetics at 800 °C are slower than that for ceria typically re-oxidized at 1000 °C or that the perovskite is far from equilibrium at this temperature. Interestingly, we observed a different behavior for the perovskites compared to ceria in the switch from oxidizing to reducing conditions at 800 °C, Fig. 6b. The perovskite undergoes a mass loss immediately after switching from Ar + CO2 to Ar in contrast to ceria, where no measurable change is visible in this step. This indicates that the mass changes for the perovskite are strongly dependent on the pCO2. We ascribe this behavior to the fast release of oxygen as a consequence of different relative pO2 in the atmosphere. Alternative explanations for this swift mass loss are the release of adsorbed CO2 or decomposition of carbonates (e.g. SrCO3). However, carbonate formation was excluded since it is neither detected by in situ XRD nor by Raman spectroscopy, see also additional discussion in the ESI S2.† For these reasons, we conclude that adsorption or carbonate formation can only have insignificant effects on the observed mass changes.
In Fig. 6c, the CO yields calculated from mass changes measured during thermochemical cycling are compared for the perovskite La0.6Sr0.4Cr1−xCoxO3−δ solid solutions towards pristine ceria. A CO yield of 168.8 μmol g−1, in Fig. 6c, for the reference measurement of undoped ceria, cycled between 1000 and 1500 °C, is in the range of values reported in the literature 105 μmol g−50 and 193 μmol g−20 under similar operation conditions. As additional comparison, the Mn- and Sr- doped LaAlO3 based perovskites had CO production with an average of 135 μmol g−1 over 80 cycles between 1000 and 1350 °C in a stagnating flow reactor.
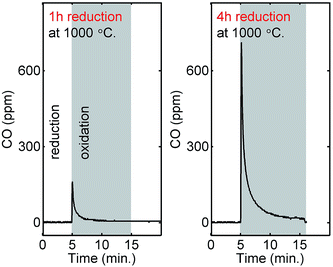
For supplementary verification of CO2 splitting, we measured the fuel production yields by using non-dispersive infrared sensors for the material with the highest performance, La0.6Sr0.4Cr0.8Co0.2O3, in a fluidized bed reactor. Fig. 7 shows the amount of produced CO as a function of time for two different cycles, the time of injection of CO2 is marked with a grey square. Owing to a lower reduction temperature, longer reduction times were needed to reach higher non-stoichiometries. In the first cycle, the material was reduced for 1 hour and in the second it was reduced for 4 hours. For the second cycle, it will have a higher non-stoichiometry and as expected we observed a higher yield of CO. The yields were 10 μmol g−1 and 63 μmol g−1 for the first and second cycle, respectively. The fact that the CO2 concentration is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in inert gas compared to 1
3 in inert gas compared to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the thermogravimetric measurements and that the reduction temperature was 200 °C lower (reduction at 1200 °C in TGA experiments) reasonably account for the lower fuel yield.
1 in the thermogravimetric measurements and that the reduction temperature was 200 °C lower (reduction at 1200 °C in TGA experiments) reasonably account for the lower fuel yield.
In real solar-to-fuel reactors, the overall process efficiency is of high importance for the viability of a material. For this model system, the thermogravimetric measurements reveal an optimum in doping with respect to fuel production. However, the composition with the highest fuel yield is not necessarily the composition with the highest efficiency. Determining process efficiency is a complex procedure determined by reactor design and operation. For example, Scheffe and co-workers raised concern about a lowered efficiency for (La,Sr)MnO3−δ perovskites compared to ceria because they require higher amounts of oxidants (H2O and CO2) leading to energy penalties in the form of heat loss.20 Yet, Ermanoski et al. showed that a smart design of the solar-to-fuel reactor enables a higher heat recovery making it possible to work with higher educt concentration.6 This makes materials with lower Gibbs free energy of oxidation, Δgoxd, and lower operating temperature than ceria more attractive. It is beyond the scope of this paper to determine the theoretical efficiency, since this requires a determination of the thermodynamic properties for all compositions in a wide pO2 and temperature range.6,9,18 To this point, we have shown that the solid solution series La0.6Sr0.4Cr1−xCoxO3−δ has the potential to replace the best performing materials because their thermodynamic properties can be tailored to a larger extent compared to materials known in the field of solar-to-fuel conversion.
We conclude that the perovskite has a CO production of 157 μmol g−1 even when operated at a lowered temperature cycle of 800–1200 °C, compared to a CO yield of 168 μmol g−1 for ceria operated at 1000–1500 °C. Thus, we report an almost equivalent fuel yield to the state-of-the-art material at 300 °C lower operating temperature. Additionally, the large variation in fuel yield of 14 μmol g−1 to 157 μmol g−1 depending on the concentration of cobalt on the B-site shows that the thermodynamic properties are highly dependent on the doping. A high degree of tunability of thermodynamic properties is beneficial when optimizing for system efficiency.
Structural stability of La0.6Sr0.4Cr0.8Co0.2O3−δ perovskites for solar-to-fuel conversion: in situ carbon dioxide redox-cycling
Promising fuel yields from H2O and CO2 splitting have been demonstrated for La0.6Sr0.4Cr0.8Co0.2O3−δ. At this point, it may be debated that the weight gains measured by thermogravimetric analysis are related to not only the splitting of CO2 but also the formation of Sr- or La-carbonates. Secondary phases and strontium carbonate formation have previously been detected by in situ XRD in perovskites with Sr on the A-site in La(Co,Fe)O3−δ compositions when exposed to CO2 in the temperature range of 550–1000 °C.51,52 Phase changes or carbonate formation may lead to degradation and decrease in performance over time.53 To clarify the structural stability and possible carbonate formation, we performed in situ X-ray powder diffraction analysis for the best performing perovskite La0.6Sr0.4Cr0.8Co0.2O3−δ material for the redox reaction with carbon dioxide. In Fig. 9, in situ X-ray diffraction data are displayed for La0.6Sr0.4Cr0.8Co0.2O3−δ for a temperature of 1200 °C and 800 °C. At the lower temperature of 800 °C, the sample was exposed to argon and a mix of 5 vol% CO2 in Ar for 5 hours. This temperature and atmosphere program was used to reproduce the instantaneous changes the sample is exposed to during a solar-thermochemical cycle and enable investigation of long-term effects of exposure to CO2. In Fig. 9a, we show XRD patterns displaying the main peak of (012) and the doublets of (110) and (104); a close up of the double peak (110) and (104) is displayed in Fig. 9b. By analyses of the redox-characteristics (under oxidation by CO2 and reduction in argon), we unequivocally show that there are neither changes in the peak shape over time nor additional diffraction lines. A slight shift of the (110) peak is related to the chemical expansion due to the incorporation of oxygen by CO2 splitting.54,55In this study, we clearly confirm that the material La0.6Sr0.4Cr0.8Co0.2O3−δ is able to split carbon dioxide and water with greater promise than state-of-the-art ceria. Through in situ structural redox-experiments we prove that it is stable in a carbon dioxide atmosphere and that intermediate carbonate formations are not to be accounted for the time tested. This is supported by fact that the carbonate vibration structural bands, e.g. characteristic SrCO3 bands at the wavenumber of ∼1071 cm−1 (ref. 56 and 57), are not traceable in our Raman experiments after thermochemical cycling of the materials.
4. Conclusion
In this work, we report for the first time that the material La0.6Sr0.4Cr1−xCoxO3−δ reveals a high potential to replace state-of-the-art ceria due to its ability to split carbon dioxide and water as a new solar-to-fuel conversion reactor material at lower temperature.Ceria is currently considered the state-of-the-art material in solar-driven thermochemical dissociation of CO2 and H2O due to favorable thermodynamics and kinetic characteristics. By thermogravimetric analysis, we found a comparably high performing perovskite material, namely La0.6Sr0.4Cr0.8Co0.2O3−δ, in the temperature range of 800–1200 °C even strongly outperforming ceria with 25 times greater CO yield compared to ceria (800–1200 °C). A comprehensive structural ex and in situ study under harsh conditions, such as simulated carbon dioxide heat redox-cycle, shows no sign of phase changes or carbonate formation for potential reactor operation. The fact that the material can be operated at a strongly lowered temperature implies that heat losses and overall material temperature gradients during solar-driven heating can be minimized. Potential operation at a higher temperature regime may be evaluated for further efficiency increase due to the high oxygen storage capacity of the material.
The novel material was chosen based on the evaluation of existing thermodynamic data on (La,Sr)CrO3−δ and (La,Sr)CoO3−δ with a criteria of release of oxygen at low temperature as well as favorable thermodynamic characteristics for water and CO2 splitting. By this comparison we demonstrate that the oxygen non-stoichiometry and thermodynamic properties of B-site doped (La,Sr)BO3−δ solid solutions can be varied to a much larger extent than for example ceria. The present work contributes with first model material experiments for which solid solution series have been synthesized to systematically investigate the effect on structure, chemistry and thermochemical syngas production for the series of La0.6Sr0.4Cr1−xCoxO3−δ. We exploit the significant variations in oxygen non-stoichiometry and thermodynamic properties to optimize fuel yields. Based on the material's insights, we show that there is a trade-off in doping: cobalt doping increases the release of oxygen in the 1st high temperature reducing step, but it comes at the price of a less favorable thermodynamics for CO2 and water splitting in the 2nd low temperature step. The fact that the thermodynamic properties of the solid solution series can be tuned to this extent, while maintaining structural integrity, makes it interesting for real solar-to-reactor systems. We anticipate that further studies on the thermodynamic properties can be used to find an optimum composition within this solid solution series for high process efficiency depending on the reactor type and operation.
5. Methods
Material synthesis
Solid solutions of La0.60Sr0.40Cr1−xCoxO3−δ (with x = 0.05, 0.10, 0.20, 0.50) were synthesized as powders via the Pechini method. For this, stoichiometric quantities of the metal nitrates, being La(NO3)3·6H2O (Fluka Analytical, ≥99%), Sr(NO3)2 (Fluka Analytical ≥99%), Cr(NO3)3·9H2O (Sigma-Aldrich ≥99%) and Co(NO3)2·H2O (Fluka Analytical, ≥98%), were mixed in a molar ratio of 60/40 with citric acid (Sigma-Aldrich, ≥99%) under continuous stirring at room temperature. Hereby, an excess of citric acid is used to ensure complexation of the metal cations. Ethylene glycol (Fluka Analytical, ≥99.5%) was added to the citric acid in a 2/3 wt. ratio. The solution was heated until a gel was formed and then calcined at 400 °C for 2 h to evaporate the organic residues. The resulting powder was ground and heat treated at 1200 °C for 24 hours, with a heating rate of 2 °C min−1, to acquire a single-phase powder and to ensure the chemical stability prior to thermogravimetric measurements.Structural and chemical analysis
In situ XRD experiments at elevated temperatures were performed using a Panalytical X'Pert Pro diffractometer equipped with an X'Celerator detector and with an Anton-Paar HTK 1200 high temperature furnace in a controlled atmosphere. A constant total flow rate of 200 sccm was used for both reduction (argon) and oxidation (argon + CO2) steps. In the oxidation step, the CO2 concentration had to be chosen lower (5% in argon) in the in situ XRD compared to the thermogravimetric measurements (50% CO2 in argon) due to experimental limitations of the XRD setup. Data were collected at 1200 °C and 800 °C over the range of 2θ = 20–60°, in steps of 0.0167°, with an effective scan time of 40 s per step and an equilibration time of 30 min. between measurements.
The unit cell parameters were determined by Rietveld whole profile fitting of the recorded ex situ XRD data using the program GSAS.58 A rhombohedral unit cell model for the space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c was successfully used for all refinements.59 In this structural fit arrangement, the cations were located on ideal structural sites, specifically (using Wyckoff nomenclature) the 6a sites (0, 0, ¼) for the La and Sr and the 6b sites (0 0 0) for the Co and Cr. The anionic oxide positions were fixed for the 8e crystallographic sites (z 0 ¼) with z = 0.54.
c was successfully used for all refinements.59 In this structural fit arrangement, the cations were located on ideal structural sites, specifically (using Wyckoff nomenclature) the 6a sites (0, 0, ¼) for the La and Sr and the 6b sites (0 0 0) for the Co and Cr. The anionic oxide positions were fixed for the 8e crystallographic sites (z 0 ¼) with z = 0.54.
Thermochemical measurements
The thermochemically driven oxygen non-stoichiometry changes of La0.60Sr0.40Cr1−xCoxO3−δ materials were studied in a thermogravimetric analyzer (TGA, NETZSCH 449C) for temperature and gas environment cycling. For each measurement, 200 mg of powder were placed in Al2O3 TGA-crucibles (NETZSCH) and cycled between 800 and 1200 °C, with heating rates of 50 °C min−1 and a total flow of 100 sccm. For reduction and oxidation, high purity Ar (Pangas, 99.999%) and CO2 (99.9%) were mixed; 50% CO2 in Ar during oxidation and 100% Ar during reduction. For the oxidation step, we used an isotherm for 1 h at 800 °C, with 10 min. equilibration in a reducing atmosphere before and after oxidation in CO2. Gas flows and timescale of the thermochemical experiments were chosen to enable a performance assessment of the proposed perovskite materials towards other materials in earlier thermogravimetric studies under similar conditions.20,50,60 Moreover, the conditions resemble reactor operation demonstrated by Chueh et al.8 with on-sun simulated operation. Although, in the simulated reactor operation lower gas flows were used (0.035L min−1 g) compared to previous thermogravimetric evaluations and this one (0.25L min−1 g).To exclude buoyancy effects, experimental runs were carried out under equivalent conditions in the same and empty crucibles for the thermogravimetric measurement. In Fig. 5a and b, the relative mass is set to zero at the beginning of the re-oxidation step to allow easy comparison of CO-yield between compositions. The relative mass change measured by thermogravimetry at the re-oxidation step under the CO2 flow is converted to CO yield, nCO, which is given by
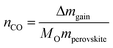 | (5) |
We compare the oxygen deficiencies and CO2/Ar cycling kinetics of the best performing La0.6Sr0.4Cr0.8Co0.2O3−δ perovskite in this study to the state-of-the art in the field being CeO2−δ (Cerac, 99.9%). For this, thermochemical cycling was either studied at a low temperature range of 800 to 1200 °C with a heating rate of 50 °C min−1 or for a high temperature range of 1000–1500 °C with a 20 °C min−1 heating rate. We used these conditions on purpose, since the first low temperature thermochemical cycling would be a range where we expected sufficient oxygen release from the perovskite, Fig. 2a and b, whereas the higher one is the state-of-the-art operation range for solar-to-fuel conversion on binary oxide ceria.8,9,50
Water splitting experiments were carried out by flushing argon through a water bubbler before entering the TGA. The temperature of water was kept at 21 °C, thus we obtained a water vapor pressure of pH2O = 2.5 atm or a concentration of 2.5% in argon.
Fuel production measurements in a fluidized bed reactor
To confirm CO2 splitting by the perovskite solution La0.6Sr0.4Cr0.8Co0.2O3−δ, we detected and quantified the amount of produced CO by using an infrared sensor in a fluidized bed reactor. The setup is described elsewhere.61 In the two-step thermochemical experiment, reduction and oxidation were performed at 1000 and 800 °C, respectively. The lower reduction temperature in this experiment compared to the thermogravimetric analysis was used due to limitations on the higher temperature of the setup. The flow was 1.5 L min−1 for N2 during reduction. During the oxidation step, the flows were 1.5 L min−1 for N2 and 0.5 L min−1 for CO2. The perovskite powders were synthesized as described above and subsequently pressed into pellets, crushed and sieved to a particle size range of 300–425 μm. Alumina particles were used as the fluidized bed.Acknowledgements
The authors want to thank Prof. A. Studart from the Laboratory of Complex Materials for the use of the TGA and SEM. Prof. R. Spolenak from the Laboratory for Nanometallurgy for the use of the Raman spectrometer and Prof. M. Niederberger from the Laboratory for Multifunctional Materials for the use of the XRD facilities and a special thanks to D. Erdem for the support with high temperature in situ XRD measurements (ETH Zurich, Switzerland). Prof. C. Müller and Q. Imtiaz are gratefully acknowledged for measurements in the fluidized bed reactor (ETH Zurich, Switzerland). Furthermore, the authors thank S. Schweiger and R. Schmitt for assistance with Raman Spectroscopy and SEM measurements, respectively. We also thank the partners of Competence Center for Energy and Mobility (CCEM-CH) for valuable discussions. The funding support by ETH, grant number ETH-05 13-1, is gratefully acknowledged.References
- I. Lubomirsky and D. Cahen, MRS Bull., 2012, 37, 412–416 CrossRef.
- D. S. Ginley and D. Cahen, Fundamentals of Materials for Energy and Environmental Sustainability, Cambridge university press, 2011 Search PubMed.
- A. Yilanci, I. Dincer and H. K. Ozturk, Prog. Energy Combust. Sci., 2009, 35, 231–244 CrossRef CAS.
- T. Kodama and N. Gokon, Chem. Rev., 2007, 107, 4048–4077 CrossRef CAS PubMed.
- R. B. Diver, J. E. Miller, M. D. Allendorf, N. P. Siegel and R. E. Hogan, J. Sol. Energy Eng., 2008, 130, 041001 CrossRef.
- I. Ermanoski, N. P. Siegel and E. B. Stechel, J. Sol. Energy Eng., 2013, 135, 031002 CrossRef.
- W. C. Chueh and S. M. Haile, Philos. Trans. R. Soc., A, 2010, 368, 3269–3294 CrossRef CAS PubMed.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- J. R. Scheffe and A. Steinfeld, Energy Fuels, 2012, 26, 1928–1936 CrossRef CAS.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef CAS.
- S. Bishop, K. Duncan and E. Wachsman, Electrochim. Acta, 2009, 54, 1436–1443 CrossRef CAS.
- S. Omar, E. Wachsman, J. L. Jones and J. Nino, J. Am. Ceram. Soc., 2009, 92, 2674–2681 CrossRef CAS.
- J. L. M. Rupp, A. Infortuna and L. J. Gauckler, J. Am. Ceram. Soc., 2007, 90, 1792–1797 CrossRef CAS.
- J. L. M. Rupp, E. Fabbri, D. Marrocchelli, J. W. Han, D. Chen, E. Traversa, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2014, 24, 1562–1574 CrossRef CAS.
- M. Kuhn, S. Bishop, J. L. M. Rupp and H. Tuller, Acta Mater., 2013, 61, 4277–4288 CrossRef CAS.
- D. Chen, Y. Cao, D. Weng and H. L. Tuller, Chem. Mater., 2014, 26, 5143–5150 CrossRef CAS.
- J. P. Eufinger, M. Daniels, K. Schmale, S. Berendts, G. Ulbrich, M. Lerch, H. D. Wiemhöfer and J. Janek, Phys. Chem. Chem. Phys., 2014, 16, 25583–25600 RSC.
- Y. Hao, C. K. Yang and S. M. Haile, Chem. Mater., 2014, 26, 6073–6082 CrossRef CAS.
- A. McDaniel, A. Ambrosini, E. Coker, J. Miller, W. Chueh, R. O'Hayre and J. Tong, Energy Procedia, 2014, 49, 2009–2018 CrossRef CAS.
- J. R. Scheffe, D. Weibel and A. Steinfeld, Energy Fuels, 2013, 27, 4250–4257 CrossRef CAS.
- J. Mizusaki, Y. Mima, S. Yamauchi, K. Fueki and H. Tagawa, J. Solid State Chem., 1989, 80, 102–111 CrossRef CAS.
- J. Mizusaki, S. Yamauchi, K. Fueki and A. Ishikawa, Solid State Ionics, 1984, 12, 119–124 CrossRef CAS.
- M. Oishi, K. Yashiro, K. Sato, J. Mizusaki and T. Kawada, J. Solid State Chem., 2008, 181, 3177–3184 CrossRef CAS.
- H. Falcon, J. Barbero, J. Alonso, M. Martínez-Lope and J. Fierro, Chem. Mater., 2002, 14, 2325–2333 CrossRef CAS.
- F. Messerschmitt, M. Kubicek, S. Schweiger and J. L. M. Rupp, Adv. Funct. Mater., 2014, 24, 7447 CrossRef.
- H. Nili, S. Walia, S. Balendhran, D. B. Strukov, M. Bhaskaran and S. Sriram, Adv. Funct. Mater., 2014, 24, 6741–6750 CrossRef CAS.
- F. Messerschmitt, M. Kubicek and J. L. M. Rupp, Adv. Funct. Mater., 2015 DOI:10.1002/adfm.201501517.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed.
- P. V. Hendriksen, P. H. Larsen, M. Mogensen, F. W. Poulsen and K. Wiik, Catal. Today, 2000, 56, 283–295 CrossRef CAS.
- U. P. Muecke, D. Beckel, A. Bernard, A. Bieberle-Hütter, S. Graf, A. Infortuna, P. Müller, J. L. M. Rupp, J. Schneider and L. J. Gauckler, Adv. Funct. Mater., 2008, 18, 3158–3168 CrossRef CAS.
- E. D. Wachsman and K. T. Lee, Science, 2011, 334, 935–939 CrossRef CAS PubMed.
- A. S. Harvey, F. J. Litterst, Z. Yang, J. L. M. Rupp, A. Infortuna and L. J. Gauckler, Phys. Chem. Chem. Phys., 2009, 11, 3090–3098 RSC.
- C.-K. Yang, Y. Yamazaki, A. Aydin and S. M. Haile, J. Mater. Chem. A, 2014, 2, 13612–13623 CAS.
- S. Dey, B. Naidu and C. Rao, Chem.–Eur. J., 2015, 21, 7077–7081 CrossRef CAS PubMed.
- A. H. McDaniel, E. C. Miller, D. Arifin, A. Ambrosini, E. N. Coker, R. O'Hayre, W. C. Chueh and J. Tong, Energy Environ. Sci., 2013, 6, 2424–2428 CAS.
- A. M. Deml, V. Stevanović, A. M. Holder, M. Sanders, R. O'Hayre and C. B. Musgrave, Chem. Mater., 2014, 26, 6595–6602 CrossRef CAS.
- A. Demont, S. Abanades and E. Beche, J. Phys. Chem. C, 2014, 118, 12682–12692 CAS.
- H. U. Anderson, M. Nasrallah, B. Flandermeyer and A. Agarwal, J. Solid State Chem., 1985, 56, 325–334 CrossRef CAS.
- P. S. Devi and M. S. Rao, J. Solid State Chem., 1992, 98, 237–244 CrossRef CAS.
- M. Romero and A. Steinfeld, Energy Environ. Sci., 2012, 5, 9234–9245 CAS.
- A. Steinfeld, Sol. Energ., 2005, 78, 603–615 CrossRef CAS.
- M. W. Chase and J. A. N. A. Force, 1998.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. Anzai, H. Kawakami, T. Takayama and H. Yamamura, Trans. Mater. Res. Soc. Jpn., 2010, 35, 503–506 CrossRef CAS.
- M. Mori, Y. Hiei and N. M. Sammes, Solid State Ionics, 2000, 135, 743–748 CrossRef CAS.
- R. K. Gupta and C. M. Whang, J. Phys.: Condens. Matter, 2007, 19, 196209 CrossRef.
- D. Hoang, A. Dittmar, M. Schneider, A. Trunschke, H. Lieske, K.-W. Brzezinka and K. Witke, Thermochim. Acta, 2003, 400, 153–163 CrossRef CAS.
- M. N. Iliev and M. V. Abrashev, J. Raman Spectrosc., 2001, 32, 805–811 CrossRef CAS.
- R. Polini, A. Falsetti, E. Traversa, O. Schäf and P. Knauth, J. Eur. Ceram. Soc., 2007, 27, 4291–4296 CrossRef CAS.
- A. Le Gal, S. Abanades and G. Flamant, Energy Fuels, 2011, 25, 4836–4845 CrossRef CAS.
- V. Esposito, M. Søgaard and P. V. Hendriksen, Solid State Ionics, 2012, 227, 46–56 CrossRef CAS.
- S. Rajesh, J. Pereira, F. Figueiredo and F. Marques, Electrochim. Acta, 2014, 125, 435–442 CrossRef CAS.
- M. Gálvez, R. Jacot, J. Scheffe, T. Cooper, G. Patzke and A. Steinfeld, Phys. Chem. Chem. Phys., 2015, 17, 6629–6634 RSC.
- J. Ovenstone, J. S. White and S. T. Misture, J. Power Sources, 2008, 181, 56–61 CrossRef CAS.
- N. H. Perry, S. R. Bishop and H. L. Tuller, J. Mater. Chem. A, 2014, 2, 18906–18916 CAS.
- M. C. Alves, M. R. Nascimento, S. J. Lima, P. S. Pizani, J. W. Espinosa, E. Longo, L. E. Soledade, A. G. Souza and I. M. Santos, Mater. Lett., 2009, 63, 118–120 CrossRef CAS.
- N. Eror, T. Loehr and U. Balachandran, Ferroelectrics, 1982, 40, 71–73 CrossRef CAS.
- A. C. Larson and R. B. V. Dreele, Los Alamos National Laboratory Report, LAUR 86-748, 2004 Search PubMed.
- R. Sonntag, S. Neov, V. Kozhukharov, D. Neov and J. Ten Elshof, Phys. B, 1997, 241, 393–396 CrossRef.
- A. Demont and S. Abanades, J. Mater. Chem. A, 2015, 3, 3536–3546 CAS.
- Q. Imtiaz, A. M. Kierzkowska, M. Broda and C. R. Müller, Environ. Sci. Technol., 2012, 46, 3561–3566 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ta02519b |
| This journal is © The Royal Society of Chemistry 2015 |