Low-activated Li-ion mobility and metal to semiconductor transition in CdP₂@Li phases

Abstract

Solids with high ion mobility are of broad interest for energy storage applications. New systems featuring low-activated ion mobility are important to improve the performance in such systems. Herein we report on a model system dealing with such improved properties. Li_0.2CdP₂ was synthesized from the elements, lithium as structure stabilizer and CdI₂ as reaction promoters in sealed silica ampoules at 823 K. It crystallizes tetragonal, in space group I4₁22 (α-CdAs₂ structure type), with lattice parameters a = 7.6691(8) Å, c = 4.4467(4) Å and V = 261.53(4) ų. After 24 h of storage in air lithium ions can be removed in a spontaneous delithiation reaction resulting in Li(OH)·H₂O formation on the surface of the crystals. Formed α′-CdP₂ adopts the α-CdAs₂ structure type. Both compounds consist of isolated cadmium atoms and helical ¹_∞[P⁻]-chains generating empty channels suitable to accommodate Li ions. The heavy atom structure was determined by X-ray diffraction methods while a full model including lithium was derived from a combined solid state NMR and quantum chemical calculation approach. An low activation barrier range in the order of 0.1 to 0.2 eV was determined by NMR spectroscopy pointing towards an extraordinary high Li mobility in Li_0.2CdP₂. Of course a Cd-based solid will have certain disadvantages like toxicity and mass for storage applications but substitution of Cd by suitable lighter elements can solve this issue.

---

Introduction

Phosphorus is an element with intriguing structure chemistry.¹ In the case of Cd the reactivity is reasonable and binaries like CdP₂,^2–4 Cd₃P₂,^5,6 CdP₄,⁷ or Cd₇P₁₀ (ref. 8) exist. Cd is a prominent element used in photo-semiconductors like CdTe⁹ or Cd₃Pn₂ (with Pn = P, As)^10,11 quantum dots for solar cell applications. While solar energy conversion applications are well established features for Cd pnictides and Cd chalcogenides due to their high electron mobility, the knowledge of ion mobility in Cd pnictides is rather small. Mixed ion and electron conducting compounds are potential candidates for batteries while pure ion conductors are also important as solid state electrolytes.^12,13 Prominent solid ion conductors like garnet-type compounds show conductivities of 10⁻³ S cm⁻¹ at room temperature and activation energies of 0.3 eV.¹⁴

CdP₂ exists in two different modifications. At room temperature, α-CdP₂ crystallizes orthorhombic, in space group Pna2₁ (ref. 2–4) while a high temperature phase β-CdP₂ occurs above 693 K, adopting the space group P4₁2₁2.³ The prominent structural feature in both cases is a helical ¹_∞[P⁻]-chain coordinated to cadmium ions. A helical arsenic chain was detected in the compound α-CdAs₂, featuring the space group I4₁22.¹⁵ An examination of the solid solution CdP₂–CdAs_s reveals a continuous series up to CdAs_2−xP_x with x = 1.8, where all representatives crystallize tetragonal, thus adopting the α-CdAs₂ structure type.¹⁶ It has been reported in ref. 16 that a cadmium polyphosphide in the α-CdAs₂ structure type could not be realized. Unfortunately, this α-CdAs₂ structure offers open channels ready for a coordination of mobile ions whereas such channels are not present in the known polymorphs.

Metal halides are prominent compounds to act as reaction promoters for the synthesis of kinetically stabilized materials and compounds adopting uncommon structure features.¹⁷ This feature, called mineralizer principle from now on, can also be used to selectively synthesize element allotropes of phosphorus.¹⁸ Recently, fibrous red phosphorus has been prepared by using CuCl₂ (ref. 19) and orthorhombic black phosphorus can be realized by a SnI₄/Sn combination.^20–22 This synthesis principle was used to synthesize the present compounds.

Herein we report on the synthesis, reactivity, quantum chemical characterization and ion mobility of Li_0.2CdP₂ and α′-CdP₂, featuring the end member of the solid solution CdAs_2−xP_x with x = 2.0. The mineralizer principle has successfully been adopted using CdI₂ as mineralizer agent.

Experimental section

Synthesis

Li_0.2CdP₂ was synthesized by reacting Li (Rockwood lithium, 99.9%), Cd (Chempur, 99.9999%) and red P (Chempur, 99.999+%) in a molar ratio of 0.25 : 0.875 : 2 in evacuated graphitized silica ampoules. CdI₂ (25 mg), acting as mineralizer, was added to a total amount of 1 g starting materials. The mixture was heated up to 823 K within 12 h, kept for 7 days at this temperature, and slowly cooled down to room temperature within 12 h afterwards. Li_0.2CdP₂ was obtained as a black powder. Impurities of cadmium or iodide were never detected the final products.

Li_0.2CdP₂ can also be prepared from the elements in ideal ratios (Li : Cd : P = 0.2 : 1 : 2) without a mineralizer, resulting in a microcrystalline black powder, but only with sparse crystals. The exchange of the mineralizer from CdI₂ to another mineralizer like CuCl₂ resulted in completely different products. Cd₃P₂ and crystals of LiP₁₅ have been identified after phase analysis. Impurities of copper or chlorine were neither detected in Cd₃P₂ nor in LiP₁₅ fractions.

α′-CdP₂ can be prepared from Li_0.2CdP₂ by a de-lithiation process upon exposing it to moist air. A white powder is formed on top of the needle-shaped Li_0.2CdP₂ crystals, after 24 h of exposure. After dissolution of the white powder in water Li₂CO₃ was found as main phase after removal of the solvent, substantiating the Li extraction from Li_0.2CdP₂. A full de-lithiation takes place after four weeks (Results and discussion section).

EDS and ICP analyses

Semi-quantitative EDS analysis was performed using a SEM 5900LV spectrometer (JEOL) scanning electron microscope equipped with an INCA energy dispersive microanalysis system (Oxford Instruments). An acceleration voltage of 30 kV was used for the measurements. Another system we used was a desktop scanning microscope JCM 6000 NeoScop™ (JEOL) equipped with an energy dispersive X-ray unit (JED 2200 JEOL). An acceleration voltage of 15 kV was applied for the measurements. The ICP analysis were performed using an Agilent Technologies (Santa Clara, CA) model 725 Series ICP OES instrument, equipped with an Echelle optics (model Vista/7XX ES), a monochromator (model Variant Liberty) and a CCD sensor (model Vista Pro 720/725_ES, resolution < 0.01 nm). Data analysis was done by the program ICP Expert II for Agilent 725 ES ICP OES.

X-ray single crystal diffraction

Li_0.2CdP₂ was stored and treated in an argon filled glovebox, while α′-CdP₂ was kept in air for 7 days and subsequently washed with water to remove Li(OH)·H₂O on the surface. Single crystals of Li_0.2CdP₂ were sealed in a 0.3 mm glass capillary prior to the measurement. Data were collected on a Bruker APEX II diffractometer equipped with a D8 goniometer (MoKα radiation, λ = 0.71069 Å, graphite monochromator, rotating anode source) at 123 K. The frames were integrated with the Bruker SAINT software package²³ using a narrow frame algorithm. Numerical absorption correction was done employing the SADABS routine.²⁴ A suitable single crystal of α′-CdP₂ was fixed on a glass capillary, and positioned on the goniometer head of an Oxford Xcalibur3 diffractometer (Sapphire 3 CCD detector; MoKα radiation, λ = 0.71073 Å, graphite monochromator). The Oxford CrysAlis RED software was used for data processing, including an empirical absorption correction with ABSPACK.²⁵

The space group I4₁22 was assigned on the basis of systematic absent reflections and the statistical analysis of the intensity distributions. The structure was solved using the superflip routine²⁶ implemented in the Jana2006 program suite.²⁷

X-ray powder diffraction

For the X-ray powder diffractometer analysis the sample kept under argon (Li_0.2CdP₂) and the sample on air (α′-CdP₂) were ground and sealed in glass capillaries. Powder XRD data were collected with a STOE STADI P X-ray powder diffractometer equipped with a DECTRIS Mythen 1K Detector using CuKα₁ radiation (λ = 1.54051 Å, curved Ge (111) monochromator). An external calibration was performed with Si (a = 5.43088 Å). Data were collected from 10.03° to 119.755° 2θ. The XRD pattern was fitted using the Rietveld routine implemented in the program Jana2006.²⁷

Electronic structure calculations

The first-principles calculations were carried out within the framework of DFT with exchange-correlation functionals in the generalized gradient approximation (GGA)^28,29 according to Perdew–Burke–Enzerhof (PBE)³⁰ and in the local density approximation according to Perdew and Zunger (LDA).³¹ Full geometry optimizations were executed with the Vienna Ab initio Simulation Package (VASP).^32,33 All atomic site parameters and cell constants were allowed to fully relax with the conjugant gradient algorithm. The interactions between the ions and the electrons are described by the projector-augmented-wave (PAW) method³⁴ with a cut-off energy of 500 eV. All calculations were performed in several subsequent steps with increasing k-grid meshes (depending on the size of the unit cell) between 2 × 2 × 2 and 12 × 12 × 12 to reach sufficient accuracy. A structure optimization was considered to be converged with a difference in total energy of less than 1 × 10⁻⁶ eV and a maximum Hellmann–Feynman force of 1 × 10⁻⁴ eV Å⁻¹. The final values of the total energies of the investigated systems were obtained with energy differences (between last and second to last step) of less than 1 × 10⁻³ eV per formula unit.

Solid state NMR

Experiments were performed on a Bruker Advance III spectrometer operating at 7 T with resonance frequencies of 116.6 MHz, 121.5 MHz and 300.13 MHz for ⁷Li, ³¹P and ¹H, respectively. A Bruker 4 mm WVT MAS probe was used for the experiments. The Li_0.2CdP₂ sample was handled in a glovebox and dry N₂ was employed for spinning and cooling the sample. Static ⁷Li NMR spectra were recorded in the temperature range 117 K < T < 561 K employing single pulse excitation and the solid echo pulse sequence for data acquisition. For the ⁷Li T₁-NMR measurements, the inversion recovery sequence was used. The temperature was calibrated employing the chemical shift of Pb(NO₃)₂ as a chemical shift thermometer.^35,3631P MAS NMR and ⁷Li MAS NMR spectra were recorded employing spinning speeds of 8–12 kHz using the Bruker system. Additional spectra at higher spinning speeds (up to 35 000 Hz) for ¹H and ³¹P were acquired on a Varian DMR2 NMR spectrometer operating at 11, 7 T using a Varian T3 MAS 1.6 mm NMR probe. Spectra are referenced as usual employing TMS for ¹H, 1 M LiCl for ⁷Li and 85% H₃PO₄ for ³¹P.

Differential scanning calorimetry (DSC)

Finely ground samples of phase pure Li_0.2CdP₂ (8.8 mg) and α′-CdP₂ (9.0 mg) were transferred to aluminum crucibles and were measured with a rate of 10 K min⁻¹ using a Netzsch DSC 200 F3 Maja machine. H₂O, In and Zn were used as standards for temperature calibration. All measurements were performed under N₂ atmosphere. No thermal effect was found in the temperature range from 123 K to 373 K for Li_0.2CdP₂. α′-CdP₂ cannot be transferred to α-CdP₂ or β-CdP₂ up to 673 K.

DC conductivity measurements

Total electric conductivities of Li_0.2CdP₂ and α′-CdP₂ have been measured using a homemade tool, which is capable to measure pressurized powdered samples (200 MPa, up to 2 mm height and 6 mm diameter) with a scale for measuring the height of the compressed powder. With a potentiostat (VMP-3, Biologic), a voltage of up to 10 V is applied to the compressed powder and the resulting current is measured. This unconventional procedure was necessary because a stable and dense pellet for impedance measurements could not be made from powdered samples in both cases. Temperature dependent conductivity measurements on single crystals are currently underway.

Results and discussion

CdP₂ shows polymorphism with two known polymorphs, a low temperature α-CdP₂ adopting the space group Pna2₁ (ref. 2–4) and a high temperature β-phase stable above 693 K, crystallizing in space group P4₁2₁2.³ A brief overview of the two CdP₂ structures is given in Fig. 1a and b.

Fig. 1 Crystal structures of (a) α-CdP₂ in the space group Pna2₁ (no. 33), (b) β-CdP₂ in the space group P4₁2₁2 (no. 92), (c) α-CdAs₂ in the space group I4₁22 (no. 98) and (d) Li_0.2CdP₂ in space group I4₁22 with displacement parameters at 90%. Li could not be detected during the structure refinement and was therefore determined from quantum chemical calculations. All structures possess helical pnictide chains. Cadmium atoms are drawn as cyan, phosphorus atoms as purple, and arsenic atoms as white spheres. Li channels are marked with arrows.

The main difference is the arrangement of ¹_∞[P⁻]-chains parallel and perpendicular towards each other featuring alternating P–P bond lengths. α-CdAs₂ contains a ¹_∞[As⁻]-chain (see Fig. 1c) with no bond length alteration and a slightly different arrangement of the Cd substructure than observed in α-CdP₂. Surprisingly, a α-CdAs₂-type CdP₂ polymorph does not exist till now – a solid solution α-CdAs_2−xP_x has only been realized up to x = 1.8.¹⁶ We therefore started systematic investigations to close this gap to x = 0.2 and call this new phase α′-CdP₂ from now on.

All our attempts to prepare α′-CdP₂, either from the elements directly or by the mineralizer principle using CdI₂ or CuCl₂, failed. CdP₄, Cd₃P₂ and β-CdP₂ were found instead. If lithium was added in small portions as starting material, Li_0.2CdP₂, adopting the α-CdAs₂ structure type, was found.

Structural characterization and elemental analysis of Li_0.2CdP₂

Single crystals of Li_0.2CdP₂, separated from a batch with the nominal composition x = 0.125, have been used to perform a single crystal X-ray structure determination. An executed neutron scattering experiment of microcrystalline Li_0.2CdP₂ has also been performed, but due to the large neutron absorption cross section of σ_a = 2520b, it was not possible to derive any structural parameters from that data.

Li_0.2CdP₂ crystallizes tetragonal, isostructural to α-CdAs₂, in space group I4₁22, with Z = 4. The lattice parameters (a = 7.6691(8) Å, c = 4.4467(4) Å and V = 261.53(4) ų; [c/a = 0.5798]) are taken from the powder analysis. Displacement parameters of Cd are slightly anisotropic, pointing towards a possible symmetry reduction. We found no evidences for a loss of the 4₁ symmetry which would directly lead to a bond length variation within the P substructure. Also a loss of centering was checked but could not be confirmed. The selected symmetry was crosschecked by X-ray powder phase analysis including Rietveld refinements (see ESI†).

The cadmium atoms are located on 4a position (0, 0, 0) while phosphorus occupies 8f (0.42546(9), 0.25, 0.125). Li could not be localized in this case. Even at 123 K we were not able to locate Li in the structure (see ESI†). This arrangement of heavy atoms leads to four channels per unit cell along the c-direction, of which two of them are filled with a helical ¹_∞[P⁻]-chain (Fig. 1d). The bond length observed within the helical ¹_∞[P⁻] chain is d(P–P) = 2.2040(6) Å, lying within the expected range for covalently bonded phosphorus (2.14–2.30 Å).¹ The Cd–P bond length of 2.6043(4) Å represents a well suited value reported for many cadmium polyphosphides. Examples are α-CdP₂ (d(Cd–P) = 2.495(15) to 2.627(15) Å)⁴ or Cd₇P₁₀ (d(Cd–P) = 2.49 to 2.85 Å).⁸ The distances between neighbored cadmium atoms are close to 4 Å. A section of the crystal structure of Li_0.2CdP₂ is given in Fig. 1d.

The composition and exact Li-content was determined from single crystals by ICP-OES resulting in Li_0.20(3)Cd_0.90(5)P_2.00(3) (or Li : Cd : P = 6.43 : 28.93 : 64.64 in at%). This finding is close to the expected composition but features a slightly reduced Cd content. An EDX analysis substantiated the 1 : 2 ratio of the heavy atoms. As shown later on by quantum chemical calculations, NMR spectroscopy, and phase analysis the Li_0.2Cd_1.0P₂ composition was substantiated. In the following, we use the idealized composition Li_0.2CdP₂ for further discussions.

Lithium mobility in Li_0.2CdP₂

Due to the high Li mobility (see later on) we tried to localize Li by other methods than scattering techniques. We therefore decided to do quantum chemical model calculations and temperature dependent solid state NMR spectroscopy to evaluate the most probable position within the structure and to check for Li mobility in the present system.

A first hint for a high Li ion mobility is the reasonable reactivity of Li_0.2CdP₂ against humid air. If Li_0.2CdP₂ is stored in air for 24 h, a white powder can be observed on the surface being identified as Li(OH)·H₂O. Details are given in the ESI.† Assuming simple exchange reactions the formation of Li(OH)·H₂O is explainable.

On the crystal surface:

10 × 0.2Li⁺(Li_0.2CdP₂) + H₂O (air) ⇆ 2LiOH + 2H⁺

LiOH + H₂O → Li(OH)·H₂O

LiOH + H⁺ ⇆ Li₂O + H₂O

After dissolution and removal of water on air:

2Li⁺ + 2OH⁻ + CO₂ (from air) ⇆ Li₂CO₃↓ + H₂O

Driving force for this de-lithiation reaction is the formation of a lithium compounds on the surface of the crystals. A possible proton exchange has been addressed by NMR spectroscopy. The proton content was determined as H_0.050(5)CdP₂ (see ESI†).

Structural characterization and elemental analysis of α′-CdP₂

Carefully washed α′-CdP₂ crystals were subject of a single crystal structure determination. The α-CdAs₂ structure type has been confirmed (see ESI†) but slightly larger lattice parameters have been observed as for Li_0.2CdP₂. Lattice parameters of a = 7.6829(2) Å, c = 4.46036(11) Å and V = 263.279(12) ų [c/a = 0.581] have been derived from the scattering data, being 0.3% larger than for the lithiated compound. The effect is not drastic but outside the 3σ criteria for all lattice parameters. Bond length of d(P–P) of 2.2104(10) Å (d(P–P) = 2.2040(6) Å in Li_0.2CdP₂) and d(Cd–P) of 2.6102(3) Å (d(Cd–P) = 2.6043(4) Å in Li_0.2CdP₂) resulted.

α′-CdP₂ can be regarded as an electron precise compound with Cd²⁺ ions and two-bonded (2b)P⁻, resulting in Cd²⁺(P⁻)₂ following the Zintl–Klemm³⁷ concept. It represents the former unknown end member of a solid solution CdAs_2−xP_x (0 < x < 1.8),¹⁶ which was reported in 1989 (see Fig. 2). The differences in cell volume between Li_0.2CdP₂ and α′-CdP₂ are not huge but α′-CdP₂ fits to the Vegard line⁴¹ while Li_xCdP₂ lies significantly below.

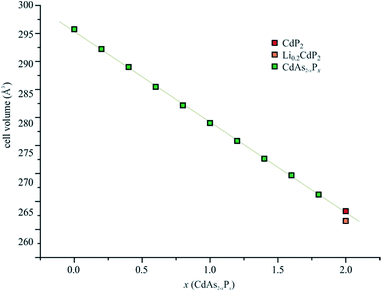Fig. 2 Cell volumes of the solid solution CdAs_2−xP_x derived from literature [ref. 16] for 0 < x < 1.8 and from single-crystal X-ray experiments for x = 2. A Vegard-like³⁸ decrease of the cell volume is observed up to the maximum P content of x = 2.

An ICP analysis of the carefully washed black crystals after full de-lithiation resulted in Cd_0.89(3)P_2.00(3). Li can be extracted quantitatively from Li_0.2CdP₂ by storage on air to form CdP₂. Following the notation we called the new phase α′-CdP₂ to illustrate the close relationship but also significant difference to α-CdP₂.

Quantum chemical calculations

Band structure calculations and DOS representations were performed for Li_0.2CdP₂ and its de-lithiated form α′-CdP₂. Li positions in Li_0.2CdP₂ were determined by a supercell approach and localized within the empty channels along the crystallographic c-axis. While α′-CdP₂ is destabilized in relation to known α-CdP₂ and β-CdP₂, a substantial stabilization is found for a Li incorporation into the empty channels (see Fig. 3 and ESI†). Substitution of Cd by Li does not lead to a significant stabilization effect and can be ruled out.

Fig. 3 0 K energies calculated by LDA and GGA for existing α- and β-CdP₂, α′-CdP₂ and Li_0.2CdP₂ (top). Band structure representation and total Density of States (DOS) for Li_0.2CdP₂ and α′-CdP₂. The integrated DOS within the black area represents 0.2 electrons, in good accordance with the Li content in Li_0.2CdP₂.

Li_0.2CdP₂ is metallic featuring a pseudo band gap 0.9 eV below the Fermi level (see Fig. 3). In contrast, α′-CdP₂ is a semiconductor with a calculated band gap of 0.77 eV (LDA) and 0.71 eV (GGA). Total conductivity measurements of microcrystalline Li_0.2CdP₂ (10⁻⁵ S cm⁻¹) and α′-CdP₂ (10⁻⁹ S cm⁻¹) exhibit a difference of four orders of magnitude at room temperature, nicely reflecting the different electronic structures. The present conductivity values from powdered samples cannot be more than a first hint due to the extreme sensitivity of the samples against mechanical stress. This feature causes disintegration of the structure upon grinding prior to the measurements. Temperature dependent conductivity measurements on single crystals are currently underway.

Obviously, the intercalation of lithium ions into the host structure leads to the closure of the band gap and the occurrence of a metal to semiconductor transition. Upon intercalation of Li into α′-CdP₂, 0.2 electrons are located in the conduction band and the band gap vanishes. The integrated DOS (i-DOS) between the Fermi level and the pseudo gap of Li_0.2CdP₂ corresponds to 0.2 electrons, in good accordance with the expected value from the formula sum (black area in Fig. 3).

Solid state NMR spectroscopy

The ³¹P-MAS-NMR spectra for α′-CdP₂ and Li_0.2CdP₂ are compiled in Fig. 4. In accordance with the crystal structure, we find a single phosphorous site in α′-CdP₂ with an isotropic chemic shift of δ_iso = −172.6 ppm. From a simulation employing the DMFIT software,³⁹ the chemical shift anisotropy (CSA) parameters were determined as δ_CS = 189.5 ppm and η_CS = 0.5. We note that the spinning sidebands on the high field side of the spectrum experience some broadening, especially at higher spinning speeds.

Fig. 4 ³¹P-MAS-NMR spectra for Li_0.2CdP₂ (a) and α′-CdP₂ (b).

We ascribe this to the combined action of the chemical shift anisotropy and extremely strong homo-nuclear dipolar coupling. The experimental data is found to be in good agreement with the results of quantum chemical calculations of the CSA parameters employing the WIEN2k software package,⁴⁰ which produces δ_iso = −171 ppm, δ_CS = 210 ppm and η_CS = 0.46.

For Li_0.2CdP₂, on the other hand, clearly two different P sites with isotropic chemical shifts of −157.4 ppm and −167.4 ppm with relative ratio of 1 : 1 can be identified. The CSA parameters for both sites are δ_CS = 182 ppm and η_CS = 0.6. The virtual identical CSA parameters for P in Li_0.2CdP₂ and the de-lithiated α′-CdP₂ sample confirm that the local ³¹P environment in both compounds is rather similar, as suggested by the XRD results. In addition the presence of two distinct P sites in Li_0.2CdP₂ indirectly confirms the presence of Li within the structure.

The static ⁷Li NMR spectra as a function of temperature in the temperature range 140 K ≤ T ≤ 295 K, acquired employing either a single pulse excitation or a solid echo pulse sequence, are collected in Fig. 5.

Fig. 5 (a) Static ⁷Li NMR spectra as a function of temperature in the temperature range 140 K ≤ T ≤ 295 K for Li_0.2CdP₂. (b) Evolution of the central signal line-width with temperature. (c) Measurement and fit for the 293 K signal of Li_0.2CdP₂.

For a I = 3/2 nucleus, the overall static line width represents the magnitude of the quadrupole coupling constant C_Q = eV_ZZQ/h, with Q denoting the quadrupolar moment, elementary charge and V_ZZ the principal component of the electric field gradient. The narrow line in the middle of the spectrum (central transition) is only affected by the homo- and hetero-nuclear dipolar interactions. Since both, the (first order) quadrupolar coupling and the dipole interaction scale with the second Legendrian 3 cos² β − 1 with β denoting the angle between the direction of the magnetic field B₀ and the principal axis of the respective interaction (quadrupolar or dipolar), the line shape will be influenced by dynamic processes, leading to an averaging of the interactions and hence a motional narrowing of the NMR line if the inverse of the corresponding correlation time exceeds the magnitude of the interaction.

In the absence of any motional process on the other hand, the line width adopts a constant line width, which is usually referred to as the rigid lattice value. From the evolution of the line shape of the static ⁷Li NMR spectra with temperature we can clearly conclude considerable Li ion mobility in Li_0.2CdP₂. At T < 180 K, the spectrum is characterized by a broad signal (m = ±1/2 to m = ±3/2 transitions) from which a quadrupolar coupling constant of C_Q = 95 kHz can be deduced. The width of the central transition at T = 140 K (4 kHz) indicates the presence of sizeable dipole coupling. Upon increasing the temperature, the overall width of the spectrum decreases to a value of 11 kHz at ambient temperature. Thus, the quadrupolar interaction is partially averaged out due to Li dynamics. For an isotropic diffusive motion, a vanishing EFG and hence zero quadrupolar coupling would be expected. The presence of a residual average quadrupolar coupling as observed here indicates a hopping process in which the Li ion traces well defined positions within the crystal structure, as observed e.g. in crystalline Li ion conductors.^41–43 In this situation, which is often termed anisotropic diffusion, the effective EFG, averaged over these positions, does not average to zero, but to a small residual value.

The evolution of the width of the central line with temperature is plotted in Fig. 5b. At ambient temperature, a line width of 800 Hz is observed. The line width does not suffer from any broadening down to temperatures of 200 K, then a broadening sets in, resulting in a line width of 3300 Hz at T = 117 K. Surprisingly, the rigid lattice regime is not reached even at these low temperatures. Employing the empirical Waugh–Fedin relation, E_A = 0.156 × T_onset, which relates the activation energy E_A of the motional process to the onset temperature T_onset, at which the motional narrowing sets in, we can give an upper limit for the activation energy of approx. 20 kJ mol⁻¹.

A more precise evaluation of the activation energy is possible from an analysis of the temperature dependence of the spin lattice relaxation time T₁, which was measured using a standard inversion recovery pulse sequence. The T₁ values were determined from measuring the magnetization built-up which was found to be exponential over the complete investigated temperature range. The data (cf.Fig. 6) exhibits a clear T₁-minimum at approx. 310 K. The activation energy and the correlation time of the dynamic process were then obtained from a simulation of the data employing the relaxation model of Bloembergen, Purcell and Pound (BPP),⁴⁹ resulting in E_A = 15 kJ mol⁻¹, τ⁰_c = 3.1 × 10⁻¹² s⁻¹.

Fig. 6 Evolution of 1/T₁ plotted as a function of the inverse temperature for Li_0.2CdP₂.

Since the low temperature side of the BPP curve is – especially in the case of disordered solids – often biased to lower values,^50,51 the low temperature T₁ data was not taken into account during the simulation. We emphasize that this value is among the lowest observed activation energies for crystalline Li ion conductors. A selection of Li ion conductors is shown in Table 1. Such a low value is in line with the best known Li ion conductors. With respect to the proposed structures for Li_0.2CdP₂, the ⁷Li NMR results clearly rule out the substitution model and favor the intercalation model.

Table 1 Activation barriers of selected fast Li-ion conductors^a

Compound	E A/eV (kJ mol^−1)	Determination method	T/K	Lit.
a IS: Impedance Spectroscopy NMR: Nuclear Magnetic Resonance.
LiFePO4	0.6 (57.9)	IS	RT	44
Li7PS6	0.16 (Li/LiClO4) (15.4)	IS	313	45
	0.33 (Pt) (31.8)	IS	313	45
NASICON	0.19 (18.3)	IS	473–773	46
LiCoO2	0.30 (29.0)	NMR	RT	47
LiNiO2	0.59 (56.9)	NMR	RT	47
Li7La3Zr2O12	0.32 (30.9)	IS	291–323	48
Li0.2CdP2	0.15 (15)	NMR	117–561	This work

---

Conclusions

Metallic Li_0.2CdP₂ was prepared by a mineralizer assisted reaction from the elements and CdI₂ as reaction promoter. Semiconducting α′-CdP₂ with a band gap of ∼0.7 eV can be synthesized via a de-lithiation process upon a simple storage process on humid air. Li(OH)·H₂O is formed on the surface of Li_0.2CdP₂ after 24 h and a complete de-lithiation to α′-CdP₂ takes place within weeks. A combined approach using diffraction techniques, spectroscopy and quantum chemistry was necessary to determine the crystal structures. Li_0.2CdP₂ shows a reasonable Li-ion mobility which was examined and confirmed by solid state NMR spectroscopy. An activation barrier range of 0.15 eV has been derived from spin lattice relaxation time (T₁) experiments, being at the low end of the activation energy spectrum known for the best solid Li-ion conducting materials. During the de-lithiation process, a metal to semiconductor transition occurs which has been examined and substantiated by quantum chemical calculations.

Acknowledgements

NE and TN thank the state of Bavaria and the DFG for the funding of an X-ray powder diffractometer.

References

1. R. Pöttgen, W. Hönle and H. G. von Schnering, Encyclopedia of Inorganic Chemistry, ed. R. B. King, Wiley, Chichester, 2nd edn, 2005, vol. VIII, pp. 4255–4308.
2. J. Goodyear and G. A. Steigmann, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 2371.
3. J. Berak and Z. Pruchnik, Rocz. Chem., 1968, 42, 1403–1410.
4. O. Olofsson and J. Gullman, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1883–1884.
5. M. von Stackelberg and R. Paulus, Z. Phys. Chem., Abt. B, 1935, 28, 427–460.
6. K. Masumoto, S. Isomura and K. Sasaki, Phys. Status Solidi A, 1971, 6, 515–523.
7. M. von Stackelberg and R. Paulus, Z. Phys. Chem., Abt. B, 1935, 28, 427–460.
8. J. Kalicinska Karut, Z. Pruchink and K. Lukaszewicz, Rocz. Chem., 1971, 45, 1991–1992.
9. X. Wu, Sol. Energy, 2004, 6, 803–814.
10. S. Miao, S. G. Hickey, B. Rellinghaus, C. Waurisch and A. Eychmüller, J. Am. Chem. Soc., 2010, 132, 5613–5615.
11. D. K. Harris, P. M. Allen, H.-S. Han, B. J. Walker, J. Lee and M. G. Bawendi, J. Am. Chem. Soc., 2011, 133, 4676–4679.
12. J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
13. A. R. West, J. Mater. Chem., 1991, 1, 157–162.
14. V. Thangadurai, S. Narayanana and D. Pinzarua, Chem. Soc. Rev., 2014, 43, 4714–4727.
15. L. Červinka and A. HrubČ, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 457–458.
16. V. A. Rubtsov, E. M. Smolarenko, V. M. Trukhan, V. N. Yakimovich and L. K. Orlik, Phys. Status Solidi A, 1989, 115, K155–K158.
17. S. Lange, M. Bawohl, R. Weihrich and T. Nilges, Angew. Chem., 2008, 120, 5736–5739 ( Angew. Chem., Int. Ed. , 2008 , 47 , 5654–5657 ).
18. F. Bachhuber, J. von Appen, R. Dronskowski, P. Schmidt, T. Nilges, A. Pfitzner and R. Weihrich, Angew. Chem., 2014, 126, 11813–11817 ( Angew. Chem., Int. Ed. , 2014 , 53 , 11629–11633 ).
19. N. Eckstein, A. Hohmann, R. Weirich, T. Nilges and P. Schmidt, Z. Anorg. Allg. Chem., 2013, 639, 2741–2743.
20. S. Lange, P. Schmidt and T. Nilges, Inorg. Chem., 2007, 46, 4028–4035.
21. T. Nilges, M. Kersting and T. Pfeifer, J. Solid State Chem., 2008, 181, 1707–1711.
22. N. Eckstein, L.-A. Jantke, T. F. Fässler, J. Mink, M. Drees and T. Nilges, Eur. J. Inorg. Chem., 2014, 30, 5135–5144.
23. Bruker SAINT, 7.68 A, Bruker AXS Inc., Madison, Wisconsin, USA, 2001.
24. Bruker SADABS, 2008/2, Bruker AXS Inc., Madison, Wisconsin, USA, 2001.
25. CrysAlis RED, Version 1.171.33.34d, Oxford Diffraction Ltd., 2009.
26. L. Palatinus and G. J. Chapuis, Appl. Crystallogr., 2007, 40, 786–790.
27. V. Petřiček, M. Dušek and L. Palatinus, JANA2006 The Crystallographic Computing System, Institute of Physics, Praha, Czech Republic, 2006.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
30. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
31. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
33. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
34. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. T. Takahashi, H. Kawashima, H. Sugisawa and T. Baba, Solid State Nucl. Magn. Reson., 1999, 15, 119.
36. A. Bielecki and D. P. Burum, J. Magn. Reson., Ser. A, 1995, 116, 215.
37. E. Zintl, Angew. Chem., 1939, 52, 1.
38. L. Z. Vegard, Z. Phys., 1921, 5, 17–26.
39. D. Massiot, F. Fayon, M. Capron, I. King, S. Le Calvé, B. Alonso, J. O. Durand, B. Bujoli, Z. Gan and G. Hoatson, Magn. Reson. Chem., 2002, 40, 70–76.
40. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augmented Plane Wave plus Local Orbitals Program for calculating Crystal Properties program suite, Technische Universiät, Wien, Austria, 2001.
41. L. van Wüllen, L. Hildebrandt and M. Jansen, Solid State Ionics, 2005, 176, 1449–1456.
42. L. van Wüllen, N. Sofina, L. Hildebrandt, C. Mühle and M. Jansen, Solid State Ionics, 2006, 117, 1665–1672.
43. L. van Wüllen, T. Echelmeyer, H.-W. Meyer and D. Wilmer, Phys. Chem. Chem. Phys., 2007, 9, 3298–3303.
44. C. Delacourt, L. Laffont, R. Bouchet, C. Wurm, J.-B. Leriche, M. Morcrette, J.-M. Tarascon and C. Masquelier, J. Electrochem. Soc., 2005, 152, A913–A921.
45. H.-J. Deiseroth, J. Maier, K. Weichert, V. Nickel, S.-T. Kong and C. Reiner, Z. Anorg. Allg. Chem., 2011, 637, 1287–1294.
46. G. Jasinski, P. Jasinski, B. Chachulski and A. Nowakowski, Mater. Sci., 2006, 24, 261–268.
47. K. Nakamura, H. Ohno, K. Okamura, Y. Michihiro, I. Nakabayashi and T. Kanashiro, Solid State Ionics, 2000, 135, 143–147.
48. R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., 2007, 119, 7925–7928.
49. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712.
50. D. Brinkmann, Magn. Reson. Rev., 1989, 14, 101.
51. R. Winter, K. Siegmund and P. Heitjans, J. Non-Cryst. Solids, 1997, 212, 215.

---

Footnote

† Electronic supplementary information (ESI) available: Cif files containing the heavy atom structures, details concerning the elemental and thermal analyses, conductivity measurements and details concerning the quantum chemical calculations. See DOI: 10.1039/c5ta00471c

---