The effect of poling conditions on the performance of piezoelectric energy harvesters fabricated by wet chemistry

Abstract

The effect of poling conditions on the power output of piezoelectric energy harvesters using sol–gel based Pb(Zr_0.53,Ti_0.47)O₃–Pb(Zn_1/3,Nb_2/3)O₃ piezoelectric thin-films has been investigated. A strong correlation was established between the poling efficiency and harvester output. A method based on simple capacitance–voltage measurements is shown to be an effective approach to estimate the power output of harvesters poled under different conditions. The poling process was found to be thermally activated with an activation energy of 0.12 eV, and the optimum poling conditions were identified (200 kV cm⁻¹, 250 °C for 50 min). The voltage output and power density obtained under optimum poling conditions were measured to be 558 V cm⁻² and 325 μW cm⁻², respectively.

---

1 Introduction

The search for alternative energy sources continues on many fronts. In particular, there has been a recent increase in activity to harvest energy from non-traditional alternate energy sources such as vibrations (via the piezoelectric effect), temperature variations (via the thermoelectric effect), and solar energy.¹ The search for ways to improve the performance of alternative sources by keeping them manufacturable and low cost is of primordial interest. Chemical based processes can help to meet those requirements. The improvement of a harvester may be divided into two main areas: the material and the device separately.

From the material standpoint, it is well known that the addition of donor dopants or higher valence dopants such as La³⁺,^2–4 and Nb⁵⁺,^5–7 to the original piezoelectric material (ABO₃ perovskite structure) contributes electrons when they substitute on the A and B sites,^5,8 improving the energy density of thin-film piezoelectric materials.⁹ We have recently reported the synthesis and integration of a piezoelectric energy harvester based on an alternative material, namely, the relaxor composition 0.9Pb(Zr_0.53,Ti_0.47)O₃–0.1Pb(Zn_1/3,Nb_2/3)O₃ or PZT–PZN.^10,11 The thin-film relaxor material was integrated into a cantilever device by a manufacturable, topside, low cost, and planar chemical-wet-etch based process.

Additionally, it is also known that the piezoelectric response of polycrystalline perovskite ceramic materials can be enhanced by externally poling the material.¹² Most reported studies of poling effects have been mainly focused on the Pb(Zr,Ti)O₃ material system.^13,14 The poling process involves the application of a strong DC field to preferentially orient the polarization in polycrystalline perovskite ceramics along the direction of the applied field. The poling conditions normally used to improve the figure of merit of piezoelectric materials include electric field, time, and temperature or light exposure, and they all can have a dramatic impact on the performance of the piezoelectric element and therefore the performance of the device.¹⁵ The improved properties of the piezo-harvester after poling depend on how well the dipoles are oriented in the desired direction, and how stable the new dipole orientations are after removing the applied field. The stability of the dipole configuration after poling is dramatically impacted by the internal bias fields that build up in the sample during poling. It is also well known that the poling field applied to ferroelectric thin films can be greater than that for bulk ceramics;¹⁵ and activation mechanisms are necessary for poling to happen. In this work, temperature, voltage, and time were used to pole the samples. However, there have also been reports showing that photoactive light exposure during poling stabilizes the new dipole configurations; light exposure has been proved to be useful for the poling of polymer films,¹⁶ and is a useful alternative for micromechanical devices integrated on a chip.^15–17

Despite these numerous reports, little information has been reported on the effect of poling conditions on the power output of integrated thin-film piezoelectric energy harvesters. In the present work, we investigate the poling effect on the electrical performance of energy harvesting devices fabricated by a wet chemistry-based release process, and made from sol–gel-based PZT–PZN thin-films. It is shown that the functional PZT–PZN cantilever performance is enhanced by the poling treatment, and a mechanism is proposed for this enhancement.

2 Experimental

2.1. Relaxor material synthesis and characterization

The energy harvesters fabricated in this study are based on a cantilever design and sol–gel solution deposition process which has been previously reported by this group.^11,18 The sol–gel synthesis we used is based on alkoxide chemistry and was carried out under a N₂ atmosphere. In this synthesis, water is required to start the reaction with metal alkoxides (Zr, Ti, Pb, Zn, and Nb) and the condensate or oligomer is the final product. Acetic acid is used as the catalyst, which enhances the electrophilic behavior of the metal alkoxide. Methanol is used as the solvent. The starting precursors used for the synthesis were Zr[OC(CH₃)₃]₄ (zirconium butoxide, solution 80 wt% in 1-butanol), Ti[OCH(CH₃)₂]₄ (titanium-isopropoxide, assay 99.99% trace metal basis), and Nb(OCH₂CH₃)₅ (niobium ethoxide). These precursors were initially reacted in CH₃COOH (acetic acid, assay 95%), and CH₃OH (methanol, assay ≥99%), followed by the addition of Pb(CH₃CO₂)₄ (lead acetate, assay 95%) and Zn(CH₃COO)₂·H₂O (zinc acetate dihydrate), and heating to 85 °C to dissolve the acetates. The final PZT–PZN solution had a concentration of 0.4 M. The dielectric constant, loss tangent, and piezoelectric coefficient (d₃₃) were measured to be 3200, 0.0171, and 182 pC/N, respectively. Capacitance and loss tangent values were measured using a Cascade Microtech probe station, coupled with a Keithley 590 CV analyzer and an Agilent 4284A LCR meter. The dielectric constant was calculated from the capacitance values. The piezoelectric coefficient was measured using an Aix ACCT dual-beam laser interferometer working in differential mode.

2.2. Cantilever and device fabrication

The sol–gel solution was then spin-coated, at 3000 rpm for 30 s on a multi-layer substrate designed to enable facile release of the cantilevers via a wet-chemistry etching process. Briefly, the cantilever stack is comprised of the following sequential layers: Si substrate, 3 μm polycrystalline silicon (poly-Si) layer deposited by low pressure chemical vapor deposition (LPCVD), 50 nm thermally grown SiO₂, 500 nm tensile-stress LPCVD Si₃N₄, and 500 nm plasma-enhanced chemical vapor deposited (PECVD) SiO₂. A layer of TiO₂ (50 nm) then was deposited on top of PECVD SiO₂, which is formed by the sputter deposition of Ti and oxidizing the same in a furnace at 1000 °C for 30 min in O₂. A sol–gel based PbTiO₃ (PT) layer was also added to improve the relaxor film phase formation, as previously reported.¹¹ The relaxor PZT–PZN thin films (0.810 μm thick) were then deposited on top of the TiO₂ layer and crystallized at 675 °C for 30 min in air to obtain phase-pure relaxor films.^10,11,19 The patterning, wet etching, and cantilever release steps were carried out in a class 1000 clean room. The first photolithography step involved patterning of 50 nm RuO₂/40 nm Cr/400 nm Au interdigitated electrodes (IDEs). The RuO₂ was sputter deposited and the Cr/Au was deposited using e-beam evaporation. The next step involved PECVD SiO₂ encapsulation to improve the long-term stability of the devices. The following step included the deposition of 40 nm Cr/400 nm Au on the bond pads for wire bonding. The cantilevers were then released using a three-step etching process: 20% HF for 1.5 min to remove the oxides, stopping on the LPCVD nitride layer; a 15 min dry etch using 100% CF₄ in a reactive ion etcher (RIE) to remove LPCVD nitride; and finally a 6.5 hour poly-Si etch using 20% KOH at 50 °C to release the cantilevers, with constant stirring during the entire etching time.

The cantilever fabrication was designed in a way to harvest energy in the d₃₃ mode, which presents several advantages over the d₃₁ mode. For instance, d₃₃ coefficients are 2–2.5 times higher than the d₃₁ coefficients, leading to an open-circuit voltage of a d₃₃ harvester that is at least 20 times higher. In addition, the d₃₃ mode eliminates the need for bottom electrodes, thus reducing the number of photomasks needed, and providing the possibility to generate higher strain at lower voltages. An example of a cantilever released using our process is shown in the SEM image in Fig. 1(a). It can be seen that the dimensions of the device are 200 μm by 600 μm. In addition, the finger width and spacing are seen to be 5 μm each. The geometry was selected by modeling several parameters such as finger spacing, finger width and other parameters using COMSOL FE software.¹⁰ Modeling was based on a 4-layered model structure, 700 nm SiO₂/500 nm Si₃N₄/810 nm PZT/600 nm Au stack, and the mechanical parameters used were provided by the COMSOL database. Cantilevers with variable finger width (I), finger spacing (D) and the space between the cantilever edge and finger arrays (E) were constructed and simulated using the Solid Mechanics (Solid) Module in order to obtain the resonance frequency, deflection, and stress of the structures. After the mechanical structural data were processed, we proceeded to create a second model using the piezoelectric devices (Pzd) and electrical circuit (Cir) module to evaluate the voltage output as a function of I, D and E, respectively; this model was performed by creating a boundary condition and introducing a function which represents the mechanical behavior of the structure upon excitation. Meshing was performed using a combination of tetrahedral elements and swept elements to optimize the mesh size, and the number of elements ranged from 5000 to 30 000 depending on the complexity of the geometry; all results were based on 3D elements.

Fig. 1 (a) SEM image of a released cantilever and (b) image of actual cantilevers wire-bonded to the chip carrier.

2.3. Device characterization

The poling study was carried out on a temperature controlled probe station. To be able to pole several cantilevers at the same time, packaging was necessary as shown in Fig. 1(b), the chip carrier is then mounted on a printed circuit board (PCB) to allow poling of several cantilevers simultaneously in a parallel array. The PCB was introduced into a furnace and connected to a voltage source (Keithley 2400).

After poling treatments, the samples were tested by mounting them to a mechanical shaker (Vibration Research Corporation model VR5800). The force generated by the shaker was proportional to the selected acceleration, which was controlled by the voltage applied to a high power amplifier (VR565 Linear Power Amplifier). The acceleration and frequency were monitored with an accelerometer mounted to the piston of the shaker. The amplifier was driven by a 12 V power supply and signals from a frequency generator. The output voltage from the cantilever was monitored using a Tektronix digital oscilloscope (TDS 210). To normalize the voltage for different cantilever designs, the measured voltage was divided by the area of the cantilever to obtain the voltage density (V cm⁻²).

3 Results and discussion

Using poling conditions previously reported for PZT thin film piezoelectrics as a starting point,^17,20 a study of the poling conditions of the relaxor PZT–PZN thin films was performed. Watanabe et al.¹⁷ reported using a field of 50 kV cm⁻¹ to pole their piezoelectric thin films, but did not specify the poling temperature or time. Yi et al.²¹ reported using 31 kV cm⁻¹ for 100 min at 200 °C as extreme conditions for poling piezoelectric thin films. Because the poling conditions in our study involved the variation of several parameters, it was necessary to define a method to quantify the efficiency of the poling process. One method is based on the observation that the capacitance–voltage (CV) curves of the relaxor piezoelectric film experience a shift along the voltage axis after poling, which is defined as ΔV in Fig. 2. The hysteresis loops corresponding to the selected CV curves are shown in the ESI file, Fig. S1,† and also exhibit a voltage shift after poling.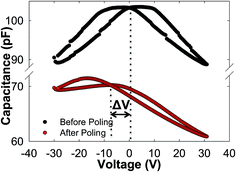

Fig. 2 C–V plots before and after poling treatment at 250 °C/100 V/50 min showing the voltage shift (ΔV) resulting from the poling process.

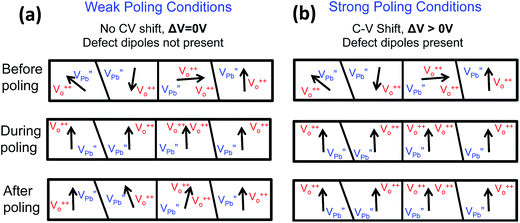
It has been suggested by many authors that the net polarization in PZT thin films is comprised of two components—the “normal” ferroelectric polarization (P_r) and a volumetric distribution of aligned defect-dipole complexes such as 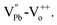^22–25 It has been shown that such defect dipoles can be reoriented and stabilized under an external bias, leading to the build-up of internal bias fields, which create rigid shifts along the voltage axis in a hysteresis loop.^26,27 We surmise that the origin of the voltage shift (ΔV) in the C–V characteristics of our samples is related to the stabilization of such defect dipoles during the poling process. If the poling conditions are strong enough, then it is possible to re-orient defect dipoles into stable configurations, leading to large voltage shifts. On the other hand, if the poling conditions are weak, a lower number of defect dipoles are oriented or stabilized, resulting in smaller voltage shifts. A schematic of this effect is shown in Fig. 3.

Fig. 3 Schematic showing the effect of poling conditions on defect-dipole formation and alignment in PZT–PZN films: (a) weak poling conditions, where randomly located point defects are present in the sample, but no defect-dipoles, and (b) strong poling conditions, where defect-dipoles are formed and aligned under the influence of a strong poling voltage, hence producing a bigger ΔV. Black arrows indicate the direction of ferroelectric polarization.

Thus, strong poling conditions result in a bigger voltage shift (ΔV), an indication of larger oriented polarization with the poling field, leading to a higher power output from the cantilevers. Therefore, we believe that it is possible to use this voltage shift (ΔV) as an indicator of the poling efficiency and power output of cantilevers. This is important, because in principle such a procedure can allow one to evaluate the potential power output of different piezoelectric films and composites without having to fabricate the full cantilever. Furthermore, we normalize this shift (ΔV) with respect to the maximum applied voltage (V_max) used to measure the CV curves, which was kept at 30 V in our study. Hence, we define ΔV% = 100 × (ΔV/V_max) as the measure of the efficiency of the poling process. Our results show that more extreme poling conditions result in the largest shift in the CV curves (largest ΔV%), and serve as an indication that new and more stable domain configurations and defect-dipole alignment have been formed after poling.

Fig. 4(a) shows the effect of increasing the poling time while keeping the voltage and temperature constant (100 V/200 °C) up to 60 min, at which time the sample breaks down. The efficiency of the poling process was measured by ΔV%. The right-hand axis shows that the relative shift in the CV curve (ΔV%) increases with poling time, in qualitative agreement with the expected increase in the efficiency of the poling process. The left-hand axis shows that the output voltage of the piezoelectric energy harvester increased with the poling efficiency.

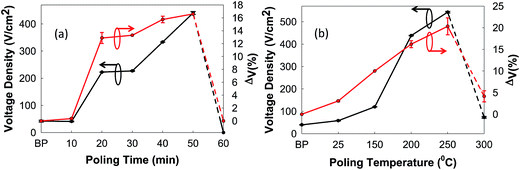Fig. 4 Output voltage density and voltage shift vs. (a) time (250 °C, 100 V) and (b) temperature (100 V, 50 min). The error bars indicate the variation in the measurement for 4 devices.

Similarly, Fig. 4(b) shows the effect of poling temperature on the output voltage of the energy harvesters while keeping the poling voltage and time constant (100 V/50 min), until breakdown at 300 °C. A similar observation can be made, where the cantilever voltage output increases with the poling efficiency.

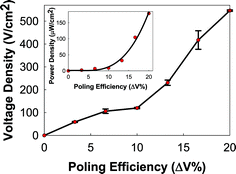
The curves of the devices fabricated with a constant thickness are shown in Fig. 4, leading to a similar breakdown field of 7.25 ± 0.6 kV cm⁻¹. The data sets in Fig. 4(a) and (b) can be combined and summarized as shown in Fig. 5, which shows the relationship between the voltage output measured from fully fabricated cantilevers as a function of the poling efficiency (ΔV%). An acceleration of 10 g and a frequency of 3.6 kHz were used. The voltage and power are normalized with respect to the device area to facilitate comparison with other reported values, as most of them are normalized by area.

Fig. 5 Plot showing the voltage output density vs. the poling efficiency (ΔV%). The inset plot shows an estimation of the output power density as a function of the poling efficiency (ΔV%). A polynomial of the 3^rd order equation is also estimated and presented. An acceleration of 10 g and a frequency of 3.6 kHz were used.

Using these results, an estimate of the power density output was calculated (inset in Fig. 5). Fitting the cantilever power output to the poling efficiency (ΔV%) resulted in a polynomial cubic behavior, as shown in eqn (1),

P = ΔV%[αΔV%² − βΔV% + δ] (1)

where P is the power output density, α, β and δ are constants obtained from the exponential fit and equaling 0.0376, 0.3368 and 0.7967, respectively, and ΔV% is the poling efficiency. This particular fitting was done assuming a load resistance of 1 MΩ. The data clearly show that there is a strong correlation between the cantilever output voltage/power and the poling efficiency, regardless of which experimental parameters are varied to pole the sample. Thus by performing a simple CV measurement before and after poling, an estimate of the power output of the cantilever device from the voltage shift in the CV curve (ΔV%) can be done. More importantly, one need not fabricate a fully released cantilever to evaluate the potential of different piezoelectric films and composites for energy harvesting. A simple CV measurement after poling shows the potential usefulness of any piezoelectric film or composite for energy harvesting from vibrations. Using this procedure, we can see that the maximum voltage output of our PZT–PZN cantilevers is obtained using the conditions 100 V/50 min/250 °C.

It is known that stringent poling conditions are needed for poling thin films as compared to bulk materials because of the mechanical clamping that the substrate exerts on the thin film.^20,25 Such strong fields have been reported to cause a shift of the C–V curve after poling due to a build-up of the internal bias field.²⁸ Warren et al.²⁶ suggested that the defect-dipoles have an effect on the total polarization and hence they might stabilize the piezoelectric material after poling or not, other authors such as Lee et al.²⁹ supported the same mechanism. Calculation of the effective activation energy to analyze the mechanism responsible for poling was performed, where the internal bias field was plotted as a function of temperature. At lower temperatures, from 25 °C to 77 °C, a linear behavior is observed in our samples and an activation energy of 0.12 eV was calculated, at higher temperatures not much change was observed, reaching a saturation point. This result suggests the movement of ionic charge carriers, as expected for defect-dipole formation. Previously reported values suggest that the activation energy for ionic movement in PZT thin films is about 0.18 eV and is 0.04 eV for electronic movement.^28,30 Finally, the voltage and power output of a thin-film cantilever poled under optimum conditions as a function of load resistance were measured. The optimum poling conditions were reduced by 10% to avoid breakdown. The cantilever device was connected to an oscilloscope through a controllable resistive load (R1). It was observed that the cantilever using the optimum poling conditions could deliver a maximum power density of 325 μW cm⁻². These results are comparable to previously reported PZT cantilevers.^18,31,32 A 70% reduction in resonance frequency was also observed for the topside wet-etch cantilevers compared to previously reported devices. Frequency reduction is an important advantage as most of the vibration sources available are lower than 1 kHz as reported previously by Roundy et al.^1,33

4 Conclusions

Functional integrated piezoelectric energy harvesting devices have been fabricated by a simple wet-chemical process. It is found that a strong correlation exists between the poling efficiency and the power output of the cantilevers. A method based on simple capacitance–voltage measurements is shown to be an effective approach to estimate the power output of harvesters. The optimum poling conditions for our devices were identified as 200 kV cm⁻¹/50 min/250 °C, resulting in an output voltage density of 558 V cm⁻² at open circuit, and a maximum power output of 325 μW cm⁻².

Acknowledgements

The authors would like to thank NSF Phase I STTR #0810391 and NSF Phase IB #0937831 projects, supplemented by a Texas Emerging Technology Fund seed grant (March 2008–Sept 2009).

References

1. S. Roundy, P. K. Wright and J. Rabaey, Comput. Commun., 2003, 26, 1131–1144.
2. F. Kulcsar, J. Am. Ceram. Soc., 1959, 42, 343–349.
3. G. H. Haertling and C. E. Land, J. Am. Ceram. Soc., 1971, 54, 1–11.
4. X. Dai, Z. Xu and D. Viehland, J. Am. Ceram. Soc., 1996, 79, 1957–1960.
5. R. B. Atkin, R. L. Holman and R. M. Fulrath, J. Am. Ceram. Soc., 1971, 54, 113–115.
6. P. G. Lucuta, F. L. Constantinescu and D. Barb, J. Am. Ceram. Soc., 1985, 68, 533–537.
7. M. Pereira, A. G. Peixoto and M. J. M. Gomes, J. Eur. Ceram. Soc., 2001, 21, 1353–1356.
8. Y. Xu, in Ferroelectric Materials and their Applications, ed. Y. Xu, Elsevier, Amsterdam, 1991, pp. 217–245,  DOI:10.1016/b978-0-444-88354-4.50010-3.
9. H. Xiyun, Z. Xia, Z. Xinsen, Q. Pinsun, C. Wenxiu and D. Aili, J. Phys.: Conf. Ser., 2009, 152, 012068.
10. E. M. A. Fuentes-Fernandez, W. Debray-Mechtaly, M. A. Quevedo-Lopez, B. Gnade, E. Leon-Salguero, P. Shah and H. N. Alshareef, Smart Mater. Res., 2012, 2012, 9.
11. E. Fuentes-Fernandez, W. Debray-Mechtaly, M. A. Quevedo-Lopez, B. Gnade, A. Rajasekaran, A. Hande, P. Shah and H. N. Alshareef, J. Electron. Mater., 2011, 40, 85–91.
12. G. Helke and K. Lubitz, in Piezoelectricity, Springer, Berlin, Heidelberg, 2008, vol. 114, ch. 4, pp. 89–130.
13. S. Priya and D. J. Inman, Energy Harvesting Technologies, Springer, US, New York, 1st edn, 2009.
14. S. Priya, C.-T. Chen, D. Fye and J. Zahnd, Jpn. J. Appl. Phys., 2005, 44, L104.
15. A. L. Kholkin, D. V. Taylor and N. Setter, presented in part at the Applications of Ferroelectrics, ISAF 98, Proceedings of the Eleventh IEEE International Symposium on, Montreux, 1998.
16. A. L. Kholkin and N. Setter, Appl. Phys. Lett., 1997, 71, 2854–2856.
17. S. Watanabe, T. Fujiu and T. Fujii, Appl. Phys. Lett., 1995, 66, 1481–1483.
18. E. Fuentes-Fernandez, L. Baldenegro-Perez, M. Quevedo-Lopez, B. Gnade, A. Hande, P. Shah and H. N. Alshareef, Solid-State Electron., 2011, 63, 89–93.
19. E. M. A. Fuentes-Fernandez, A. M. Salomon-Preciado, B. E. Gnade, M. A. Quevedo-Lopez, P. Shah and H. N. Alshareef, J. Electron. Mater., 2014, 43, 3898–3904.
20. A. J. Moulson and J. M. Herbert, in Electroceramics, John Wiley & Sons, Ltd, 2003, pp. 5–93,  DOI:10.1002/0470867965.ch2.
21. G. Yi, Z. Wu and M. Sayer, J. Appl. Phys., 1988, 64, 2717–2724.
22. G. E. Pike, W. L. Warren, D. Dimos, B. A. Tuttle, R. Ramesh, J. Lee, V. G. Keramidas and J. T. Evans, Appl. Phys. Lett., 1995, 66, 484–486.
23. I. K. Yoo, S. B. Desu and J. Xing, MRS Online Proc. Libr., 1993, 310, 165.
24. S. L. Miller, J. R. Schwank, R. D. Nasby and M. S. Rodgers, J. Appl. Phys., 1991, 70, 2849–2860.
25. S. Trolier-McKinstry and P. Muralt, J. Electroceram., 2004, 12, 7–17.
26. W. L. Warren, H. N. Al-Shareef, D. Dimos, B. A. Tuttle and G. E. Pike, Appl. Phys. Lett., 1996, 68, 1681–1683.
27. J. Lettieri, M. A. Zurbuchen, Y. Jia, D. G. Schlom, S. K. Streiffer and M. E. Hawley, Appl. Phys. Lett., 2000, 77, 3090–3092.
28. A. L. Kholkin, D. V. Taylor and N. Setter, presented in part at the Applications of Ferroelectrics, ISAF 98, Proceedings of the Eleventh IEEE International Symposium on, Montreux, 1998.
29. E. G. Lee, K. S. Kim, J. K. Lee, W. Y. Jang, J. G. Lee and S. J. Kim, J. Korean Phys. Soc., 2003, 42, 158–161.
30. W. L. Warren, D. Dimos, B. A. Tuttle, R. D. Nasby and G. E. Pike, Appl. Phys. Lett., 1994, 65, 1018–1020.
31. S.-H. Kim, Y.-S. Choi, C.-E. Kim and D.-Y. Yang, Thin Solid Films, 1998, 325, 72–78.
32. Y. B. Jeon, R. Sood, J. H. Jeong and S. G. Kim, Sens. Actuators, A, 2005, 122, 16–22.
33. S. Roundy and P. K. Wright, Smart Mater. Struct., 2004, 13, 1131.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ta00447k

‡ Present address: Materials Science and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia.

---