Formation of bilayer clathrate hydrates

Abstract

We report molecular dynamics (MD) simulation evidence for a new family of two-dimensional (2D) clathrate hydrates. Particular attention is placed on the effect of the size and hydrophilicity of guest-molecules on the formation of 2D clathrate hydrates. Among the MD simulations undertaken, the spontaneous formation of bilayer (BL) clathrate hydrates in nanoslits are found with five different hydrophobic guest molecules, namely, ethane (C₂H₆), ethene (C₂H₄), allene (C₃H₄), carbon dioxide (CO₂) and hydrogen (H₂) molecules. Our simulations suggest that the host cages in a water framework are likely BL-hexagonal cages with single occupancy for H₂ or BL-heptagonal cages for CO₂. With a further increase in guest size, the host cages for C₂H₆, C₂H₄, and C₃H₄ are BL-octagonal cages with single occupancy, and their long molecular axis tends to be normal to the surface of clathrate hydrates. In addition, for hydrophilic guest molecules, such as NH₃ and H₂S, which can form strong hydrogen bonds with water, we find that most guest molecules can preferentially displace water molecules from the lattice sites of the water framework, instead of being separately trapped within the water cages. Structural analogy between the 2D and 3D clathrates enlightens us to predict the stability of several bulk gas hydrates, namely, “ethane clathrate III”, “CH₄ ice-i” and “H₂ ice-i”. Our findings can not only enrich clathrate structures in the hydrate family but may also improve the understanding of hydrate formation in microporous media.

---

Introduction

Clathrate hydrates, which are ice-like crystalline compounds comprised of guest molecules trapped inside hydrogen-bonded water cages, can be formed spontaneously by cooling and/or compressing a mixture of guest molecules and water.¹ Understanding the microscopic mechanism of clathrate hydrate formation has become an enduring research topic, not only because it belongs to the fundamental subjects of crystal growth from mixtures and self-ordering of water around guest molecules,² but also because it has important implications to energy resources, environment, chemical industries and geological hazard prevention.^3–9

Over the past decade, considerable research efforts have been made to explore the structures and physical properties of clathrate hydrates.^10–23 However, the microscopic mechanism for the nucleation and growth of bulk clathrate hydrate is still not fully understood. This is because of the inability of precisely recording the time and spatial domain of a nucleation event experimentally, and also due to the very long computing time required in a typical molecular dynamics (MD) theoretical simulation of clathrate hydrate nucleation (a rare event).²¹ Recently, several simulation studies have shown that low-dimensional clathrate gas hydrates, as well as guest-free hydrates, can be spontaneously formed on the time scale of nanoseconds in a highly confined environment.^24–33 Moreover, the host cages formed in low-dimensional clathrate hydrates differ from those in bulk clathrate hydrates due to geometrical constraints. The predicted low-dimensional clathrate hydrates not only enrich the gas hydrate family, but also open a door towards an improved understanding of hydrate formation in sediments or in porous media.

Previous experimental and theoretical studies indicate that hydrate nucleation and growth are strongly dependent on the size of the guest molecules.^16,17 In this article, we perform systematic studies on the effect of guest-molecule size on the formation of two-dimensional (2D) gas hydrate (GH) using MD simulations. Our focus is on the bilayer (BL) clathrate hydrates formed in nanoslits with the guest molecules being ethane (C₂H₆), ethene (C₂H₄), allene (C₃H₄), carbon dioxide (CO₂), or the smallest, hydrogen (H₂) molecules. In addition, the formation of BL clathrate hydrates with the guest molecules being either NH₃ or H₂S molecules are examined because both guest molecules can entail strong H-bonding interaction with water molecules. We find that most hydrophilic guest molecules can preferentially displace water molecules from the lattice sites of the water framework, instead of being separately trapped within the water cages. Based on these insights from the 2D simulations, we speculate a series of 3D stable clathrate structures.

Model and methods

Classical MD simulations were performed to achieve the spontaneous formation of BL-clathrate hydrates when the binary fluid mixtures of water and guest molecules are confined in a nanoslit (width D = 0.8 nm to accommodate two layers of water²⁶). The water molecule is described by the TIP5P model,³⁴ while the TIP4P model was also examined for test simulations, which gave the same qualitative results of the bilayer hydrates formation as with those achieved with the TIP5P model (see ESI† for details). The OPLS potential models were chosen to simulate the C₂H₆, C₂H₄ and C₃H₄, NH₃ and H₂S molecules.^35,36 For representing proper electrostatic interaction, hydrogen molecule (H₂) was specifically modeled as a quadrupole with −0.64e charge at the center and +0.325e charge positioned at the two ends.³⁷ CO₂ molecule was treated using the EPM2 model.³⁸ A cut-off of 1.0 nm was used for interatomic interactions. Note that the cut-off method has been previously used to study the bilayer water.^32,33 Another widely used method for treating long-range electrostatic interactions in 2D structures is the slab-adapted Ewald sum method.³⁹ As summarized in a recent review,²⁹ both methods generally yield qualitatively the same bilayer ice and bilayer methane hydrate structures, although the ferroelectric monolayer ice phases can be obtained by only using the slab-adapted Ewald sum method.^28,29 The guest molecules–wall and water–wall interactions were described by the 9–3 Lennard-Jones (LJ) potential function. The LJ and Coulombic potential parameters are listed in the ESI (Table S1†). All the MD simulations were performed using the GROMACS 4.5 package⁴⁰ with periodic boundary conditions in the lateral directions (i.e., x and y directions that are parallel to the confining walls). The z direction is normal to the confining walls. Temperature and pressure were controlled by a Nosé–Hoover thermostat⁴¹ and Parrinello–Rahman barostat,⁴² respectively.

Results and discussion

In the first series of MD simulations, the simulation system consists of a binary fluid mixture of water and ethane molecules (with a H₂O/C₂H₆ ratio = 576 : 72 = 8 : 1, on the basis of test MD simulations). The lateral pressure (P_L) was set within the range of 200 MPa to 1 GPa to examine the pressure effect. The fluid system is initially equilibrated at a high temperature and then isobarically cooled in steps to a low temperature. Once the fluid system turns into a solid and reaches thermodynamic equilibrium at the low temperature, the temperature was increased again in steps. For all independent MD simulations with a different lateral pressure in the range of 200 MPa to 1 GPa, marked hysteresis-loop behavior for the internal energy versus temperature is seen (Fig. 1), suggesting the occurrence of a strong first-order phase transition for the confined binary mixture. Moreover, the inherent structure (obtained via applying the steepest-descent method to the final snapshot at the low temperature³⁰) of the solid phase depends on the lateral pressure (see ESI Fig. S1†). At a relatively low pressure (P_L = 200 MPa, Fig. S1a†), most of the ethane molecules congregate together within a cavity, behaving like a gas bubble, whereas other ethane molecules are separately encapsulated inside the BL octagonal water cages (with one ethane molecule per octagonal cage). These BL-octagonal water cages are part of a BL-amorphous ice, which exhibits empty BL-pentagonal and BL-hexagonal cages, as well as a small fraction of BL-heptagonal and BL-tetragonal cages.³⁰ With increasing pressure (P_L = 500 MPa, Fig. S1b and P_L = 800 MPa, Fig. S1c†), more and more ethane molecules are involved in the formation of BL gas hydrates, i.e., separately enclosed in the BL-octagonal cages. At the highest lateral pressure considered (P_L = 1 GPa), most of the ethane molecules are enclosed in the BL-octagonal cages (Fig. S1d†), while BL-tetragons connect the BL-octagonal cages (except with some defects, e.g., BL-pentagons); thus, a less perfect BL-octagon–tetragon hydrate was observed. Notably, double occupancy, i.e., two ethane molecules being encapsulated in every single BL-decagonal cage, was also observed (Fig. S1d†). However, phase-separated ethane gas bubbles still exist in the BL clathrate hydrate. More importantly, the MD trajectory (ESI Movie S1†) shows that the ethane molecules in the “bubble” appear to be crystalline, which is different from bulk clathrate simulations, where the guest molecule bubbles were fluid. Perhaps, this behavior produces the kinetic barrier that hinders the formation of a perfect BL-clathrate.

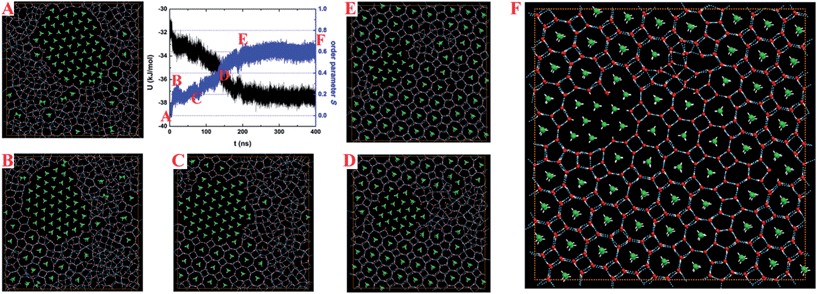
Fig. 1 Temperature-dependence of the potential energy U at various P_L for a mixture of water and ethane molecules confined in the nanoslit.

When the solid hydrate is heated, three types of behaviors were observed at different lateral pressures: (1) for P_L = 200 MPa, the crystalline structure shows a slight change; (2) for P_L = 800 MPa or 1 GPa, an increasing number of ethane molecules are separately enclosed in BL-octagonal cages, corresponding to the dip in potential–energy curves (Fig. 1C and D, at 330–340 K and 370–380 K, respectively); (3) for P_L = 500 MPa, when the system was heated to 340 K, coexisting liquid-water/ethane-bubble/BL-clathrate can be observed, which remains unchanged at 350 K. This result corresponds to the potential energy step at a temperature range of 340–350 K for P_L = 500 MPa (Fig. 1B).

On the basis of the inherent structures shown in Fig. S1† and the structural features of the BL-octagon–tetragon ethane hydrate (the details will be discussed below), every ethane molecule encaged in the BL-octagonal cages is perpendicular to the confining walls, i.e., parallel to the z axis. To characterize the degree of nucleation and growth for the BL-clathrate, an order parameter S is defined as follows:

where θ_i is the angle between the long molecular axis of the i-th ethane molecule and the z axis, N_A is the number of isolated ethane molecules encapsulated in the water cage (here, the isolated ethane molecule is defined such that every ethane molecule is entirely surrounded by water molecules, i.e., the ethane molecule is enclosed inside the BL-water cage), and N is the total number of ethane molecules. The summation of N_A in eqn (1) implies that ethane molecules involved in ethane bubbles are excluded from the summation. Thus, the order parameter S is 1 for the perfect BL-clathrate structure and 0 for phase-separated liquid.

Fig. 2 shows the time-dependent potential energy U and order parameter S for typical nucleation and growth of BL-clathrate hydrate (see Movie S1†) at 370 K and 1 GPa, starting from a phase-separated liquid water with an ethane bubble (pre-equilibrated at 380 K and 1 GPa; Fig. 2A). In the first several nanoseconds, stochastic nucleation events of ethane-containing BL-octagonal cages arise. At ∼7.5 ns, a clear jump in S from zero to ∼0.2 and a small drop in U (by ∼1 kJ mol⁻¹) can be seen, indicating a post-nucleation process (Fig. 2B). Beyond 75 ns, with more and more ethane molecules being separately incorporated into BL octagonal cages (Fig. 2C and D), marked growth of ethane hydrate was observed, as indicated by the precipitous increase of S and decrease of U. At ∼200 ns, a small domain of ethane bubble was enclosed in the hydrate (Fig. 2E), hindering its further growth. Some BL-pentagonal “defects”, which were formed to connect the BL-octagonal cages, result in a less perfect BL-clathrate hydrate (Fig. 2F).

Fig. 2 Time-dependent potential energy U (black curve) and order parameter S (blue curve) for the confined ethane–water system during the course of nucleation and growth of the BL-clathrate hydrate at T = 370 K and P_L = 1 GPa. Snapshots (A) through (F) display the structural evolution at different time-stages of the MD simulation marked in the time-dependent S curve. Color code: O, red; H, white; C, green; hydrogen bond, blue dotted line.

To remove the ethane bubble and the BL-pentagonal “defects”, we designed a thermodynamic path in the MD simulation to achieve a near-perfect BL-ethane hydrate crystal, including the cyclic heating/annealing, stepwise compression, and long-time incubation. Starting from a three-phase coexistence structure, as shown in Fig. 3A, which was obtained at 350 K on heating at 500 MPa, the lateral pressure of the system was increased to 600 MPa for 20 ns and then to 700 MPa for 100 ns. Subsequently, the temperature and lateral pressure of the system were increased instantly to 360 K and 800 MPa for 50 ns. The MD trajectory (Movie S2†) and order parameters S (Fig. S2†) demonstrate that the octagon-square domain grows gradually. Furthermore, the temperature and pressure of the system were increased instantly to 390 K and 1 GPa, and maintained for 200 ns (Movie S3†). Most ethane molecules were separately encapsulated in the BL-octagonal cages, which were connected by BL-tetragons (Fig. 3B). Finally, we performed a simulation for 160 ns at 430 K and 1.5 GPa to produce a perfect BL-clathrate hydrate (as shown in Fig. 3C and Movie S4†). Note that for the perfect BL-clathrate, order parameter S ∼ 0.8 is less than 1 (Fig. S2†), suggesting that the ethane axis was tilting with respect to the z axis because of thermal motion. As temperature decreases, the majority of ethane molecules in the hydrate are aligned vertically (Fig. S3†). In addition, the inherent structures show that ethane molecules are normal to the confining wall due to the absence of thermal motion. It can also been seen from Fig. 3B that some water molecules are separately enclosed in water cages (blue marked), i.e. interstitial water, indicating the transformation among the water cages through water pair insertions/removals and rotations. Similar behavior was observed from the MD simulation of bulk hydrate growth,²² and these interstitial water molecules may facilitate the growth of hydrate crystals.

Fig. 3 A designed thermodynamic path in the MD simulation to grow a nearly-perfect BL ethane clathrate crystal. (A) A three-phase coexistence structure at 350 K and 500 MPa. (B) A less perfect BL-clathrate hydrate at 390 K and 1 GPa. (C) Top and side views of the inherent structure of a perfect BL-clathrate hydrate at 430 K and 1.5 GPa. The blue spheres in (B) represent the water molecules separately enclosed in water cages, i.e., interstitial water.

Both Fig. 2 and 3 demonstrate that the crystallization of the BL ethane clathrate proceeds via a multistep nucleation and growth. First, most ethane molecules gather together and form a dense bubble. The ethane bubble persists in solution, and at the nucleation stage, the ethane molecules at the edge of bubble or those dissolved in solution are trapped in the BL-octagonal cages to form clathrate nuclei. However, these early BL-octagonal cages can easily collapse before becoming critical nuclei, which consists of at least four octagons according to observation of the MD trajectories. Second, the nuclei that are larger in size than the critical nucleus grow and some BL-polygon “defects” (BL-pentagons in particular) are formed within the solid nuclei, resulting in a seed of amorphous clathrate. Note that the bubble and BL-pentagonal defects can block the formation of a perfect BL-clathrate. As shown in Fig. 3C, starting from the three-phase coexistence, upon cyclic heating/annealing, stepwise compression, and long-time incubation, the BL amorphous clathrate develops into a nearly-perfect BL-clathrate crystal. This multistep nucleation mechanism is consistent with the two-step nucleation mechanism revealed in bulk clathrates.^{15–18,21–23}

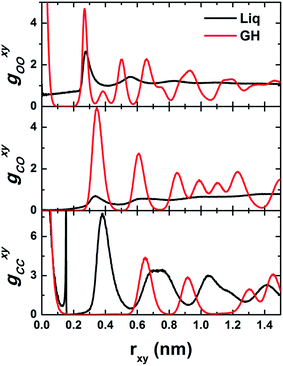
To gain more insight into the structural features of BL-octagon–tetragon ethane hydrate, we examined the lateral site–site radial distribution functions (RDFs) and the transverse density profiles (TDPs) of phase-separated liquid at 1 GPa and 450 K and a perfect BL-clathrate, as shown in Fig. 4 and 5. The oxygen (O)–oxygen (O) RDF (g_OO^xy) of liquid exhibits a typical liquid behavior, including a pre-peak representing a bilayer liquid, and a prominent first peak at r_xy ∼ 0.28 nm, followed by decaying peaks and eventually approaches to unity, indicating a disordered state, while g_OO^xy of the clathrate hydrate shows features of sharp peaks owing to the long-range order: the first peak (at r_xy ∼ 0) corresponds to the solid bilayer and the hydrogen bonding between two monolayer water (normal to the walls), and the second peak (at r_xy ∼ 0.27 nm) indicates the in-plane hydrogen bonds. Moreover, the methyl (C)–methyl (C) RDF (g_CC^xy) for phase-separated liquid also shows sharp peaks. However, this does indicate a long-range order, but a high-density ethane bubble, which can be also seen from the methyl (C)–oxygen (O) RDF (g_CO^xy) in which the first peak of liquid is very low (<1). The first and second peaks of g_CC^xy for phase-separated liquid suggest that some ethane molecules are oriented normal to the walls (at r_xy ∼ 0) and some are parallel to the walls (at r_xy ∼ 0.15 nm). However, the g_CC^xy of clathrate hydrate exhibits long-range order, and the first peak indicates that the ethane molecules are normal to the walls (at r_xy ∼ 0). The second peak (at r_xy ∼ 0.65 nm) corresponds to the lateral distance between the center of nearest-neighbor octagons, while the third peak (at r_xy ∼ 0.92) corresponds to the lateral distance between the center of second nearest-neighbor octagons (connected by tetragons). The disappearance of the peak at r_xy ∼ 0.15 nm suggests that all ethane molecules are normal to the walls. The first peak of g_CO^xy for clathrate hydrate corresponds to the “radius” of octagons (the lateral distance between ethane molecules and their nearest-neighbor waters, which form the octagons).

Fig. 4 Computed lateral site–site radial distribution functions (RDFs) g(r_xy) for phase-separated liquid (Liq) and bilayer-gas hydrate (GH).

Fig. 5 Transverse density profiles for phase-separated liquid and gas hydrate.

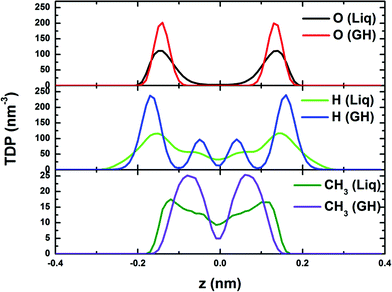
Fig. 5 shows the computed transverse density profiles of oxygen, hydrogen and ethane (methyl, CH₃) in the z-direction (normal to the confining walls). The distribution of oxygen for the BL-clathrate hydrate exhibits two sharp peaks, suggesting a solid state, whereas these peaks for the phase-separated liquid are broad. The distribution of hydrogen atoms in the BL-clathrate hydrate exhibits four sharp peaks, two close to the peaks of oxygen, indicating that the OH bond is parallel to the confining walls, and another two at the distance of 0.1 nm from the peak of oxygen, indicating that the OH bond is normal to the confining walls. The amplitude of the peaks for hydrogen that are parallel to the confining walls is about three times higher than that normal to the confining walls, indicating that among the four water molecules in one tetragon, two are parallel to the confining walls, and other two are normal to the confining walls. The distribution of methyl (CH₃) groups in the phase-separated liquid is also broad, while that for the BL-clathrate hydrate, two sharp peaks with a distance of 0.15 nm, close to C–C bond length of ethane molecule, suggesting that the ethane molecule in BL-clathrate hydrate is normal to the confining walls.

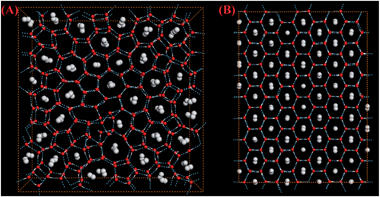
From Fig. 3C, one can see that the water framework of BL ethane clathrate is identical to that of BL methane clathrate,²⁶i.e., the Archimedean 4·8² (square-octagon) pattern, even though an ethane molecule has a longer molecular axis than that of CH₄. Actually, if the long molecular axis of ethane is normal to the surface of the clathrate hydrate, the lateral size of ethane is comparable to that of CH₄. Therefore, both molecules can give rise to the same water framework. To further test this conjecture, we also performed several independent simulations for binary fluid mixtures of water–ethene and water–allene. All of these molecules have similar lateral size, while the perpendicular length of allene is longer than that of ethane. It turns out that ethene and allene can also form nearly-perfect clathrate hydrates, and their water frameworks also exhibit the Archimedean 4·8² (square-octagon) pattern (see Fig. S4–S6†). In addition, the molecular axis of both ethene and allene molecules is also normal to the plane of BL-clathrate hydrates. More importantly, the stabilities of the BL-square-octagon clathrates for the three linear molecules are confirmed by ab initio computation (see ESI† for details).

Thus far, we have shown that the three linear molecules can lead to the same water framework as the CH₄ guest. How about guest molecules smaller than CH₄? To address this question, we performed another series of independent MD simulations to seek BL CO₂ and H₂ hydrates from two types of initial configurations. First, we constructed a perfect BL-clathrate hydrate (4·8² pattern) with either CO₂ or H₂ molecules replacing the ethane molecules. We then started the MD simulation (in the NVT ensemble) with the BL-hydrate for CO₂ (H₂) as the initial structure and at 100 K, followed by stepwise increases in temperature towards 300 K. For the CO₂ hydrate, the BL-octagonal cages start to collapse when the temperature reaches 240 K. Eventually, most of the BL-octagonal cages are transformed to BL-heptagonal cages connected by BL-pentagons (Movie S5†).

Another MD simulation was started from a binary fluid mixture of water and CO₂ (see Fig. 6). In particular, a mixture of 50 CO₂ and 400 water molecules was equilibrated at 800 K and 1 GPa, followed by an instant cooling to 250 K. After an equilibration of 20 ns, a mixture of gas and hydrate was formed, where some CO₂ molecules are separately enclosed in BL-octagonal or BL-heptagonal cages, while many CO₂ molecules are not dissolved into water. To render more CO₂ molecules dissolved into water, the gas and hydrate mixture was heated to 300 K and compressed at 1 GPa for 40 ns (Fig. 6A). Subsequently, the system was equilibrated at 325 K and 1.5 GPa for 260 ns (Fig. 6B) from which an amorphous-like BL CO₂ hydrate structure was formed (see Fig. 6C). Because CO₂ molecules can be separately encapsulated in either heptagonal or octagonal cages (Fig. 6C), some CO₂ molecules were aligned in a horizontal direction at low temperatures. Fig. S7A† shows the CO₂ molecular orientation versus temperature with respect to the z direction (surface normal of the clathrate) in the BL-amorphous hydrate. As temperature decreases, the majority of CO₂ in the hydrate are aligned in the z direction (θ being ∼16 degree), while others are aligned horizontally (θ being ∼90 degree) below 50 K. Fig. S7B† shows that the order parameter S of CO₂ increases as temperature decreases.

Fig. 6 (A) An image of mixed CO₂ gas and hydrate at 300 K and 1 GPa. (B) Time-dependent S during system equilibration at 325 K and 1.5 GPa for 260 ns. As more CO₂ dissolved into bilayer water, more CO₂ are aligned normal to the surface of clathrate. (C) An image of hydrate structure at 260 ns, which is amorphous-like. Most of the CO₂ molecules are located within the BL-heptagonal cages, while a small number of them are trapped inside BL-octagonal cages. Color code: O, red; H, white; C, grey.

Next, starting with a constructed H₂ hydrate, a similar NVT MD simulation shows that the BL-octagonal cages collapse at 150 K, indicating that the H₂ BL-clathrate with 4·8² pattern was mechanically unstable even at very low temperature. Another MD simulation starts with a binary fluid mixture of water and H₂ (with 20% mole fraction of H₂) at 300 K and 1 GPa, which leads to a BL amorphous hydrate (Fig. 7A). In this amorphous structure, there are not only BL-hexagonal cages occupied by single H₂, but also BL-heptagonal cages accommodating two H₂ molecules (i.e., double occupancy), BL-octagonal cages that encage three H₂ molecules, and BL-nonagonal cages encapsulating four H₂ molecules. Note that the water framework of the BL amorphous hydrate was identical to the BL-amorphous ice.³⁰ We know that the BL-amorphous ice is a metastable phase, whereas the BL-hexagonal ice is the thermodynamically stable phase because the latter can be obtained by annealing the former through repeated cycles of cooling and heating.^26,31 Thus, we speculate that a possible ideal BL H₂ clathrate could be a BL-hexagonal crystal with single occupancy of H₂ in each hexagonal cage (Fig. 7B). To verify this speculation, we examined the thermal stability of such a BL-hexagon H₂ clathrate crystal via an MD simulation in an NVT ensemble for temperature changes from 100 to 300 K. For T ≤ 270 K, the constructed BL-hexagonal H₂ clathrate does not show signs of decomposition or cage collapse. At 280 K, the cages start to collapse (Movie S6†). The stability of the BL-hexagonal H₂ clathrate was also confirmed by ab initio computation (see ESI† for details). The thermodynamic path to achieve the near-perfect BL-hexagonal H₂ clathrate will be investigated in the future.

Fig. 7 (A) An image of a BL amorphous H₂ clathrate. (B) A constructed perfect BL-hexagonal H₂ clathrate. Red spheres represent oxygen, white small spheres represent the hydrogen of water, big white spheres represent hydrogen molecules, and blue dotted lines represent hydrogen bonds.

As a summary, for the smallest diatomic molecule H₂, the host cage is likely to be a BL-hexagon for single occupancy, BL-heptagon for double occupancy, BL-octagon for triple occupancy, and BL-nonagon for quadruple occupancy. For CO₂ with a size between that of H₂ and CH₄, the host cage is likely to be a BL-heptagon for single occupancy. With further increase in molecular size, for CH₄ (ref. 26) and linear molecules with similar lateral size, such as C₂H₆, C₂H₄, and C₃H₄, the host cage is a BL-octagon with single occupancy. The long molecular axis of the latter three molecules tends to be normal to the surface of clathrate hydrates.

Thus far, all the guest molecules we have considered are hydrophobic. It is commonly believed that highly hydrophilic molecules cannot serve as guest molecules because they tend to disrupt the hydrogen-bonding networks. However, there are actual evidences from experiments and MD simulations of stable clathrates with some guests forming strong hydrogen bonds with water.^43–47 Can these hydrophilic molecules support stable BL-clathrates as well? To explore this possibility, we first examined the stability of a constructed BL-clathrate NH₃ hydrate with the 4·8² pattern because NH₃ was comparable to CH₄ in size. Based on MD simulations (in the NVT ensemble) with temperature increasing in steps from 100 to 300 K, we see signs of cage collapse at 180 K (Movie S7†). Alternatively, we examined the possibility of the spontaneous formation of BL NH₃ hydrate by starting the MD simulation (in the NP_LT ensemble with the ratio of H₂O/NH₃ = 576/72 = 8/1) from a high temperature fluid (equilibrated at 1000 K and 1 GPa), followed by an instant quench to 250 K. After 100 ns, the obtained hydrate structure resembles that of BL-rhombic ice⁴⁸ with the exception that some water molecules are displaced by NH₃ molecules from the lattice sites of the rhombic structure (Fig. 8A, and Movie S8†).

Fig. 8 (A) The inherent structure of a BL mixture of water and NH₃. (B) An image of the structure obtained via heating the “perfect” binary C₂H₆ and NH₃ hydrate to 300 K. (C) The final image obtained from the simulation (starting from a fluid mixture, the system was instantly cooled to 250 K at fixed lateral pressure, and then heated again to 260–270 K). Color code: O, red; H, white; N, blue; C, green; hydrogen bond, blue dotted line.

We note a recent simulation and experimental study shows that the addition of methane molecules can stabilize the very unstable NH₃ clathrate, although the mixed clathrate is still far less stable than that of a pure methane clathrate.⁴⁷ Enlightened by this study, we examined the stability of a perfect BL-ethane hydrate with the 4·8² pattern and with a portion of guests replaced by NH₃ molecules. Although the main water framework consisting of cages containing C₂H₆ remains stable at 300 K, the cages containing NH₃ starts to collapse even at 160 K, and the NH₃ and water molecules form BL-polygons (Fig. 8B and Movie S9†). The collapse of the NH₃ cages suggests that the hydrophilic molecules (such as NH₃) can destabilize the clathrate structure.

We also examined the possibility of the formation of binary C₂H₆ and NH₃ hydrate by cooling a fluid mixture of C₂H₆, NH₃ and water (with a ratio of H₂O/C₂H₆/NH₃ = 576/63/9 = 64/7/1). Remarkably, a mixed clathrate was eventually formed (see Fig. 8C). Here, the frame-structure of BL water (besides some BL-polygon defects) was identical to that of BL-ethane clathrate, i.e., 4·8² pattern. The ethane molecules were separately encapsulated in the BL-octagonal cages, while NH₃ molecules preferentially displaced some water molecules from the lattice sites (Movie S10†). NH₃ molecules in cages were also observed. More interestingly, the MD trajectory shows that the NH₃ molecules diffuse much more rapidly, while the hydrophobic guests and their surrounding water molecules stay in place (Movies S8–S10†). The rapid diffusion of NH₃ molecules may be the reason for the destabilization of the NH₃ clathrate. Interestingly, for another hydrophilic molecule, i.e., H₂S molecule, similar behavior was also observed from the MD simulations of BL-H₂S hydrate (see Fig. S8 and Movie S11†).

Additional remarks on connection with 3D methane hydrates

(1) We have demonstrated the formation of 2D BL-clathrate ethane, ethene or allene hydrates, where the guest molecules preferred to be entrapped inside BL-octagonal cages. Are there any structural analogy between the 2D and 3D (bulk) ethane clathrates? In other words, can these linear molecules be separately entrapped in “octagonal” cages in bulk clathrates? One hint can be gained from the structures of the high-pressure methane and argon hydrate III phases^49,50 because in these bulk hydrates, their typical 2D plane was composed of tetragons and octagons. Motivated by this hint, we performed an MD simulation test and confirmed that indeed the methane hydrate III can be stable at room temperature and 3 GPa (Fig. S9†). Next, we constructed a new “ethane clathrate III”, whose water framework resembles that of the methane hydrate III. Here, ethane molecules are separately enclosed in octagonal cages. The “ethane clathrate III” was first optimized at zero temperature with a fixed volume. Then, the system was heated at several different pressures. Our MD simulation shows that the “ethane clathrate III” was stable at 3 GPa and temperatures below 320 K (Fig. 9A).

Fig. 9 Images of (A) the constructed “ethane clathrate III” at 3 GPa and 300 K and (B) constructed “CH₄ ice-i” at 200 MPa and 230 K.

(2) Another hint can be gained from the “ice-i”, which is a stable guest-free ice clathrate observed only in computer simulations.⁵¹ We constructed a new methane clathrate (CH₄ ice-i) in which the methane molecules were separately entrapped by “octagonal cages” (see Fig. 9B). The new solid hydrate was heated stepwise at a fixed pressure (200 MPa). The melting temperature of “CH₄ ice-i” was about 240 K, close to that of guest-free bulk ice clathrate (ice-i melts at 250 K and 200 MPa).⁵¹ We also examined the stability of “ethane ice-i” and found that the hand-made hydrate was not stable even at 0 K. However, when the Lennard-Jones parameters of CH₃ were reduced to those of hydrogen (i.e., σ = 0.266 nm and ε = 0.125 kJ mol⁻¹) while keeping the bond length (CH₃–CH₃) unchanged, the “ethane ice-i” was stable, suggesting that “hydrogen ice-i” may be a stable hydrate. The stability of the bulk “hydrogen ice-i” using the first-principles method will be investigated in the future.

Conclusions

Based on numerous MD simulations, a number of stable BL crystalline and amorphous gas hydrates with either hydrophobic or hydrophilic guest molecules were obtained within a nanoslit. Our MD results demonstrate that the host water cages depend on the size of the guest molecule. For example, for the smallest diatomic molecule, H₂, despite the amorphous structure observed, the BL-hexagonal clathrate was mechanically most stable for a single occupancy of a H₂ molecule per cage. For a larger guest molecule, CO₂, the amorphous clathrate entails mostly the BL-heptagonal cages with single occupancy of a CO₂ molecule per cage. For several molecules with sizes larger than CO₂, i.e., CH₄,²⁶ or linear molecules, such as C₂H₆, C₂H₄, and C₃H₄, the BL-square-octagonal clathrate structure was formed, where the three linear molecules can be accommodated within the BL-octagonal cages by adjusting their molecular orientation. This adjustment of the molecular orientation of linear molecules may be a reason that seemingly different guests can be enclosed in the same type of water cage in bulk clathrate hydrate.

In addition, for hydrophilic guest molecules, such as NH₃ and H₂S, which can form strong hydrogen bonds with water, most of the guest molecules can preferentially displace water molecules, one for each, from lattice sites of the water framework rather than being separately trapped within water cages. Furthermore, for a mixture of C₂H₆ and NH₃, a mixed clathrate identical to BL-ethane clathrate, in which the ethane molecules are separately encapsulated in BL-octagonal cages and NH₃ molecules preferentially displace some water molecules from the lattice sites, was observed. Our simulations also show that the NH₃ molecules diffuse much more rapidly, while the hydrophobic guests and their surrounding water molecules stay in place. The rapid diffusion of NH₃ may be the reason for the destabilization of the clathrate.

Finally, the structural analogy between the 2D and 3D (bulk) ethane clathrates was analyzed. Motivated from the unique feature of “BL-octagonal cages” in many 2D clathrate hydrates, we predicted the stability of bulk “ethane clathrate III”, “CH₄ ice-i” and “H₂ ice-i”. These newly predicted bulk clathrate hydrates as well as their structural similarity with 2D BL clathrate hydrates require future experimental confirmation.

Acknowledgements

This work is supported by the MOST (2011CB921400), the NSFC (21121003, 2123307), the Fundamental Research Funds for the Central Universities (WK2060030012), and CAS (XDB01020300, XDB10030402). XCZ is supported by grants from the University of Nebraska Center for Energy Sciences Research and a grant from USTC for (1000plan) Qianren-B summer research. WHZ and XCZ are also supported by a grant (1401042004) from Bureau of Science & Technology of Anhui Province.

Notes and references

1. E. D. Sloan and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC Press, Boca Raton, FL, 3rd edn, 2008.
2. J. Vatamanu and P. G. Kusalik, J. Phys. Chem. B, 2006, 110, 15896–15904.
3. E. D. Sloan, Nature, 2003, 426, 353–359.
4. L. J. Florusse, C. J. Peters, J. Schoonman, K. C. Hester, C. A. Koh, S. F. Dec, K. N. Marsh and E. D. Sloan, Science, 2004, 306, 469–471.
5. W. L. Mao, H.-k. Mao, A. F. Goncharov, V. V. Struzhkin, Q. Guo, J. Hu, J. Shu, R. J. Hemley, M. Somayazulu and Y. Zhao, Science, 2002, 297, 2247–2249.
6. Y. Park, D.-Y. Kim, J.-W. Lee, D.-G. Huh, K.-P. Park, J. Lee and H. Lee, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12690–12694.
7. K. Kaiho, T. Arinobu, R. Ishiwatari, H. E. G. Morgans, H. Okada, N. Takeda, K. Tazaki, G. Zhou, Y. Kajiwara, R. Matsumoto, A. Hirai, N. Niitsuma and H. Wada, Paleoceanography, 1996, 11, 447–465.
8. C. R. Fisher, I. R. MacDonald, R. Sassen, C. M. Young, S. A. Macko, S. Hourdez, R. S. Carney, S. Joye and E. McMullin, Naturwissenschaften, 2000, 87, 184–187.
9. D. J. Milton, Science, 1974, 183, 654–656.
10. D. K. Staykova, W. F. Kuhs, A. N. Salamatin and T. Hansen, J. Phys. Chem. B, 2003, 107, 10299–10311.
11. A. Klapproth, E. Goreshnik, D. Staykova, H. Klein and W. F. Kuhs, Can. J. Phys., 2003, 81, 503–518.
12. J. M. Schicks and J. A. Ripmeester, Angew. Chem., Int. Ed., 2004, 43, 3310–3313.
13. M. M. Murshed and W. F. Kuhs, J. Phys. Chem. B, 2009, 113, 5172–5180.
14. H. Ohno, T. A. Strobel, S. F. Dec, E. D. Sloan Jr and C. A. Koh, J. Phys. Chem. A, 2009, 113, 1711–1716.
15. L. C. Jacobson, W. Hujo and V. Molinero, J. Am. Chem. Soc., 2010, 132, 11806–11811.
16. L. C. Jacobson, W. Hujo and V. Molinero, J. Phys. Chem. B, 2010, 114, 13796–13807.
17. J. S. Loveday and R. J. Nelmes, Phys. Chem. Chem. Phys., 2008, 10, 937–950.
18. J. Vatamanu and P. G. Kusalik, Phys. Chem. Chem. Phys., 2010, 12, 15065–15072.
19. L. C. Jacobson and V. Molinero, J. Am. Chem. Soc., 2011, 133, 6458–6463.
20. G.-J. Guo, Y.-G. Zhang, C.-J. Liu and K.-H. Li, Phys. Chem. Chem. Phys., 2011, 13, 12048–12057.
21. M. R. Walsh, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Science, 2009, 326, 1095–1098.
22. M. R. Walsh, J. D. Rainey, P. G. Lafond, D.-H. Park, G. T. Beckham, M. D. Jones, K.-H. Lee, C. A. Koh, E. D. Sloan, D. T. Wu and A. K. Sum, Phys. Chem. Chem. Phys., 2011, 13, 19951–19959.
23. M. R. Walsh, G. T. Beckham, C. A. Koh, E. D. Sloan, D. T. Wu and A. K. Sum, J. Phys. Chem. C, 2011, 115, 21241–21248.
24. H. Tanaka and K. Koga, J. Chem. Phys., 2005, 123, 094706.
25. J. Bai, C. A. Angell and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5718–5722.
26. J. Bai and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21240–21245.
27. W. Zhao, L. Wang, J. Bai, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2014, 136, 10661–10668.
28. W. Zhao, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Chem. Sci., 2014, 5, 1757–1764.
29. W. Zhao, L. Wang, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Acc. Chem. Res., 2014, 47, 2505–2513.
30. K. Koga, H. Tanaka and X. C. Zeng, Nature, 2000, 408, 564–567.
31. J. Bai, X. C. Zeng, K. Koga and H. Tanaka, Mol. Simul., 2003, 29, 619–626.
32. S. Han, M. Y. Choi, P. Kumar and H. E. Stanley, Nat. Phys., 2010, 6, 685–689.
33. P. Kumar, S. V. Buldyrev, F. W. Starr, N. Giovambattista and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051503.
34. M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922.
35. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
36. R. C. Rizzo and W. L. Jorgensen, J. Am. Chem. Soc., 1999, 121, 4827–4836.
37. S. Figueroa-Gerstenmaier, S. Giudice, L. Cavallo and G. Milano, Phys. Chem. Chem. Phys., 2009, 11, 3935–3942.
38. J. G. Harris and K. H. Yung, J. Phys. Chem., 1995, 99, 12021–12024.
39. I. C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155.
40. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
41. S. Nose, Mol. Phys., 1984, 52, 255–268; W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
42. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
43. T. C. W. Mak, J. Chem. Phys., 1965, 43, 2799–2805.
44. K. Koga and H. Tanaka, J. Chem. Phys., 1996, 104, 263–272.
45. S. Alavi, R. Susilo and J. A. Ripmeester, J. Chem. Phys., 2009, 130, 174501.
46. V. Buch, J. P. Devlin, I. A. Monreal, B. Jagoda-Cwikilik, N. Uras-Aytemiz and L. Cwiklik, Phys. Chem. Chem. Phys., 2009, 11, 10245–10265.
47. K. Shin, R. Kumar, K. A. Udachin, S. Alavi and J. A. Ripmeester, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14785–14790.
48. R. Zangi and A. E. Mark, J. Chem. Phys., 2003, 119, 1694–1700.
49. J. S. Loveday, R. J. Nelmes, M. Guthrie, D. D. Klug and J. S. Tse, Phys. Rev. Lett., 2001, 87, 215501.
50. A. Y. Manakov, A. G. Ogienko, M. Tkacz, J. Lipkowski, A. S. Stoporev and N. V. Kutaev, J. Phys. Chem. B, 2011, 115, 9564–9569.
51. C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2004, 120, 9175–9184; C. J. Fennell and J. D. Gezelter, J. Chem. Theory Comput., 2005, 1, 662–667.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1–S9, Table S1, independent MD simulations with the TIP4P water model, the density-functional theory structural optimizations, and Movies S1–S11. See DOI: 10.1039/c4ta06857b

‡ Both authors contributed equally to this work.

---