Open Access Article
Open Access ArticleNanostructural changes in crystallizable controlling units determine the temperature-memory of polymers†
Ulrich
Nöchel‡
a,
Chaganti Srinivasa
Reddy‡§
a,
Ke
Wang¶
a,
Jing
Cui||
a,
Ivo
Zizak
b,
Marc
Behl
a,
Karl
Kratz
a and
Andreas
Lendlein
*ac
aInstitute of Biomaterial Science, Helmholtz-Zentrum Geesthacht, Kantstr. 55, 14513 Teltow, Germany. E-mail: andreas.lendlein@hzg.de
bHelmholtz-Zentrum Berlin, Institute for Nanometer Optics and Technology, Albert-Einstein-Str. 15, 12489 Berlin, Germany
cInstitute of Chemistry, University Potsdam, Karl-Liebknecht-Str. 24-25, 14476 Potsdam, Germany
First published on 3rd March 2015
Abstract
Temperature-memory polymers remember the temperature, where they were deformed recently, enabled by broad thermal transitions. In this study, we explored a series of crosslinked poly[ethylene-co-(vinyl acetate)] networks (cPEVAs) comprising crystallizable polyethylene (PE) controlling units exhibiting a pronounced temperature-memory effect (TME) between 16 and 99 °C related to a broad melting transition (∼100 °C). The nanostructural changes in such cPEVAs during programming and activation of the TME were analyzed via in situ X-ray scattering and specific annealing experiments. Different contributions to the mechanism of memorizing high or low deformation temperatures (Tdeform) were observed in cPEVA, which can be associated to the average PE crystal sizes. At high deformation temperatures (>50 °C), newly formed PE crystals, which are established during cooling when fixing the temporary shape, dominated the TME mechanism. In contrast, at low Tdeform (<50 °C), corresponding to a cold drawing scenario, the deformation led preferably to a disruption of existing large crystals into smaller ones, which then fix the temporary shape upon cooling. The observed mechanism of memorizing a deformation temperature might enable the prediction of the TME behavior and the knowledge based design of other TMPs with crystallizable controlling units.
1. Introduction
Thermo-sensitive polymer networks exhibiting a temperature-memory effect (TME)1–8 typically exhibit a broad thermal transition ΔTtrans9 or two overlapping thermal transitions, which could also exhibit multi-shape effects.10–12 Temperature-memory polymers (TMPs) can memorize the temperature Tdeform within ΔTtrans, where they have been deformed during programming. The original shape of the programmed TMP is recalled when response temperatures Tsw are exceeded, whereby Tsw are equal to or above Tdeform. The temperature interval ΔTtrans, which can be either a glass (Tg) or melting (Tm) transition, can be considered as an ensemble of individual sharp transitions (Ttrans,i), whereby each single sharp transition can be utilized as reversible physical crosslinks for fixation of the temporary shape. In this context, first theoretical model approaches have recently been introduced for the description of amorphous TMPs.2,13,14 Still, it is relevant to understand and experimentally confirm the mechanistic aspects of TME in polymers with crystallizable controlling units. One example for polymers having a broad ΔTm and showing excellent temperature-memory properties over a temperature interval of up to 90 °C is crosslinked poly[ethylene-co-(vinyl acetate)] (cPEVA) comprising amorphous vinyl acetate (VA) segments and crystallizable polyethylene (PE) segments.4 The broad ΔTm in cPEVA is a result of the sequence structure of the copolymer and in particular the distribution of PE segment lengths, which are related to the thickness of the crystalline lamellae. The broadness of ΔTm in cPEVA can be influenced by either the weight fraction of VA co-monomer or the crosslink density of the polymer network.We hypothesized that the TME capability of cPEVA is enabled by specific nanostructures of the crystals, which remember the temperature of the deformation. Several contributions might influence the crystallizable controlling units when a temperature-memory creation procedure (TMCP) is applied, which includes a deformation step at certain Tdeform within ΔTm. First, the temperature (Tdeform) prior deformation could be considered as an isothermal treatment, permitting the variation of crystal dimensions. Second, the deformation step could lead into a rearrangement of the crystal structure (e.g. orientation of crystals) and third, the contribution of the cooling step when fixing the temporary shape will influence the nanostructure responsible for memorizing different Tdeforms. These changes of the semi-crystalline nanostructure would be caused both by the temperature within the melting range and the deformation to the temporary shape.
In this study, we explored the nanostructural changes during temperature-memory programming and recovery for a series of cPEVAs with regard to the contribution of temperature treatment by means of specific annealing experiments as well as DSC analysis, the influence of the deformation step during temperature-memory creation procedure at different temperatures, and the contribution of the cooling step on the formed semi-crystalline nanostructure via in situ X-ray scattering techniques (small- and wide-angle X-ray scattering SAXS/WAXS). In this way, the effect of applying different Tdeforms on the nanostructure of PE crystalline domains in programmed cPEVAs and therefore on the TME mechanism could be revealed.
In the following we describe the thermomechanical characterization of the cPEVA copolymer networks. Their nanostructure is explored by SAXS and WAXS and compared to theoretical dimensions. The thermal contribution to the TME is investigated by annealing experiments of non-deformed samples and analyzed by DSC. The contribution of the mechanical deformation at Tdeform and the contribution of the cooling step to changes of the nanostructure of the crystallizable controlling units are investigated in situ by SAXS and WAXS. Finally, mechanisms at high and low Tdeform are deduced from these experiments and temperature dependent pathways for the TME are presented.
2. Experimental
2.1. Materials
Poly[ethylene-co-(vinyl acetate)]s (DuPont, Wilmington, USA) with vinyl acetate contents of 18 wt% and 28 wt% (data of supplier) and the thermosensitive initiator dicumyl peroxide (DCP) (Sigma-Aldrich, Taufkirchen, Germany) were used as received. Copolymer networks were prepared as described in reference,15i.e., PEVAs were mixed with 0.5, 1, or 2 wt% DCP in a twin-screw extruder (EuroPrismLab, Thermo Fisher Scientific, MA, USA) at 110 °C and 50 rpm. The obtained PEVA/DCP blends were compression molded into films with 1 mm thickness at 200 °C at 20 bar for 25 min.2.2. Thermogravimetric analysis (TGA)
TGA measurements were carried out on a TGA 209 (NETZSCH, Selb, Germany) in the temperature range from 25 °C to 700 °C with a heating rate of 20 K min−1. The composition of cPEVA was analyzed according to the weight loss of acetic acid groups observed in the temperature range from 300 °C to 410 °C,16 where the vinyl acetate weight content (VAC) was calculated by eqn (1). | (1) |
2.3. 1H-NMR spectroscopy
1H-NMR spectroscopy was recorded at 25 °C on a 500 MHz Advance spectrometer (Bruker, Karlsruhe, Germany) using tetramethylsilane (TMS) as internal standard. Experiments were performed at 500 MHz (1H) resonance frequency with the spectral width of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. Samples were dissolved in toluene-d8 at 50 °C for 18 h prior to the measurements. The assigned chemical shifts were: (a) –COOCH3– (methylene protons near the carboxyl group, δ = 1.8 ppm), (b) –CH– (methylene protons near the carboxyl group, δ = 5.0 ppm), and (c) –CH2– (linear methylene protons, δ = 1.3–1.6 ppm) (see ESI Fig. S1†).
000 Hz. Samples were dissolved in toluene-d8 at 50 °C for 18 h prior to the measurements. The assigned chemical shifts were: (a) –COOCH3– (methylene protons near the carboxyl group, δ = 1.8 ppm), (b) –CH– (methylene protons near the carboxyl group, δ = 5.0 ppm), and (c) –CH2– (linear methylene protons, δ = 1.3–1.6 ppm) (see ESI Fig. S1†).
The 1H-NMR data were used for calculation of the theoretical average segment length of PE sequences using the formula n0 = 1 + 2Fe/Fv, where n0 is the segment length, Fe the ethylene mole fraction, and Fv the VA mole fraction.17
2.4. Swelling experiments
The gel content (G) was determined by gravimetric relation of the non-extracted reaction product to the purified polymer network. The purification procedure consisted of extraction with toluene at 50 °C for 24 h, removing all un-reacted fractions and drying the samples at 50 °C under vacuum until constant weight was reached (eqn (2)). cPEVAs purified by extraction were used for determination of equilibrium swelling Q in toluene (eqn (3)): | (2) |
 | (3) |
2.5. Differential scanning calorimetry (DSC)
DSC measurements were performed on a DSC 204 Phoenix (NETZSCH, Selb, Germany) applying a heating–cooling–heating cycle at heating and cooling rates of 10 K min−1 between −100 and 150 °C. The melting temperatures of cPEVAs were obtained from the second heating run. Furthermore, the melting enthalpy related weight crystallinity (wc) of cPEVAs was calculated from DSC endothermic curves obtained from second heating according to eqn (4). | (4) |
2.6. Annealing experiments
For annealing the copolymer networks, samples were placed in the thermo-chamber of the tensile tester and were heated to 90 °C and then cooled towards 20 °C in steps of 10 °C at a rate of 5 °C min−1. The samples were kept for 2 h under isothermal conditions after each 10 °C cooling step at this particular temperature. Annealed specimens were analyzed using the first DSC heating run at 10 K min−1 between −20 and 120 °C.2.7. Tensile tests
Tensile tests were performed on a Z1.0 (Zwick-Roell, Ulm, Germany) equipped with a thermo chamber and a temperature controller (Eurotherm e2408, Limburg, Germany) using standard test specimen (ISO 527-2/1BB) at a strain rate of 5 mm min−1. Stress–strain curves were recorded at ambient temperature and at Thigh (100 °C for cPEVA20 and at 80 °C for cPEVA31). A pre-force of 50 mN was applied prior data recording. Young's modulus (E), elongation at break (εb) and tensile strength (σb) were determined. Additionally, the obtained stress–strain data at Thigh were analyzed by Mooney–Rivlin equations for calculation of the crosslink density (νc) (eqn (5) and (6)) of cPEVAs.19,20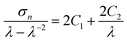 | (5) |
 | (6) |
2.8. Cyclic, thermomechanical tensile tests
Testing machine and specimen dimensions were the same as described for tensile tests. Each test cycle consisted of a temperature-memory creation procedure (TMCP), where the temporary shape was created at Tdeform, and a recovery module under stress-free conditions (see ESI Fig. S3a†). The first cycle was used as a preconditioning cycle to erase the thermomechanical history of the samples.The extent, to which the applied deformation (εm) could be fixed, was quantified by the shape fixity ratio Rf, which was calculated according to eqn (7). Similarly the ability of the material to recover its original shape was quantified by the shape recovery ratio Rr using eqn (8). ESI Fig. 3a† shows the schematic illustration of the TMCP and both recovery modules in a temperature–strain–stress 3D plot.
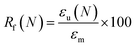 | (7) |
 | (8) |
2.9. X-ray scattering techniques
Integration of intensity vs. scattering angle 2θ led to one-dimensional curves for analysis. The peaks of the two phases (amorphous and crystalline) were fitted with Pearson VII functions. The crystallinity index (xc) was determined from the areas of crystalline and amorphous peaks using eqn (9).
 | (9) |
The average lateral crystal size (lc) was calculated from the (110) reflection by the Scherrer method with k = 0.9.21 Integration of intensity versus azimuthal angle χ data led into one-dimensional curves for analysis of the degree of crystal orientation.
3. Results and discussion
3.1. Characterization of copolymer networks
Two series of crosslinked poly[ethylene-co-(vinyl acetate)] comprising two different vinyl acetate contents (VAC of 20 wt% and 31 wt%) and three different crosslink densities (achieved by crosslinking with dicumyl peroxide (DCP) weight contents of 0.5, 1, and 2 wt%), and thus providing various melting transition intervals and crystallinities, were synthesized. Samples were denoted as cPEVAxxDyy, where xx represents the vinyl acetate content (VAC) and yy the DCP wt% in the starting mixture. Gel contents with G > 85% were observed for all cPEVAs, when the DCP content was 1 and 2 wt% in the starting reaction mixture G > 90% was reached. The VAC of the copolymer networks was determined via thermogravimetric analysis (TGA), revealing a VAC of 20 wt% and 31 wt% for the cPEVA20 and the cPEVA31 series respectively (Table 1). Data for cPEVA20 series were adopted from ref. 15. The theoretical average segment length of polyethylene (PE) sequences (n0) was determined from the 1H-NMR spectra (ESI Fig. S1†), here n0 = 24 and 13 PE repeating units (–CH2–CH2–) for the cPEVA20 and the cPEVA31 series were calculated respectively.| Sample IDa | DCP [wt%] | VACb [wt%] | G [%] | Q [%] | x c [%] | w c [%] | 2C1f [MPa] | 2C2f [MPa] | ν c [mol m−3] |
|---|---|---|---|---|---|---|---|---|---|
| a The first two-digit number in sample ID was given according to the experimental value of VA-contents in cPEVAs determined by TGA measurements and the last two-digit number was given according to the content of DCP in wt% in crosslinking reaction. b VA-contents in cPEVAs determined by TGA measurements. c Gel content G and degree of swelling Q of cPEVAs was determined in toluene at 50 °C. d Crystallinity index as calculated from WAXS. e Weight crystallinity as calculated from DSC measurements. f Mooney–Rivlin constants 2C1 and 2C2 and crosslink density (νc) were obtained based on the results of tensile tests at Thigh > Tm according to Mooney–Rivlin equations. g Data of cPEVA20 series were adopted from ref. 15. | |||||||||
| cPEVA20D05 | 0.5 | 20 ± 2 | 85 ± 1 | 1300 ± 10 | 27.4 ± 0.7 | 23.8 | 0.21 ± 0.03 | 0.47 ± 0.03 | 69 ± 9 |
| cPEVA20D10 | 1 | 20 ± 2 | 92 ± 1 | 840 ± 10 | 26.8 ± 0.7 | 23.3 | 0.47 ± 0.03 | 0.89 ± 0.1 | 150 ± 10 |
| cPEVA20D20 | 2 | 20 ± 2 | 96 ± 1 | 630 ± 10 | 25.1 ± 0.9 | 24.4 | 0.81 ± 0.05 | 1.10 ± 0.04 | 260 ± 15 |
| cPEVA31D05 | 0.5 | 31 ± 2 | 88 ± 1 | 1510 ± 10 | 15.7 ± 1.3 | 15.6 | 0.24 ± 0.01 | 0.94 ± 0.09 | 81 ± 4 |
| cPEVA31D10 | 1 | 31 ± 2 | 94 ± 1 | 960 ± 10 | 14.3 ± 0.7 | 15.3 | 0.44 ± 0.02 | 1.16 ± 0.1 | 149 ± 6 |
| cPEVA31D20 | 2 | 31 ± 2 | 96 ± 1 | 640 ± 10 | 14.1 ± 2.2 | 14.4 | 0.96 ± 0.04 | 1.42 ± 0.11 | 326 ± 13 |
The equilibrium degree of swelling (Q) was found to decrease from 1510% to 630% with increasing DCP content in the starting mixture. The crosslink density, as determined by Mooney–Rivlin analysis (Table 1), increased from νc = 70 mol m−3 to 260 mol m−3 for cPEVA20 and from νc = 80 mol m−3 to 325 mol m−3 for cPEVA31 series with increasing DCP content, which was in good correlation with the obtained Q values. The Mooney–Rivlin constant 2C1, which is mainly related to the number of covalent netpoints in the networks, was found to increase with increasing DCP content in the starting reaction mixture. Similarly 2C2, representing the contribution of physical crosslinks like entanglements, increased with increasing DCP content.
Differential scanning calorimetry (DSC) analysis was employed to investigate thermal properties of the cPEVAs. The melting and crystallization peak temperatures of the copolymer networks obtained in DSC experiments decreased with increasing VA-content from Tm = 81 °C to 84 °C (Tc = 53 °C to 57 °C) for cPEVA20s towards Tm = 65 °C to 68 °C (Tc = 36 °C to 39 °C) for the cPEVA31 series (Table 2). Data for cPEVA20 series were adopted from ref. 15. At the same time the melting temperature interval (ΔTm) was found to decrease from ΔTm ≈ 95 °C for cPEVA20s to ΔTm ≈ 80 °C for cPEVA31s (ESI Fig. S2†), while the same trend was observed for the melting enthalpy (ΔHm) decreasing from ΔHm around 67 to 70 J g−1 (cPEVA20s) to significantly lower values of 41 to 44 J g−1 for the copolymer networks with lower VAC. This observation can be attributed to the shorter PE average segment length of 13 repeating units in cPEVA31 samples resulting in the formation of smaller or thinner crystals, which melt at lower temperatures. Besides the substantial impact of the VAC on the thermal properties, the variation of the crosslinking density resulted only in minor changes of the thermal characteristics, where Tc and Tm slightly decreased with increasing crosslink density, while ΔTm and ΔHm remained almost unchanged.
| Sample ID | T m [°C] | T c [°C] | ΔHma [J g−1] | Ambient temperatureb | T high | ||||
|---|---|---|---|---|---|---|---|---|---|
| E [MPa] | σ b [MPa] | ε b [%] | E [MPa] | σ b [MPa] | ε b [%] | ||||
| a Data determined by DSC: melting transition temperature (Tm); crystallization temperature (Tc) and overall melting enthalpy (ΔHm). b Young's modulus (E), elongation at break (εb), and its corresponding stress (σb) were determined by tensile tests at ambient temperature and at Thigh = 100 °C for cPEVA20s and at Thigh = 80 °C for cPEVA31s. c Data of cPEVA20 series were adopted from ref. 15. | |||||||||
| cPEVA20D05 | 84 | 57 | 68.3 | 27 ± 3 | 17 ± 2 | 700 ± 80 | 0.5 ± 0.1 | 0.8 ± 0.1 | 740 ± 100 |
| cPEVA20D10 | 83 | 56 | 67.1 | 26 ± 4 | 17 ± 5 | 660 ± 50 | 0.7 ± 0.1 | 0.7 ± 0.1 | 380 ± 90 |
| cPEVA20D20 | 81 | 53 | 70.1 | 28 ± 1 | 15 ± 1 | 635 ± 10 | 1.2 ± 0.1 | 0.9 ± 0.1 | 190 ± 50 |
| cPEVA31D05 | 68 | 39 | 45.0 | 12 ± 1 | 14 ± 2 | 755 ± 50 | 0.6 ± 0.1 | 1.6 ± 0.1 | 1010 ± 50 |
| cPEVA31D10 | 66 | 38 | 44.0 | 11 ± 1 | 16 ± 5 | 700 ± 60 | 1.0 ± 0.1 | 1.3 ± 0.1 | 515 ± 30 |
| cPEVA31D20 | 65 | 36 | 41.2 | 11 ± 1 | 14 ± 3 | 615 ± 10 | 1.5 ± 0.1 | 1.1 ± 0.2 | 200 ± 50 |
The results of the tensile tests are summarized in Table 2. At ambient temperature the elastic modulus (E) was higher for the cPEVA20 series (∼27 MPa) than for the cPEVA31 series (∼11 MPa), which was attributed to additional physical netpoints (i.e. PE crystals) in the cPEVA20 series, which had a higher degree of crystallinity. Elongation at break (εb) at ambient temperature decreased from 700% to 635% for the cPEVA20 series and from 755% to 615% for the cPEVA31 series when crosslinking density increased. As the decrease in εb was low, we concluded that the PE crystals as physical netpoints dominated the elastic properties. The corresponding stress at break (σb) was almost constant within a series, being ∼16 MPa for cPEVA20s and ∼14 MPa for cPEVA31s. At Thigh > Tm, i.e. in the viscoelastic state, the mechanical properties were only influenced by the chemical crosslinks and the entanglements of the polymer chains. E increased from 0.5 to 1.2 MPa for cPEVA20s and from 0.6 to 1.5 MPa for cPEVA31s with increasing crosslink density. Also εb was reduced with increasing crosslink density, decreasing from 740% to 190% for cPEVA20s and from 1010% to 200% for cPEVA31s. Here a good correlation to the results from the Mooney–Rivlin analysis was observed.
The overall crystallinity determined from wide-angle X-ray scattering (xc) or DSC (wc) experiments was similar, being around 25% for the cPEVA20 and about 15% for the cPEVA31 series (Table 1). This observation indicates that the amount of crystals was not affected by the introduced crosslinks.
The nanostructure of cPEVAs was analyzed by small- and wide-angle X-ray scattering (SAXS and WAXS) measurements at ambient temperature. Crystallinity index (xc) and average lateral crystal extension (lc) were determined from the (110) reflection of PE in the WAXS pattern, while the average long period (L) and the average lamella crystal thickness (dc) were obtained from SAXS data. The calculated results are listed in Table 3. All non-programmed samples exhibited isotropic Debye–Scherrer rings in WAXS and circular correlation rings in SAXS experiments, indicating that the crystalline domains are randomly arranged. The L and dc were almost similar for both cPEVA series with values about L ≈ 12 nm and dc ≈ 6 nm (c.f.Table 3). As L was found to be approximately two times dc in cPEVAs, the crystallinity within a stack can be anticipated as ≈50%. Their structure might consist of stacks of alternating crystalline-amorphous PE lamellae, which are surrounded by a mixed amorphous PE-VA matrix comprising short PE-segments, unable to form crystals.
| ε = 0% | ε m = 150% | ε u at Tlowe | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T deform [°C] | L [nm] | l c [nm] | d c [nm] | x c [%] | T deform [°C] | L [nm] | l c [nm] | d c [nm] | x c [%] | T deform [°C] | L [nm] | l c [nm] | d c [nm] | x c [%] |
| a Long period determined from CDF. b Average lateral crystal extension determined from (110) reflection. c Average crystal thickness determined from CDF. d Crystallinity determined from WAXS. e Measurements performed at Tlow = 10 °C on samples, which were deformed at Tdeform and cooled to Tlow = 10 °C to fix the temporary shape (εu). | ||||||||||||||
| cPEVA20D20 | ||||||||||||||
| 25 | 11.4 ± 0.5 | 10.4 ± 0.5 | 6.0 ± 0.5 | 27 ± 2 | 25 | 12.2 ± 0.5 | 4.9 ± 0.5 | 5.9 ± 0.5 | 28 ± 2 | 25 | 12.6 ± 0.5 | 5.3 ± 0.5 | 5.9 ± 0.5 | 30 ± 2 |
| 40 | 12.6 ± 0.5 | 9.8 ± 0.5 | 6.5 ± 0.5 | 20 ± 2 | 40 | 13.2 ± 0.5 | 9.9 ± 0.5 | 5.5 ± 0.5 | 20 ± 2 | 40 | 11.4 ± 0.5 | 6.6 ± 0.5 | 4.3 ± 0.5 | 28 ± 2 |
| 65 | 14.9 ± 0.5 | 9.0 ± 0.5 | 7.7 ± 0.5 | 11 ± 2 | 65 | 18.9 ± 0.5 | 9.6 ± 0.5 | 9.0 ± 0.5 | 9 ± 2 | 65 | 14.3 ± 0.5 | 10.2 ± 0.5 | 6.1 ± 0.5 | 28 ± 2 |
| 90 | 12.5 ± 0.5 | 10.4 ± 0.5 | 5.4 ± 0.5 | 29 ± 2 | ||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||||
| cPEVA31D20 | ||||||||||||||
| 25 | 11.5 ± 0.5 | 6.1 ± 0.5 | 5.9 ± 0.5 | 14 ± 2 | 25 | 11.5 ± 0.5 | 5.2 ± 0.5 | 4.5 ± 0.5 | 15 ± 2 | 25 | 11.0 ± 0.5 | 6.5 ± 0.5 | 4.4 ± 0.5 | 16 ± 2 |
| 40 | 12.4 ± 0.5 | 5.2 ± 0.5 | 6.4 ± 0.5 | 12 ± 2 | 40 | 14.9 ± 0.5 | 5.4 ± 0.5 | 7.2 ± 0.5 | 11 ± 2 | 40 | 13.1 ± 0.5 | 6.0 ± 0.5 | 5.4 ± 0.5 | 14 ± 2 |
| 55 | 14.1 ± 0.5 | 4.4 ± 0.5 | 7.0 ± 0.5 | 9 ± 2 | 55 | 18.4 ± 0.5 | 5.4 ± 0.5 | 8.2 ± 0.5 | 7 ± 2 | 55 | 13.1 ± 0.5 | 6.6 ± 0.5 | 6.0 ± 0.5 | 14 ± 2 |
| 70 | 12.5 ± 0.5 | 7.2 ± 0.5 | 4.8 ± 0.5 | 13 ± 2 | ||||||||||
Based on the obtained average PE crystal thickness of 6 nm it can be assumed that the ordered PE nanostructure is related to PE segments with an average segment length of about 20 to 25 repeating units, which was in good correlation with the theoretical calculations from the NMR spectroscopy data for cPEVA20s. For the cPEVA31 series, with a calculated average segment length of 13 repeating units, one would expect an average crystal thickness around 3 nm, but in WAXS experiments we observed also a dc ≈ 6 nm. This difference might be attributed to a non-statistical distribution of the VA moieties within the copolymer matrix and thus larger PE segment lengths than predicted by the theory.
As the deformation temperature Tdeform was assumed to be the key parameter for creation of a TME in polymers, we further investigated the crystalline thickness as function of temperature exemplarily for cPEVA31D20 and cPEVA20D20. The non-deformed samples were heated in 10 K steps from 25 °C to 75 °C and SAXS patterns were recorded. In Fig. 1a and Table 3 the resulting dcvs. temperature data are presented, showing a continuous increase of the crystal thickness with increasing temperature. The maximum dcs were 8.5 nm for cPEVA20D20 at 75 °C and 7.5 nm for cPEVA31D20 at 63 °C, whereby the lower maximum dc of cPEVA31D20 can be attributed to a lower PE-segment length.
3.2. Temperature-memory capability
The applied Tdeforms for the TME experiments were chosen to span the whole melting temperature interval ΔTm obtained in DSC experiments. Thus Tdeforms for cPEVA20s ranged from 10 to 90 °C and for cPEVA31s deformation temperatures from 10 to 70 °C were utilized (for details see Experimental section). The temperature-memory capability of cPEVAs was investigated by cyclic thermomechanical tensile tests (see Scheme in ESI Fig. S3a†) and the obtained results are summarized in ESI Table S1 and S2.† The temporary shape in semi-crystalline shape-memory polymers is fixed by crystallizable switching segments, which act as temporary physical netpoints. In a classical thermally-induced SME cycle the sample is deformed at Thigh > Tm, where the switching segment is amorphous, and cooled to Tlow < Tm allowing crystallization of the switching segment and thus the formation of temporary netpoints which retain the temporary shape. By reheating to Thigh the temporary netpoints are disassembled by melting of the switching segment and the permanent shape is recovered.All investigated cPEVAs exhibited excellent temperature-memory properties demonstrated by an almost linear correlation between the Tdeform and the response temperature Tsw (Fig. 2). The recorded stress–temperature–strain plots obtained under stress-free conditions are exemplarily displayed for cPEVA20D10 in ESI Fig. 3b.† The stress at εm was increasing when Tdeform was decreased, which was attributed to the higher crystallinity of the sample. For equal Tdeform the stress increased with increasing crosslink density, which was related to the additional covalent netpoints. High shape recovery ratios of Rr ≥ 87% were achieved for all copolymers independent from the applied Tdeform, indicating the high entropic elasticity of the polymer networks at Thigh, reflecting the excellent stabilization of the permanent shape by the chemical crosslinks. In contrast, the shape fixity ratios were found to decrease with decreasing Tdeform from Rf around 100% to Rf values of 50 to 60% for Tdeform = 10 °C (c.f.Fig. 2). Rf values above 100% were attributed to crystallization induced elongation upon cooling at constant stress as previously reported.25
3.3. Annealing experiments
Annealing experiments were conducted on cPEVAs to investigate the contribution of the isothermal crystallization to the crystal structure. For doing so, non-deformed specimens were annealed stepwise in the thermo-chamber of the tensile tester and were analyzed by a first DSC heating run. The resulting thermograms are shown in Fig. 1.As mentioned before the broad ΔTm of cPEVAs can be treated as an infinite number of sharp single melting temperatures, whereby each individual transition would be controlled by a crystal population of a distinct thickness. Therefore, the broad ΔTm in cPEVAs can be assumed as broad distribution of crystal lamellae thicknesses, which are related to the PE-segment length distribution. Here, the Thomson–Gibbs equation (eqn (10)) describes the relation between crystal thickness dc and its melting temperature Tm.26,27 Where Tm0 is the melting temperature of an infinitely large PE-crystal (414.4 K)28 and γe is the top and bottom surface energy of the crystalline lamellae (33 erg cm−2).
 | (10) |
A stepwise annealing protocol, where the samples were first heated to 90 °C and then cooled to 20 °C in subsequent steps of 10 K, while allowing isothermal crystallization at each temperature, was applied to separate different crystal populations within ΔTm from each other (see Experimental section). The annealed samples were analyzed by DSC heating experiments. In Fig. 1b the DSC curves obtained in the first heating run of cPEVA20d05 and cPEVA31D05 are shown. Both cPEVA series exhibited multiple distinct melting peaks (P0 to P4/P5) corresponding to the applied individual annealing temperatures, which was similar to the behavior reported for annealed non-crosslinked PEVA29,30 comprising multiple Tms. The Tms could be related to the corresponding theoretical lamellae thickness (Fig. 1a) representing the contribution of the isothermal crystallization step during TMCP. Theoretical thickness increased from 3.9 nm for Tm = 15 °C to 8.3 nm for Tm = 80 °C, indicating the formation of thick and thermally stable crystals when increased isothermal crystallization temperature was applied. The theoretical dc values were smaller than the dc determined from SAXS, especially at low temperatures, because SAXS showed the average lamellae thickness with contributions from the entire crystal population. The influence of the annealing treatment on cPEVAs could be interpreted as follows: The peak P5 at 80 °C could only be observed for cPEVA20s comprising a higher PE segment length. A pronounced influence of the crosslink density on the peak area of the P4 and P5 became only apparent for cPEVA20 samples, while cPEVA31 networks were not affected by the variation of the crosslink density (Fig. 1c and d). Here the peak area of P5 was found to decrease with rising crosslink density, which can be attributed to a reduction of PE-segment length leading to the formation of thinner crystal lamellae resulting in an increase in the peak area of P4. In contrast the peaks P0, P1, P2 and P4 were not affected by increasing the crosslink density (Fig. 1c). Summarizing, higher Tdeform, which correspond to isothermal crystallization at higher temperatures, would favor the creation of thick crystalline lamellae. In contrast lower Tdeform would promote thin crystals. By cooling to Tlow additional crystallization occurs in both cases but the resulting average crystal thickness would be increased when a higher Tdeform was applied. In this way higher or lower Tdeform will contribute to the TME.
3.4. Nanostructural investigations by SAXS/WAXS – mechanistic aspects of TME
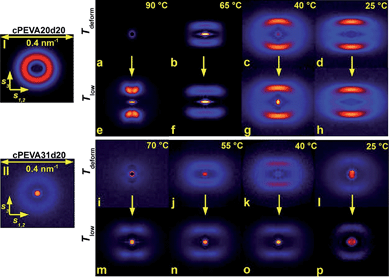
In addition to the contribution of the isothermal crystallization at Tdeform, the deformation step was expected to have significant influence on the crystal structure responsible for memorizing Tdeform. Thus the crystalline PE nanostructures were analyzed before and after deformation at Tdeform as well as after completion of the TMCP at Tlow. In this way the contributions of the deformation step and the cooling step on the crystallizable controlling units responsible for the TME should by elucidated. The obtained WAXS patterns as well as the azimuthal profiles are shown in Fig. 3 for cPEVA20D20 and in ESI Fig. 4† for cPEVA31D20, while the respective SAXS patterns are displayed in Fig. 4. The analyzed structural parameters such as the degree of crystallinity (xc), the average lateral crystal size (lc), the average crystal thickness (dc) and the longitudinal long period (L) calculated from SAXS and WAXS diffraction patterns are listed in Table 3. It has to be pointed out that at the highest Tdeforms (i.e. 90 °C for cPEVA20D20 and 70 °C for cPEVA31D20) the specimens are amorphous as all crystals are in the molten state and in this way the TMCP and the recovery could be considered as a classical shape-memory experiment.The illustrated WAXS patterns (Fig. 3a–h and ESI Fig. 4a–h†) represent the structures at ambient temperature before deformation, when deformed to εm = 150% at different Tdeforms (cPEVA20D20: 90, 65, 40 and 25 °C; cPEVA31D20: 70, 55, 40 and 25 °C) and at Tlow = 10 °C after completion of TMCP. For all samples the main (hk0) reflections, i.e. (110) and (200) were found on the equatorial part, reflecting that the orientation of the polymer chains is parallel to the strain direction. The meridional part of the pattern did not exhibit any reflections. The overall degree of crystallinity of both programmed copolymer samples was found to be similar to the original non-programmed sample with xc in the range of 27 to 30% for cPEVA20D20 and xc values from 13 to 16% for cPEVA31D20. With increasing Tdeformxc was found to systematically decrease to xc = 9% (cPEVA20D20 at 65 °C) or 7% (cPEVA31D20 at 55 °C) while almost no difference between elongated and non-elongated test specimen could be observed, which suggested that strain-induced crystallization processes are not involved during TMCP.
Different azimuthal profiles related to the (110) peak were obtained for copolymers with different VAC equivalent to a different PE segment length. Here cPEVA20D20 (Fig. 3) showed a lower degree of orientation compared to cPEVA31D20 (ESI Fig. 4†), which exhibited sharper peak profiles (χ direction), which were attributed to a higher mobility of smaller crystals and therefore a higher orientation after application of the deformation. A broadening of the azimuthal profiles in χ direction was observed with increasing Tdeform. Interestingly at Tdeform = 90 °C a somehow bimodal azimuthal profile was observed, which might be attributed to a structure of tilted lamellae.31
The average lateral crystal size (lc) determined from the (110) reflection of the programmed cPEVA20D20 samples at ambient temperature was found to increase from lc = 5.3 nm to lc = 10.4 nm with increasing Tdeform from 25 °C to 90 °C. The samples programmed at higher Tdeforms of 90 °C and 65 °C exhibited a similar lc around 10 nm like the original non-programmed sample. This leads to the conclusion that at high Tdeform, where only a few or almost no PE crystals are present after deformation, the crystal growth during cooling to Tlow is not hindered and larger crystals can be formed. Significantly lower lc values in the range of 5 to 7 nm were found at lower deformation temperatures. This might be explained by the disruption of existing PE crystals into smaller microfibril-like structures during the deformation at lower Tdeform. The new crystalline structures formed during further cooling to Tlow are hindered in extension by the small structures generated during deformation, which resulted in an overall reduction of the lateral extension of the crystalline domains. Similar findings have been reported for a cold drawn polyethylene-octene copolymer.32
In contrast for cPEVA31D20 having a lower PE segment length the lc-values remained almost constant around 6 to 7 nm independent from the applied Tdeform, which corresponds to the lc of the non-programmed sample.
In addition to the crystallinity and the lateral crystal size data, the in situ SAXS experiments provide information about the longitudinal long period L, including one amorphous and one crystalline layer, and the average thickness of the crystalline lamella dc. In Fig. 4 various SAXS patterns obtained for the original non-deformed cPEVA20D20 and cPEVA31D20 sample at ambient temperature (Fig. 4I and II), at different Tdeform with εm = 150% (Fig. 4a–d and i–l) and after completion of TMCP at Tlow (Fig. 4e–h and m–p) are shown. Both non-programmed samples cPEVA20D20 and cPEVA31D20 exhibited an isotropic structure with a long period around L = 11.5 nm and a crystalline thickness of dc ≈ 6.0 nm. At the desired deformation temperatures without elongating the sample the isotropic structure remained and the values for L and dc increased with raising temperature, while at Tdeform = 90 °C (cPEVA20D20) and at Tdeform = 70 °C (cPEVA31D20) no discrete scattering pattern could be observed.
In the following first the further SAXS data obtained for cPEVA20D20 will be discussed. Also after deformation to εm = 150% at Tdeform = 90 °C no discrete scattering pattern could be observed, while after cooling to Tlow and releasing the stress in the temporary shape a four point pattern was obtained (Fig. 4e). This pattern exhibits a typical correlation in the s3 direction of elongation, which can be attributed to a structure of tilted lamellae. When lower Tdeforms of 65, 40 and 25 °C were applied the SAXS patterns achieved during deformation at Tdeform and after completion of TMCP differed strongly from those obtained at 90 °C. Here a relatively broad lateral distribution of the maxima was generated with patterns having a distinct streak parallel to the equator (s1,2), which indicate a microfibrillar or cylinder-like structure.33 Such a transformation from the point reflections in the non-deformed state to a microfibrillar or cylinder-like structure can be attributed to inter- and intra-lamellar slipping processes and crystallite fragmentation during deformation at low Tdeforms.34
The SAXS pattern obtained for cPEVA31D20, with exception of Tdeform = 70 °C, where the sample was completely amorphous, had a four-point character similar to cPEVA20D20 (Fig. 4i–p), whereby these pattern appear more layer-like, which can be attributed to a pronounced cylinder-like structure of the crystalline PE domains.
Programming at Tdeform = 90 °C, where the copolymer network is completely amorphous, resulted in similar values for the long period (L = 12.5 nm) and the crystalline thickness (dc = 5.4 nm) as in the original state. Here, the cooling to Tlow = 10 °C generated a subsequent increasing population of crystalline domains, starting with the formation of thicker crystals at higher temperatures and ending with thinner crystals at lower temperatures, which are placed in between the previously formed ones. A similar trend was observed when the sample was deformed at Tdeform = 65 °C, where a crystalline fraction of xc = 9% remained and a L of 18.9 nm and a dc of 9.0 nm represented the existing PE crystals. After cooling to Tlow the long period as well as the average crystal thickness decreased to L = 14.3 nm and dc of 6.1 nm, respectively.
After deformation at lower Tdeforms of 40 °C and 25 °C long periods of L = 13.2 nm and L = 12.2 were obtained, which are slightly higher compared to the values observed for the non-deformed samples at the same Tdeforms, whereas the crystal thickness was reduced to values of 5.5 to 5.9 nm. After cooling from Tdeform = 40 °C to Tlow both the longitudinal long period and the crystal thickness were found to be slightly reduced to L = 11.4 nm and dc = 4.3 nm. Together with the increase in xc and the decrease in lc obtained from WAXS experiments this indicated that less laterally extended crystals are intersected between the existing crystalline domains. When programmed at 25 °C L and dc were not affected during cooling to Tlow = 10 °C, while xc increased substantially, which indicated that a small fraction of identical crystalline structures were inserted in between existing crystals upon cooling.
During programming at lower Tdeforms the predominant process was the structural rearrangement of existing PE crystallites, which was dictated by the deformation.
A similar trend for the changes in the crystalline nanostructure was observed for cPEVA31D20 when programmed at higher TdeformS of 70, 55 or lower TdeformS of 40 and 25 °C, but less pronounced (see Table 3).
Based on the observations from WAXS/SAXS and annealing experiments two different contributions to the nanostructural changes in cPEVA responsible for the memorization of the deformation temperature depending on the choice of Tdeform were proposed, which are schematically displayed in Fig. 5. Starting from the non-deformed sample with a broad distribution of crystal thickness as reflected by its broad melting transition (DSC results), heating to higher Tdeform (Fig. 5a–e) results in a few remaining thicker crystals, which are thermally stable at these temperatures, as confirmed by SAXS measurements. Annealing at this Tdeform increased the thermally stable crystal fraction. When the deformation is applied these crystals are tilted and oriented, whereby some crystal thickening might occur. By cooling to Tlow, oriented PE chains crystallize and finally relatively thick crystals are generated. The now established nanostructure of the temporary shape has a broader crystal thickness distribution compared to the starting structure. In order to induce the TME by reheating, higher temperatures need to be exceeded to melt these thicker crystals and in this way the sample remembers the higher Tdeform.
At lower Tdeforms (Fig. 5a–e') the overall starting nanostructure is almost maintained during the initial heating step as only a few thinner crystals are melting. Annealing at low temperatures would increase the thermally less stable crystal fraction. When the deformation is applied, rearrangement of the nanostructure takes place in such way that thicker and larger crystals were disrupted into smaller and thinner (and less lateral extended) ones, which are oriented. By cooling to Tlow = 10 °C only a few thinner crystals can grow as the space for crystallization is already occupied. Finally, the temporary shape comprises a nanostructure with thin and small oriented crystals, which melt at low temperatures during reheating and in this way the sample remembers the lower Tdeform applied during programming.
4. Conclusions
Series of cPEVAs with two different VACs comprising a broad melting temperature range and three different crosslink densities were prepared, which exhibited a pronounced temperature-memory effect. The contribution of the temperature applied during TMCP was explored by annealing experiments, which revealed preferential formation of thick crystals when higher temperatures were applied. In situ X-ray investigations were employed to investigate the nanostructural changes of the crystallizable PE controlling units during functionalization and activation of the temperature-memory effect, especially regarding the contribution of the deformation step. It could be shown that two different mechanisms are responsible for memorizing higher or lower Tdeform. At higher Tdeforms predominantly newly formed large crystal structures were established during cooling to Tlow, which are controlling the TME. In contrast, at lower Tdeforms, which is comparable to a cold drawing scenario, the TME was determined by the rearrangement of existing crystalline structures during deformation, whereby large crystalline structures are disrupted into smaller ones related to low response temperatures. The observed nanostructural changes during TMCP were found to be almost independent from the composition of the investigated cPEVAs. The mechanism of the TME in semi-crystalline cPEVAs with contributions from thermal treatment and mechanical deformation might be extended to other TMPs comprising crystallizable controlling units and in this way enable a knowledge based design.Notes and references
- P. Miaudet, A. Derre, M. Maugey, C. Zakri, P. M. Piccione, R. Inoubli and P. Poulin, Science, 2007, 318, 1294–1296 CrossRef CAS PubMed.
- H. A. Khonakdar, S. H. Jafari, S. Rasouli, J. Morshedian and H. Abedini, Macromol. Theory Simul., 2007, 16, 43–52 CrossRef CAS.
- J. Cui, K. Kratz and A. Lendlein, Smart Mater. Struct., 2010, 19, 065019 CrossRef.
- K. Kratz, S. A. Madbouly, W. Wagermaier and A. Lendlein, Adv. Mater., 2011, 23, 4058–4062 CrossRef CAS PubMed.
- T. Xie, K. A. Page and S. A. Eastman, Adv. Funct. Mater., 2011, 21, 2057–2066 CrossRef CAS.
- K. Kratz, U. Voigt and A. Lendlein, Adv. Funct. Mater., 2012, 22, 3057–3065 CrossRef CAS.
- D. M. Feldkamp and I. A. Rousseau, Macromol. Mater. Eng., 2010, 295, 726–734 CrossRef CAS.
- M. Y. Razzaq, M. Behl and A. Lendlein, Adv. Funct. Mater., 2012, 22, 184–191 CrossRef CAS.
- T. Xie, Nature, 2010, 464, 267–270 CrossRef CAS PubMed.
- I. S. Kolesov and H.-J. Radusch, eXPRESS Polym. Lett., 2008, 2, 461–473 CrossRef CAS.
- J. Li, T. Liu, S. Xia, Y. Pan, Z. Zheng, X. Ding and Y. Peng, J. Mater. Chem., 2011, 21, 12213–12217 RSC.
- Q. Zhang, S. Song, J. Feng and P. Wu, J. Mater. Chem., 2012, 22, 24776–24782 RSC.
- L. Sun and W. M. Huang, Soft Matter, 2010, 6, 4403–4406 RSC.
- M. Heuchel, T. Sauter, K. Kratz and A. Lendlein, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 621–637 CrossRef CAS.
- U. Nöchel, U. N. Kumar, K. Wang, K. Kratz, M. Behl and A. Lendlein, Macromol. Chem. Phys., 2014, 215, 2446–2456 CrossRef.
- W. W. Zhao, X. G. Zhong, L. Yu, Y. F. Zhang and J. Z. Sun, Polymer, 1994, 35, 3348–3350 CrossRef CAS.
- H. N. Sung and J. H. Noggle, J. Polym. Sci., Polym. Phys. Ed., 1981, 19, 1593–1602 CrossRef CAS.
- Polymer Handbook, ed. J. Brandrup and E. H. Immergut, Wiley Interscience, New York, Chicester, Brisbane, Toronto, Singapore, 3rd edn, 1989 Search PubMed.
- M. Mooney, J. Appl. Phys., 1940, 11, 582–592 CrossRef PubMed.
- N. Sombatsompop, Polym.-Plast. Technol. Eng., 1998, 37, 333–349 CrossRef CAS.
- A. L. Patterson, Phys. Rev., 1939, 56, 978–981 CrossRef CAS.
- N. Stribeck, J. Appl. Crystallogr., 2001, 34, 496–503 CrossRef CAS.
- C. G. Vonk, Colloid Polym. Sci., 1979, 257, 1021–1032 CAS.
- N. Stribeck, E. Buzdugan, P. Ghioca, S. Serban and R. Gehrke, Macromol. Chem. Phys., 2002, 203, 636–644 CrossRef CAS.
- R. Alamo, R. Domszy and L. Mandelkern, J. Phys. Chem., 1984, 88, 6587–6595 CrossRef CAS.
- Q. Jiang, C. C. Yang and J. C. Li, Macromol. Theory Simul., 2003, 12, 57–60 CrossRef CAS.
- B. Wunderlich and G. Czornyj, Macromolecules, 1977, 10, 906–913 CrossRef CAS.
- G. W. H. Höhne, Polymer, 2002, 43, 4689–4698 CrossRef.
- M. Y. Keating and E. F. McCord, Thermochim. Acta, 1994, 243, 129–145 CrossRef CAS.
- X. Shi, J. Jin, S. Chen and J. Zhang, J. Appl. Polym. Sci., 2009, 113, 2863–2871 CrossRef CAS.
- N. S. Murthy and D. T. Grubb, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1277–1286 CrossRef CAS.
- N. Stribeck, R. Androsch and S. S. Funari, Macromol. Chem. Phys., 2003, 204, 1202–1216 CrossRef CAS.
- R. Androsch, N. Stribeck, T. Lüpke and S. S. Funari, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 1919–1930 CrossRef CAS.
- S. Hobeika, Y. Men and G. Strobl, Macromolecules, 2000, 33, 1827–1833 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ta06586g |
| ‡ Authors contributed equally. |
| § Present address: The Centre for Research on Adaptive Nanostructures and Nanodevices and School of Physics, Trinity College Dublin, Dublin 2, Ireland. |
| ¶ Present address: Institute of Materials Physics and Technology, Hamburg University of Technology, 21073 Hamburg, Germany. |
| || Present address: BASF Advanced Chemicals Co. Ltd, 200137 Shanghai, China. |
| This journal is © The Royal Society of Chemistry 2015 |