Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correction: Wrapping of ellipsoidal nano-particles by fluid membranes
Sabyasachi
Dasgupta
,
Thorsten
Auth
and
Gerhard
Gompper
Theoretical Soft Matter and Biophysics, Institute of Complex Systems and Institute for Advanced Simulations, Forschungszentrum Jülich, D-52425 Jülich, Germany. E-mail: s.dasgupta@fz-juelich.de
First published on 26th August 2015
Abstract
Correction for ‘Wrapping of ellipsoidal nano-particles by fluid membranes’ by Sabyasachi Dasgupta et al., Soft Matter, 2013, 9, 5473–5482.
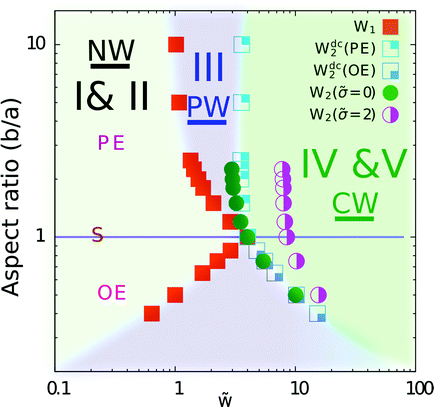
Phase transitions have been calculated for ellipsoidal particles with various aspect ratios. The values for the adhesion strength for the transitions depend on both particle size and aspect ratio. Calculations are conveniently carried out for fixed small axes of prolate particles or long axes of oblate particles, fixed surface area, or fixed volume. We have calculated adhesion strengths for transitions between partially-wrapped and completely-wrapped states using particles with the same surface area A, and adhesion strengths for binding of the particles to the membrane using particles with the same length of their small axis a. The data is plotted as a function of the reduced adhesion strength
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 2wa2/κ. In the original publication, we missed a factor 4πa2/A in the scaling of the values for the effective adhesion strength for calculations with fixed surface area. In addition there is a misprint in eqn (5), the corrected equation is:
= 2wa2/κ. In the original publication, we missed a factor 4πa2/A in the scaling of the values for the effective adhesion strength for calculations with fixed surface area. In addition there is a misprint in eqn (5), the corrected equation is: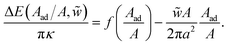 | (5) |
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) = 2wa2/κ and
= 2wa2/κ and ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = σa2/κ. The transitions shift to smaller adhesion strengths for prolate particles, where a is the short axis, and to larger adhesion strengths for oblate particles, where a is the long axis. For spherical particles 4πa2/A = 1, therefore the results presented in Fig. 3 remain unaffected.
= σa2/κ. The transitions shift to smaller adhesion strengths for prolate particles, where a is the short axis, and to larger adhesion strengths for oblate particles, where a is the long axis. For spherical particles 4πa2/A = 1, therefore the results presented in Fig. 3 remain unaffected.
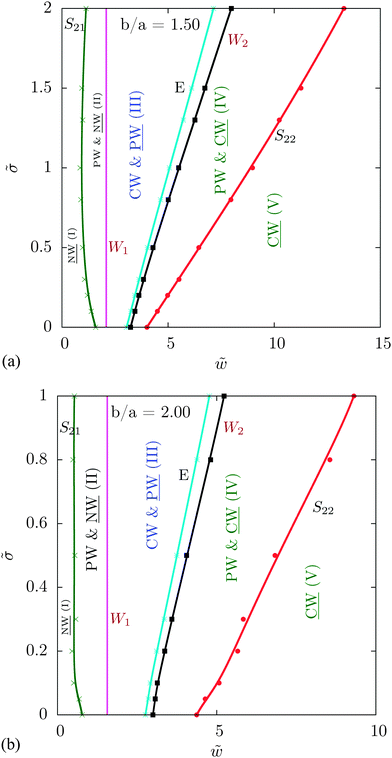 | ||
| Fig. 7 Wrapping states for prolate ellipsoidal particles with aspect ratios (a) 1.5 and (b) 2, plotted analogously to Fig. 6. | ||
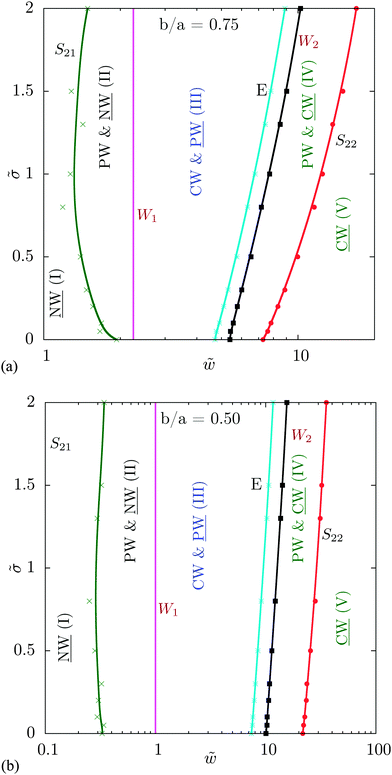 | ||
| Fig. 8 Wrapping states for oblate ellipsoidal particles with aspect ratios (a) 0.75 and (b) 0.5, plotted analogously to Fig. 6. | ||
The phase diagrams presented here are most easily interpreted for ellipsoidal particles with fixed length of the axis a, because of the choice of ![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) for the reduced adhesion strength. Instead, in the original Fig. 11, the W2 transition is shown for reduced adhesion strength
for the reduced adhesion strength. Instead, in the original Fig. 11, the W2 transition is shown for reduced adhesion strength ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) = wA/(2πκ), which can be most easily interpreted for particles with fixed surface area A. Almost all data presented in the corrected figures can be rescaled to be used for particles with fixed A – besides the transition for
= wA/(2πκ), which can be most easily interpreted for particles with fixed surface area A. Almost all data presented in the corrected figures can be rescaled to be used for particles with fixed A – besides the transition for ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) = 2 in Fig. 11 that applies only for fixed length of the small axis. In the corrected Fig. 11, the transition W2 for prolate ellipsoids is almost independent of the particle aspect ratio; the increased bending energy cost to wrap the tips of the ellipsoidal particles with higher aspect ratio is compensated for by the increased adhesion energy gain because of the larger particle surface area.
= 2 in Fig. 11 that applies only for fixed length of the small axis. In the corrected Fig. 11, the transition W2 for prolate ellipsoids is almost independent of the particle aspect ratio; the increased bending energy cost to wrap the tips of the ellipsoidal particles with higher aspect ratio is compensated for by the increased adhesion energy gain because of the larger particle surface area.
The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
| This journal is © The Royal Society of Chemistry 2015 |