Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Measurement of molecular mixing at a conjugated polymer interface by specular and off-specular neutron scattering†
David
James
a,
Anthony M.
Higgins
*a,
Paul
Rees
a,
Mark
Geoghegan
 b,
M. Rowan
Brown
a,
Shion-Seng
Chang
a,
Dyfrig
Môn
a,
Robert
Cubitt
c,
Robert
Dalgliesh
d and
Philipp
Gutfreund
c
b,
M. Rowan
Brown
a,
Shion-Seng
Chang
a,
Dyfrig
Môn
a,
Robert
Cubitt
c,
Robert
Dalgliesh
d and
Philipp
Gutfreund
c
aCollege of Engineering, Swansea University, Fabian Way, Crymlyn Burrows, Swansea, SA1 8EN, Wales, UK. E-mail: a.m.higgins@swansea.ac.uk
bDepartment of Physics and Astronomy, University of Sheffield, Hounsfield Road, Sheffield, S3 7RH, UK
cInstitut Laue-Langevin, 71 Avenue des Martyrs, 38000 Grenoble, France
dISIS, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX11 OQX, UK
First published on 28th September 2015
Abstract
Measurements have been performed on thermally equilibrated conjugated-polymer/insulating-polymer bilayers, using specular and off-specular neutron reflectivity. While specular reflectivity is only sensitive to the structure normal to the sample, off-specular measurements can probe the structure of the buried polymer/polymer interface in the plane of the sample. Systematic analysis of the scattering from a set of samples with varying insulating-polymer-thickness, using the distorted-wave Born approximation (DWBA), has allowed a robust determination of the intrinsic width at the buried polymer/polymer interface. The quantification of this width (12 Å ± 4 Å) allows us to examine aspects of the conjugated polymer conformation at the interface, by appealing to self-consistent field theory (SCFT) predictions for equilibrium polymer/polymer interfaces in the cases of flexible and semi-flexible chains. This analysis enables us to infer that mixing at this particular interface cannot be described in terms of polymer chain segments that adopt conformations similar to a random walk. Instead, a more plausible explanation is that the conjugated polymer chain segments become significantly oriented in the plane of the interface. It is important to point out that we are only able to reach this conclusion following the extensive analysis of reflectivity data, followed by comparison with SCFT predictions. It is not simply the case that conjugated polymers would be expected to adopt this kind of oriented conformation at the interface, because of their relatively high chain stiffness. It is the combination of a high stiffness and a relatively narrow intrinsic interfacial width that results in a deviation from flexible chain behaviour.
Introduction
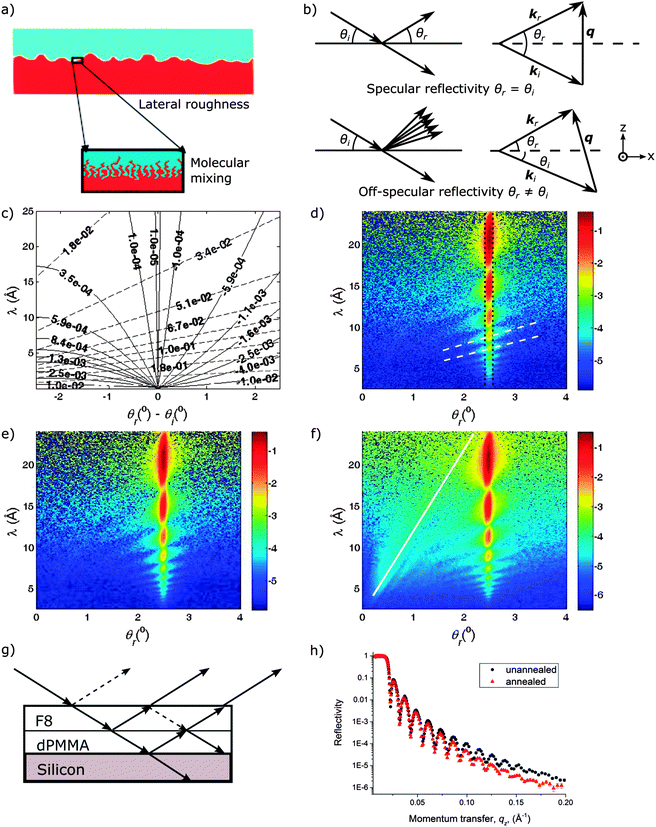
Conjugated polymer interfaces are at the heart of plastic electronic devices such as solar cells, light-emitting diodes (LEDs) and field-effect-transistors (FETs). The structure of these interfaces is known to be an important factor in photophysical processes and charge transport, and is therefore a key determinant of device performance. Examples include (i) the influence of the relative positioning/orientation of polymer chain segments on the photophysics at conjugated polymer heterojunctions,1,2 (ii) the impact of (total) interfacial roughness at conjugated polymer heterojunctions on photoluminescence3 and charge separation efficiency4 and (iii) the impact of interfacial roughness5–7 and molecular orientation, on charge mobility at the dielectric–semiconducting interface within polymer-based FETs.8 However, a full characterisation of the structure at such interfaces is currently lacking. One important aspect of the structure is the lateral lengthscale on which interfacial roughness manifests itself. The possibility of two distinct contributions to the roughness at a buried interface is illustrated in Fig. 1(a). One contribution to the roughness at a polymer–polymer interface is the local (nanoscale) composition profile, due to mixing of the polymer chains at a molecular level, parameterised by the intrinsic interfacial width, σi.9 A second contribution to interface roughness (which we call lateral roughness, σlat) occurs due to deviations of the interface position from a plane, on larger length scales (due, for example, to thermally excited capillary waves at a liquid–liquid interface).10Recent studies using specular neutron reflectivity3,11 and resonant soft X-ray reflectivity4 have quantified the total roughness (given as (σi2 + σlat2)1/2)10 at buried conjugated polymer heterojunctions. Molecular mixing and lateral roughness at conjugated polymer interfaces are expected to have considerably different effects on interfacial processes such as charge separation, charge (re-)combination, photon emission and charge transport. However, specular reflection techniques are sensitive to the total roughness only, and are not able to distinguish these two contributions. Some inference regarding the magnitude of the contributions can be drawn from photophysical measurements on bilayers,3 or by appealing to theoretical arguments (such as provided by capillary wave theory at equilibrated polymer–polymer interfaces).10,11 Both of these approaches have their limitations; (i) the use of photophysical measurements to infer interfacial structure is reliant on a thorough understanding of the influence of structure on photophysics. Even for the relatively simple and well-understood photophysics at play in ref. 3, the analysis provides semi-quantitative information on the intrinsic interfacial width only. For heterojunctions found within organic solar cells (so-called type II heterojunctions) the photophysics is in general considerably more complex1,12,13 and therefore the ability to fully determine the influence of heterojunction structure on device properties requires more precise characterisation of the nanoscale interface structure; (ii) even for amorphous polymer melts, it is known that standard capillary-wave theory does not correctly describe the lateral roughness at the surface/interface of entangled polymer thin-films.14 Appeals to capillary wave theory to quantify lateral roughness at interfaces containing semi-flexible/liquid-crystalline conjugated polymers would therefore be unwise at present, and are not possible for the non-equilibrium interfaces often found within working devices. For these reasons the ability to quantify intrinsic mixing and lateral roughness purely from scattering measurements would represent a significant advance.
Measurements of off-specular scattering,15–18 offer the opportunity to quantify both the lateral roughness and intrinsic width at buried interfaces. X-rays have been utilised to characterise structure at polymer surfaces,14 and buried liquid interfaces where there is sufficient contrast.19 Neutrons have been used where enhanced contrast, via deuteration, is desired; e.g. in lipid bilayer systems.18 In this paper we demonstrate the successful application of off-specular neutron scattering to characterise the in-plane structure at buried conjugated polymer interfaces. Our ultimate aims are to understand the physics of interface formation, and to facilitate more complete comparative studies between interface structure and device performance. To address the first of these aims we focus here on a model system, consisting of thermally equilibrated interfaces between one of the most well-studied conjugated polymers poly(9,9′,dioctyl fluorine) (F8) and poly(methyl methacrylate) (PMMA). F8 is a nematic liquid-crystalline polymer with a crystalline/nematic transition at ∼160 °C,11 and PMMA is an amorphous polymer, with a bulk glass transition temperature of ∼115 °C,20 that is commonly used as a gate dielectric in polymeric FETs. The choice of an equilibrium interface allows us to interpret our findings within the framework of existing equilibrium statistical mechanics theories of polymer interface structure. Combining specular and off-specular reflectivity, enables us to separate the lateral roughness and intrinsic mixing in this system. We find that the amplitude of the total and the lateral roughness grows with film thickness, agreeing qualitatively with the predictions of capillary-wave theory and polymer brush theory.10,14,21 The intrinsic width shows no systematic dependence on film thickness and has a Gaussian width10 with a mean value of ∼12 Å. Comparison with self-consistent field theory for semi-flexible polymers22 allows us to infer that the conjugated polymer chains at this interface adopt a strongly orientated conformation within the mixed interfacial region, that is qualitatively distinct from the predicted behaviour at flexible polymer–polymer interfaces.9,23
Experimental section
Batches of F8 with number-average molecular weight (Mn) of 100 kg mol−1 and 88 kg mol−1, both with a polydispersity index (PDI) of 2, (referenced to polystyrene standards) were provided by CDT Ltd, Cambridge, UK. Deuterated poly(methyl methacrylate) (dPMMA), with Mn of 124 kg mol−1 and a PDI of 1.02 was purchased from Polymer Laboratories, Church Stretton, UK. Films of dPMMA of various thickness were fabricated by spin-coating from toluene solutions onto 2′′ diameter single crystal silicon blocks (〈111〉 orientation, supplied by Compart Technology Ltd, UK). F8 films were spin-coated onto freshly cleaved mica substrates. The F8 films were floated off the mica substrates onto the surface of de-ionized water, and then deposited on top of the silicon/dPMMA samples to make bilayers. The bilayer samples were allowed to dry at room temperature, and then placed under vacuum for 24 hours. Samples were then annealed under vacuum for three hours at 180 °C, and then rapidly quenched on a metal block at room temperature. Previous measurements have shown that this is sufficient time for equilibration of this polymer–polymer interface.24 The temperature of 180 °C is well above the glass transition temperature of bulk PMMA and the crystalline–nematic transition temperature of the F8. Annealing at this temperature followed by rapid quenching was performed to preserve the structure of the equilibrium liquid–liquid interface by preventing any crystallisation of the F8 that could potentially occur with slower cooling.25Specular and off-specular neutron reflectivity measurements were performed simultaneously, on the reflectometer D17 at the Institut Laue-Langevin (ILL), Grenoble, France.26 Some additional specular reflectivity measurements were performed on the reflectometer CRISP at ISIS. Measurements at D17 were performed in time-of-flight (TOF) mode using a broad neutron wavelength (λ) range. Neutrons were incident on the sample at an angle, θi, and detected on an area detector at reflected angles, θr. The components of the momentum transfer vector, q(qx, qy, qz), in the experiments are defined in Fig. 1(b). The experiments utilised an incident ‘ribbon beam’ defined by a 30 mm width slit in the y-direction (the direction perpendicular to the plane containing the incident and specularly reflected beam). The scattered intensity on the detector was summed in the y-direction. This corresponds to integration over qy and leaves the scattered intensity measurement as a function of qx and qz. The experimentally accessible values of qx and qz in the off-specular TOF measurements are shown in Fig. 1(c). The collection of specular reflectivity with qz ranging from below the silicon critical edge to 0.2 Å−1 required the use of two incident angles, 0.6° and 2.5°. To obtain a resolution, Δqz/qz, (where Δqz is the uncertainty in qz) ranging from ∼2% to ∼5% across the qz range with good specular reflectivity statistics, required typical measurement times of 30 minutes and 60 minutes for the incident angles of 0.6° and 2.5° respectively. Off-specular scattering with good measurement statistics was obtained by counting for significantly longer (typically 8–15 hours) at the incident angle of 2.5°. The angular resolution was defined by a pair of narrow slits (in the z-direction) before the sample. The width of these slits (of order 1 mm) was chosen to under-illuminate the samples, and was fixed to give an angular resolution of 0.05° at the incident angle of 2.5°, for all measurements. The chopper settings for the incident angle of 2.5° were chosen to give a wavelength resolution, Δλ/λ (where Δλ is the uncertainty in λ) of 1%. In the modelling of the simultaneous specular/off-specular fits (combined fits), described below, these resolution effects were included by convolving the calculated models with Gaussian functions in both the λ and θr directions. To minimise background scattering from air, all measurements were performed with the sample located within a vacuum chamber with quartz windows.27 This chamber occupied almost all of the space between the incident neutron guide/slit and the evacuated detector tube (leaving an air gap of a few millimetres on either side of the chamber). To assess the various potential sources of background scattering, we measured the intensity of neutrons on the detector; (i) with the sample removed from the beam and the chamber evacuated, (ii) with the sample removed from the beam but the chamber full of air, (iii) with a silicon-only sample in the beam and (iv) with a silicon/F8 sample in the beam. This procedure revealed that the most important contribution to the background scattering came from the air. The second most important source of background counts came from the silicon substrate. The background scattering from the F8 film was found to be negligible. In the bilayer reflectivity data reduction at 2.5° the background counts, obtained with the sample removed from the beam and the chamber evacuated, were subtracted from the measured bilayer counts. Specular and off-specular reflectivity data were fitted by minimising the goodness-of-fit (χ2) parameter using a differential evolution algorithm.28 The main details of the models used are given in the Results and discussion. Further details of the model implementation and fitting are given in the ESI.†
Atomic force microscopy (AFM) measurements were performed using a Park Systems XE100 in contact mode. Root-mean-square (rms) roughness measurements on sample surfaces were obtained by imaging over an area of 45 μm × 45 μm. The square-root of this area is of the same order as the typical in-plane coherence length of the neutrons in the reflectivity experiments.29,30 The Hurst parameter, h,15 (which parameterises the height–height correlation function, as described in the Results and discussion section) is obtained from AFM by performing scans on 1 μm × 1 μm areas of sample surfaces. The height-difference function of the surface (as defined in Teichert et al.31 and Sinha et al.15) can be obtained from these AFM scans.31 On sufficiently small lengthscales (smaller than the in-plane cut-off length of the height–height correlation/height-difference functions) the gradient of a log–log plot of the height-difference function gives 2h.32
Results and discussion
Fig. 1(d)–(f) show intensity maps in θr − λ space from a silicon/dPMMA/F8 bilayer and a silicon/dPMMA single layer. The geometry of the bilayer, with a high scattering-length-density (SLD) bottom layer, ensures that the scattering is dominated by two high-contrast interfaces, the buried polymer–polymer interface and the polymer–substrate interface, with relatively little scattering from the F8 surface (see Fig. 1(g)). The high-intensity scattering at θr = 2.5° in Fig. 1(d)–(f) is the specular reflectivity, with fringes corresponding to the thickness of the dPMMA layer. The dashed vertical lines represent the extent of the specular reflectivity (given by the angular resolution), from which reflectivity versus qz curves are extracted. Significant off-specular scattering is evident in all three intensity maps. These show two distinct types of feature; (i) lines of intensity pointing towards the origin in θr − λ space (Yoneda scattering)15,33 and (ii) lines of intensity along constant qz contours. Yoneda scattering is due to lateral roughness at an individual interface, while the scattering along lines of constant qz is due to correlations between the lateral undulations at different interfaces.16Fig. 1(e) and (f) show that correlations between different interfaces within the bilayer samples, are present before and after annealing. They are also present in the dPMMA single layer (Fig. 1(d)). AFM measurements (see ESI,† Fig. S3) on the silicon substrates used in this study show a surface with lateral height variations that have an rms roughness of 4.3 Å. Deposition of a dPMMA layer onto the silicon results in correlations between the height variations at the silicon–dPMMA interface and at the dPMMA surface. It is these correlations that give rise to the scattering along lines of constant qz in Fig. 1(d)–(f). This is further demonstrated by measurements that were performed on a second batch of silicon substrates that had a significantly lower roughness (rms roughness ∼ 1.6 Å). These showed no strong scattering along lines of constant qz (see ESI,† Fig. S6). Fig. 1(e) and (f) show that there is an increase in the intensity of the Yoneda scattering, and in the scattered intensity between the Yoneda scattering and the specular reflectivity, on annealing. Qualitatively, we can state that this increase in the off-specular scattering is due to increased lateral roughness at the polymer–polymer interface. A reduction in the overall intensity of the specular reflectivity and damping of the interference fringes (Keissig fringes) on annealing (see Fig. 1(h)) is also indicative of increased (total) interface roughness. However, while the signatures of interfacial roughness and the correlations between interfaces are apparent in Fig. 1(e)–(g), our ability to separate the degree of molecular mixing at equilibrated F8–dPMMA interfaces from the extent of the lateral roughness at these interfaces, relies on thorough analysis of the full θr − λ scattering maps from a systematic set of samples. Quantitative data analysis is performed by combining the standard optical-matrix method23 to model the true specular reflectivity (proportional to the product of two Dirac delta function δ(qx) δ(qy)15) and the distorted-wave Born approximation (DWBA)15 to model the diffuse scattering (which represents scattering that is not a delta function and has, in general, non-zero scattered intensity at both specular and non-specular locations).The DWBA applied to a single interface (a semi-infinite sample) by Sinha et al.15 has been extended to multiple interfaces by a number of authors.16,34,35 Sinha et al. split the scattering potential V into two parts; V = V1(r) + V2(r), where r(x,y,z) is a position vector. The first part V1(r) represents the interaction of neutrons with an ideal smooth interface between scattering media and the second part V2(r) is the perturbation due to interfacial roughness (lateral roughness).16,36 The expressions for V1(r) and V2(r) for a single interface, with an average location at z = 0, are given in Sinha et al.15 eqn (4.5) and (4.6).15
Within the DWBA the scattering T matrix15 is approximated as
〈2|T|1〉 = 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2|V1|ϕ1〉 + 〈 2|V1|ϕ1〉 + 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2|V2|ψ1〉, 2|V2|ψ1〉, | (1) |
| |ϕ1〉 = eikin(z)·r. | (2) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2 are exact plane wave eigenstates for a smooth surface and are given by eqn (4.7) and (4.11) in Sinha et al.15 In a multilayer system these equations are written as34
2 are exact plane wave eigenstates for a smooth surface and are given by eqn (4.7) and (4.11) in Sinha et al.15 In a multilayer system these equations are written as34ψ1(r) = T1(z)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eik1(z)·r + R1(z) eik1(z)·r + R1(z)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eik1′(z)·r eik1′(z)·r | (3) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2(r) = T2*(z) 2(r) = T2*(z)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eik2*(z)·r + R2*(z) eik2*(z)·r + R2*(z)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eik2′*(z)·r. eik2′*(z)·r. | (4) |
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 2 is time-reversed, and has complex reflection and transmission amplitudes T2 and R2 respectively. The wave vectors k1(z) and k2(z) correspond to the incoming waves in each eigenstate and the wave vectors k1′(z) and k2′(z) correspond to the outgoing waves.
2 is time-reversed, and has complex reflection and transmission amplitudes T2 and R2 respectively. The wave vectors k1(z) and k2(z) correspond to the incoming waves in each eigenstate and the wave vectors k1′(z) and k2′(z) correspond to the outgoing waves.
The work by Sinha et al.15 for off-specular reflectivity from a single interface is extended by Schlomka et al.34 and Holý et al.35,36 to systems with multiple interfaces. Following Holý et al.,36 we define a multilayer system containing N interfaces, as consisting of N − 1 layers of finite thickness between a semi-infinite substrate and semi-infinite air/vacuum. The layers are labelled with the subscript j (or k), with j = 1 representing the air/vacuum and j = N + 1 representing the substrate. The wave vector components in each layer are dependent on the layer refractive index and therefore k1(z) can be written kj1 where j is the index of the layer (similarly for k2(z)). The mean height of the jth interface (the interface between layers j and j + 1) is written zj (as in Sinha et al. and Holý et al. the origin of the z-axis is located at the sample/air interface and the positive z direction is defined as pointing out from the sample surface.)
The differential scattering cross-section is proportional to the probability of scattering from the state ψ1(r) ψ2(r) given by15
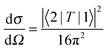 | (5) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) (k1)|2 is related to the reflectivity of the ideal interface |R(k1)|2 by
(k1)|2 is related to the reflectivity of the ideal interface |R(k1)|2 by | (6) |
When evaluating the diffuse scattering, Sinha et al.15 approximated the wave functions above the average interface location (at z = 0), but below the actual sample/air interface, by the wave functions below the interface in the case of a smooth interface (eqn (3) and (4)). This greatly simplifies the evaluation of the matrix elements in eqn (1). When doing this in our study we chose the analytic continuation that is equivalent to that given in Schlomka et al.34Table 1, Case II. (NB; in Schlomka et al. the interfaces are indexed differently to Holý et al. In Schlomka et al. the jth interface is that between layers j − 1 and j. In Schlomka et al., Table 1, the superscript m is the index of the momentum transfer and the subscript j is the index of the layer. We, instead follow the nomenclature of Holý et al.36 and parameterize the terms equivalent to Schlomka et al.Table 1 with a superscript j, representing the layer index and a subscript m representing the momentum transfer index).
| dPMMA thickness (Å); off-specular only fit | dPMMA thickness (Å); combined fit | Hurst parameter, h, at dPMMA/F8 interface; off-specular only fit | Hurst parameter, h, at dPMMA/F8 interface; combined fit | ξ (μm); off-specular only fit | ξ (μm); combined fit | |
|---|---|---|---|---|---|---|
| Sample 1 | 161.8 | 162.5 | 0.61 | 0.61 | 1.7 | 1.2 |
| Sample 2 | 215.1 | 215.1 | 0.6 | 0.6 | 1.5 | 1.2 |
| Sample 3 | 418.9 | 423.5 | 0.1 | 0.16 | 7.1 | 0.4 |
| Sample 4 | 480.7 | 482.2 | 0.21 | 0.18 | 11.3 | 0.5 |
| Sample 5 | 650.2 | 647.2 | 0.2 | 0.12 | 6.0 | 2.0 |
Taking the configurational average and ignoring for the moment correlations between the lateral roughness of different interfaces, the diffuse differential cross-section is given by34,36
 | (7) |
 | (8) |
| m, n = 0,…,3, j, k = 1,…,N, |
| qj0z = kj1z + kj2z |
| qj1z = kj1z − kj2z |
| qj2z = −qj1z |
| qj3z = −qj0z. | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−(R/ξj)2hj, where σlat,j is the lateral roughness of interface j, ξj is the cut-off length, hj is the Hurst parameter and
e−(R/ξj)2hj, where σlat,j is the lateral roughness of interface j, ξj is the cut-off length, hj is the Hurst parameter and 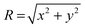 .
.
To take into account potential height correlations between different interfaces the following terms are added to the diffuse cross section.
 | (10) |
 .16
.16
Since the scattering in the samples is dominated by the two high-contrast interfaces, the dPMMA/F8 interface and the silicon/dPMMA interface, cjk(x,y) is set to zero for all other interface pairs. Following the approach of Schlomka et al. (ref. 34 eqn (5)) correlations between height fluctuations at the silicon/dPMMA and dPMMA/F8 interfaces were parameterised using the cj(x,y) functions for each interface plus a single additional parameter; the perpendicular cut-off distance, ξ⊥,jk. Small values of ξ⊥,jk compared to the distance between interfaces j and k correspond to low correlation between these interfaces, whereas large values of ξ⊥,jk correspond to strongly correlated lateral roughness at these two interfaces. The form of eqn (7)–(10) implies that the diffuse scattering is dependent on both the lateral roughness (via the cjk(x,y) terms inside the integral in Qjkmn and the 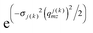 terms in the prefactors) and the intrinsic roughness (given that the σj(k) term in the exponent of the prefactors is the total roughness).
terms in the prefactors) and the intrinsic roughness (given that the σj(k) term in the exponent of the prefactors is the total roughness).
Reflectivity measurements were performed on a set of thermally equilibrated F8–dPMMA bilayers, in which the thickness of the F8 layer was kept constant (at 1000 Å) and the thickness of the dPMMA layer was varied between approximately 120 Å and 850 Å. Our initial approach to analysing this data was to extract the specular reflectivity (the reflectivity arising from scattering within the ‘specular strip’; -the region shown by the vertical dotted lines in Fig. 1(d)) and fit this data under the assumption that all of this scattering arises from composition gradients that are purely normal to the substrate (i.e. we ignore the presence of diffuse scattering within the specular strip). We use a bilayer model in which the thickness and SLD of the dPMMA layer, and the (total) roughness at the dPMMA/F8 interface were allowed to vary. The SLD and thickness of the F8 layer were fixed at the values obtained from fitting the specular reflectivity of a single annealed F8 layer. The F8 surface roughness was fixed at the value measured by AFM. Fig. 2 shows that good fits can be obtained with the bilayer model, and that these show a larger roughness for thicker dPMMA layers. The robustness of this conclusion with-respect-to the inclusion or neglect of a native silicon-oxide layer in the model in shown in the ESI† (Fig. S4). Off-specular reflectivity with good statistics was obtained from five of these samples, with different thicknesses of dPMMA layer. Our next steps were to; (i) fit the off-specular data on its own (i.e. without fitting the data within the specular strip) and (ii) fit the combined specular and off-specular reflectivity simultaneously. In both cases the data was fitted by calculating the differential scattering cross-section in θr − λ space, and using the total roughness and the lateral roughness at the dPMMA/F8 interface as fit parameters. All other interfaces were modelled by setting the total roughness to be equal to lateral roughness (i.e. the intrinsic interfacial width was set to zero at these interfaces). The following systematic methodology was used to analyse the data. Firstly we performed AFM measurements on the silicon substrate, and then AFM and reflectivity measurements on a single dPMMA film deposited onto the silicon. From the AFM we extracted σlat for the silicon surface, and σlat and h for the dPMMA surface. We then fitted the off-specular reflectivity measurements on the dPMMA single layer, with the silicon substrate and dPMMA surface parameters fixed to these values, using ξ and h for the silicon/dPMMA interface, and ξ for the dPMMA surface as fit parameters. All subsequent bilayer fits were then performed with the silicon/dPMMA interface parameters (σlat, ξ and h) fixed at the values from this dPMMA single layer fit. There is also a prefactor in the model that scales the diffuse scattering with respect to the true specular reflectivity.15,34 This is an instrumental constant (for a given detector, angle of incidence and slit geometry), and was fixed in the bilayer fits at the value obtained from the dPMMA single layer fit.
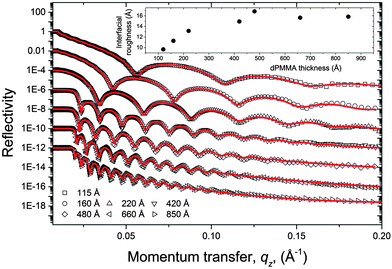
Experimental data and combined fits of the specular and off-specular reflectivity for two different thicknesses of dPMMA are shown in Fig. 3. The fits are of good quality and our bilayer model reproduces the observed features well. The enhanced Yoneda scattering for the thicker dPMMA layer that we observe, is evidence of larger lateral roughness at the dPMMA/F8 interface. The roughness parameters from the fits for all five bilayers are shown in Fig. 4, while the remaining fit parameters are given in Table 1. Fig. 4(a) displays the total roughness extracted from the fits to the specular-only data and the off-specular-only data, plus the combined specular and off-specular fits. There is some scatter in the plot, but Fig. 4(a) shows an increase in the total interface roughness with dPMMA film thickness. It is clear that fitting only the specular reflectivity, with the assumption that we can ignore the diffuse scattering at the specular condition (Fig. 4(a) closed circles), significantly underestimates the total interface roughness. It is also clear that fitting only the off-specular data results in systematically higher values of the total roughness in comparison with the combined specular and off-specular fits. We also fitted the specular reflectivity, after subtraction of the diffuse scattering intensity within the specular strip (obtained from an extrapolation of the fit to the off-specular-only data). The total roughness parameter obtained by this procedure is also displayed in Fig. 4(a) (open triangles). These values are in reasonable agreement with those from the combined specular and off-specular fits (filled triangles) and help to demonstrate the robustness of the data analysis methodology. Fig. 4(b) plots the fitted lateral dPMMA/F8 interface roughness from the off-specular-only and from the combined specular and off-specular fits, showing a general increase with film thickness. This behaviour is in line with expectations due to the smaller lengthscale cut-off to the capillary-wave spectrum at a polymer interface for thinner films. This restriction in the wavelength of capillary-wave fluctuations (and hence the amplitude of the lateral roughness) in thin films, can occur due to either dispersion forces10,23,40 or substrate pinning of polymer chains (even for films considerably thicker than the radius of gyration of the polymer).14 In contrast the fitted intrinsic interfacial width shown in Fig. 4(c) shows no clear dependence on film thickness. There is some scatter in the calculated intrinsic width, particularly for the thicker dPMMA films. It is likely that this is due to the fact that as the lateral roughness becomes a larger component of the total roughness (as occurs for thicker dPMMA films), the calculation of the intrinsic roughness (calculated from the difference between the squares of σtotal and σlat) becomes more prone to error. Averaging all five data points for the combined fit parameters in Fig. 4(c) gives an intrinsic interfacial width of 12 Å ± 4 Å.
The robustness of these findings was further investigated by repeating the fitting procedure on the set of bilayer samples using several different methodologies. These procedures were; (i) allowing the scaling parameter between the true specular and the diffuse scattering to vary in the bilayer fits, rather than being fixed at the value obtained for the dPMMA single layer; (ii) inserting a silicon-oxide layer with variable thickness and SLD (but with the same values of σlat, ξ and h at the silicon-oxide/dPMMA interface as at the silicon/silicon-oxide interface) into the model; (iii) fixing the values of the cut-off length ξ for the dPMMA/F8 interface in the combined specular and off-specular fits, at the values obtained when only the off-specular data is fitted (this was performed because the fits for the thicker dPMMA layers returned significantly different ξ parameters for the off-specular-only fits and for the combined specular/off-specular fits). Examples of the fits with a silicon-oxide layer (Fig. S5) and the extracted fit parameters for all three of these methodologies (Tables S1–S3) are shown in the ESI.† Tables S1–S3 (ESI†) show that our findings for the magnitude of both σi and σlat, and their dependence on dPMMA thickness are robust with-respect-to these different fitting methodologies. It is important to point out that the robustness of these findings is in contrast to the results for a second set of experiments that we performed using a different batch of silicon (〈111〉 orientation from Prolog Semicor, Ukraine) with lower rms roughness. The off-specular reflectivity from samples made on these substrates (for both dPMMA single layers and bilayers) lacked any strong scattering due to correlations between different interfaces, and it did not prove possible to robustly fit such data (see ESI† for further details).
Having obtained a reasonably consistent and robust estimate of the intrinsic width of the dPMMA/F8 interface at equilibrium, we now examine the implications of our findings within theoretical frameworks that look at polymer–polymer composition profiles using self-consistent field theory (SCFT) (in the limit of infinite molecular weight polymers). Morse and Fredrickson (MF)22 predict qualitative differences in the mixing behaviour at semiflexible polymer–polymer interfaces, depending on the value of κχ, where κ is a dimensionless bending modulus, proportional to the persistence length of the polymer (assumed, in the theory, to be the same for both polymers), and χ is the Flory–Huggins interaction parameter.22 For κχ ≪ 1 the MF theory predicts the same intrinsic interfacial width as the Helfand and Tagami (HT)9 result for Gaussian chains. This states that the width of the predicted hyperbolic tangent composition profile, ω, is given by ω = b/(6χ)1/2, where b is the statistical segment length23 of the polymer (a given value of ω corresponds to a Gaussian roughness, σi, equal to (2π)1/2ω10,23). Helfand and Sapse (HS)41 extended the theory for Gaussian chains to consider the case where the chain stiffness on the two sides of the interface was different. For one polymer with a significantly higher value of b than the other, the interface width is dominated by the stiffer polymer and has a characteristic size given by the HT result multiplied by a factor of  .23,41 For κχ ≫ 1 the MF prediction is completely different. Rather than the interface width increasing with b, the system enters a regime in which increases in chain stiffness result in a narrowing of the interface. In this regime the polymer adopts a more strongly oriented conformation, and has a width that is narrower than the HT result by a factor of order (κχ)−1.
.23,41 For κχ ≫ 1 the MF prediction is completely different. Rather than the interface width increasing with b, the system enters a regime in which increases in chain stiffness result in a narrowing of the interface. In this regime the polymer adopts a more strongly oriented conformation, and has a width that is narrower than the HT result by a factor of order (κχ)−1.
We now compare our results with the predictions of MF theory, to enable us to gain some insight into the nature of the interfacial mixing of our polymer pair in terms of the conformation of chain segments at the interface. Our first approach uses the extracted values of σi, combined with the literature value for the persistence length of F8,25 to calculate values for χ, using the HS theory. Substitution of the extracted values for σi from Fig. 4(c) into the HS result, returns a value of χ such that κχ is significantly larger than one; -taking values for σi at the extremes of the range, 6 Å and 17 Å, the HS calculation returns values for κχ between 3 and 22 (if the HT equation is used instead of the HS equation values of κχ between 6 and 45 are obtained). This range of calculated values for κχ completely invalidates the use of the HS (or HT) equation in the first place. This lack of internal consistency implies that, on the lengthscale of the intrinsic interfacial width, these polymers do not mix in a way that can be modelled as loops of flexible Gaussian chain. We now examine our results in comparison to the higher stiffness MF regime predictions. Quantitative comparison with the MF theory in the regime in which κχ ≫ 1 is complicated by the fact that (i) the theory does not explicitly consider asymmetry in the chain stiffness, and (ii) the theory predicts only an order of magnitude for the prefactor, with no numerical coefficients. Nevertheless, if we calculate the value of χ and hence κχ using the MF theory, with the assumption that the prefactor by which the HT width should be multiplied is equal to (κχ)−1, we can at least estimate the potential applicability of this regime. Making this assumption returns values of κχ of order 2-to-4, which (without providing conformation that we are clearly in the higher stiffness MF regime) does not flatly contradict the requirement that this product should be significantly larger than one. We also point out that for the molecular weights used in this work, the calculated values of χ multiplied by the degree of polymerisation of the polymers, N, return values that justify the use of the infinite molecular weight assumption, implicit in the HT, HS and MF theories (i.e. χN ≫ 1).42,43 These comparisons lead us to conclude that mixing at the interface cannot be described in terms of polymer chain segments that adopt conformations similar to a random walk. Instead, a more plausible explanation is that the conjugated polymer chain segments become significantly oriented in the plane of the interface.44 We would like to point out that we are only able to reach this conclusion following the extensive analysis of reflectivity data, followed by comparison with SCFT predictions. It is not simply the case that the polymers would be expected to adopt this kind of oriented conformation at the interface, simply because of the relatively high chain stiffness of the F8. It is the combination of a high stiffness and a relatively narrow intrinsic interfacial width that results in a deviation from flexible chain behaviour. At significantly broader interfaces, such as we have found exist at some polyfluorene heterojunctions,3,11 it may well be possible for these relatively stiff polymers to exhibit mixing that can be described by the Gaussian chain (HT) model.
Conclusions
A systematic series of measurements on a set of model conjugated-polymer/insulating-polymer bilayers has been performed using specular and off-specular neutron reflectivity. The use of off-specular measurements has allowed sensitivity to the structure of the buried polymer/polymer interface in the plane of the sample, in addition to the usual probing of average composition normal to the sample, achieved by specular reflectivity. This three-dimensional characterisation, allied to detailed quantitative analysis of the diffuse scattering resulting from height correlations within and between the two high-contrast interfaces has allowed a robust determination of the intrinsic width at the buried polymer/polymer interface. Comparison of this measurement with theoretical predictions for the intrinsic width at polymer/polymer interfaces gives insight into the nature of the conjugated polymer conformation at the interface. The ability to gain this insight directly from structural measurements alone is an important step forward. It is hoped that this will enable a significant enhancement of the understanding of (i) the physical processes influencing local composition and conformation at conjugated polymer interfaces, and (ii) the relationship between the structure of well-controlled/well-characterised interfaces and optoelectronic behaviour, in a variety of conjugated polymer-based systems.Acknowledgements
We acknowledge ISIS and ILL for the award of beam time, and thank the staff at the beam-lines CRISP at ISIS and D17 at ILL for their support during the experiments. We thank CDT Ltd for supplying the F8. David James and Dyfrig Môn thank EPSRC for the award of studentships via the Doctoral Training Grant to Swansea University.References
- P. Sreearunothai, A. C. Morteani, I. Avilov, J. Cornil, D. Beljonne, R. H. Friend, R. T. Phillips, C. Silva and L. M. Herz, Phys. Rev. Lett., 2006, 96(11), 117403 CrossRef CAS PubMed.
- Y.-S. Huang, S. Westenhoff, I. Avilov, P. Sreearunothai, J. M. Hodgkiss, C. Deleener, R. H. Friend and D. Beljonne, Nat. Mater., 2008, 7(6), 483–489 CrossRef CAS PubMed.
- A. M. Higgins, A. Cadby, D. G. Lidzey, R. M. Dalgliesh, M. Geoghegan, R. A. L. Jones, S. J. Martin and S. Y. Heriot, Adv. Funct. Mater., 2009, 19(1), 157–163 CrossRef CAS.
- H. Yan, S. Swaraj, C. Wang, I. Hwang, N. C. Greenham, C. Groves, H. Ade and C. R. McNeill, Adv. Funct. Mater., 2010, 20(24), 4329–4337 CrossRef CAS.
- M. L. Chabinyc, R. A. Street and J. E. Northrup, Appl. Phys. Lett., 2007, 90(12), 123508 CrossRef.
- L. L. Chua, P. K. H. Ho, H. Sirringhaus and R. H. Friend, Adv. Mater., 2004, 16(18), 1609–1615 CrossRef CAS.
- S. S. Chang, A. B. Rodriguez, A. M. Higgins, C. Liu, M. Geoghegan, H. Sirringhaus, F. Cousin, R. M. Dalgleish and Y. Deng, Soft Matter, 2008, 4(11), 2220–2224 RSC.
- B. A. Collins, J. E. Cochran, H. Yan, E. Gann, C. Hub, R. Fink, C. Wang, T. Schuettfort, C. R. McNeill, M. L. Chabinyc and H. Ade, Nat. Mater., 2012, 11(6), 536–543 CrossRef CAS PubMed.
- E. Helfand and Y. Tagami, J. Polym. Sci., Part B: Polym. Lett., 1971, 9(10), 741–746 CrossRef CAS.
- M. Sferrazza, C. Xiao, R. A. L. Jones, D. G. Bucknall, J. Webster and J. Penfold, Phys. Rev. Lett., 1997, 78(19), 3693–3696 CrossRef CAS.
- A. M. Higgins, S. J. Martin, M. Geoghegan, S. Y. Heriot, R. L. Thompson, R. Cubitt, R. M. Dalgliesh, I. Grizzi and R. A. L. Jones, Macromolecules, 2006, 39(19), 6699–6707 CrossRef CAS.
- A. C. Morteani, P. Sreearunothai, L. M. Herz, R. H. Friend and C. Silva, Phys. Rev. Lett., 2004, 92(24), 247402 CrossRef PubMed.
- W. J. Huang, R. Sun, J. Tao, L. D. Menard, R. G. Nuzzo and J. M. Zuo, Nat. Mater., 2008, 7(4), 308–313 CrossRef CAS PubMed.
- Y.-S. Seo, T. Koga, J. Sokolov, M. H. Rafailovich, M. Tolan and S. Sinha, Phys. Rev. Lett., 2005, 94(15), 157802 CrossRef PubMed.
- S. K. Sinha, E. B. Sirota, S. Garoff and H. B. Stanley, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38(4), 2297–2311 CrossRef.
- R. Pynn, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(2), 602–612 CrossRef.
- J. Daillant, S. Mora, C. Fradin, M. Alba, A. Braslau and D. Luzet, Appl. Surf. Sci., 2001, 182(3–4), 223–230 CrossRef CAS.
- M. S. Jablin, M. Zhernenkov, B. P. Toperverg, M. Dubey, H. L. Smith, A. Vidyasagar, R. Toomey, A. J. Hurd and J. Majewski, Phys. Rev. Lett., 2011, 106(13), 138101 CrossRef PubMed.
- B. R. McClain, M. Yoon, J. D. Litster and S. G. J. Mochrie, Eur. Phys. J. B, 1999, 10(1), 45–52 CrossRef CAS.
- C. B. Roth, A. Pound, S. W. Kamp, C. A. Murray and J. R. Dutcher, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 20(4), 441–448 CrossRef CAS PubMed.
- G. H. Fredrickson, A. Ajdari, L. Leibler and J. P. Carton, Macromolecules, 1992, 25(11), 2882–2889 CrossRef CAS.
- D. C. Morse and G. H. Fredrickson, Phys. Rev. Lett., 1994, 73(24), 3235–3238 CrossRef CAS PubMed.
- R. A. L. Jones and R. W. Richards, Polymers at surfaces and interfaces, Cambridge University Press, 1999 Search PubMed.
- A. M. Higgins, P. C. Jukes, S. J. Martin, M. Geoghegan, R. A. L. Jones and R. Cubitt, Appl. Phys. Lett., 2002, 81(26), 4949–4951 CrossRef CAS.
- M. Grell, D. D. C. Bradley, M. Inbasekaran and E. P. Woo, Adv. Mater., 1997, 9(10), 798–802 CrossRef CAS.
- R. Cubitt and G. Fragneto, Appl. Phys. A: Mater. Sci. Process., 2002, 74(1), s329–s331 CrossRef CAS.
- D. W. James, PhD thesis, Swansea University, 2011.
- R. Storn and K. Price, Journal of Global Optimization, 1997, 11(4), 341–359 CrossRef.
- T. P. Russell, Mater. Sci. Rep., 1990, 5(4), 171–271 CrossRef CAS.
- R. M. Richardson, J. R. P. Webster and A. Zarbakhsh, J. Appl. Crystallogr., 1997, 30(6), 943–947 CrossRef CAS.
- C. Teichert, J. F. MacKay, D. E. Savage, M. G. Lagally, M. Brohl and P. Wagner, Appl. Phys. Lett., 1995, 66(18), 2346–2348 CrossRef CAS.
- H. N. Yang, G. C. Wang and T. M. Lu, Diffraction from Rough Surfaces and Dynamic Growth Fronts, World Scientific, 1993, pp. 38–81 Search PubMed.
- Y. Yoneda, Phys. Rev., 1963, 131(5), 2010–2013 CrossRef.
- J. P. Schlomka, M. Tolan, L. Schwalowsky, O. H. Seeck, J. Stettner and W. Press, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(4), 2311–2321 CrossRef CAS.
- V. Holý and T. Baumbach, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(15), 10668–10676 CrossRef.
- V. Holý, J. Kuběna, I. Ohlídal, K. Lischka and W. Plotz, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(23), 15896–15903 CrossRef.
- L. Névot and P. Croce, Rev. Phys. Appl., 1980, 15(3), 761–779 CrossRef.
- V. W. Stone, X. Arys, R. Legras and A. M. Jonas, Macromolecules, 2000, 33(8), 3031–3041 CrossRef CAS.
- B. Akgun, D. R. Lee, H. Kim, H. Zhang, O. Prucker, J. Wang, J. Rühe and M. D. Foster, Macromolecules, 2007, 40(17), 6361–6369 CrossRef CAS.
- A. K. Doerr, M. Tolan, W. Prange, J. P. Schlomka, T. Seydel, W. Press, D. Smilgies and B. Struth, Phys. Rev. Lett., 1999, 83(17), 3470–3473 CrossRef CAS.
- E. Helfand and A. M. Sapse, J. Chem. Phys., 1975, 62(4), 1327–1331 CrossRef CAS.
- H. Tang and K. F. Freed, J. Chem. Phys., 1991, 94(9), 6307–6322 CrossRef CAS.
- D. Broseta, G. H. Fredrickson, E. Helfand and L. Leibler, Macromolecules, 1990, 23(1), 132–139 CrossRef CAS.
- We note that the MF theory contains no nematic terms in the Hamiltonian. The inclusion of such terms would be expected to further increase polymer orientation and reduce interfacial width. However, as far as we are aware, no studies exist in which interface widths are systematically calculated as a function of the strength of the nematic terms, alongside the bending modulus and χ parameter. The neglect/inclusion of such terms would not alter the conclusion that our results imply that mixing at the interface cannot be interpreted within the flexible Gaussian chain model, and that more highly oriented polymer conformations at the interface provide a more plausible interpretation.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02008e |
| This journal is © The Royal Society of Chemistry 2015 |