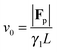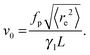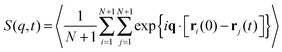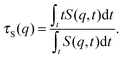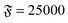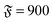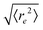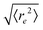DOI:
10.1039/C5SM01683E
(Paper)
Soft Matter, 2015,
11, 7181-7190
Self-propelled worm-like filaments: spontaneous spiral formation, structure, and dynamics†
Received
8th July 2015
, Accepted 5th August 2015
First published on 6th August 2015
Abstract
Worm-like filaments that are propelled homogeneously along their tangent vector are studied by Brownian dynamics simulations. Systems in two dimensions are investigated, corresponding to filaments adsorbed to interfaces or surfaces. A large parameter space covering weak and strong propulsion, as well as flexible and stiff filaments is explored. For strongly propelled and flexible filaments, the free-swimming filaments spontaneously form stable spirals. The propulsion force has a strong impact on dynamic properties, such as the rotational and translational mean square displacement and the rate of conformational sampling. In particular, when the active self-propulsion dominates thermal diffusion, but is too weak for spiral formation, the rotational diffusion coefficient has an activity-induced contribution given by vc/ξP, where vc is the contour velocity and ξP the persistence length. In contrast, structural properties are hardly affected by the activity of the system, as long as no spirals form. The model mimics common features of biological systems, such as microtubules and actin filaments on motility assays or slender bacteria, and artificially designed microswimmers.
1 Introduction
Its importance in biology and its enormous potential impact in technical applications makes active soft matter a field of rapidly growing interest and progress.1–3 Flexible slender bodies are of particular importance. The majority of natural swimmers propel themselves using flexible, hair-like structures like cilia and flagella.1 Another important example are actin filaments and microtubules, major constituents of the cytoskeleton, whose capability to buckle decisively controls the mechanical properties of the cell body.4 Flexibility is the crucial ingredient for the formation of small-scale spirals5 and possibly also for large-scale swirls6 of microtubules on motility assays. Even the structure of slender bacteria can be dominated by their flexibility.7 Electrohydrodynamic convection can propel colloid chains because they are flexible,8 just as the swimming mechanism of assembled magnetic beads in an oscillating external magnetic field is possible because of the swimmer's flexibility.9 Flexibility is of course also the feature that allows for the instabilities leading to cilia-like beating in artificially bundled microtubules.10,11
Despite its importance, the number of theoretical studies of active agents that incorporate flexibility is still relatively small, and can roughly be subdivided into works that focus on buckling phenomena and on free-swimming agents. Symmetry breaking instabilities leading to rotation and beating motion of active filaments on motility assays can be described with a phenomenological ordinary differential equation for the filaments.12 The propulsion force of motor proteins has been predicted based on a Langevin model for buckled, rotating actin filaments and microtubules.13 Numerical studies with Lattice-Boltzmann simulations and Brownian or multi-particle collision dynamics have demonstrated that clamped of pinned filaments composed of stresslets or propelled beads can show cilia-like beating or rotation.14,15
The behaviour of free-swimming actin filaments on motility assays was reproduced in early numerical studies using the Langevin equation.16 However, it was only recently that theoretical study of flexible, active filaments that can move freely has received significant attention. Lattice-Boltzmann simulations reveal that spontaneous symmetry breaking in chains of stresslets can lead to rotational or translational filament motion.17 Brownian dynamics simulations of short self-propelled filaments suggest that different types of motion occur for single filaments18 and that spontaneous rotational motion can arise for pairs of filaments.19 A combination of Brownian dynamics simulations and analytic theory shows that shot noise in worm-like filaments leads to temporal superdiffusive filament movement and faster-decaying tangent–tangent correlation functions.20 Finally, chains of active colloids connected by springs have the same Flory exponent but a different prefactor of the scaling law compared to chains of passive colloids, as shown recently both analytically for beads without volume exclusion and numerically with Brownian dynamics simulations for beads with volume exclusion.21
The free-swimming behaviour of a worm-like filament that is tangentially propelled with a homogeneous force is still unexplored and is the subject of this work. The model is introduced in Section 2. Results for the structural and dynamic properties over a wide range or propulsion forces and filament flexibilities are presented in Section 3. We find that the filament can spontaneously form spirals, which is the mechanism that dominates the behaviour of flexible filaments for large propulsion forces. The relevance of our observations for natural and artificial active agents is discussed in Section 4. We present our conclusions in Section 5.
2 Model and methods
We study a single, active, worm-like filament, which is modelled as a sequence of N + 1 beads connected via stiff springs. The overdamped equation of motion is given by| | 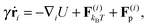 | (1) |
where ri are the coordinates of bead i, γ is the friction coefficient, U is the configurational energy, 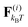 is the thermal noise force, and F(i)p is the active force that drives the system out of equilibrium. The configurational potential energy
is the thermal noise force, and F(i)p is the active force that drives the system out of equilibrium. The configurational potential energy| | | U = Ubond + Uangle + UEV | (2) |
is composed of a bond contribution between neighbouring beads| | 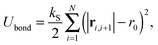 | (3) |
a bending energy| | 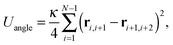 | (4) |
and an excluded volume term modelled with repulsive Lennard-Jones interactions| | 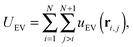 | (5) |
| | 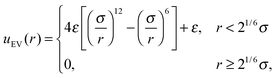 | (6) |
where ri,j = ri − rj is the vector between the position of the beads i and j, kS is the spring constant for the bond potential, r0 is the equilibrium bond length, κ is the bending rigidity, and ε and σ are the characteristic volume-exclusion energy and effective filament diameter (bead size).
The drag force γṙi is the velocity of each bead times the friction coefficient γ. The thermal force 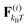 is modelled as white noise with zero mean and variance 2kBTγ/Δt as described in ref. 22. Note that hydrodynamic interactions (HI) are not included in our model. The model is thus in particular valid for (i) neutral swimmers, for which HI are known to be of minor importance,23–25 (ii) swimmers near a wall, where HI is of less importance,26,27 and (iii) microorganisms that glide on a surface, such as nematodes like C. elegans.28,29
is modelled as white noise with zero mean and variance 2kBTγ/Δt as described in ref. 22. Note that hydrodynamic interactions (HI) are not included in our model. The model is thus in particular valid for (i) neutral swimmers, for which HI are known to be of minor importance,23–25 (ii) swimmers near a wall, where HI is of less importance,26,27 and (iii) microorganisms that glide on a surface, such as nematodes like C. elegans.28,29
Without propulsion force, F(i)p = 0, the model matches the well-known worm-like chain model for semi-flexible polymers.30,31 For active filaments, we use a force per unit length fp that acts tangentially along all bonds, i.e.,
| | 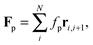 | (7) |
as illustrated in
Fig. 1. The force along each bond is distributed equally onto both adjacent beads.
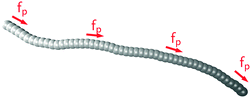 |
| | Fig. 1 Filament model: beads are connected via stiff springs. The active force acts tangentially along all bonds. Colour gradient indicates the force direction. | |
We consider systems with parameters chosen such that (i) kS is sufficiently large that the bond length is approximately constant r0, that (ii) the local filament curvature is low such that the bead discretization does not violate the worm-like polymer description, and that (iii) the thickness of the chain has negligible impact on the results. When these requirements are met, the system is fully characterized by two dimensionless numbers,
| | 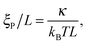 | (8) |
| | 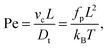 | (9) |
where
L =
Nr0 and
ξP are the length and persistence length of the chain, respectively.
ξP/
L is a measure for the bending rigidity of the filament. The Péclet number Pe is the ratio of convective to diffusive transport and measures the degree of activity. For its definition, we use that the filament has a contour velocity
vc =
fp/
γl, and that the translational diffusion coefficient
Dt =
kBT/
γlL, where we have introduced the friction per unit length
γl =
γ(
N + 1)/
L.
The ratio of these numbers
| | 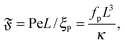 | (10) |
which we call the flexure number, provides a ratio of activity to bending rigidity. Previous studies showed that this number is decisive for buckling instabilities of active filaments.
12,15 It will be shown below that this is also a determining quantity for spiral stability and rotational diffusion.
Simulations were performed in two dimensions, where volume exclusion interactions have major importance. Equations of motions were integrated using an Euler scheme. Simulation parameters and results are reported in dimensionless form, where length are measured in units of the filament length L, energies in units of the thermal energy kBT, and time in units of the characteristic time for the filament to diffuse its own body length
In our simulations we used
kS = 4000
kBT/
r02,
r0 =
σ =
L/
N, and
ε =
kBT if not stated otherwise. A large parameter space for Pe and
ξP/
L was explored by varying
fp,
N, and
κ.
N was varied in the range from 25 to 200 from the highest to the lowest
ξP/
L. Almost all simulations were run for more than 5
τ. An initial period of the simulation output is discarded in the analysis. The timestep Δ
t was adjusted to the remaining settings to ensure stable simulations. A list with all simulation settings is given in the ESI.
† Unless explicitly mentioned, results refer to simulations that were started with a perfectly straight conformation.
All simulations were performed using the LAMMPS molecular simulation package32 with in-house modifications to describe the angle potential, the propulsion forces, and to solve the overdamped equations of motion.
3 Results
The characteristic filament behaviour depends on its bending rigidity and activity and can be divided into three regimes (see Fig. 2). At low Pe or high ξP/L, the “polymer regime”, the active filament structurally resembles the passive filament with Pe = 0. The main difference compared to the passive filament is that the active force drives the filament along its contour, leading to a directed translational motion—we name this characteristic movement “railway motion”. At high Pe and low ξP/L, the filament spontaneously winds up to a spiral. The “spiral state” is characterized by ballistic rotation but only diffusive translation. Spirals can spontaneously break up. Their lifetime determines whether spiral formation has a minor impact on the overall filament behaviour, the “weak spiral regime” at intermediate Pe, or whether spirals are dominating, the “strong spiral regime” at large Pe. Because spiral formation has a major impact on both the structure and the dynamics, features related to spiral formation are addressed first. Structural and dynamic properties of the elongated and spiral state are presented afterwards.
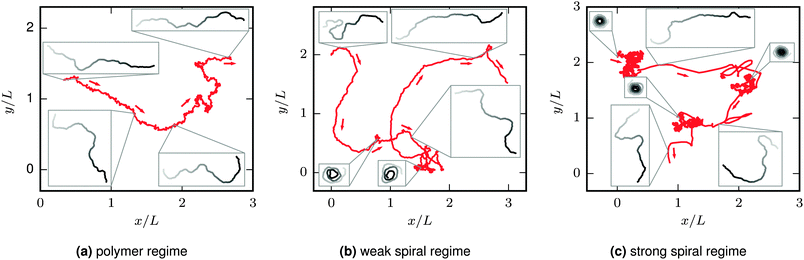 |
| | Fig. 2 Trajectories of the center of mass of the filament (red) and filament configurations from selected snapshots (grayscale, leading tip black). Arrows point in the direction of movement. ξP/L = 0.2 (with N = 100) in all plots; Pe increases from left to right. At Pe = 200 (left), there is not sign of spiral formation. At Pe = 1000 (middle) spirals form occasionally, but the overall behaviour is dominated by an elongated chain. At Pe = 5000 (right), the spiral state is predominant. The chain has a directed motion in the elongated state. In the spiral state, the translational motion is almost purely diffusive. This leads to separated clusters in the trajectories for simulations in the strong spiral regime, visible for example in the upper left of the right image. The length of the depicted trajectories corresponds to approximately 0.13τ (left), 0.13τ (middle), and 0.6τ (right). Videos of the simulations of these examples are given in the ESI.† | |
3.1 Spiral formation
The processes that lead to the formation and break-up of spirals are depicted in Fig. 3. Spontaneous spiral formation (cf.Fig. 3a) results from the leading tip colliding with a subsequent part of the chain. Volume exclusion then forces the tip to bent. By further forward movement, the chain winds to a spiral. Two spiral break-up mechanisms occurred in our simulations. The first is the thermally activated mechanism in Fig. 3b. The leading tip of the wound-up chain spontaneously changes direction and the spiral deforms. This break-up mechanism requires strong local bending and is therefore predominant for small ξP. The second mechanism is spiral break-up by widening and is depicted in Fig. 3c. The bending potential widens the spiral until the leading tip looses contact to the filament end. This break-up mechanism is predominant when ξP is too large for spontaneous spiral break-up. Because high stiffness is also unfavourable for spiral formation, spiral break-up by widening was almost exclusively observed in simulations that started with a spiral configuration.
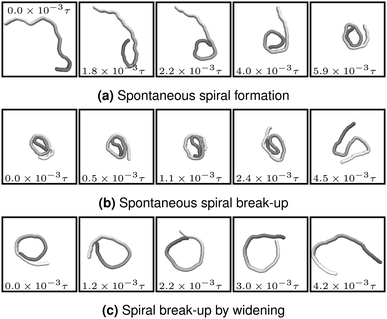 |
| | Fig. 3 Spiral formation and break-up mechanisms. Numbers in each panel provide the elapsed time. Leading tip is black. N = 100 in each case. (a and b) ξP/L = 0.4, Pe = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 000, 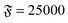 . (c) ξP/L = 1.0, Pe = 900, . (c) ξP/L = 1.0, Pe = 900, 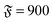 . . | |
To understand spiral formation more quantitatively, we introduce the spiral number
| | 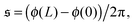 | (12) |
where
ϕ(
s) is the bond orientation at position
s along the contour of the filament, as measure for the instantaneous chain configuration. The definition is illustrated for three sample structures in
Fig. 4a. It effectively measures how often the filament wraps around itself. The time evolution of
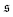
is depicted in
Fig. 4b for the same Pe and
ξP/
L as in
Fig. 2. At Pe = 200,
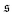
is always close to zero. At Pe = 1000,
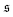
behaves similarly, except that peaks with larger values for
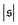
occur occasionally,
i.e., when spirals with a short lifetime form. At Pe = 5000, extended plateaus develop at large
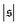
. The spirals are wound up stronger and have a much longer lifetime.
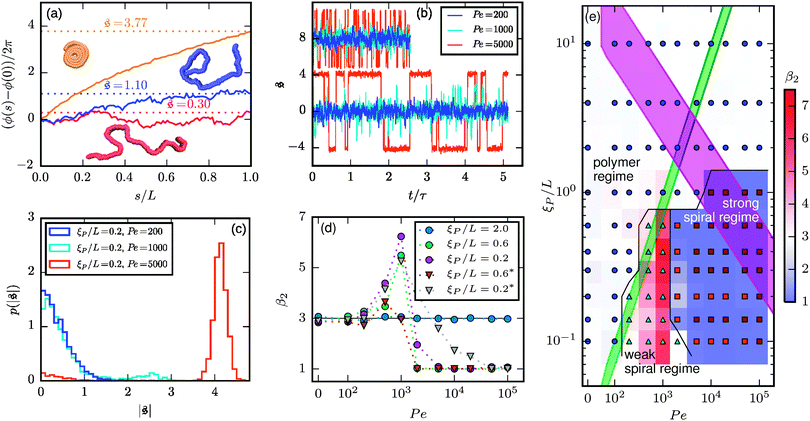 |
| | Fig. 4 (a) Definition of the spiral number 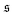 . The measure can effectively distinguish between elongated (red), weakly wound-up (blue), and strongly wound-up (orange) conformations. (b) Evolution of the spiral number for the examples given in Fig. 2 with ξP/L = 0.2 (N = 100). Lines centered around . The measure can effectively distinguish between elongated (red), weakly wound-up (blue), and strongly wound-up (orange) conformations. (b) Evolution of the spiral number for the examples given in Fig. 2 with ξP/L = 0.2 (N = 100). Lines centered around 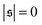 display results for σ = L/N; lines centered around display results for σ = L/N; lines centered around 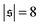 (shifted upwards for clarity) show results for σ = 2L/N. (c) Probability distributions of the absolute value of the spiral number (shifted upwards for clarity) show results for σ = 2L/N. (c) Probability distributions of the absolute value of the spiral number 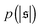 for the same examples with σ = L/N. (d) Kurtosis β2 for selected filament rigidities. Circles: σ = L/N, triangles: σ = 2L/N. (e) Phase diagram. Background colour: kurtosis. Blue circles: polymer regime. Cyan triangles: weak spiral regime. Light and dark red squares: strong spiral regime. For the dark red squares, spirals did not break up during the simulations once formed. Black lines are a guide to the eye. Green area: threshold for spiral stability against break-up by widening. Spirals above this threshold will unfold by widening, spirals below will not. Purple: parameter space that can be obtained by actin filaments on a myosin carpet at T = 300 K using parameters for fp and κ from ref. 12. for the same examples with σ = L/N. (d) Kurtosis β2 for selected filament rigidities. Circles: σ = L/N, triangles: σ = 2L/N. (e) Phase diagram. Background colour: kurtosis. Blue circles: polymer regime. Cyan triangles: weak spiral regime. Light and dark red squares: strong spiral regime. For the dark red squares, spirals did not break up during the simulations once formed. Black lines are a guide to the eye. Green area: threshold for spiral stability against break-up by widening. Spirals above this threshold will unfold by widening, spirals below will not. Purple: parameter space that can be obtained by actin filaments on a myosin carpet at T = 300 K using parameters for fp and κ from ref. 12. | |
Probability distributions 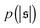 are depicted in Fig. 4c. For the simulation without spirals (Pe = 200), the histogram resembles the right half of a Gaussian distribution. For the simulation in the weak spiral regime,
are depicted in Fig. 4c. For the simulation without spirals (Pe = 200), the histogram resembles the right half of a Gaussian distribution. For the simulation in the weak spiral regime, 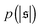 is similar for low
is similar for low 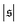 , but also has a small peak at
, but also has a small peak at 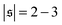 . For strong spiral formation at Pe = 5000,
. For strong spiral formation at Pe = 5000, 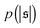 has only a small peak at low
has only a small peak at low 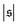 , which corresponds to the elongated state, and a large peak at large
, which corresponds to the elongated state, and a large peak at large 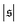 , the predominating spiral state. It turns out that the different regimes can be well distinguished by the kurtosis
, the predominating spiral state. It turns out that the different regimes can be well distinguished by the kurtosis
| | 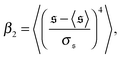 | (13) |
where 〈…〉 denotes the ensemble average and
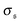
is the standard deviation of
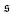
. Results for the kurtosis are shown in
Fig. 4d for selected
ξP/
L.
β2 ≈ 3 in the polymer regime, as expected for Gaussian distributions. In the weak spiral regime, the small peak at larger values increases the numerator in
eqn (13) and has only a weak impact on
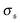
, leading to an increase of
β2. When the spiral state is dominating,
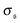
grows drastically, resulting in a much smaller kurtosis
β2. Note that to reduce statistical uncertainties we symmetrized the
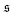
-distribution in the computation of
β2 by counting each measured
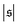
as
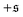
and
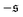
and only used data from the spiral state for simulations that do not show spiral break-up.
With the kurtosis as measure to characterize spiral formation, a phase diagram can be constructed as depicted in Fig. 4e. Low filament rigidity ξP and high propulsion Pe is beneficial for spiral formation. In particular, for a fixed propulsion strength per unit length, any chain will form spirals if it is sufficiently long, because increasing the chain length without modifying any other parameter corresponds to moving to the lower right in the phase diagram.
The dimensionless numbers ξP/L and Pe completely characterize the system if the filament diameter—or the filament aspect ratio—is of minor importance. This is the true in the entire polymer regime, where volume-exclusions interactions hardly come into play because of the elongated chain structure. For the spiral regimes, the aspect ratio has an impact on the structure of the spiral and does in this way influence the results. Which features of the spiral regime can be approximated well by the dimensionless numbers can be understood from the spiral formation and break-up mechanisms. The aspect ratio is hardly relevant for spiral formation and spiral break-up by widening, where the decisive moments are when the filament tip collides with subsequent parts of the chain, or when it looses contact to the chain end, respectively. That break-up by widening is characterized well by the dimensionless numbers is also confirmed by a series of simulations that we start from a spiral configuration in which we vary N, fp, κ, and kBT. It turns out that spirals will break up by widening if
| | 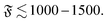 | (14) |
In contrast, spontaneous spiral break-up by a change of orientation of the leading tip is dependent on a strong local curvature close to the tip and the structure of the spiral, which in turn is dependent on the filament diameter. The dimensionless description does therefore not provide a full characterization of the strong spiral regime, where spontaneous spiral break-up is the only mechanism to escape the spiral state. This is also confirmed by results for spirals that never broke up (cf. dark red squares in Fig. 4e); results for ξP/L = 0.2 and ξP/L = 0.14 show non-monotonic behaviour in the direction of ξP/L. This is a result of a combination of that the dimensionless description is only partially valid in this regime and that we chose N = 200 for ξP/L < 0.2 but N = 100 for 0.2 ≥ ξP/L ≥ 2.0 in our simulations, i.e., the aspect ratio L/σ is halved in our simulations for filaments with ξP/L < 0.2.
Finally, the bead discretization with the chosen parameters favours a staggered arrangement of beads of contacting parts of the filament,33,34 which implies an effective sliding friction between these parts. To study the importance of this effect, we increase the diameter of the beads at fixed bond length so that neighboring beads are heavily overlapping, which leads to a strongly smoothened interaction potential. Results for an increased diameter σ = 2L/N are shown in Fig. 4b and d. We find that the spiral formation frequency is hardly affected by smoothening the filament surface. In contrast, spontaneous spiral break-up is largely alleviated for the smoother filament, leading to decreased spiral life-time, as can be seen from the evolution of 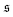 for Pe = 5000 in Fig. 4b. Smoother filaments thus show a qualitatively similar phase behaviour with slightly moved phase boundaries.
for Pe = 5000 in Fig. 4b. Smoother filaments thus show a qualitatively similar phase behaviour with slightly moved phase boundaries.
3.2 Structural properties
The structural properties of the filament conformations can be best understood from the end-to-end vector re, as depicted in Fig. 5. As long as no spirals form, simulation results are in good agreement with the Kratky–Porod model (valid for worm-like, non-active polymers without volume-exclusion interactions) that predicts30,31| | 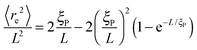 | (15) |
in two dimensions. At low ξP/L, volume-exclusion interactions lead to slight deviations between the Kratky–Porod model and the simulation results. Strong deviations between the Kratky–Porod model and simulation results only occur in the strong spiral region in the phase diagram. The same trend was observed for the tangent–tangent correlation function, the radius of gyration, and the static structure factor, but is not reported here to avoid unnecessary repetition.
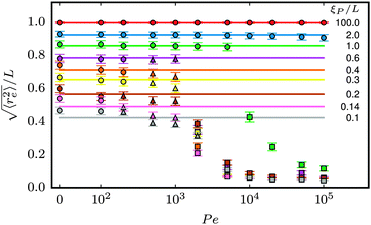 |
| | Fig. 5 Symbols: mean end-to-end distance 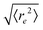 over Pe for different values of ξP/L. Solid lines: over Pe for different values of ξP/L. Solid lines: 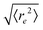 as predicted from the Kratky–Porod model. The symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime, squares: strong spiral regime. N varies from 25 to 200 from large to small ξP/L. as predicted from the Kratky–Porod model. The symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime, squares: strong spiral regime. N varies from 25 to 200 from large to small ξP/L. | |
3.3 Dynamic properties
The characteristic filament motion can be understood from the mean square displacement (MSD) of a bead j + i relative to bead j, as shown in Fig. 6. For comparison, the MSD of the reference bead j of a passive filament is also shown. Note that the displacement of this bead is subdiffusive at the short lag times shown here.35 Displacement functions of the propelled beads are always larger than in the passive case. The curves show three distinct regimes. At small lag times, the MSDs of active filaments display plateaus due to the average distance of the two beads j + i and j along the filament. At large lag times, the increased motion caused by activity effects the MSDs of the propelled beads to grow more rapidly than that of the passive bead. The relevant part of the MSD that shows that the characteristic filament motion is movement along its contour is at intermediate lag times, where the MSDs of the propelled beads pass through minima that touch the reference MSD for thermal motion. At that lag time, the bead j + i has moved approximately to the position of bead j at zero lag time. The beads have moved along the chain contour, similar to the movement of a train on a railway. The deviation from the exact starting position of bead j exactly matches the thermal motion, which results in the MSDs of the propelled beads touching the MSD of the passive filament. Thus, the characteristic movement of the filament is motion along its contour superimposed with thermal noise, as depicted in Fig. 7a. Note that ξP/L = 0.3 was selected in Fig. 6 because this corresponds to a rather flexible filament, where stronger deviations from the characteristic railway motion might be expected. This type of motion was observed in all simulations in the polymer regime and weak spiral regime. In the strong spiral regime, the MSDs of the propelled beads even fall below the reference line for purely thermal motion.
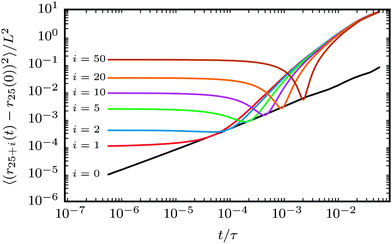 |
| | Fig. 6 Mean square displacement of bead 25 + i with respect to bead j = 25 (N = 100). ξP/L = 0.3 for all lines. Black line: Pe = 0, coloured lines: Pe = 1000 (weak spiral regime). Black line describes purely diffusive motion of the leading bead j. | |
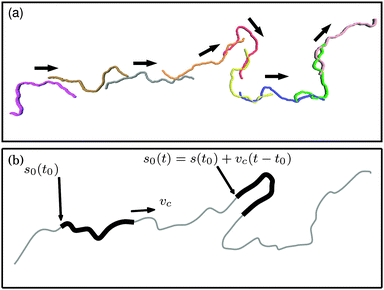 |
| | Fig. 7 (a) Series of snapshots of a filament with ξP/L = 0.3 (with N = 100) and Pe = 1000. The chain moves along its contour superimposed with thermally activated motion. Colouring is to improve the distinctness of the chains. (b) Idealized railway motion in the absence of diffusion. The filament (thick black line) moves with velocity vc along the contour of an infinite chain with same ξP (gray line). s0(t) runs along the contour of the infinite chain and marks the end point of the filament. | |
The rotational diffusion can be accessed from the orientation of the end-to-end vector θ. Its mean square rotation (MSR) is given in Fig. 8a. Note that complete rotations around the axis are accounted for in our computations. θ(t) can therefore be much larger than 2π. In both the spiral and the elongated state, there is a regime at short lag times in which the MSR is dominated by the internal filament flexibility. For the spiral state, this regime is followed by a ballistic regime with MSR ∝ t2. For simulations in which the spirals break up spontaneously, a subsequent regime at high times with MSR ∝ t is expected but could not be detected in our simulations because of finite simulation time and strong noise at large lag times in the MSR. For the elongated state, the regime dominated by internal flexibility is followed by a diffusive regime with MSR ∝ t.
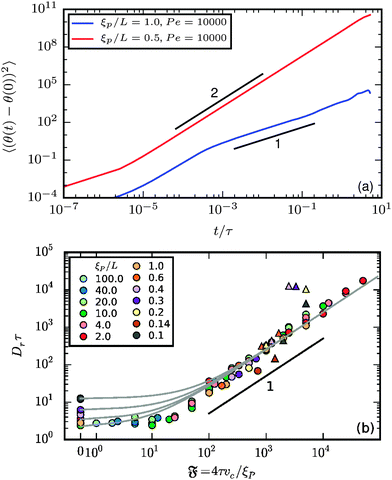 |
| | Fig. 8 (a) Mean square rotation of the end-to-end vector; the red line is from the strong spiral regime, the blue from the polymer regime (N = 100). (b) Rotational diffusion coefficient Dr as a function of the flexure number 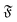 . Symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime. Gray lines are predictions with eqn (24) for different Dr,p; for the lowermost line Dr,p = 9/4τ−1. N varies from 25 to 200 from large to small ξP/L. . Symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime. Gray lines are predictions with eqn (24) for different Dr,p; for the lowermost line Dr,p = 9/4τ−1. N varies from 25 to 200 from large to small ξP/L. | |
The rotational diffusion coefficient Dr can be extracted by fitting MSR = 2Drt to the regime of the MSR with gradient unity on a double-log scale. Measured Dr are given in Fig. 8b as a function of the flexure number 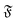 . The diffusion coefficients collapse to a single curve, which has a plateau at low
. The diffusion coefficients collapse to a single curve, which has a plateau at low 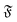 and then grows linearly. Strong deviations from this trend are only observed at high
and then grows linearly. Strong deviations from this trend are only observed at high 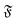 when the filament is in the weak spiral regime, and at
when the filament is in the weak spiral regime, and at 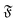 = Pe = 0 for flexible filaments, where strong deviations from a rod-like shape increase Dr.
= Pe = 0 for flexible filaments, where strong deviations from a rod-like shape increase Dr.
The rotational diffusion coefficient Dr can be predicted from the characteristic railway motion in Fig. 7 and the relation of the rotational diffusion coefficient to the autocorrelation function of the end-to-end tangent vector te
| | | 〈te(t)·te(0)〉 = e−Drt, | (16) |
which is valid for lag times
t that are sufficiently large such that variation of
te is not dominated by non-diffusive behaviour at early lag times caused by the filament flexibility (
cf.Fig. 8a). With
| | 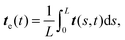 | (17) |
where
t(
s,
t) is the tangent vector at position
s of the filament at time
t, the left hand side of
eqn (16) becomes
| | 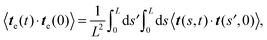 | (18) |
where the order of summations has been changed to arrive at the right-hand side of
eqn (18). As a representation of the characteristic railway motion (
cf.Fig. 7b), we write
| | | t(s,t) = t(s + vct,0). | (19) |
Note that this equation disregards the passive equilibrium rotation
Dr,p. With
eqn (19) and the expression for the tangent–tangent correlation function of worm-like polymers,
30,31 the integrand in
eqn (18) becomes
| | 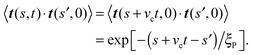 | (20) |
Integrating
eqn (18) provides
| | | 〈te(t)·te(0)〉 = −ξP2/L2(e−vct/ξP(2 − eL/ξP − e−L/ξP)). | (21) |
A second order Taylor expansion in (small)
L/
ξP then gives
| | | 〈te(t)·te(0)〉 = exp[−vct/ξP], | (22) |
so that a comparison with
eqn (16) finally yields the activity-induced rotational diffusion
Note that
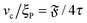
. Assuming that uncorrelated activity-induced and thermal rotation
Dr,a and
Dr,p contribute to the overall rotation, we write
where
Dr,p depends on
ξP/
L and has the lower bound
Dr,p = (9/4)
τ−1 for rod-like filaments.
36 As can be seen from
Fig. 8b,
eqn (24) matches the simulated rotational diffusion coefficient accurately.
The characteristics of the center-of-mass MSD are shown in Fig. 9. For the polymer regime, the typical S-shape of subsequent short-time diffusive, intermediate-time ballistic, and long-time effective diffusive behaviour develops;37 stronger propulsion increases the MSD. An important difference compared to rigid bodies is that the transition time τr = 1/Dr to long-time diffusive behaviour is dependent on the propulsion strength.
 |
| | Fig. 9 Mean square displacement of the center of mass. Dashed coloured lines: simulation results. Gray solid lines: predictions using eqn (25). (a) Results for ξP = 4.0 (polymer regime, N = 50) and different values of Pe increasing from 0 to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. v0 is predicted from eqn (27), Dr from eqn (24) with Dr,p = 9/4τ−1. (b) Results for ξP/L = 0.3 (spirals at large Pe, N = 100). v0 from eqn (27), Dr is determined from a fit to the measured MSD, because eqn (24) is only valid in the polymer regime. Spiral formation leads to a decreased MSD. 000. v0 is predicted from eqn (27), Dr from eqn (24) with Dr,p = 9/4τ−1. (b) Results for ξP/L = 0.3 (spirals at large Pe, N = 100). v0 from eqn (27), Dr is determined from a fit to the measured MSD, because eqn (24) is only valid in the polymer regime. Spiral formation leads to a decreased MSD. | |
When spiral formation becomes important, the general trend of the MSD changes, as shown in Fig. 9b for a flexible filament. In the polymer regime or weak spiral regime, increasing Pe leads to a larger displacement. In the strong spiral regime, however, the MSD decreases. For very stable spirals, the MSD is only weakly affected by the propulsion and almost matches the case of purely diffusive motion.
The MSD for active point particles, spheres, or stiff rods is given by1
| | | 〈(rc(t) − rc(0))2 〉 = 4Dtt + (2v02/Dr2)[Drt + exp(−Drt) − 1], | (25) |
where
Dt is the translational diffusion coefficient and
v0 is a ballistic velocity. It turns out that
eqn (25) can be used to describe the MSD for active filaments, when the three coefficients
Dt,
v0, and
Dr are chosen properly. The translational diffusion coefficient is
Dt =
L2/4
τ =
kBT/
γlL. We predict the rotational diffusion coefficient
Dr with
eqn (24). Finally the effective velocity can be expressed
via| | 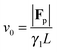 | (26) |
as a balance of the net external force |
Fp| with the total friction force
γlLv0. |
Fp| can conveniently be expressed as the propulsive force per bond
fp times the end-to-end vector, thus leading to
| | 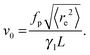 | (27) |
As shown in
Fig. 9, using these correlations for the coefficients provides an accurate prediction of the MSD.
The last item we address is the effect of propulsion on conformational sampling. Fig. 10a shows results for the dynamic structure factor
| | 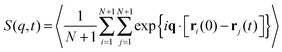 | (28) |
averaged over different directions of
q. In the phase without spirals,
S(
q,
t)/
S(
q,0) decays more rapidly with increasing Pe, indicating a faster change of conformations with increasing propulsion. When spirals form,
S(
q,
t)/
S(
q,0) is independent of Pe and larger than
S(
q,
t)/
S(
q,0) at Pe = 0, indicating a slow change of conformations, which agrees with the observation of hardly any internal motion of the chain in this regime in our simulation output. Note that for the strong spiral regime, the data is from simulations where spirals formed spontaneously and did not break up. The depicted data is a result of averaging over the spiral states only.
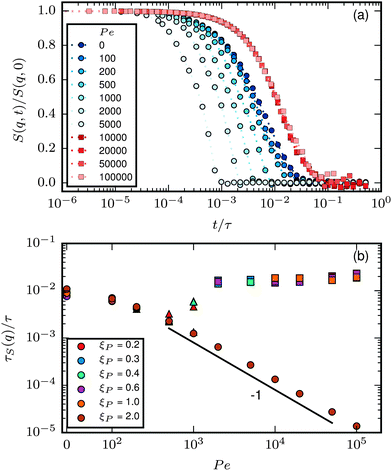 |
| | Fig. 10 (a) S(q,t)/S(q,0) for ξP/L = 1.0, N = 100, q ≈ 5π/L and different Pe. (b) τS(q) for q ≈ 5π/L. Circles correspond to the polymer regime, triangles to the weak spiral regime, and squares to the strong spiral regime in both plots. | |
To better quantify the behaviour of S(q,t), we compute the characteristic decay time of the dynamic structure factor
| | 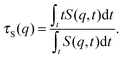 | (29) |
Results for
τS(
q) at
q ≈ 5π/
L, a
q-vector large enough to capture the behaviour of mainly the internal degrees of freedom, are given in
Fig. 10b.
τS(
q) decays slowly at low Pe. At high Pe,
τS decays inversely proportional to Pe when no spirals form. This is consistent with the picture that instantaneous conformations are essentially identical to those of passive filaments, but they are traversed with velocity
vc, corresponding to
τ ∝ Pe
−1. In the strong spiral regime,
τS is large and independent of Pe, which is a sign for that conformational changes are irrelevant and that
τS is determined by the quasi-diffusive center of mass movement. Note that the measured
τS at different
ξP/
L collapse to a single line for both the polymer and the strong spiral regime.
4 Discussion
The spontaneous formation of spirals is the feature dominating the overall behaviour of self-propelled filaments, both for dynamic and structural properties. Formation of spirals was previously observed for long, slender bacteria surrounded by short bacteria.7 It was concluded that interaction with other active particles is a prerequisite for spiral formation. In contrast, the study at hand shows that spirals can form even for isolated filaments, as long as (i) the filament is sufficiently flexible, (ii) the propulsion is sufficiently strong, and (iii) excluded volume interactions force the tip of the filament to wind up.
The first two conditions will be met automatically for any real system by choosing L sufficiently large and leaving all other parameters constant (leading to increased Pe and decreased ξP/L, i.e., favouring spirals). Meeting the third condition can in general not be achieved so easily. A free-swimming filament in three dimensions or a filament in two dimensions with low resistance of crossing its own body will not form spirals. This is also one reason why spiral formation has not yet been observed in more experimental studies. Agents that are similar to our model are actin filaments or microtubules on a motility assay. The former have a high crossing probability,38 formation of spirals is therefore not expected. The area enclosing the actin-filament parameter space in Fig. 4 must thus be understood as that the regime where the flexibilities and propulsion strengths permit spiral formation can in principle be reached in real systems, and not so much as that sufficiently long actin filaments will form spirals. Microtubules on dynein carpets, which have a much lower crossing probability,6,34 will possibly form spirals if they are grown to sufficient size.
Overall, except for slender bacteria,7 we are unaware of a microscopic example in which spiral formation was observed. Yet, the formation of spirals is a feature that deserves more attention in the future. First, formation of spirals is an extremely simple non-equilibrium phenomenon that, in contrast to many other phenomena of active matter, arises for a single self-propelled particle and cannot easily be mapped qualitatively to passive systems in which activity is replaced by attractive forces. It can thus be used as a model phenomenon for the study of non-equilibrium thermodynamics. Second, our model is very simple; a realization in experiment seems possible within the near future. Finally, the formation of spirals leads to a sudden, strong change in structural and dynamic properties. The effect can thus potentially be used as a switch on the microscopic scale.
5 Summary and outlook
We report an extensive study for the behaviour of dilute, self-propelled, worm-like filaments in two dimensions. The spontaneous formation and break-up of spirals is the feature that dominates the filament behaviour. Spiral formation is favoured by strong propulsion and low bending rigidity. Propulsion has a noticeable impact on structural properties only when spirals are dominating. The Kratky–Porod model30 is therefore valid for filaments that are weakly propelled or have high bending rigidity. When spiral formation becomes significant, structural properties change drastically.
The characteristic filament motion is what we call the railway behaviour. The chain moves along its own contour superimposed with noise. With the understanding of the structural properties and the characteristic motion, rotational diffusion and the center-of-mass mean square displacement can be predicted to high accuracy when no spirals form. In contrast to rigid bodies, propulsion has an impact on the rotational diffusion coefficient. Finally, propulsion enhances conformational sampling in the regime without spirals.
An obvious next step is understanding the collective motion of such active filaments. We expect that our single filament results will help to understand the collective behaviour, which is nonetheless strongly influenced by the additional interactions. In particular collision with other constituents might enhance spiral formation and lead to swirl-like patterns.
Acknowledgements
We thank Thorsten Auth for helpful discussion. Financial support by the Deutsche Forschungsgemeinschaft via SPP 1726 “Microswimmers” is gratefully acknowledged.
References
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- M. E. Cates and F. C. MacKintosh, Soft Matter, 2011, 7, 3050–3051 RSC.
- O. C. Rodriguez, A. W. Schaefer, C. A. Mandato, P. Forscher, W. M. Bement and C. M. Waterman-Storer, Nat. Cell Biol., 2003, 5, 599–609 CrossRef CAS PubMed.
- A. M. Rashedul Kabir, S. Wada, D. Inoue, Y. Tamura, T. Kajihara, H. Mayama, K. Sada, A. Kakugo and J. P. Gong, Soft Matter, 2012, 8, 10863–10867 RSC.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- S.-N. Lin, W.-C. Lo and C.-J. Lo, Soft Matter, 2014, 10, 760–766 RSC.
- Y. Sasaki, Y. Takikawa, V. S. R. Jampani, H. Hoshikawa, T. Seto, C. Bahr, S. Herminghaus, Y. Hidaka and H. Orihara, Soft Matter, 2014, 10, 8813–8820 RSC.
- P. J. Vach and D. Faivre, Sci. Rep., 2015, 5, 9364 CrossRef CAS PubMed.
- T. Sanchez, D. Welch, D. Nicastro and Z. Dogic, Science, 2011, 333, 456–459 CrossRef CAS PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- K. Sekimoto, N. Mori, K. Tawada and Y. Toyoshima, Phys. Rev. Lett., 1995, 75, 172–175 CrossRef CAS PubMed.
- L. Bourdieu, T. Duke, M. Elowitz, D. Winkelmann, S. Leibler and A. Libchaber, Phys. Rev. Lett., 1995, 75, 176–179 CrossRef CAS PubMed.
- A. Laskar, R. Singh, S. Ghose, G. Jayaraman, P. B. S. Kumar and R. Adhikari, Sci. Rep., 2013, 3, 1964 Search PubMed.
- R. Chelakkot, A. Gopinath, L. Mahadevan and M. F. Hagan, J. R. Soc., Interface, 2014, 11, 20130884 CrossRef PubMed.
-
Z. Farkas, I. Derényi and T. Vicsek, Structure and Dynamics of Confined Polymers, Springer Netherlands, 2002, vol. 87, pp. 327–332 Search PubMed.
- G. Jayaraman, S. Ramachandran, S. Ghose, A. Laskar, M. S. Bhamla, P. B. S. Kumar and R. Adhikari, Phys. Rev. Lett., 2012, 109, 158302 CrossRef PubMed.
- H. Jiang and Z. Hou, Soft Matter, 2014, 10, 9248–9253 RSC.
- H. Jiang and Z. Hou, Soft Matter, 2014, 10, 1012–1017 RSC.
- A. Ghosh and N. S. Gov, Biophys. J., 2014, 107, 1065–1073 CrossRef CAS PubMed.
- A. Kaiser, S. Babel, B. ten Hagen, C. von Ferber and H. Löwen, J. Chem. Phys., 2015, 142, 124905 CrossRef PubMed.
- B. Dünweg and W. Paul, Int. J. Mod. Phys. C, 1991, 02, 817–827 CrossRef.
- M. T. Downton and H. Stark, J. Phys.: Condens. Matter, 2009, 21, 204101 CrossRef PubMed.
- I. O. Götze and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041921 CrossRef.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef.
- J. Elgeti and G. Gompper, Europhys. Lett., 2009, 85, 38002 CrossRef.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- J. Gray and H. W. Lissmann, J. Exp. Biol., 1964, 41, 135–154 CAS.
- J. Korta, D. A. Clark, C. V. Gabel, L. Mahadevan and A. D. T. Samuel, J. Exp. Biol., 2007, 210, 2383–2389 CrossRef PubMed.
- O. Kratky and G. Porod, J. Colloid Sci., 1949, 4, 35–70 CrossRef CAS PubMed.
- N. Saitô, K. Takahashi and Y. Yunoki, J. Phys. Soc. Jpn., 1967, 22, 219–226 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- Y. Yang, V. Marceau and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031904 CrossRef.
- M. Abkenar, K. Marx, T. Auth and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062314 CrossRef.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS.
-
I. Teraoka, Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., New York, 2002 Search PubMed.
- X. Zheng, B. ten Hagen, A. Kaiser, M. Wu, H. Cui, Z. Silber-Li and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 032304 CrossRef.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Videos of swimming filaments from the three characteristic regimes, as well as details of the simulations. See DOI: 10.1039/c5sm01683e |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
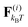 is the thermal noise force, and F(i)p is the active force that drives the system out of equilibrium. The configurational potential energy
is the thermal noise force, and F(i)p is the active force that drives the system out of equilibrium. The configurational potential energy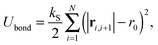
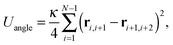
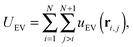
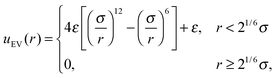
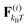 is modelled as white noise with zero mean and variance 2kBTγ/Δt as described in ref. 22. Note that hydrodynamic interactions (HI) are not included in our model. The model is thus in particular valid for (i) neutral swimmers, for which HI are known to be of minor importance,23–25 (ii) swimmers near a wall, where HI is of less importance,26,27 and (iii) microorganisms that glide on a surface, such as nematodes like C. elegans.28,29
is modelled as white noise with zero mean and variance 2kBTγ/Δt as described in ref. 22. Note that hydrodynamic interactions (HI) are not included in our model. The model is thus in particular valid for (i) neutral swimmers, for which HI are known to be of minor importance,23–25 (ii) swimmers near a wall, where HI is of less importance,26,27 and (iii) microorganisms that glide on a surface, such as nematodes like C. elegans.28,29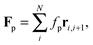

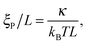
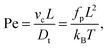
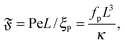

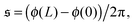
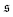 is depicted in Fig. 4b for the same Pe and ξP/L as in Fig. 2. At Pe = 200,
is depicted in Fig. 4b for the same Pe and ξP/L as in Fig. 2. At Pe = 200, 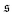 is always close to zero. At Pe = 1000,
is always close to zero. At Pe = 1000, 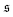 behaves similarly, except that peaks with larger values for
behaves similarly, except that peaks with larger values for 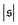 occur occasionally, i.e., when spirals with a short lifetime form. At Pe = 5000, extended plateaus develop at large
occur occasionally, i.e., when spirals with a short lifetime form. At Pe = 5000, extended plateaus develop at large 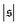 . The spirals are wound up stronger and have a much longer lifetime.
. The spirals are wound up stronger and have a much longer lifetime.

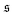 . The measure can effectively distinguish between elongated (red), weakly wound-up (blue), and strongly wound-up (orange) conformations. (b) Evolution of the spiral number for the examples given in Fig. 2 with ξP/L = 0.2 (N = 100). Lines centered around
. The measure can effectively distinguish between elongated (red), weakly wound-up (blue), and strongly wound-up (orange) conformations. (b) Evolution of the spiral number for the examples given in Fig. 2 with ξP/L = 0.2 (N = 100). Lines centered around 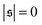 display results for σ = L/N; lines centered around
display results for σ = L/N; lines centered around 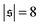 (shifted upwards for clarity) show results for σ = 2L/N. (c) Probability distributions of the absolute value of the spiral number
(shifted upwards for clarity) show results for σ = 2L/N. (c) Probability distributions of the absolute value of the spiral number 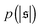 for the same examples with σ = L/N. (d) Kurtosis β2 for selected filament rigidities. Circles: σ = L/N, triangles: σ = 2L/N. (e) Phase diagram. Background colour: kurtosis. Blue circles: polymer regime. Cyan triangles: weak spiral regime. Light and dark red squares: strong spiral regime. For the dark red squares, spirals did not break up during the simulations once formed. Black lines are a guide to the eye. Green area: threshold for spiral stability against break-up by widening. Spirals above this threshold will unfold by widening, spirals below will not. Purple: parameter space that can be obtained by actin filaments on a myosin carpet at T = 300 K using parameters for fp and κ from ref. 12.
for the same examples with σ = L/N. (d) Kurtosis β2 for selected filament rigidities. Circles: σ = L/N, triangles: σ = 2L/N. (e) Phase diagram. Background colour: kurtosis. Blue circles: polymer regime. Cyan triangles: weak spiral regime. Light and dark red squares: strong spiral regime. For the dark red squares, spirals did not break up during the simulations once formed. Black lines are a guide to the eye. Green area: threshold for spiral stability against break-up by widening. Spirals above this threshold will unfold by widening, spirals below will not. Purple: parameter space that can be obtained by actin filaments on a myosin carpet at T = 300 K using parameters for fp and κ from ref. 12.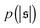 are depicted in Fig. 4c. For the simulation without spirals (Pe = 200), the histogram resembles the right half of a Gaussian distribution. For the simulation in the weak spiral regime,
are depicted in Fig. 4c. For the simulation without spirals (Pe = 200), the histogram resembles the right half of a Gaussian distribution. For the simulation in the weak spiral regime, 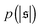 is similar for low
is similar for low 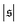 , but also has a small peak at
, but also has a small peak at 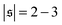 . For strong spiral formation at Pe = 5000,
. For strong spiral formation at Pe = 5000, 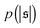 has only a small peak at low
has only a small peak at low 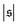 , which corresponds to the elongated state, and a large peak at large
, which corresponds to the elongated state, and a large peak at large 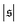 , the predominating spiral state. It turns out that the different regimes can be well distinguished by the kurtosis
, the predominating spiral state. It turns out that the different regimes can be well distinguished by the kurtosis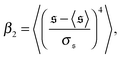
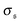 is the standard deviation of
is the standard deviation of 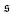 . Results for the kurtosis are shown in Fig. 4d for selected ξP/L. β2 ≈ 3 in the polymer regime, as expected for Gaussian distributions. In the weak spiral regime, the small peak at larger values increases the numerator in eqn (13) and has only a weak impact on
. Results for the kurtosis are shown in Fig. 4d for selected ξP/L. β2 ≈ 3 in the polymer regime, as expected for Gaussian distributions. In the weak spiral regime, the small peak at larger values increases the numerator in eqn (13) and has only a weak impact on 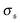 , leading to an increase of β2. When the spiral state is dominating,
, leading to an increase of β2. When the spiral state is dominating, 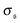 grows drastically, resulting in a much smaller kurtosis β2. Note that to reduce statistical uncertainties we symmetrized the
grows drastically, resulting in a much smaller kurtosis β2. Note that to reduce statistical uncertainties we symmetrized the 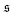 -distribution in the computation of β2 by counting each measured
-distribution in the computation of β2 by counting each measured 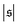 as
as 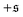 and
and 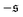 and only used data from the spiral state for simulations that do not show spiral break-up.
and only used data from the spiral state for simulations that do not show spiral break-up.
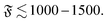
 for Pe = 5000 in Fig. 4b. Smoother filaments thus show a qualitatively similar phase behaviour with slightly moved phase boundaries.
for Pe = 5000 in Fig. 4b. Smoother filaments thus show a qualitatively similar phase behaviour with slightly moved phase boundaries.

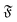 . Symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime. Gray lines are predictions with eqn (24) for different Dr,p; for the lowermost line Dr,p = 9/4τ−1. N varies from 25 to 200 from large to small ξP/L.
. Symbol shape indicates the region in the phase diagram: circle: polymer regime; triangle: weak spiral regime. Gray lines are predictions with eqn (24) for different Dr,p; for the lowermost line Dr,p = 9/4τ−1. N varies from 25 to 200 from large to small ξP/L.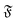 . The diffusion coefficients collapse to a single curve, which has a plateau at low
. The diffusion coefficients collapse to a single curve, which has a plateau at low 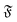 and then grows linearly. Strong deviations from this trend are only observed at high
and then grows linearly. Strong deviations from this trend are only observed at high 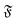 when the filament is in the weak spiral regime, and at
when the filament is in the weak spiral regime, and at 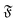 = Pe = 0 for flexible filaments, where strong deviations from a rod-like shape increase Dr.
= Pe = 0 for flexible filaments, where strong deviations from a rod-like shape increase Dr.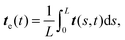
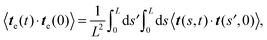
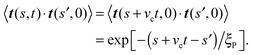
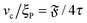 . Assuming that uncorrelated activity-induced and thermal rotation Dr,a and Dr,p contribute to the overall rotation, we write
. Assuming that uncorrelated activity-induced and thermal rotation Dr,a and Dr,p contribute to the overall rotation, we write
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. v0 is predicted from eqn (27), Dr from eqn (24) with Dr,p = 9/4τ−1. (b) Results for ξP/L = 0.3 (spirals at large Pe, N = 100). v0 from eqn (27), Dr is determined from a fit to the measured MSD, because eqn (24) is only valid in the polymer regime. Spiral formation leads to a decreased MSD.
000. v0 is predicted from eqn (27), Dr from eqn (24) with Dr,p = 9/4τ−1. (b) Results for ξP/L = 0.3 (spirals at large Pe, N = 100). v0 from eqn (27), Dr is determined from a fit to the measured MSD, because eqn (24) is only valid in the polymer regime. Spiral formation leads to a decreased MSD.