Cyclic polymers revealing topology effects upon self-assemblies, dynamics and responses

Abstract

A variety of single- and multicyclic polymers having programmed chemical structures with guaranteed purity have now become obtainable owing to a number of synthetic breakthroughs achieved in recent years. Accordingly, a broadening range of studies has been undertaken to gain updated insights on fundamental polymer properties of cyclic polymers in either solution or bulk, in either static or dynamic states, and in self-assemblies, leading to unusual properties and functions of polymer materials based on their cyclic topologies. In this article, we review recent studies aiming to achieve distinctive properties and functions by cyclic polymers unattainable by their linear or branched counterparts. We focus, in particular, on selected examples of unprecedented topology effects of cyclic polymers upon self-assemblies, dynamics and responses, to highlight current progress in Topological Polymer Chemistry.

---

Takuya Yamamoto

Takuya Yamamoto received his BS degree in 1999 and PhD degree in 2004 from the University of Utah. He joined the JST ERATO Aida Nanospace Project as a researcher in 2005. Since 2008, he has been an assistant professor of the Department of Organic and Polymeric Materials, Tokyo Institute of Technology. His current research interests include the synthesis and self-assembly of cyclic polymers for the development of functional materials.

Yasuyuki Tezuka

Yasuyuki Tezuka is a Professor of the Tokyo Institute of Technology. He is a graduate of The University of Tokyo, and received his doctorate degree from Ghent University (Belgium) in 1982. He then joined Nagaoka University of Technology (Japan) as an assistant professor. In 1994, he moved to the Tokyo Institute of Technology, and has been a professor since 2003 in the Department of Organic and Polymeric Materials. He received the Tokyo Tech Award of Best Teacher, 2004, and The Award of the Society of Polymer Science, Japan (2010). He has served as Editor in Chief of Reactive and Functional Polymers since 2012. His current research is focused on topological polymer chemistry, in particular on the design of topologically unique macromolecular architectures, and of novel polymer materials by their topology effects.

---

1. Cyclic polymers and topology effects thereof

There are abundant examples where the form of objects directs their functions and properties at all dimensions and scales. In polymer chemistry and polymer materials science, on the other hand, the choice of macromolecular structures has mostly been limited to linear or randomly branched forms. During the past decade, however, a variety of precisely controlled polymer topologies has been constructed along with the introduction of intriguing synthetic techniques.¹ In particular, an important class of polymers having cyclic and multicyclic topologies has now become obtainable with unprecedented structural precision, and their qualities are now satisfactorily guaranteed by the newly introduced spectroscopic and chromatographic techniques, including MALDI-TOF mass, and critical-condition HPLC.² The expansion of the choice of reliable polymer samples has now inspired modeling/simulation studies in order to reveal any topology effects, which have significantly benefited from the ongoing progress of computational techniques toward the consideration of more and more complex and larger systems in a rigorous manner.³ These developments have also allowed experimental verification studies over classical or newly proposed theoretical models on the fundamental static/dynamic properties uniquely achieved by cyclic and multicyclic polymers.^2,3 Moreover, conceptually novel ways to realize the unprecedented properties and functions simply based on the form, i.e. topology, of the polymer molecules, and their eventual applications in polymer materials design have now started to be studied.^2–4

Cyclic biopolymers, frequently encountered in DNAs, peptides and polysaccharides, have long attracted significant interest due to their sophisticated topology-based functions, and have been valuable resources for designing functions and properties in synthetic polymer materials.⁵ Synthetic single cyclic (ring) polymers, in particular, have been studied theoretically as well as experimentally to understand the fundamental properties of randomly coiled polymer molecules which uniquely rely on the chain topology of either the linear or cyclic form.⁶ It has been shown that the hydrodynamic volume, i.e., 3D size, of ring polymers is distinctively smaller than that of their linear counterparts. Moreover, the diffusion properties are notably affected by the shape or topology of the polymer molecules. Indeed, the diffusion process of linear/branched polymers conforms to a reptation mechanism with snake-like motion in which the chain ends are critical in the dynamics, but ring polymers, in the absence of chain ends, distinctly show a speculatively amoeba-like motion.^7,8

It is also notable that the elimination of end groups by ring polymers from their linear counterparts results in distinctive properties, as typically observed in the glass transition temperature (T_g). The T_g of ring polymers is noticeably higher than that of linear polymers of identical molar mass, i.e. chain length, while the distinction tends to diminish along with the increase of the polymer chain length. Hence, in a strict sense, this is regarded as a chain-length (or chain-end concentration) dependent property, in contrast to the intrinsic ones like the hydrodynamic volume, which are independent of the polymer chain length. Nevertheless, as the elimination of the chain ends of linear polymers inevitably transforms the topology into a ring form, either the intrinsic or chain-end concentration dependent properties could be referred to as topology effects.²

While principal and fundamental properties of simple ring polymers are comprehensively addressed by seminal works produced during the early periods in polymer science dating back to the middle of the preceding century,⁶ a variety of homopolymers and copolymers of not only simple ring but also complex cyclic forms have now been purposely produced to investigate the topology effects in a more comprehensive and rigorous manner. Recent works reporting the diverse topology effects of cyclic polymers are collected in Table 1, classified into several sub-areas to cover the current scope of research activities. It is notable, in particular, that an increasing number of works are focusing on the topology effects in a variety of self-assembly states, i.e., micelles/interfaces, complex/complexations, gels/gelation, etc. (Table 1, A). This trend is explained by the fact that any topology effects could be amplified in self-assembly states, and in comparison, the linear/cyclic distinction in single polymer molecules is not obviously significant.²

Table 1 Recent reports on topology effects of cyclic polymers

Topology effect	Polymer type^a	Preparation method^b	Ref.
a PEO: poly(ethylene oxide) or polyethylene glycol, PS: polystyrene, poly(NCA): poly(N-carboxyanhydride), PCL: poly(ε-caprolactone), PAA: poly(acrylic acid), PMMA: poly(methyl methacrylate), PLA: poly(lactic acid), poly(THF): poly(tetrahydrofuran), PE: polyethylene, and -der denotes -derivative. b MPC: metathesis polymer cyclization, ATRP: atom-transfer radical polymerization, REMP: ring-expansion metathesis polymerization, ESA–CF: electrostatic self-assembly and covalent fixation.
(A) Self-assemblies
1. Micelles and emulsions	PEO–polyacrylate, PS–PEO block	End-linking (MPC)	11, 12, 15 and 16
	Poly(NCA)	Ring-expansion (NHC)	42
	PCL–PS-der block with PEO graft	End-linking (ATRP-click)	43
	Polyacrylate–PAA block	End-linking (ATRP-click)	44
	PEO–PCL block	End-linking (click)	45
	Poly(glycidyl ethers), dicyclic, etc.	End-linking (click)	46
	PS–PAA, dicyclic block	End-linking (click)	47
	Simulation	n.a.	48
2. Stereocomplexes	PLA	Ring-expansion (NHC)	49
	PMMA	End-linking (click)	50
	PLA	MPC	18 and 19
3. Gels	Poly(cyclooctene)-der	Ring-expansion (REMP)	51
	PS, polysiloxane, PEO	End-linking (amidation)	52 and 53
	Poly(NCA) copolymer	Ring-expansion (NHC)	54
	Poly(alkylene phosphate)	Ring-expansion (NHC)	55
4. Bulk properties (melting, glass transition, phase spacing, etc.)	Polyester (lactones)	Ring-expansion (NHC)	56
	PS and deuterated PS	End-linking (MPC)	57
	Poly(NCA)	Ring-expansion (NHC)	54
	PS–PEO block copolymer	End-linking (click)	58
	PS, multicyclics	End-linking (click)	59
(B) Dynamics/conformations
1. Diffusion	Poly(THF), cyclic and dicyclic	End-linking (ESA–CF)	21, 23 and 24
	PS and deuterated PS	End-linking (living PS)	60 and 61
	Simulation	n.a.	62 and 63
2. Crystallization kinetics	Poly(THF)	End-linking (ESA–CF)	64
	PE	Ring-expansion (REMP)	65
	PCL	End-linking (click)	66
	Poly(NCA)-der	Ring-expansion (NHC)	67
3. Rheology/entanglement	PS, PEO, polyisoprene	End-linking (living precursors)	63
	Simulation	n.a.	68 and 69
4. Blends/composites	PS and POSS or C60	End-linking (click)	70
	PCL and CNT	End-linking (click)	71
5. Conformations	PS	End-linking (living PS)	72
	Amylose	Enzymatic	73
	Simulations	n.a.	62, 63 and 74–89
(C) Responses
1. Photo responses	PS-der	End-linking (living PS)	90
	PMMA-der	End-linking (ATRP-click)	91 and 92
	Polythiophene	End-linking (condensation)	93
2. Thermo/chemoresponses	Poly(aldehyde)	Ring-expansion (cationic)	94–96
3. Topological transformation	PEO	Reversible (metal coordination)	97
	PS	Reversible (H-bonding)	98
	PS	Reversible (metal coordination)	99
(D) Bioconjugates
1. Biotransportation	PAA-der-PEG graft	End-linking (ATRP-click)	100
	Oligopeptides	End-linking (S–S bonding)	101
2. Gene/DNA delivery	PMMA-der (cationic)	End-linking (ATRP-click)	102
	Polyethylene imine	End-linking (click)	103
(E) Nanoobjects
1. Nanostructures	Poly(norbornene)-der	Ring-expansion (REMP)	104
2. Nanostructures(metalated)	Poly(norbornene)-der	Ring-expansion (REMP)	105

---

Another area of persisting research interest includes the topology effects upon dynamics and conformational properties of ring polymers, in contrast to their linear counterparts, covering diffusion behavior, crystallization kinetics, entanglements, etc. (Table 1, B). Indeed, an increasing number of simulation/modelling studies have appeared in recent years, undoubtedly due to the enormous progress in computational and calculation technologies, and also inspired by new synthetic developments to afford appropriate polymer samples used for experimental verification studies. In turn, these new modelling/simulation works have been inducing further experimental studies toward the precision synthesis of new target polymers. Such extensive research efforts, in particular upon polymer dynamics, are again explained by the fact that the non-reptation mechanism unique for ring polymer dynamics is expected to create a distinction from their linear polymer counterparts.

It is remarkable, moreover, that new approaches have appeared to study the topology effects of cyclic polymers by making use of adaptive polymer materials responding to either photonic, thermal, electronic or chemical stimuli under non-equilibrium conditions (Table 1, C). Also in biomedical fields, the topology effects of cyclic polymers compared to their conventional linear counterparts was exploited to achieve controlled/improved bio-transportation as well as gene/DNA delivery (Table 1, D). Finally, cyclic polymers are now applied as structural scaffolds to construct nano-objects of unique non-linear forms, which will become a first step toward eventual nanotechnological applications (Table 1, E).

We have reported various topology effects of cyclic and multicyclic polymers, obtainable through precision synthesis protocols, including metathesis polymer cyclization (MPC)⁹ as well as electrostatic self-assembly and covalent fixation (ESA–CF)¹⁰ processes. In the following section, we show first the topology effects of cyclic polymers upon self-assemblies, by using cyclic amphiphilic block copolymers to form micelles, in particular.^11–13 The elimination of chain ends in cyclic surfactants, forming the densely packed hydrophobic segment core and prohibiting the dynamic bridging between micelles, was found to cause the significant stabilization of micelles. In addition, the topology effect of linear and cyclic surfactants upon the stabilization of a water/toluene emulsion was revealed.^14,15 The self-assembly of either linear or cyclic polymer surfactants at the toluene/water interface was considered to cause the amplified topology effect in their emulsion. Furthermore, linear and cyclic amphiphilic block copolymers having a liquid crystalline and hydrophobic segment were synthesized, and the topology effect was observed upon their self-assembly structure formation in comparison with their linear counterpart. The subsequent electric field application caused distinctive responses in their morphologies.¹⁶

In the next section, we discuss a set of linear and cyclic poly(THF)s consisting exclusively of monomer units, and of linear and cyclic stereoregular polylactide homo and block copolymers to examine the topology effect upon their crystallization kinetics and stereocomplex structures/properties.^17,18 Furthermore, a cyclic polylactide incorporating a photo-cleavable unit is introduced for the photo-induced cyclic-linear topological transformation, causing a topology effect upon the thermal properties.¹⁹

In the final section, we show the single-molecule spectroscopic study to reveal the topology effect upon the polymer diffusion, by using a pair of linear and monocyclic polymers as well as a set of 4-armed star and dicyclic (8-shaped) polymer samples prepared by the ESA–CF process, in which a fluorescent unit was commonly incorporated.²⁰ The newly developed spectroscopic technique was demonstrated to disclose the topology effect in the diffusion process of the different polymer topologies of either linear branched, single cyclic or dicyclic forms.^21–24

2. Topology effects upon self-assemblies

2.1 Micelles from cyclic amphiphilic block copolymers

Self-assembly is a versatile process to construct functional nanostructures with molecular-level precision, and micelles as well as vesicles made from surfactant molecules, including amphiphilic block copolymers, are typical examples with wide application possibilities.²⁵ Notably, in nature, a class of thermophilic archaea, single-cell microorganisms coping with hostile environments like the high-temperatures of hot springs and submarine volcanoes, have cyclic lipids as their cell membrane component.²⁶

Inspired by this unique topology effect of the self-assembly of cyclic lipids exploited by biosystems, we prepared a series of linear amphiphilic allyl-telechelic A–B–A type block copolymers having poly(n-butyl acrylate) (PBA) and poly(ethylene oxide) (PEO) segments (PBA–PEO–PBA) and their cyclized PBA–PEO block copolymer counterparts using the MPC protocol (Fig. 1(a) and (b), respectively).²⁷ The flower-like micelles were commonly formed by the self-assembly of linear or cyclic block copolymers with similar critical micelle concentrations (Fig. 1(c) and (d), respectively).

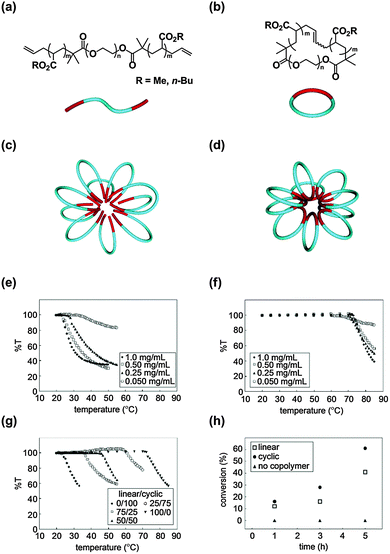Fig. 1 Chemical structures of (a) linear and (b) cyclic amphiphilic block copolymers. Schematic representation of a (c) linear polymer micelle and (d) cyclic polymer micelle. Temperature-dependent transparency (%T) of micellar solutions of (e) linear, (f) cyclic, and (g) a mixture of the linear and cyclic amphiphilic block copolymers. (h) Time-dependent conversion of the halogen exchange reaction. Reproduced from ref. 11, copyright 2010 American Chemical Society, and from ref. 12, copyright 2013 Nature Publishing Group.

A remarkable topology effect was seen on the stabilization of micelles by a cyclized block copolymer versus its linear counterpart, as a result of the amplification of the topology effect of self-assemblies.^11,12 Using cloud point (T_c) measurements, the linear polymer micelles were observed to turn turbid at 24–27 °C (Fig. 1(e)), while the cyclic counterparts were stable up to as high as 71–74 °C (Fig. 1(f)). Therefore, the linear to cyclic transformation of the topology of the polymer surfactant resulted in the drastic improvement in the thermal stability of the micelles, despite the chemical structures and molecular weights remaining unaltered. Furthermore, the T_c was systematically tuned using a series of micelles prepared by simply mixing the cyclic block copolymer and the linear precursor at various compositions (Fig. 1(g)).

In addition, a pair of linear and cyclic amphiphilic block copolymers having poly(methyl acrylate) (PMA) as the hydrophobic segment were prepared with PEO as the hydrophilic counterpart, and the salt stabilities of the resulting micelles were compared.¹² As an example, the micelle formed from the cyclic PMA–PEO surfactants was stable at concentrations up to as high as 270 mg mL⁻¹ NaCl, in contrast to the linear PEO–PMA–PEO micelles which precipitated at only 10 mg mL⁻¹ NaCl. Accordingly, the cyclic polymer micelles were proven to be stable not only against higher temperatures but also higher salt concentrations. Moreover, the T_c of the micelles was systematically controlled in the wide temperature and salt concentration ranges by simply adjusting the mixing ratio of the cyclic and linear amphiphiles.¹¹ By taking advantage of this topology effect, a unique micellar catalyst was developed for the halogen exchange reaction.¹² The catalytic reaction using the cyclic amphiphile was accelerated by 1.5 folds in comparison with the corresponding process with the linear counterpart catalyst (Fig. 1(h)).¹²

The higher stability of the micelles of the A–B type cyclic PBA–PEO versus the A–B–A type linear counterparts was further elucidated using X-ray structural analysis in solution.¹³ It was shown, in particular, that the density of the hydrophobic PBA core was significantly higher for the cyclic polymer micelles (d = 1.06–1.23 g cm⁻³), than for the linear counterparts (0.93–1.08 g cm⁻³). The density of the core of the cyclic polymer micelles was comparable to that of the bulk PBA (d = 1.08 g cm⁻³), which is in accordance with the absence of the chain ends and thus free volumes for the cyclic polymer surfactant.

For the flower-like micelles formed by the linear block copolymer surfactant, one of the chain ends could jump out from the core of the micelle, and cause the bridging between micelles after dehydration. Consequently, the linear block copolymer micelles could result in agglomeration at relatively low temperatures, in contrast to the thermally robust cyclic counterparts, in which the bridging motion is unlikely to proceed due to the absence of chain ends.¹¹

2.2 Emulsion stabilization by cyclic amphiphilic block copolymers

Emulsion stabilization by polymer surfactants has routinely been employed in diverse applications, including coating formation, pharmaceutical/cosmetic formulation, food processing, detergents preparation, etc.²⁸ Hence, cyclic polymer surfactants will become potentially attractive emulsion modifiers, since both cyclic and linear polymer surfactants are chemically identical and are considered inherently compatible with each other.

We prepared a linear block copolymer precursor, PS–PEO–PS, having olefinic end groups, as well as a cyclic PS–PEO block copolymer by making use of the MPC procedure (Fig. 2(a) and (b), respectively).²⁹ The emulsion stabilization of a pair of the PS–PEO–PS linear and the PS–PEO cyclic block copolymer surfactants was measured, as the linear PS–PEO block copolymers have so far been employed in relevant studies on their self-assemblies, like micelles, vesicles and other complex aggregates,³⁰ and in particular, on the formation of simple to complex emulsion structures by the toluene/water system.³¹

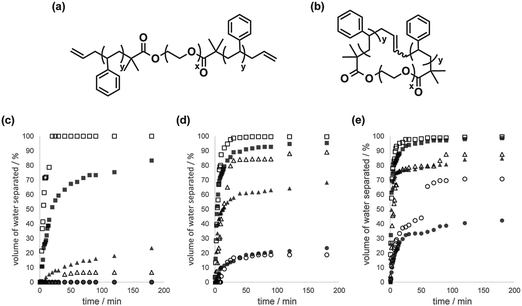Fig. 2 Chemical structures of (a) allyl-telechelic PS–PEO–PS and (b) cyclized PS–PEO surfactants. Time-dependent volume fraction of the separated water layer from the water phase of the emulsion, in the presence of linear PS–PEO–PS (■, ▲, ●) and cyclized PS–PEO (□, △, ○) with a surfactant concentration of 0.1 g L⁻¹ in toluene at a toluene/water ratio of (c) 10 mL/5 mL, (d) 10 mL/10 mL, and (e) 10 mL/15 mL at 25 °C (●, ○), 50 °C (▲, △), and 75 °C (■, □). Reproduced from ref. 15. Copyright 2015 Nature Publishing Group.

The macroscopic phase separation of water–toluene emulsions was monitored by the presence of either the linear PS–PEO–PS or the cyclized PS–PEO surfactants.¹⁵ Thus, a prescribed amount of the linear or cyclic polymer surfactant was dissolved in toluene (10 mL), and the solution was introduced to a 30 mL graduated glass cylinder. A series of volumes (5, 10 or 15 mL) of distilled water were then slowly added to form a two-phase solution. The graduated cylinder was vigorously agitated to give an emulsified solution and placed in a thermostated water bath at either 25, 50 or 75 °C. The phase separation process of the emulsified layer in the water phase, i.e., an oil-in-water emulsion, was subsequently monitored (Fig. 2(c), (d) and (e), respectively). The phase separation was, as anticipated, quicker at higher temperature and made faster by reducing the amount of water. At the same time, the phase separation kinetics were noticeably affected by the type of surfactant, and was significantly faster for emulsions containing the cyclic surfactant, particularly for toluene/water (10 mL/5 mL) at 75 °C (linear, ■; cyclic, □ in Fig. 2(c)), toluene/water (10 mL/10 mL) at 50 °C (linear, ▲; cyclic, △ in Fig. 2(d)), and toluene/water (10 mL/15 mL) at 25 °C (linear, ●; cyclic, ○ in Fig. 2(e)).

In the present emulsion system, the phase separation presumably proceeded through the coalescence of the oil droplets, promoted by the mass transfer of the block copolymer surfactants, initially located at the interface of the water/toluene phase.¹⁵ And they tend to translocate gradually into the oil droplet phase as both the PS and PEO segments of the surfactant molecule are soluble in toluene. During this process, the linear surfactant is expected to cause the bridging between the oil droplets with the extended chain conformation. Consequently, the coalescence of the oil droplets involves the translocation of the hydrophobic PS segments of the linear surfactants passing across the water phase between oil droplets, in contrast to the case with cyclic surfactants, where the mass transfer proceeds simply upon dehydration. Accordingly, the bridging process undergone exclusively by the linear surfactants could suppress the merging of the oil droplets, and the eventual phase separation. As in the stabilization of the micelles by cyclized block copolymers, the topology effect on the present emulsion stabilization is ascribed to the bridging by the surfactant having hydrophobic end segments, but this motion is inherently suppressed for the cyclic counterpart.

2.3 Self-assemblies of cyclic amphiphilic block copolymers having a liquid crystalline segment and their response behaviors

Liquid crystalline (LC) polymers have been extensively studied as they are able to respond to an electric or magnetic field owing to the rigidity and dielectric anisotropy of the polymer chain.³² We prepared a pair of linear and cyclized amphiphilic copolymers having a hydrophilic poly(acrylic acid) segment (AA_m), combined with a common main-chain LC polymer component of poly(3-methylpentamethylene-4,4′-bibenzoate) (BB_n) (Fig. 3(a) and (b), respectively).³³ The topology effect upon their self-assemblies and, moreover, on their electric or magnetic field-responses was investigated accordingly.¹⁶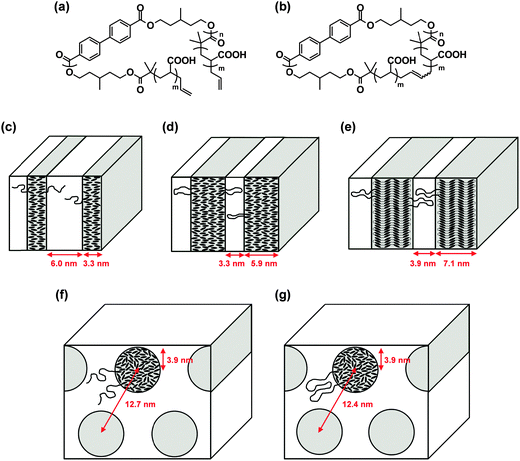

Fig. 3 Chemical structures of (a) linear AA_mBB_nAA_m and (b) cyclic AA_2mBB_n. Schematic illustration of the phase separation models of (c) linear AA₂₁BB₉AA₂₁, (d) cyclic AA₃₃BB₁₀, (e) cyclic AA₅₁BB₁₈, (f) linear AA₄₄BB₉AA₄₄, and (g) cyclic AA₁₀₀BB₉. Reproduced from ref. 16. Copyright 2015 Royal Society of Chemistry.

First, the solid state morphology of the linear and the cyclized block copolymers of different compositions was studied using small-angle X-ray scattering (SAXS) and wide-angle X-ray diffraction (WAXD). Linear AA₂₁BB₉AA₂₁ (Fig. 3(c)), cyclic AA₃₃BB₁₀ (Fig. 3(d)), and cyclic AA₅₁BB₁₈ (Fig. 3(e)) formed lamellar microdomains, where only the BB_n segment of cyclic AA₅₁BB₁₈ gave a smectic CA phase (Fig. 3(e)). In contrast, linear AA₄₄BB₉AA₄₄ (Fig. 3(f)) and cyclic AA₁₀₀BB₉ (Fig. 3(g)) formed cylindrical microdomains. Furthermore, these amphiphilic block copolymers self-assembled in water to form cylindrical micelles or vesicles, depending on the polymer concentration of the initial THF solution (Fig. 4(a) and (b)). By the application of an electric field, the vesicles formed from linear AA₂₅BB₁₄AA₂₅ and cyclic AA₅₁BB₁₈ turned into substantially larger aggregates, presumably due to the reorganization of the LC segment in the bilayer (Fig. 4(c) and (d), respectively).

Fig. 4 TEM images of the self-assembled structures from linear AA₂₅BB₁₄AA₂₅ and cyclic AA₅₁BB₁₈ using an initial THF solution with a polymer concentration 10 mg mL⁻¹ before and after applying an electric field (E) of 1.5 V mm⁻¹ for 2 min. (a) Linear, before E, stained with TI-blue. (b) Cyclic, before E, stained with TI-blue. (c) Linear, after E. (d) Cyclic, after E. Reproduced from ref. 16. Copyright 2015 Royal Society of Chemistry.

3. Topology effects upon crystallization

3.1 Crystallization kinetics by a defect-free cyclic poly(THF)

A class of ring polymers consisting exclusively of the monomer unit, in which not only chemically but also geometrically irregular chain-end or branched structures are completely eliminated, are considered defect-free, and are important for the rigorous examination of the fundamental properties of randomly coiled long-chain ring polymers, in comparison with their linear counterparts, both in solution and in bulk.¹⁷

Thus, we prepared a ring poly(THF) with a linking structure of a 2-butenoxy group, through the MPC process, with a uniform-size, telechelic poly(THF) having allyl end groups.⁹ Remarkably, the subsequent hydrogenation reaction of this linking group is capable of producing an oxytetramethylene group, identical to the monomer unit. By making use of this procedure, we prepared a series of defect-free ring poly(THF)s having different molecular weights, and their relevant linear counterparts, whose structures correspond to those formed through the bond-breaking at the middle position of the butane(tetramethylene) unit of the ring polymers and the subsequent addition of two hydrogen atoms.¹⁷ We subsequently compared the isothermal crystallization kinetics of these model polymers, since a distinctive polymer topology effect is anticipated for the ring polymer versus the linear counterpart.

Remarkable ring topology effects were revealed in the spherulite growth rates and spherulite morphologies in comparison with the relevant linear counterparts. Thus, the crystallization rate was slower for the cyclic poly(THF), and the unusual spherulite structure was formed.^17,34 The slower growth rate for the cyclic polymer was accounted for by their conformational constraints suppressing the propagation at the crystallization front. Interestingly, a faster crystallization rate was observed for cyclic poly(ε-caprolactone) in comparison with its linear counterpart,³⁵ and the faster diffusion of the cyclic polymers compared to the linear counterparts was postulated to be critical in this topology effect.

3.2 Stereocomplex formation by cyclic stereoregular polylactides

The stereocomplex formation process by a pair of complementary polymer components of either cyclic or linear form is expected to control the complexation kinetics, the complex structures and their eventual stabilization, by reflecting the presence/absence of the conformational constraint by cyclic/linear polymer components, and to cause the subsequent topology effects. Polylactides are known as a typical example to form stereocomplexes by the combination of polymers having opposite stereoregularities.³⁶ Thus, a series of cyclic poly(L-lactide), PLLA, and poly(D-lactide), PDLA, as well as linear and cyclic stereoblock polylactides were systematically prepared through the click linking of telechelic polymer precursors having either azide or alkyne groups at the designated chain end of the polylactides, and also having allyl groups at another chain end. They were subsequently cyclized using the MPC protocol to give the corresponding cyclic PLAs of opposite segment orientations.¹⁸

The homocrystals and stereocomplexes obtained by these linear and cyclic polylactides were first studied using WAXD as well as SAXS techniques, and subsequently the melting points (T_m) were measured to observe the topology effect upon the stereocomplex structures of the linear and the cyclic stereoregular homopolymers and block copolymers. Moreover, a pair of linear and cyclic PLLA and PDLA, having an o-nitrobenzyl group as a photocleavable linker unit, were prepared (Fig. 5(a) and (b), respectively).¹⁹ Thus, the cyclic polymer topology could be transformed into the linear form using UV irradiation causing the chain cleavage reaction at the single prescribed location, while the molecular weight and the polymer chain structure remained intact. This photo-responsive topological conversion could result in the simultaneous rearrangement of the stereocomplex structures. Thus, the T_m of the stereocomplex of the linear PLLA/PDLA was observed at 209 °C compared to that of the cyclic PLLA/PDLA, which was measured to be 167 °C before UV irradiation. The difference of as large as 40 °C between these T_m values corresponds to the lamellae thickness of the crystalline phase (l_c) with the extended chain conformation of the linear polylactide in contrast to the folded conformation of the cyclic counterpart (Fig. 5(c) and (d), respectively). Upon UV irradiation of the cyclic PLLA and PDLA having a photocleavable linker unit in solution, the T_m of the recovered product increased up to 211 °C, in accordance with the topological transformation of polylactides from the cyclic to the linear form.

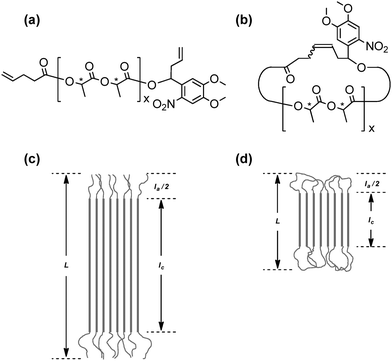Fig. 5 Chemical structures of photocleavable (a) linear and (b) cyclized polylactides. Schematic illustrations of the lamellar structures of (c) linear and (d) cyclized homocrystals and stereocomplexes of the photocleavable polylactides. L, long period; I_a, amorphous thickness; I_c, crystal thickness. Reproduced from ref. 19. Copyright 2015 Royal Society of Chemistry.

4. Topology effects of cyclic and dicyclic polymers upon diffusion revealed by single molecule spectroscopy

The diffusion process of linear or branched polymer molecules conforms to a reptation mechanism, in which polymer molecules are allowed to undergo snake-like motion, and their chain ends are critically important in their dynamics.⁷ On the other hand, ring polymers in the absence the chain ends are distinct from linear counterparts in their diffusion process, which is yet to be fully addressed, and an alternative topology-directed mechanism such as amoeba-like motion is postulated.⁸ In order to gain insights in the diffusion mechanism of cyclic polymers, single-molecular fluorescent spectroscopy has now been developed.^37,38 In contrast to traditional experimental methods to characterize diffusive and relaxation dynamics of polymers with ensemble averages, single-molecule imaging is used to reveal the heterogeneities of polymer dynamics. As unconventional and complicated chain dynamics and interactions are assumed to operate in cyclic and multicyclic polymers, single-molecule approaches should become a powerful means for investigating their dynamics, as shown in the case of linear and cyclic DNAs.²²

Thus, we prepared first a pair of linear and monocyclic poly(THF)s using the ESA–CF protocol, containing a perylene diimide either at the centre position of the linear polymer or at the prescribed inner position of the cyclic polymer samples. Each polymer sample was then mixed in a linear poly(THF) matrix at semidilute or bulk conditions under an extremely high dilution of 32–35 ppb. The diffusion process of the single molecules was monitored and analysed using a single-molecule localization and tracking method. Thus, the locations of the molecules in each image frame were precisely determined by two-dimensional Gaussian fitting, and the diffusion coefficients of individual molecules (D) were determined using mean-squared displacement (MSD) analysis of the trajectories. Finally, the D distributions were determined and compared with theoretical probability distributions.^21,23

Remarkably, a unimodal distribution of D was revealed for the linear polymer system, in contrast to a bimodal distribution for the cyclic counterparts. This distinction was explained by the fact that part of the cyclic polymers was threaded with the linear matrix of polymers leading to slower diffusion, while those without threading were faster than the average diffusion of the linear polymers. Such topology effects upon the diffusion dynamics, often undetectable through the ensemble average techniques, are uniquely disclosed by means of the single-molecular spectroscopy technique.^21,23

Moreover, a pair of 8-shaped and four-armed star-shaped polymers were also prepared by the ESA–CF process, in which a perylene diimide fluorophore unit was purposely introduced at the core of the 8-shaped and four-armed star-shaped polymer structures (Fig. 6(a) and (b), respectively).²⁰ This pair of perylene diimide-labelled, 8-shaped and four-armed star-shaped poly(THF)s was then mixed with a linear poly(THF) matrix to form a melt state at elevated temperatures, and was subjected to single-molecular fluorescent spectroscopy.

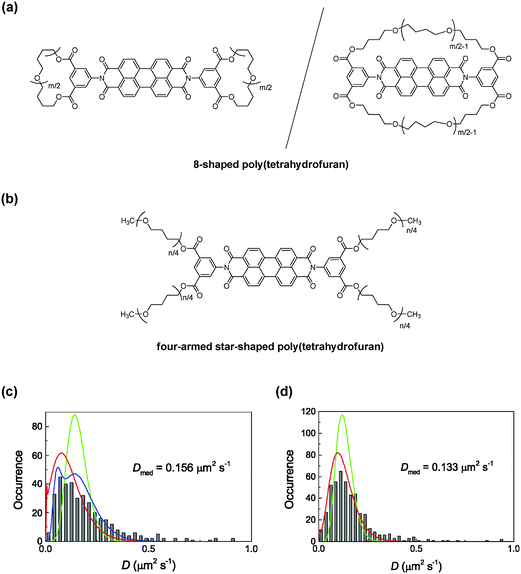Fig. 6 Chemical structures of (a) 8-shaped and (b) four-armed star-shaped poly(THF) incorporating a perylene diimide unit. Frequency histograms (grey bars) of the diffusion coefficient calculated for (c) 8-shaped and (d) four-armed star-shaped polymers in a linear poly(THF) matrix. The green, red, and blue lines indicate homogeneous diffusion models, single Gaussian models, and double Gaussian models, respectively. Reproduced from ref. 24. Copyright 2015 Royal Society of Chemistry.

The obtained frequency histograms of D values for 8-shaped and four-armed star-shaped polymers, calculated by the MSD analysis of the diffusion trajectories, are shown in Fig. 6(c) and (d), respectively.²⁴ The mean D value of the 8-shaped polymers in the melt state (D = 0.156 μm² s⁻¹) was comparable to that of the monocyclic polymer (D = 0.155 μm² s⁻¹) with a similar ring size. On the other hand, multi-armed star polymers have D values depending on the number of arms. Notably, moreover, the slower diffusion component found for the 8-shaped polymers (D = 0.061 μm² s⁻¹, shown in a blue line in Fig. 6(c)) was much smaller than that for the four-armed star polymer (D = 0.133 μm² s⁻¹) although the total chain length in the 8-shaped polymers was similar to that in the four-armed star polymer. These results coincided with a simulation study, which predicted the slower diffusion of cyclic chains by the threading with linear chains, as was shown in the monocyclic and linear polymers. As the total chain length in the four-armed star-shaped polymer and the 8-shaped polymers was comparable, the faster diffusion observed for the latter should correspond to the suppression of the threading and/or the contracted dicyclic conformation.

5. Concluding remarks

Cyclic polymers have been considered as a material of great potential, and we have observed important developments in recent years towards efficient and innovative synthetic processes, and new purification and characterization techniques. Thereby a variety of single- and multicyclic polymers having programmed chemical structures with guaranteed qualities have now become obtainable. By taking advantage of this significant progress, unprecedented opportunities have now been realized to disclose unusual polymer properties by cyclic polymers, in either solution or bulk, in either static or dynamic states, and in self-assemblies, ready for eventual applications. Topology effects are considered as a unique means to control polymer properties, in which no excessive change in molecular weights or chemical structures are involved, and thus any precaution over chemical toxicity or environmental pollution are not additionally required. Thus, one could apply the topology effect in polymer material design in order to purposely improve any properties of conventional polymeric materials. Moreover, any topology effects of cyclic polymers can be exploited in the tuning of a wide range of sophisticated functions based on dynamic physicochemical systems, as in the typical example of soft stimuli-responsive polymer materials.³⁹ Also in the future, a variety of topology effects of not only simple ring polymers but also of multicyclic polymers^40,41 are anticipated to be disclosed, and to be applied in practice for the routine methodology of polymer materials designs.

Acknowledgements

A series of our works have been supported partly by KAKENHI (26288099, 15H01595 and 15K13703 to T.Y., and 26310206 to Y.T.).

References

1. Complex Macromolecular Architectures: Synthesis, Characterization, and Self-Assembly, ed. N. Hadjichristidis, A. Hirao, Y. Tezuka and F. Du Prez, Wiley, Singapore, 2011.
2. Topological Polymer Chemistry: Progress of Cyclic Polymers in Syntheses, Properties and Functions, ed. Y. Tezuka, World Scientific, Singapore, 2013.
3. Cyclic Polymers: New Developments, Special Issue in Reactive and Functional Polymers, ed. S. M. Grayson, Y. D. Y. L. Getzler and D. Zhang, Elsevier, Amsterdam, 2014.
4. T. Yamamoto and Y. Tezuka, Polym. Chem., 2011, 2, 1930–1941.
5. Cyclic Polymers, ed. J. A. Semlyen, Kluwer Academic Publishers, New York, 2nd edn, 2002.
6. J. Roovers, in Topological Polymer Chemistry: Progress of Cyclic Polymers in Syntheses, Properties and Functions, ed. Y. Tezuka, World Scientific, Singapore, 2013, ch. 9, pp. 137–156.
7. P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1979.
8. T. McLeish, Science, 2002, 297, 2005–2006.
9. Y. Tezuka and R. Komiya, Macromolecules, 2002, 35, 8667–8669.
10. H. Oike, H. Imaizumi, T. Mouri, Y. Yoshioka, A. Uchibori and Y. Tezuka, J. Am. Chem. Soc., 2000, 122, 9592–9599.
11. S. Honda, T. Yamamoto and Y. Tezuka, J. Am. Chem. Soc., 2010, 132, 10251–10253.
12. S. Honda, T. Yamamoto and Y. Tezuka, Nat. Commun., 2013, 4, 1574.
13. K. Heo, Y. Y. Kim, Y. Kitazawa, M. Kim, K. S. Jin, T. Yamamoto and M. Ree, ACS Macro Lett., 2014, 3, 233–239.
14. E. Baba and T. Yamamoto, in Topological Polymer Chemistry: Progress of Cyclic Polymers in Syntheses, Properties and Functions, ed. Y. Tezuka, World Scientific, Singapore, 2013, ch. 16, pp. 329–347.
15. E. Baba, T. Yatsunami, T. Yamamoto and Y. Tezuka, Polym. J., 2015, 47, 408–412.
16. S. Honda, M. Koga, M. Tokita, T. Yamamoto and Y. Tezuka, Polym. Chem., 2015, 6, 4167–4176.
17. Y. Tezuka, T. Ohtsuka, K. Adachi, R. Komiya, N. Ohno and N. Okui, Macromol. Rapid Commun., 2008, 29, 1237–1241.
18. N. Sugai, T. Yamamoto and Y. Tezuka, ACS Macro Lett., 2012, 1, 902–906.
19. N. Sugai, S. Asai, Y. Tezuka and T. Yamamoto, Polym. Chem., 2015, 6, 3591–3600.
20. S. Fujiwara, T. Yamamoto, Y. Tezuka and S. Habuchi, React. Funct. Polym., 2014, 80, 3–8.
21. S. Habuchi, N. Satoh, T. Yamamoto, Y. Tezuka and M. Vacha, Angew. Chem., Int. Ed., 2010, 49, 1418–1421.
22. S. Habuchi, in Topological Polymer Chemistry: Progress of Cyclic Polymers in Syntheses, Properties and Functions, ed. Y. Tezuka, World Scientific, Singapore, 2013, ch. 13, pp. 265–290.
23. S. Habuchi, S. Fujiwara, T. Yamamoto, M. Vacha and Y. Tezuka, Anal. Chem., 2013, 85, 7369–7376.
24. S. Habuchi, S. Fujiwara, T. Yamamoto and Y. Tezuka, Polym. Chem., 2015, 6, 4109–4115.
25. Bioinspired and Biomimetic Polymer Systems for Drug and Gene Delivery, ed. Z. Gu, Wiley-VCH, Weinheim, 2014.
26. M. Kates, in The Biochemistry of Archaea (Archaebacteria), ed. M. Kates, D. J. Kushner and A. T. Matheson, Elsevier, Amsterdam, 1993, ch. 9, pp. 261–295.
27. K. Adachi, S. Honda, S. Hayashi and Y. Tezuka, Macromolecules, 2008, 41, 7898–7903.
28. Emulsion Formation and Stability, ed. T. Tadros, Wiley-VCH, Weinheim, 2013.
29. E. Baba, S. Honda, T. Yamamoto and Y. Tezuka, Polym. Chem., 2012, 3, 1903–1909.
30. Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985.
31. L. Hong, G. Sun, J. Cai and T. Ngai, Langmuir, 2012, 28, 2332–2336.
32. A. M. Donald, A. H. Windle and S. Hanna, Liquid Crystalline Polymers, Cambridge University Press, Cambridge, 2nd edn, 2006.
33. R. Ishige, T. Ishii, M. Tokita, M. Koga, S. Kang and J. Watanabe, Macromolecules, 2011, 44, 4586–4588.
34. H. Takeshita and T. Shiomi, in Topological Polymer Chemistry: Progress of Cyclic Polymers in Syntheses, Properties and Functions, ed. Y. Tezuka, World Scientific, Singapore, 2013, ch. 15, pp. 317–328.
35. M. E. Córdova, A. T. Lorenzo, A. J. Müller, J. N. Hoskins and S. M. Grayson, Macromolecules, 2011, 44, 1742–1746.
36. X. Yan, F. Wang, B. Zheng and F. Huang, Chem. Soc. Rev., 2012, 41, 6042–6065.
37. A. Deres, G. A. Floudas, K. Müllen, M. Van der Auweraer, F. De Schryver, J. Enderlein, H. Uji-i and J. Hofkens, Macromolecules, 2011, 44, 9703–9709.
38. S. Habuchi, T. Oba and M. Vacha, Phys. Chem. Chem. Phys., 2011, 13, 7001–7007.
39. C. Guerrero-Sanchez, D. Wouters, S. Hoeppener, R. Hoogenboom and U. S. Schubert, Soft Matter, 2011, 7, 3827–3831.
40. T. Suzuki, T. Yamamoto and Y. Tezuka, J. Am. Chem. Soc., 2014, 136, 10148–10155.
41. H. Heguri, T. Yamamoto and Y. Tezuka, Angew. Chem., Int. Ed., 2015, 54, 8688–8692.
42. C. U. Lee, T. P. Smart, L. Guo, T. H. Epps and D. H. Zhang, Macromolecules, 2011, 44, 9574–9585.
43. T. Cai, W. J. Yang, K.-G. Neoh and E.-T. Kang, Polym. Chem., 2012, 3, 1061–1068.
44. L. Li, J. Yang and J. Zhou, Macromolecules, 2013, 46, 2808–2817.
45. B. Zhang, H. Zhang, Y. Li, J. N. Hoskins and S. M. Grayson, ACS Macro Lett., 2013, 2, 845–848.
46. T. Isono, Y. Satoh, K. Miyachi, Y. Chen, S. Sato, K. Tajima, T. Satoh and T. Kakuchi, Macromolecules, 2014, 47, 2853–2863.
47. X. Wang, L. Li, X. Ye and C. Wu, Macromolecules, 2014, 47, 2487–2495.
48. A. Kalogirou, O. A. Moultos, L. N. Gergidis and C. Vlahos, Macromolecules, 2014, 47, 5851–5859.
49. E. J. Shin, A. E. Jones and R. M. Waymouth, Macromolecules, 2012, 45, 595–598.
50. J. M. Ren, K. Satoh, T. K. Goh, A. Blencowe, K. Nagai, K. Ishitake, A. J. Christofferson, G. Yiapanis, I. Yarovsky, M. Kamigaito and G. G. Qiao, Angew. Chem., Int. Ed., 2014, 53, 459–464.
51. K. Zhang, M. A. Lackey, J. Cui and G. N. Tew, J. Am. Chem. Soc., 2011, 133, 4140–4148.
52. K. Miki, Y. Inamoto, S. Inoue, T. Uno, T. Itoh and M. Kubo, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 5882–5890.
53. S. H. Lahasky, X. Hu and D. Zhang, ACS Macro Lett., 2012, 1, 580–584.
54. C.-U. Lee, L. Lu, J. Chen, J. C. Garno and D. Zhang, ACS Macro Lett., 2013, 2, 436–440.
55. T. S. Stukenbroeker, D. Solis-Ibarra and R. M. Waymouth, Macromolecules, 2014, 47, 8224–8230.
56. E. J. Shin, H. A. Brown, S. Gonzalez, W. Jeong, J. L. Hedrick and R. M. Waymouth, Angew. Chem., Int. Ed., 2011, 50, 6388–6391.
57. S.-F. Wang, X. Li, R. L. Agapov, C. Wesdemiotis and M. D. Foster, ACS Macro Lett., 2012, 1, 1024–1027.
58. J. E. Poelma, K. Ono, D. Miyajima, T. Aida, K. Satoh and C. J. Hawker, ACS Nano, 2012, 6, 10845–10854.
59. Md. D. Hossain, D. Lu, Z. Jia and M. J. Monteiro, ACS Macro Lett., 2014, 3, 1254–1257.
60. D. Kawaguchi, Y. Ohta, A. Takano and Y. Matsushita, Macromolecules, 2012, 45, 6748–6752.
61. D. Kawaguchi, Polym. J., 2013, 45, 783–789.
62. W. Chen, J. Chen, L. Liu, X. Xu and L. An, Macromolecules, 2013, 46, 7542–7549.
63. R. Pasquino, T. C. Vasilakopoulos, Y. C. Jeong, H. Lee, S. Rogers, G. Sakellariou, J. Allgaier, A. Takano, A. R. Brás, T. Chang, S. Gooßen, W. Pyckhout-Hintzen, A. Wischnewski, N. Hadjichristidis, D. Richter, M. Rubinstein and D. Vlassopoulos, ACS Macro Lett., 2013, 2, 874–878.
64. H. Takeshita, M. Poovarodom, T. Kiya, F. Arai, K. Takenaka, M. Miya and T. Shiomi, Polymer, 2012, 53, 5375–5384.
65. T. Kitahara, S. Yamazaki and K. Kimura, Kobunshi Ronbunshu, 2011, 68, 694–701.
66. H.-H. Su, H.-L. Chen, A. Díaz, M. T. Casas, J. Puiggalí, J. N. Hoskins, S. M. Grayson, R. A. Pérez and A. J. Müller, Polymer, 2013, 54, 846–859.
67. C.-U. Lee, A. Li, K. Ghale and D. Zhang, Macromolecules, 2013, 46, 8213–8223.
68. A. Rosa, E. Orlandini, L. Tubiana and C. Micheletti, Macromolecules, 2011, 44, 8668–8680.
69. C. B. Renner and P. S. Doyle, ACS Macro Lett., 2014, 3, 963–967.
70. Z. Lin, P. Lu, X. Yu, W.-B. Zhang, M. Huang, K. Wu, K. Guo, C. Wesdemiotis, X. Zhu, Z. Zhang, K. Yue and S. Z. D. Cheng, Macromolecules, 2014, 47, 4160–4168.
71. R. A. Pérez, J. V. López, J. N. Hoskins, B. Zhang, S. M. Grayson, M. T. Casas, J. Puiggalí and A. J. Müller, Macromolecules, 2014, 47, 3553–3566.
72. A. Takano, Y. Ohta, K. Masuoka, K. Matsubara, T. Nakano, A. Hieno, M. Itakura, K. Takahashi, S. Kinugasa, D. Kawaguchi, Y. Takahashi and Y. Matsushita, Macromolecules, 2012, 45, 369–373.
73. K. Terao, N. Asano, S. Kitamura and T. Sato, ACS Macro Lett., 2012, 1, 1291–1294.
74. A. Narros, A. J. Moreno and C. N. Likos, Macromolecules, 2013, 46, 9437–9445.
75. J. Suzuki, A. Takano and Y. Matsushita, J. Chem. Phys., 2013, 138, 024902.
76. M. Z. Slimani, P. Bacova, M. Bernabei, A. Narros, C. N. Likos and A. J. Moreno, ACS Macro Lett., 2014, 3, 611–616.
77. J. Cao, J. Qin and S. T. Milner, Macromolecules, 2014, 47, 2479–2486.
78. D. Michieletto, D. Marenduzzo, E. Orandini, G. P. Alexander and M. S. Turner, ACS Macro Lett., 2014, 3, 255–259.
79. R. Tsubouchi, D. Ida, T. Yoshizaki and H. Yamakawa, Macromolecules, 2014, 47, 1449–1454.
80. P. Polanowski, J. K. Jeszka and A. Sikorski, Macromolecules, 2014, 47, 4830–4839.
81. J. S. Myung, F. Taslimi, R. G. Winkler and G. Gompper, Macromolecules, 2014, 47, 4118–4125.
82. J. Suzuki, A. Takano and Y. Matsushita, J. Chem. Phys., 2013, 139, 184904.
83. T. Deguchi, Kobunshi Ronbunshu, 2011, 68, 767–772.
84. N. Hirayama, K. Tsurusaki and T. Deguchi, Kobunshi Ronbunshu, 2011, 68, 804–810.
85. C. Fu, W. Ouyang, Z. Sun and L. Ana, J. Chem. Phys., 2007, 127, 044903.
86. J. U. Kim, Y.-B. Yang and W. B. Lee, Macromolecules, 2012, 45, 3263–3269.
87. M. Lang, J. Fischer and J.-U. Sommer, Macromolecules, 2012, 45, 7642–7648.
88. S. Y. Reigh and D. Y. Yoon, ACS Macro Lett., 2013, 2, 296–300.
89. M. Lang, Macromolecules, 2013, 46, 1158–1166.
90. R. Chen, J. Ling and T. E. Hogen-Esch, Macromolecules, 2009, 42, 6015–6022.
91. H. Zhang, N. Zhou, X. Zhu, X. Chen, Z. Zhang, W. Zhang, J. Zhu, Z. Hu and X. Zhu, Macromol. Rapid Commun., 2012, 33, 1845–1851.
92. Y. Cai, J. Lu, F. Zhou, X. Zhou, N. Zhou, Z. Zhang and X. Zhu, Macromol. Rapid Commun., 2014, 35, 901–907.
93. O. Coulembier, G. Deshayes, M. Surin, J. De Winter, F. Boon, C. Delcourt, P. Leclère, R. Lazzaroni, P. Gerbaux and P. Dubois, Polym. Chem., 2013, 4, 237–241.
94. J. A. Kaitz, C. E. Diesendruck and J. S. Moore, Macromolecules, 2013, 46, 8121–8128.
95. J. A. Kaitz, C. E. Diesendruck and J. S. Moore, Macromolecules, 2014, 47, 3603–3607.
96. J. A. Kaitz and J. S. Moore, Macromolecules, 2014, 47, 5509–5513.
97. M. Schappacher and A. Deffieux, Macromolecules, 2011, 44, 4503–4510.
98. O. Altintas, P. Krolla-Sidenstein, H. Gliemann and C. Barner-Kowollik, Macromolecules, 2014, 47, 5877–5888.
99. J. Willenbacher, O. Altintas, P. W. Roesky and C. Barner-Kowollik, Macromol. Rapid Commun., 2014, 35, 45–51.
100. B. Chen, K. Jerger, J. M. J. Fréchet and F. C. Szoka, Jr., J. Controlled Release, 2009, 140, 203–209.
101. Z. Qian, X. Xu, J. F. Amacher, D. R. Madden, E. Cormet-Boyaka and D. Pei, Angew. Chem., Int. Ed., 2015, 54, 5874–5878.
102. H. Wei, D. S. H. Chu, J. Zhao, J. A. Pahang and S. H. Pun, ACS Macro Lett., 2013, 2, 1047–1050.
103. M. A. Cortez, W. T. Godbey, Y. Fang, M. E. Payne, B. J. Cafferty, K. A. Kosakowska and S. M. Grayson, J. Am. Chem. Soc., 2015, 137, 6541–6549.
104. M. Glassner, J. P. Blinco and C. Barner-Kowollik, Macromol. Rapid Commun., 2011, 32, 724–728.
105. K. Zhang, Y. Zha, B. Peng, Y. Chen and G. N. Tew, J. Am. Chem. Soc., 2013, 135, 15994–15997.

---