Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of fluid–colloid interactions on the mobility of a thermophoretic microswimmer in non-ideal fluids
Dmitry A.
Fedosov
*,
Ankush
Sengupta
and
Gerhard
Gompper
Theoretical Soft Matter and Biophysics, Institute of Complex Systems and Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: d.fedosov@fz-juelich.de
First published on 21st July 2015
Abstract
Janus colloids propelled by light, e.g., thermophoretic particles, offer promising prospects as artificial microswimmers. However, their swimming behavior and its dependence on fluid properties and fluid–colloid interactions remain poorly understood. Here, we investigate the behavior of a thermophoretic Janus colloid in its own temperature gradient using numerical simulations. The dissipative particle dynamics method with energy conservation is used to investigate the behavior in non-ideal and ideal-gas like fluids for different fluid–colloid interactions, boundary conditions, and temperature-controlling strategies. The fluid–colloid interactions appear to have a strong effect on the colloid behavior, since they directly affect heat exchange between the colloid surface and the fluid. The simulation results show that a reduction of the heat exchange at the fluid–colloid interface leads to an enhancement of colloid's thermophoretic mobility. The colloid behavior is found to be different in non-ideal and ideal fluids, suggesting that fluid compressibility plays a significant role. The flow field around the colloid surface is found to be dominated by a source-dipole, in agreement with the recent theoretical and simulation predictions. Finally, different temperature-control strategies do not appear to have a strong effect on the colloid's swimming velocity.
1 Introduction
The construction of nano- and micro-machines, which can move through a fluid environment, is one of the grand challenges confronting nanoscience today.1–4 Several strategies and physical mechanisms have been employed so far to generate self-propulsion in a fluid.5,6 One approach is biomimetic, where the flagellar propulsion of sperm, bacteria, or cilia is recreated with synthetic soft materials and actuators. Some recent examples include artificial sperm7 and artificial cilia;8 however, in most of these cases, the machines are rather of millimeter than of sub-micrometer size. Nano- to micrometer length scales are reached by artificial cilia made from microtubules and motorproteins,9 and by magnetic nano- and microscrews rotated by an external magnetic field.10 Another approach is physico-chemical, where non-equilibrium concentration fields or temperature distributions in the fluid environment are generated around the swimmer and are employed for propulsion, without any movable parts of the swimmer itself. Here, diffusiophoretic11–16 and thermophoretic17–22 Janus colloids have been studied most intensively. For diffusiophoretic swimmers, a semi-spherical cap on the colloidal Janus particle catalyzes a reaction in the fluid and thereby generates a spatially inhomogeneous non-equilibrium distribution of reaction agents and products. For thermophoresis, a semi-spherical cap on a colloidal Janus particle absorbs light from an external light source, and is thereby heated, and generates a local temperature gradient. An interesting combination of the two has also been investigated, where the onset of the chemical reaction is triggered by the external light intensity.16 Light-controlled microswimmers have the advantage that their motion can be controlled easily by a variation of the light intensity.A particularly interesting type of thermophoretic microswimmers has been suggested by Volpe et al.23 This is again a colloidal particle with a metallic, light-absorbing cap; however, this Janus colloid is immersed in a binary fluid mixture at an ambient temperature just below its lower demixing critical point. A slight heating of the cap then leads to a local demixing of the fluid mixture, which generates the driving force for swimming. An advantage of this mechanism is that it works for much smaller power of the light source than that for thermophoretic microswimmers in single-component fluids.
The study of thermophoretic swimming in binary fluids23 demonstrates that the interaction of the fluid with the colloid surface plays an important role. In particular, it was shown by Volpe et al.23 that the swimming direction depends on which of the two components partially wets the colloid surface. However, theoretical studies have only considered either fluids on the level of the incompressible Navier–Stokes equation,21 or fluids with an ideal-gas equation of state.20,22,24 Thus, as a first step toward an understanding of thermophoretic self-propulsion in real fluid mixtures, we investigate a system with a single-component fluid with a non-ideal equation of state and a variety of boundary conditions (BCs) on the colloid surface. In particular, we investigate the influence of no-slip and slip BCs and fluid–colloid interactions. In addition, the behavior of a thermophoretic swimmer is studied for different temperature controls and gradients. We find that local fluid–colloid interactions and temperature gradients near the colloid's surface control its swimming velocity. The models with non-ideal and ideal fluids lead to qualitatively different trends in the colloid mobility. Finally, the flow field around a swimming thermophoretic colloid is mainly determined by the source-dipole term in agreement with recent theoretical predictions.21
2 Models and methods
We consider a spherical Janus colloid immersed in a single-component fluid. In order to correctly describe the hydrodynamics of a thermophoretic microswimmer, the fluid model has to properly conserve momentum and energy locally. We employ here the version of dissipative-particle-dynamics (DPD) approach25,26 with energy conservation.27,282.1 Dissipative particle dynamics with energy conservation (eDPD)
In the standard (isothermal) DPD approach,25,26 the fluid is modeled by a set of N particles, each of mass m, interacting through a weak conservative (FCij), a dissipative (FDij), and random (FRij) pairwise forces, where the subscripts i, j refer to particle indices. The pairwise additive forces are given byFCij = aωC(rij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, |
FDij = −γωD(rij)(vij·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij) ij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, |
FRij = σωR(rij)ξijΔt−1/2![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij, ij, | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij is its unit vector, and vij = vi − vj with r and v being the particle positions and velocities, respectively. The parameter a is the conservative force coefficient, which affects fluid compressibility. γ and σ are the friction and noise amplitudes, which are related through the fluctuation–dissipation balance26 as σ2 = 2γkBT, where kB is the Boltzmann constant and T is the temperature. All forces are short-ranged with a cutoff radius rc, and vanish for rij > rc. The conservative force profile is defined by ωC(rij) = (1 − rij/rc) for rij ≤ rc, while the spatial dependence of the dissipative (ωD) and random (ωR) weight functions is determined by ωR(rij) = (1 − rij/rc)s for rij ≤ rc and the relation ωD = (ωR)2 derived from the fluctuation–dissipation theorem.26 Here, s is the exponent which affects inter-particle friction and fluid viscosity such that s < 1 is advantageous in order to achieve a sufficiently large fluid viscosity.29,30ξij is a Gaussian distributed random variable with zero mean and unit variance with the requirement ξij = ξji for momentum conservation. Finally, Δt is the simulation time step.
ij = rij/rij is its unit vector, and vij = vi − vj with r and v being the particle positions and velocities, respectively. The parameter a is the conservative force coefficient, which affects fluid compressibility. γ and σ are the friction and noise amplitudes, which are related through the fluctuation–dissipation balance26 as σ2 = 2γkBT, where kB is the Boltzmann constant and T is the temperature. All forces are short-ranged with a cutoff radius rc, and vanish for rij > rc. The conservative force profile is defined by ωC(rij) = (1 − rij/rc) for rij ≤ rc, while the spatial dependence of the dissipative (ωD) and random (ωR) weight functions is determined by ωR(rij) = (1 − rij/rc)s for rij ≤ rc and the relation ωD = (ωR)2 derived from the fluctuation–dissipation theorem.26 Here, s is the exponent which affects inter-particle friction and fluid viscosity such that s < 1 is advantageous in order to achieve a sufficiently large fluid viscosity.29,30ξij is a Gaussian distributed random variable with zero mean and unit variance with the requirement ξij = ξji for momentum conservation. Finally, Δt is the simulation time step.
The particle dynamics is determined by the equations of motion as
 | (2) |
In the energy-conserving DPD (eDPD) method,27,28 each fluid particle i, in addition to its position and velocity, also possesses an internal energy εi. We assume that the internal energy of a particle is related to the temperature value Ti as εi = CvTi, where Cv is the specific heat of a fluid.27 Then, the evolution equation for particle temperature can be written in the following form
 | (3) |
Local heat conduction between particles is defined as27,28
 | (4) |
 | (5) |
To connect particle dynamics to its internal temperature (or energy),27,28 the force coefficients in eqn (1) become functions of temperature and should be replaced by the corresponding aij(Ti,Tj), γij(Ti,Tj), and σij(Ti,Tj) coefficients. Recently, it has been suggested that the conservative force coefficient aij should depend linearly on temperature in order to properly reproduce fluid compressibility.32 However, in the current work we employ a constant conservative force coefficient such that aij(Ti,Tj) = aF. For simplicity, we also assume no temperature dependence of the random force coefficient such that σij(Ti,Tj) = σ. Then, the corresponding friction coefficient is given by
 | (6) |
The work fluxes qwij can be derived from the total energy E of a simulated system. The total energy of the system,  , should be constant and thus, a change in mechanical energy Emech should correspond to the change in the internal energy such that
, should be constant and thus, a change in mechanical energy Emech should correspond to the change in the internal energy such that  . The mechanical energy consists of kinetic and potential contributions given by
. The mechanical energy consists of kinetic and potential contributions given by
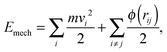 | (7) |
 . Thus, we calculate the changes in kinetic and potential energies locally after each integration step and adjust the internal energy of each particle accordingly. This method leads to exact conservation of the total energy of a system, and we have verified that it properly represents temperature gradients in a fluid. A similar idea has been used in ref. 33, where energy conservation has been implemented locally for each pair of interacting fluid particles.
. Thus, we calculate the changes in kinetic and potential energies locally after each integration step and adjust the internal energy of each particle accordingly. This method leads to exact conservation of the total energy of a system, and we have verified that it properly represents temperature gradients in a fluid. A similar idea has been used in ref. 33, where energy conservation has been implemented locally for each pair of interacting fluid particles.
2.2 Janus colloid and boundary conditions
The Janus colloid is modeled with Ns = 4000 DPD particles placed on the surface of a sphere with radius Rs = 4rc corresponding to the surface density of ρs ≈ 20/rc2. The colloid is centered at the origin, with the hot (cold) side positioned in the half-space x < 0 (x > 0). The colloid particles are frozen at their positions on the spherical surface, see Fig. 1. It is important to note that a colloid moving in a resting fluid and a colloid fixed at a position with certain orientation are essentially identical; the main difference is just a transformation of the reference frame. In the former case, the colloid is moving in the fluid, while in the latter case the fluid is moving around the colloid. The two cases are equivalent for small rotational and translational diffusion coefficients, i.e. for sufficiently large colloids. There might be deviations for small colloids, when the relaxation time of the temperature profile becomes comparable to the rotational diffusion time.In the simulations, one or both sides of the colloid surface are maintained at constant temperature. The steady-state behavior of the system is ensured by the constancy of the temperature gradient in the fluid and of the flow field in the co-moving frame of the colloid. The fluid particles are present both outside and inside the colloidal shell, in order to ensure a proper pressure balance on both sides of the colloid surface. Thus, the fluid particles inside and outside the colloid interact through the conservative force in eqn (1). However, the friction coefficient between the inside and outside fluids is set to zero, since viscous interactions between them are shielded by the colloid wall. This means that γij = σij = 0 whenever (i, j) represents a pair of fluid particles intercepted by the colloid surface.
Two separate cases of boundary conditions (BCs) are considered including either bounce-back collisions or specular reflection of the fluid particles at the fluid–colloid interface. This applies to collisions both at the inside and the outside of the colloidal shell. The reflections of fluid particles are necessary to prevent the entry of a fluid particle from the exterior to the interior of the colloidal shell, or vice versa, since the conservative interactions between fluid and colloid particles are too soft to guarantee no inter-fluid mixing. On the other hand, the two different collision rules realize different BCs at the colloid surface. The bounce-back collisions implement a no-slip (or stick) BCs, since the particle velocity is inverted at the colloid surface (i.e.v → −v) resulting on average in a vanishing tangential component of the fluid velocity. In the case of specular reflections, the velocity component parallel to the local tangent plane of the colloid surface remains unchanged, while the perpendicular component is inverted. This realizes slip BCs.
In addition to the above mentioned BCs, the fluid particles also interact pairwise with the immobile DPD particles comprising the colloid surface. Therefore, different halves of the Janus particle possess not only dissimilar thermal properties, but also may have different fluid–colloid interactions (see Fig. 1). This is done by assigning different pair-interaction coefficients for the particles at the two halves of the colloid with the surrounding fluid particles. The particles of the two distinct hemispheres are labeled as A and B. Given that the fluid particles i and j interact with a coefficient aij = aF, the coefficients for fluid–colloid interactions will be referred to as aiA and aiB for the two halves, respectively. Then, aiA < aF mimics an effectively “solvophilic” surface, while aiA > aF mimics an effectively “solvophobic” surface. In experiments, Janus particles can be chemically functionalized to generate hydrophilic or hydrophobic interaction with the host fluid.34 Such chemical functionalization can affect the particle behavior in addition to the temperature gradient. Thus, changing the fluid–cap interaction strength for both caps A and B allows us to access surface-tuning capabilities together with the thermophoretic control in our model. The dissipative and random force coefficients for fluid–colloid interactions are set to zero (γiA = σiA = γiB = σiB = 0), since the bounce-back and specular reflections of particles at the colloid interface already define the type of BCs employed. Finally, the fluid and the colloid exchange heat locally within rc following eqn (4). In order that the fluid particles can approach the colloid particles close enough and exchange heat, a shorter cut-off radius for the fluid–colloid conservative interactions, rc′ = 0.25rc, has been used.
The temperature gradient across the colloid is maintained by setting an elevated temperature Thot for the immobile particles comprising cap A, while the particles comprising cap B are kept at a lower temperature Tcold throughout the course of the simulation, see Fig. 2(a). In experiments, however, one-half of the Janus colloid is heated by allowing the metal-capped half to absorb heat from an incident laser field.17,35 The bulk fluid in this case remains at a colder temperature, and thus maintains a temperature gradient across the colloid diameter without the need to additionally cool the other half of the colloid. Therefore, we have also examined the case where we keep the particles of cap A at an elevated temperature Thot and impose the temperature Tcold for the fluid particles appearing within a narrow slice of 1.5rc at the two periodic boundaries parallel to the symmetry axis of the Janus colloid (Fig. 2(b)). In this case, we let the temperature of all other particles, including those of cap B, relax to an intermediate steady-state value. Similarly, we have also compared these cases with the situation when all the periodic boundaries are kept at the lower temperature Tcold within a slice of 1.5rc, while the particles of cap A are maintained at the higher temperature Thot (Fig. 2(c)). We denote a maximal temperature difference across the colloid as ΔT = TA − TB, which is equal to Thot − Tcold for the case where the temperature is controlled on both sides of the Janus colloid. For the other two cases, where the temperature is maintained only at one side of the colloid, ΔT = Thot − TB with TB measured directly from the simulation data. The differences in Janus-colloid behavior with respect to the different temperature-control strategies will be discussed.
2.3 Simulation setup and parameters
In the simulations, a cubic box of size Lx = Ly = Lz = 25rc with periodic BCs is used. We employ m = 1 to define the unit of mass, rc = 1 to define the unit of length, and is the unit of time, where kB = 1 and
is the unit of time, where kB = 1 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = (Thot + Tcold)/2 is the average temperature, which has been set to
= (Thot + Tcold)/2 is the average temperature, which has been set to ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.64 in simulations. For the normalization of different colloid properties, we will also use the rotational diffusion coefficient Dr = kB
= 0.64 in simulations. For the normalization of different colloid properties, we will also use the rotational diffusion coefficient Dr = kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /(8πηRs3), where η is the fluid's dynamic viscosity at
/(8πηRs3), where η is the fluid's dynamic viscosity at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) . Other parameters include the density of fluid particles ρf = 3/rc3, the conservative force coefficient aF = 39kB
. Other parameters include the density of fluid particles ρf = 3/rc3, the conservative force coefficient aF = 39kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /rc, the random force coefficient
/rc, the random force coefficient  , the exponent s = 0.25, the specific heat Cv = 200kB, and the nominal strength of interparticle heat conductivity k0 = 0.00125/τ. The fluid viscosity for aF = 39kB
, the exponent s = 0.25, the specific heat Cv = 200kB, and the nominal strength of interparticle heat conductivity k0 = 0.00125/τ. The fluid viscosity for aF = 39kB![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /rc at
/rc at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) is equal to
is equal to  , and thus
, and thus  . We will also employ a fluid with aF = 0 whose viscosity is equal to
. We will also employ a fluid with aF = 0 whose viscosity is equal to  resulting in
resulting in 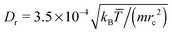 . The simulations were performed with discrete timesteps Δt = 0.004τ and data were collected after an initial relaxation time of 2 × 105 timesteps, in order to ensure a proper steady state. The relaxation to the steady state has been monitored by observing a stable time-independent temperature gradient and flow field. The steady-state averages were calculated by collecting data over another 8 × 106 timesteps.
. The simulations were performed with discrete timesteps Δt = 0.004τ and data were collected after an initial relaxation time of 2 × 105 timesteps, in order to ensure a proper steady state. The relaxation to the steady state has been monitored by observing a stable time-independent temperature gradient and flow field. The steady-state averages were calculated by collecting data over another 8 × 106 timesteps.
3 Results
We study the dynamics of the model thermophoretic Janus colloid in the host fluid medium under various temperature conditions and surface interactions. The center of the Janus colloid is fixed at the origin of the reference frame as discussed in Section 2.2 such that we can conveniently study the translational motion of the colloid by measuring the fluid velocity far from the colloid surface. All our results are shown for steady-state conditions.3.1 Temperature dependence of self-propulsion
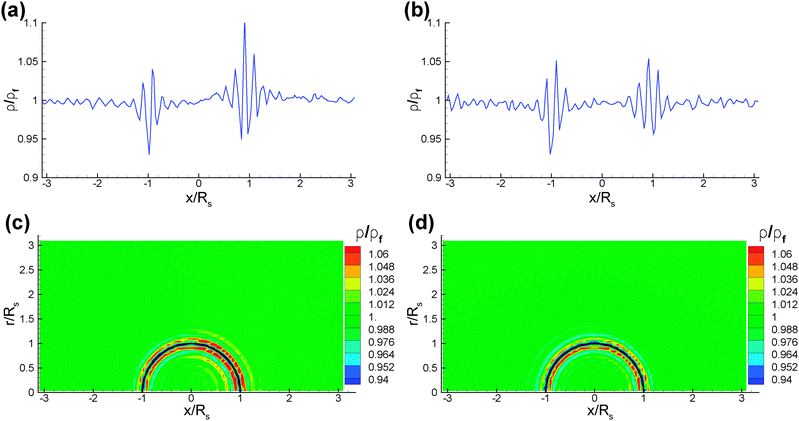
Fig. 2 shows the temperature profiles around the colloid in the steady-state for the different temperature-control strategies described above. The temperature profiles are axisymmetric allowing us to average simulation data over the full azimuthal angle. Clearly, the temperature profiles are very different in the three cases. In Fig. 2(a), a very strong temperature gradient develops at the interface between the two caps; this interfacial gradient is much smaller in Fig. 2(b) and (c), which is both due to the smaller temperature difference between the two caps and the temperature variation on the non-heated cap itself. The comparison of the profiles of Fig. 2(b) and (c) shows minor differences in the close vicinity of the colloid surface, but a much slower decay along the symmetry axis in Fig. 2(b).In all three cases, we also measure the density profiles of the fluid near the colloid surface. Fig. 3 shows the fluid density cuts along the x-axis and the corresponding density profiles in two dimensions. We find a layering of the interacting fluid particles at the fluid–colloid surface. Such a layering is well known for hard-core particles near a hard wall,36 and is thus related to the repulsive interaction of fluid particles among themselves and with the colloid surface. These density modulations at the colloid wall decay to the mean bulk density (ρf = 3/rc3) rapidly over a length scale of two to three times rc. However, the density patterns are similar for different temperature-control strategies. Also, density profiles do not show any appreciable differences for the various BCs, in particular the bounce-back and the specular reflection BCs at the fluid–colloid interface. The fluid density profiles in case of a hot cap (Thot/![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 1.3) and a temperature fixed to be Tcold/
= 1.3) and a temperature fixed to be Tcold/![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.7 at the periodic boundaries in all directions are nearly identical to those in Fig. 3(b) and (d) for the temperature control only at the periodic boundaries in the y-direction.
= 0.7 at the periodic boundaries in all directions are nearly identical to those in Fig. 3(b) and (d) for the temperature control only at the periodic boundaries in the y-direction.
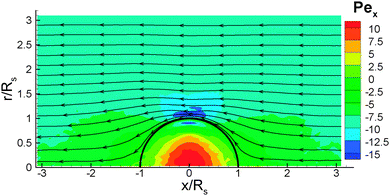
The non-zero temperature difference across the colloid diameter results in the spontaneous generation of a far-field flow velocity in the fluid in the co-moving frame of the colloid (see Fig. 4). We measure this flow velocity by averaging over the velocities of all the DPD fluid particles far away from the colloid with coordinates |r| > 2Rs. In the laboratory frame, this flow velocity is the same in magnitude and opposite in direction to the self-propulsion velocity vp of the colloid. We find that vp increases linearly with increase in the maximal temperature difference ΔT across the colloid at fixed average temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) , as shown in Fig. 5 in terms of a particle Peclet number Pep = vp/(2RsDr). Pep can be also interpreted as a non-dimensional swimming velocity of the colloid. Defining the corresponding proportionality constant as the thermophoretic mobility, μ = vp/ΔT, we can readily obtain μ from the slope. The thermophoretic mobility is determined by the surface properties of the Janus particle, the interactions within the fluid, and the average temperature
, as shown in Fig. 5 in terms of a particle Peclet number Pep = vp/(2RsDr). Pep can be also interpreted as a non-dimensional swimming velocity of the colloid. Defining the corresponding proportionality constant as the thermophoretic mobility, μ = vp/ΔT, we can readily obtain μ from the slope. The thermophoretic mobility is determined by the surface properties of the Janus particle, the interactions within the fluid, and the average temperature ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) , but obviously independent of ΔT, and thus, it is a convenient quantity to characterize a thermophoretic microswimmer. We can then use the thermophoretic mobility μ to study the dependence of self-propulsion on the surface properties of the colloid in relation to the host fluid. Subsequently, our simulation results will be presented mostly in terms of a non-dimensional mobility μ* = Pep
, but obviously independent of ΔT, and thus, it is a convenient quantity to characterize a thermophoretic microswimmer. We can then use the thermophoretic mobility μ to study the dependence of self-propulsion on the surface properties of the colloid in relation to the host fluid. Subsequently, our simulation results will be presented mostly in terms of a non-dimensional mobility μ* = Pep![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /ΔT = μ
/ΔT = μ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) /(2RsDr).
/(2RsDr).
3.2 Dependence of thermophoretic mobility on fluid–colloid interactions
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.6. The mobility increases with increasing cap repulsion strength, and levels off to some saturation value at very high repulsion strength.
= 0.6. The mobility increases with increasing cap repulsion strength, and levels off to some saturation value at very high repulsion strength.
Fig. 6 reveals an interesting dependence of μ* on the slip or stick BCs. Within the numerical accuracy, we find that the saturation value at high repulsion strength does not depend on whether bounce-back or specular-reflection collisions are employed at the colloid surface. This can easily be understood by considering the fact that at high repulsion strengths hardly any fluid particles can reach the colloid surface anymore, so that the type of surface reflection becomes irrelevant. However, for low cap repulsion strengths, the stick BCs generate larger fluid flow (and thus, propulsion velocity) than the slip BCs for a given temperature difference and cap repulsion strength. In fact, in the absence of cap repulsion, the thermophoretic mobility disappears in the case of slip BCs.
Fig. 5 also shows the velocity-temperature graphs for asymmetric cap repulsion strengths. Fig. 5(b) concerns the case when the hot cap A interacts with a lower interaction coefficient with the fluid particles compared to the fluid–fluid interaction (aiA < aF), to mimic a solvophilic cap interaction. This interaction is kept fixed and the interaction of the cold cap B with the fluid is increased from solvophilic (aiB < aF) to solvophobic (aiB > aF) strengths. In Fig. 5(c), the cold cap B is instead maintained at a solvophilic interaction strength (aiB < aF), and the interaction aiA on the hot cap A is varied. These two cases are not identical, because the A-cap is always the hot and the B-cap is always the cold side. The velocity response to the temperature difference remains linear for all cases. The non-dimensional thermophoretic mobility μ* extracted from these data for the case of ΔT/![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.6 is shown in Fig. 6. As for the symmetric case, μ* is found to increase with increasing repulsion strength aiA or aiB. Fig. 6(a) and (b) also provide the comparison of mobilities for stick and slip BCs, which show similar trends as for the symmetric case, with an increase in μ* and its final saturation as the cap repulsion strength is elevated.
= 0.6 is shown in Fig. 6. As for the symmetric case, μ* is found to increase with increasing repulsion strength aiA or aiB. Fig. 6(a) and (b) also provide the comparison of mobilities for stick and slip BCs, which show similar trends as for the symmetric case, with an increase in μ* and its final saturation as the cap repulsion strength is elevated.
The thermophoretic mobility obtained from these two very different asymmetric fluid–cap interaction cases remains essentially identical (within our numerical accuracy), although it is much lower than the corresponding mobility for symmetric fluid–cap interactions (where the larger value of the two repulsion strengths in the asymmetric case is the same as acap in the symmetric case). In particular, the saturation value of μ* in the asymmetric case is considerably smaller than that for the symmetric case. Furthermore, Fig. 6 shows that the increase of the mobility due to cap repulsion is about twice as large for the symmetric than for the (highly) asymmetric cases. Together, this indicates that the thermophoretic mobility can be understood as a superposition of the mobilities generated by the two caps independently. This indicates that the temperature gradient between the cap and the fluid, rather than that at the interface between the two caps, is responsible for the propulsion. Fig. 6 also shows that the insensitivity of the thermophoretic mobility to the exchange of repulsion strengths is also not affected by the type of BCs at the colloid–fluid interface. However, the slip BCs always generate lower mobilities compared to stick boundary BCs, in particular for lower values of fluid–cap interaction strengths.
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and TB = Tcold = 0.7
and TB = Tcold = 0.7![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) (illustrated in Fig. 2(a)). We now consider the case where the A-cap is held at a fixed temperature Thot, and the fluid far away from the colloid (and near the periodic boundaries of the simulation box) is held at a lower value Tcold, while the temperature of the other cap (B) is free to adjust, as illustrated in Fig. 2(b) and (c). In this case, TB is measured directly from the simulation data. The temperature distribution is nearly independent of the fluid–colloid interactions and the type of BCs, and the measured values of temperature at the cold side are TB = 1.11
(illustrated in Fig. 2(a)). We now consider the case where the A-cap is held at a fixed temperature Thot, and the fluid far away from the colloid (and near the periodic boundaries of the simulation box) is held at a lower value Tcold, while the temperature of the other cap (B) is free to adjust, as illustrated in Fig. 2(b) and (c). In this case, TB is measured directly from the simulation data. The temperature distribution is nearly independent of the fluid–colloid interactions and the type of BCs, and the measured values of temperature at the cold side are TB = 1.11![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) when the two periodic boundaries parallel to the symmetry axis of the Janus colloid are kept at the temperature Tcold and TB = 1.09
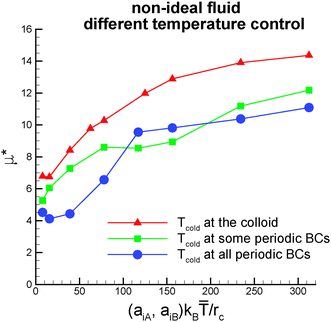
when the two periodic boundaries parallel to the symmetry axis of the Janus colloid are kept at the temperature Tcold and TB = 1.09![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) when all periodic boundaries are maintained at Tcold. The results for the non-dimensional thermophoretic mobility displayed in Fig. 7 show that the qualitative trends remain unaltered. However, μ* is slightly lower than for the case of fixed temperature TB = Tcold. This is due to the fact that temperature gradients at the interface between the cold and hot sides of the colloid are stronger for the case of the temperature control TB = Tcold directly at the colloid.
when all periodic boundaries are maintained at Tcold. The results for the non-dimensional thermophoretic mobility displayed in Fig. 7 show that the qualitative trends remain unaltered. However, μ* is slightly lower than for the case of fixed temperature TB = Tcold. This is due to the fact that temperature gradients at the interface between the cold and hot sides of the colloid are stronger for the case of the temperature control TB = Tcold directly at the colloid.
3.3 Thermophoretic propulsion in “ideal” fluids
The coefficient aF of the conservative interaction between fluid particles plays an important role in determining the compressibility of the fluid, but also affects the diffusion coefficient and the fluid viscosity. Here, decreasing aF increases the fluid compressibility. Further, we investigate the extreme case when aF = 0, i.e., the case obtained when the fluid is most compressible. In this case, the equation of state is that of an ideal gas, similar to the MPC fluid model in ref. 20 and 24. The thermophoretic mobility of the Janus colloid is then again measured in this host fluid medium for both bounce-back and specular reflection BCs, and its dependence on the fluid–colloid interaction strength for both symmetric and asymmetric cap cases is determined.In the case of bounce-back BCs at the colloid–fluid interface, the thermophoretic mobilities as a function of the fluid–cap interaction strength are shown in Fig. 8(a). We find an initial decrease of the mobility with increasing cap–fluid interaction strength, followed by a subsequent weak recovery, and finally saturation with further increase of the interaction strength, for both symmetric and asymmetric fluid–cap interactions. This dependence of the thermophoretic mobility is qualitatively different from the behavior of a Janus colloid in a non-ideal fluid (with aF > 0). Also, the propulsion velocity in the ideal fluid for the symmetric cap case remains lower than that for asymmetric cap, again in contrast to the non-ideal fluid case. Our results show that in addition to an enhancement of mobility with cap asymmetry, the magnitude can be further controlled by interchanging the temperature of the caps, unlike the non-ideal fluid scenario.
For specular-reflection BCs in Fig. 8(b), we obtain a reversal of propulsion direction of the colloid in the ideal fluid by tuning the fluid–cap interaction. In the low fluid–cap interaction regime, the computed mobility is negative, which is equivalent to swimming in the direction towards the colloid's hot side. With increasing fluid–cap interaction strength, the corresponding mobility changes sign and becomes positive, i.e. the propulsion direction is inverted and the colloid swims toward its cold side. Over the entire range of the fluid–cap interactions studied in Fig. 8(b), the mobility increased gradually with the interaction strength before leveling off at very large fluid–cap interactions.
A comparison of Fig. 8(a) and (b) reveals that the trends of the mobilities over the entire range of cap repulsions for specular reflections and bounce-back collisions are quite different. In particular, the saturation value of the mobility for the colloid with symmetric caps remains higher than that with asymmetric caps for specular reflections unlike the bounce-back situation. Furthermore, interchanging the temperatures of the asymmetric caps leads to a change in the propulsion velocity, quite unlike the situation of non-ideal fluids.
In comparison to the MPC simulations in ref. 20 and 24, we also observe a reversal in the swimming direction by tuning the fluid–cap interaction strength. However, the direction reversal occurs only for the case of specular reflections (i.e., slip BCs) and relatively small fluid–cap interaction strength. In these simulations, the fluid–cap interaction can be considered purely repulsive, since aF = 0 of the suspending fluid. Thus, in case of bounce-back reflections the colloid always swims toward the cold side similar to the results for non-ideal fluid case, while in case of slip BCs, the colloid moves toward the cold side for strong fluid–cap repulsion and toward the hot side for weak fluid–cap repulsive interactions. This trend seems to be rather opposite to that in ref. 20 and 24, where fluid–colloid repulsive interactions lead to a swimming direction toward the hot side, while fluid–colloid attractive interactions result in swimming toward the cold side. In addition, the swimming direction of a Janus thermophoretic colloid has not been affected by the type of BCs (i.e., slip or no-slip) in the MPC simulations.20,24
3.4 Flow field around thermophoretic Janus colloids
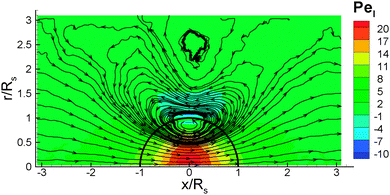
As the colloid swims, the flow field generated in the fluid can be found from our simulations. Fig. 9 shows the flow field in the lab frame, obtained by adding the velocity of self-propulsion vp to the fluid velocity v, since its magnitude has an opposite sign to the far-field fluid velocity (see Fig. 4 for example). The flow field indicates that the source-dipole contribution dominates, which is consistent with the conclusions from theory21 and simulations24,39 for a thermophoretic colloidal swimmer. The flow field in Fig. 9 is very similar to the theoretical predictions for a thin-cap limit21 (i.e., the thermal conductivity of the cap does not play a role), supporting the validity of the simulation results. The corresponding flow-field in MPC simulations24,39 is very close to a source-dipole approximation in the theory.21Finally, we determine the radial component vrsph of the velocity field v + vp in spherical coordinates as a function of the distance from the center of the colloid, see Fig. 10. The radial component of the velocity is measured at a particular angle, θ, relative to the symmetry axis of the colloid. Within the statistical accuracy of our simulations, we observe a power-law dependence with rsph, which is consistent with an inverse cubic power, vrsph ∼ 1/rsph3, for both an ideal-gas fluid with aF = 0, and a DPD fluid with non-zero aF. This behavior is unaffected by the different BCs used, and is in good agreement with the theoretical predictions21 and MPC simulations.24,39 We also compute the radial velocity as a function of the angle θ at a distance rsph = 1.5Rs from the center. The results are shown in Fig. 11 for different fluid interaction strengths and different BCs. We find an asymmetric radial velocity distribution around the colloid from the cold cap pole (θ = 0°) to the hot cap pole (θ = 180°). This dependence is in qualitative agreement with the theoretical predictions of ref. 21.
4 Discussion and conclusions
The swimming velocity of a thermophoretic Janus colloid strongly depends on different fluid–colloid interactions and BCs. The choice of BCs (i.e., slip or no-slip) affects viscous friction exerted on the colloid by the fluid, while different strengths of fluid–colloid repulsive interactions alter both, the heat exchange between the fluid and the colloid surface and the near-wall density fluctuations illustrated in Fig. 3. Thus, the repulsive strengths aiA and aiB also have an effect on the viscous friction for the case of bounce-back reflections. Perhaps, the simplest case is that with specular reflections in Fig. 6(b), since viscous friction between the colloid and the fluid can be neglected. In this case, the colloid mobility increases with increasing interaction strength, or equivalently when fluid particles are pushed further away from the surface of the swimmer. We expect that a larger distance between fluid particles and the colloid surface should lead to a reduction of heat exchange between the colloid and the fluid. In Fig. 6(b) for small aiA and aiB values, a fast heat exchange between the colloid and the fluid is expected. As the heat exchange is getting reduced for increasing fluid–colloid interaction strength, the swimming velocity is increasing. This indicates again that the temperature gradient between the cap and the fluid mainly determines colloid propulsion.The comparison of Fig. 6(a) and (b) for the stick and slip BCs have shown that the no-slip BCs also result in an enhancement of the swimming velocity for the low strengths of fluid–colloid interactions. This finding is rather counter-intuitive, since no-slip BCs lead to an additional friction on the colloid exerted by the fluid. Bounce-back reflections do not affect fluid particle distribution near the colloid in comparison to specular reflections, and therefore, it is plausible to expect no change in heat exchange between the colloid and the fluid at least through the heat conduction term in eqn (4). The particle kinetic energy also remains conserved for both bounce-back and specular reflections. One should expect differences in the potential energy for the different collision rules. For example, bounce-back reflections may lead to a slight elevation of temperature (2–5%) near a wall in comparison to a specular type of reflections, which has been found for the standard isothermal (non-energy-conserving) DPD.40 A local increase of temperature near the colloid surface would reduce conductivity between the colloid and the fluid, which would be consistent with an increase of the swimming velocity as discussed above for the fluid–colloid interactions. However, currently we cannot exclude that other effects are present and the interplay between viscous friction and heat exchange between the colloid and the fluid for various parameters needs to be investigated in much more detail.
Results for the ideal fluid have shown swimming trends qualitatively different from those for a non-ideal liquid. For instance, in case of bounce-back reflections the swimming velocity first decreases with increasing the fluid–colloid repulsive interaction strength for an ideal fluid (Fig. 8(a)), while in the corresponding case for a non-ideal fluid (Fig. 6(a)) the swimming velocity is increasing when the fluid–colloid interactions are getting stronger. In the case of specular reflections, the trends of an increase of the swimming velocity with increasing the fluid–colloid interaction strength (Fig. 6(b) and 8(b)) are similar for both fluid types; however, for the ideal-fluid case the swimming velocity changes its sign, which means that the thermophoretic swimmer changes its swimming direction. From Fig. 8(a) and (b) we can also conclude that the swimmer's velocity in case of an ideal fluid becomes nearly independent of the repulsion strength and type of the fluid particle reflection, when aiA ≳ 100 and aiB ≳ 100, since such a repulsion strength is large enough to nearly push all fluid particles away from a layer of the cutoff radius rc′ of the fluid–colloid repulsive interaction evidenced from fluid-density distributions. Note that this occurs due to a high compressibility of an ideal fluid, while for a non-ideal fluid the layer of rc′ still remains populated by fluid particles. Therefore, the heat exchange between the colloid and the fluid is expected to be affected by the fluid–colloid interactions much more for ideal fluids than that for non-ideal liquids. Another difference between the ideal and non-ideal fluid cases is density gradients, which are much stronger for an ideal fluid than for a non-ideal liquid, even though temperature distributions are not drastically different. For the case of a non-ideal fluid, the changes in density are within a few percent from an average fluid density, while for the ideal-fluid case the density may change up to 30–40% from an average density. Thus, the fluid-density changes are more realistic in the non-ideal fluid case. However, currently it is not clear how these differences between the ideal and non-ideal fluid cases lead to different swimming behavior of the thermophoretic colloid.
A qualitative explanation for the behavior of a (homogeneous) colloidal particle in a temperature gradient has been sketched in ref. 41 for MPC simulations. A temperature gradient results in an inverse gradient of density and thus, the density around the cold side is larger than that at the hot side. Hence, a higher density on one side may result in a stronger interaction and lead to the colloid motion. A change in fluid–colloid interactions (e.g., repulsion or attraction) may invert this balance and force a colloid to move to an opposite direction. This idea is equivalent to having a pressure gradient across the colloid poles and the fluid–colloid interactions seem to provide a control for it. However, this argument for the generation of a pressure difference is not completely conclusive, because for an ideal gas in local thermodynamic equilibrium, the pressure p = kBTρ should be constant due to mechanic stability.
Swimming of the Janus colloid toward the hot side in Fig. 8(b) for a case of ideal fluid, specular reflections, and weak fluid–colloid interactions is consistent with this proposition. Note that in case of specular reflections no exchange of momentum occurs between the fluid and colloid in the tangential direction, and therefore, a driving force for the swimming colloid is likely to come from a pressure gradient across the colloid poles. Then, as we increase the repulsion between the fluid and colloid in Fig. 8(b), the pressure difference is turned around and the thermophoretic swimmer moves toward an opposite direction. The comparison of the specular-reflection case in Fig. 8(b) to the bounce-back BCs in Fig. 8(a) indicates that exchange of momentum between the fluid and colloid in the tangential direction also contributes to the swimmer propulsion, since the mobility of colloid is different for these two conditions. Note that no pressure differences are expected between the specular and bounce-back cases, because both conditions lead to the same density distributions and the same exchange of momentum between the fluid and colloid in the normal direction. Currently, we cannot identify the swimming effect due to the tangential momentum exchange, but it is clearly present in these systems.
The application of the idea above to the case of a non-ideal fluid is not so straightforward, because the density gradients in this case are much smaller than in the case of an ideal fluid, as already mentioned. In fact, Fig. 6(b) for specular BCs indicates that a colloid does not swim for the case of vanishing fluid–colloid interactions, which implies no pressure gradient across the colloid poles. As the repulsion between the fluid and colloid is increased in Fig. 6(b), the swimmer starts moving toward the cold side indicating that a pressure difference across the colloid poles must have developed. The comparison of results in Fig. 6(a) and (b) for specular and bounce-back BCs, respectively, implies again that the exchange of momentum between the fluid and colloid in the tangential direction must contribute to colloid's swimming. Here, for the case of bounce-back BCs in Fig. 6(a), the colloid has a non-zero swimming velocity for vanishing fluid–colloid interactions. Thus, the effect of tangential momentum exchange on the propulsion of a thermophoretic swimmer needs to be investigated further.
Finally, we would like to discuss the differences between our simulations with an ideal fluid and the MPC simulations of a similar Janus-colloid swimmer.20,22,24 Note that a direct comparison has not been intended. A seeming dissimilarity is the dependence of swimming velocity on the fluid–colloid interaction strength. In the present simulations the thermophoretic colloid swims toward the cold side if we increase the repulsive strength of fluid–colloid interactions, while in ref. 20 and 24 repulsive interactions between a colloid and a fluid result in the motion toward the hot side. A closer look at the details of the simulation setups reveals that the fluid–colloid interactions in these two studies may have a different meaning. In our setup, the repulsive interactions directly affect heat exchange between the colloid and the fluid, since larger distances between them reduce the exchange of heat. In ref. 20 and 24 the temperature in a thin layer near the colloid is controlled, and thus, the repulsive interactions affect the number of particles to be thermalized in this layer. Hence, in the present simulations repulsive interactions affect conductivity between the colloid and the fluid, while in ref. 20 and 24 such conductivity effects are omitted, which is equivalent to a very high colloid–fluid conductivity such that a thin layer of fluid particles near the colloid receives heat instantly. Another difference between the two simulation setups is temperature control. In our simulations, generated heat is taken away at the cold side of the colloid or far away from the colloid, while in ref. 20 and 24 the excess heat is taken away uniformly from the whole fluid. This may result in different temperature distributions around the colloid affecting its swimming behavior. Finally, there exist a fundamental difference between the simulation methods. In MPC, heat exchange and temperature gradients are sustained only through the kinetic energy of fluid particles, while in eDPD an internal energy is simulated explicitly. In fact, the internal energy is much larger than the contributions from kinetic and potential energies, since Cv ≫ 1. Simulations with Cv ≈ 1 appear not to be stable in eDPD, since then there is a chance that internal temperature of a particle may become negative, for instance, due to the random conductivity term in eqn (4). The discussed reasons do not allow us to make a detailed comparison, which would require more consistent setups.
In conclusion, we have presented simulations of the dynamics of a thermophoretic colloid for different fluid–colloid interactions and temperature controls. Different temperature-control strategies have a minor effect on the colloid swimming velocity. The fluid–colloid interactions have a strong effect on the colloid behavior and directly affect heat exchange between the colloid surface and the fluid. Our results show that a reduction of the heat exchange leads to an enhancement of colloid's thermophoretic mobility, since larger temperature gradients near the colloid surface are formed. The flow-field generated by the colloid appears to be dominated by a source-dipole contribution in agreement with the recent theoretical21 and simulation20,24 predictions. However, the differences in colloid's mobility between the cases with non-ideal and ideal fluids and in comparison to the MPC simulations20,24 are yet to be understood. We hope that this work will generate further efforts and discussions in this area of research.
Acknowledgements
We would like to thank Marisol Ripoll for discussions. Dmitry A. Fedosov acknowledges funding by the Alexander von Humboldt Foundation. We also gratefully acknowledge a CPU time grant by the Jülich Supercomputing Center. Partial financial support by the Deutsche Forschungsgemeinschaft via the priority program “Microswimmers” (SPP 1726) is thankfully acknowledged.References
- R. A. L. Jones, Soft machines: nanotechnology and life, Oxford University Press, New York, 2004 Search PubMed.
- G. A. Ozin, I. Manners, S. Fournier-Bidoz and A. Arsenault, Adv. Mater., 2005, 17, 3011–3018 CrossRef CAS.
- W. F. Paxton, S. Sundararajan, T. E. Mallouk and A. Sen, Angew. Chem., Int. Ed., 2006, 45, 5420–5429 CrossRef CAS PubMed.
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- B. J. Williams, S. V. Anand, J. Rajagopalan and M. T. A. Saif, Nat. Commun., 2014, 5, 3081 Search PubMed.
- S. Sareh, J. Rossiter, A. Conn, K. Drescher and R. E. Goldstein, J. R. Soc., Interface, 2013, 10, 20120666 CrossRef PubMed.
- T. Sanchez, D. Welch, D. Nicastro and Z. Dogic, Science, 2011, 333, 456–459 CrossRef CAS PubMed.
- D. Schamel, A. G. Mark, J. G. Gibbs, C. Miksch, K. I. Morozov, A. M. Leshansky and P. Fischer, ACS Nano, 2014, 8, 8794–8801 CrossRef CAS PubMed.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef.
- S. Thakur and R. Kapral, J. Chem. Phys., 2011, 135, 024509 CrossRef PubMed.
- M. N. Popescu, S. Dietrich, M. Tasinkevych and J. Ralston, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 351–367 CrossRef CAS PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- D. Rings, R. Schachoff, M. Selmke, F. Cichos and K. Kroy, Phys. Rev. Lett., 2010, 105, 090604 CrossRef PubMed.
- R. Golestanian, Physics, 2010, 3, 108 CrossRef.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061401 CrossRef.
- T. Bickel, A. Majee and A. Würger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012301 CrossRef.
- P. de Buyl and R. Kapral, Nanoscale, 2013, 5, 1337–1344 RSC.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810–8815 RSC.
- M. Yang, A. Wysocki and M. Ripoll, Soft Matter, 2014, 10, 6208–6218 RSC.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef.
- P. Español, Europhys. Lett., 1997, 40, 631–636 CrossRef.
- J. B. Avalos and A. D. Mackie, Europhys. Lett., 1997, 40, 141–146 CrossRef CAS.
- X. Fan, N. Phan-Thien, S. Chen, X. Wu and T. Y. Ng, Phys. Fluids, 2006, 18, 063102 CrossRef.
- D. A. Fedosov, G. E. Karniadakis and B. Caswell, J. Chem. Phys., 2008, 128, 144903 CrossRef PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Clarendon Press, New York, 1991 Search PubMed.
- Z. Li, Y.-H. Tang, H. Lei, B. Caswell and G. E. Karniadakis, J. Comput. Phys., 2014, 265, 113–127 CrossRef CAS.
- M. Lísal, J. K. Brennan and J. B. Avalos, J. Chem. Phys., 2011, 135, 204105 CrossRef PubMed.
- Q. Chen, J. K. Whitmer, S. Jiang, S. C. Bae, E. Luijten and S. Granick, Science, 2011, 331, 199–202 CrossRef CAS PubMed.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- J. R. Henderson and F. van Swol, Mol. Phys., 1984, 51, 991–1010 CrossRef CAS.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Adv. Polym. Sci., 2009, 221, 1–87 CAS.
- M. Yang and M. Ripoll, Soft Matter, 2013, 9, 4661–4671 RSC.
- D. C. Visser, H. C. J. Hoefsloot and P. D. Iedema, J. Comput. Phys., 2005, 205, 626–639 CrossRef.
- D. Lüsebrink, M. Yang and M. Ripoll, J. Phys.: Condens. Matter, 2012, 24, 284132 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2015 |