DOI:
10.1039/C5SM01333J
(Paper)
Soft Matter, 2015,
11, 5947-5954
Modeling the stretching of wormlike chains in the presence of excluded volume†
Received
30th May 2015
, Accepted 23rd June 2015
First published on 24th June 2015
Abstract
We propose an interpolation formula (the EV-WLC relation) for the force–extension behavior of wormlike chains in the presence of hard-core excluded volume interactions, analogous to the classic interpolation formula from Marko and Siggia for ideal wormlike chains. Using pruned-enriched Rosenbluth method (PERM) simulations of asymptotically long, discrete wormlike chains in an external force, we show that the error in the EV-WLC interpolation formula to describe discrete wormlike chains is systematically smaller than the error in the Marko–Siggia interpolation formula, except for the saturation region in which both formulas have the same limiting behavior. We anticipate that the EV-WLC interpolation formula will prove useful in the coarse-graining of wormlike chain models for dynamic simulations. Related results for the excess free energy due to excluded volume provide strong support for the physical basis of the Pincus regime.
1 Introduction
Stretching a polymer chain in the presence of an external force is a classic problem in polymer physics.1 In general, entropic and enthalpic intramolecular interactions must be considered for an accurate description of polymer elasticity.2 An ideal flexible polymer chain with no enthalpic interactions (which, for our purposes, means no excluded volume) can be modeled as a simple random walk with a Gaussian distribution function for the end-to-end extension. In the limit of low forces, equilibrium thermodynamics suggests that the force f required to stretch a chain is linear in the extension. For an ideal freely-jointed chain, the (dimensionless) entropic force is given by the Hookean expression| |  | (1) |
where F = flp/kBT is the dimensionless force for a chain of persistence length lp with kBT being the Boltzmann factor, and z = X/L is the fractional extension for a chain of contour length L with X being the extension along the force direction. For most practical situations, the elasticity needs to be modified to consider the effects of high forces (i.e. finite extensibility) and excluded volume interactions. In the limit of high forces, a partition function approach can be used to describe the elasticity of an ideal freely-jointed chain,| |  | (2) |
where  is the Langevin function, which has no analytical inverse.
is the Langevin function, which has no analytical inverse.
Wormlike chains represent a different class of macromolecules with a uniform distribution of bending stiffness along the polymer backbone. Over 20 years ago, Marko and Siggia3 proposed the interpolation formula
| |  | (3) |
to describe the extension of a wormlike chain under tension. The Marko–Siggia formula correctly limits to
eqn (1) in the low-force limit and the saturation value
FWLC ≅ [2(1 −
z)]
−2 in the high-force limit.
Eqn (3) only deviates by a few percent from the force–extension result computed numerically from the Hamiltonian of an ideal wormlike chain.
3 As a result, the Marko–Siggia force relation has found widespread use, most notably in the description of the force–extension behavior of DNA
4 below the B-to-S transition at 70 pN.
5,6 It is used ubiquitously as the spring-force in bead-spring models of wormlike chains such as DNA.
7,8
For real polymer chains, incorporation of excluded volume interactions is challenging and has been considered using renormalization approaches.1 In a classic paper, Pincus used scaling theory to show that the restoring force for real polymers scales non-linearly with extension in the limit of low forces,9
Clearly, the elastic behavior for real polymer chains is strikingly different than the Hookean response for ideal chains.
A key limitation of the Marko–Siggia and Langevin force relations is that these relations were obtained for ideal chains, and thus cannot account for the excluded volume interactions and the concomitant nonlinear-low force elasticity of a real chain. For very stiff chains, where the persistence length lp is much larger than the backbone width w, the excluded volume is weak.10,11 However, for single-stranded DNA and many synthetic polymers, the monomer anisotropy ratio lp/w is modest and excluded volume effects can be important.10 It would be highly desirable to have an interpolation formula similar to eqn (3) to interpret force–extension experiments with such molecules.12,13 Such a formula is even more important for modeling the behavior of these polymers in flow using coarse-grained, bead-spring models. For efficient modeling, each spring must represent a large number of persistence lengths. When bead-spring models are used to study polymer dynamics at the relatively low flow strengths encountered in many experimental systems, excluded volume within a spring can become important.
In the present contribution, we propose an interpolation formula for wormlike chains that connects the Pincus regime9 in the presence of strong excluded volume interactions to the Marko–Siggia result3 for ideal wormlike chains. Using simulations of a discrete wormlike chain model, we show that this interpolation formula provides a good description of the force–extension behavior for all values of the monomer anisotropy ratio lp/w we studied over experimentally relevant values of the fractional extension. A key challenge in our work is simulating chains with high resolution of the chain backbone up to a sufficiently high molecular weight to observe the Pincus regime.14 While it is possible to reach such high molecular weights by reducing the number of degrees of freedom with a lattice model15 or by reducing the resolution of the chain backbone with a bead-rod model,16 the off-lattice pruned-enriched Rosenbluth method (PERM) used previously to study discrete wormlike chains in free solution10 and in confinement17–21 is readily adapted to the force–extension problem.15 Using this approach, we are able to simulate asymptotically long chains down to small values of the fractional extension (z ≈ 0.1) over a wide range of lp/w values, thereby accessing all of the relevant regimes. The results of these simulations not only allow us to assess the accuracy of our interpolation formula relative to the Marko–Siggia force relation, but also provide strong support for the existence of the Pincus regime.
2 Interpolation formula for the stretching of real wormlike chains
We propose that eqn (3) should be replaced by an excluded volume-wormlike chain (EV-WLC) interpolation formula consisting of two parts,The quantity| |  | (6) |
is the dominant contribution for small z, with the constant 0.21 determined from a fit to our simulation data. Conversely, the term| |  | (7) |
is the dominant contribution at high z. Note that the leading-order term in Fhigh is O(z2) for small z. Since the constant 0.21 in eqn (6) was determined by fitting to simulation data for a discrete wormlike chain model, this parameter may differ for an interpolation formula describing a continuous wormlike chain model. However, it is worth keeping in mind that the overall form of the EV-WLC interpolation formula (i.e., the limiting behavior and the crossovers between different regimes) does not assume a discrete wormlike chain model.
The rationale for this formula is threefold:
First, when the chain is strongly stretched (z ≈ 1), excluded volume should not be important and the Marko–Siggia result for ideal chains applies. It is readily confirmed that eqn (5) reduces to eqn (3) in this limit. Note that this saturation value is correct for a continuous wormlike chain. For a discrete wormlike chain, which we will use for our simulations here, the saturation value shifts from the wormlike chain behavior F ∼ (1 − z)−2 to the freely-jointed chain result F ∼ (1 − z)−1 for sufficiently high forces.22
Second, for small values of the extension, the leading-order behavior of eqn (5) should reduce to Pincus’s scaling result for weak stretching in the presence of excluded volume.9 Pincus’s theory is based on the existence of a tensile screening length ξt = kBT/f that competes with the Flory radius RF = L3/5lp1/5w1/5 for a wormlike chain of contour length L.2 The force–extension behavior can be obtained by a scaling argument where tensile blobs of size ξt contain a contour length
| | | Lblob = ξt5/3lp−1/3w−1/3 | (8) |
The fractional extension is then given by
z =
ξt/
Lblob, leading to
9This is indeed the leading-order behavior of
Flow. Since
Fhigh ∼
O(
z2) for small
z, and it is also the leading-order behavior of
eqn (5) for small
z.
Third, Flow should exhibit a crossover from Pincus behavior to ideal wormlike chain behavior. The Pincus regime crosses over to the ideal scaling regime when the tensile blob size is commensurate with the thermal blob size, ξt ≅ lp2/w.16 The crossover point is
with a corresponding fractional extension
This is indeed the fractional extension where the two quantities in the denominator of
Flow are balanced.
Before moving on, we should note that eqn (5) is not intended to be a model for freely-jointed chains. The force–extension interpolation behavior of freely-jointed chains has been addressed previously in a similar interpolation approach by Radhakrishnan and Underhill.23Eqn (5) should not reduce to a freely-jointed chain model in the limit lp = w because the saturation behavior of the wormlike chain model is qualitatively different than a freely-jointed chain model.22 For this reason, we only consider cases lp > w to test the EV-WLC formula.
3 Simulation method
We obtained force–extension data for a discrete wormlike chain model10,24 using pruned-enriched Rosenbluth method (PERM) simulations.25 Our simulations are the off-lattice analog of previous lattice simulations by Hsu and Binder.15 The discrete wormlike chain model consists of a series of N inextensible bonds of length a. We use touching beads such that a = w, where w is the width of the chain. The contour length of the chain is thus L = Nw = (Nb − 1)w, where Nb is the number of beads. A bending energy| |  | (12) |
is imposed between contiguous trios of beads, where β = (kBT)−1 is the inverse Boltzmann factor and θj is the angle formed by the beads. The bending energy parameter κ is related to the persistence length by21,26| |  | (13) |
Excluded volume interactions are treated by a hard core potential| |  | (14) |
between non-contiguous beads.
In each tour of the PERM simulations, the first bead is placed at the origin. Due to the translational invariance of the imposed force, this initial condition leads to no loss of generality. For the nth chain growth step, we make k = 5 trial moves by selecting points on the unit sphere from the discrete wormlike chain distribution in the absence of excluded volume or the external force.17 As a result, the reference state for our simulations is an ideal discrete wormlike chain at zero force. The jth trial move to place the nth bead at position r(j)n is assigned an atmosphere
| | | a(j)n = exp[−β(UEV − f·r(j)n)] | (15) |
where
UEV is the excluded volume caused by placing this bead and
f is the force. We then select one of the
k trial moves with probability
| | 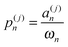 | (16) |
where
| |  | (17) |
is the Rosenbluth weight for step
n.
During a given tour, we track the cumulative weight of a configuration,
| |  | (18) |
and enforce pruning and enriching steps
via Grassberger’s algorithm.
25 If at some step
n a chain’s cumulative weight is too high relative to the target weight, we “enrich” by generating a copy of the configuration and splitting the weight
Wn between the two copies. Conversely, if at some step
n the chain’s cumulative weight is too low relative to the target weight, it is “pruned” and growth terminates at that step. In Grassberger’s algorithm, the target weight is adjusted on-the-fly based on the current status of the simulation to improve sampling efficiency.
25 For each value of
lp/
w, we conducted at least 10
5 tours so that the standard error of the mean, assumed to be the sampling error, is small compared to the symbol size in the plots.
As a chain growth method, PERM naturally produces equilibrium data as a function of molecular weight. For a chain consisting of n steps, the average fractional extension is
| |  | (19) |
where
W(t)n is the cumulative weight of configuration
t in the ensemble and
z(t)n is the corresponding extension of the configuration in that tour
| |  | (20) |
with
r(t)n the vector position of the
nth bead of configuration
t and (
n − 1)
w is the contour length at step
n. We run our simulations to sufficiently high molecular weights such that
z becomes independent of
n. The number of beads used for the data in this paper appear in Tables S1 and S2 in the ESI.
† As a result, we simply report the asymptotic value of
z in what follows. Evidence in support of this claim is provided in Fig. S1 of the ESI.
†
In the course of our discussion, it will also prove useful to compute the excess free energy ΔFEV caused by excluded volume. For this calculation, we repeat our simulations at a force f setting UEV = 0. In PERM, the free energy for growth out to step n relative to the reference state is
where the angle brackets indicate an average value. The excess free energy for chains grown out to step
n is then given by
20| |  | (22) |
where
Widealn is the cumulative weight from PERM simulations in the absence of excluded volume.
4 Results
We begin by comparing the simulation data we obtained for real discrete wormlike chains to the response of ideal continuous wormlike chains given by the Marko–Siggia interpolation formula in eqn (3). As shown in Fig. 1, the force–extension behavior at high stretch is insensitive to the monomer anisotropy ratio lp/w. However, the elastic behavior depends on the monomer anisotropy ratio at low forces. For a stiff chain, the deviation between the Marko–Siggia interpolation formula and the simulation data is small, even at rather small values of the fractional extension. For the more flexible chain, the deviation from the Marko–Siggia interpolation formulation is substantial and persists over a wide range of fractional extensions. In both cases, the EV-WLC interpolation formula reasonably captures both the saturation behavior at high forces and the deviation from the Marko–Siggia interpolation formula at low forces.
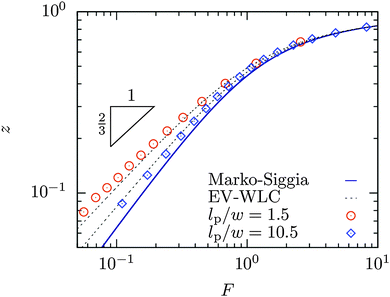 |
| | Fig. 1 Comparison between discrete wormlike chain simulation data and the Marko–Siggia interpolation formula (solid line) in eqn (3) and the EV-WLC interpolation formula (dashed lines) in eqn (5) for a relatively flexible chain (lp/w = 1.5) and a stiff chain (lp/w = 10.5). The triangle indicates the Pincus scaling in eqn (4). Similar plots for other values of lp/w are provided as Fig. S2 in the ESI.† | |
We included the Pincus scaling in eqn (4) beside the low-force data in Fig. 1. The data do appear to follow Pincus scaling for sufficiently low forces, and we will address this issue in a quantitative manner shortly. For the moment, it suffices to note that the Pincus scaling is not a good description of the chain for all forces, which follows directly from its derivation.9 As a result, we defer the error in the Pincus scaling to a later point, and focus for the moment exclusively on the Marko–Siggia interpolation formula and the EV-WLC interpolation formula.
The most important question to resolve, from a practical standpoint, is when the stretching of semiflexible chains should be modeled by the Marko–Siggia interpolation formula in eqn (3) and when the EV-WLC interpolation formula in eqn (5) provides a better description. To answer this question in a quantitative manner, we evaluated the error in these formulas for discrete wormlike chains as
| |  | (23) |
with
z being the value obtained from the simulation and
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif)
being the value from the interpolation formulas in
eqn (3) or (5). Naturally, the error is a function of the force.
Fig. 2 shows the error for the data in
Fig. 1. As expected, the error in the Marko–Siggia formula increases as the force decreases due to excluded volume effects. Moreover, for the stiff chain with
lp/
w = 10.5, we see that the Marko–Siggia interpolation formula indeed only exhibits errors of a few percent once the excluded volume effects are suppressed at high forces. The error also increases for the EV-WLC formula as the force decreases, since the interpolation formula only approximately captures the crossover between Pincus scaling and the Hookean response.
 |
| | Fig. 2 Plot of the error ε (eqn (23)) between simulation data and the Marko–Siggia interpolation formula (red circles) and the EV-WLC interpolation (blue triangles) as a function of dimensionless force F for (a) a relatively flexible chain (lp/w = 1.5) and (b) a stiff chain (lp/w = 10.5). Similar plots for other values of lp/w are provided as Fig. S3 in the ESI.† | |
The data in Fig. 2 also provide insight into modeling the stretching of double-stranded DNA, which is a very common model polymer whose monomer anisotropy in a high ionic strength buffer is similar to lp/w = 10.5.10 Our data for discrete wormlike chains support the use of the Marko–Siggia interpolation formula in models of double-stranded DNA in flow.7,8 However, it is worth noting that lp/w decreases as the ionic strength decreases because the electrostatic interactions affect the persistence length and the width differently.10 For very low ionic strengths, the EV-WLC interpolation formula may prove to be more accurate for double-stranded DNA than the Marko–Siggia formula.
We have obtained data at many different monomer anisotropies, and plots similar to Fig. 1 and 2 for these other values of lp/w are provided as Fig. S2 and S3 in the ESI.†Fig. 3 summarizes the overall result, reporting the average error over all forces where we have obtained data. The average error for the EV-WLC interpolation is always smaller than the average error in the Marko–Siggia interpolation formula, independent of lp/w. A closer inspection of the error as a function of force in Fig. 2 and the additional data provided in Fig. S3 of the ESI† shows that this trend persists for all values of the force except the saturation regime, where the two interpolation formulas are essentially the same. Thus, we expect that the EV-WLC interpolation formula in eqn (5) will prove quite useful for modeling relatively flexible wormlike chains.
 |
| | Fig. 3 Average error, εavg, for the Marko–Siggia and EV-WLC interpolation formulas as a function of lp/w. | |
The error in both the Marko–Siggia and EV-WLC formulas both increase as the chain becomes more flexible. For the Marko–Siggia interpolation formula, we suspect that much of this error is due to a failure capture the low-force behavior, as Fig. 3 reports the average value of the error over all forces. For the EV-WLC formula, we previously proposed that the error arises primarily due to the approximate way that eqn (5) treats the cross-over between the Pincus scaling and Hookean behavior. However, for both the Marko–Siggia and EV-WLC formulas, some of the error may also arise from the use of theories for continuous chains to describe data obtained from simulations of discrete wormlike chains. Indeed, as lp/w decreases, the discreteness of the model becomes increasingly important. For both interpolation formulas, the error in the interpolation formula increases as the discreteness of the model increases.
In the course of obtaining the force–extension data required to produce Fig. 3, we obtained a large amount of data that should correspond to the Pincus regime. Thus, it is worthwhile to take a moment to see whether our data are consistent with eqn (9) and (11) and to assess quantitatively the error between the Pincus force law and the simulation data. For this purpose, we also included data for a freely-jointed chain (lp = w) in Fig. 4. While the freely-jointed chain does not give the same limiting behavior as a wormlike chain at high extensions, it produces a Pincus regime. Fig. 4a provides a rescaled force–extension plot demonstrating the collapse in the Pincus regime with a crossover corresponding to eqn (11). To test the scaling in eqn (9), we extracted the data corresponding to the Pincus regime and used linear regression to determine the prefactor and exponent for the scaling law. This analysis led to an exponent F0.71. This exponent is consistent with Pincus’s analysis using the Flory radius2RF = Lνw2ν−1l2−3νp, which leads to16
| | | F ∼ zν/(1−ν)(lp/w)(2ν−1)/(1−ν) | (24) |
The change in the exponent from
z ∼
F2/3 in
eqn (9) to
z ∼
F0.71 in
eqn (24) using
ν = 0.587597 as the Flory exponent
27 is identical to the case of the scaling law for the extension of semiflexible polymers confined in channels in the de Gennes regime.
28 For the data in
Fig. 4 corresponding to the Pincus regime, the force–extension
| |  | (25) |
where the prefactor is obtained from the linear regression in
Fig. 4, leads to an average error of 0.036.
Fig. 4b provides the corresponding values of the excess free energy due to excluded volume, demonstrating that the onset of excluded volume interactions is coincident with the Pincus scaling for the chain extension.
 |
| | Fig. 4 Plot of (a) the rescaled extension zlp/w versus the rescaled force Flp/w and (b) excess free energy per unit length, βΔFEV/L, for different values of lp/w. The vertical dot-dashed line denotes the boundary of the (shaded) Pincus regime. The dashed line in panel (a) is the regression result to the Pincus regime. The symbols for different values of lp/w are the same in panel (a) and (b). | |
5 Discussion
The key result of our paper is the development and evaluation of the EV-WLC interpolation formula in eqn (5). Based on the error analysis in Fig. 3 it appears that the EV-WLC interpolation formula provides a good description of the force–extension behavior of wormlike chains. However, we need to be careful about extending the EV-WLC interpolation formula in eqn (5) to polymers with isotropic monomers where lp becomes very close to the chain width w. As pointed out by Dobrynin et al.,22 at very high forces, the saturation behavior switches from the wormlike chain result to the flexible chain result (i.e. the Langevin function) as the bending energy decreases. In principle, it should be possible incorporate this crossover for the saturation behavior for arbitrary stiffness κ into our EV-WLC interpolation formula, since Dobrynin et al.22 have already determined how to interpolate between the flexible and wormlike stretching for ideal chains.
The EV-WLC interpolation formula is most useful for modest ratios of lp/w, and these values characterize a number of important polymer systems. Single-stranded DNA is a polymer with enormous biological relevance that exhibits nearly isotropic monomers. There is a growing experimental interest in using single-stranded DNA as a model polymer.11,29 Using biochemical synthesis methods, single-stranded DNA molecules with ≈104 bases containing designer sequences with minimal base paring can readily be synthesized and uniformly labeled with fluorescent dyes, thereby enabling the direct visualization of single chain dynamics using fluorescence microscopy.29 Due to the very small persistence length of single-stranded DNA (lp ≈ 1–2 nm under modest salt concentrations),12 single-stranded DNA chains with contour lengths L ≈ 15–20 μm correspond to NK ≈ 7500–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Kuhn segments compared to only NK ≈ 150–190 for double-stranded DNA of similar contour length. The ability to study single chain dynamics of long chain, highly flexible polymers opens a new window into observing non-linear phenomena and chain dynamics in flow, which are heavily influenced by dominant EV and intramolecular hydrodynamic interactions.30 From this perspective, the non-equilibrium flow dynamics of highly flexible polymers such as single-stranded DNA is expected to differ qualitatively compared to linear λ-DNA of similar contour length L. Our enthusiasm towards using the EV-WLC model for single-stranded DNA is tempered by the possibility that the results could be affected by torsional constraints, which are included in some coarse-grained models, such as the 3-SPN model,31 but not in others, such as OX-DNA.32 Ultimately, the importance (or lack thereof) of torsion on the force–extension behavior of ssDNA is a question that needs to be resolved experimentally. Our EV-WLC formula provides a framework for addressing this question, since it assumes no torsional potential.
000 Kuhn segments compared to only NK ≈ 150–190 for double-stranded DNA of similar contour length. The ability to study single chain dynamics of long chain, highly flexible polymers opens a new window into observing non-linear phenomena and chain dynamics in flow, which are heavily influenced by dominant EV and intramolecular hydrodynamic interactions.30 From this perspective, the non-equilibrium flow dynamics of highly flexible polymers such as single-stranded DNA is expected to differ qualitatively compared to linear λ-DNA of similar contour length L. Our enthusiasm towards using the EV-WLC model for single-stranded DNA is tempered by the possibility that the results could be affected by torsional constraints, which are included in some coarse-grained models, such as the 3-SPN model,31 but not in others, such as OX-DNA.32 Ultimately, the importance (or lack thereof) of torsion on the force–extension behavior of ssDNA is a question that needs to be resolved experimentally. Our EV-WLC formula provides a framework for addressing this question, since it assumes no torsional potential.
On the chemistry side, a broad class of synthetic polymers would also be described by the EV-WLC interpolation formula. In particular, we anticipate that the EV-WLC formula will describe the elastic behavior of synthetic polymers that have bulky side groups but do not form helical structures, thereby maintaining modest values of lp/w. In many ways, we do not yet know which polymers will be described by the EV-WLC formula because the low-force elasticity has not yet been rigorously investigated for most synthetic polymers using single molecule force spectroscopy. Whereas AFM can faithfully measure the high-force elasticity of single polymers, magnetic tweezers are one method capable of interrogating the low-force regime; however, this approach has only been applied to a handful of polymers such as single-stranded DNA12 and poly(ethylene glycol).13
Poly(ethylene glycol) or PEG presents an interesting case in the context of developing interpolation formulas for chain elasticity. Gaub and coworkers33 performed AFM measurements on PEG and observed that the polymer forms water-mediated superstructures in aqueous solutions. As a result, and perhaps unexpectedly, PEG is well described by the Marko–Siggia force relation (eqn (3)) in the limit of high forces in water. On the other hand, stretching PEG in an aprotic solvent (hexadecane) resulted in force–extension curves that were well fit by the inverse Langevin function (eqn (2)), which is characteristic of stretching a flexible polymer in a theta solvent in the absence of EV interactions. Recently, magnetic tweezers were used to probe the force–extension behavior of PEG in the low force regime,13 which revealed that PEG exhibits both the Pincus and Hookean regimes in aqueous solutions. However, the Pincus regime only survives up to very small extensions z ≈ 0.06, perhaps due to local rigidification of the polymer backbone due to the formation of superstructures in aqueous solution. From this view, it is clear that the existence of solvent–polymer interactions for PEG results in an increase in monomer rigidity and somewhat unexpected behavior. Overall, the lessons from these results clearly illustrate that the details of the chemistry, solvent interactions, and local molecular structure are key to determining the emergent force–extension behavior for any macromolecule.
The availability of the EV-WLC interpolation formula opens up a new avenue for coarse-grained modeling of such polymers in flow. In typical bead-spring models, a polymer chain is described by a series of beads (friction points) connected by massless springs. The entropic penalty for stretching the chain is captured by a spring force, while enthalpic effects arising from intramolecular excluded volume interactions are imposed by a pairwise potential between beads. An alternate approach is to use eqn (5) to simultaneously capture the effects of stretching and the internal excluded volume interactions due to the subchain represented by the spring. We envision that such a model could prove very useful for modeling the dynamics of such polymers in flow.
While our primary emphasis in this paper is the development and testing of the EV-WLC interpolation formula, the results we have obtained for stretching in the Pincus regime should also be viewed in light of the existing simulation and experimental literature. From the simulation side, our data are part of a growing body of literature14–16 demonstrating the existence of the Pincus regime, that is, a low-force non-linear elasticity for polymers in a good solvent. Our key contributions in this respect are methodological, showing that off-lattice PERM simulations of a discrete wormlike chain model can reach sufficiently high molecular weights to observe Pincus scaling even for rather stiff chains, and in the thermodynamics of the Pincus regime, with Fig. 4b clearly demonstrating that the Pincus regime exists due to excluded volume interactions. From the experimental side, moving forward, it will be worthwhile to see how our data relate to the force–extension properties of single-stranded DNA12 and new classes of synthetic polymers that can be studied using magnetic tweezers.13
6 Conclusions
In the present contribution, we have shown that an interpolation formula that incorporates excluded volume interactions leads to more accurate predictions of the force–extension behavior of discrete wormlike chains than the classic Marko–Siggia interpolation formula, which was developed for ideal continuous wormlike chains. The EV-WLC interpolation formula will prove particularly important for polymers with relatively small range of monomer anisotropies lp/w, as these values characterize many important experimental systems such as single-stranded DNA and synthetic polymers that contain bulky side groups but do not form helices. We anticipate that the EV-WLC interpolation formula will prove useful as a model for the force–extension behavior of such polymers as such experimental data become available.12,13 Even more importantly, we expect that the EV-WLC interpolation formula will provide a quantitatively accurate force law for coarse-grained simulations of these polymers in flow.
Acknowledgements
We thank Abhriam Muralidhar for useful discussions on PERM. This work is supported by the NSF Grant No. CBET-1262286 to KDD and NSF Grant No. CBET-1254340 and the Camille & Henry Dreyfus Foundation to CMS. We also acknowledge the computational resources provided by the Minnesota Supercomputing Institute.
References
-
P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, 1979 Search PubMed.
-
M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Science, 1994, 265, 1599–1600 CAS.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J.-L. Viovy, D. Chatenay and F. Caron, Science, 1996, 271, 792–794 CAS.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS.
- E. S. G. Shaqfeh, J. Non-Newtonian Fluid Mech., 2005, 130, 1–28 CrossRef CAS PubMed.
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- P. Pincus, Macromolecules, 1976, 9, 386–388 CrossRef CAS.
- D. R. Tree, A. Muralidhar, P. S. Doyle and K. D. Dorfman, Macromolecules, 2013, 46, 8369–8382 CrossRef CAS PubMed.
- F. Latinwo and C. M. Schroeder, Soft Matter, 2011, 7, 7907–7913 RSC.
- O. A. Saleh, D. B. McIntosh, P. Pincus and N. Ribeck, Phys. Rev. Lett., 2009, 102, 068301 CrossRef CAS.
- A. Dittmore, D. B. McIntosh, S. Halliday and O. A. Saleh, Phys. Rev. Lett., 2011, 107, 148301 CrossRef.
- M. J. Stevens, D. B. McIntosh and O. A. Saleh, Macromolecules, 2013, 46, 6369–6373 CrossRef CAS.
- H.-P. Hsu and K. Binder, J. Chem. Phys., 2012, 136, 024901 CrossRef PubMed.
- L. Dai and P. S. Doyle, Macromolecules, 2013, 46, 6336–6344 CrossRef CAS.
- D. R. Tree, Y. Wang and K. D. Dorfman, Phys. Rev. Lett., 2013, 110, 208103 CrossRef.
- D. R. Tree, W. F. Reinhart and K. D. Dorfman, Macromolecules, 2014, 47, 3672–3684 CrossRef CAS.
- A. Muralidhar, D. R. Tree and K. D. Dorfman, Macromolecules, 2014, 47, 8446–8458 CrossRef CAS.
- A. Muralidhar, D. R. Tree, Y. Wang and K. D. Dorfman, J. Chem. Phys., 2014, 140, 084905 CrossRef PubMed.
- A. Muralidhar and K. D. Dorfman, Macromolecules, 2015, 48, 2829–2839 CrossRef CAS.
- A. V. Dobrynin, J. M. Y. Carrillo and M. Rubinstein, Macromolecules, 2010, 43, 9181–9190 CrossRef CAS PubMed.
- R. Radhakrishnan and P. T. Underhill, Soft Matter, 2012, 8, 6991–7003 RSC.
- J. Wang and H. Gao, J. Chem. Phys., 2005, 123, 084906 CrossRef PubMed.
- P. Grassberger, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 3682 CrossRef CAS.
-
P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, CRC Press, Boca Raton, 2007 Search PubMed.
- N. Clisby, Phys. Rev. Lett., 2010, 104, 055702 CrossRef.
- Y. Wang, D. R. Tree and K. D. Dorfman, Macromolecules, 2011, 44, 6594–6604 CrossRef CAS PubMed.
- C. A. Brockman, S. J. Kim and C. M. Schroeder, Soft Matter, 2011, 7, 8005–8012 RSC.
-
R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, 1999 Search PubMed.
- T. A. Knotts, N. Rathore, D. C. Schwartz and J. J. de Pablo, J. Chem. Phys., 2007, 126, 084901 CrossRef PubMed.
- T. E. Ouldridge, A. A. Louis and J. P. K. Doye, J. Chem. Phys., 2011, 134, 085101 CrossRef PubMed.
- F. Oesterhelt, M. Rief and H. Gaub, New J. Phys., 1999, 1, 6 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Data supporting that z is independent of contour length, a listing of molecular weights for all reported results, and plots equivalent to Fig. S1 and S2 for other values of lp/w. See DOI: 10.1039/c5sm01333j |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

 is the Langevin function, which has no analytical inverse.
is the Langevin function, which has no analytical inverse.






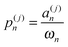







![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) being the value from the interpolation formulas in eqn (3) or (5). Naturally, the error is a function of the force. Fig. 2 shows the error for the data in Fig. 1. As expected, the error in the Marko–Siggia formula increases as the force decreases due to excluded volume effects. Moreover, for the stiff chain with lp/w = 10.5, we see that the Marko–Siggia interpolation formula indeed only exhibits errors of a few percent once the excluded volume effects are suppressed at high forces. The error also increases for the EV-WLC formula as the force decreases, since the interpolation formula only approximately captures the crossover between Pincus scaling and the Hookean response.
being the value from the interpolation formulas in eqn (3) or (5). Naturally, the error is a function of the force. Fig. 2 shows the error for the data in Fig. 1. As expected, the error in the Marko–Siggia formula increases as the force decreases due to excluded volume effects. Moreover, for the stiff chain with lp/w = 10.5, we see that the Marko–Siggia interpolation formula indeed only exhibits errors of a few percent once the excluded volume effects are suppressed at high forces. The error also increases for the EV-WLC formula as the force decreases, since the interpolation formula only approximately captures the crossover between Pincus scaling and the Hookean response.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Kuhn segments compared to only NK ≈ 150–190 for double-stranded DNA of similar contour length. The ability to study single chain dynamics of long chain, highly flexible polymers opens a new window into observing non-linear phenomena and chain dynamics in flow, which are heavily influenced by dominant EV and intramolecular hydrodynamic interactions.30 From this perspective, the non-equilibrium flow dynamics of highly flexible polymers such as single-stranded DNA is expected to differ qualitatively compared to linear λ-DNA of similar contour length L. Our enthusiasm towards using the EV-WLC model for single-stranded DNA is tempered by the possibility that the results could be affected by torsional constraints, which are included in some coarse-grained models, such as the 3-SPN model,31 but not in others, such as OX-DNA.32 Ultimately, the importance (or lack thereof) of torsion on the force–extension behavior of ssDNA is a question that needs to be resolved experimentally. Our EV-WLC formula provides a framework for addressing this question, since it assumes no torsional potential.
000 Kuhn segments compared to only NK ≈ 150–190 for double-stranded DNA of similar contour length. The ability to study single chain dynamics of long chain, highly flexible polymers opens a new window into observing non-linear phenomena and chain dynamics in flow, which are heavily influenced by dominant EV and intramolecular hydrodynamic interactions.30 From this perspective, the non-equilibrium flow dynamics of highly flexible polymers such as single-stranded DNA is expected to differ qualitatively compared to linear λ-DNA of similar contour length L. Our enthusiasm towards using the EV-WLC model for single-stranded DNA is tempered by the possibility that the results could be affected by torsional constraints, which are included in some coarse-grained models, such as the 3-SPN model,31 but not in others, such as OX-DNA.32 Ultimately, the importance (or lack thereof) of torsion on the force–extension behavior of ssDNA is a question that needs to be resolved experimentally. Our EV-WLC formula provides a framework for addressing this question, since it assumes no torsional potential.
