Avalanche-like fluidization of a non-Brownian particle gel

Abstract

We report on the fluidization dynamics of an attractive gel composed of non-Brownian particles made of fused silica colloids. Extensive rheology coupled to ultrasonic velocimetry allows us to characterize the global stress response together with the local dynamics of the gel during shear startup experiments. In practice, after being rejuvenated by a preshear, the gel is left to age for a time t_w before being subjected to a constant shear rate [small gamma, Greek, dot above]. We investigate in detail the effects of both t_w and [small gamma, Greek, dot above] on the fluidization dynamics and build a detailed state diagram of the gel response to shear startup flows. The gel may display either transient shear banding towards complete fluidization or steady-state shear banding. In the former case, we unravel that the progressive fluidization occurs by successive steps that appear as peaks on the global stress relaxation signal. Flow imaging reveals that the shear band grows until complete fluidization of the material by sudden avalanche-like events which are distributed heterogeneously along the vorticity direction and correlated to large peaks in the slip velocity at the moving wall. These features are robust over a wide range of t_w and [small gamma, Greek, dot above] values, although the very details of the fluidization scenario vary with [small gamma, Greek, dot above]. Finally, the critical shear rate [small gamma, Greek, dot above]* that separates steady-state shear-banding from steady-state homogeneous flow depends on the width of the shear cell and exhibits a nonlinear dependence with t_w. Our work brings about valuable experimental data on transient flows of attractive dispersions, highlighting the subtle interplay between shear, wall slip and aging whose modeling constitutes a major challenge that has not been met yet.

---

1 Introduction

Yield stress materials denote assemblies of mesoscopic constituents such as colloids, droplets or bubbles that display macroscopic properties intermediate between those of fluids and solids.^1,2 At rest, or under low stress, yield stress materials display a solid-like behaviour whereas they flow like liquids above a certain threshold, referred to as yield stress.^3–5 Their solid-like behaviour at rest originates either from a densely packed microstructure composed of soft objects⁶ such as in dense emulsions,⁷ jammed microgels,^8–10etc., or from the existence of weak attractive interactions that bind the constituents together and result in the formation of a sample-spanning network.¹¹ In the latter case, solid-like properties emerge even at low packing fractions. This defines a category referred to as attractive gels,¹² which encompass various systems such as clay suspensions,^13–15 carbon black gels^16,17 and colloid–polymer mixtures.¹⁸ All sorts of colloids and larger particles of different shapes and attraction potentials also comply with this definition.^19,20

Over the past ten years, the rheological behaviour of attractive gels has proved to be by far one of the most challenging aspects to understand among non-Newtonian fluids. In particular, their mechanical properties at rest are strongly time-dependent: attractive gels display reversible aging dynamics driven by the weak attractive forces between its constituents²¹ and that can be reversed by shear. As a result, the elastic properties of gels display a slow logarithmic or weak power-law increase with time,^22–25 until complete demixing of the system, which is historically referred to as syneresis.²⁶ To make matters worse, particles are often denser than the surrounding fluid which fosters syneresis and may trigger the collapse of the gel.^27–31 Such density mismatch is further suspected to influence the behaviour of these systems under flow, although clear experimental evidence is still lacking.³² Nonetheless, it is now well established that the behaviour of attractive gels under external shear involves heterogeneous flows that are highly sensitive to preshear history, boundary conditions, and/or finite size effects. For instance, one can emphasize the case of LAPONITE® suspensions whose steady-state flow properties were shown to be influenced by the nature of boundaries: under external shear, smooth walls lead to the complete fluidization of the gel and to linear velocity profiles, while rough boundary conditions allow the growth of a steady shear band.^33,34 Moreover, as an illustration of the impact of confinement on flows of attractive gels, one can mention the spectacular shear-induced structuration observed at moderate shear rates and reported in silica suspensions,³⁵ gels of anisotropic particles,³⁶ attractive emulsions³⁷ and carbon black gels.^38–40 In such cases, the gel rearranges to form a striped pattern of logrolling flocs aligned along the vorticity direction, whose origin and formation mechanism are still highly debated.⁴¹

Beyond the effects of bounding walls and confinement, attractive interactions alone are also responsible for long-lasting transients under external shear. On the one hand, experiments performed under constant^42–46 and oscillatory^43,47,48 stress reveal that the fluidization process of attractive gels, initially at rest, may take up to tens of hours. Experiments coupled to velocimetry have revealed that such a process is mostly activated, as evidenced by the Arrhenius-like dependence of the fluidization time with the applied shear stress,^43,45 and that it is strongly heterogeneous in both the vorticity and the flow directions.⁴⁸ On the other hand, attractive gels show an overshoot in the stress response to shear startup experiments. Such behaviour, which strongly depends on the preshear history, corresponds to the orientation and subsequent rupture of the gel microstructure into clusters.^{19,25,49–51} Beyond the yield point, attractive gels either display homogeneous or shear-banded flows depending on the applied shear rate and on the boundary conditions.⁵² However, only a handful of studies have investigated the influence of the sample age, i.e. the duration separating preshear from the start of the experiment, on such a shear-rate-induced fluidization scenario.⁵³ Recently, Martin and Hu have shown on LAPONITE® suspensions⁵⁴ that aged-enough samples tend to exhibit long-lasting though transient shear-banding, and that shear-banding may also be trapped by the rapid aging of the non-flowing band and become permanent. The latter scenario is remarkable as it strongly differs from the classic shear-banding scheme which relies on the mechanical instability of the sample under scrutiny.^55,56 This study highlights the interplay between the sample age and the shear and strongly urges the investigation of the impact of sample age on the shear-induced fluidization scenario in other attractive gels.

To summarize, attractive gels entirely behave neither as solids nor as fluids over a wide range of timescales. In the landscape of non-Newtonian fluids, they define a rather singular category of materials rightfully referred to as the “Twilight zone” in the early classification established by L. Bilmes,⁵⁷ which was recently adapted to complex fluids by G. H. McKinley.⁵⁸ We barely start to understand the (transient) rheology of attractive gels and more experiments are obviously needed to shed some light on the heterogeneous flow of such highly time-dependent materials.

In the present manuscript we report spatially resolved data on the fluidization dynamics of an attractive gel composed of weakly attractive non-Brownian particles. Velocimetry performed in a concentric cylinder geometry simultaneously to shear startup experiments reveals that the steady-state behaviour is a subtle function of both the time t_w during which the system was left to age before the beginning of the experiment and the value [small gamma, Greek, dot above] of the applied shear rate. Extensive experiments allow us to build a state diagram of steady-state flows in the ([small gamma, Greek, dot above], t_w) plane. Two distinct regions roughly emerge: (i) homogeneous flows for shear rates larger than a critical value [small gamma, Greek, dot above]* that weakly increases with the aging time and (ii) steady-state shear banding elsewhere. As a key result of this work, the complete fluidization observed in the upper region of the state diagram involves a transient shear band that is progressively eroded through a series of dramatic fluidization events. These avalanche-like processes show as large peaks in the temporal evolution of both the global shear stress and the slip velocity measured at the moving wall of the shear cell. As further confirmed by two-dimensional ultrasonic imaging, this fluidization process is spatially heterogeneous and may occur at different locations along the vorticity direction. Finally, for a range of parameters ([small gamma, Greek, dot above], t_w) in the vicinity of the boundary between the two main regions of the state diagram, we observe large fluctuations in the stress and slip velocity signals, although the system does not reach complete fluidization. Such avalanche-like events are strongly coupled to variations in both the width of the shear band and the slip velocity. To our knowledge the present work is among the first experimental evidence of local avalanche-like fluidization events in a weak attractive gel under shear. It also provides an extensive data set to test the relevance of the flow stability criteria for shear banding⁵⁹ and stands as a new challenge for spatially resolved models.^60–62

2 Materials and methods

2.1 Experimental setup

The experimental setup allows us to perform time-resolved velocimetry simultaneously with standard rheometry. The rheological measurements are performed in a polished Taylor–Couette (concentric cylinder) cell made of Plexiglas (gap e = 2 mm) in which the inner Mooney–Couette cylinder of angle 2.3°, height 60 mm and radius 23 mm is connected to a stress-controlled rheometer (ARG2, TA Instruments) and positioned at 100 μm from the bottom of the outer cylinder. A solvent trap located at the top of the rotor and a homemade lid are used to prevent evaporation efficiently up to about 9 hours. The Taylor–Couette cell is embedded in a water tank connected to a thermal bath which allows us to keep the sample at a constant temperature T = 23.5 ± 0.1 °C.

Local velocity profiles across the gap of the Taylor–Couette cell are recorded simultaneously with the global rheology by means of two different ultrasonic probes immersed in the water tank, which also ensures acoustic coupling to the shear cell. The first ultrasonic probe is a single high-frequency focused transducer that allows us to record the azimuthal velocity v as a function of the radial position r across the gap at the middle height of the shear cell, i.e. at 30 mm from the bottom. Full technical details on this one-dimensional ultrasonic velocimetry (1D-USV) technique can be found in a previous publication.⁶³ The second ultrasonic probe consists of a linear array of 128 transducers placed vertically at about 15 mm from the cell bottom. This transducer array is 32 mm high and gives access to images of the azimuthal velocity as a function of the radial position r and vertical position z over about 50% of the cell height. This two-dimensional ultrasonic velocimetry (2D-USV) technique is thoroughly described in ref. 64. Both devices can be used simultaneously and roughly face each other in the water tank, i.e. they are separated by an azimuthal angle of about 180°. While the 1D-USV setup has the advantage of a better spatial resolution (about 40 μm against 100 μm), only the 2D-USV setup allows us to detect and monitor the presence of flow heterogeneities along the vorticity direction.

Both velocimetry techniques require that the ultrasonic beam crossing the gap of the shear cell is backscattered either by the fluid microstructure itself or by acoustic tracers added during sample preparation when the system is acoustically transparent.^63,64 Here, we shall emphasize that the microstructure of the sample further detailed below conveniently backscatters ultrasound in the single scattering regime, which allows us to monitor the fluid velocity in a fully non-invasive way.

2.2 Sample preparation and rheological properties

Our Ludox gels are prepared following the same recipe as that used by Møller et al. in ref. 65. As we shall show below, the system is composed of non-Brownian particles made of permanently fused silica colloids. These particles are themselves reversibly aggregated in brine due to van der Waals forces leading to a space-spanning gel with solid-like properties at rest.

A stable suspension of silica colloids (Ludox TM-40, Sigma-Aldrich, 40 wt% in silica colloids) of typical diameter 20 nm [see Fig. 1(a) for a scanning electron microscopy (SEM) image of a dilute sample (Supra 55, VP Zeiss)] and pH = 9.0 ± 0.5 is first poured without any further purification into a 10 wt% deionized aqueous solution of sodium chloride (Merck Millipore) up to a Ludox : NaCl mass ratio of 6 : 13, corresponding to a final volume fraction of 7% in silica colloids and a final pH of 7.6 ± 0.2. The mixture, which instantaneously becomes white and optically opaque, is then shaken intensely by hand for 2 min and left at rest for at least 15 h before being studied. Such a drastic change in the sample turbidity strongly suggests the rapid formation of aggregates at the micron scale. Indeed, direct observations using different techniques confirm the existence of a much coarser microstructure than the initial nanometric silica colloids. On the one hand, SEM images of a dried droplet extracted from a fresh sample that has been previously diluted in a NaCl solution unveil the presence of particles whose size ranges from a few microns up to a hundred microns [Fig. 1(b)]. On the other hand, bright-field microscopy images (ECLIPSE Ti, Nikon) of the sample neither altered nor diluted further confirm the existence of these micron-sized particles [Fig. 1(c)–(e)], which are stable in time and robust to repeated shear, as confirmed by similar observations performed on samples subjected to different shear histories (images not shown).

Fig. 1 SEM images of (a) the stock colloidal suspension (Ludox TM-40) used to prepare the sample and (b) the non-Brownian aggregates composing the sample which form almost instantaneously after mixing the colloidal suspension with a concentrated NaCl solution. The inset in (b) shows a single typical aggregate made of fused silica colloids. Images are obtained as follows: both the suspension and the gel have been diluted by a factor 1000 (except for the main figure in (b) where the gel has been diluted 100×), the first one in deionized water and the second one in 6.8 wt% NaCl which corresponds to the final salt concentration in the gel. The samples are then left to dry on a pin stub before being imaged. (c)–(e) Bright-field microscopy images representative of the gel microstructure at three different magnifications. The sample has been presheared for 2 min at 500 s⁻¹ before being imaged about 10 minutes later in a homemade observation cell made of a glass slide topped with a cover slip and sealed with UV glue.

To account for the formation of such a large scale microstructure, which to our knowledge has not been reported in the literature previously,^65,66 we propose the following scenario. Above pH = 7, silica colloids are negatively charged and bear silanol (Si–OH) and dissociated silanol groups that are poorly hydrated.⁶⁷ In most of the previous studies, NaCl is added in a relatively small amount (typically 0.05–0.5 M) such that electrostatic repulsion is screened leading to the slow reversible aggregation of individual colloids until the formation of a colloidal gel.^68–70 Here, we add a much larger amount of salt (1.2 M) to the colloidal suspension, which leads to an ion exchange where protons are replaced by sodium ions.^71,72 The loss of hydrogen bonding between the colloids and the solvent triggers the fast and irreversible aggregation of the silica colloids through the formation of interparticle siloxane bonds,^73–75 resulting in the formation of the non-Brownian particles described above. Finally, these non-Brownian particles also aggregate reversibly due to van der Waals forces and form a space-spanning network, i.e. a gel, whose mechanical behaviour is studied below. Note that such a microstructure scatters ultrasound efficiently, allowing us to use both 1D- and 2D-USV without requiring any seeding of the sample with tracer particles.

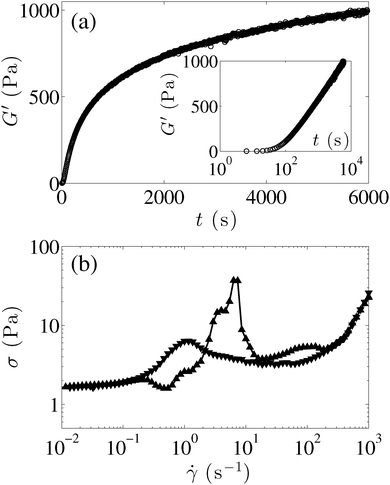
The rheological features of the gel are displayed in Fig. 2. A strong preshear of [small gamma, Greek, dot above]_p = 500 s⁻¹ applied for 2 min fully fluidizes the system, which quickly rebuilds once the preshear is stopped and subsequently shows pronounced aging. Indeed, the small amplitude oscillatory shear reveals that the elastic modulus G′ becomes larger than the viscous modulus G′′ within about 20 s [see Fig. S1 in the ESI†] and that G′ further increases logarithmically over more than 2 h [Fig. 2(a)]. Such aging dynamics are reproducible for a given preshear protocol and lead to the formation of a solid-like gel. The latter shows an elastic modulus that is nearly frequency independent and a critical yield strain of about 7% that weakly depends on the sample age [see Fig. S2 and S3 in the ESI†].

Fig. 2 (a) Elastic modulus G′ vs. time t after a preshear at [small gamma, Greek, dot above]_p = 500 s⁻¹ for 2 min. Inset: the same data set in semilogarithmic scales. Measurements performed under oscillatory shear stress in the linear regime with frequency 1 Hz and stress amplitude 0.05 Pa. (b) Flow curve σ vs. [small gamma, Greek, dot above] obtained by first decreasing [small gamma, Greek, dot above] continuously from 10³ to 10⁻² s⁻¹ in 75 logarithmically spaced points of duration δt = 8 s (▼) and then increasing [small gamma, Greek, dot above] over the same range (▲).

Such a solid-like behaviour is also reflected in the nonlinear rheology of the gel. Fig. 2(b) shows the flow curve σ vs. [small gamma, Greek, dot above] measured by sweeping down the shear rate from 10³ to 10⁻² s⁻¹ and back up. The flow curve shows an apparent yield stress of a few Pascals and displays a complex non-monotonic shape together with strong hysteresis. Velocity profiles recorded simultaneously for the up and down shear rate sweeps shown in Fig. 2 reveal that wall slip and heterogeneous flows are involved over a large range of shear rates, below 20 s⁻¹ during the decreasing ramp and up to about 200 s⁻¹ during the increasing ramp [see Fig. S4 in the ESI†]. In particular, the large stress peak observed in Fig. 2(b) at [small gamma, Greek, dot above] ≃ 7 s⁻¹ while ramping up the shear rate is the signature of the partial fluidization of the sample which moves as a plug and totally slips at both walls for 7 ≲ [small gamma, Greek, dot above] ≲ 100 s⁻¹, before finally starting to flow homogeneously on the reversible branch at high shear rates, i.e. above about 200 s⁻¹.

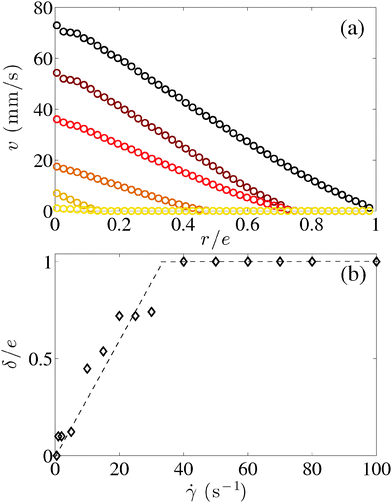
Furthermore, in Fig. 2(b), the shear stress σ shows a minimum in between [small gamma, Greek, dot above] ≃ 20 s⁻¹ and 40 s⁻¹ on the decreasing shear rate sweep, which hints at the existence of a critical shear-rate [small gamma, Greek, dot above]_c below which no homogeneous flow is possible.^76,77 The latter result is confirmed by performing steady-state measurements at a constant applied shear rate starting from the liquid state, i.e. on a fully fluidized sample, in order to avoid long-lasting transients that go along with shear startup experiments on a sample at rest, and which are at the core of Section 3. Here, discrete shear rates of decreasing values ranging from 500 s⁻¹ down to 0.1 s⁻¹ are successively applied for at least 300 s each. The flow remains homogeneous down to [small gamma, Greek, dot above]_c ∼ 35 s⁻¹ below which the sample exhibits an arrested band [Fig. 3(a)]. Such a value of [small gamma, Greek, dot above]_c is comparable to the one reported in a previous work on very similar Ludox gels.⁶⁵ Moreover, as the shear rate is decreased below [small gamma, Greek, dot above]_c, the size of the fluidized band δ decreases roughly linearly with [small gamma, Greek, dot above] [Fig. 3(b)] in agreement with the classical “lever rule”.^65,76,77 The deviation of δ from a straight line could be related to the wall slip that is present at the rotor.

Fig. 3 (a) Steady-state velocity profiles across the gap at different shear rates: [small gamma, Greek, dot above] = 40, 30, 20, 10, 5 and 1 s⁻¹ from top to bottom. The parameter r denotes the distance to the rotor. These data have been recorded starting from large shear rates (500 s⁻¹) and decreasing [small gamma, Greek, dot above] by successive steps of long enough duration to achieve a steady state at every imposed shear rate. (b) Size of the fluidized band δ normalized by the gap width e vs. the applied shear rate [small gamma, Greek, dot above]. The dashed line corresponds to the standard “lever rule” with [small gamma, Greek, dot above]_c = 35 s⁻¹.

To conclude this subsection, complex cycles of hysteresis such as the one reported in Fig. 2 have also been reported for numerous other attractive gels including carbon black gels⁴⁵ and clay suspensions.^34,78 Although significant progress has been made in extracting quantitative information from hysteresis loops,⁷⁹ we rather chose to focus our study on shear startup experiments in order to fully decouple the fluid dynamics from any time-dependent effect related to the experimental protocol. The present experiments are all thus performed on a sample prepared in a solid-like state, so as to investigate the shear-induced fluidization scenario of the non-Brownian particle gel. In practice, after preparing the gel in a well-defined and reproducible initial state, thanks to preshearing, we monitor the stress response of the material to a constant shear rate over long durations. The results are discussed in Section 3.

2.3 Experimental protocol

Prior to any shear startup experiment, the sample is presheared at [small gamma, Greek, dot above]_p = 500 s⁻¹ for 2 min in order to erase any previous shear history.⁸⁰ We check systematically that the velocity profiles during the preshear step become homogeneous across the gap within a duration shorter than 2 min. The system is then left to rebuild for a duration t_w that ranges between 1 and 100 min, and during which we apply small amplitude oscillatory shear stress (stress amplitude σ = 0.05 Pa, frequency f = 1 Hz) to monitor the evolution of the linear viscoelastic properties of gels and make sure that for a given value of t_w, the gel reaches an initial state that is reproducible from one experiment to another. Finally, a constant shear rate [small gamma, Greek, dot above] is applied to the material over a long duration (>1000 s) while we monitor the stress response together with local velocity profiles.

3 Results

3.1 Global rheology and one-dimensional velocity profiles

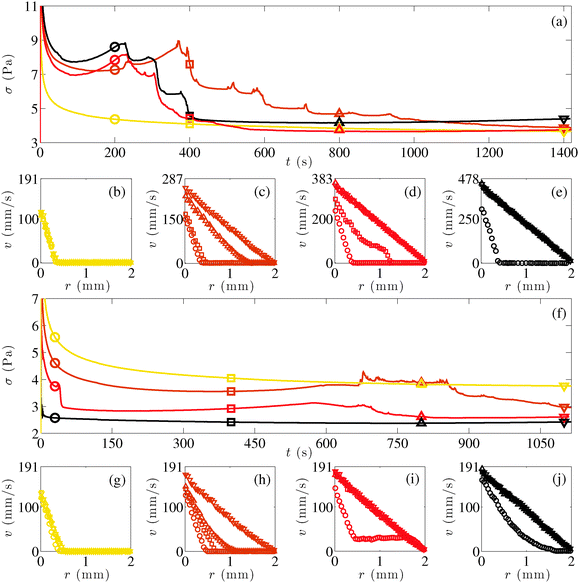
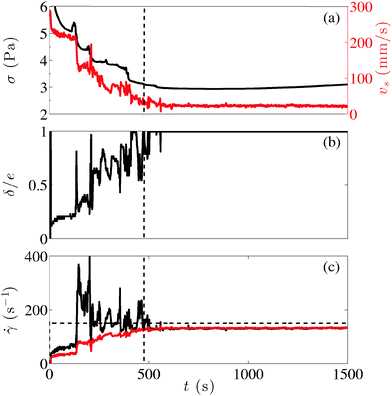
We first fix the duration between the preshear and the start of the experiment to t_w = 60 min and discuss the material response for shear startup experiments performed at different shear rates. For shear rates lower than about 150 s⁻¹, the stress relaxes smoothly towards a constant value as illustrated in Fig. 4(a) for an experiment performed at [small gamma, Greek, dot above] = 100 s⁻¹. Velocity profiles acquired simultaneously reveal that the material remains at rest near the stator, while it flows in the vicinity of the rotor where it shows strong wall slip [Fig. 4(b)]: the sample displays steady-state shear banding. For larger shear rates, one observes a completely different scenario, both from global and local measurements. The stress displays a series of spike-like relaxation events, during which stress increases of small amplitude are followed by large drops [Fig. 4(a)]. Local measurements show that the gel flows heterogeneously. However, the shear band is only transient and the system always ends up being homogeneously sheared at a steady state [Fig. 4(c)–(e)]. Qualitatively, the width of the shear band increases while strong wall slip is observed at the rotor, until the whole gap is fluidized and the wall slip becomes negligible. This scenario is robustly observed at different shear rates and full fluidization occurs sooner for larger shear rates [Fig. 4(a)]. A quantitative analysis of the velocity profiles is further proposed in Section 3.3.

Fig. 4 (a) Shear stress response σ(t) for different applied shear rates [color, [small gamma, Greek, dot above] (s⁻¹)]: [, 100]; [, 150]; [, 200]; [–, 250]. (b)–(e) Velocity profile v(r) across the gap, where r is the distance to the rotor at different times [symbol, time (s)]: [○, 200]; [□, 400]; [△, 800]; [▽, 1400]. Each color corresponds to each applied shear rate in (a). The rotor velocity corresponds to the upper bound of the vertical axis. The sample is left to age for t_w = 60 min before each experiment. (f) Shear stress response σ(t) for different waiting times t_w [color, t_w (min)]: [, 100]; [, 30]; [, 5]; [–, 1]. Experiments performed at [small gamma, Greek, dot above] = 100 s⁻¹. (g)–(j) Velocity profile at different times [symbol, time (s)]: [○, 30]; [□, 400]; [△, 800]; [▽, 1100]. Each color corresponds to each value of t_w in (f). The rotor velocity corresponds to the upper bound of the vertical axis.

To evidence the impact of the aging time t_w on the material response, Fig. 4(f)–(j) shows similar experiments performed for different t_w values at the same shear rate [small gamma, Greek, dot above] = 100 s⁻¹. For long waiting times between the preshear and the start of the experiments, e.g. t_w = 100 min, one observes a smooth stress relaxation here again associated with steady shear-banded velocity profiles [Fig. 4(f) and (g)]. Decreasing t_w to 30 or 5 minutes leads to a gel of lower elastic modulus. Local measurements further reveal that these weaker gels go through a transient shear-banding regime and that in both cases the steady state is homogeneous [Fig. 4(h) and (i)]. Here, unlike the case of transient shear banding reported in Fig. 4(a) for large shear rates in samples left to age for t_w = 60 min where fluidization corresponds to a long series of successive stress relaxations, fluidization proceeds in a single stress drop together with small noisy fluctuations [Fig. 4(f)]. Finally, one observes that very young gels (t_w = 1 min) barely show any heterogeneous velocity profile during the startup flow and reach a homogeneous steady state within a few tens of seconds [Fig. 4(j)]. In summary, the longer the sample ages after preshear, the more likely it is to exhibit a long-lasting heterogeneous fluidization scenario or to display steady shear banding.

3.2 Flow state diagram

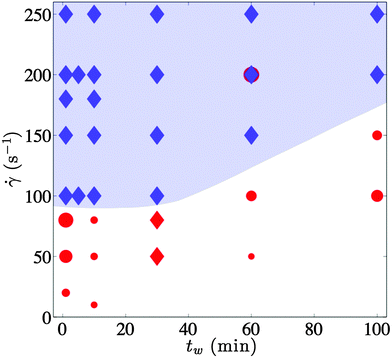
To go one step further and get an overall picture of the material response, we have performed extensive shear startup experiments by varying systematically both the aging time (1 ≤ t_w ≤ 100 min) and the applied shear rate (10 ≤ [small gamma, Greek, dot above] ≤ 250 s⁻¹). The entire data set is summarized in the flow state diagram pictured in Fig. 5, where different symbols code for the three different scenarios that we may distinguish at the end of each startup experiment lasting typically for 1500 to 3600 s. In the steady state, the attractive gel may either fully fluidize after a transient phase possibly involving strong fluctuations ( in Fig. 5), as observed in the upper part of the state diagram for large shear rates quite independent of the sample age, or exhibit shear banding. The boundary between these two regimes defines a critical shear rate [small gamma, Greek, dot above]* that depends in a nonlinear fashion on the sample age t_w. Furthermore, we can discriminate between two types of behaviour when shear banding is observed.

Fig. 5 Flow state diagram in the (sample age t_w, applied shear rate [small gamma, Greek, dot above]) plane. In the steady state, the gel may either be fully fluidized (, blue region) or display shear banding. Steady shear banding is represented in () symbol whose size encodes the portion of the gap that is being sheared. Unsteady banding, which denotes flows where the band width and the slip velocity at the rotor display significant fluctuations, is represented by ().

First, steady shear banding ( in Fig. 5), for which both the width δ of the shear band and the slip velocity v_s at the rotor display negligible fluctuations in the steady state, is observed in particular at low aging times t_w ≲ 20 min and low enough shear rates, typically below 100 s⁻¹. In that case, the width of the arrested band may decrease (t_w = 1 s) or remain constant (t_w = 10 s and 100 s) for increasing shear rates.

Second, we have also observed unsteady shear banding ( in Fig. 5). In this case both global and local measurements display significant fluctuations in the steady state. These fluctuations are strikingly similar to those observed during the transients leading to complete fluidization in the upper part of the diagram. However here the material never gets entirely fluidized and the shear band width δ does not show a systematic evolution towards δ = e so that an unsteady shear band persists in the steady state at least within the finite duration of the experiments. These fluctuations are investigated in more detail in the next section.

3.3 Linking global rheology to the local dynamics

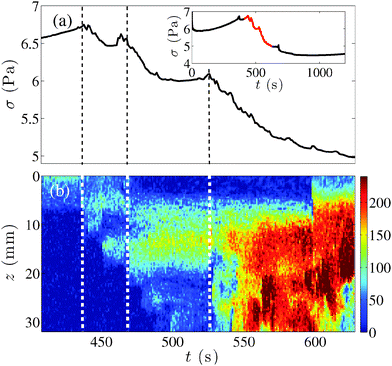
In this section, we focus on the strong fluctuations that are observed (i) during transient regimes leading to complete fluidization and (ii) during unsteady shear-banded flows at the steady state. Global rheological data together with the detailed analysis of the corresponding local measurements are reported in Fig. 6 and 7 respectively, (see also the corresponding Movies S1 and S2 in the ESI†). Local data are analyzed as follows: linear fits of the velocity profiles in the fluidized part of the gap are used to estimate the local shear rate and extrapolate the sample velocity v(0) at the rotor. The width δ of the shear band is obtained as the abscissa of the intersection between the fit and the zero velocity axis, while the slip velocity is given by v_s = v₀ − v(0), where v₀ is the rotor velocity. Finally, the global shear rate is defined as v(0)/e.

Fig. 6 Full fluidization observed for [small gamma, Greek, dot above] = 150 s⁻¹ and t_w = 30 min. (a) Shear stress σ (–) and slip velocity v_s () vs. time. (b) Width δ of the fluidized shear band normalized by the gap width e vs. time. (c) Local shear rate within the shear band (–) and global shear rate () vs. time. The horizontal dotted line indicates the shear rate applied by the rheometer. In (a)–(c), the vertical dashed line indicates the fluidization time τ_f.

Fig. 7 Unsteady shear banding observed for [small gamma, Greek, dot above] = 50 s⁻¹ and t_w = 30 min. (a) Shear stress σ (–) and slip velocity v_s () vs. time. (b) Width δ of the fluidized shear band normalized by the gap width e vs. time. (c) Local shear rate within the shear band (–) and global shear rate () vs. time. The horizontal dotted line indicates the shear rate applied by the rheometer.

We first discuss Fig. 6, which shows a case of full fluidization for [small gamma, Greek, dot above] = 150 s⁻¹ on a gel left to age for t_w = 30 min. The stress relaxes by successive jumps until full fluidization, which occurs at t = τ_f ≃ 507 s and after that σ remains roughly constant [Fig. 6(a)]. The temporal evolutions of δ [Fig. 6(b)] and of the local shear rate [Fig. 6(c)] show that fluidization occurs by successive spatial “avalanches” that are directly correlated to the stress drops. During the whole fluidization process, the slip velocity at the rotor v_s decreases towards a negligible value that is reached at t = τ_f, diminishing by jumps that are in phase with the stress evolution.

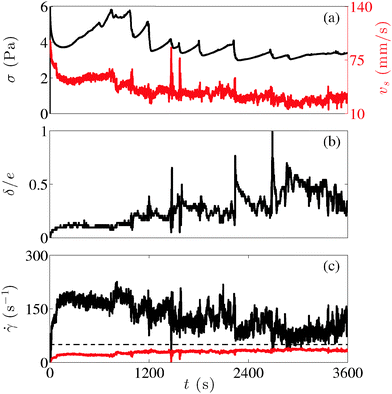
Fig. 7 focuses on spatiotemporal fluctuations observed during steady-state shear-banded flows for the same aging time (t_w = 30 min) as in Fig. 6 but sheared at a lower shear rate ([small gamma, Greek, dot above] = 50 s⁻¹). The stress exhibits periods of slow increase followed by rapid drops [Fig. 7(a)]. Within an hour, about half of the gap gets fluidized and the size of the fluidized band shows a pronounced increase during a short period of times, which are synchronized with the stress drops [Fig. 7(b)]. The dynamics of the fluid at the rotor is strongly correlated to the global fluctuations, as evidenced by the sudden peaks of the slip velocity when the stress drops. Note that, although the slip velocity decreases in average over the whole duration of the experiment, it remains at a high level of about 20%, in noticeable contrast to the fully fluidized scenario described in the previous paragraph. Such oscillatory dynamics in the vicinity of the rotor are reminiscent of stick-slip. Indeed, the fluidized band shows a time interval during which the local shear rate remains constant [Fig. 7(c)], while the band width slowly decreases. As a result, the stress slowly builds up, until the fluidized band experiences a large slip event at the moving wall and gets rejuvenated. These dynamics look similar to the stick-slip motion reported in clays in the pioneering work of Pignon et al.⁸¹ However, in the latter case, stick-slip occurs along fracture planes located in the bulk sample, while here slip at the wall appears to play a key role.

Finally, we shall emphasize that in both types of scenarios, the peaks in both the stress and the slip velocity are only seen in the presence of shear banding. Although it is not clear which of the shear banding or the slip at the rotor is the cause of the oscillations, these peculiar dynamics hint toward a subtle flow-microstructure coupling that certainly deserves more investigation.

3.4 Local scenario within an avalanche

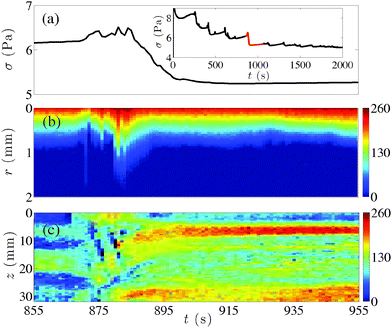
To get better insight on the avalanche-like fluidization scenario, we now focus on the single stress drop shown in Fig. 8(a). This event is extracted from the shear startup experiments performed at [small gamma, Greek, dot above] = 150 s⁻¹ for t_w = 10 min and the steady-state flow corresponds to a fully fluidized sample [inset of Fig. 8(a)]. The velocity profiles recorded simultaneously with 1D-USV are plotted as a spatiotemporal diagram in Fig. 8(b). Quite surprisingly the one-dimensional flow profiles before and after the stress drop are very similar as they all show shear localization over about half the gap. By the time the stress reaches its maximum value, about 80% of the gap is sheared. Then shear abruptly localizes again over about 1 mm close to the rotor at the beginning of the stress relaxation. Therefore, although the strong fluctuations of v(r, t) observed before the stress peak appear to be correlated to those of σ(t), the drop of about 15% in the stress value cannot be explained by these one-dimensional data in a straightforward manner. We emphasize that the 1D-USV measurements are performed at a given height of the Taylor–Couette cell so that they may reflect the evolution of global rheology only if the flow is homogeneous along the vorticity direction. As a matter of fact, velocity profiles v(r, z, t) recorded simultaneously over the whole height of the Taylor–Couette cell through 2D-USV demonstrate that the flow is strongly heterogeneous in the vertical direction z. Fig. 8(c) shows a spatiotemporal plot of the fluid velocity along the vertical axis z at a fixed radial position r₀ = 0.2 mm close to the rotor (see also Movie S3 in the ESI†). Depending on the position along the z-axis, the material can simultaneously be either solid-like as evidenced by areas of very low velocities in Fig. 8(c) (see, for instance, at the top of the region of interest for z ≲ 5 mm) or fluid-like and flow at high velocities as observed for z ≃ 8 and z ≃ 30 mm. Note that the 1D-USV measurements are performed at z₀ ≃ 15 mm and are fully consistent with the 2D-USV data. Our measurements further reveal that the particular avalanche-like event analyzed here only corresponds to partial fluidization: at the end of the stress drop, the flow is still heterogeneous, even though arrested regions for t ≲ 870 s have given way to flowing regions arranged in a vertically banded structure for t ≳ 890 s. In fact, the inset of Fig. 8(a) shows that several subsequent stress drop events still have to take place before complete fluidization of the sample.

Fig. 8 (a) Stress σ vs. time during a single stress drop event extracted from the shear startup experiment during which the material is fully fluidized ([small gamma, Greek, dot above] = 150 s⁻¹, t_w = 10 min). Inset: Stress vs. time for the whole experiment. The signal pictured in the main graph appears in red. (b) Spatiotemporal diagram of the velocity data v(r, t) as a function of position r and time t. The radial position r is measured from the rotating inner wall. Data obtained with 1D-USV. (c) Spatiotemporal diagram of the velocity data v(r₀, z, t) as a function of the vertical position z and time t at r₀ = 0.2 mm. Data obtained with 2D-USV. The vertical position z is measured from the top of the transducer array. In both (b) and (c), the fluid velocity is color coded in mm s⁻¹.

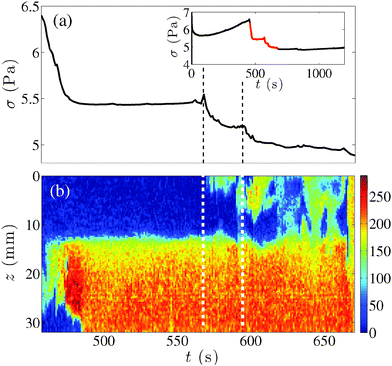
To test the existence of a local fluidization scenario that would be generic to all avalanche-like events, we analyze additional experiments in the full fluidization region of the state diagram at [small gamma, Greek, dot above] = 180 and 200 s⁻¹. The temporal evolution of the shear stress is reported, respectively, in Fig. 9(a) and 10(a) and the corresponding 2D-USV measurements v(r₀, z, t) are displayed as spatiotemporal diagrams in Fig. 9(b) and 10(b) for a radial position r₀ = 0.7 mm (see also Movies S4 and S5 in the ESI†). Here again, the temporal evolution of the velocity field is strongly heterogeneous along the vertical direction in both experiments. Furthermore, despite the fact that these two experiments are performed at comparable shear rates, the local fluidization scenario is strikingly different. In the shear startup experiment reported in Fig. 9, the lower part of the region of interest is fully fluidized after the first stress relaxation while the upper part of the sample necessitates two supplemental avalanches to in turn fully fluidize. On the other hand, the fluidization process shown in Fig. 10 starts from the upper part of the region of interest before extending to the lower part of the Taylor–Couette cell. Here, each avalanche-like event involves large pieces of the sample with a typical vertical extension of about 5 mm [see events marked by white dotted lines in Fig. 10(a)]. Some of these events only show up in the stress response as very small peaks while their local signature is much more impressive (see, e.g., the event at t ≃ 600 s). For t ≃ 400–500 s, the sample even appears to fluidize, or at least set into motion, through regular steps occuring from top to bottom with a characteristic time of 10–20 s. The experiments shown in Fig. 9 and 10 allow us to conclude that the peaks in the stress signal may encompass very different local scenarios. Since both experiments were performed with the same aging time t_w = 1 min, these results illustrate the high sensitivity to “initial conditions”, i.e. to the possibly different arrangement of the heterogeneous microstructure after the aging process, and the subtle interplay between aging and shear banding with no systematic failure scenario along the cell height.

Fig. 9 (a) Stress σ vs. time during a single stress relaxation episode extracted from the shear startup experiment at the end of which the material is fully fluidized ([small gamma, Greek, dot above] = 180 s⁻¹, t_w = 1 min). (b) Spatiotemporal diagram of the velocity data v(r₀, z, t) as a function of the vertical position z and time t at r₀ = 0.7 mm. Data obtained with 2D-USV. The vertical position z is measured from the top of the transducer array. The fluid velocity is color coded in mm s⁻¹.

Fig. 10 (a) Stress σ vs. time during a single stress relaxation episode extracted from the shear startup experiment at the end of which the material is fully fluidized ([small gamma, Greek, dot above] = 200 s⁻¹, t_w = 1 min). (b) Spatiotemporal diagram of the velocity data v(r₀, z, t) as a function of the vertical position z and time t, at r₀ = 0.7 mm. Data obtained with 2D-USV. The vertical position z is measured from the top of the transducer array. The fluid velocity is color coded in mm s⁻¹.

4 Discussion

On the one hand, we conclude from Section 2.2 that the gel under scrutiny displays a discontinuous yielding transition that is very similar to the one reported in other attractive gels.^65,77,82 Indeed, one observes that, when the initial condition is a completely fluidized state, applying a series of shear rates of decreasing values leads to the growth of a steady-state arrested band below a critical shear rate [small gamma, Greek, dot above]_c. The value of [small gamma, Greek, dot above]_c is inherent to the sample and results from the flow instability at low shear rates. This is fully consistent with previous results on Ludox gels.⁶⁵ On the other hand, the shear startup experiments reported in Section 3 and performed on the sample prepared in the solid state allow us to identify a second critical shear rate [small gamma, Greek, dot above]* > [small gamma, Greek, dot above]_c. For applied shear rates such as [small gamma, Greek, dot above]_c < [small gamma, Greek, dot above] < [small gamma, Greek, dot above]*, the sample gets only partially fluidized and exhibits steady-state shear banding, while long-lasting yet transient shear banding is observed for [small gamma, Greek, dot above] > [small gamma, Greek, dot above]*. Such a behaviour can be interpreted in the framework recently described by Martin and Hu for LAPONITE® samples.⁵⁴ Under external shear, the sample in the vicinity of the rotor that is initially at rest gets fluidized, while the sample close to the stator remains at rest and keeps aging. Depending on the intensity of the shear rate, such a heterogeneous velocity profile may either be trapped by the sample aging and become permanent as observed below [small gamma, Greek, dot above]*, or become homogeneous after a transient shear-banding regime whose duration decreases for increasing values of [small gamma, Greek, dot above]. Such an argument allows us to understand that [small gamma, Greek, dot above]* will be sensitive to the gap size and to the cell geometry, which we have verified by performing identical shear startup experiments with different gap widths. These experiments show that [small gamma, Greek, dot above]* decreases as the gap size is reduced [see Fig. S6 in the ESI†]. Therefore, steady-state shear banding trapped by aging should be distinguished from shear banding resulting from the intrinsic flow instability which should not depend on the geometry. Finally, we have shown in Section 3.2 that [small gamma, Greek, dot above]* is a nonlinear function of the sample age t_w, again in contrast to [small gamma, Greek, dot above]_c.

Regarding the transient fluidization dynamics, our work unravels the existence of very characteristic peaks in the global rheological data. These peaks correspond to local avalanches associated with the abrupt fluidization of shear-banded velocity profiles. An avalanche proceeds in two steps. First, the sample ages as evidenced by the slow increase of the stress indicative of progressive consolidation, while the shear band remains roughly fixed. Second, the sample suddenly fluidizes before localizing again, at least partially, while the stress drops and the shear rate increases. This scenario strikingly recalls the transient shear banding reported on LAPONITE® clay suspensions⁵⁴ and fits well with the stability criterion recently proposed by Fielding et al.^59,62 In practice though, the physical origin of the avalanche-like and successive stress relaxation events remains to be determined. Aging is more pronounced in our system than in the attractive gels that have been studied previously^22,83,84 as evidenced from the large values of dG′/d log t after preshear [see the inset of Fig. 2(a)]. Therefore, syneresis driven by the aggregation and/or sedimentation of the colloidal flocs due to their density mismatch with the surrounding fluid could also play a role and interfere with the traditional picture of a competition between aging and shear rejuvenation.⁸⁵ As syneresis is negligible in most of the colloidal gels that have been the topic of rheophysical studies so far, it could also explain why such stress oscillations have, to our knowledge, never been reported in the literature.

An alternative explanation for the stress oscillations could be related to confinement. Indeed, as the size distribution of the fused silica aggregates is wide and extends up to 100 μm, the sample mesostructure most likely involves aggregates whose size becomes comparable to that of the gap, at least for long enough rest durations t_w. In this framework, stress oscillations would result from a competition between shear-induced structuration as described in the Introduction and the strong aging of the sample. Such an interpretation would also account for the stick-slip like motion of the fluidized band at the moving wall. Nonetheless, despite systematic monitoring of the sample during shear startup experiments, no structuration or spatial pattern could be observed. Moreover, supplemental shear startup experiments in narrower gaps show that for a given shear rate, stronger confinement leads to the disappearance of the stress oscillations and homogeneous velocity profiles [see Fig. S6 in the ESI†]. This last result strongly suggests that confinement alone cannot account for stress oscillations.

Finally, the present study has focused on experiments performed under smooth boundary conditions, revealing the presence of strong wall slip associated with heterogeneous, shear-banded flows while fully fluidized states show negligible wall slip. Yet the roughness and/or chemical nature of the walls are known to have a crucial influence not only on rheological measurements but also on the local flow both close to the walls and in the bulk.^{33,34,45,86,87} Therefore the influence of boundary conditions on the complex fluidization scenario reported here appears as the next key question to address in future work. As a first step, we report preliminary tests on the role of boundary conditions in the above results in the ESI.† The flow curve measured under “rough” boundary conditions in a sand-blasted Plexiglas Taylor–Couette cell with a typical roughness of 1 μm (compare with a few tens of nanometers for the “smooth” cell used so far) shows a smaller, yet significant hysteresis [see Fig. S1(b) in the ESI†] as well as wall slip at low shear rates (see Fig. S5 in the ESI†). Furthermore, one can see a strong difference between the velocity profiles recorded simultaneously with the flow curve, respectively, with the rough and smooth boundary conditions (compare Fig. S4 and S5 in the ESI†) although the surface roughness of the rough boundary does not match exactly the size of the microstructure. In particular, the transient fluidization episode reported around [small gamma, Greek, dot above] ≃ 7 s⁻¹ with smooth boundary conditions [Fig. S2(b) and S4 in the ESI†] is absent with rough walls (see Fig. S5 in the ESI†). These preliminary results illustrate the strong impact of the boundary conditions and urge for systematic experiments so as to quantify the impact of the boundary conditions, especially on the state diagram reported in Fig. 5.

5 Conclusion

We have investigated the local scenario associated with the shear-induced fluidization of an attractive gel made of non-Brownian particles. We have identified a critical shear rate [small gamma, Greek, dot above]* that separates steady shear-banded flows from full fluidization and that exhibits a nonlinear dependence with the sample age t_w. This critical shear rate [small gamma, Greek, dot above]* is much larger than the one signaling flow instability in experiments starting from fluidized states and depends on the shear cell geometry as well as possibly on the preshear intensity imposed prior to the shear startup experiment. As a key result, we have shown that for shear rates larger than [small gamma, Greek, dot above]*, the fluidization of the sample involves successive local avalanche-like events that are heterogeneously distributed along the cell height and dynamics of which is strongly coupled to both the slip behaviour at the wall and the width of the shear band. Such avalanches appear in the stress signal as peaks, whose individual properties are strongly reminiscent of stick-slip phenomena. Future work will focus on the early stage of shear startup experiments, and in particular on the stress overshoot that occurs before the stress relaxation, as well as on the influence of the boundaries and confinement on the fluidization scenario.

Acknowledgements

The authors thank J.-P. Chapel, B. Keshavarz and G. Ovarlez for stimulating discussions, T. Gibaud for allowing us to use his microscope, J. Laurent for her precious assistance with the SEM experiments as well as two anonymous referees for their constructive remarks on our manuscript. This work was supported by JSPS and CNRS under the Japan-France Research Cooperative Program (PRC CNRS/JSPS RheoVolc). A.K. acknowledges support by JSPS Kakenhi Grant No. 265204. S.M. acknowledges funding from Institut Universitaire de France and the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013) and ERC Grant Agreement No. 258803.

References

1. P. Coussot, J. Non-Newtonian Fluid Mech., 2014, 211, 31–49.
2. D. Bonn, J. Paredes, M. Denn, L. Berthier, T. Divoux and S. Manneville, 2015, arXiv:1502.05281.
3. P. C. F. Møller, A. Fall and D. Bonn, Europhys. Lett., 2009, 87, 38004.
4. G. Ovarlez, S. Cohen-Addad, K. Krishan, J. Goyon and P. Coussot, J. Non-Newtonian Fluid Mech., 2013, 193, 68–79.
5. N. Balmforth, I. Frigaard and G. Ovarlez, Annu. Rev. Fluid Mech., 2014, 46, 121–146.
6. R. Bonnecaze and M. Cloitre, Adv. Polym. Sci., 2010, 236, 117–161.
7. T. G. Mason, J. Bibette and D. A. Weitz, J. Colloid Interface Sci., 1996, 179, 439–448.
8. M. Cloitre, M. Borrega, F. Monti and L. Leibler, C. R. Phys., 2003, 4, 221–230.
9. J. Seth, M. Cloitre and R. Bonnecaze, J. Rheol., 2006, 50, 353–376.
10. M. Siebenbürger, M. Fuchs and M. Ballauff, Soft Matter, 2012, 8, 4014–4024.
11. P. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
12. P. Lu and D. Weitz, Annu. Rev. Condens. Matter Phys., 2013, 4, 217–233.
13. A. Mourchid, A. Delville, J. Lambard, E. Lécolier and P. Levitz, Langmuir, 1995, 11, 1942–1950.
14. F. Pignon, A. Magnin, J.-M. Piau, B. Cabane, P. Lindner and O. Diat, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 3281–3289.
15. E. Paineau, I. Bihannic, C. Baravian, A.-M. Philippe, P. Davidson, P. Levitz, S. Funari, C. Rochas and L. Michot, Langmuir, 2011, 27, 5562–5573.
16. V. Trappe and D. A. Weitz, Phys. Rev. Lett., 2000, 85, 449–452.
17. V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775.
18. K. Pham, S. Egelhaaf, P. Pusey and W. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 011503.
19. E. Mock and C. Zukoski, J. Rheol., 2007, 51, 541–559.
20. N. Reddy, Z. Zhang, M. Lettinga, J. Dhont and J. Vermant, J. Rheol., 2012, 56, 1153–1174.
21. L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 2000, 84, 2275–2278.
22. C. Derec, G. Ducouret, A. Ajdari and F. Lequeux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061403.
23. G. Ovarlez and X. Chateau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061403.
24. A. Negi and C. Osuji, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 010404.
25. N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470.
26. G. Scherer, J. Non-Cryst. Solids, 1989, 108, 18–27.
27. S. Manley, J. Skotheim, L. Mahadevan and D. Weitz, Phys. Rev. Lett., 2005, 94, 218302.
28. R. Buscall, T. H. Choudhury, M. A. Faers, J. W. Goodwin, P. A. Luckham and S. J. Partridge, Soft Matter, 2009, 5, 1345–1349.
29. G. Brambilla, S. Buzzaccaro, R. Piazza, L. Berthier and L. Cipelletti, Phys. Rev. Lett., 2011, 106, 118302.
30. L. J. Teece, M. A. Faers and P. Bartlett, Soft Matter, 2011, 7, 1341–1351.
31. P. Barlett, L. Teece and M. Faers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021404.
32. R. Buscall and I. McGowan, Faraday Discuss. Chem. Soc., 1983, 76, 277–290.
33. T. Gibaud, C. Barentin and S. Manneville, Phys. Rev. Lett., 2008, 101, 258302.
34. T. Gibaud, C. Barentin, N. Taberlet and S. Manneville, Soft Matter, 2009, 5, 3026–3037.
35. J. J. V. DeGroot, C. W. Macosko, T. Kume and T. Hashimoto, J. Colloid Interface Sci., 1994, 166, 404–413.
36. R. Navarrete, L. Scriven and C. Macosko, J. Colloid Interface Sci., 1996, 180, 200–211.
37. A. Montesi, A. Peña and M. Pasquali, Phys. Rev. Lett., 2004, 92, 058303.
38. C. O. Osuji, C. Kim and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 060402(R).
39. A. Negi and C. Osuji, Rheol. Acta, 2009, 48, 871–881.
40. V. Grenard, N. Taberlet and S. Manneville, Soft Matter, 2011, 7, 3920–3928.
41. J. Vermant and M. J. Solomon, J. Phys.: Condens. Matter, 2005, 17, R187–R216.
42. V. Gopalakrishnan and C. Zukoski, J. Rheol., 2007, 51, 623–644.
43. T. Gibaud, D. Frelat and S. Manneville, Soft Matter, 2010, 6, 3482–3488.
44. J. Sprakel, S. Lindström, T. Kodger and D. Weitz, Phys. Rev. Lett., 2011, 106, 248303.
45. V. Grenard, T. Divoux, N. Taberlet and S. Manneville, Soft Matter, 2014, 10, 1555–1571.
46. A. Stickland, A. Kumar, T. Kusuma, P. Scales, A. Tindley, S. Biggs and R. Buscall, Rheol. Acta, 2015, 54, 337–352.
47. H. Chan and A. Mohraz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041403.
48. C. Perge, N. Taberlet, T. Gibaud and S. Manneville, J. Rheol., 2014, 58, 1331–1357.
49. P. Varadan and M. Solomon, Langmuir, 2001, 17, 2918–2929.
50. A. Mohraz and M. Solomon, J. Rheol., 2005, 49, 657–681.
51. B. Rajaram and A. Mohraz, Soft Matter, 2010, 6, 2246–2259.
52. T. Divoux, M.-A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103.
53. J. S. Raynaud, P. Moucheront, J. C. Baudez, F. Bertrand, J. P. Guilbaud and P. Coussot, J. Rheol., 2002, 46, 709–732.
54. J. Martin and Y. Hu, Soft Matter, 2012, 8, 6940–6949.
55. G. Ovarlez, S. Rodts, X. Chateau and P. Coussot, Rheol. Acta, 2009, 48, 831–844.
56. A. Fall, J. Paredes and D. Bonn, Phys. Rev. Lett., 2010, 105, 225502.
57. L. Bilmes, Nature, 1942, 150, 432–433.
58. G. McKinley, Rheol. Bull., 2015, 84, 14–17.
59. R. Moorcroft and S. Fielding, Phys. Rev. Lett., 2013, 110, 086001.
60. J. Colombo, A. Widmer-Cooper and E. Del Gado, Phys. Rev. Lett., 2013, 110, 198301.
61. J. Colombo and E. Del Gado, J. Rheol., 2014, 58, 1089–1116.
62. S. Fielding, Rep. Prog. Phys., 2014, 77, 102601.
63. S. Manneville, L. Bécu and A. Colin, Eur. Phys. J.: Appl. Phys., 2004, 28, 361–373.
64. T. Gallot, C. Perge, V. Grenard, M.-A. Fardin, N. Taberlet and S. Manneville, Rev. Sci. Instrum., 2013, 84, 045107.
65. P. C. F. Møller, S. Rodts, M. A. J. Michels and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041507.
66. M. Kobayashi, F. Juillerat, P. Galletto, P. Bowen and M. Borkovec, Langmuir, 2005, 21, 5761–5769.
67. W. Heston, R. Iler and G. Sears, J. Chem. Phys., 1960, 64, 147–150.
68. J. Trompette and M. Clifton, J. Colloid Interface Sci., 2004, 276, 475–482.
69. X. J. Cao, H. Z. Cummins and J. F. Morris, Soft Matter, 2010, 6, 5425–5433.
70. D. Truzzolillo, V. Roger, C. Dupas, S. Mora and L. Cipelletti, E-print cond-mat/1411.2265.
71. L. Allen and E. Matijević, J. Colloid Interface Sci., 1969, 31, 287–296.
72. L. Allen and E. Matijević, J. Colloid Interface Sci., 1970, 33, 420–429.
73. J. Depasse and A. Watillon, J. Colloid Interface Sci., 1970, 33, 430–438.
74. J. Depasse, J. Colloid Interface Sci., 1997, 194, 260–262.
75. E. Drabarek, J. Bartlett, H. Hanley, J. Woolfrey and C. Muzny, Int. J. Thermophys., 2002, 23, 145–160.
76. P. Coussot, J. S. Raynaud, F. Bertrand, P. Moucheront, J. P. Guilbaud, H. T. Huynh, S. Jarny and D. Lesueur, Phys. Rev. Lett., 2002, 88, 218301.
77. A. Ragouilliaux, B. Herzhaft, F. Bertrand and P. Coussot, Rheol. Acta, 2006, 46, 261–271.
78. A. ten Brinke, L. Bailey, H. Lekkerkerker and G. Maitland, Soft Matter, 2007, 3, 1145–1162.
79. T. Divoux, V. Grenard and S. Manneville, Phys. Rev. Lett., 2013, 110, 018304.
80. V. Viasnoff and F. Lequeux, Phys. Rev. Lett., 2002, 89, 065701.
81. F. Pignon, A. Magnin and J.-M. Piau, J. Rheol., 1996, 40, 573–587.
82. P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, J. Rheol., 2002, 46, 573–589.
83. P. Coussot, H. Tabuteau, X. Chateau, L. Tocquer and G. Ovarlez, J. Rheol., 2006, 50, 975–994.
84. G. Ovarlez and P. Coussot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011406.
85. P. C. F. Møller, J. Mewis and D. Bonn, Soft Matter, 2006, 2, 274–283.
86. J. Seth, C. Locatelli-Champagne, F. Monti, R. Bonnecaze and M. Cloitre, Soft Matter, 2012, 8, 140–148.
87. V. Mansard, L. Bocquet and A. Colin, Soft Matter, 2014, 10, 6984–6989.

---

Footnote

† Electronic supplementary information (ESI) available: Five movies and six supplemental figures together with their descriptions and explanations. See DOI: 10.1039/c5sm01259g

---