Microscopic segregation of hydrophilic ions in critical binary aqueous solvents

Abstract

Solid surfaces suspended in critical aqueous binary mixtures containing hydrophilic salt have recently been found to exhibit anomalous interactions, and a possible mechanism is provided by the asymmetric solvation preferences of weakly and strongly hydrophilic cations and anions, respectively. Here we address this mechanism by studying interfacial ion distributions in a critical binary mixture of water and 2,6-dimethylpyridine containing potassium chloride at temperatures below the lower critical point, using grazing-incidence X-ray fluorescence from the liquid–vapour interface. Our data provide direct and unambiguous experimental evidence for microscopic segregation of hydrophilic ions in critical aqueous binary mixtures, thereby supporting the important role of asymmetric ion solvation in the above mentioned anomalous force. However, the experimental data are only qualitatively reproduced by state-of-the-art theoretical calculations, demonstrating the need of a microscopic theoretical model including asymmetric ion solvation.

---

1 Introduction

Binary liquid mixtures exhibit diverging concentration fluctuations upon approaching the critical point of demixing. The spatial confinement of these concentration fluctuations, for example between suspended colloidal particles, leads to the emergence of a force between the confining surfaces – the so-called critical Casimir force.¹ While this critical force had been observed indirectly already earlier via the thickness of wetting films,² its recent direct observation³ has sparked significant interest in the phenomenon. Since the spatial extent of this force is governed by the correlation length of the solvent's critical fluctuations, it is strongly dependent on the temperature of the system. Moreover, its sign depends on the adsorption preferences of the confining surfaces; if the same liquid component wets both surfaces an attraction emerges, whereas opposite wetting preferences results in a repulsion. Given this tunability, critical Casimir forces are currently being employed for reversible control of colloidal assembly, utilising both temperature^4,5 and adsorption preferences⁶ as external parameters.

Although the critical Casimir forces are well understood in pure binary solvents,^7,8 this is not the case upon adding salt. In particular, the complex coupling between ion distributions and critical fluctuations in binary aqueous mixtures containing hydrophilic salt has been observed to induce an attraction between suspended hydrophilic and hydrophobic surfaces, although the electrical double layer and critical Casimir forces are expected to be mutually repulsive.⁹ Several models,^10–13 at different level of theory, have been devised to rationalise this surprising experimental observation. A key ingredient in many of these theoretical models^10–12 is an unequal partitioning of ions due to asymmetric solvation preferences; the combination of strongly hydrophilic anions and only weakly hydrophilic cations induces an accumulation of positive charge near the suspended hydrophobic surface, thus leading to its anomalous attraction to the negatively charged hydrophilic surface. However, such microscopic segregation of hydrophilic ions in critical binary aqueous solvents is yet to be directly observed experimentally.

In this paper, we address experimentally the unequal partitioning of hydrophilic cations and anions in a critical binary aqueous solvent. For this purpose we apply grazing-incidence X-ray fluorescence (GIXF) to probe ion density profiles at the liquid–vapour interface, which is preferentially adsorbed by the nonaqueous component. Following ref. 3 and 9, the critical mixture is composed of water and 2,6-dimethylpyridine, and we use potassium chloride (KCl) as the added hydrophilic salt. The results of our study can be summarised as follows. Most importantly, our GIXF data provide direct experimental evidence for microscopic segregation of hydrophilic ions in critical binary aqueous mixtures. This finding provides support for the important role of asymmetric ion solvation in the above mentioned anomalous forces between hydrophilic and hydrophobic surfaces suspended in salt-containing critical binary aqueous solvents. However, the experimental GIXF data are found to be in only qualitative, but not quantitative, agreement with state-of-the-art theoretical predictions for interfacial ion distributions in critical binary liquid mixtures,¹⁴ demonstrating the need for developing a microscopic theoretical model which includes asymmetric ion solvation.

2 Experimental

Materials

The sample was a binary liquid mixture of water (Millipore; dielectric constant ε ≈ 80) and 2,6-dimethylpyridine (also known as 2,6-lutidine; Sigma-Aldrich, purity ≥99%; ε ≈ 7). Except for the phase diagram of Fig. 1 (discussed below), we obtained all data presented here using a 2,6-dimethylpyridine volume fraction of ϕ = 0.3 and 10 mM added potassium chloride (Sigma-Aldrich, purity ≥99%). We used all chemicals as received.

Fig. 1 Coexistence points for the mixture of water and 2,6-dimethylpyridine. The data are presented as a function of 2,6-dimethylpyridine volume fraction ϕ. The blue circles depict data for the pure binary solvent, while the red diamonds have been obtained upon adding 10 mM KCl. The error bars are smaller than the symbol size.

Phase diagrams

We prepared sample sets by varying the 2,6-dimethylpyridine content in the range of ϕ = 0.15–0.6 by volume fraction. Next we placed the samples in 75 × 10 mm sealed glass test tubes and further in a temperature-controlled water bath (Grant Instruments, temperature stability ≈0.1 K). For each sample, we increased the temperature in steps of 0.1 K, and we allowed the samples to equilibrate for ≈15 minutes after each temperature increment. We determined the phase separation points visually based on the onset of critical opalescence.

GIXF experiment

We carried out the GIXF experiment at beamline ID10 of the European Synchrotron Radiation Facility. We used an incident X-ray energy of 8 keV, which for this system leads to a critical angle of total reflection θ_C = 0.152°, and we recorded the fluorescence spectra using an energy-dispersive detector (Vortex, SII NanoTechnology). During the experiment we kept the sample under helium atmosphere in order to avoid parasitic argon fluorescence. We collected data at several temperatures well below T_C (i.e., T_C − T = 4–10 K), using a custom-made sample cell with a temperature stability within ≈0.1 K.

3 Results and discussion

Bulk properties

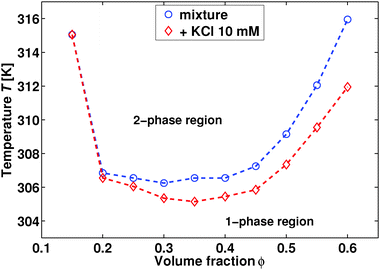
The addition of ions modifies hydrogen bonding and may thus affect bulk properties of binary aqueous solvents, such as the phase diagram or the correlation length of the critical fluctuations. In order to set the stage, we therefore present in Fig. 1 the experimental phase diagram for our binary mixture of water and 2,6-dimethylpyridine. The neat binary solvent exhibits an immiscibility loop with a lower critical point at ϕ_C ≈ 0.30, in line with previous studies.¹⁵ Upon adding 10 mM KCl we observe two effects: (i) a lowering of the critical point by ≈2 K and (ii) a minor shift of the critical composition by Δϕ_C ≤ 0.05. The former finding is in agreement with previous studies on this particular system,¹⁶ while the latter one is reminiscent of earlier reports on the phase behaviour of binary mixtures containing inorganic salts.¹⁷

Let us next turn to the bulk correlation length ξ(T) of the critical fluctuations. For the pure critical mixture of water and 2,6-dimethylpyridine we have ξ(T) = ξ₀(1 − T/T_C)^−ν, where ν ≈ 0.63 is a critical exponent and ξ₀ = 0.2 ± 0.02 nm.¹⁵ For this particular critical mixture it is known that ξ(T) is unaffected by the addition of 10 mM KCl.⁹ In the rest of this study, we will therefore focus on the mixture of water and 2,6-dimethylpyridine with ϕ = 0.3 and 10 mM added KCl. Nevertheless, we have verified that the same result is obtained in GIXF experiments using either ϕ = 0.3 or 0.35 for the 2,6-dimethylpyridine composition.

Grazing-incidence X-ray fluorescence

In order to gain more insight into the ion–solvent coupling, we have probed cation and anion distributions at several degrees below the critical point. For this purpose we use GIXF, which is an emerging surface-sensitive technique^18,19 that has recently been applied for studies on specific ion adsorption at aqueous electrolyte surfaces²⁰ and ion distributions in biological membranes.²¹ In these experiments the incident X-ray beam hits the liquid–vapour interface at a grazing angle, leading to an evanescent wave propagation in the sample. The evanescent wave, in turn, excites the different chemical species and finally leads to fluorescence emission. Moreover, by varying the angle of incidence in the vicinity of the critical angle the penetration depth of the exponentially decaying evanescent X-ray field can be tuned; below the critical angle the sample is probed within a depth of about five nm, providing sensitivity to interfacial ion distributions, while above θ_C the bulk sample is probed. Formally the fluorescence intensity I_±(θ) from cations and anions (denoted respectively as + and −) at an incidence angle θ is given byHere the liquid phase is found at z ≥ 0 (with the liquid surface at z = 0), while I₀(z,θ) denotes the intensity distribution of X-rays in the sample (henceforth called the illumination profile), n_±(z) the ion number density profile, and μ_± the tabulated²² linear absorption coefficient for the emitted fluorescence line. The prefactor C_±(θ) contains terms such as acceptance angle and quantum efficiency of the detector, i.e., factors which do not depend on the ion distributions in the sample. For an illustration of the experiment, see Fig. 2.

Fig. 2 Illustration of the GIXF experiment at the liquid–vapour interface. The light blue and white regions depict the liquid and vapour phases, respectively, while the black solid and dashed-dotted lines denote the illumination profile I₀(z,θ) across the liquid–vapour interface for incidence angles of θ = 0.7θ_C and of θ = 1.0θ_C. The solid blue and dashed red lines exemplify cation and anion number density profiles n_±(z), and the inset shows the volume fraction profile ϕ(z) of 2,6-dimethylpyridine (see text for details).

The GIXF data is exemplified in Fig. 3. More specifically, Fig. 3a shows a typical GIXF spectrum collected from a mixture of water and 2,6-dimethylpyridine containing 10 mM KCl, in this particular case obtained using an incidence angle of θ = 0.2°. From these data we can clearly identify the main characteristic anion and cation emission lines – the chloride and potassium Kα lines at ∼2.6 keV and ∼3.3 keV, respectively. Following previous studies (see, e.g., ref. 23), we collected GIXF spectra for several angles of incidence, each of which were normalised and further fitted with multiple Gaussian peaks and a linear background in order to extract the intensities of the characteristic emission lines. Using this procedure we obtained anion (Cl⁻ Kα) and cation (K⁺ Kα) GIXF intensities (over more than four orders of magnitude) as a function of incidence angle θ, as shown in Fig. 3b. As mentioned earlier, for incidence angles below θ_C these data are sensitive to the interfacial ion distributions.

Fig. 3 GIXF data obtained from a mixture of water and 2,6-dimethylpyridine containing 10 mM KCl. (a) A typical spectrum, collected using an incidence angle of θ = 0.2°. The main fluorescence signal from chloride (Cl⁻ Kα, energy ∼2.6 keV) and potassium (K⁺ Kα, ∼3.3 keV) ions are explicitly depicted in the figure. (b) Experimental normalised GIXF intensity as a function of incidence angle θ. Cation (blue solid line) and anion (red dashed line) data are shown separately.

The data of Fig. 3 further highlight two reasons for choosing KCl as the added salt, both of which are essential for the success of the present experiment. From a methodological point of view, the X-ray emission lines of potassium and chloride are relatively closely spaced in energy, allowing the cation and anion fluorescence signals to be monitored simultaneously (see Fig. 3a). This feature is the reason for choosing KCl rather than KBr, which was studied in ref. 9. In terms of physics, in turn, chloride strongly prefers water over 2,6-dimethylpyridine while potassium only has a weak preference for water. This solvation asymmetry of the two hydrophilic ionic species, which is expected for several different combinations of binary aqueous solvents and ionic species,²⁴ governs the microscopic charge segregation studied here.

Relative GIXF intensity

In order to facilitate the comparison between cation and anion data, we show in Fig. 4 the relative GIXF intensity I₊/I₋versus incidence angle θ. Most importantly, the prefactors C_±(θ) of eqn (1) cancel out via this normalisation procedure. By presenting the GIXF data in this manner, we thereby highlight the differences between cation and anion concentrations near the interface.

Fig. 4 Relative GIXF intensity I₊/I₋versus incidence angle θ for the critical mixture of water and 2,6-dimethylpyridine containing 10 mM KCl. Experimental data are shown for room temperature, T_C − T = 8 K, corresponding to a bulk correlation length of ξ = 2.0 nm. The solid and dashed-dotted lines are based on the theoretical model of eqn (2), using cation solvation contrasts f₊ = 2.5 and 0, respectively (see text for details). The vertical dashed line represents the critical angle of total reflection, θ_C.

Based on these data, we can directly make the important observation that the relative GIXF intensity I₊/I₋ is larger than unity for small incidence angles θ ≤ θ_C. This finding, which we have verified in two separate experiments and for several different temperatures in the range T_C − T = 4–10 K, can only be explained by a relative excess of cations compared to anions close to the liquid–vapour interface. We note that the effect is also visible on the logarithmic scale of Fig. 3b. To the best our knowledge, this is the first direct experimental evidence of microscopic segregation of hydrophilic ions in binary aqueous mixtures. We will discuss this observation in more detail later with the aid of theoretical modelling.

Adsorption preferences

The data of Fig. 4 also provide indirect information about adsorption preferences of the two liquids at the interface. It is known that for binary liquid mixtures in which the two components exhibit a large difference in surface tension, the component with the smaller surface tension saturates the liquid–vapour interface. In this case an excess of the preferentially adsorbed liquid component is observed within a distance ∼ξ from the surface. This is also the case for the present system, where 2,6-dimethylpyridine has been found to adsorb at the interface, owing to its lower surface tension (γ ≈ 30 mN m⁻¹ in ambient atmosphere) compared to water (γ ≈ 70 mN m⁻¹).²⁵ This result is supported by our data of Fig. 4; preferential adsorption of 2,6-dimethylpyridine at the interface leads to relative interfacial excess of the ionic species exhibiting only a weak preference for water over the non-aqueous liquid component, viz. potassium in our study. In the subsequent theoretical GIXF modelling, we will therefore assume that 2,6-dimethylpyridine saturates the liquid–vapour interface.

Theoretical modelling

To gain more insight into the mechanisms of the microscopic charge segregation observed in Fig. 4, we model the GIXF data of eqn (1) using the theoretical illumination profile I₀(z,θ) and ion density profiles n_±(z). For determination of the illumination profile we use a so-called matrix propagation method,²⁶ and we have verified that it suffices to assume a sharp interface and a constant electron density in the liquid phase. In brief, we determine I₀(z,θ) by solving Maxwell's equations for a stratified medium in a matrix formalism, using tabulated²⁷ optical constants as input. This approach gives identical results to those obtained using Parrat's recursive scheme.²¹ The application of the matrix propagation method to GIXF has been presented elsewhere.²³

In order to obtain theoretical ion density profiles, we use a simplified model by Bier and co-workers. This model provides approximate n_±(z) in good agreement with state-of-the-art mean-field theories,^10,14 in which equilibrium ion distributions are obtained by minimising a grand potential given by several free energy contributions such as the mixing entropy of solvent components and ions, energy cost of solvent inhomogeneties, ion solvation, adsorption preferences of the interface, and an external electrostatic potential in the case of charged interfaces. In the case of an uncharged liquid–vapour interface saturated by the non-aqueous component, the adopted model yields¹⁴

n_±(z) = n⁰_± exp{−V_±[ϕ(z)] + V_±(ϕ₀)}, (2)

with the liquid phase again being situated at z ≥ 0. Here n⁰_± = n_±(∞) is the bulk number density of the ions, V_±(ϕ)k_BT an effective solvent-mediated ion potential with V_±(ϕ) = −log{1 − ϕ [1 − exp(−f_±)]} and k_BT the thermal energy, f_±k_BT the free energy cost of transferring a cation (+) or an anion (−) from water to 2,6-dimethylpyridine, and ϕ₀ = ϕ(∞) the bulk volume fraction of the latter component. Within this model ϕ(z) is an approximate volume fraction profile of 2,6-dimethylpyridine (see inset of Fig. 2), which is determined in the absence of solvent–ion coupling using a temperature-dependent Flory–Huggins-type interaction parameter χ and the bulk correlation length ξ of the solvent. In essence, eqn (2) describes Boltzmann distributions of non-interacting ions in a free-energy potential induced by the preferential solvation of cations and anions; given an inhomogeneous distribution of solvent components, i.e. ϕ(z) ≠ constant, the difference between n₊(z) and n₋(z) is driven by different free energies of transfer, f₊ and f₋, for the two ionic species.

In practice, we carry out our model calculations using eqn (2) as follows. First, we are not aware of tabulated solvation contrasts between water and 2,6-dimethylpyridine. Therefore we employ instead the values f₊ = 2.5 and f₋ = 15 for the free energies of transfer of K⁺ and Cl⁻ ions from water to pyridine²⁴ [see Fig. 2 for the resulting n_±(z)]. Second, we have chosen the Flory–Huggins-type parameter χ, which represents the interactions between solvent molecules, such as to reproduce the bulk correlation length ξ = 2.0 nm.^10,14 Third, since we are not sensitive to surface roughness in the range of grazing angles used in the present study, we neglect it in our modelling.

GIXF experiment versus theory

In Fig. 4 we present as the solid line the model calculation thus obtained. The model qualitatively describes the experimental data, i.e. I₊/I₋ > 1 for small incidence angles θ ≤ θ_C, although it systematically underestimates the relative interfacial excess of cations compared to anions. In order to quantify the magnitude of the difference between the model and the experimental data, we also present as the dashed-dotted line the corresponding model calculation using a hypothetical cation solvation contrast f₊ = 0, which means that K⁺ would not show preference for any of the solvent components. By introducing this value for f₊ we are, in effect, magnifying the difference between n₊(z) and n₋(z) near the interface. In this case the agreement between the model and the experimental data is semi-quantitative for all incidence angles θ. The good agreement in this latter case should, of course, not be taken to imply that the cation does not have a preference for water over 2,6-dimethylpyridine; rather, it reflects the approximations in our model calculations.

What are the main reasons for the quantitative difference between experiment and theory of Fig. 4? We can think of several possible explanations. First, the solvation contrasts f_± may be different for 2,6-dimethylpyridine compared to those for pyridine adopted here. While the number density profile n₋(z) of the strongly hydrophilic anions are insensitive to small variations in f₋, a minor change in f₊ of the weakly hydrophilic cations, due to the addition of two methyl groups, would modify n₊(z) and the ensuing relative GIXF intensity I₊/I₋. Given the current interest in salt-containing critical binary aqueous solvents, it would be important to obtain better estimates of the solvation contrasts f_±. Second, the addition of ions may modify the adsorption preferences of the liquid components at the interface, although both experiments⁹ and theory^13,14 imply that this effect is negligible at weakly charged, hydrophobic interfaces. Third, the use of the mean-field value ϕ = 0.5, instead of the experimental value ϕ ≈ 0.3, may quantitatively affect the GIXF data. Finally, the model neglects molecular-scale ordering of the solvent, the finite size of the ions, and ion–ion interactions, which may affect the interfacial ion distributions.²⁸ A possible approach to reproduce our experimental findings could thus be the coarse-graining scheme of ref. 13, but including asymmetric ion solvation.

4 Conclusions

In conclusion, we report the first direct experimental observation of microscopic segregation of hydrophilic ions in aqueous binary mixtures. Such unequal ion partitioning has recently been employed to explain anomalous forces between solid surfaces suspended in a critical binary solvent consisting of water and 2,6-dimethylpyridine.^10–12 Our experimental observation thus shows the importance of preferential ion solvation when describing colloidal interactions in salt-containing critical binary liquid mixtures. It should be noted, however, that our finding does not rule out the second proposed mechanism for the anomalous forces, namely salt-induced modification of adsorption preferences.¹³

Finally we comment briefly on the broader impact of the microscopic segregation of hydrophilic ions in binary aqueous mixtures, as reported here. Our direct experimental observation highlights the importance of preferential ion solvation for the modification of electric double layers, and hence double layer interactions, in aqueous mixtures containing salt.²⁹ Consequently, it is highly relevant for a range of soft-matter systems, from charge-stabilised ‘emulsifier’-free water-in-oil emulsions³⁰ to bicontinuous interfacially jammed emulsion gels³¹ (i.e., bijels).

Acknowledgements

We thank the European Synchrotron Radiation Facility for providing beamtime and the Swedish Research Council (Grant No. 621-2012-3897) for financial support.

References

1. M. E. Fischer and P. G. de Gennes, C. R. Seances Acad. Sci., Ser. B, 1978, 287, 207–209.
2. M. Fukuto, Y. F. Fano and P. S. Pershan, Phys. Rev. Lett., 2005, 94, 135702.
3. C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172–175.
4. D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. H. Wegdam and P. Schall, Phys. Rev. Lett., 2009, 103, 156101.
5. V. D. Nguyen, S. Faber, Z. Hu, G. H. Wegdam and P. Schall, Nat. Commun., 2013, 4, 1584.
6. F. Soyka, O. Zvyagolskaya, C. Hertlein, L. Helden and C. Bechinger, Phys. Rev. Lett., 2008, 101, 208301.
7. M. Krech, The Casimir Effect In Critical Systems, World Scientific, 1994.
8. A. Gambassi, A. Maciołek, C. Hertlein, U. Nellen, L. Helden, C. Bechinger and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 80, 061143.
9. U. Nellen, J. Dietrich, L. Helden, S. Chodankar, K. Nygård, J. F. van der Veen and C. Bechinger, Soft Matter, 2011, 7, 5360–5364.
10. M. Bier, A. Gambassi, M. Oettel and S. Dietrich, EPL, 2011, 95, 60001.
11. R. Okamoto and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 051401.
12. S. Samin and Y. Tsori, J. Chem. Phys., 2012, 136, 154908.
13. F. Pousaneh, A. Ciach and A. Maciołek, Soft Matter, 2014, 10, 470–483.
14. M. Bier, A. Gambassi and S. Dietrich, J. Chem. Phys., 2012, 137, 1034504.
15. E. Gülari, A. F. Collings, R. L. Schmidt and C. J. Pings, J. Chem. Phys., 1972, 56, 6169–6179.
16. C. Y. Seah, C. A. Grattoni and R. A. Dawe, Fluid Phase Equilib., 1993, 89, 345–350.
17. V. Balevicius and H. Fuess, Phys. Chem. Chem. Phys., 1999, 1, 1507–1510.
18. M. J. Bedzyk, G. M. Bommarito and J. S. Schildkraut, Phys. Rev. Lett., 1989, 62, 1376–1379.
19. W. B. Yun and J. M. Bloch, J. Appl. Phys., 1990, 68, 1421–1428.
20. V. Padmanabhan, J. Daillant, L. Belloni, S. Mora, M. Alba and O. Konovalov, Phys. Rev. Lett., 2007, 99, 086105.
21. E. Schneck, T. Schubert, O. V. Konovalov, B. E. Quinn, T. Gutsmann, K. Brandenburg, R. G. Oliveira, D. A. Pink and M. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9147–9151.
22. I. Orlic, K. K. Loh, C. H. Sow, S. M. Tang and P. Thong, Nucl. Instrum. Methods Phys. Res., Sect. B, 1993, 74, 352–361.
23. W. Abuillan, E. Schneck, A. Körner, K. Brandenburg, T. Gutsmann, T. Gill, A. Vorobiev, O. Konovalov and M. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012705.
24. H. D. Inerowicz, W. Li and I. Persson, J. Chem. Soc., Faraday Trans., 1994, 90, 2223–2234.
25. J. H. J. Cho, B. M. Law and K. Gray, J. Chem. Phys., 2002, 116, 3058–3062.
26. K. Ohta and H. Ishida, Appl. Opt., 1990, 29, 1952–1959.
27. B. L. Henke, E. M. Gullikson and J. C. Davis, At. Data Nucl. Data Tables, 1993, 54, 181–342.
28. N. Laanait, M. Mihaylov, B. Hou, H. Yu, P. Vanýsek, M. Meron, B. Lin, I. Benjamin and M. L. Schlossman, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20326–20331.
29. J. Zwanikken and R. van Roij, Phys. Rev. Lett., 2007, 99, 178301.
30. M. E. Leunissen, A. van Blaaderen, A. D. Hollingsworth, M. T. Sullivan and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2585–2590.
31. E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2006, 6, 966–971.

---