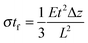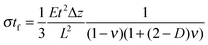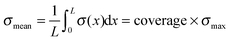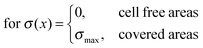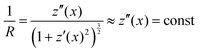Contractile cell forces deform macroscopic cantilevers and quantify biomaterial performance

Abstract

Cells require adhesion to survive, proliferate and migrate, as well as for wound healing and many other functions. The strength of contractile cell forces on an underlying surface is a highly relevant quantity to measure the affinity of cells to a rigid surface with and without coating. Here we show with experimental and theoretical studies that these forces create surface stresses that are sufficient to induce measurable bending of macroscopic cantilevers. Since contractile forces are linked to the formation of focal contacts, results give information on adhesion promoting qualities and allow a comparison of very diverse materials. In exemplary studies, in vitro fibroblast adhesion on the magnetic shape memory alloy Fe–Pd and on the L-lysine derived plasma-functionalized polymer PPLL was determined. We show that cells on Fe–Pd are able to induce surface stresses three times as high as on pure titanium cantilevers. A further increase was observed for PPLL, where the contractile forces are four times higher than on the titanium reference. In addition, we performed finite element simulations on the beam bending to back up the calculation of contractile forces from cantilever bending under non-homogenous surface stress. Our findings consolidate the role of contractile forces as a meaningful measure of biomaterial performance.

---

1 Introduction

Cellular adhesion is a prerequisite for cell survival, proliferation and migration, since external stimuli to the cell from the extra cellular matrix (ECM) are required to regulate protein expression and further pathways within the cell.¹ However, the link between cell and matrix not only serves for signaling purposes, but is furthermore required for mechanical stability. This connection is mediated by focal adhesions, which establish the connection between the cells' cytoskeleton and ECM proteins and enable cells to exert contractile forces onto rigid surfaces balancing inward directed forces the material exerts on the cell.² In fact the contractile force generated by fibroblasts is closely linked to their matrix adhesion.³

To this end, one of the most important goals in developing modern biomaterials for applications requiring good initial cell adhesion is to provide the conditions for a natural organization of the ECM on the material. But the mere adhesion of ECM proteins to the material is not sufficient to also confirm good cellular adhesion. Also the conformation of the molecules is an important factor whether cells are able to establish a hold. Therefore in vitro testing with primary or immortalized cells is an important prerequisite to make statements about the adhesion promoting properties of a biomaterial candidate.

Early developed methods concentrated on investigating cellular adhesion instead of its manifestation in the form of contractile forces. They simply determine the portion of adherent cells compared to those seeded, and how much they spread after longer incubation times,⁴ or their resistance to shear flow.⁵ For more quantitative results, one of the most common techniques is based on immunostaining of ECM proteins. Antibodies can recognize a certain protein fragment with very high precision. It is possible to specifically label adhesive proteins like vinculin, or α_ν and β₁ integrin subunits, which correspond to the location of focal contacts and thus the anchoring points of contractile forces.^6,7 With this method one can easily compare the expression of focal contacts on similar materials as for example done for different metals by Turner et al.⁸ However, giving an actual value for the force a cell exerts on its support materials is not possible. More detailed information can be acquired by directly measuring the force needed to remove a cell from its substrate, which is for example done by peel-off tests⁹ or single-cell force spectroscopy,^10–12 which both use a modified atomic force microscopy (AFM) setup. The problem here however is that only single cells are tested, which is not only a time-consuming measurement on an expensive setup. As a method operating on a microscopic scale, it also requires some knowledge of surface proteins and adhesion receptors.¹³ This is not the case for macroscopic measurements, where averaging over thousands of cells is possible.

Since direct force measurements turn out to be very challenging, a different and highly promising approach is to measure the effect of these forces on their substrate. The underlying idea dates back to as much as 35 years ago by investigating the effect of cell contractile forces on wrinkle formation in soft silicon rubber.¹⁴ The method was recently refined by Tan et al.,¹⁵ who seeded cells on micropillars and calculated forces from their bending, while Schwarz et al.¹⁶ used labeled gels to visualize substrate deformation. Although giving valuable insights on cell force distributions, the methods are only suitable for highly flexible materials such as silicon and PDMS elastomers employed in those studies. A comparison of a larger variety of surfaces including high stiffness metals is still lacking.

A different type of approach is established within the area of surface physics, in which the phenomenon of surface stress is widely investigated and numerous methods exist to indirectly measure this quantity. Concepts that determine absolute stress values by measuring surface phonon properties or atomic structures¹⁷ of thin specimens compared to bulks of the same material¹⁸ are not applicable in combination with living cells. However, the absolute stress is usually not the property of interest, and it is sufficient to know the change in surface stress when comparing substrates with and without cells. Therefore, measuring cell-adhesion induced changes in curvature of a macroscopic cantilever¹⁹ is the method of choice, leaving unnecessarily difficult aspects like the bending due to atomic structure or coatings of the cantilever out of the equation. The tensile stress results from contractile forces within a cell and attractive interactions between neighboring atoms within a surface layer that induce stresses in solid thin films.²⁰

Attempts to apply this method to cell biology were made before with silicon micro cantilever arrays,²¹ but lack an in-depth study of the physics behind the process. Furthermore, a rescaling to macroscopic cantilevers is desirable to obtain maximal generality with respect to the surface of interest, improve statistics and gain better experimental feasibility. The higher generality of macroscopic approaches results from the fact that the tested surface material can be applied as thin films, not influencing the bulk cantilevers elastic properties, as we will discuss in the course of this work. Therefore a wide spectrum of surface layers can be investigated reaching from biopolymers up to metals with Young's moduli of some kPa up to several 100 GPa, respectively.

Opposing to the objections of Raiteri et al.,²² observed stresses are sufficient to induce measurable deformations in macroscopic cantilevers, as we will show by performing finite element calculations.

We justify this claim by demonstrating adhesion measurements exemplarily on two very different, yet equally promising and interesting materials applied as thin films: the hard metal alloy iron–palladium (Fe₇Pd₃) and the soft polymeric plasma functionalized poly-L-lysine (PPLL) coating.

Fe–Pd is a ferromagnetic shape memory alloy²³ and as such a smart material with a unique set of properties. It is superelastic and can respond to external magnetic fields with deformations and strains of theoretically up to 6%.²⁴ Moreover, it offers great potential for medical applications due to its biocompatibility^25,26 and a surface chemistry favoring biomolecule adhesion.²⁷ On the other hand PPLL is a coating that was developed as prototype of a new promising plasma functionalization technique. It shows similar properties as fermented poly-L-lysine, which is widely used to increase biocompatibility and bioactivity of various materials,^28–30 but exceeds it in robustness, ductility and functionality.³¹

Conclusively, our study gives new insights on contractile forces with a quantitative comparison of cell behavior on materials with very diverse properties. Furthermore, finite element simulations of the cantilever bending induced by inhomogeneous stress distributions from living cells are employed to model the interaction of cells with the cantilever and interpret the experimental findings.

2 From bending to forces – setup and analysis

2.1 Cantilever bending experiment

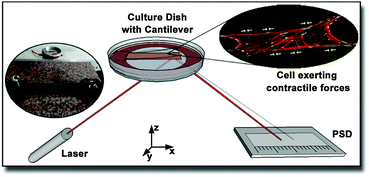
The principle of this contractile force measurement relies on determining the difference in deformation of a cantilever due to the absence or presence of adherent cells. The fully home-built setup is sketched in Fig. 1. A laser was pointed towards a glued reflector plate on the bottom side of the cantilever and then reflected onto a one dimensional position sensitive detector (PSD) from Sitek Electro Optics (PSD 1L20-CP3), attached to a home-built amplifier electronics, as described previously.³² Since diffusively reflected light from cell culture medium and dish can differ from cantilever to cantilever, the linearity and scaling of the PSD were calibrated for each measurement individually, as described in the ESI.† The cell-covered cantilever was clamped on one side into a serum-free cell culture medium filled culture dish and the position of the reflected laser spot was measured after some relaxation time. While continuously tracking the laser spot deflection, 2 ml of 10× trypsin–EDTA solution (Biochrom L2153) were added to the medium around the cantilever to detach the cells. To compensate the additional fluid weight, 2 ml of medium were removed simultaneously from the culture dish. After a short mixing time, a change in cantilever deflection could be observed due to the detachment of cells. The missing contractile stress on the upper side of the cantilever caused a bending downwards resulting in a shifting of the laser spot towards the laser. The laser spot position in dependence of the time was captured by a self-written LabView routine. To confirm a complete detachment of the cells from the cantilever, the surface was examined with fluorescence microscopy. Exemplary pictures before and after trypsin treatment are provided in the ESI.† Note that the imaging does not require fixation of the cells, since no immunofluorescence labeling is applied. Only samples with less than ten residual cells per mm² were considered for further analysis.

Fig. 1 Schematic and inset photograph of the bending beam setup to measure the deflection of a cantilever exposed to contractile forces of living cells. The change in position of a laser beam deflected on the bended beam is measured with a position sensitive detector.

2.2 Surface stress determination with finite element calculations

The cantilever bending due to surface stresses on one side is a very intuitive process, yet not trivial to calculate in most cases. One could assume that the behavior is described by Stoney's formula proposed in 1909 to calculate spontaneous bending of wafers due to a thin film on top of them,³³ but two very important requirements of this method are not matched in our case. First, the cell layer on top does not have a defined thickness as it is the case for solid thin films. Second, the stress is not distributed equally over the whole substrate surface but concentrates at the location of focal contacts. Determining the stress from thin film theory by assuming constant cell height of 3.4 μm, as it was done by Köser et al.,²¹ results in stress values on the order of MPa and thus forces per cell in a mN range, which is clearly unrealistic. Therefore, we decided to iteratively calculate stresses with finite element simulations on each individual sample. After several convergence tests described in the results section, the following routine was established.

From fluorescence micrographs obtained before the measurement, cells were counted and the cantilever surface area covered by cells on the cantilever surface was calculated. From these values, the parameters coverage and spacing were derived. Coverage describes the area populated by cells divided by the total surface area of the cantilever. Spacing is the hypothetical distance from one cell's center to the next if they were evenly distributed along the long axis of the cantilever. From these values, a matching stress profile was designed and applied to the top side of the cantilever. Finite element simulations were performed with COMSOL Multiphysics 4.1. The cantilever was modeled as a block consisting of titanium with the dimensions 25 mm × 10 mm × 0.1 mm and the elastic properties in terms of the Young's modulus E = 105 GPa and Poisson ratio ν = 0.33, as provided by the COMSOL databank. The coating's elastic properties are negligible due to its very small thickness of 50 nm compared to the bulk thickness of 0.1 mm. Negligible in this regard means that for metallic coatings with Young's moduli up to double that of titanium (105 GPa), the position of the neutral axis would move by 0.1%, while for soft coatings with Young's moduli around 100 kPa, the effect would diminish to as few as 10⁻⁷% using the relations giving by Wyser et al.³⁴ for thin film laminates.

For the stress a value according to Stoney's formula was chosen as first approximation. The thereby simulated cantilever surface shape was fitted linearly in a 5 mm region prior to the tip to determine the position and tilt of the reflector plate. Through simple algebra and ray optics, the position of the laser spot on the PSD was calculated by taking the position and length of the cantilever, the laser position and angle, and the PSD position into account. This value is subtracted from the position of the reflection from the undeformed cantilever to get the difference Δl.

On the other hand, Δl was obtained from experimental data. Fig. 2 shows typical curves of the relative laser spot position over time for two cantilevers that were covered with different amounts of cells. It was calculated from the sum and difference signal of the PSD considering the linearity calibration for the respective sample. The noise in the signal at the 100 s mark results from adding trypsin to the medium. The moving fluid made the laser spot reflection diffuse until the system equilibrated again. In the end, simulated and measured values were compared and simulations were iteratively repeated with different stress values until both values for Δl were identical.

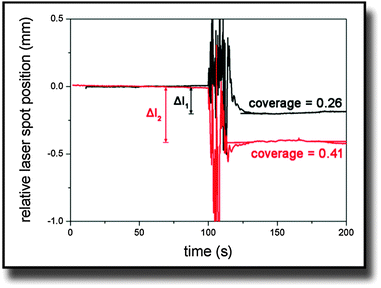Fig. 2 Typical curves of the laser spot position on the PSD after being deflected at the bending cantilever. Trypsin was added at the 100 s mark and causes the noisy behavior.

3 Results

3.1 Finite element simulations of cantilever bending

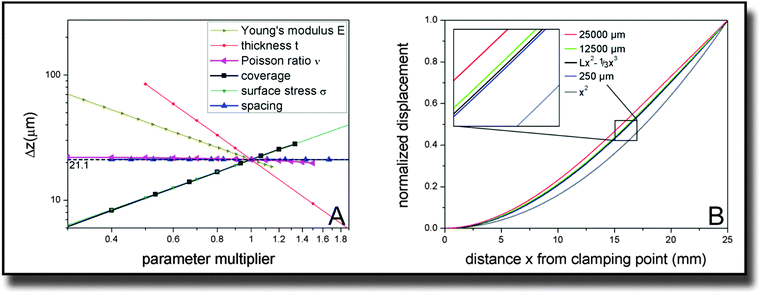
In our study, fibroblast cell monolayers were seeded onto a macroscopic metallic cantilever. Due to interaction of the cells with the cantilever and contractile forces of the cells parallel to the surface, a bending of the cantilever was detected. The simulation parameters for calculating contractile forces from measured deflection were established by performing several convergence tests and parametric studies of which we want to summarize the results in the following.

For later comparison with cantilever bending theories, the key quantity for measuring the influence of different parameter sets is the displacement at the far end of the cantilever, 25 mm away from the clamping. The reference parameter set is described by the dimensions of the cantilever (width × length × thickness with W = 10 mm, L = 25 mm, t = 0.1 mm), its Young's modulus E = 105 GPa, its Poisson ratio ν = 0.33, and the external parameters defined by the adherent cells, which are coverage = 0.75, spacing = 250 μm and tensile stress on covered areas σ = 1000 pN μm⁻². With these parameters, the tip deflection is Δz = 21.1 μm. The z-direction denotes the direction of the cantilever thickness.

In order to verify that the established ∼E⁻¹ and ∼t⁻² behavior is unchanged by the presence of cells, we varied these internal parameters along with the Poisson ratio ν. Fig. 3(A) confirms the expectations. The dependence with respect to the Poisson ratio is much smaller than for the other parameters and also does not follow such a simple power law. Fitting a parabola function results in the equation Δz(ν) ∼ (1 + 0.0115ν − 0.427ν²) with an accuracy of R² > 0.999.

Fig. 3 (A) Parametric studies from finite element simulations of the cantilever bending in dependence of mechanical properties of the material and cell properties, plotted in a double logarithmic scale to directly derive power law behavior and (B) simulated shape of the cantilever for different spacing between the cells.

More interestingly, we also varied the distribution and size of the cells on top of the cantilever. The coverage has a directly proportional effect on the cantilever displacement. The same is true for the tensile stress the cells exert on the surface. The spacing parameter is varied up to hypothetical values that are unrealistic in the context of cells but still give valid information on the system. While the cantilever tip deflection drops slightly for very high values of the space per cell, it approaches a constant value for the displayed, more realistic dimensions of up to 500 μm.

Of course not only the maximum deflection at the end of the cantilever gives information about the elastic behavior. Therefore also the curve shape of the displacement over the whole length of the cantilever was investigated and is displayed in Fig. 3(B). Differences in the behavior are only visible for very high values of the spacing parameter. For a spacing parameter of 25 000 μm representing a hypothetical single huge cell stretched over the whole cantilever, the simulated bending was smallest. However, already for 12 500 μm spacing representing two cells, the shape of the curve converges towards the behavior, that is consistently exhibited for smaller spacing values, particularly below 250 μm. The calculation of two giant cells is of course a mere theoretical dalliance that does not imply that we are able to detect 2 single cells. However it shows that cell size effects are negligible in realistic orders of magnitude. In addition to the normalized curves for these three characteristic values, two ideal curves of the shape z(x) = Lx² − 1/3x³ and x² are plotted in Fig. 3(B) with z being the direction along the cantilever thickness and x along its length. The cubic behavior fits the small spacing data very precisely (R² > 0.9999).

3.2 Cell-induced surface stresses

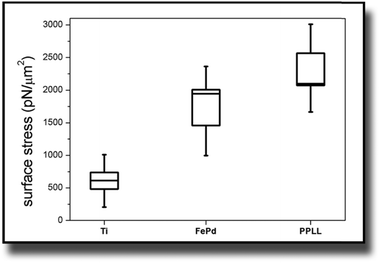
The considerations of Section 3.1 are prerequisites for calculating actual stress values from the measured deflection. This section shows the results for this cell induced tensile surface stress on pure titanium. Additionally the results were compared to measurements on Fe–Pd sputtered titanium and on L-lysine plasma functionalized titanium.

The boxplots in Fig. 4 show the mean of the measured values ± standard errors. The whiskers indicate minimum and maximum of the data set. For titanium, an average surface stress of σ = (610 ± 130) pN μm⁻² was measured. The stress is increased on titanium substrates with Fe–Pd coating, where the mean value is σ = (1733 ± 273) pN μm⁻² and highest on titanium with a continuous L-lysine polymer film reaching σ = (2321 ± 247) pN μm⁻².

Fig. 4 Boxplot of the surface stress values of NIH/3T3 cells on different surfaces calculated from the measured cantilever deflection. Whiskers range between minimum and maximum. Boxes indicate standard error.

4 Discussion

Most approaches to correlate cantilever bending with surface stress originate from Stoney's formula in 1909
with surface stress σt_f, Young's modulus E, substrate thickness t, cantilever length L and tip deflection Δz.³² Although this relation gives values that overestimate the value obtained from finite element simulations by around 60%, the proportionality 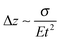is confirmed by our parametric studies. Reasons for the derivation are the non-uniform stress distribution and that Stoney did not consider effects of the bending in the in-plane direction perpendicular to the tensile stress due to a non-zero Poisson ratio. To remedy the latter factor, we included the dimensionality parameter D in our calculations, which was defined in the work of Dahmen et al.³⁵ It depends on the aspect ratio of the cantilever. In case of a perfect two-dimensional (D = 2) behavior for very long cantilevers, a factor (1 − ν) must be considered. The shorter the cantilever with respect to its width, the more one-dimensional (D = 1) is the behavior, leading to a correction factor (1 − ν) × (1 + ν). In the transition between these regimes, Stoney's formula transforms to

With an approximate dimensionality of D = 1.8 in our case, the derivation from the simulated results remains only 15%. However, our simulations did not confirm the dependency of the deflection on the Poisson ratio. In case of the best fitting dimensionality D = 1.57, the correction factor found in our simulations still deviates by 0.58ν. This additional linear term results from the areas unstrained within the cantilever through which the conversion to transverse strain is corroborated.

Besides the material properties of the cantilever, also the coverage of the cantilever with cells and the spacing between those have an influence on the bending. However, the spacing only changes the total cantilever displacement in case of very large stress inducing elements (we do not want to call them cells here since these spacing values are far from realistic cell sizes). As soon as the spacing is small compared to the cantilever dimensions, its influence vanishes and one can assume a mean stress field acting with a constant value on the whole length of the cantilever. Parametric studies proved that the magnitude of this mean field is influenced by the coverage in a simple linear manner:

We thus find that the introduction of coverage is required, while the spacing parameter does not influence the mean field. This independence of particular cell spacing coincides with the findings of Schwarz et al.,¹⁶ who showed that the force distribution of a cellular focal contact can be described by a multipole expansion, and can be considered as point-like force at high distances.

Stoney's formula furthermore assumes a constant radius of curvature over the whole cantilever due to a constant stress induced moment acting on the surface. In the approximation of small curvatures, this would imply

and thus a parabola shaped cantilever surface. This is not the case as we observe a cubic progression of the shape z(x) ∼ Lx² − 1/3x³ as displayed in Fig. 3(B), hinting towards a momentum that increases linearly towards the clamping of the cantilever. This can also be explained with the influence of the Poisson ratio in combination with the cell-free surfaces, since the cantilever behavior gets more and more one-dimensional towards the clamping.

With this, the conversion from stresses to cantilever deflections is set, but another very important question to discuss is, whether obtained stress really results from the cells. This is confirmed by control measurements with cells seeded on the bottom side of the cantilever that are added to the ESI.† Another indicator for really measuring an effect from the cells is the agreement of the results with values reported in literature. Dembo and Wang³⁶ reported stresses of 2000 pN μm⁻² for NIH/3T3 fibroblasts on soft polyacrylamide substrates. Assuming that this stress results from the strength of integrin–fibrinogen bonds, one can predict the number of such bonds within a cell. Using 150 pN as force of one such bond³⁷ and a density of 300 integrin bonds per μm² within a focal contact,³⁸ we can calculate an expected density of focal contacts within a single cell from the measured mean surface stress and get (3.8 ± 0.6)% for Fe–Pd and (5.2 ± 0.6)% for PPLL coated samples. Considering the up to now poorly characterized strength of single integrin bonds, these values are in good agreement with earlier reported results for adherent NIH/3T3 fibroblasts after 1 day incubation of 2.9%²⁵ and 4.6%³¹ on Fe–Pd and PPLL, respectively. Despite the differences resulting from comparing various measurement methods, we were able to calculate reliable surface stress values. Therefore both Fe–Pd and PPLL show an enhancing effect on the formation and growth of focal contacts in comparison to a titanium substrate. Moreover, our findings give a quantitative measure for improved bioactivity of PPLL coated films compared to uncoated metals.

5 Conclusions

Traction forces exerted by cells on substrates are a highly relevant quantity to systematically address interaction of cells with substrate surfaces. While it of course does not replace established biocompatibility assays investigating cellular morphology and focal contact expression, it adds a new complementing view point that has high relevance in biomaterial performance. To achieve this, an intuitive versatile apparatus was used for measuring macroscopic influences of adherent cells on the bending of their support material, which can be functionalized with thin films of biomaterials. These thin films do no influence the bending properties of the cantilever and thus allow comparison of a broad spectrum of surfaces. Particularly due to this simplicity and clearness in design, it was a key objective of this work to confirm the results by comparing them to existing bending beam and cell adhesion theories. The results showed that the measured effect can be mainly attributed to the cells while other surface stress phenomena only contribute to a negligible amount. In combination with finite element simulations, we were able to develop a theory how cells bend an underlying support material. As proof of principle, we measured the forces exerted on titanium as reference material and on the same titanium cantilevers coated with two very diverse materials of biomedical interest, namely a ferromagnetic shape memory alloy iron–palladium and an adhesion promoting L-lysine based coating, polymerized by plasma functionalization. The stresses from cells on Fe–Pd exceed those on titanium by a factor of three, while the PPLL coating allows the cells to interact four times as strong as on titanium.

Both these results encourage the usage of the cantilever bending method for an easy-to-employ assessment of contractile forces on surfaces as different as solid metals and soft polymers in a physiological environment.

6 Experimental

6.1 Cantilever preparation

The cantilever was cut from a titanium foil (Advent Research Materials, Catalogue No. TI228724) with a thickness of 100 μm. The precise dimensions of 10 mm × 37 mm were achieved by laser cutting, such that the free bending length of the cantilever after clamping would be 25 mm. To ensure a consistency in bending behavior, roughness, and elastic properties, the same bulk cantilever material from the same titanium foil was also used as support for the testing of other materials and only the surface was modified, by applying closed thin films of the respective material. Fe–Pd films were sputtered onto Ti foils described above from an Fe₇Pd₃ alloy target (ACI Alloys). Prior to sputtering, the chamber was evacuated and flooded with an argon flow of 3.5 sccm to achieve a sputtering pressure of 5 × 10⁻³ mbar. The argon plasma was excited by an RF input power of 45 W. The resulting films have a thickness of 50 nm.

The special plasma treated lysine-based polymer coating was applied within a continuous-flow pulsed plasma reactor which was previously described in greater detail.³¹ The precursor L-lysine solution, consisting of monomer powder (CAS 56-87-1, Sigma-Aldrich Chemie GmbH) and pure ethanol (CAS 64-17-5, Merck KGaA) with a concentration of 0.009 mol l⁻¹, was injected at a flow rate of 0.24 ml min⁻¹ into a pulsed argon plasma with 10 W input power and duty cycle of 2%. Under the influence of the plasma, lysine monomers were cleaved into radicals and deposited on the titanium foil, where they recombined to a highly cross-linked, closed polymeric network. The film thickness after one hour of deposition was 50 nm.

6.2 Cell culture

The embryonic murine fibroblast cell line NIH/3T3 (ATCC, Manassas, VA) was used due to their strongly adhesive nature and their high contractility compared to many other cell types. Cells were cultured in Dulbecco's Modified Eagles Medium (Biochrom, F0435), supplemented with 10% calf serum and 1% penicillin–streptomycin antibiotic solution (PS). Cells were incubated at 37 °C in 5% CO₂ humidified atmosphere. Medium was changed every two to three days.

One day before the respective measurement, cells were seeded onto the according cantilever in full culture medium in high enough densities to ensure a measurable contractile effect but also low enough to ensure growth in monolayers (∼10 000 cells per cm²). Measurements were carried out in supplement-free DMEM so that the detaching effect of trypsin is not inhibited.

6.3 Cell imaging and counting

For an accurate estimation of contractile cell forces, the number of cells on the measured beam must be known not only after seeding but directly before measuring. To count the cells on the intransparent materials, a vital fluorescent staining was required. Therefore CellTracker Red (Invitrogen C34552) was first diluted in serum-free medium to a final working concentration of 2 μM and incubated with the cells for 45 minutes. Subsequently, cells were gently washed with phosphate buffered saline (PBS) and then stored in serum-free culture medium for less than 2 hours before the measurement. Images were taken with a Zeiss Axio Scope A1 fluorescence microscope with 5× objective magnification both before the measurement and directly afterwards to count the cells and confirm that they were all released from the cantilever. The micrographs were processed using ImageJ³⁹ for contrast enhancement and noise reduction. Afterwards, cells were counted manually to calculate the spacing parameter and the percentage of the area covered by cells was determined by a self-written edge detection routine, which distinguishes background from foreground through a manually adjusted brightness threshold value. For each of the measured surfaces, the final values are averaged over measurements from at least six samples, each containing more than 100 000 cells per cm². Results are given as mean value ± standard error of these six measurements.

Acknowledgements

We thank BSc N. John and Dr M. Ehrhard for help with cantilever preparation and laser cutting, respectively, Mr S. Daum at the workshop of the Leibniz Institute of Surface Modification for manufacturing the setups framework, as well as Prof. Dr J. Käs for general support. This work is funded in parts by the European Social Fund (ESF), the German Science Foundation (DFG), Project “BIOSTRAIN” and Federal Ministry of Education and Research (BMBF 1315883) and was performed within the Leipzig Graduate School of Natural Sciences BuildMoNa, established within the German Excellence Initiative by the DFG.

References

1. M. M. Stevens and J. H. George, Science, 2005, 310, 1135–1138.
2. D. Ingber, Curr. Opin. Cell Biol., 1991, 3, 841–848.
3. N. Q. Balaban, U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi and B. Geiger, Nat. Cell Biol., 2001, 3, 466–472.
4. M. Humphries, Mol. Biotechnol., 2001, 18, 57–61.
5. C. Dong and X. X. Lei, J. Biomech., 2000, 33, 35–43.
6. I. I. Singer, J. Cell Biol., 1982, 92, 398–408.
7. C. T. Mierke, P. Kollmannsberger, D. P. Zitterbart, J. Smith, B. Fabry and W. H. Goldmann, Biophys. J., 2008, 94, 661–670.
8. N. Turner, M. Armitage, R. Butler and G. Ireland, Cell Biol. Int., 2004, 28, 541–547.
9. C. Selhuber-Unkel, T. Erdmann, M. López-García, H. Kessler, U. Schwarz and J. Spatz, Biophys. J., 2010, 98, 543–551.
10. P. Bertoncini, S. Le Chevalier, S. Lavenus, P. Layrolle and G. Louarn, J. Mol. Recognit., 2012, 25, 262–269.
11. D. J. Müller, J. Helenius, D. Alsteens and Y. F. Dufrêne, Nat. Chem. Biol., 2009, 5, 383–390.
12. P.-H. Puech, A. Taubenberger, F. Ulrich, M. Krieg, D. J. Muller and C.-P. Heisenberg, J. Cell Sci., 2005, 118, 4199–4206.
13. J. Helenius, C.-P. Heisenberg, H. E. Gaub and D. J. Müller, J. Cell Sci., 2008, 121, 1785–1791.
14. A. K. Harris, P. Wild and D. Stopak, Science, 1980, 208, 177–179.
15. J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1484–1489.
16. U. Schwarz, N. Balaban, D. Riveline, A. Bershadsky, B. Geiger and S. Safran, Biophys. J., 2002, 83, 1380–1394.
17. M. Murakami, J. Angelillo, H.-C. Huang, A. Segmuller and C. Kircher, Thin Solid Films, 1979, 60, 1–9.
18. D. Sander, Curr. Opin. Solid State Mater. Sci., 2003, 7, 51–57.
19. R. Koch, J. Phys.: Condens. Matter, 1994, 6, 9519.
20. D. Sander, Z. Tian and J. Kirschner, Sensors, 2008, 8, 4466–4486.
21. J. Köser, S. Gaiser and B. Müller, Eur. Cells Mater., 2011, 21, 479–486 ; discussion 486–487.
22. R. Raiteri, M. Grattarola, H.-J. Butt and P. Skládal, Sens. Actuators, B, 2001, 79, 115–126.
23. R. D. James and M. Wuttig, Philos. Mag. A, 1998, 77, 1273–1299.
24. T. Kakeshita and T. Fukuda, Mater. Sci. Forum, 2002, 531–536.
25. U. Allenstein, Y. Ma, A. Arabi-Hashemi, M. Zink and S. Mayr, Acta Biomater., 2013, 9, 5845–5853.
26. M. Zink and S. Mayr, Mater. Sci. Technol., 2014, 30, 1579–1589.
27. M. Zink, F. Szillat, U. Allenstein and S. G. Mayr, Adv. Funct. Mater., 2013, 23, 1383–1391.
28. C. Shan, H. Yang, D. Han, Q. Zhang, A. Ivaska and L. Niu, Langmuir, 2009, 25, 12030–12033.
29. M. Hu, E. E. Sabelman, S. Lai, E. K. Timek, F. Zhang, V. R. Hentz and W. C. Lineaweaver, J. Biomed. Mater. Res., 1999, 47, 79–84.
30. Y. Zhang, J. Li, Y. Shen, M. Wang and J. Li, J. Phys. Chem. B, 2004, 108, 15343–15346.
31. U. Allenstein, F. Szillat, A. Weidt, M. Zink and S. G. Mayr, J. Mater. Chem. B, 2014, 2, 7739–7746.
32. S. G. Mayr and K. Samwer, Phys. Rev. Lett., 2001, 87, 036105.
33. G. G. Stoney, Proc. R. Soc. London, Ser. A, 1909, 82, 172–175.
34. Y. Wyser, C. Pelletier and J. Lange, Packag. Technol. Sci., 2001, 14, 97–108.
35. K. Dahmen, S. Lehwald and H. Ibach, Surf. Sci., 2000, 446, 161–173.
36. M. Dembo and Y.-L. Wang, Biophys. J., 1999, 76, 2307–2316.
37. R. I. Litvinov, H. Shuman, J. S. Bennett and J. W. Weisel, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7426–7431.
38. S. W. Moore, P. Roca-Cusachs and M. P. Sheetz, Dev. Cell, 2010, 19, 194–206.
39. W. Rasband, ImageJ, version 1.49, U. S. National Institutes of Health, Bethesda, Maryland, USA, 1997–2011.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01212k

---