 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Celebrating Soft Matter's 10th Anniversary: Influencing the charge of poly(methyl methacrylate) latexes in nonpolar solvents
Gregory N.
Smith†
 a,
James E.
Hallett
b and
Julian
Eastoe
*a
a,
James E.
Hallett
b and
Julian
Eastoe
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: Julian.Eastoe@bristol.ac.uk
bH. H. Wills Physics Laboratory, University of Bristol, BS8 1TL, UK
First published on 7th September 2015
Abstract
Sterically-stabilized poly(methyl methacrylate) (PMMA) latexes dispersed in nonpolar solvents are a classic, well-studied system in colloid science. This is because they can easily be synthesized with a narrow size distribution and because they interact essentially as hard spheres. These PMMA latexes can be charged using several methods (by adding surfactants, incorporating ionizable groups, or dispersing in autoionizable solvents), and due to the low relative permittivity of the solvents (εr ≈ 2 for alkanes to εr ≈ 8 for halogenated solvents), the charges have long-range interactions. The number of studies of these PMMA particles as charged species has increased over the past ten years, after few studies immediately following their discovery. A large number of variations in both the physical and chemical properties of the system (size, concentration, surfactant type, or solvent, as a few examples) have been studied by many groups. By considering the literature on these particles as a whole, it is possible to determine the variables that have an effect on the charge of particles. An understanding of the process of charge formation will add to understanding how to control charge in nonaqueous solvents as well as make it possible to develop improved technologically relevant applications for charged polymer nanoparticles.
1 Introduction
Ten years have passed since Hsu, Dufresne, and Weitz published the paper “Charge Stabilization in Nonpolar Solvents”, and this article helped revive interest in surfactant-induced charging of colloids in nonpolar solvents.1 The results showed the importance and tunability of charge on dispersions of model colloids and suggested that this phenomenon would be useful in industrial colloid science. The formation and application of charges in nonpolar solvents generally have been discussed in several interesting reviews: by Novotny in 1987,2 by Morrison in 1993,3 and by Smith and Eastoe in 2013.4The charge of many types of colloids in low dielectric media has been reported. In addition to polymer nanoparticles, carbon black,5,6 mineral oxides,7,8 pigments,9–11 and aerosols12 have all been studied. In this article, the focus is a specific system of charged colloids: polymer brush stabilized poly(methyl methacrylate) (PMMA) latexes, where typically poly(12-hydroxystearic acid) (PHSA) is used as the steric stabilizer. By studying a specific system of colloids in detail, a better understanding of charged colloids in nonpolar solvents generally can be obtained. These latexes represent an excellent model system because their synthesis results in colloids with a very low size distribution that act essentially as hard spheres.13,14 The particles are commonly dispersed in nonpolar solvents with low relative permittivities (εr ≈ 2), such as dodecane or hexadecane. This reduces the dispersion attraction between colloids but can enhance the effect of charge. Charges are difficult to stabilize in nonpolar solvents; for example, AOT has a dissociation constant in alkanes of 10−5.1,15 Also, interactions are long-range; this can be encapsulated by considering the Bjerrum length (λB = e2/4πε0εrkBT; ε0 is the vacuum permittivity and kBT is the thermal energy),16 which is the separation between two point charges where the electrostatic interaction is equal to the thermal energy. For nonpolar solvents, λB = 28 nm, and for water, λB < 1 nm. When species are charged, the interaction potentials can be as great as in water for charge numbers that are orders of magnitude lower.1Fig. 1 shows an example of the dramatic effect of charge formation in nonpolar solvents from Hsu, Dufresne, and Weitz's 2005 paper. The addition of the anionic, double-tailed surfactant Aerosol OT (AOT) to a dispersion of PMMA latexes results in particles that are further separated and more ordered.1
 | ||
| Fig. 1 Charge stabilization of a nonpolar suspension of PMMA latexes in dodecane. The images are optical micrographs of PMMA latexes in pure dodecane (a) and a 12 mM solution of AOT in dodecane (b). The field of view is 135 × 108 μm2. Reprinted with permission from Hsu et al.1 Copyright 2005 American Chemical Society. | ||
Although PMMA latexes are primarily sterically stabilized, they may also possess a surface charge, as observed by several groups.17–20 The number of charges on PMMA particles in alkane solvents is typically very low (Z ≲ 20e). While seemingly a small number of charges, due to the low relative permittivity of the solvent and weak screening, the residual charge can influence the interparticle interactions; for example, crystallization phase behavior is shifted by even one electron per sphere.17 Avoiding the presence of water, known to influence the charge of inorganic colloids in nonpolar solvents,21,22 is crucial to understanding how to control the charge of PMMA latexes. Greater charges can be introduced using several methods. Kitahara et al. produced the first academic report of surfactant-charged polymer latexes in 1981, using salts of alkylammonium and dioctylsulfosuccinate surfactants to charge lauryl methacrylate-stabilized PMMA dispersions.23 Despite the development of PHSA-stabilized PMMA particles in collaboration with ICI and the University of Bristol in the 1970s and 1980s,24,25 there were no reports of surfactant-charged PHSA-stabilized PMMA latexes until decades later.26–28 In addition to using surfactants, there are other methods of producing charged polymer colloids in nonpolar solvents. Polymerizable ionic monomers or salts can be added during the particle synthesis, introducing a dissociable group into the colloids.29,30 Latexes in density-matched solvent mixtures including brominated solvents can also charged by solvent decomposition.31–34
The nature of the formation of charges is different for these three methods. The reduced mobilities (μ* = μ/μ0 where μ0 = e/6πηλB; η is the viscosity of the fluid) for three systems of charged PMMA latexes as a function of volume fraction (ϕ) are shown in Fig. 2. There are two systems containing background electrolyte. The results from these are similar; the mobility tends to a plateau at low ϕ. Vissers et al. studied dyed latexes in a mixed solvent of cis-decalin and cyclohexyl bromide (CHB);35 Smith et al. studied AOT charged latexes in dodecane.36 On the other hand, the results from particles with no background electrolyte are very different. Gillespie et al. studied ionic monomer charged latexes in dodecane, and μ* continues to increase as ϕ is decreased.37 As can be clearly seen, the three charging methods are not equivalent.
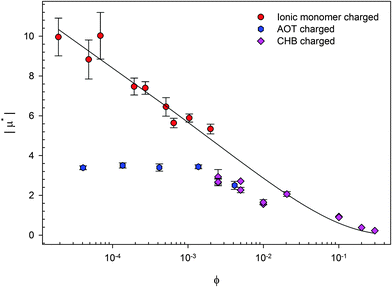 | ||
| Fig. 2 Reduced mobility (μ* = μ/μ0) for three systems of charged PMMA latexes as a function of volume fraction (ϕ). Gillespie et al. studied ionic monomer charged latexes,37 Smith et al. studied surfactant (AOT) charged latexes,36 and Vissers et al. studied solvent (cyclohexyl bromide, CHB) charged latexes.35 The line is Ohshima's prediction of the electrophoretic mobility in a salt-free medium.38 The results show that the mobility of latexes depends on the method used to charge the particles. | ||
In this review, the effects of varying either physical or chemical properties on the electrophoretic mobility and surface potential of charged, sterically-stabilized PMMA latexes are considered. Physical variations include volume fraction, size, and ion screening; chemical variations include solvent, surfactant type, and fluorescent dye, as a few examples. The effect of varying parameters (such as adding surfactant and changing the charging method) can clearly be seen in Fig. 1 and 2. Many groups have studied these particles using different methods and charging agents, and therefore, it is only possible to determine the correlations between variables and particle charge by considering the literature as a whole. By analyzing all the variations studied so far in the literature, those that do or do not have an influence on the charge of particles can be identified.
2 Physical variations
Physical variations involve changes that control the interactions between particles. These include the concentration of particles, their size, and the amount of ion screening (controlled by the concentration of surfactants or other salts). The effects of varying these will be discussed in relation to charged colloids in water, to show the differences between these extreme solvents. Due to the much lower relative permittivity of nonpolar solvents compared to water, the double layers will be thicker and charge interactions will be more long ranged.2.1 Particle volume fraction
In most dilute suspensions of colloids in water, the electrophoretic mobility and ζ potential are usually independent of particle concentration, although unusual volume fraction-dependent electrophoretic mobilities of sulfate-terminated polystyrene particles have been observed in highly deionized aqueous suspensions.39–42 The large relative permittivity of water (εr = 80.1 at 293 K)43 and high solubility of many electrolytes results in a very short screening length,44 typically a few nanometers. For micrometer-sized particles, this typically results in a κa ≫ 1; the same particles in nonpolar solvents usually have a κa ≤ 1. For large κa, all particles and their associated double layers essentially do not interact with each other except at very high volume fractions, so the charge contributions are essentially the same at all volume fractions. Ohshima determined a general expression for how the electrophoretic mobility varies as a function of both κa and ϕ.45 For lower values of κa, the mobility deviates from infinite dilution at much lower volume fractions than for higher values. The reduced mobilities for three systems of charged colloids in nonpolar solvents are shown in Fig. 2. At low volume fractions, the two systems containing electrolyte (AOT and CHB charged latexes) approach a ϕ-independent mobility.There are several mechanisms that can result in a decrease in electrophoretic mobility at high volume fraction. These can be divided into entropic, hydrodynamic, and electrostatic. The entropic argument can simply be reduced to, as the volume fraction increases, the charging equilibrium is different. For example, the adsorption of the charging agent, such as AOT, per particle reaches a plateau value at large charging agent concentrations.46 At high volume fractions there are fewer charge additives per particle and eventually each particle is no longer saturated with charge additive.15,47 Another entropic charging argument is that, if the dissociation of surface groups is at equilibrium with the solvent ion content, then an increase in volume fraction will favor association of some of these surface groups to maintain the counterion concentration.48
Different theoretical descriptions have been put forward to consider these surface charge equilibria and how they relate to the surface potential and particle charge. For example, it is often assumed that particle surface charge density is constant, which would yield a particle charge that increases with the square of the particle radius. However, instead a linear relationship is often observed. Strubbe et al. studied the charging mechanism in a system with an excess of chargeable sites, a charge neutral particle placed in a solvent where an electrolyte ion has a greater affinity for the particle surface or where a charged surface group has a higher solubility in the solvent. By considering the preferential dissociation or adsorption of electrolyte or surface ions, a linear relationship between particle size and particle charge could be obtained.49 The surface potential was found to increase with the number of surface charging sites and ion concentration up to a saturation point. Furthermore, this model resulted in a surface potential independent of particle size, provided the particle had a sufficiently large number of chargeable sites. Roberts et al. found a form of this model to be a good description for the electrophoretic charge (measured through ζ potential and conductivity measurements) of PMMA charged with different surfactants as a function of surfactant concentration.15
Hydrodynamic arguments are related to the physical interactions between particles and the resulting flow as they become more crowded,50 or through Poiseuille flow, where flow of the solvent alters the particle mobility across a cell.35 However, provided these hydrodynamic contributions are accounted for by considering relative velocity or a change in viscosity, the reduced electrophoretic mobility should be unchanged from the static case. Finally, the electrostatic mechanism for electrophoretic mobility reduction is related to the interactions between particle double layers and the changing electrolyte content. The Holm group showed through both experiments and simulations that increasing the volume fraction is analogous to increasing the salt concentration (alternatively, increasing κeffa of the system), as a constant number of dissociated surface counterions must occupy a smaller volume available for each particle.42,51 Increasing κeffa (for κa < 3, typical for nonpolar solvents) at a fixed surface potential results in a decrease in electrophoretic mobility in the O'Brien and White description (who derived full numerical solutions to the linearized Poisson–Boltzmann and Navier–Stokes equations to produce accurate dilute ζ potential values up to 250 mV as a function of κa);52 the effect may be less pronounced if the number of charges on the particle also decreases with increased volume fraction. In an infinitely dilute system, the counterion charge density (and so, the electrical potential) tends toward zero at long distances. In a dilute system, this is essentially the case for all particles. However, as the particle volume fraction increases beyond a critical value, neighboring potential tails begin to overlap, increasing the mid-plane potential. There are various potential arguments used in the literature (encapsulated by the boundary conditions at the particle surface and at long distances53), but in essence, the effective potential distribution around the particle is modified by the overlapping potential from neighboring particles, which manifests in a change in electrophoretic mobility.41,54,55 There is a considerable body of work devoted to consolidating the effective interactions or mobilities measured in non-dilute systems with quite diverse theoretical descriptions.56–61 As previously mentioned, Roberts et al. used a variation of the model proposed by Strubbe et al. and applied it specifically to the problem of AOT particle charge.15,49 Cao et al. used a modified form of the model proposed by Roberts et al. (intended to describe the charge of the AOT–PMMA system in dodecane), specifically including the contribution of volume fraction and radius, to describe the influence of AOT on the charge of colloidal titania and polystyrene in dodecane with a more comprehensive sweep of parameters.47 Their data broadly reproduced trends predicted by the model (although not for a PMMA system): that surface potential would increase with the number of micelles per particle until a saturation point, at which point it would gradually decay (for a fixed volume fraction) and that surface potential would display a constant value below a critical volume fraction and radius, that increased with a higher number of micelles per particle, above which it would decrease. Kanai et al. studied the structure of the AOT-charged PMMA particles at high volume fractions in a density and refractive-index matched mixture of cis-decalin and tetrachloroethylene.48 At low concentrations (1 mM), confocal microscopy measurements of the radial distribution function were consistent with a charge-stabilized fluid. At higher AOT concentrations, they observed the formation of charge-stabilized Wigner crystals, with the formation of a body-centered cubic (BCC) phase. At even higher AOT concentrations a face-centered cubic (FCC) structure was present. At the highest AOT concentrations (200 mM), they observed reentrant melting to a fluid phase as the screening length was significantly reduced, and the radial distribution function was essentially the same as at 1 mM AOT. The positions of the phase boundaries showed some dependence on PMMA particle size. To explain this unusual behavior, they constructed a Poisson–Boltzmann (PB) cell model where they defined the surface charge as a function of the ratio of chargeable surface sites and surface and bulk micellar equilibrium constants. By solving the PB equation in a spherical Wigner-cell,57 they obtained values for the surface charge and potential, Donnan potential, and far-field background charge density. They used this information to map the colloidal dispersion onto a one-component plasma (OCP) of n point particles of charge ZOCP, maintaining electroneutrality with the background charge density. The OCP crystallizes for Coulombic coupling parameter Γ > 106; therefore, the phase boundary for crystallization and reentrant melting was determined to be at this point. By solving the PB equation for the different volume fractions and AOT concentrations used experimentally, the OCP Γ could be determined for each state point. Remarkably, the phase boundaries measured experimentally for both crystallization and reentrant melting were in close agreement with the model description, despite its simplicity (although the BCC–FCC transition was not predicted). In aqueous systems, Makino and Ohshima62 analyzed data by Agnihotri et al.63 of the ζ potential of gold nanoparticles of different sizes. Based on the observation that ζ potential changes with electrolyte concentration, so is an ill-defined parameter to describe a colloidal system, they developed an analytical method to relate electrophoretic mobility to particle surface charge density. They found that although the ζ potential of the different gold systems changed with electrolyte concentration, the surface charge density was reasonably constant and variations were attributed to electrolyte ion adsorption.
For ionic monomer charged particles, which do not contain any electrolyte, the mobility continues to increase as the volume fraction is decreased (μ* ∝ ln(1/ϕ)).38,64 Gillespie et al. attributed this volume fraction dependence to counterion condensation at higher volume fractions, due to the balance of configurational entropy of the counterions and the electrostatic interactions.37 At even lower volume fractions, a limit should be reached where the potential and mobility depend solely on the bare surface charge rather than the effective surface charge (reduced due to counterion condensation).38,64,65 In these ionic monomer charged latexes in nonpolar solvents, the bare charged limit has yet to be reached.
2.2 Particle size
In water (particularly aqueous electrolyte solutions), changing the size of colloids will not influence the magnitude of the ζ potential, as long as the particles have homogenous charge densities. For extreme κa, there are approximations to determine the ζ potential from measurements of the electrophoretic mobility. For κa ≫ 1 (thin double layers), the Helmholtz–Smoluchowski equation is applicable, and this is generally the case in aqueous electrolyte solutions. For κa < 1 (thick double layers), the Hückel–Onsager equation is applicable.66 In either of these extremes, the ζ potential should be independent of size. However, for PMMA latexes charged by AOT, for example, κa ≈ 1,1,19,46,67 and neither of these approximations is appropriate. Therefore, the size of the particles needs to be considered.It is not immediately obvious why changing the size of PMMA particles charged by AOT should result in different surface potentials. For particle diameters in excess of 300 nm, the surface potential is apparently the same regardless of particle size, shown in Fig. 3. There is some variation in the magnitude of the surface potential as a function of size, ranging from ζ* ≈ −1 to −6, but this is not systematic. (ζ* is the reduced ζ potential, eζ/kBT.) The average surface potential shown in Fig. 3 taken from the literature is ζ* = −2.6. Although there is no apparent correlation between particle size and potential, some recent measurements on small particles suggest that for particles smaller than 300 nm, the surface potential is lower (Fig. 3). Although the parameter κa is taken into account when calculating the particle charge from electrophoretic mobility or interaction measurements, differently sized PMMA are not strictly chemically identical. The main difference is that there are differences in composition between differently sized PMMA latexes; there is more stabilizer in smaller particles. Approximately 25% of total reaction weight for particles of diameter smaller than 100 nm is stabilizer, compared to 5% for larger particles, due to the larger total surface area of the synthesized particles. Whether AOT has an affinity for particular groups within the PMMA core or on the particle surface is an open question. Recent work indicates that AOT percolates homogeneously through the whole of the latex.68 It may be that AOT preferentially adsorbs or dissociates in regions of “pure” PMMA, rather than close to the surface, either in the stabilizer layer or where the stabilizer backbone is bonded to the PMMA matrix. This contribution would be negligible for large particles but would become increasingly significant for small particle sizes as, for example, either a higher ratio of the methacrylic acid monomer would be chemically locked to the stabilizer backbone25 or a higher percentage of the particle volume would consist of stabilizer.
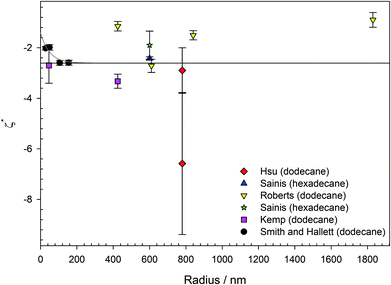 | ||
| Fig. 3 Reduced surface potential (ζ* = eζ/kBT) for AOT charged PMMA latexes in either dodecane or hexadecane. Lines are guides to the eye. Data were obtained using either electrophoresis (phase-analysis light scattering and optical tweezer microelectrophoresis) or interaction measurements (microscopy and blinking optical tweezers). The largest surfactant concentration for a given particle size from each study is taken (3.5 < [AOT] < 200 mM), all above the inverse micelle CMC.69,70 There is scatter but no systematic variation in the surface potential for particles larger than 300 nm (average ζ* = −2.6), shown by the solid black line. For smaller particles, the surface potential appears to decrease in magnitude, shown by the solid grey line. Data were taken from the literature: red diamonds (electrophoresis and interaction), Hsu et al.;1 blue upward triangle (interaction), Sainis et al.;67 yellow downward triangles (electrophoresis), Roberts et al.;15 green star (interaction), Sainis et al.;19 pink squares (electrophoresis), Kemp et al.;46 and black circles (electrophoresis), this study. | ||
For CHB charged latexes, the charge of particles does not seem to depend on the size of the particles. Both the surface potential (ζ* ≈ 5) and surface charge density (∼50e μm−2) are constant for latexes from 0.5 ≲ a ≲ 2 μm.71 Without investigating smaller latexes, however, it is not possible to know whether or not there would be a reduction in surface potential for smaller particles as is the case for AOT charged particles.
The situation is different for ionic monomer charged particles, as they are in a salt-free medium. Ramanathan showed that for highly charged particles there is a critical radius for counterion condensation to occur.72 Gillespie et al. experimentally demonstrated this by measuring the reduced mobility of ionic monomer particles of different sizes at fixed volume fractions (μ* ∝ ln(1/ϕ)), and their results are shown in Fig. 4. The mobility of small particles (a ≲ 300 nm) is much lower than the asymptote at large a. This demonstrates that the surface charge density is fixed and that counterion condensation is absent for small particles. The data shown in Fig. 4 is well reproduced by a two-state variational model. Manning showed that the fraction of condensed ions in a salt free system can be determined by considering the two different populations of ions present: condensed and free.73,74 The fraction of condensed ions can determined by minimizing the free energy of the system through reduction of the electrostatic energy and increase of the configurational entropy of the ions. Free energy minimization with respect to the condensed fraction α yields the following expression.
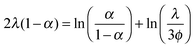 | (1) |
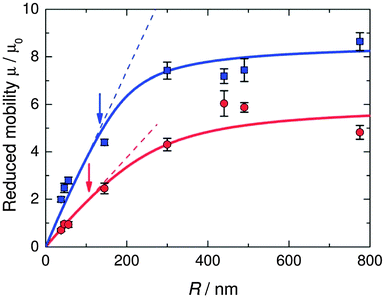 | ||
| Fig. 4 Reduced mobility (μ* = μ/μ0) of ionic monomer charged latexes at fixed volume fractions (blue squares, ϕ = 10−4; red circles, ϕ = 10−3). The solid curves represent fits to the data using the Poisson–Boltzmann equation and Ohshima's expressions for the electrophoretic mobility in salt-free dispersions.38,64 The dashed lines represent linear fits to the data at small radius. The arrows mark the critical radius for counterion condensation. Reproduced from Gillespie et al.37 with permission of The Royal Society of Chemistry. | ||
2.3 Ion screening
In water, the addition of ionic surfactants can lead to flocculation of charge stabilized colloids; this is due to two consequences of adding the surfactants. As salts, they screen the Coulombic repulsion between the colloids, resulting in a secondary attractive minimum in the interparticle interactions.75 Also, surfactants with the opposite charge to the surface adsorb onto the particles, neutralizing the charge.76 In nonpolar solvents, PMMA latexes are sterically-stabilized rather than charge stabilized, so adding surfactant increases the charge of the particles. Also, no secondary minimum is reached, because van der Waals attraction is weak and double layers are thicker. In water, surfactants form ions through salt dissociation; in nonpolar solvents, surfactants form ions through a disproportionation mechanism in the same way as water-in-oil microemulsions.77As the surfactant concentration is increased, two things vary. The amount of ion screening increases, due to a larger number of background ions; this has been observed as an increase in solution conductivity.1,19,46,78 Also, the amount of surfactant incorporated into the particles increases; this has been measured using small-angle neutron scattering.68
Neither of these variations has a significant effect on the surface potential of the PMMA latexes.1,19,46 Reduced ζ potentials (ζ* = eζ/kBT) are shown in Fig. 5. The two sets of data are measured using electrophoresis: single-particle optical microelectrophoresis or SPOM, which requires low volume fractions of ϕ ≈ 10−5, and phase-analysis light scattering or PALS, which requires higher volume fractions of ϕ ≈ 10−4. That the measurements are very similar at volume fractions that differ by 50 times shows that it is the concentration of surfactant that determines the particle charge. Only surfactant concentrations above 0.1 mM, the CMC for inverse micelle formation, are considered.69,70 Below this concentration, the potential decreases to 0.
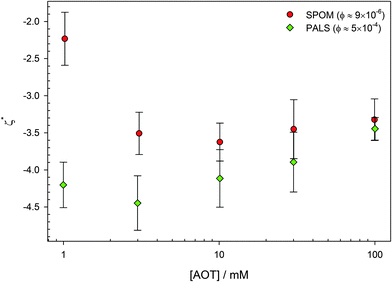 | ||
| Fig. 5 Reduced ζ potential (ζ* = eζ/kBT) as a function of AOT concentration for 425 nm radius PMMA latexes in dodecane. Two techniques are used, optical tweezer single-particle microelectrophoresis (SPOM) and phase-analysis light scattering (PALS). The two methods use very different particle concentrations (shown in the legend), and this shows that it is the surfactant concentration that determines ζ*. The magnitude of ζ* is also independent of concentration, as has been found by others.1,19,46 Data is reproduced from Kemp.79 | ||
The constant potential as a function of surfactant concentration suggests that the charging of particles by AOT surfactant is due to the preferential adsorption of charged species. More surfactant may be adsorbed at 100 mM than 1 mM,68 but the number of dissociated surfactant molecules is the same.
For other methods used to generate charged particles, the amount of ion screening is fixed, and the method used to charge the particles does not modify it. For ionic monomer charged particles, there is no background electrolyte, and the suspensions are salt-free.37 For CHB charged particles, there is a constant amount of screening, as the bromide ions arising from solvent decomposition determine the ionic background, and the surface potential of the particles is constant regardless of changes in particle concentration or size.35,71
3 Chemical variations
Chemical variations involve changes to the chemical composition for systems with the same charging method. These include properties of the charging agents (their ionicity, constituent ions, or hydrophobicity), the particles (their stabilizer or component chemicals), and of the entire system (the solvent or presence of water). As many of these are specific to charged species in nonpolar solvents, rather than comparing the variations to colloids dispersed in water, they will be compared to other systems of charged colloids in nonpolar solvents, where appropriate.3.1 Charging agent
As introduced in Section 1, there are three main ways of charging polymer particles in nonpolar solvents.PMMA latexes can be charged by the addition of surfactants, which form inverse micelles, to the solvent. In the Hsu, Dufresne, and Weitz paper of 2005, AOT was used,1 and this surfactant has frequently been used as a charge control additive. Polymerizable ionic monomers and other ionizable small molecules can be added during the synthesis of the latexes, and these particles can be charged without the addition of a surfactant.29,30 Latexes can also be charged in density-matched solvents containing halogenated solvents due to the autoionization of the solvent into free halide ions.31–34
Of the proposed mechanisms for particle charging in nonaqueous solvents,3 acid–base interactions are unlikely to be the origin of charge for these particles given the lack of dissociable protons on the PMMA latexes. Therefore, preferential adsorption seems like the most likely explanation for the charging of latexes by surfactants or halogenated solvents.4 In the case of ionic monomer or salt containing particles, the origin of charge is a preferential dissociation of one component.
3.2 Surfactant ionicity
From the reports in the literature, ionic surfactants are required to charge PHSA-stabilized PMMA latexes. Two nonionic charging agents have been tested. Sainis et al. used polyisobutylene succinimide surfactant,67 and Roberts et al. used the PMMA-graft-PHSA stabilizer copolymer.15 Both can act as electrolytes, but they do not charge PMMA latexes. As a contrast to sterically-stabilized PMMA, aqueous dispersible PMMA is charged positively in hexane by nonionic sorbitan oleate surfactants.80 The mechanism of charging will be different for these two types of PMMA, presumably acid–base interactions for aqueous dispersible PMMA and preferential adsorption for sterically-stabilized PMMA latexes.3,4Of the ionic surfactants studied, the vast majority are anionic. Aerosol OT (AOT) is the primary anionic surfactant used, and it charges particles negatively.1,15,18,23,46,68,81,82 AOT is frequently used as a charging agent, but there is nothing particularly special about the 2-ethylhexyl tailgroup.83,84 Other sodium dialkylsulfosuccinate surfactants have been found to be similarly effective to AOT as charging agents.36 Counterion-exchanged AOT surfactants also charge particles negatively, except for manganese AOT, which charged particles positively.23 Octanoate surfactants with divalent metals (zirconium or calcium) charge particles positively.15,18,27 The difference between AOT and octanoate surfactants is likely due to the complexation between the metal cation, a single surfactant, and carbonyl groups on the particles; this results in a net positive charge.
Kitahara et al. are the only group to report the charging of PMMA latexes by cationic surfactants (carboxylic acid anions and alkylamine cations), and they found that the particles were positively charged.23
3.3 Surfactant counterion
The surfactant counterion has been varied for two surfactants: the AOT series and the octanoate series. The polarity of the charge will be discussed in this section rather than the magnitude. The reduced mobilities (μ* = μ/μ0) of PMMA latexes charged by four different surfactants (sodium AOT, calcium AOT, calcium octanoate, and zirconyl 2-ethylhexanoate) as a function of surfactant concentration are shown in Fig. 6. Only data above the CMC for inverse micelle formation (∼0.1 mM) are shown so that the counterions will be inverse micelles rather than monomers.69,70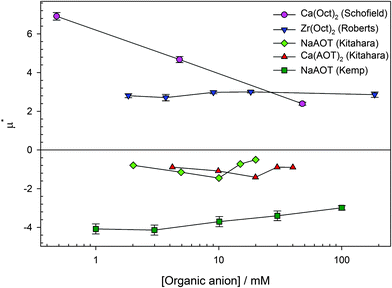 | ||
| Fig. 6 Reduced mobility (μ* = μ/μ0) for PMMA latexes charged by four surfactants, shown in the legend. The organic anion of the surfactant (dioctylsulfosuccinate or octanoate/2-ethylhexanoate) seems to dictate the polarity of the particle charge rather than the inorganic cation. Dioctylsulfosuccinate (AOT) surfactants charge particles negatively, and isooctanoate/2-ethylhexanoate (Oct) surfactants charge particles positively. The data are measured using electrophoresis equipment (either light scattering or optical tweezers) and are from several sources (Ca(Oct)2 from Schofield,28 Zr(Oct)2 from Roberts,85 NaAOT and Ca(AOT)2 from Kitahara et al.,23 and NaAOT from Kemp79). | ||
In the first study of AOT charging of PMMA latexes by Kitahara et al., they studied salts of AOT with four different counterions (Na+, Mn2+, Co2+, and Ca2+). They found that NaAOT, Co(AOT)2, and Ca(AOT)2 surfactants charged particles negatively but that Mn(AOT)2 surfactant charged particles positively. They were unable to explain why Mn(AOT)2 behaved differently to the other surfactants.23 Other than the study by Kitahara et al., the inorganic cation does not seem to dictate the charge of PMMA latexes. Aside from Mn(AOT)2, all AOT salts seem to charge particles negatively.
The inorganic counterion of octanoate (either isooctanoate or 2-ethylhexanoate) surfactants does not dictate the charge of PMMA latexes either. Two counterions have been studied, calcium27,28 and zirconium.15,18,85 Both surfactants charge particles positively.
3.4 Surfactant organic ion
For ionic surfactants, either the counterion or surfactant ion can be varied. As discussed in Section 3.3, the counterion was found to have limited effect on the polarity of the particle charge. Of all the surfactants studied in the literature, calcium surfactants are an interesting case, as they have been studied with different organic anions (shown in Fig. 6). Schofield used calcium octanoate as a charging agent and found that it charged particles positively.27,28 Kitahara et al. used calcium AOT as a charging agent and found that it charged particles negatively.23The dissociation of the two surfactants should be identical; they will both form singly charged CaX+ and X− groups, where X is the organic ion. The charge of the particle will then depend on whether the CaX+ or the X− group preferentially adsorbs. The reason that a different ion would preferentially adsorb between the two surfactants is not clear. Both groups assign the X− moiety as more hydrophobic (equivalently solvophilic). Schofield and Ottewill assert that the Ca2+ containing salt will complex with esters in the latexes,27 but Kitahara et al. state that the more hydrophobic ion will adsorb onto the particles.23 These two explanations are inconsistent. The origin of the difference in the polarity of the charge arising from these two calcium surfactants is unclear, but it is clear that the organic ion determines the charge of the particles.
3.5 Incorporated charging agent
Bartlett et al. developed a method to produce charged PMMA latexes through the incorporation of charging additives rather than the through the addition of surfactants. They have primarily used a polymerizable ionic monomer, consisting of a tetraalkylammonium cation that is bound to the particles and a fluorinated tetraphenylborate anion that can dissociate, but they have also added non-polymerizable hydrophobic salts to the particle synthesis. The non-polymerizable salts produced particles that were negatively charged, and the polymerizable ionic monomer produced particles that were positively charged (as expected) with a larger surface potential.29 The charge of the ionic monomer particles did not depend on the chemical properties of the monomer (spacer or alkylammonium chain length). The particles are in a counterion-dominated regime where their electrophoretic mobility and surface potential are determined by counterion condensation and are less than the bare charge.64,65 In the bare charge limit (at very low ϕ), the properties of the alkylammonium cation may influence the charge, but at higher volume fractions, the effective mobility is restricted by the requirements of counterion condensation, obscuring any difference between different charging species. The dependence of the charge on ionic monomer concentration is unclear. Some studies showed a dependence,86 and some did not.37 There were differences in the solvent conditions as well as amount of centrifugation used to clean the particles, which may explain the discrepancy.3.6 Charging dyed particles
Royall et al. showed that fluorescently labeled PMMA latexes can be charged by adding halide anions into the system; they used tetrabutylammonium chloride (TBAC). Particles with different fluorescent dyes were both positively charged, although with different magnitudes, but the addition of 40 μM TBAC inverted the charge of the particles.87An interesting application of inverting particle charge is that oppositely charged latexes can be produced. Both Leunissen et al. and Bartlett and Campbell reported colloidal crystals of oppositely charged particles in 2005;33,34 an example is shown in Fig. 7. Vissers et al. also reported the formation of lanes when oppositely charged particles were driven by electric fields.88 The presence of halide anions is required to modify the charge of the particles. Leunissen et al. and Vissers et al. introduced bromide ions through the tetrabutylammonium bromide salt,33,88 and Bartlett and Campbell introduced bromide ions by adding a ferromagnetic wire to catalyze the autoionization of the CHB solvent.34
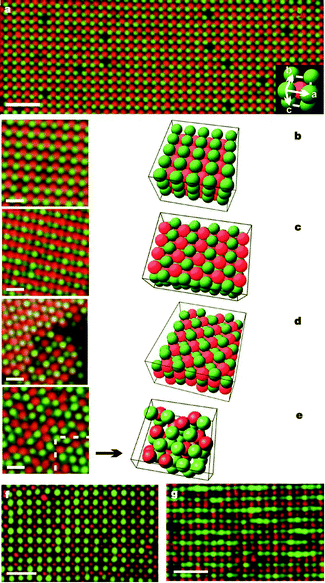 | ||
| Fig. 7 CsCl-type binary crystals formed from oppositely charged colloids. All particles were dispersed in salt-containing CHB–decalin solutions. In subfigures (a–e), red particles are positive PMMA latexes and green particles are negative PMMA latexes; in subfigures (f and g), green particles are positive PMMA latexes and red particles are negative silica. Reprinted by permission from Macmillan Publishers Ltd: Nature, Leunissen et al., 2005.33 | ||
3.7 Surfactant hydrophobicity
There has been little work in systematically varying the hydrophobicity (equivalently solvophilicity) of surfactants and determining the effect on charging PMMA latexes. This could, however, partly explain the differences in charging for different organic ions, discussed in Section 3.4. Differences have been observed for other colloids in nonpolar solvents. For example, Gacek and Berg recently found differences in how surfactants with different hydrophobic–lipophilic balances charged mineral oxide particles.89 Similar results have been found for PMMA latexes. The triple-chain analogue of AOT, which is more hydrophobic than AOT itself, is a more effective charging agent than AOT at equimolar concentrations.363.8 Particle stabilizer
Poly(12-hydroxystearic acid) (PHSA) has by far been the most common steric stabilizer used for producing PMMA latexes in nonpolar solvents, since their development in the 1970s and 1980s.24,25 PHSA is incorporated into the latex using a brush copolymer consisting of PHSA brushes and a backbone of methyl methacrylate and glycidyl methacrylate.90 There are other possible stabilizers that can be used; the primary requirements for good steric stabilizers are that there is a high surface coverage and that the solvent is good for the stabilizing chains. In addition to PHSA, poly(dimethylsiloxane) (PDMS), polyethylene, polypropylene, polyisobutylene, and poly(alkyl acrylate) stabilizers have been used to generate PMMA latexes in alkane solvents.91 Several groups have recently prepared latexes for electrophoretic display applications using PHSA alternatives. Richez et al. prepared PDMS-stabilized latexes,92 and Farrand et al. prepared poly(octadecyl acrylate) and poly(2-ethylhexyl acrylate) stabilized latexes.93None of these studies produced charged particles though. PHSA-stabilized PMMA latexes have been used to produce all surfactant, ionic monomer, and solvent or dye charged particles discussed so far, with the exception of Kitahara et al. They produced latexes that were stabilized by copolymers of butyl or lauryl methacrylate. They found that the particles were negatively charged by AOT, but they did not discuss particle size or concentration, making it difficult to directly compare to other experimental results.23 Several surprising results have been found for PDMS-stabilized latexes. Sánchez found that AOT does not charge particles in decalin and destabilizes particles in dodecane.94 Lin et al. found that AOT charges particles in decalin to a similar degree as PHSA-stabilized ones (|μ*| ≈ 4), although the particles decelerated as they moved electrophoretically across a microfluidic cell. Additionally, the PDMS-stabilized particles without any charging additive were highly charged, with 170e per particle.95
These are the only studies of charged latexes stabilized by non-PHSA polymers, despite additional stabilizers being identified in recent decades. This is a parameter that is worth exploring further.
3.9 Particle synthesis
Recently, there has been some work into the effect of locking the PHSA stabilizer to the surface. A catalyst, such as diethanolamine, is added to enable the reaction between epoxide groups on the stabilizer and methacrylic acid groups on the latex. This covalently links the PHSA brush copolymer stabilizer to the particle surface, which is only entangled after the first step.25This step does not need to performed to produce stable latexes, as has been shown for ionic monomer charged latexes.30 Gillespie et al. measured μ* for ionic monomer charged particles, some of which had been locked and some of which had not, and they found that the electrophoretic mobilities for different particles were effectively the same.37
This is not the case for particles charged by CHB solvent decomposition. van der Linden et al. measured the electrophoretic mobility of dyed PMMA latexes using confocal microscopy, and they found that latexes that had been locked were more highly charged than those that had not. They attributed this to complexation between free protons and the 2-(dimethylamino)ethanol (DMAE) catalyst. By systematically varying the conditions relating to the locking stage (temperature, catalyst, and concentration), they determined that the DMAE catalyst is chemically incorporated into the latexes, and therefore that locked latexes include groups that can complex with H+ ions and increase their positive charge.71 The choice of locking catalyst can dictate whether or not protons can be complexed. Basic amines, such as diethanolamine or DMAE, can lead to positively charged particles,24,25,71 and alkyl amines, such as triethylamine or N,N-dimethyldodecylamine, can reduce particle charging.71,96 This is particularly relevant to particles charged by CHB solvent decomposition, but it is a variable that should be considered further for all charging methods to understand how to control the charge of PMMA latexes.
3.10 Solvent type
The effect of varying solvent depends on the method that is used to charge particles. The charge of latexes where charging agents are added (such as surfactants in alkanes) does not depend on the solvent. On the other hand, the charge of latexes where the charging agents are a component of the particle or the solvent (such as ionic monomers or CHB) can depend on the solvent. The relative permittivity of the solvent is important for determining the magnitude of charge dissociation; the conductivities of tetraalkylammonium salts and AOT surfactant are known to vary in different solvents.97,98 This ability to study solvent effects requires that varying the solvent does not change the stability of the particles. While generally not an issue, differences in stability have been reported in the literature. For example, PHSA-stabilized latexes are stable in hexadecane,19,67,99–101 but PDMS-stabilized latexes are not.102For surfactant-charged particles in alkanes, varying the solvent has no influence on the electrophoretic mobility other than through the change in viscosity. For example, the reduced mobilities (μ* = μ/μ0) of AOT-charged latexes at the same volume fraction and the same surfactant concentration are identical (Table 1), as μ0 normalizes for the solution viscosity.82
| Solvent | μ* |
|---|---|
| Octane | −3.8 ± 0.6 |
| Dodecane | −3.9 ± 0.6 |
| Hexadecane | −4.1 ± 0.8 |
For ionic monomer charged latexes, the charge of particles depends on the polarity of the solvent. This is because the charge arises from the dissociation of an ion from the surface, and the solubility of the ion will dictate the particle charge. Sánchez and Bartlett measured the charge of latexes including an ionic monomer in mixtures of dodecane and pentanol (2.0 ≤ εr ≤ 15.1), and found that the particle charge decreased as the amount of pentanol, and consequently εr, was increased.29
For dyed particles dispersed in density-matched solvents, the charge was attributed to the self-ionization of the cyclohexyl bromide (CHB) solvent used for density and refractive index matching.87 The weak charge of dyed colloids was originally attributed to the dye incorporated for fluorescence microscopy.31 However, later work showed that neither removing water from the solvent nor producing particles without dye resulted in uncharged particles.32,103 Therefore, it appears that the solvent itself is responsible for the particle charge.
Thermotropic liquid crystals (LCs) are another “solvent” often used with PMMA particles. However, this solvent system is not used to investigate charge but rather to study the formation of defect-induced soft solid materials. The PHSA stabilizer on the PMMA surface strongly orients liquid crystal molecules in a radial configuration, distorting the local liquid crystal director. A nematic liquid crystal acts to minimize distortion by bringing these defects together, and at sufficiently high particle loadings can form percolating gel-like structures, capable of supporting their own weight.104 Furthermore, PMMA particles dispersed in isotropic 5CB that are then cooled into the nematic phase form a similar free-standing structure, induced by highly localized aggregation of particles at the boundaries of nucleating nematic regions, forming a so-called soft solid.105–107 The dielectric environment is more complicated in these systems due to their birefringence, and although many liquid crystal mixtures possess low dielectric constants in both parallel and perpendicular orientation (3 < ε‖, ε⊥ < 8),108,109 the majority of studies on PMMA–LC composites use 4-cyano-4′-pentylbiphenyl, more commonly known as 5CB. It possesses an intermediate dielectric constant of 11.4 in the isotropic phase (when heated above the clearing point at 35.6 °C), and ε‖ = 19.7 and ε⊥ = 6.6 in the nematic phase.110
The charge of ionic monomer-charged and unmodified PMMA latexes has been measured in both isotropic and nematic 5CB. While the unmodified particle system showed no noticeable charge, the results for the ionic liquid-modified system were qualitatively the same as Lavrentovich et al.111 for hydrophobically-coated silica spheres: the electrophoretic velocity was directly proportional to field strength in isotropic 5CB but was field dependent for nematic 5CB.112 Directly comparing these results to conventional solvents, due to the difficulties in defining the dielectric constant and viscosity, is challenging. The ability to produce charged particles in nematic liquid crystals is very interesting, however, due to the development of technologies such as electrophoretic liquid crystal displays.113
3.11 Presence of water
The presence of water in nonpolar solvents is known to influence properties of the system. For example, Eicke and Christen showed that the CMC of AOT in nonpolar solvents depends on the amount of water,114 and both Tettey and Lee and Gacek et al. showed that trace amounts of moisture can influence the charge of silica particles in nonpolar solvents.21,22 The effect of added water has differing effects on the charge of PMMA latexes, depending on the method used to charge the particles.For particles charged by CHB decomposition, water does not seem to dictate the charge of the particles, as drying and distilling the CHB do not influence the interparticle interactions.32,87 Instead, water can be used as a bulk ion reservoir to remove ions from the CHB.115,116
Water has profound, well-known effects on solutions of surfactants in nonpolar solvents. The conductivity of water-containing microemulsion droplets is different than surfactant inverse micelles due to charge fluctuation.77 For particles charged by AOT surfactant, water has a clear influence on their charge. Wood et al. exposed AOT charged PMMA latexes in dry dodecane to moisture, and they found that charge of the particles reversed from −10e to +10e after 30 min exposure to water.81 The electrokinetic properties of PMMA latexes have been measured to determine the electrophoretic mobility and charge of small particles with a w ratio (w = [H2O]/[AOT]) of 41. The ζ potential determined from optical tweezer microelectrophoresis of 425 nm latexes was found to decrease for microemulsions (ζ* = −3.5 for AOT inverse micelles and ζ* = −1.7 for AOT microemulsions). However, the dimensionless charge (ZλB/a) determined from conductivity for two different PMMA latexes was found to be approximately the same (2.6 for AOT inverse micelle charged 610 nm latexes and 2.8 for microemulsion charged 42 nm latexes).15,46
4 Conclusions
By considering the literature of charged PMMA latexes as a whole, it is possible to determine the variables that can be used to control the particle charge. Some groups have studied systematic variations, but by comparing different methods of charging particles and different techniques, the relationship between the variable and the charge becomes clearer. This contributes to understanding how to control the charge of these latexes and can be applied to charged colloids in low dielectric fluids more generally. For example, the effect of varying particle size and surface charge density has been studied for AOT charged latexes,15 ionic monomer charged latexes,37 and CHB charged latexes.71 The surface potential of AOT charged latexes and CHB charged latexes appears to be independent of particle size, and the surface charge density of ionic monomer latexes is also constant. However, the electrophoretic mobility of ionic monomer charged latexes shows some dependence on particle size, as there is a critical radius beyond which counterion condensation becomes significant. This is a consequence of how the particles are charged, so by considering the studies together, it is possible to see the effect of varying the charging method. The advantage of considering PMMA latexes is that there are several methods to charge them, and this reveals the detail of changing properties of both the charging agent and the dispersant.Of the physical variations studied, changing the volume fraction seems to have the largest effect on the particles, particularly at higher volume fractions. The particle size and double layer thickness (controlled by the surfactant or salt concentration) have less of an effect, only showing deviations at very small particle sizes or surfactant concentrations below the CMC. In general, the electrophoretic mobility can be controlled by varying volume fraction, size, or surfactant concentration, but the electrokinetic potential is constant. This is due to the relationship between electrophoretic mobility and ζ potential, which is different in nonpolar solvents than in water due to the thick double layer.45,52,66
Of the chemical variations studied, the charging method used has a large effect on the particle charge. This is because the location of the charging agent is different for the three methods, either chemically bound to the particle, added as an external species, or a byproduct of solvent decomposition. For surfactant charged PMMA particles, the ionicity of the surfactant is important; nonionic species do not charge particles whereas ionic surfactants do. This is in contrast to other colloids dispersed in nonpolar media, where nonionic surfactants can act as charging agents due to acid–base interactions.117 Changing the solvent does not vary the electrophoretic mobility of AOT charged particles in alkane solvents, beyond increasing the viscosity, as expected from the definition of μ0. For CHB charged particles, changing the dye or drying the solvent does not modify the charge of the particles; it is determined by the concentration of bromide ions in the solvent. For ionic monomer charged particles, changing the size of the bound cation does not modify the charge of the particles; the counterion controls the ion dissociation. These observations are particular to PMMA latexes, as such charging methods cannot be used for other types of colloids, but this shows that it is crucial to consider the interactions of the charging agent with the particle and the solvent to fully understand the formation of charge.
By choosing a well-studied model colloidal system, it is possible to determine how to influence the charge of colloids in nonpolar solvents. Physical electrokinetic models can be applied to understand the electrophoresis of colloids in nonpolar solvents, but the results may initially seem counterintuitive when compared to water. By considering the reduction in relative permittivity and subsequent increase in the thickness of the double layer, the results are generally as expected. The interaction of the charging agent, whether a surfactant, salt, or dissociated surface species, with the solvent and the particle surface is key to understanding the charge of the colloid. Interfacial interactions are particularly important.
Gaining an understanding of how to control the charge of polymer particles will be important for guiding the application of charged species in nonpolar solvents. Charged particles in nonaqueous media are already widely used in applications, such as in electrophoretic electronic paper displays,118 and will be equally important in the future. Many of the possible technologies that have been proposed for next-generation electronic paper devices require control of charged species.113,119 Research by many groups, particularly over the past 10 years, has shown that producing charge on particles in nonpolar solvents continues to provide surprising, technologically-relevant results, with a rich variety of properties achievable through careful tuning of the colloidal system. Technological requirements may demand deviations from the simple case of AOT as the charging agent, at an intermediate surfactant concentration, and at a low latex volume fraction. When this is the case, it is clearly not a perfect model system. By establishing the variables that influence the charging of latexes in nonpolar solvents, this review provides guidance to predicting how these deviations will control their electrophoretic mobility and interparticle interactions.
Acknowledgements
GNS acknowledges Merck Chemicals Ltd. UK, an affiliate of Merck KGaA, Darmstadt, Germany, and the UK Engineering and Physical Sciences Research Council (EPSRC) for the provision of a CASE PhD studentship. JEH is supported by EPSRC CDT grant EP/G036780/1.References
- M. F. Hsu, E. R. Dufresne and D. A. Weitz, Langmuir, 2005, 21, 4881–4887 CrossRef CAS PubMed.
- V. Novotny, Colloids Surf., 1987, 24, 361–375 CrossRef CAS.
- I. D. Morrison, Colloids Surf., A, 1993, 71, 1–37 CrossRef CAS.
- G. N. Smith and J. Eastoe, Phys. Chem. Chem. Phys., 2013, 15, 424–439 RSC.
- J. L. van der Minne and P. H. J. Hermanie, J. Colloid Sci., 1952, 7, 600–615 CrossRef CAS.
- J. L. van der Minne and P. H. J. Hermanie, J. Colloid Sci., 1953, 8, 38–52 CrossRef CAS.
- R. I. Keir, Suparno and J. C. Thomas, Langmuir, 2002, 18, 1463–1465 CrossRef CAS.
- M. Gacek, G. Brooks and J. C. Berg, Langmuir, 2012, 28, 3032–3036 CrossRef CAS PubMed.
- P. Jenkins, S. Basu, R. I. Keir, J. Ralston, J. C. Thomas and B. M. Wolffenbuttel, J. Colloid Interface Sci., 1999, 211, 252–263 CrossRef CAS PubMed.
- M. E. Parent, J. Yang, Y. Jeon, M. F. Toney, Z.-L. Zhou and D. Henze, Langmuir, 2011, 27, 11845–11851 CrossRef CAS PubMed.
- M. M. Gacek and J. C. Berg, Electrophoresis, 2014, 35, 1766–1772 CrossRef CAS PubMed.
- R. C. Flagan, Aerosol Sci. Technol., 1998, 28, 301–380 CrossRef CAS PubMed.
- P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342 CrossRef CAS PubMed.
- C. P. Royall, W. C. K. Poon and E. R. Weeks, Soft Matter, 2013, 9, 17–27 RSC.
- G. S. Roberts, R. Sanchez, R. Kemp, T. Wood and P. Bartlett, Langmuir, 2008, 24, 6530–6541 CrossRef CAS PubMed.
- N. Bjerrum, K. Dan. Vidensk. Selsk., Mat.-Fys. Medd., 1926, 7, 1–48 CAS.
- S. Auer, W. C. K. Poon and D. Frenkel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 020401 CrossRef CAS.
- G. S. Roberts, T. A. Wood, W. J. Frith and P. Bartlett, J. Chem. Phys., 2007, 126, 194503 CrossRef PubMed.
- S. K. Sainis, J. W. Merrill and E. R. Dufresne, Langmuir, 2008, 24, 13334–13337 CrossRef CAS PubMed.
- F. Beunis, F. Strubbe, K. Neyts and D. Petrov, Phys. Rev. Lett., 2012, 108, 016101 CrossRef.
- M. Gacek, D. Bergsman, E. Michor and J. C. Berg, Langmuir, 2012, 28, 11633–11638 CrossRef CAS PubMed.
- K. E. Tettey and D. Lee, Soft Matter, 2013, 9, 7242–7250 RSC.
- A. Kitahara, T. Satoh, S. Kawasaki and K. Kon-No, J. Colloid Interface Sci., 1982, 86, 105–110 CrossRef CAS.
- R. J. R. Cairns, R. H. Ottewill, D. W. J. Osmond and I. Wagstraff, J. Colloid Interface Sci., 1976, 54, 45–51 CrossRef CAS.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78 CrossRef CAS.
- P. M. Adriani and A. P. Gast, Faraday Discuss. Chem. Soc., 1990, 90, 17–29 RSC.
- R. H. Ottewill, A. R. Rennie and A. Schofield, in Trends in Colloid and Interface Science IV, ed. M. Zulauf, P. Lindner and P. Terech, Steinkopff, 1990, vol. 81, pp. 1–5 Search PubMed.
- A. B. Schofield, PhD thesis, University of Bristol, 1993.
- R. Sánchez and P. Bartlett, Soft Matter, 2011, 7, 887–890 RSC.
- N. Greinert, M. Uerdingen, L. Beylage, N. Ignatyev, J. H. Wilson, M. J. Goulding, R. Kemp, A. N. Smith, P. Bartlett, P. Barthen, W. Frank and R. S. Garcia, Particles for Electrophoretic Displays, WO2012/072218 A1, 2012 Search PubMed.
- U. Gasser, E. R. Weeks, A. Schofield, P. N. Pusey and D. A. Weitz, Science, 2001, 292, 258–262 CrossRef CAS PubMed.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Nature, 2005, 437, 235–240 CrossRef CAS PubMed.
- P. Bartlett and A. I. Campbell, Phys. Rev. Lett., 2005, 95, 128302 CrossRef.
- T. Vissers, A. Imhof, F. Carrique, A. V. Delgado and A. van Blaaderen, J. Colloid Interface Sci., 2011, 361, 443–455 CrossRef CAS PubMed.
- G. N. Smith and J. Eastoe, in preparation.
- D. A. J. Gillespie, J. E. Hallett, O. Elujoba, A. F. Che Hamzah, R. M. Richardson and P. Bartlett, Soft Matter, 2014, 10, 566–577 RSC.
- H. Ohshima, J. Colloid Interface Sci., 2003, 262, 294–297 CrossRef CAS.
- M. Evers, N. Garbow, D. Hessinger and T. Palberg, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6774–6784 CrossRef CAS.
- M. Medebach and T. Palberg, J. Phys.: Condens. Matter, 2004, 16, 5653–5658 CrossRef CAS.
- T. Palberg, M. Medebach, N. Garbow, M. Evers, A. B. Fontecha, H. Reiber and E. Bartsch, J. Phys.: Condens. Matter, 2004, 16, S4039 CrossRef CAS.
- V. Lobaskin, B. Dünweg, M. Medebach, T. Palberg and C. Holm, Phys. Rev. Lett., 2007, 98, 176105 CrossRef.
- C. Wohlfarth, CRC Handbook of Chemistry and Physics, CRC Press, 95th edn, 2014–2015, internet version Search PubMed.
- D. Fermin and J. Riley, in Colloid science: principles, methods, and applications, ed. T. Cosgrove, Wiley, Chichester, 2nd edn, 2010, ch. Charge in Colloidal Systems, pp. 23–43 Search PubMed.
- H. Ohshima, J. Colloid Interface Sci., 1997, 188, 481–485 CrossRef CAS.
- R. Kemp, R. Sanchez, K. J. Mutch and P. Bartlett, Langmuir, 2010, 26, 6967–6976 CrossRef CAS PubMed.
- H. Cao, N. Lu, B. Ding and M. Qi, Phys. Chem. Chem. Phys., 2013, 15, 12227–12234 RSC.
- T. Kanai, N. Boon, P. J. Lu, E. Sloutskin, A. B. Schofield, F. Smallenburg, R. van Roij, M. Dijkstra and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 030301 CrossRef.
- F. Strubbe, F. Beunis, M. Marescaux and K. Neyts, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031405 CrossRef.
- A. Wysocki, C. P. Royall, R. G. Winkler, G. Gompper, H. Tanaka, A. van Blaaderen and H. Löwen, Soft Matter, 2009, 5, 1340–1344 RSC.
- B. Dünweg, V. Lobaskin, K. Seethalakshmy-Hariharan and C. Holm, J. Phys.: Condens. Matter, 2008, 20, 404214 CrossRef.
- R. W. O'Brien and L. R. White, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1607–1626 RSC.
- F. Carrique, J. Cuquejo, F. J. Arroyo, M. L. Jiménez and A. V. Delgado, Adv. Colloid Interface Sci., 2005, 118, 43–50 CrossRef CAS PubMed.
- K. Kim, Y. Nakayama and R. Yamamoto, Phys. Rev. Lett., 2006, 96, 208302 CrossRef.
- F. Carrique, F. J. Arroyo, M. L. Jiménez and A. V. Delgado, J. Phys. Chem. B, 2003, 107, 3199–3206 CrossRef CAS.
- E. K. Zholkovskij, S. S. Dukhin, N. A. Mishchuk, J. H. Masliyah and J. Czarnecki, Colloids Surf., A, 2001, 192, 235–251 CrossRef CAS.
- E. Trizac, L. Bocquet, M. Aubouy and H. H. von Grünberg, Langmuir, 2003, 19, 4027–4033 CrossRef CAS.
- C. Haro-Pérez, M. Quesada-Pérez, J. Callejas-Fernández, P. Schurtenberger and R. Hidalgo-Álvarez, J. Phys.: Condens. Matter, 2006, 18, L363–L369 CrossRef PubMed.
- F. Carrique, E. Ruiz-Reina, F. J. Arroyo and A. V. Delgado, J. Phys. Chem. B, 2006, 110, 18313–18323 CrossRef CAS PubMed.
- F. Carrique, E. Ruiz-Reina, F. J. Arroyo, M. L. Jiménez and A. V. Delgado, Langmuir, 2008, 24, 2395–2406 CrossRef CAS PubMed.
- T. E. Colla, Y. Levin and E. Trizac, J. Chem. Phys., 2009, 131, 074115 CrossRef PubMed.
- K. Makino and H. Ohshima, Langmuir, 2010, 26, 18016–18019 CrossRef CAS PubMed.
- S. M. Agnihotri, H. Ohshima, H. Terada, K. Tomoda and K. Makino, Langmuir, 2009, 25, 4804–4807 CrossRef CAS PubMed.
- H. Ohshima, J. Colloid Interface Sci., 2002, 248, 499–503 CrossRef CAS PubMed.
- H. Ohshima, J. Colloid Interface Sci., 2002, 247, 18–23 CrossRef CAS PubMed.
- A. V. Delgado, F. González-Caballero, R. J. Hunter, L. K. Koopal and J. Lyklema, Pure Appl. Chem., 2005, 77, 1753–1805 CAS.
- S. K. Sainis, V. Germain, C. O. Mejean and E. R. Dufresne, Langmuir, 2008, 24, 1160–1164 CrossRef CAS PubMed.
- G. N. Smith, S. Alexander, P. Brown, D. A. J. Gillespie, I. Grillo, R. K. Heenan, C. James, R. Kemp, S. E. Rogers and J. Eastoe, Langmuir, 2014, 30, 3422–3431 CrossRef CAS PubMed.
- M. Kotlarchyk, J. S. Huang and S.-H. Chen, J. Phys. Chem., 1985, 89, 4382–4386 CrossRef CAS.
- G. N. Smith, P. Brown, S. E. Rogers and J. Eastoe, Langmuir, 2013, 29, 3252–3258 CrossRef CAS PubMed.
- M. N. van der Linden, J. C. P. Stiefelhagen, G. Heessels-Gürboaa, J. E. S. van der Hoeven, N. A. Elbers, M. Dijkstra and A. van Blaaderen, Langmuir, 2015, 31, 65–75 CrossRef CAS PubMed.
- G. V. Ramanathan, J. Chem. Phys., 1988, 88, 3887–3892 CrossRef CAS PubMed.
- I. Borukhov, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3598–3615 CrossRef CAS PubMed.
- G. S. Manning, J. Phys. Chem. B, 2007, 111, 8554–8559 CrossRef CAS PubMed.
- J. Eastman, in Colloid science: principles, methods, and applications, ed. T. Cosgrove, Wiley, Chichester, 2nd edn, 2010, ch. 2, pp. 45–59 Search PubMed.
- B. Dobiáš, in Coagulation and Flocculation, ed. H. Stechemesser and B. Dobiáš, Taylor & Francis, London, 2nd edn, 2005, ch. 10, pp. 663–765 Search PubMed.
- H. F. Eicke, M. Borkovec and B. Das-Gupta, J. Phys. Chem., 1989, 93, 314–317 CrossRef CAS.
- J. Schmidt, R. Prignitz, D. Peschka, A. Münch, B. Wagner, E. Bänsch and W. Peukert, J. Colloid Interface Sci., 2012, 386, 240–251 CrossRef CAS PubMed.
- R. Kemp, PhD thesis, University of Bristol, 2009.
- C. E. Espinosa, Q. Guo, V. Singh and S. H. Behrens, Langmuir, 2010, 26, 16941–16948 CrossRef CAS PubMed.
- T. A. Wood, G. S. Roberts, S. Eaimkhong and P. Bartlett, Faraday Discuss., 2008, 137, 319–333 RSC.
- G. N. Smith, I. Grillo, S. E. Rogers and J. Eastoe, J. Colloid Interface Sci., 2015, 449, 205–214 CrossRef CAS PubMed.
- S. Nave, J. Eastoe and J. Penfold, Langmuir, 2000, 16, 8733–8740 CrossRef CAS.
- S. Nave, J. Eastoe, R. K. Heenan, D. Steytler and I. Grillo, Langmuir, 2000, 16, 8741–8748 CrossRef CAS.
- G. S. Roberts, PhD thesis, University of Bristol, 2007.
- G. Hussain, A. Robinson and P. Bartlett, Langmuir, 2013, 29, 4204–4213 CrossRef CAS PubMed.
- C. P. Royall, M. E. Leunissen and A. van Blaaderen, J. Phys.: Condens. Matter, 2003, 15, S3581–S3596 CrossRef CAS.
- T. Vissers, A. Wysocki, M. Rex, H. Lowen, C. P. Royall, A. Imhof and A. van Blaaderen, Soft Matter, 2011, 7, 2352–2356 RSC.
- M. M. Gacek and J. C. Berg, J. Colloid Interface Sci., 2015, 449, 192–197 CrossRef CAS PubMed.
- M. T. Elsesser and A. D. Hollingsworth, Langmuir, 2010, 26, 17989–17996 CrossRef CAS PubMed.
- A. P. Richez, H. N. Yow, S. Biggs and O. J. Cayre, Prog. Polym. Sci., 2013, 38, 897–931 CrossRef CAS PubMed.
- A. P. Richez, L. Farrand, M. Goulding, J. H. Wilson, S. Lawson, S. Biggs and O. J. Cayre, Langmuir, 2014, 30, 1220–1228 CrossRef CAS PubMed.
- L. D. Farrand, C. Topping, K. Belsey and S. Holder, Particles for Electrophoretic Displays, WO2014/166583 A1, 2014 Search PubMed.
- R. Sánchez, 2012, arXiv e-prints, 1211.3155.
- T. Lin, T. E. Kodger and D. A. Weitz, Soft Matter, 2013, 9, 5173–5177 RSC.
- M. K. Klein, A. Zumbusch and P. Pfleiderer, J. Mater. Chem. C, 2013, 1, 7228–7236 RSC.
- A. P. Abbott and D. J. Schiffrin, J. Chem. Soc., Faraday Trans., 1990, 86, 1453–1459 RSC.
- E. L. Michor and J. C. Berg, Langmuir, 2014, 30, 12520–12524 CrossRef CAS PubMed.
- S. K. Sainis, V. Germain and E. R. Dufresne, Phys. Rev. Lett., 2007, 99, 018303 CrossRef.
- J. W. Merrill, S. K. Sainis and E. R. Dufresne, Phys. Rev. Lett., 2009, 103, 138301 CrossRef.
- J. W. Merrill, S. K. Sainis, J. Blawzdziewicz and E. R. Dufresne, Soft Matter, 2010, 6, 2187–2192 RSC.
- S. M. Klein, V. N. Manoharan, D. J. Pine and F. F. Lange, Colloid Polym. Sci., 2003, 282, 7–13 CAS.
- G. Bosma, C. Pathmamanoharan, E. H. A. de Hoog, W. K. Kegel, A. van Blaaderen and H. N. W. Lekkerkerker, J. Colloid Interface Sci., 2002, 245, 292–300 CrossRef CAS PubMed.
- T. A. Wood, J. S. Lintuvuori, A. B. Schofield, D. Marenduzzo and W. C. K. Poon, Science, 2011, 334, 79–83 CrossRef CAS PubMed.
- S. P. Meeker, W. C. K. Poon, J. Crain and E. M. Terentjev, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, R6083–R6086 CrossRef CAS.
- D. Vollmer, G. Hinze, W. C. K. Poon, J. Cleaver and M. E. Cates, J. Phys.: Condens. Matter, 2004, 16, L227 CrossRef CAS.
- J. Cleaver, D. Vollmer, J. Crain and W. Poon, Mol. Cryst. Liq. Cryst., 2004, 409, 59–68 CrossRef CAS PubMed.
- L. Wei, L. Eskildsen, J. Weirich, L. Scolari, T. T. Alkeskjold and A. Bjarklev, Appl. Opt., 2009, 48, 497–503 CrossRef.
- N. Podoliak, O. Buchnev, M. Herrington, E. Mavrona, M. Kaczmarek, A. G. Kanaras, E. Stratakis, J.-F. Blach, J.-F. Henninot and M. Warenghem, RSC Adv., 2014, 4, 46068–46074 RSC.
- A. Bogi and S. Faetti, Liq. Cryst., 2001, 28, 729–739 CrossRef CAS PubMed.
- O. D. Lavrentovich, I. Lazo and O. P. Pishnyak, Nature, 2010, 467, 947–950 CrossRef CAS PubMed.
- J. E. Hallett, P. Bartlett and R. M. Richardson, in preparation.
- S. Klein, Liq. Cryst. Rev., 2013, 1, 52–64 CrossRef CAS PubMed.
- H.-F. Eicke and H. Christen, Helv. Chim. Acta, 1978, 61, 2258–2263 CrossRef CAS PubMed.
- M. E. Leunissen, PhD thesis, Universiteit Utrecht, 2007.
- M. E. Leunissen, A. van Blaaderen, A. D. Hollingsworth, M. T. Sullivan and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2585–2590 CrossRef CAS PubMed.
- M. M. Gacek and J. C. Berg, Adv. Colloid Interface Sci., 2015, 220, 108–123 CrossRef CAS PubMed.
- B. Comiskey, J. D. Albert, H. Yoshizawa and J. Jacobson, Nature, 1998, 394, 253–255 CrossRef CAS.
- J. Heikenfeld, P. Drzaic, J.-S. Yeo and T. Koch, J. Soc. Inf. Disp., 2011, 19, 129–156 CrossRef.
Footnote |
| † Current address: Department of Chemistry, University of Sheffield, Brook Hill, Sheffield, South Yorkshire, S3 7HF, UK. |
| This journal is © The Royal Society of Chemistry 2015 |



