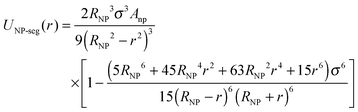Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rouse mode analysis of chain relaxation in polymer nanocomposites
Jagannathan T.
Kalathi
ab,
Sanat K.
Kumar
*a,
Michael
Rubinstein
c and
Gary S.
Grest
d
aDepartment of Chemical Engineering, Columbia University, New York, NY 10027, USA. E-mail: sk2794@columbia.edu
bDepartment of Chemical Engineering, National Institute of Technology Karnataka, Surathkal, KA 575025, India
cDepartment of Chemistry, University of North Carolina, Chapel Hill, NC 27599, USA
dSandia National Laboratories, Albuquerque, NM 87185, USA
First published on 20th April 2015
Abstract
Large-scale molecular dynamics simulations are used to study the internal relaxations of chains in nanoparticle (NP)/polymer composites. We examine the Rouse modes of the chains, a quantity that is closest in spirit to the self-intermediate scattering function, typically determined in an (incoherent) inelastic neutron scattering experiment. Our simulations show that for weakly interacting mixtures of NPs and polymers, the effective monomeric relaxation rates are faster than in a neat melt when the NPs are smaller than the entanglement mesh size. In this case, the NPs serve to reduce both the monomeric friction and the entanglements in the polymer melt, as in the case of a polymer–solvent system. However, for NPs larger than half the entanglement mesh size, the effective monomer relaxation is essentially unaffected for low NP concentrations. Even in this case, we observe a strong reduction in chain entanglements for larger NP loadings. Thus, the role of NPs is to always reduce the number of entanglements, with this effect only becoming pronounced for small NPs or for high concentrations of large NPs. Our studies of the relaxation of single chains resonate with recent neutron spin echo (NSE) experiments, which deduce a similar entanglement dilution effect.
Introduction
Adding nanoparticles (NPs) to polymer matrices can substantially enhance their optical, mechanical and thermal properties.1–3 The resulting polymer nanocomposites (PNCs) have found widespread use in e.g., packaging4,5 and solar cells.6–8 As a consequence there have been many investigations9–18 to understand the dynamics of polymers in nanocomposites to optimize properties and to facilitate their processing. Since polymer chains relax over a wide range of time and length scales, it is important to understand how the presence of NPs in polymer composites affects their relaxations across these different length and time scales.In our previous studies, using molecular dynamics (MD) simulations, we showed that the shear viscosity of a polymer melt can be significantly reduced when it is filled with small energetically neutral NPs (smaller than roughly half the entanglement mesh size).19 We deduced that small NPs act akin to solvent molecules and reduce the viscosity of a polymer melt in this “plasticization” limit. This effect is reversed for larger NPs, in which case they increase the viscosity of the polymer, as may be expected using classical theories such as those formulated by Einstein and by Batchelor.20 The reduction of viscosity seen for small NPs can also be overcome by increasing the attractive strength of NP–polymer interactions.
The diffusivities of the NP in a polymer melt are also found to be strongly dependent on their size.21 For NPs smaller than the polymer's entanglement mesh size, the relaxation times and NP diffusivity are described by the Stokes–Einstein relationship, where the viscosity is set by the segment of polymer chain with end-to-end distance comparable to the NP diameter. However, for NPs with diameters larger than the entanglement mesh size it appears that the competition of full chain relaxation vs. NP hopping through entanglement gates controls NP diffusion22 – however, there is no ready means to apply the Stokes–Einstein formula here.
Schneider et al.10 experimentally studied the relaxation of entangled poly(ethylene-alt-propylene) (PEP) chains (tube diameter ∼ 5 nm) filled with silica NPs (average diameter ∼ 17 nm). The silica volume fraction was varied in the range 0 ≤ ϕNP ≤ 0.6, where the ϕNP is calculated from the measured weight fraction of silica in the nanocomposite, and by assuming silica and polymer densities of 2.2 and ∼1 gm cm−1,3 respectively. Chain dynamics in these nanocomposites, with non-attractive interactions, are explored using neutron spin echo spectroscopy (NSE) and the resulting collective dynamic scattering function data analyzed using the idea of a tube-like confinement for chain relaxation below the reptation time. This procedure yields the following primary conclusions: (i) the monomeric relaxation rates (see below for definition) are unaffected by the addition of NPs, even at high particle loadings; (ii) chain conformations remain Gaussian for all loadings considered; and (iii) the tube diameter determined from analysis of NSE data decreases monotonically with added NPs. It is argued that there are two contributions to overall chain dynamics, and how they are affected by the addition of the NPs. The number of topological chain–chain entanglements decreases with increased NP loading, i.e., the chains disentangle from each other since a part of the system volume is occupied by the NPs. This is (more than) compensated by the geometric constraints that NPs present to chain dynamics. Since the second factor dominates at large loadings, the NSE reports an increase in chain relaxation time, while at the same time a reduction in the number of intra-chain entanglements.
Several of these experimental deductions have been considered by Li et al.,17 who conducted MD simulations on melts of well-entangled chains of length N = 500 with a single sized (10σ, where σ is the diameter of the chain monomers) NP (comparable to the size of the tube diameter). They used a primitive path analysis (PPA) assuming that the NPs were “phantoms” – that is the NPs are penetrable in the PPA and hence do not interfere with the chain “straightening” inherent in this calculation. The simulation-derived collective scattering functions were used to deduce the net effective tube diameter, which defines this collective motion (and presumably convolutes the effects of the NPs in chain dynamics and also chain–chain entanglements) in apparently good agreement with the experiments of Schneider et al. However, there is some uncertainty about the role of the NPs in the PPA: while Li et al., use a phantom description where the chains can penetrate the NPs (which will naturally yield an entanglement dilution effect as seen in the experiments), there is a second possibility where the NPs are held fixed and impenetrable to the polymer chains, which would yield an increase in the number of entanglements. The latter scenario should clearly be operative if the chains are strongly adsorbed (strongly favorable NP–polymer interactions). However since attractive NP–polymer interactions are necessary to ensure the miscibility of the mixture,23,24 absent the experimental results, it is a priori unclear which of these descriptions is accurate. Clearly, a method that does not involve the PPA would help to unequivocally clarify this point.
A related issue is the role of polymer–NP attractions. Specifically, Smith et al.18 carried out MD simulations and found slower chain dynamics in attractive PNCs, compared to repulsive systems. This has been attributed to heterogeneity in relaxation of chains arising from polymers adsorbed on the NPs.
The main objective of this work is to examine the role of NPs on chain relaxation in nanocomposites for both unentangled and entangled melts. NPs ranging in size from the chain monomer to ∼1.5 times the tube diameter are studied, particularly because it has been conjectured that NP diffusion (and hence presumably dynamics) change dramatically in character when their size goes from well below the entanglement mesh size to well above it.25 We use the Rouse modes of the chains (which are equivalent to the normal modes of short chain melts) to show that the addition of weakly attractive NPs always reduces interchain entanglements, with these effects having different origins for small vs. large NPs. For NPs larger than the entanglement mesh size the dominant effect comes from the fact that some part of the volume is taken up by the NPs (“entanglement dilution”). For small NPs, there is both a reduction of monomer friction and a decrease of entanglement density. As an experimental direction, we propose that probing the self-intermediate scattering function of the polymer might give direct evidence into this entanglement dilution effect. This would directly complement previous NSE measurements and could help to separate out the NP induced entanglement dilution effects from the NP confinement effect on chain motion. The role of the interaction strength between a NP and the polymer is also studied. We present a scaling model explaining some of the observed phenomena.
Rouse description of chain dynamics
The simplest model for polymer chain dynamics in a melt, the Rouse model,26 has three parameters, the monomeric friction (ζ), chain connectivity (modeled through harmonic springs with mean-squared bond length b2) and the degree of polymerization of the chains (N). This model is known to describe the dynamics of short, unentangled melts reasonably well, though deviations appear at monomeric length scales, which are affected by local excluded volume interactions and chain stiffness.27 For long, entangled chains, the Rouse model describes the dynamics at intermediate time/length scales even though the longer scale dynamics are strongly affected by constraints formed by surrounding chains.The Rouse modes, p = 0, 1, 2,…, N − 1, of a chain of length N are defined as:28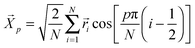 . The p = 0 mode describes the motion of the chain center-of-mass, while the modes with p ≥ 1 describe internal relaxations with a mode number p corresponding to a sub-chain of (N − 1)/p segments. The autocorrelation of the Rouse modes,
. The p = 0 mode describes the motion of the chain center-of-mass, while the modes with p ≥ 1 describe internal relaxations with a mode number p corresponding to a sub-chain of (N − 1)/p segments. The autocorrelation of the Rouse modes, 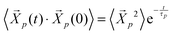 is predicted to decay exponentially and independently for each mode p for an ideal chain with a relaxation time τp where
is predicted to decay exponentially and independently for each mode p for an ideal chain with a relaxation time τp where 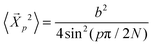 and
and 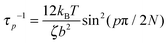 . Simulations of homopolymer melts have found that the Rouse mode autocorrelations are better described by a stretched exponential form:14,16,17
. Simulations of homopolymer melts have found that the Rouse mode autocorrelations are better described by a stretched exponential form:14,16,17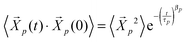 . The effective relaxation times of mode p can be obtained by integrating this relaxation function:14,16,17,29
. The effective relaxation times of mode p can be obtained by integrating this relaxation function:14,16,17,29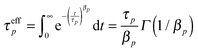 where Γ(x) is the gamma function. The effective monomeric relaxation rate is
where Γ(x) is the gamma function. The effective monomeric relaxation rate is 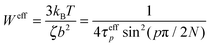 , and for the Rouse model this quantity should be independent of mode number and only depend on the monomer friction, temperature and the statistical segment length b.
, and for the Rouse model this quantity should be independent of mode number and only depend on the monomer friction, temperature and the statistical segment length b.
It is well known that the Rouse modes are not the correct normal modes of long polymer melts in the entangled regime.30 They clearly violate the fundamental principle of mode decoupling in the Rouse model, but provide a useful description for comparing chain relaxation in polymer nanocomposites to homopolymer melts. More pertinently, experimentalists often model chain dynamics in the language of the Rouse model. Understanding experimental results therefore leads us to analyze the simulations in the same manner. In our previous work29 on neat melts of short unentangled chains we found that the stretching exponent that defines the Rouse mode autocorrelation functions, βp, increases from ∼0.8 for large p to ∼1 for the p = 1 mode. The situation for entangled chains is quite different. For long well-entangled chains, the large p modes have a stretching exponent ∼0.8. However, βp decreases with decreasing mode number, reaching a minimum of ∼0.5 for modes that are in the vicinity of the entanglement length Ne. Li et al.16 also found that the minimum in βp occurs for N/p ∼ Ne. Previous work by Padding and Briels16 and by Shaffer14 suggest that this minimum in βp is due to kinetic constraints on the chains.31,32 To summarize, there are two essential results that we shall employ here to understand the role of NPs on chain dynamics. First, for well-entangled chains the minimum value of βp ∼ 0.5 which occurs for N/p ∼ Ne. Second, as one decreases the chain length towards Ne, the minimum value of βp no longer occurs at βp ∼ 0.5 (it becomes progressively higher for shorter chains), and the location of this minimum, i.e., N/p, is no longer at Ne, but rather at some smaller value.
Model
Polymer chains are represented by the Kremer–Grest coarse-grained bead-spring model.33 Non-bonded monomers interact through the Lennard-Jones (LJ) 12-6 potential: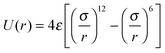 for r ≤ rc, where ε is the LJ energy scale and σ is the monomer diameter. The LJ interaction is cut-off at rc = 2.5σ. The LJ timescale is
for r ≤ rc, where ε is the LJ energy scale and σ is the monomer diameter. The LJ interaction is cut-off at rc = 2.5σ. The LJ timescale is 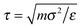 , where m is the mass of a monomer. Two successive segments of a chain are connected by a finitely extensible nonlinear elastic (FENE)33 potential:
, where m is the mass of a monomer. Two successive segments of a chain are connected by a finitely extensible nonlinear elastic (FENE)33 potential: 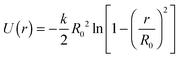 with k = 30ε/σ2 and R0 = 1.5σ.33,34 These parameter values ensure the non-crossability of the chains. In addition, a three-body bending potential of the form Ubend = kθ(1 + cos
with k = 30ε/σ2 and R0 = 1.5σ.33,34 These parameter values ensure the non-crossability of the chains. In addition, a three-body bending potential of the form Ubend = kθ(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) with kθ = 0.75ε, is used to control the stiffness of the chains. The entanglement length Ne for this value of kθ is ≈45.19,35,36 We have considered chains of length N = 10–400 to study the chain relaxation in both unentangled and entangled melts filled with NPs (nanocomposites) as well as without NPs (neat melts).
θ) with kθ = 0.75ε, is used to control the stiffness of the chains. The entanglement length Ne for this value of kθ is ≈45.19,35,36 We have considered chains of length N = 10–400 to study the chain relaxation in both unentangled and entangled melts filled with NPs (nanocomposites) as well as without NPs (neat melts).
The NPs are modeled as bare smooth spheres of diameter, σNP, composed of uniformly distributed monomers of the size of a polymer segment with a mass density, ρNP* = ρNPσ3 = 1. Under these assumptions, the Lennard-Jones interactions between a polymer segment and the NP-segments are integrated over all the NP spheres to obtain the effective interaction:37–40
The Hamaker constant for NP–NP interactions is Ann = 4π2εnnρNP2σ6. Since we use the same LJ potential for the interactions between two polymer-beads and between two beads comprising a NP, εnn = ε, we have Ann = 39.48ε. We employed a cut-off distance rc = σNP so that inter-NP interactions are purely repulsive. In a similar vein, NP-chain monomer interactions are governed by Anp = 24πεnpρNPσ3. While εnp = ε yields Anp = 75.3ε, we find NP agglomeration for this interaction energy and a cut-off distance 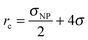 .23 Instead, we use a larger Anp = 100ε for σNP > 3σ and 120ε for σNP = 3σ (and smaller NPs) to avoid NP agglomeration,23 but the NPs are still neutral to the polymer as evident from NP–polymer radial distribution functions, shown below. We have also considered higher interaction strengths Anp in a few cases to study its effect on chain relaxation.
.23 Instead, we use a larger Anp = 100ε for σNP > 3σ and 120ε for σNP = 3σ (and smaller NPs) to avoid NP agglomeration,23 but the NPs are still neutral to the polymer as evident from NP–polymer radial distribution functions, shown below. We have also considered higher interaction strengths Anp in a few cases to study its effect on chain relaxation.
Most of the results presented here are for NPs of diameter σNP = 1–15σ at fixed NP loading 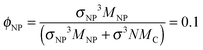 , where N, MNP and MC are the chain length, number of NPs and number of polymer chains, respectively (Table 1). Though we have studied N = 10, 20, 40, 60, 80, 100, 200 and 400 we mainly discuss N = 40, 100 and 400. To test the effect of increasing NP loading, we also simulated a system with ϕNP = 0.6 for N = 400 and σNP = 10. All of the simulations are carried out using the large scale atomic molecular massively parallel simulator (LAMMPS).41 The initial configurations of neat and NP-filled polymer systems are prepared at random at a constant number density while allowing for overlaps among beads. The overlaps are removed by initially using a soft potential between polymer monomers, and then by gradually increasing the strength of the potential. After all overlaps are removed, the LJ interactions between polymer monomers is turned on and the volume of the simulation cell is allowed to adjust at a constant reduced pressure P = 0. Systems of chain length N = 100–400 are equilibrated following the double-bridging procedure.34 The shorter N melts are equilibrated by running isobarically, and then at constant volume until the chains have moved their own size multiple times. After equilibration, the systems are run at constant volume at temperature
, where N, MNP and MC are the chain length, number of NPs and number of polymer chains, respectively (Table 1). Though we have studied N = 10, 20, 40, 60, 80, 100, 200 and 400 we mainly discuss N = 40, 100 and 400. To test the effect of increasing NP loading, we also simulated a system with ϕNP = 0.6 for N = 400 and σNP = 10. All of the simulations are carried out using the large scale atomic molecular massively parallel simulator (LAMMPS).41 The initial configurations of neat and NP-filled polymer systems are prepared at random at a constant number density while allowing for overlaps among beads. The overlaps are removed by initially using a soft potential between polymer monomers, and then by gradually increasing the strength of the potential. After all overlaps are removed, the LJ interactions between polymer monomers is turned on and the volume of the simulation cell is allowed to adjust at a constant reduced pressure P = 0. Systems of chain length N = 100–400 are equilibrated following the double-bridging procedure.34 The shorter N melts are equilibrated by running isobarically, and then at constant volume until the chains have moved their own size multiple times. After equilibration, the systems are run at constant volume at temperature 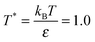 with a Langevin thermostat with damping constant Γ = 0.1τ−1. For longer chain lengths we find that the average pressure P = (0 ± 0.05)ε/σ3, whereas for shorter chains P = (0 ± 0.1)ε/σ3. The number of chains and NPs, and volume of simulation cell of the system studied in the present work along with static properties of chains are listed in Table 1.
with a Langevin thermostat with damping constant Γ = 0.1τ−1. For longer chain lengths we find that the average pressure P = (0 ± 0.05)ε/σ3, whereas for shorter chains P = (0 ± 0.1)ε/σ3. The number of chains and NPs, and volume of simulation cell of the system studied in the present work along with static properties of chains are listed in Table 1.
| NP diameter σNP | Chain length N | Number of chains MC | Number of NP MNP | Volume fraction of NP φNP | Length of simulation box L (σ) | 〈Rg2〉1/2 (σ) |
|---|---|---|---|---|---|---|
| 15 | 10 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188 188 |
5 | 0.10 | 57.11 | 1.58 |
| 15 | 20 | 7594 | 5 | 0.10 | 56.88 | 2.36 |
| 15 | 40 | 3800 | 5 | 0.10 | 56.80 | 3.45 |
| 15 | 60 | 2500 | 5 | 0.10 | 56.52 | 4.27 |
| 15 | 80 | 1880 | 5 | 0.10 | 56.55 | 4.97 |
| 15 | 100 | 1800 | 6 | 0.10 | 60.03 | 5.58 |
| 15 | 200 | 1215 | 8 | 0.10 | 66.30 | 7.95 |
| 15 | 400 | 600 | 8 | 0.10 | 66.02 | 11.26 |
| 10 | 10 | 9000 | 10 | 0.10 | 48.07 | 1.58 |
| 10 | 20 | 4500 | 10 | 0.10 | 47.87 | 2.36 |
| 10 | 40 | 2000 | 10 | 0.11 | 46.04 | 3.44 |
| 10 | 60 | 1500 | 10 | 0.10 | 47.74 | 4.27 |
| 10 | 80 | 2250 | 20 | 0.10 | 60.13 | 4.96 |
| 10 | 100 | 900 | 10 | 0.10 | 47.72 | 5.57 |
| 10 | 150 | 900 | 15 | 0.10 | 54.62 | 6.87 |
| 10 | 200 | 500 | 11 | 0.10 | 49.41 | 7.95 |
| 10 | 400 | 500 | 23 | 0.10 | 62.29 | 11.39 |
| 10 | 400 | 500 | 300 | 0.60 | 75.81 | 11.33 |
| 8 | 10 | 9210 | 20 | 0.10 | 48.51 | 1.58 |
| 8 | 100 | 500 | 11 | 0.10 | 39.29 | 5.72 |
| 8 | 400 | 500 | 45 | 0.10 | 62.39 | 11.37 |
| 5 | 10 | 3000 | 27 | 0.10 | 33.58 | 1.57 |
| 5 | 20 | 2000 | 40 | 0.11 | 36.92 | 2.36 |
| 5 | 40 | 1000 | 40 | 0.11 | 36.84 | 3.44 |
| 5 | 60 | 500 | 27 | 0.10 | 33.36 | 4.27 |
| 5 | 100 | 500 | 45 | 0.10 | 39.54 | 5.58 |
| 5 | 150 | 500 | 67 | 0.10 | 45.21 | 6.88 |
| 5 | 200 | 500 | 90 | 0.10 | 49.77 | 7.97 |
| 5 | 400 | 517 | 200 | 0.11 | 63.49 | 11.57 |
| 3 | 10 | 1000 | 42 | 0.10 | 23.54 | 1.57 |
| 3 | 20 | 500 | 42 | 0.10 | 23.45 | 2.36 |
| 3 | 40 | 1000 | 185 | 0.11 | 37.31 | 3.45 |
| 3 | 100 | 500 | 206 | 0.10 | 39.94 | 5.59 |
| 3 | 200 | 500 | 411 | 0.10 | 50.29 | 7.99 |
| 3 | 400 | 500 | 825 | 0.10 | 63.37 | 11.26 |
| 1 | 10 | 500 | 555 | 0.10 | 18.75 | 1.58 |
| 1 | 20 | 500 | 1111 | 0.10 | 23.56 | 2.38 |
| 1 | 40 | 500 | 2300 | 0.10 | 29.65 | 3.48 |
| 1 | 100 | 500 | 5555 | 0.10 | 40.14 | 5.81 |
| 1 | 200 | 500 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111 111 |
0.10 | 50.56 | 8.31 |
| 1 | 400 | 500 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.12 | 64.07 | 11.94 |
| Neat | 10 | 500 | — | — | 17.95 | 1.58 |
| Neat | 20 | 1000 | — | — | 28.37 | 2.36 |
| Neat | 40 | 500 | — | — | 28.28 | 3.45 |
| Neat | 60 | 500 | — | — | 32.38 | 4.40 |
| Neat | 80 | 500 | — | — | 35.62 | 5.10 |
| Neat | 100 | 500 | — | — | 38.37 | 5.74 |
| Neat | 150 | 500 | — | — | 43.91 | 6.91 |
| Neat | 200 | 500 | — | — | 48.33 | 8.20 |
| Neat | 400 | 500 | — | — | 60.80 | 11.43 |
Results
Role of NP size and chain length
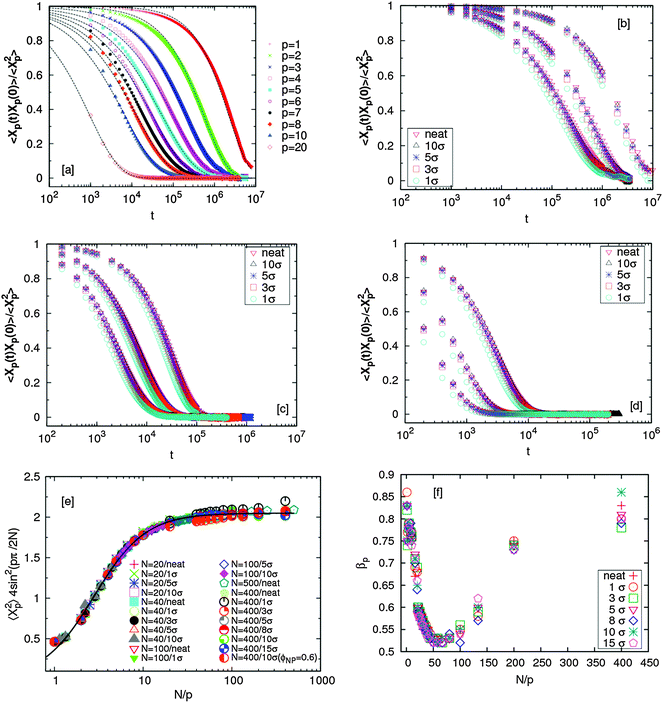
The autocorrelation function of the Rouse modes for chains in the nanocomposites along with neat systems are shown in Fig. 1(a)–(d). The N = 400 chain melts filled with NPs of different sizes were simulated for up to time scales of ∼8 × 106τ. All the autocorrelation functions (except for p = 1 in a few cases) have decayed to zero, implying that the chains are substantially relaxed.The amplitudes of the autocorrelation function of the Rouse modes for different chain lengths fall on a master curve for chain lengths N = 20–400 (Fig. 1(e)). We find that this master curve follows 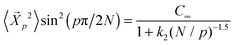 where C∞ = 2.05 and k2 = 4.69. Here we remind the reader that the Rouse model predicts that
where C∞ = 2.05 and k2 = 4.69. Here we remind the reader that the Rouse model predicts that 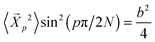 independent of p, and hence the amplitudes depend purely on static chain conformations. Consistent with this fact, the
independent of p, and hence the amplitudes depend purely on static chain conformations. Consistent with this fact, the 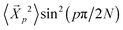 become asymptotically independent of p, and the characteristic ratio C∞ ∼ 2.05 is obtained asymptotically for
become asymptotically independent of p, and the characteristic ratio C∞ ∼ 2.05 is obtained asymptotically for 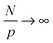 . When
. When 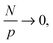 chain bending (stiffness), and excluded volume interactions affect this function. However, the important conclusion here is that chain conformations are essentially unaffected by the NPs at all length scales.17,42
chain bending (stiffness), and excluded volume interactions affect this function. However, the important conclusion here is that chain conformations are essentially unaffected by the NPs at all length scales.17,42
There are also several pieces of information that can be deduced on the role of NPs on chain dynamics. First, we focus on the stretching exponent, βp. Fig. 1(f) shows that a minimum value of βp ∼ 0.5 is attained in all cases, consistent with the fact that the N = 400 chains are long enough to proper delineate the role of the NPs on entanglements at this particle concentration. The location of this minimum changes from ∼50 ± 4 (neat melt) to ∼65 (for NPs with σNP = 1 and 3) and then ∼55 for all larger NPs (5 ≤ σNP ≤ 15) (see Table 2). The results from the larger NPs are consistent with the notion that we have added 10% by volume of the NPs. These NP must result in a reduction in the number of entanglements, and our results suggest that this effect is about a 20% increase in Ne, as quantified in this fashion. More generally, these findings are consistent with our previous conjectures that small NPs act as plasticizers and reduce the entanglement density (and thus increase the entanglement length). For σNP = 1 and 3 we find that Ne is about 40% larger than the value obtained for large NPs.
| NP size | N/p | Uncertainty (+/−) |
|---|---|---|
| Neat melt | 50 | 4 |
| 1σ | 66 | 3 |
| 3σ | 64 | 3 |
| 5σ | 56 | 4 |
| 8σ | 54 | 3 |
| 10σ | 56 | 3 |
| 15σ | 54 | 3 |
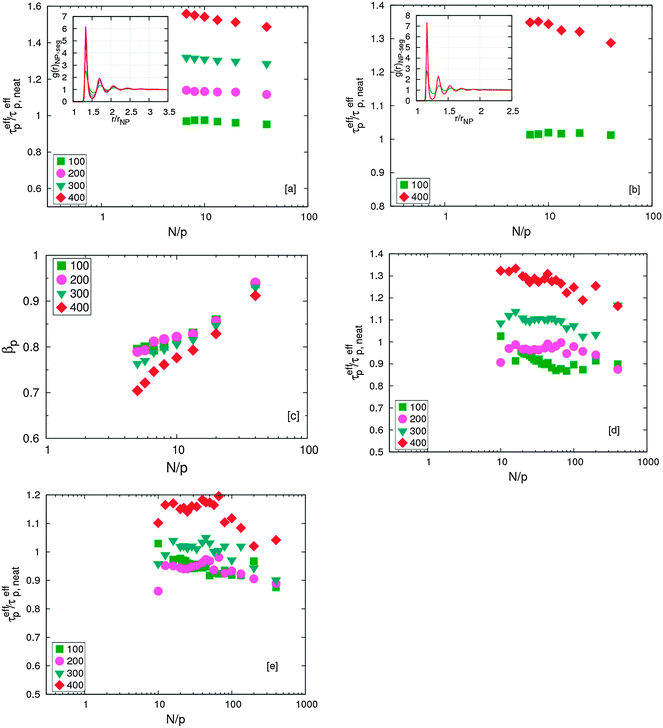
To independently verify these conclusions, we compare the relaxation times of the different modes for chains in the PNCs for three different degrees of polymerization N filled with NPs of different sizes for ϕNP = 0.1 to neat melts without NPs [Fig. 2(a)–(c)]. For the shortest chain length (N = 40), which corresponds to an unentangled melt, the relaxation time ratio of the pth modes are effectively independent of mode number p except for the smallest NP size which show a decrease of this ratio. The smallest NPs are expected to reduce the monomeric friction, i.e., they act as a solvent for the polymer. These effects decrease with increasing particle size, and for the largest NPs the monomeric relaxation time ratio is effectively equal to unity. These findings for the shortest chains are in good agreement with the experiments of Schneider et al.11
 | ||
| Fig. 2 Normalized effective relaxation times of p-th mode for chains in nanocomposites for different NP sizes at ϕNP = 0.1: (a) N = 40; (b) N = 100; (c) N = 400. (d) Effect of NP loading for N = 400, σNP = 10σ (Closed triangles correspond to σNP = 10σ in N = 500 at similar NP loading from ref. 17). (e) Corresponding plot for the stretching exponent βp. | ||
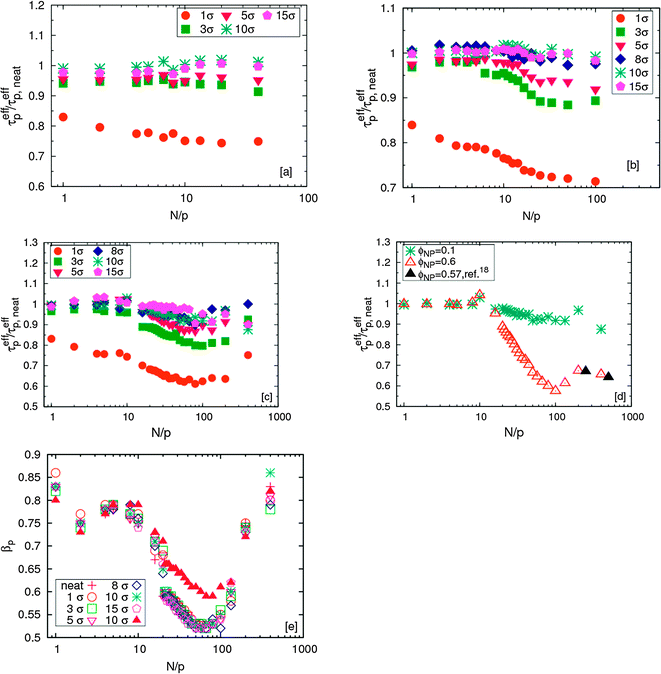
The trends for the long chains are richer. For small N/p, we see a plateau for 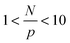 that depends on NP size. We believe that this plateau is related to the effect of NPs on monomer friction (Fig. 2(c)). There also appears to be a monotonic decrease of the relaxation time ratio for larger N/p, and finally a plateau for
that depends on NP size. We believe that this plateau is related to the effect of NPs on monomer friction (Fig. 2(c)). There also appears to be a monotonic decrease of the relaxation time ratio for larger N/p, and finally a plateau for 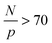 .19 We assume that the relaxation time for a chain follows the crossover ansatz that smoothly bridges between the Rouse model and reptation dynamics:
.19 We assume that the relaxation time for a chain follows the crossover ansatz that smoothly bridges between the Rouse model and reptation dynamics: 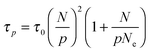 , where τ0 is the monomer relaxation time. In this ansatz, the large p modes directly yield information on the monomer friction and how it is modified by the addition of the NPs. In contrast, in the limit of p = 1, the plateau is directly proportional to the ratio of τ0/Ne in the PNC compared to that in the pure melt. Our results for the longest chains clearly show that the monomeric relaxation times are decreased by (∼30%) by the addition of σNP = σ NPs. However, this effect disappears for larger NPs, i.e., 3σ and larger. This is in good agreement with our previous results.19 More interesting are the findings that are apparent in the low p modes: for small NPs, which act as a diluent, there is an additional speedup, which we attribute to a reduction in entanglements. Our relaxation time ansatz suggests that
, where τ0 is the monomer relaxation time. In this ansatz, the large p modes directly yield information on the monomer friction and how it is modified by the addition of the NPs. In contrast, in the limit of p = 1, the plateau is directly proportional to the ratio of τ0/Ne in the PNC compared to that in the pure melt. Our results for the longest chains clearly show that the monomeric relaxation times are decreased by (∼30%) by the addition of σNP = σ NPs. However, this effect disappears for larger NPs, i.e., 3σ and larger. This is in good agreement with our previous results.19 More interesting are the findings that are apparent in the low p modes: for small NPs, which act as a diluent, there is an additional speedup, which we attribute to a reduction in entanglements. Our relaxation time ansatz suggests that 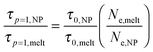 , from which it follows that Ne,melt/Ne,NP ∼ 0.9 in this regime for N = 400, which is in very good agreement with the results obtained from the stretching exponents discussed above.19 Our results also show that the entanglement length recovers its melt value with increasing NP size, but that even for σNP = 15σ, Ne,NP is ∼10% larger than the pure melt, Fig. 2(c) and (e).
, from which it follows that Ne,melt/Ne,NP ∼ 0.9 in this regime for N = 400, which is in very good agreement with the results obtained from the stretching exponents discussed above.19 Our results also show that the entanglement length recovers its melt value with increasing NP size, but that even for σNP = 15σ, Ne,NP is ∼10% larger than the pure melt, Fig. 2(c) and (e).
These results are also in reasonable agreement with our previous work, where a primitive path analysis (PPA)19 with penetrable NPs, suggested that the presence of NPs smaller than the tube diameter increased the entanglement molecular weight even at low concentrations. These results are also consistent with the effect of NP size on zero-shear viscosity where smaller NPs act as plasticizers and reduce the viscosity. These effects disappear once the particle size becomes comparable to the tube diameter, where the additional confinement effects of the NPs on chain motion results in an increased viscosity relative to the pure melt (see Discussion for more on this topic).
The monomeric relaxation rates, Weff, of different chain lengths melts with the smallest and the largest NP size studied are compared with that of neat melts in Fig. 3. It is evident that small NPs plasticize the melts and hence the relaxation rates are always higher than that of the neat melt. However, the largest NP do not affect the relaxation of chains and Weff of the neat and filled melts overlap for all modes to within the uncertainties in the simulations.15,43
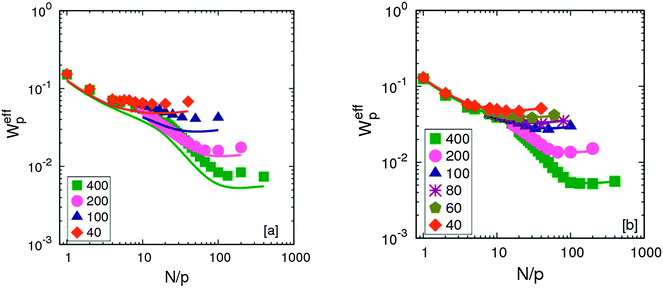 | ||
| Fig. 3 Monomeric relaxation rates for different chain lengths at ϕNP = 0.1 for (a) σNP = 1σ and (b) σNP = 15σ. Solid lines correspond to neat melts. | ||
Effect of NP loading
To show the effect of NP loading we studied chains of length N = 400 filled with NPs of size σNP = 10σ at a higher ϕNP = 0.6. The relaxation times of the longest modes of the chains at this higher NP loading are decreased relative to those at ϕNP = 0.1 (Fig. 2(d)) and are akin to the values for σNP = 1σ (Fig. 2(c)). In contrast, segmental level dynamics seems to be not affected much, as evidenced by the fact that the ratio of effective relaxation times tends to unity when N/p → 1. Based on our conjecture for the relaxation times, we conclude that the entanglement length is increased by 5–10% for low loadings, but that we see a near doubling of the entanglement length for large loadings. Support for this conclusion follows from the stretching exponent βp. As Fig. 2(e) shows, on loading, the curve shifts up as seen previously for simulations of neat melts with increasing N. Since the minimum value of the exponent ∼0.6, by comparison to our data for pure melts, these data imply that the entanglement chain length must have approximately doubled to cause such a vertical shift in the exponents (see last paragraph of Introduction). This result is consistent with one aspect of Li et al.,17 who suggested that chain entanglements are reduced when the NPs are treated as phantom entities in the PPA. Our results suggest that, when one considers the internal relaxations of the chains alone, then, it is appropriate to treat the NPs as penetrable objects in a PPA analysis especially in this limit where the chains only interact weakly with the NPs. The additional confining role of NPs on chain dynamics only seems to affect the collective dynamics as captured in the NSE experiments, and maybe in the macroscopic viscosity measurements.Role of NP–polymer interactions
Finally, we note that the interaction strength between the NPs and the polymer plays an important role in modifying chain dynamics.18 As the interaction strength between the polymer and NP increases, the polymer begins to adsorb on the NP. This adsorbed, effectively “frozen” layer of polymer segments effectively slows down chain relaxation. It is also notable that this slow dynamics is a strong function of the interfacial layer of adsorbed polymers. This is evident from Fig. 4 – the relaxation time of chains increases by 50–60% in the case of σNP = 5σ whereas it is only 30–40% larger in the presence of σNP = 10σ particles for the same volume fraction. The interfacial area available for adsorption of polymer in case of σNP = 5σ particles is higher than σNP = 10σ NPs. The lowering of βp as Anp increases, indicate that the relaxation of chains are slowed down and become more heterogeneous. These results are consistent with past findings.18Discussion
There are a few salient features that are worthy of further discussion. First, in Fig. 2(d), we, show that results from the previous work of Li et al.17 are in good agreement with our Rouse mode results at a loading of ϕNP = 0.6. To translate the volume fraction of Li et al. (defined as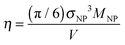 ) into our definition, we use our formula
) into our definition, we use our formula 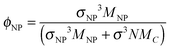 ; the Li et al. data at η = 0.31 thus corresponds to ϕNP = 0.57.
; the Li et al. data at η = 0.31 thus corresponds to ϕNP = 0.57.
A second point that emerges is that the NSE experiments, though relevant to understanding the composite effect of NPs on polymer dynamics, are not sensitive to exclusively probe inter-chain entanglement effects in the presence of NPs. Our results clearly show (as do the previous work of Li et al.) that the Rouse modes characterizing the internal dynamics of single chains are extremely sensitive to chain–chain entanglements without any interference from the confining effects of the NPs. Since the motion of chains are best characterized in the framework of the van Hove (or the self-intermediate scattering) function, we propose that experiments that focus on other methods for delineating this quantity might shed new light on the relaxations of these systems.
It is also interesting to focus on the novelty of the current work relative to the published literature. Li et al.17 for example considered a very similar situation, but they only considered a single NP size, but then varied the NP loading. Our work, in contrast, allows for the polymer length, NP size and NP loading to vary, thus providing a much more complete picture of the dynamics of these filled systems. Smith et al.18 studied the role of attractions on chains dynamics. Our previous work in this area looked at the effect of NP on the viscosity of polymer melts,19 and also the Rouse modes of neat melts29 – the current work looks at the Rouse modes of chains in the presence of NPs.
Finally, we focus on understanding the consequence of our results on the viscosity of nanocomposites filled with NPs. In this work we split this effect into NP contributions to the relaxation time and to modulus. The product of these two effects yields the role of NP on viscosity. The viscosity of the nanocomposites can be written as an integral of the stress relaxation function 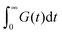 which can be split into short-time modes with wavelength smaller than the particle size:
which can be split into short-time modes with wavelength smaller than the particle size: 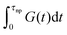 and long-time modes
and long-time modes 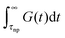 . The effective viscosity of a neat melt of polymers of size equal to the particle size
. The effective viscosity of a neat melt of polymers of size equal to the particle size 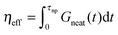 is hardened by particles smaller than tube diameter σNP < a with volume fraction ϕNP as described by Einstein equation
is hardened by particles smaller than tube diameter σNP < a with volume fraction ϕNP as described by Einstein equation 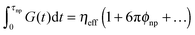 . This hardening occurs due to an increase of modulus of PNC without a change of relaxation rates of short time modes. For long-time modes NPs act as diluents and their contribution can be estimated as
. This hardening occurs due to an increase of modulus of PNC without a change of relaxation rates of short time modes. For long-time modes NPs act as diluents and their contribution can be estimated as 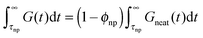 where
where 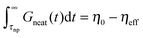 with bulk viscosity of neat melt η0. Thus, the total viscosity of the nanocomposites is η = η0 + ϕnp[(6π + 1)ηeff − η0] that can be either larger or smaller than viscosity η0 of the neat melt depending on the relative value of (6π + 1)ηeff and η0 (or relative value of particle and polymer size). This conclusion is in good agreement with our previous simulation results,19,29 which showed that the critical variable for determining the effect of NP on viscosity was the NP size relative to a characteristic chain size. For short, unentangled chains this corresponds to the radius of gyration of the chains, while for longer chains it is the entanglement mesh size.
with bulk viscosity of neat melt η0. Thus, the total viscosity of the nanocomposites is η = η0 + ϕnp[(6π + 1)ηeff − η0] that can be either larger or smaller than viscosity η0 of the neat melt depending on the relative value of (6π + 1)ηeff and η0 (or relative value of particle and polymer size). This conclusion is in good agreement with our previous simulation results,19,29 which showed that the critical variable for determining the effect of NP on viscosity was the NP size relative to a characteristic chain size. For short, unentangled chains this corresponds to the radius of gyration of the chains, while for longer chains it is the entanglement mesh size.
Conclusions
The Rouse mode results on effectively athermal nanocomposites show that, in the case of short (unentangled) chains, the NPs only affect the monomer friction, and that too only for NPs that are comparable in size to a solvent molecule or a monomer. The NPs do not affect the mode structure of the chains or the monomeric relaxation rates – conclusions that are consistent with the recent experimental findings of Richter and his coworkers.11 The behavior of long, entangled chains (with ∼10 entanglement strands per chain) in the presence of NPs is much more interesting. As in the case of the short chains, we find a renormalization of the monomer friction on the addition of small NPs, but no such modification for NPs larger than half the entanglement mesh size. The modification of relaxation times show a mode dependence that only disappears for chain segments which are approximately twice as long as the entanglement strands. From this large sub-chain behavior we conjecture that the entanglement length has a strong dependence on the NP size at a fixed particle loading (10%) – for the case of small NPs, we see an effect akin to that observed when solvent molecules are added to a polymer, and the entanglement length increases by ∼20%. This effect is NP size dependent and decreases to a ∼10% effect for NPs whose size is roughly half the bulk tube diameter or larger. These conclusions are strongly dependent on NP loading, and for large enough loading for the one size studied (σNP = 10σ) we see no effect on monomer friction but a significant reduction in chain entanglements. We thus also conclude that for weakly attractive NPs only a weak reduction in the tube diameter, and any slowing down that occurs is because the NPs act as confinement points (or barriers) to chain motion. We propose that the NSE experiments, which measure the collective structure factor, convolute these two opposing effects. We therefore suggest that methods that probe the self-intermediate scattering function of the chains might be able to more critically probe the NP-driven reduction of entanglements that is seen in the different simulations that have been performed for the case of weakly interacting mixtures.Acknowledgements
We thank Dieter Richter for detailed comments and discussion. JTK and SKK acknowledge financial support from the National Science Foundation (DMR-1006514). MR would like to acknowledge financial support from the National Science Foundation under grants DMR-1309892, DMR-1436201, DMR-1121107, and DMR-1122483, the National Institutes of Health under 1-P01-HL108808-01A1 and the Cystic Fibrosis Foundation. This research used resources obtained through the Advanced Scientific Computing Research (ASCR) Leadership Computing Challenge (ALCC) at the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the United States Department of Energy under Contract No. DE-AC02-05CH11231. This work was performed, in part, at the Center for Integrated Nanotechnologies, a US Department of Energy, Office of Basic Energy Sciences user facility. Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the US Department of Energy's National Nuclear Security Administration under contract DE-AC04-94AL85000.References
- D. C. Edwards, J. Mater. Sci., 1990, 25(10), 4175–4185 CrossRef CAS.
- K. Yurekli, R. Krishnamoorti, M. F. Tse, K. O. Mcelrath, A. H. Tsou and H. C. Wang, J. Polym. Sci., Part B: Polym. Phys., 2001, 39(2), 256–275 CrossRef CAS.
- A. J. Crosby and J. Y. Lee, Polym. Rev., 2007, 47(2), 217–229 CrossRef CAS PubMed.
- H. M. C. D. Azeredo, Food Res. Int., 2009, 42(9), 1240–1253 CrossRef PubMed.
- A. Sorrentino, G. Gorrasi and V. Vittoria, Trends Food Sci. Technol., 2007, 18(2), 84–95 CrossRef CAS PubMed.
- W. U. Huynh, J. J. Dittmer, W. C. Libby, G. L. Whiting and A. P. Alivisatos, Adv. Funct. Mater., 2003, 13(1), 73–79 CrossRef CAS PubMed.
- D. Y. Godovsky, Device Applications of Polymer-Nanocomposites, in Biopolymers PVA Hydrogels, Anionic Polymerisation Nanocomposites, Springer, Berlin, Heidelberg, 2000, vol. 153, pp. 163–205 Search PubMed.
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295(5564), 2425–2427 CrossRef CAS PubMed.
- M. Vladkov and J. L. Barrat, Macromol. Theory Simul., 2006, 15(3), 252–262 CrossRef CAS PubMed.
- G. J. Schneider, K. Nusser, L. Willner, P. Falus and D. Richter, Macromolecules, 2011, 44(15), 5857–5860 CrossRef CAS.
- G. J. Schneider, K. Nusser, S. Neueder, M. Brodeck, L. Willner, B. Farago, O. Holderer, W. J. Briels and D. Richter, Soft Matter, 2013, 9(16), 4336–4348 RSC.
- C. Bennemann, J. Baschnagel, W. Paul and K. Binder, Comput. Theor. Polym. Sci., 1999, 9(3–4), 217–226 CrossRef CAS.
- K. Nusser, G. J. Schneider and D. Richter, Soft Matter, 2011, 7(18), 7988–7991 RSC.
- J. S. Shaffer, J. Chem. Phys., 1995, 103(2), 761–772 CrossRef CAS PubMed.
- R. Perez-Aparicio, F. Alvarez, A. Arbe, L. Willner, D. Richter, P. Falus and J. Colmenero, Macromolecules, 2011, 44(8), 3129–3139 CrossRef CAS.
- J. T. Padding and W. J. Briels, J. Chem. Phys., 2002, 117(2), 925–943 CrossRef CAS PubMed.
- Y. Li, M. Kroger and W. K. Liu, Phys. Rev. Lett., 2012, 109(11), 118001 CrossRef.
- G. D. Smith, D. Bedrov, L. W. Li and O. Byutner, J. Chem. Phys., 2002, 117(20), 9478–9489 CrossRef CAS PubMed.
- J. T. Kalathi, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2012, 109(19), 198301 CrossRef.
- G. K. Batchelor, J. Fluid Mech., 1977, 83, 97–117 CrossRef.
- J. T. Kalathi, U. Yamamoto, K. S. Schweizer, G. S. Grest and S. K. Kumar, Phys. Rev. Lett., 2014, 112(10), 108301 CrossRef.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2015, 48(3), 847–862 CrossRef CAS PubMed.
- D. Meng, S. K. Kumar, S. Cheng and G. S. Grest, Soft Matter, 2013, 9(22), 5417–5427 RSC.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Soft Matter, 2012, 8(18), 5002–5010 RSC.
- L. H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2011, 44(19), 7853–7863 CrossRef CAS PubMed.
- P. E. Rouse, J. Chem. Phys., 1953, 21(7), 1272–1280 CrossRef CAS PubMed.
- M. Mondello, G. S. Grest, E. B. Webb and P. Peczak, J. Chem. Phys., 1998, 109(2), 798–805 CrossRef CAS PubMed.
- A. Kopf, B. Dunweg and W. Paul, J. Chem. Phys., 1997, 107(17), 6945–6955 CrossRef CAS PubMed.
- J. T. Kalathi, S. K. Kumar, M. Rubinstein and G. S. Grest, Macromolecules, 2014, 47(19), 6925–6931 CrossRef CAS PubMed.
- A. E. Likhtman, in Polymer Science: A Comprehensive Review, ed. A. R. Khokhlov and F. Kremer, Elsevier, 2012, vol. 1 Search PubMed.
- L. Larini, A. Ottochian, C. De Michele and D. Leporini, Nat. Phys., 2008, 4(1), 42–45 CrossRef CAS.
- A. Ottochian, C. De Michele and D. Leporini, Philos. Mag., 2008, 88(33–35), 4057–4062 CrossRef CAS PubMed.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92(8), 5057–5086 CrossRef CAS PubMed.
- R. Auhl, R. Everaers, G. S. Grest, K. Kremer and S. J. Plimpton, J. Chem. Phys., 2003, 119(24), 12718–12728 CrossRef CAS PubMed.
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303(5659), 823–826 CrossRef CAS PubMed.
- S. K. Sukumaran, G. S. Grest, K. Kremer and R. Everaers, J. Polym. Sci., Part B: Polym. Phys., 2005, 43(8), 917–933 CrossRef CAS PubMed.
- G. S. Grest, Q. Wang, P. J. in 't Veld and D. J. Keffer, J. Chem. Phys., 2011, 134(14), 144902 CrossRef PubMed.
- P. J. in 't Veld, S. J. Plimpton and G. S. Grest, Comput. Phys. Commun., 2008, 179(5), 320–329 CrossRef PubMed.
- P. J. in 't Veld, M. A. Horsch, J. B. Lechman and G. S. Grest, J. Chem. Phys., 2008, 129(16), 164504 CrossRef PubMed.
- R. Everaers and M. R. Ejtehadi, Phys. Rev. E, 2003, 67(4), 041710 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- M. K. Crawford, R. J. Smalley, G. Cohen, B. Hogan, B. Wood, S. K. Kumar, Y. B. Melnichenko, L. He, W. Guise and B. Hammouda, Phys. Rev. Lett., 2013, 110(19), 196001 CrossRef CAS.
- M. Brodeck, F. Alvarez, A. Arbe, F. Juranyi, T. Unruh, O. Holderer, J. Colmenero and D. Richter, J. Chem. Phys., 2009, 130(9), 094908 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |