Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of aggregate formation on the viscosity of protein solutions†
Lucrèce
Nicoud
a,
Marco
Lattuada
b,
Andrew
Yates
c and
Massimo
Morbidelli‡
*a
aDepartment of Chemistry and Applied Biosciences, ETH Zurich, Switzerland
bAdolphe Merkle Institute, University of Fribourg, Chemin des Verdiers 4, CH-1700 Fribourg, Switzerland
cUCB Pharma, Braine l'Alleud, Belgium
First published on 10th June 2015
Abstract
Gaining knowledge on the stability and viscosity of concentrated therapeutic protein solutions is of great relevance to the pharmaceutical industry. In this work, we borrow key concepts from colloid science to rationalize the impact of aggregate formation on the changes in viscosity of a concentrated monoclonal antibody solution. In particular, we monitor the kinetics of aggregate growth under thermal stress by static and dynamic light scattering, and we follow the rise in solution viscosity by measuring the diffusion coefficient of tracer nanoparticles with dynamic light scattering. Moreover, we characterize aggregate morphology in the frame of the fractal geometry. We show that the curves of the increase in viscosity with time monitored at three different protein concentrations collapse on one single master curve when the reaction profiles are normalized based on an effective volume fraction occupied by the aggregates, which depends on the aggregate size, concentration and morphology. Importantly, we find that the viscosity of an aggregate sample is lower than the viscosity of a monomeric sample of a similar occupied volume fraction due to the polydispersity of the aggregate distribution.
Introduction
Improving our understanding of protein stability in crowded environments is of primary importance in various research areas. From the study of cellular proteins in living organisms to the processing of therapeutic proteins in the pharmaceutical industry, most of the protein solutions finding relevant applications in biology and biopharmacy are indeed encountered in highly concentrated conditions. In this work, we focus on the stability of monoclonal antibodies (mAbs), which represent promising therapeutics in the treatment of a number of human diseases and now occupy the largest part of the biopharmaceutical market.1 MAb-based drugs generally require administration at high protein concentrations, in the order of 80 g L−1 or more. However, guaranteeing drug stability at such high concentration is challenging due to the strong aggregation propensity of proteins.2 As the presence of protein aggregates may severely compromise drug efficacy and drug safety, there is a crucial need to gain fundamental knowledge on the mechanism of protein aggregation at high concentration.3,4Another difficulty arising in concentrated protein formulations is the increase in solution viscosity, which can heavily complicate product handling and delivery by injection.3 The viscosity of protein solutions has been shown to be highly sensitive to the protein amino acid sequence and to the buffer composition,5–8 but also to the presence of protein aggregates.9–11 Since excessively high solution viscosities would hinder the commercialization of potential drug candidates, it is paramount to characterize the solution viscosity during the early stages of product formulation. Due to the limited amount of material available during drug development, effort is put towards the design of new methods for measuring solution viscosity at the microliter scale.12,13 Moreover, the analysis of traditional rheological data of protein solutions is a rather delicate task and requires some caution due to the complex behavior of proteins under shear.14,15 In this work, we follow the methodology proposed by He et al.,13 which consists of measuring the diffusion coefficient of tracer nanoparticles immersed in concentrated protein solutions with dynamic light scattering. While the experiments of the initial work were carried out under native conditions, we extend the technique to denaturing conditions with a view to quantifying the impact of aggregation on the solution viscosity. This method, which offers the advantages of being relatively time and material saving, allows one to measure the increase in solution viscosity in situ without shearing the sample, which may potentially induce rearrangement or breakage of loose aggregates.
Even though the irreversible aggregation and the reversible self-association of protein molecules have already been reported to increase the solution viscosity,9–11 a theoretical framework allowing the prediction of the impact of aggregate concentration, size and morphology on solution viscosity is still lacking. Herein, we propose to borrow key concepts from colloid science to rationalize the impact of the formation of irreversible protein aggregates on the increase of solution viscosity. Indeed, even though proteins in aqueous media are molecular mixtures, and thus represent true solutions, they can be treated in many respects as colloidal dispersions. As a matter of fact, protein molecules lie in the colloidal range: they are sufficiently small to be subjected to Brownian motion and sufficiently large compared to solvent molecules so that the solvent can be regarded as a continuum.
In this context, we study the heat-induced aggregation of a model monoclonal antibody, and we correlate the increase in the solution viscosity with the increase in the aggregate occupied volume fraction. This type of accelerated studies, although performed under thermal stress, can provide fundamental insights into the aggregation process, which may prove to be relevant under storage conditions too. The key notion of occupied volume fraction, which has already been proven to be useful to study the rheology of aggregating colloidal dispersions,16,17 is applied here to a protein system. Since the occupied volume fraction depends not only on the aggregate size and concentration, but also on the aggregate structure and compactness, we characterize the aggregate morphology experimentally by using light scattering techniques. We quantify aggregate morphology in the frame of the fractal morphology, which allows one to quantify aggregate compactness through the definition of one measurable parameter, the fractal dimension. The concept of fractal scaling has been proven to provide a simple and valuable description of irregular aggregates for a large variety of colloidal systems,18–22 and for proteins in particular.23–27
Materials and methods
Antibody sample preparation
The monoclonal antibody used for this study was a glycosylated IgG1 of industrial origin, with theoretical isoelectric point lying between 8 and 9.2.The antibody solution was stored at a protein concentration of 70 g L−1 in a buffer solution at pH 6.5 containing 20 mM histidine and 250 mM sorbitol. Prior to aggregation experiments, the antibody stock solution was dialyzed against a 20 mM histidine buffer at pH 6.5 by using dialysis cassettes with a cut-off molecular weight of 7 kDa (Slide A Lyzers cassettes, Thermo Fisher Scientific) in order to remove sorbitol. The dialysis was performed at 4 °C under gentle stirring for at least 18 hours. The dialysis buffer was renewed two times (once after 2 h and once after 4 h of dialysis) and the volume of the dialysis buffer was five hundred-fold larger than the volume of the sample to be dialyzed. The protein concentration of the stock solution after dialysis was checked by UV absorption at 280 nm.
All the samples for the aggregation studies (performed in the protein concentration range 20–60 g L−1) were prepared by diluting the dialyzed stock solution to the targeted concentration with a 20 mM histidine buffer at pH 6.5. For the viscosity measurements of the monomeric protein solution at concentrations larger than 60 g L−1, the protein solution was concentrated by centrifugal ultrafiltration using a 30 kDa cut-off molecular weight membrane (Vivaspin 500, VS0121, Sartorius).
All the chemicals required for buffer preparation of the highest purity available were purchased from Sigma. The buffer solutions were filtered through a 0.1 μm cut-off membrane filter (Millipore).
Dynamic light scattering
Isothermal aggregation kinetic measurements were performed under thermal stress at the temperature of 70 °C, which is approximately the melting temperature of the mAb, as revealed by circular dichroism experiments carried out in a previous study.23 The increase in the average aggregate hydrodynamic radius with time was monitored by dynamic light scattering (DLS) measurements performed both in batch mode by using a Zetasizer Nano (Malvern), and after elution in a size exclusion chromatography column by using a Dawn-Heleos II device equipped with a DLS module (Wyatt, Santa Barbara, CA, USA) and assembled on an Agilent series HPLC unit (Santa Clara, CA, USA).It was shown in a previous study that mAb-1 aggregates are irreversible upon dilution and are not significantly impacted by the cooling required for off-line analysis at room temperature.23
The points and error bars reported in the plots correspond to the average and standard deviation of measurements performed on at least two independent aggregate samples.
The aggregate size was estimated from the extrapolation to zero protein concentration by performing successive dilutions, as further explained in the main text.
DLS measurements were performed at the fixed angle of θ = 173° by using a laser with wavelength λ = 633 nm. Briefly, the fitting of the autocorrelation function with the method of cumulants allows the determination of the average diffusion coefficient 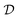 , which is connected to the average hydrodynamic radius of the aggregates 〈Rh〉 by the Stokes–Einstein equation:
, which is connected to the average hydrodynamic radius of the aggregates 〈Rh〉 by the Stokes–Einstein equation:
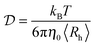 | (1) |
The mean aggregate size provided by the methods of cumulants is the so-called z-average. It is mathematically stable and relatively insensitive to noise, making it the preferred parameter to estimate the aggregate size from DLS measurements. Therefore, unless otherwise stated, the reported values of the hydrodynamic radius correspond to the z-average. Nevertheless, the volume and the number average size, which are computed from the volume and number aggregate distributions, respectively, were also considered with a view to assessing the impact of the selected averaging method on the estimated mean aggregate size (see Discussion section).
It was verified by this technique that the non-heated antibody does not associate in the range of concentrations investigated in this study (see Fig. S2 in the ESI†).
Fractal dimension measurement
The aggregate morphology was investigated by static and dynamic light scattering measurements. The aggregate fractal dimension df and the scaling prefactor kf were estimated from the correlation between the aggregate weight-average molecular weight 〈MW〉 and the aggregate average hydrodynamic radius 〈Rh〉 according to: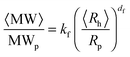 | (2) |
Aggregate samples of different sizes were produced by heating protein samples in a block heater (Rotilabo H 250, Roth, Karlsruhe) for various incubation times. The samples were analyzed through a size exclusion chromatography column equipped with an inline multi-angle light scattering detector, as described in the previous section. The aggregate weight-average molecular weight and the aggregate average hydrodynamic radius were determined from the static and dynamic light scattering results, respectively, by using the Astra software (Wyatt, Santa Barbara, CA, USA), as further detailed in the ESI.† The log linearization of eqn (2) for aggregates of different sizes allows the determination of the scaling parameters df and kf.
It was verified that these measurements give results that are consistent with the static light scattering data reported in our previous work, where it was shown that df = 1.85 at the protein concentration of 1 g L−1 from the dependence of the structure factor on the q-vector.23
Tracer nanoparticle synthesis
Poly(methyl methacrylate) (PMMA) based nanoparticles were synthetized through bulk emulsion polymerization in a three-neck round-bottom flask equipped with a reflux condenser and a thermocouple. Stripped deionized water was introduced in the reactor and heated to 70 °C with an oil bath placed on a hot-plate stirrer. The reactor atmosphere was kept inert by flushing the reaction set-up with nitrogen. The surfactant (hexadecyltrimethylammonium bromide, abbreviated as CTAB) and the monomers (methyl methacrylate and 2-methacryloyloxyethyltrimethylamonium, abbreviated as MMA and META, respectively) were then added in the reactor. Finally, the initiator (2,2′-(diazene-1,2-diyl) bis(2-methylpropanimidamide) dihydrochloride, abbreviated as INI) was injected to initiate the polymerization. The reaction volume was 100 mL, with the following mass concentrations: 5% wMMA/wTOT, 0.06% wMETA/wTOT, 0.0125% wCTAB/wMMA, and 0.02% wINI/wMMA. The reaction time was 2 h.The synthesized nanoparticles had a final hydrodynamic radius Rt = 99 nm and a zeta potential of 49.7 ± 0.9 mV, as measured using a Zetasizer Nano (Malvern). Positively charged nanoparticles were produced with the purpose of reducing attractive interactions with the antibody molecules which carry a net positive charge, as evidenced by the positive value of the zeta potential (5.7 ± 3.5 mV).23
Viscosity measurement
The viscosity of protein solutions was estimated by measuring the diffusion coefficient of the tracer nanoparticles with dynamic light scattering, both in the solvent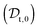 and in the concentrated protein solution
and in the concentrated protein solution 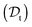 . According to the Stokes–Einstein equation applied to the tracer particle of hydrodynamic radius Rt, both in solvent and in the protein solution:
. According to the Stokes–Einstein equation applied to the tracer particle of hydrodynamic radius Rt, both in solvent and in the protein solution: | (3) |
It follows that the solution viscosity η can be estimated according to:
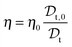 | (4) |
This technique has been shown previously to provide similar values than traditional measurements performed using a rheometer provided that the tracer particles are sufficiently large as compared to the surrounding protein molecules, and that the tracer particles are stable in the protein solution.13,29
In this study, this method was used to measure both the viscosity of monomeric protein solutions at 25 °C, and to evaluate the increase in solution viscosity due to aggregate formation at the elevated temperature of 70 °C. The aggregation experiments were performed in situ in a quartz cuvette covered with a custom made plastic cap to limit sample evaporation. The total sample volume was 65 μL and the volume fraction of tracer nanoparticles was 1.4 × 10−3. The dilution of the protein by addition of the nanoparticles was accounted for during sample preparation. The points and error bars reported in the plots correspond to the average and standard deviation of measurements performed on at least two independent samples.
In order to prove the applicability of this technique to the system under investigation, we performed rheological measurements with monomeric protein solutions under stable conditions. It can be seen in Fig. S3 of the ESI,† that viscosity results obtained from the measure of the diffusion coefficient of tracer nanoparticles by DLS, and viscosity values obtained from rheometry are in very close agreement.
The main limitation of the DLS technique is related to the interactions between the tracer nanoparticles and the protein molecules, which can potentially lead to nanoparticle aggregation.29 We proved experimentally that the tracer nanoparticles are stable under the conditions of interest, and that they are not affecting the kinetics of mAb aggregation by successively verifying that: (i) the elevated temperature required to induce mAb aggregation does not destabilize the nanoparticles (Fig. S4(a), ESI†); (ii) the nanoparticles are stable in the presence of mAb molecules under native conditions (Fig. S4(a), ESI†); (iii) the size of the nanoparticles is unchanged after mAb aggregation has been induced at high temperature (Fig. S4(b), ESI†); (iv) the measured viscosity is independent of the concentration of tracer particles (Fig. S5, ESI†). These data are reported in the ESI.†
Moreover, the accurate measurement of the solution viscosity from the diffusion coefficient of tracer nanoparticles relies on the assumption that the nanoparticles do not interact via long-range electrostatic interactions with the protein molecules.30 The validity of this assumption can be assessed from the comparison between the Debye length, which quantifies the thickness of the diffusive layer, and the size of the nanoparticles. To do so, the Debye length can be computed from the inverse of the Debye parameter, which is defined as:
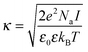 | (5) |
In a buffer of 20 mM histidine, it is computed that the Debye length is equal to 3.8 and 4.1 nm, at the temperatures of 25 and 70 °C, respectively. The Debye length is thus much smaller than the tracer particle size, implying that the electrostatic inter-particle interactions are short-ranged. Therefore, it can reasonably be assumed that the viscosity measurements are not affected by the electrostatic repulsion between the nanoparticles and the protein molecules.
Results
Aggregation kinetics experiments were performed at neutral pH under thermal stress (pH 6.5, 70 °C) at three mAb concentrations (20, 40, and 60 g L−1). First, we report the results of the increase in solution viscosity with time. Then, we correlate the observed increase in viscosity with the increase in aggregate size at each protein concentration. Finally, we show that the increase in solution viscosity can be rationalized by using the concept of occupied volume fraction, which accounts for protein concentration, aggregate size and aggregate fractal dimension.Kinetics of aggregation
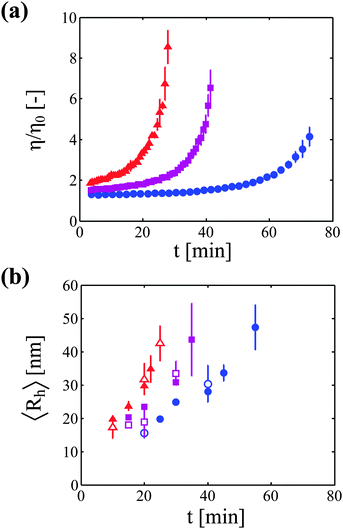
The increase in solution viscosity with time was estimated from the diffusion coefficient of tracer nanoparticles measured by DLS in situ. As explained in the Materials and methods section, preliminary experiments have been performed in order to prove the validity of this technique (data are shown in the ESI†). In particular, it has been shown that this technique provides viscosity values which are similar to those obtained from rheological measurements for monomeric protein solutions under stable conditions. Moreover, it has been demonstrated that the nanoparticles are stable in the mAb solution, and that the viscosity measurements are independent of the concentration of tracer particles.Fig. 1a shows the kinetics of viscosity increase for the three considered protein concentrations. It can be seen that, as expected, the higher the protein concentration, the faster is the rise in solution viscosity.
In a second type of experiments, the growth of protein aggregates with time was monitored (in the absence of nanoparticles) with DLS. Fig. 1b shows the increase in hydrodynamic radius for the three investigated protein concentrations measured both in batch and in flowing modes.
It is worth mentioning that the accurate determination of the protein aggregate size requires performing measurements under dilute conditions. Indeed, the value of the diffusion coefficient 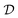 measured by DLS is affected both by protein–protein interactions and by hydrodynamics effects (including viscosity effects), which become significant at high protein concentration. These non-ideal effects can be quantified by the interaction parameter kD, which is defined as the first order concentration dependence of the diffusion coefficient:
measured by DLS is affected both by protein–protein interactions and by hydrodynamics effects (including viscosity effects), which become significant at high protein concentration. These non-ideal effects can be quantified by the interaction parameter kD, which is defined as the first order concentration dependence of the diffusion coefficient:
 | (6) |
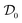 is the extrapolation of the diffusion coefficient to zero protein concentration.
is the extrapolation of the diffusion coefficient to zero protein concentration.
For a solute of molecular weight MW and of partial specific volume ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , the interaction parameter kD can be related to the second virial coefficient B22 and to the first order concentration dependence of the friction coefficient kS according to:31
, the interaction parameter kD can be related to the second virial coefficient B22 and to the first order concentration dependence of the friction coefficient kS according to:31
kD = 2B22MW − kS − ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) | (7) |
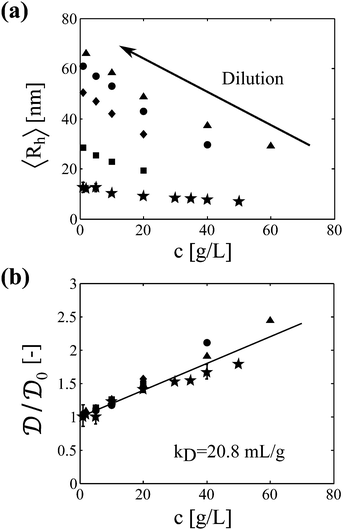
Samples analyzed by SEC-DLS are extensively diluted during elution in the chromatography column and thus reach the light scattering detector at sufficiently low protein concentration. Samples analyzed by batch DLS instead require manual dilution before analysis, which is performed at room temperature to avoid further aggregation. It is worth mentioning here that the mAb aggregates were shown to be irreversible upon dilution in a previous study.23 In Fig. 2a, we show the impact of protein concentration on the apparent hydrodynamic radius measured by DLS (considering the solvent viscosity) for a monomeric sample and for four aggregated samples of various sizes. It can be seen that the measured hydrodynamic radius dramatically increases upon sample dilution. In Fig. 2b, these results are presented in terms of diffusion coefficients normalized by the diffusion coefficient under dilute conditions. Interestingly, the data points from the five independent samples follow the same linear trend. This shows that, at least for the system under investigation, one single interaction parameter kD is sufficient to describe both the monomeric and the aggregated protein solutions. It is also interesting to note that no deviation from the linear trend is observed up to the high concentration of 60 g L−1, suggesting that higher order terms in eqn (6) can be neglected in the investigated range of protein concentrations.
It is worth highlighting that the batch and SEC-DLS measurements give access to conceptually different quantities: while batch experiments provide the average hydrodynamic radius of the whole sample, SEC-DLS experiments provide the average hydrodynamic radius of the aggregate population only, i.e. excluding the monomer. However, in this specific case, most of the monomer is already consumed at the incubation time points where DLS analysis is carried out, as shown in Fig. S6 of the ESI.† Moreover, as the scattered intensity increases with the scatterer radius to the power of 6, the contribution of the residual monomer to the total scattered intensity is negligible as compared to the contribution of the aggregates. Therefore, both batch and SEC-DLS measurements provide very similar values of the average hydrodynamic radius for the system under investigation, as can be seen in Fig. 1b. The good agreement between the two sets of data also supports the validity of the SEC-DLS analysis, ruling out possible artifacts due to aggregate breakage or interactions with the column matrix.
Occupied volume fraction
We now correlate the increase in solution viscosity with the increase in aggregate size. In Fig. 3a, the measured solution viscosity is plotted as a function of the aggregate hydrodynamic radius for each protein concentration and each incubation time. It appears clearly from this set of experimental data that the solution viscosity increases both with the aggregate size and with the protein concentration.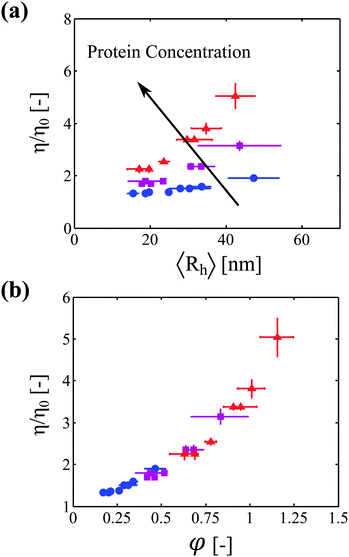 | ||
Fig. 3 (a) Viscosity increase as a function of aggregate size for three different protein concentrations: 20 g L−1 ( ), 40 g L−1 ( ), 40 g L−1 ( ), and 60 g L−1 ( ), and 60 g L−1 ( ). (b) Viscosity increase as a function of the estimated volume fraction (defined by eqn (11)) for the same three protein concentrations. All the data from (a) collapse on one single master curve. ). (b) Viscosity increase as a function of the estimated volume fraction (defined by eqn (11)) for the same three protein concentrations. All the data from (a) collapse on one single master curve. | ||
In the following, we aim at rationalizing the increase in solution viscosity with time by introducing an effective volume fraction occupied by the aggregates, which accounts for the two contributions identified experimentally: the aggregate size and the protein concentration. Accordingly, we define the occupied volume fraction ϕ as:
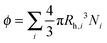 | (8) |
By approximating the aggregate population to a monodisperse population of average radius 〈Rh〉 and average number concentration 〈N〉, we can estimate an approximate volume fraction φ with:
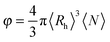 | (9) |
The average concentration of aggregates can be estimated from the initial concentration of primary particles (i.e. the initial protein concentration N0) divided by the average number of primary particles per aggregate (which is equal to the ratio between the average aggregate molecular weight 〈MW〉 and the molecular weight of the monomeric protein MWp):
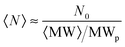 | (10) |
Moreover, the average aggregate molecular weight can be estimated from the aggregate radius by using the fractal scaling introduced in eqn (2). The concept of fractal scaling indeed provides a simple mathematical correlation between the aggregate mass and the aggregate size through the definition of the fractal dimension, which is a measurable parameter.
Finally, by combining eqn (2), (9) and (10), it results that the occupied volume fraction can be evaluated from the following equation:
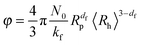 | (11) |
The above relationship shows that the impact of aggregation on the occupied volume fraction strongly depends on the aggregate morphology through the fractal dimension df and the scaling prefactor kf. For a system characterized by an aggregate fractal dimension smaller than 3, the increase in aggregate size with time leads to an increase in the occupied volume fraction. The more open are the aggregates, i.e. the lower is the fractal dimension, the more pronounced is this effect.
It is worth highlighting that an estimate of the occupied volume fraction can be obtained using eqn (11) only for fractal aggregates. Nevertheless, we believe that the key concept of occupied volume fraction (as defined by eqn (8)) is general enough to be applied to any kind of aggregate geometry. Although defining the occupied volume of non-fractal aggregates would require more theoretical work than the approximation proposed in eqn (11), the general approach of correlating viscosity increase with the occupied volume fraction should remain valid even for non-fractal aggregates.
Aggregate fractal morphology
The proper estimation of the occupied volume fraction thus requires the characterization of aggregate morphology, and in particular the evaluation of the parameters df and kf. These two parameters can be assessed experimentally directly from the correlation between the aggregate molecular weight (measured by SLS) and the aggregate hydrodynamic radius (measured by DLS) by using eqn (2). Fig. 4 shows the correlation between aggregate mass and aggregate radius, as determined from a multi-angle light scattering device, for four protein concentrations: 1, 20, 40 and 60 g L−1.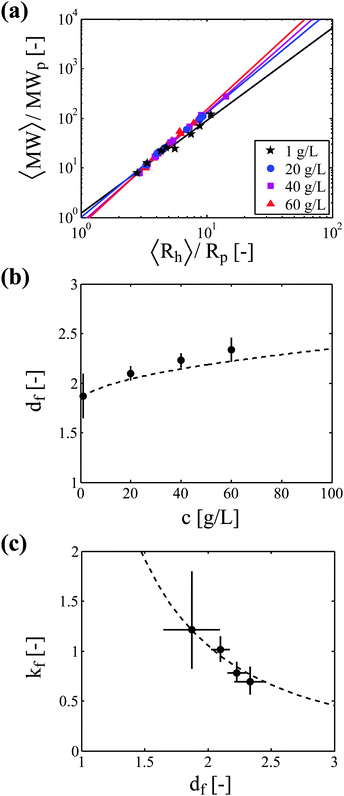 | ||
| Fig. 4 Impact of protein concentration on aggregate morphology. (a) Correlation between aggregate molecular weight and aggregate hydrodynamic radius from light scattering experiments. Lines correspond to the power law fitting of the experimental data. (b) The fractal dimension of aggregates increases with protein concentration. Experimental data (symbols) are compared to the correlation (dashed line) proposed by Gonzales et al. (eqn (12)). (c) The scaling prefactor decreases with the aggregate fractal dimension. Experimental data (symbols) are compared to the correlation (dashed line) proposed by Ehrl et al. (eqn (13)). Error bars in (b) and (c) represent the 90% confidence interval for the parameter determination from the regressions shown in (a). | ||
Fig. 4b shows the aggregate fractal dimension obtained from the power law fitting of the experimental data with eqn (2). It can be observed that the aggregate fractal dimension increases with the protein concentration, i.e. denser aggregates are produced at higher protein concentrations. One possible reason is that in concentrated systems the colliding clusters are likely to be entangled, thus favoring the formation of bonds in the core rather than at the tips of the clusters. The impact of the initial volume fraction φ0 on the fractal dimension df has been quantitatively investigated by means of Monte-Carlo simulations by Gonzales et al.,32 who report the following square root type relationship under diffusion limited conditions:
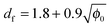 | (12) |
The experimental df values obtained in this work follow a fairly similar trend, as shown in Fig. 4b.
The power law fitting of the experimental data presented in Fig. 4a provides not only the aggregate fractal dimension df, but also the scaling prefactor kf. In Fig. 4c, we plot for each protein concentration the value of the scaling prefactor as a function of the measured aggregate fractal dimension. It can be seen that the prefactor values are close to unity and decrease with increasing fractal dimensions. This reverse correlation between kf and df has already been reported in the literature,33–35 and Ehrl et al. proposed the following empirical fitting:36
| kf = 4.46df−2.08 | (13) |
The experimental values of the prefactor obtained in this work can be well described by the above correlation, as shown in Fig. 4c.
Master curve
Knowing the values of the aggregate fractal dimension df and of the prefactor kf, it is possible to estimate the occupied volume fraction for a given aggregate size and protein concentration through eqn (11). In Fig. 3b, we plot the solution viscosity as a function of the occupied volume fraction for the three investigated protein concentrations. Most remarkably, all the data points, which were collected at several incubation times and several protein concentrations collapse on one single master curve. This demonstrates that the impact of aggregate formation on the increase in viscosity of protein solutions can be successfully rationalized by using the key concept of occupied volume fraction.Discussion
We studied the impact of irreversible aggregate formation on the viscosity increase of a mAb solution subjected to thermal stress in the protein concentration range from 20 to 60 g L−1. The rise in viscosity was monitored by measuring the diffusion coefficient of tracer nanoparticles by using dynamic light scattering in situ, while the kinetics of aggregate growth was followed by off-line DLS measurements performed both in batch and in flowing modes. The two types of measurements provided similar values of the aggregate hydrodynamic radius provided that the samples analyzed by batch DLS were diluted to a sufficiently low protein concentration (i.e. at around 1 g L−1).Protein–Protein interactions
Interestingly, we found that the diffusion coefficients of aggregates of different sizes have similar dependence on the protein concentration compared to the monomer. This suggests that protein interactions can be estimated in a coarse-grained manner by using a single interaction coefficient kD, both in a monomeric and in an aggregated solution. In the following, we attempt to deepen this finding and its implications on the second virial coefficient between protein aggregates. In order to do so, we simplify the expression of kD given by eqn (7) by estimating the contribution of the various terms for this specific system. First, the partial specific volume, which is in the order of 0.7 mL g−1,37 is neglected with respect to kD, which was evaluated here to kD = 20.8 mL g−1. Second, it is assumed that the sedimentation coefficient kS can be approximated by the diffusion coefficient kD. Indeed, kS was reported to be of the same order of magnitude than kD for several monoclonal antibodies characterized by kD values in the order of 20 mL g−1, which are values typically encountered at low ionic strength.6,38 These two simplifications imply that eqn (7) reduces to:| kD = B22MW | (14) |
Since it was shown experimentally that the diffusion coefficient kD of several aggregated samples is similar to the one of the monomeric protein, it follows that the second virial coefficient between aggregates of molecular weight MWA (denoted as BA22) can be roughly estimated from the second virial coefficient between monomeric molecules of molecular weight MWp (denoted as BM22) according to:
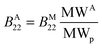 | (15) |
Nevertheless, it must be underlined once more that eqn (15) is valid only under the assumptions of kS ≈ kD and ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ≪ kD.
≪ kD.
Master curve
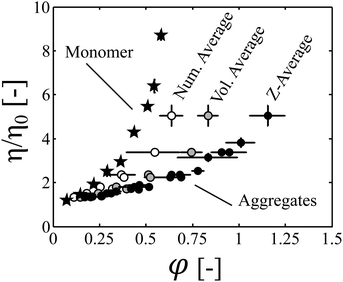
The increase in the volume fraction during time was then computed from the protein concentration, aggregate size and fractal dimension, which was measured by SLS. We showed that when plotted as a function of the occupied volume fraction, the kinetics of viscosity increase obtained at three different protein concentrations collapse on one single master curve (Fig. 3b).It is then interesting to compare this master curve, which was constructed by analyzing aggregated samples of various sizes and protein concentrations, with a similar curve obtained with monomeric samples only, which were prepared at several protein concentrations. In Fig. 5, we plot the data obtained with aggregated samples under thermal stress (black circles) and compare them to viscosity measurements performed on monomeric samples at room temperature (back stars). The results are presented in terms of normalized viscosity in order to remove the impact of temperature on the solvent viscosity. It can be observed that the two curves do not collapse. Indeed, the curve obtained with monomeric samples lies above the curve constructed with aggregated samples. Three main possible reasons can be put forth to explain this observation:
(i) The evaluated occupied volume fraction is overestimated because clusters interpenetrate due to the high protein concentrations.
(ii) The evaluated occupied volume fraction is overestimated because the average value of the hydrodynamic radius which was considered to compute the occupied volume fraction is biased towards large aggregate sizes. Indeed, for a given aggregate size distribution, several values of the average size can be computed, and the z-average, which is commonly evaluated in DLS experiments, gives prominence to large aggregate sizes.
(iii) At a given occupied volume fraction, the viscosity of a monomeric solution is higher than the viscosity of an aggregated sample due to the polydispersity (i.e. the broadness) of the aggregate distribution. Polydisperisty is indeed known to decrease the viscosity of colloidal dispersions.39–42
It can be observed in Fig. 5 that even at the early-stages of the aggregation process (let say for φ values up to 0.3), where cluster overlapping can be considered negligible, the viscosity of the monomeric protein solutions is even larger than the viscosity of aggregated samples of similar volume fractions. This suggests that assumption (i) alone is unlikely to explain the observed results.
In order to assess the likelihood of explanation (ii), we estimated the impact of the choice of the definition used to compute the average aggregate size on the computed occupied volume fraction. In order to do so, we compared the results obtained with the z-average to those obtained with the number average and the volume average aggregate radius for the batch DLS measurements. In Fig. 5, it can be seen that the selected type of average strongly impacts the value of the estimated volume fraction. In particular, for a given aggregate population, the volume fraction computed based on an average aggregate size scales in this order: number average < volume average < z-average. Nevertheless, it is worth highlighting that for each type of average, a master curve is obtained when the kinetic profiles acquired at different protein concentrations are normalized based on the occupied volume fraction. This shows that, even though the absolute values of φ must be taken with some caution due to the difficulty of estimating the occupied volume fraction from experimental data, the concept of occupied volume fraction is key to rationalize the viscosity increase during aggregation. Moreover, we demonstrate in the ESI,† that the volume fractions computed from the number and volume average aggregate radius provide, respectively, a lower and an upper boundary for the real occupied volume fraction. Since the master curve obtained when considering the number average hydrodynamic radius (which underestimates the real occupied volume fraction) lies below the curve obtained with monomeric protein solutions, explanation (ii) can be ruled out.
Therefore, we conclude from this analysis that aggregate polydispersity plays a prominent role in decreasing the solution viscosity at constant volume fraction.
Conclusion
In this work, the effect of irreversible aggregate formation on the change in viscosity of a concentrated monoclonal antibody solution was investigated. We showed that the increase in viscosity during aggregation can be rationalized by using the key concept of occupied volume fraction, which depends on aggregate concentration, size and morphology. For this purpose, we monitored the increase in solution viscosity by following the reduction in the diffusion coefficient of tracer nanoparticles with DLS in situ, while aggregate size and morphology were determined by combining static and dynamic light scattering experiments. Moreover, it was shown that aggregates are fractal objects, which are characterized by a fractal dimension increasing with protein concentration. Finally, we showed that the increase in solution viscosity with time monitored at three different protein concentrations collapse on one single master curve when the reaction profiles are normalized based on the effective volume fraction. Crucially, it was found that the viscosity of an aggregated protein solution is lower than the viscosity of a monomeric protein solution of similar occupied volume fraction due to the polydispersity of the aggregate distribution. These findings are valuable in better understanding the behavior of concentrated protein solutions.Acknowledgements
The authors thank UCB Pharma (Braine l'Alleud, Belgium) for material supplying and financial support. Financial support from the Fondation Claude et Giuliana and from the Swiss National Foundation (grant No. 200020147137/1 and grant number PP00P2133597/1) is gratefully acknowledged. We also thank Bastian Brand (ETH Zurich) for his advice on nanoparticle synthesis, David Pfister (ETH Zurich), Paolo Arosio (University of Cambridge), Jan Massant (UCB Pharma) and Edith Norrant (UCB Pharma) for interesting discussions.References
- S. Aggarwal, Nat. Biotechnol., 2012, 30, 1191–1197 CrossRef CAS PubMed.
- M. Vázquez-Rey and D. A. Lang, Biotechnol. Bioeng., 2011, 108, 1494–1508 CrossRef PubMed.
- S. J. Shire, Z. Shahrokh and J. Liu, J. Pharm. Sci., 2004, 93, 1390–1402 CrossRef CAS PubMed.
- C. J. Roberts, T. K. Das and E. Sahin, Int. J. Pharm., 2011, 418, 318–333 CrossRef CAS PubMed.
- R. Chari, K. Jerath, A. V. Badkar and D. S. Kalonia, Pharm. Res., 2009, 26, 2607–2618 CrossRef CAS PubMed.
- B. D. Connolly, C. Petry, S. Yadav, B. Demeule, N. Ciaccio, J. M. R. Moore, S. J. Shire and Y. R. Gokarn, Biophys. J., 2012, 103, 69–78 CrossRef CAS PubMed.
- W. J. Galush, L. N. Le and J. M. Moore, J. Pharm. Sci., 2012, 101, 1012–1020 CrossRef CAS PubMed.
- F. He, C. E. Woods, J. R. Litowski, L. A. Roschen, H. S. Gadgil, V. I. Razinkov and B. A. Kerwin, Pharm. Res., 2011, 28, 1552–1560 CrossRef CAS PubMed.
- W. G. Lilyestrom, S. Yadav, S. J. Shire and T. M. Scherer, J. Phys. Chem. B, 2013, 117, 6373–6384 CrossRef CAS PubMed.
- J. Liu, M. D. Nguyen, J. D. Andya and S. J. Shire, J. Pharm. Sci., 2005, 94, 1928–1940 CrossRef CAS PubMed.
- S. Amin, G. V. Barnett, J. A. Pathak, C. J. Roberts and P. S. Sarangapani, Curr. Opin. Colloid Interface Sci., 2014, 19, 438–449 CrossRef CAS PubMed.
- A. Saluja and D. S. Kalonia, AAPS PharmSciTech, 2004, 5, 68–81 CrossRef PubMed.
- F. He, G. W. Becker, J. R. Litowski, L. O. Narhi, D. N. Brems and V. I. Razinkov, Anal. Biochem., 2010, 399, 141–143 CrossRef CAS PubMed.
- J. A. Pathak, R. R. Sologuren and R. Narwal, Biophys. J., 2013, 104, 913–923 CrossRef CAS PubMed.
- M. M. Castellanos, J. A. Pathak and R. H. Colby, Soft Matter, 2014, 10, 122 RSC.
- D. B. Genovese, Adv. Colloid Interface Sci., 2012, 171–172, 1–16 CrossRef CAS PubMed.
- H. Barnes, A handbook of elementary rheology, University of Wales Institute of Non-Newtonian Fluid Mechanics, 2000 Search PubMed.
- P. Meakin, Adv. Colloid Interface Sci., 1987, 28, 249–331 CrossRef.
- V. I. Roldughin, Usp. Khim., 2003, 72, 931–959 Search PubMed.
- E. F. Mikhailov and S. S. Vlasenko, Usp. Fiz. Nauk., 1995, 165, 263–283 CrossRef CAS.
- R. Botet and R. Jullien, Phase Transitions, 1990, 24–26, 691–736 CrossRef PubMed.
- R. Jullien, Contemp. Phys., 1987, 28, 477–493 CrossRef PubMed.
- L. Nicoud, P. Arosio, M. Sozo, A. Yates, E. Norrant and M. Morbidelli, J. Phys. Chem. B, 2014, 118, 10595–10606 CrossRef CAS PubMed.
- P. Arosio, S. Rima, M. Lattuada and M. Morbidelli, J. Phys. Chem. B, 2012, 116, 7066–7075 CrossRef CAS PubMed.
- P. Grancic, V. Illeova, M. Polakovic and J. Sefcik, Chem. Eng. Sci., 2012, 70, 14–21 CrossRef CAS PubMed.
- S. Ikeda, E. A. Foegeding and T. Hagiwara, Langmuir, 1999, 15, 8584–8589 CrossRef CAS.
- L. Nicoud, M. Owczarz, P. Arosio and M. Morbidelli, Biotechnol. J., 2015, 10, 367–378 CrossRef CAS PubMed.
- T. Arakawa, D. Ejima, T. Li and J. S. Philo, J. Pharm. Sci., 2010, 99, 1674–1692 CAS.
- M. Wagner, K. Reiche, A. Blume and P. Garidel, Pharm. Dev. Technol., 2013, 18, 963–970 CrossRef CAS PubMed.
- J. G. E. Webster and H. Eren, Measurement, Instrumentation, and Sensors Handbook, Spatial, Mechanical, Thermal, and Radiation Measurement, 2nd edn, 2014 Search PubMed.
- C. Tanford, Physical Chemistry of Macromolecules, 1961 Search PubMed.
- A. E. González, F. Martínez-López, A. Moncho-Jordá and R. Hidalgo-Álvarez, Phys. A, 2002, 314, 235–245 CrossRef.
- C. M. Sorensen and G. C. Roberts, J. Colloid Interface Sci., 1997, 186, 447–452 CrossRef CAS.
- M. Lattuada, H. Wu and M. Morbidelli, J. Colloid Interface Sci., 2003, 268, 106–120 CrossRef CAS PubMed.
- A. M. Brasil, T. L. Farias and M. G. Carvalho, Aerosol. Sci. Technol., 2000, 33, 440–454 CrossRef CAS PubMed.
- L. Ehrl, M. Soos and M. Lattuada, J. Phys. Chem. B, 2009, 113, 10587–10599 CrossRef CAS PubMed.
- H. Fischer, I. Polikarpov and A. F. Craievich, Protein Sci., 2004, 13, 2825–2828 CrossRef CAS PubMed.
- A. Saluja, R. M. Fesinmeyer, S. Hogan, D. N. Brems and Y. R. Gokarn, Biophys. J., 2010, 99, 2657–2665 CrossRef CAS PubMed.
- R. A. Lionberger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 061408 CrossRef.
- J. Kovář and I. Fortelný, Rheol. Acta, 1984, 23, 454–456 CrossRef.
- N. J. Wagner and A. T. J. M. Woutersen, J. Fluid Mech., 1994, 278, 267–287 CrossRef CAS.
- D. J. Jeffrey and A. Acrivos, AIChE J., 1976, 22, 417–432 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm00513b |
| ‡ Institute for Chemical and Bioengineering, Department of Chemistry & Applied Biosciences, ETH Zurich, Vladimir-Prelog-Weg 1, CH-8093 Zurich, Switzerland. E-mail: E-mail: massimo.morbidelli@chem.ethz.ch; Tel: +41 44 632 30 34. |
| This journal is © The Royal Society of Chemistry 2015 |