 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Studying the concentration dependence of the aggregation number of a micellar model system by SANS
Matthias
Amann
*a,
Lutz
Willner
*a,
Jörg
Stellbrink
a,
Aurel
Radulescu
b and
Dieter
Richter
a
aJülich Centre for Neutron Science JCNS-1 & Institute of Complex Systems ICS-1, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany. E-mail: m.amann@fz-juelich.de; l.willner@fz-juelich.de
bJülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at MLZ, 85747 Garching, Germany
First published on 13th April 2015
Abstract
We present a small-angle neutron scattering (SANS) structural characterization of n-alkyl-PEO polymer micelles in aqueous solution with special focus on the dependence of the micellar aggregation number on increasing concentration. The single micellar properties in the dilute region up to the overlap concentration ϕ* are determined by exploiting the well characterized unimer exchange kinetics of the model system in a freezing and diluting experiment. The micellar solutions are brought to thermodynamic equilibrium at high temperatures, where unimer exchange is fast, and are then cooled to low temperatures and diluted to concentrations in the limit of infinite dilution. At low temperatures the kinetics, and therefore the key mechanism for micellar rearrangement, is frozen on the experimental time scale, thus preserving the micellar structure in the dilution process. Information about the single micellar structure in the semidilute and concentrated region are extracted from structure factor analysis at high concentrations where the micelles order into fcc and bcc close packed lattices and the aggregation number can be calculated by geometrical arguments. This approach enables us to investigate the aggregation behavior in a wide concentration regime from dilute to 6·ϕ*, showing a constant aggregation number with concentration over a large concentration regime up to a critical concentration about three times ϕ*. When exceeding this critical concentration, the aggregation number was found to increase with increasing concentration. This behavior is compared to scaling theories for star-like polymer micelles.
1 Introduction
A classical feature of block copolymers is the spontaneous self-assembly in selective solvents into micellar aggregates. Structure and more recently kinetics have been widely studied by theory, experiment and computer simulation as summarized in numerous books1,2 and review articles.3–7Several thermodynamic theories have been developed to describe and predict structural properties of block copolymer micelles. These theories can be roughly divided into mean-field8–10 and scaling approaches.11–13 Mean-field theories generally allow to calculate detailed thermodynamic and structural parameters of micelles but are limited to relatively homogeneous systems with weak interactions. For the case of block copolymer micelles exhibiting strong excluded volume interactions the mean-field ansatz is usually not appropriate. For such systems the micellar parameters can be successfully calculated and predicted by scaling theories, utilizing self-similar properties of polymers. Within scaling theories for spherical micelles three limiting structural cases have been discussed: crew-cut, intermediate and star-like.
A large number of theoretical11,12 and experimental studies14–19 were concerned with star-like spherical micelles which are obtained by highly asymmetric amphiphilic block-copolymers.11,15 This class of micelles show characteristics very similar to regular star polymers20,21 and for this reason they are often used as star substitutes in particular for a high degree of branching.22 The advantage of block copolymer micelles is the much easier availability of the underlying block copolymer, whereas the preparation and characterization of model star polymers is time consuming and requires superior synthetic skills.23 Furthermore, the properties of block copolymer micelles can be easily tuned by changing e.g. solvent quality, temperature, solvent selectivity, block copolymer composition and molecular weight, which is inherently impossible for regular star polymers.
Both, regular star polymers and block copolymer micelles are considered to be excellent soft colloidal model systems for studying interparticle interactions and the formation of ordered structures in dilute and semi-dilute concentrations.16–18,24,25 For these systems, the softness of the colloidal particle is intimately connected with the degree of branching, i.e. the number of arms or aggregation number, Nagg.22
A famous and widely used concept to describe interactions of star-like spherical micelles or regular star polymers is the repulsive pair potential derived by Likos et al.26 This potential is ultra-soft for low aggregation numbers and approaches the hard-sphere limit for high aggregation numbers. Accordingly, Nagg sensitively affects the potential and consequently has a strong impact on the expected phase behavior of these systems.
Good agreement between theory and experimental data have been achieved using amphiphilic diblock copolymers of the type poly(ethylene-alt-propylene)–poly(ethylene oxide) (PEP–PEO) in water or water–N,N-dimethylformamide mixtures.16,17 However, crystalline lattices in these systems were found to be often suppressed by the formation of a glassy state. It has been discussed and shown by Nicolai et al.27–29 that for micellar systems a fast dynamic molecular exchange is necessary for the formation of ordered phases. The rate of chain exchange in polymeric micelles is directly accessible by TR-SANS experiments.7 Using this method it has directly been shown that PEP–PEO micelles in water are frozen, i.e. the main mechanism for reaching and attaining thermodynamic equilibrium is blocked.30,31
For micellar systems with dynamic chain exchange however the interpretation of the interaction and the corresponding phase behavior at higher concentrations remains complicated as one has to take into account possible changes of Nagg with increasing concentration. The change in aggregation number at higher concentrations was predicted by scaling theory12,32 and observed experimentally by Puaud et al.28,29 The coupling between micelle aggregation and ordered phases of block copolymer micelles have also been explored by Grason33 using a mean-field model. This model predicts thermotropic and lyotropic transitions from face-centered cubic to body-centered cubic ordered phases which were found to be controlled by micellar aggregation. For a systematic and thorough interpretation of the interaction and phase behavior of a highly dynamic micellar system it is therefore inevitable to determine the concentration dependence of the aggregation number from dilute to concentrated solutions.
In this work we present a detailed study of the aggregation number of a micellar model system by small-angle neutron scattering (SANS) covering a very broad range of concentrations. As model system we have used a poly(ethylene oxide) mono-n-octacosyl ether (C28-PEO5, with 5 being the nominal molecular weight of the polymer in kg mol−1) in aqueous solution. Structure and kinetics of this system have been well characterized.19,34 Because of the high asymmetry in composition and the high incompatibility of the n-alkane with water this block copolymer forms star-like micelles with high aggregation numbers in dilute solution. The equilibrium kinetics was measured by TR-SANS using the kinetic zero average contrast method.34–36 It was found that the kinetics of C28-PEO5 follows a classical Arrhenius behavior where chain exchange can be tuned from very slow to very fast within a convenient temperature range around room temperature. Generally, single particle properties (P(Q)) are difficult to access at finite concentrations since P(Q) is superimposed by inter particle contributions (S(Q)). Classical labeling techniques, e.g. zero average contrast method where S(Q) cancels,37,38 cannot be applied as chain exchange would lead to a continuous decrease of scattering contrast. In order to still measure form factors P(Q) and to determine Nagg at higher concentrations we have created a freezing and diluting experiment exploiting the known exchange kinetics35 and the temperature independent aggregation behavior19 of this particular micellar system. This method could be applied in the dilute region up to concentrations slightly exceeding the overlap concentration, ϕ*. Aggregation numbers of micelles at higher concentrations were extracted from crystalline lattices using simple geometrical arguments. In this way we could determine aggregation numbers over the whole important concentration range. In this paper we present a brief summary of the scaling theory and a detailed description of experiments and results including the freezing and diluting experiment. SANS measurements and data evaluation will be presented and the results are discussed in terms of the scaling prediction.
2 Theoretical background
A–B block copolymers will spontaneously self-assemble when dispersed in a selective solvent. If the solvent is selective for the A block, microdomains of collapsed B-block forming a micellar core surrounded by a swollen corona of A-block will be formed. The structure of these aggregates primarily depends on the degree of polymerization N = NA + NB, the block ratio NA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NB of the polymer and the interactions between the constituents. Generally, the structure of the micelle can be described thermodynamically by the free energy per aggregated chain Fmic which can be summarized by three main contributions:8
NB of the polymer and the interactions between the constituents. Generally, the structure of the micelle can be described thermodynamically by the free energy per aggregated chain Fmic which can be summarized by three main contributions:8| Fmic = Fcore + Fcorona + Fint | (1) |
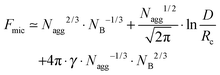 | (2) |
 | (3) |
Therefore, for a quantitative evaluation of the concentration dependence of the aggregation number both ϕ* and ϕ** are needed. The overlap concentration ϕ* is directly accessible by viscosity measurements or by geometrical arguments when Rm is known. As the crossover from the two scaling regimes above and below ϕ* needs to be continuous both expressions should be valid at ϕ = ϕ*, so that x = x0 at this concentration. Following this approach, one can find the following expression for ϕ**:
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ** = ln ϕ** = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ* + ln(D/Rcore) ϕ* + ln(D/Rcore) | (4) |
3 Experimental section
3.1 Materials
The poly(ethylene oxide) mono-n-octacosyl ether C28-PEO5 was synthesized by living anionic ring opening polymerization of ethylene oxide (EO) (Fluka) in toluene at 95 °C. As initiator system a 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 mixture of 1-octacosanol (C28H57–OH) (Aldrich) with its corresponding potassium-1-alkoxide (C28H57–O−K+) was used as described in ref. 19. The molecular weight of the alkoxide block Mn(C28H57O) = 409.8 g mol−1 was given by the choice of the initiator. The molecular weight Mn(PEO) = 4581 g mol−1 and the degree of polymerization N(PEO) = 104 of the PEO polymer was calculated from 1H-NMR spectra using the integral intensity of the alkyl-block as internal reference for the calculations, giving a total molar mass of the C28-PEO5 polymer of Mn ≃ 5 × 103 g mol−1. The polydispersity index Mw/Mn ≤ 1.04 was determined by size exclusion chromatography (SEC) with tetrahydrofuran/N,N-dimethylacetamid (85/15) as eluent at 50 °C using three Agilent PlusPore GPC columns with a continuous distribution of pore sizes and PEO standards for calibration. The chromatogram showed small contents of a polymer (≤1%) at elution volumes corresponding to approximately twice the alkane-PEO molecular weight. The origin of this polymer may be due to the presence of spurious amounts of water and/or other impurities in the reaction mixture which can act as bifunctional initiator for the EO polymerization reaction.
20 mixture of 1-octacosanol (C28H57–OH) (Aldrich) with its corresponding potassium-1-alkoxide (C28H57–O−K+) was used as described in ref. 19. The molecular weight of the alkoxide block Mn(C28H57O) = 409.8 g mol−1 was given by the choice of the initiator. The molecular weight Mn(PEO) = 4581 g mol−1 and the degree of polymerization N(PEO) = 104 of the PEO polymer was calculated from 1H-NMR spectra using the integral intensity of the alkyl-block as internal reference for the calculations, giving a total molar mass of the C28-PEO5 polymer of Mn ≃ 5 × 103 g mol−1. The polydispersity index Mw/Mn ≤ 1.04 was determined by size exclusion chromatography (SEC) with tetrahydrofuran/N,N-dimethylacetamid (85/15) as eluent at 50 °C using three Agilent PlusPore GPC columns with a continuous distribution of pore sizes and PEO standards for calibration. The chromatogram showed small contents of a polymer (≤1%) at elution volumes corresponding to approximately twice the alkane-PEO molecular weight. The origin of this polymer may be due to the presence of spurious amounts of water and/or other impurities in the reaction mixture which can act as bifunctional initiator for the EO polymerization reaction.
The micellar solutions were prepared according to the following general mixing protocols. Stock solutions of polymer volume fractions of ϕ = 1%, 12% and 15% were prepared by weighing in the pure components. The mixtures were heated to 60 °C up to 12 hours to ensure complete dissolution and micellar equilibration due to fast chain exchange kinetics.34 Subsequently, they were cooled down to room temperature within 4 hours under shaking. Additional solutions were prepared by diluting: a solution with ϕ = 0.25% was prepared from the 1% stock solution, solutions with ϕ = 2.7%, 5.4% and 8.5% were prepared from the 12% stock solution and solutions with ϕ = 7.3% and 10% were prepared from the 15% stock solution, respectively. The diluted solutions were again equilibrated by heating to 60 °C for 3 hours. It should be noted that up to 15% all solutions were liquid at 60 °C whereas at 20 °C samples become increasingly more viscous with increasing concentration. Specimens with higher concentrations were prepared by individually weighing in the pure components. Visually homogeneous solutions were obtained by several successive heating to 60 °C, centrifugation at 40 °C and cooling cycles as these samples were solid-like over the whole temperature range. This procedure allows complete dissolution and micellar equilibration even in the high concentration regime, where chain exchange kinetics is expected to be significantly slower than in dilute solutions.32,42 After experiments, polymers were recovered by freeze-drying and tested for degradation. SEC measurements however did not reveal any changes in molecular weight and molecular weight distribution.
For SANS measurements the solutions were filled into standard Hellma Quartz cells with 2 mm (samples with ϕ ≤ 7.3%) and 1 mm (samples with ϕ ≥ 8.5%) path length. Samples larger than 15% polymer volume fraction were transferred into the cells by means of a Hamilton syringe. This was easily possible because the solids show a strong shear thinning effect.
The overlap concentration was determined by viscosity measurements as function of polymer concentration with a strain controlled TA instruments ARES-G2 rheometer using couette geometry. The dependence of the zero-shear viscosity η0 on the concentration was analyzed with a model for solutions of spherical particles introduced by Krieger and Dougherty.43 The solutions were prepared using D2O as solvent and were measured at T = 15 °C to keep conformity with the SANS experiments, giving an overlap concentration of ϕ*(T = 15 °C) = 8.9%.
3.2 SANS and data evaluation
SANS experiments were performed at KWS-244 located at Heinz-Meier Leibnitz Zentrum (MLZ) in Garching, Germany. All measurements of C28-PEO5 were made using full contrast conditions, i.e. proteated polymer in D2O. The scattering length densities of solvent and polymer were calculated according to with the scattering length bi of individual atoms in the alkyl-block, the PEO repeating unit or water molecules and M the respective molecular weight. For the mass density d of the alkane block (C28H57), the value of the corresponding n-octacosane was taken, assuming the formation of a fully segregated micellar core. For the PEO-block the solution density according to Sommer et al.45 was taken. The calculated scattering length densities are ρalkane = −0.335 × 1010 cm−2, ρPEO = 0.676 × 1010 cm−2 and ρD2O = 6.362 × 10−10 cm−2.
with the scattering length bi of individual atoms in the alkyl-block, the PEO repeating unit or water molecules and M the respective molecular weight. For the mass density d of the alkane block (C28H57), the value of the corresponding n-octacosane was taken, assuming the formation of a fully segregated micellar core. For the PEO-block the solution density according to Sommer et al.45 was taken. The calculated scattering length densities are ρalkane = −0.335 × 1010 cm−2, ρPEO = 0.676 × 1010 cm−2 and ρD2O = 6.362 × 10−10 cm−2.
Sample to detector distances of 2 m and 8 m with a collimation length set to 8 m and a neutron wavelength of 7 Å with a wavelength spread of Δλ/λ = 20% were used to cover a Q-range from 0.006 ≤ Q [Å−1] ≤ 0.2 where Q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the momentum transfer and 2θ is the scattering angle. Samples with ϕ ≥ 7.3% were measured at a neutron wavelength of 5 Å and a collimation length of 20 m using the double-disc chopper and time-of-flight data acquisition mode of the KWS-2, greatly increasing the resolution of the instrument to Δλ/λ = 5%.46 Scattered intensities were corrected for detector pixel efficiency, empty cell scattering and background signal due to electronic noise, gamma radiation and fast unmoderated neutrons. The data were set to absolute scale using plexiglas as secondary internal standard. The obtained macroscopic differential cross-section dΣ/dΩ(Q) [cm−1] was further corrected for contributions of solvent and incoherent scattering. The scattering of the solvent was measured separately while the incoherent scattering of the polymer was calculated. The complete data reduction process was performed with the QtiKWS computer software provided by the MLZ in Garching.44 All measurements were carried out at a temperature of T = 15 °C.
θ is the momentum transfer and 2θ is the scattering angle. Samples with ϕ ≥ 7.3% were measured at a neutron wavelength of 5 Å and a collimation length of 20 m using the double-disc chopper and time-of-flight data acquisition mode of the KWS-2, greatly increasing the resolution of the instrument to Δλ/λ = 5%.46 Scattered intensities were corrected for detector pixel efficiency, empty cell scattering and background signal due to electronic noise, gamma radiation and fast unmoderated neutrons. The data were set to absolute scale using plexiglas as secondary internal standard. The obtained macroscopic differential cross-section dΣ/dΩ(Q) [cm−1] was further corrected for contributions of solvent and incoherent scattering. The scattering of the solvent was measured separately while the incoherent scattering of the polymer was calculated. The complete data reduction process was performed with the QtiKWS computer software provided by the MLZ in Garching.44 All measurements were carried out at a temperature of T = 15 °C.
The micellar solutions in the dilute limit, where structure factor effects can be neglected, i.e. S(Q) ≈ 1, were analyzed with the following general approach:
 | (5) |
 | (6) |
 | (7) |
 | (8) |
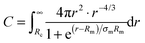 denotes a normalization constant obtained by integrating the density profile over the volume. The parameter σint is a measure of the surface roughness of the core–corona interface. To limit the corona to a finite size, a Fermi cut-off function is used in eqn (8) with σm set to 10% of Rm.
denotes a normalization constant obtained by integrating the density profile over the volume. The parameter σint is a measure of the surface roughness of the core–corona interface. To limit the corona to a finite size, a Fermi cut-off function is used in eqn (8) with σm set to 10% of Rm.
The term B(Q) in eqn (6) refers to the internal, local short range correlations of polymer segments in the corona (“blob scattering”) which have to be added incoherently:
 | (9) |
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) as an effective virial type parameter that scales with effective concentration of corona chains. The form factor of a polymer chain Pchain(Q) can be approximated by an empiric approach for self-avoiding chains introduced by Beaucage:48
as an effective virial type parameter that scales with effective concentration of corona chains. The form factor of a polymer chain Pchain(Q) can be approximated by an empiric approach for self-avoiding chains introduced by Beaucage:48 | (10) |
3.3 Exchange kinetics
The equilibrium chain exchange kinetics of C28-PEO5 micelles in aqueous solution has been studied in detail by Zinn et al.34–36 Due to the importance of the kinetics for our work we will shortly summarize the main features of the single chain exchange kinetics for this particular system. The exchange kinetics was measured by TR-SANS in combination with the kinetic zero-average contrast (KZAC) technique.7,30 It was found that the exchange can be described by a thermally activated first order kinetic process which is characterized by a single relaxation rate following an Arrhenius form:| 1/k(T) = τ(T) = τ0·exp(EA/RT) | (11) |
3.4 Freezing and diluting experiment
As mentioned in Section 1 the determination of single micellar properties is challenging at concentrations where structure factor contributions cannot be accounted for by a second virial coefficient. In this work, we have employed an experiment which exploits the well known exchange kinetics of our model system to examine the micellar form factor in particular the aggregation number Nagg at elevated concentrations. The micellar solutions were prepared and equilibrated according to the procedure presented in Section 3.1. Afterwards, the solutions or solids were cooled to T = 15 °C. A fraction of the cooled solutions was taken, weighed and diluted to a concentration of ϕ = 0.25% with the corresponding amount of pre-cooled solvent. In order to achieve a homogeneous dilution, the mixture was shaken mechanically. It is important to note that the aggregation number will be preserved during the process since the chain exchange as the main mechanism for structural rearrangement is almost frozen. The micellar size however increases due to increasing hydration of PEO at lower temperatures.19,51 SANS measurements of the diluted solutions were made directly after the freezing and diluting process, carefully holding the temperature at 15 °C. The obtained scattering curves of the diluted micellar solutions were then analyzed with the micellar core–shell model presented in Section 3.2.With increasing concentration of the stock solution, it takes increasingly more time to dilute the solid-like samples with pre-cooled D2O to volume fractions of ϕ = 0.25%. Dilution times tdil to obtain homogeneous solutions are shown in Table 1 where additionally the times tmeas from the beginning of the dilution processes to the end of the SANS measurements are depicted. Due to practical reasons, the long time scales necessary for diluting and measuring limit the accessible concentration range for the experiment to concentrations up to 15%. Increasing the speed of the freezing and diluting process at this temperature would require a much stronger agitation of the samples, which could also lead to the unlocking of chain exchange and micellar rearrangement.52
| ϕ (%) | t dil (min) | t meas (min) |
|---|---|---|
| 2.7 | 9 | 37 |
| 5.4 | 10 | 38 |
| 7.3 | 10 | 38 |
| 8.5 | 15 | 43 |
| 10 | 16 | 44 |
| 12 | 25 | 53 |
| 15 | 90 | 118 |
4 Results & discussion
The macroscopic scattering cross section dΣ/dΩ(Q) normalized by the volume fraction of C28-PEO5 micelles in dilute solution (ϕ = 0.25%) is shown in Fig. 1 in a double logarithmic representation. This SANS curve can be considered as the reference for the data obtained from samples of the freezing and diluting experiment.The scattering pattern shows characteristic features of star-like polymer micelles: a low Q Guinier Plateau and a Q−1.7 power law dependence at high Q arising from the blob scattering of the polymer in the shell. Both regions are connected by a steep decrease in intensity at intermediate Q. The global micellar parameters, Nagg, Rm were extracted from core–shell model fits using least-square fit routines. The core radius Rc was calculated by:
 | (12) |
For a detailed description of the data modeling we refer to ref. 19, here only a brief summary is given. During the fitting procedure, the scattering length densities ρc,sh,D2O were taken as calculated in Section 3.2, the block molar volumes Vc,sh as obtained from the polymer characterization, and volume fraction ϕ as calculated from the solution preparation. These parameters were kept constant throughout the analysis leading to a significant reduction of fit parameters. The parameter ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) was found to describe the data best when fixed to a value of
was found to describe the data best when fixed to a value of ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) = 0.2 for all fits. The parameter σint describing the surface roughness of the core–corona interface was set to σint = 8 Å. The length scale ξ of the “blobs” in the micellar corona was fixed to 48 Å. The global micellar parameters are rather insensitive to changes of ξ and σint which influence the fit in the high Q-regime where statistics are generally poor. Keeping the above parameters constant, the best fit yields a micellar radius of Rm = 111 Å, an aggregation number of Nagg = 100 and a core radius of Rc = 27 Å. The fit is shown as a solid line in Fig. 1 revealing an excellent agreement with the experimental data. As shown by Zinn et al.19 a typical second virial coefficient for such systems of about A2 = 1 × 10−4 cm3 mol g−2 has basically no effect on the global fit parameters at 0.25%. Also polydispersity effects could be neglected which is understandable as micelles at equilibrium are generally narrowly distributed.
= 0.2 for all fits. The parameter σint describing the surface roughness of the core–corona interface was set to σint = 8 Å. The length scale ξ of the “blobs” in the micellar corona was fixed to 48 Å. The global micellar parameters are rather insensitive to changes of ξ and σint which influence the fit in the high Q-regime where statistics are generally poor. Keeping the above parameters constant, the best fit yields a micellar radius of Rm = 111 Å, an aggregation number of Nagg = 100 and a core radius of Rc = 27 Å. The fit is shown as a solid line in Fig. 1 revealing an excellent agreement with the experimental data. As shown by Zinn et al.19 a typical second virial coefficient for such systems of about A2 = 1 × 10−4 cm3 mol g−2 has basically no effect on the global fit parameters at 0.25%. Also polydispersity effects could be neglected which is understandable as micelles at equilibrium are generally narrowly distributed.
The SANS data of the diluted solutions of different concentrations up to ϕ = 15% are shown in Fig. 1. These data were offset by multiplicative constants for better visibility. The data were individually fitted with the core–shell model following the same fitting procedures and keeping the same parameters constant as described above for the reference sample. The fit results for Nagg and Rm of these analysis are shown in Table 2, corresponding fits as solid lines in Fig. 1. It can be seen that the scattering pattern is independent of the parent concentration from which it was frozen and diluted, showing only minor differences from the reference sample. The micellar radius Rm was found to be constant with concentration. Nagg shows some minor deviations around a mean Nagg = 100 ± 5 which are within the errors of the model fits independent of concentration. However, as an exception from this observation, the sample diluted from a 12% solution shows a much smaller aggregation number. This can be explained by the normalization of the absolute intensity to the concentration and the therefore high sensitivity to concentration errors which can occur during sample preparation and especially during the freezing and diluting process. Furthermore, additional fluctuations of the absolute intensity can occur by uncertainties during absolute calibration and data reduction. Taking this into account, Nagg can be considered to be constant within experimental accuracy in the investigated concentration regime as the deviations do not follow an apparent trend (Table 2).
| ϕ (%) | N agg | R M (Å) | R C (Å) |
|---|---|---|---|
| 0.25 (ref) | 100 ± 3 | 111 ± 4 | 27 ± 2 |
| 2.7 | 105 ± 4 | 110 ± 4 | 27 ± 2 |
| 5.4 | 98 ± 3 | 110 ± 4 | 26 ± 2 |
| 7.3 | 100 ± 3 | 112 ± 4 | 27 ± 2 |
| 8.5 | 96 ± 3 | 110 ± 4 | 26 ± 2 |
| 10 | 96 ± 3 | 110 ± 4 | 26 ± 2 |
| 12 | 88 ± 3 | 110 ± 4 | 25 ± 2 |
| 15 | 100 ± 3 | 112 ± 4 | 27 ± 2 |
In addition to the diluted samples at ϕ = 0.25%, SANS measurements were performed on the concentrated micellar solutions. The data were collected with an improved wave length resolution of Δλ/λ = 5% employing the time-of-flight option at KWS-246 at MLZ in Garching. At volume fractions in the range 7.3% ≤ ϕ < 30% the scattering pattern reveal ordering of micelles into fcc crystals whereas at concentrations of ϕ ≥ 30% bcc crystals were identified. Scattering curves at 9% and 30% volume fraction are exemplarily shown in Fig. 2. We will use the position of the first structure factor peak Qmax which refers to the distance of the 111 lattice planes in the fcc crystal or 110 lattice planes in a bcc crystal, respectively. From this we can calculate the lattice parameter a for the different crystal structures according to:
 | (13) |
 | (14) |
 | (15) |
 | (16) |
| ϕ (%) | Structure | a (Å) | N agg |
|---|---|---|---|
| 7.3 | fcc | 371 | 134 |
| 8.5 | fcc | 357 | 133 |
| 10 | fcc | 331 | 125 |
| 12 | fcc | 322 | 139 |
| 15 | fcc | 298 | 139 |
| 20 | fcc | 265 | 128 |
| 30 | bcc | 185 | 133 |
| 50 | bcc | 164 | 157 |
| 72 | bcc | 177 | 280 |
The values for the aggregation numbers Nagg obtained from the cooling and dilution experiment and from the crystal structure analysis are shown in Fig. 3 as a function of polymer volume fraction normalized to the overlap concentration ϕ*. We note that for this plot ϕ* is corrected for a temperature induced change of micellar size. This is necessary because we have to recall that the corona shrinks upon heating since the solvent quality of water for PEO decreases with increasing temperature. Zinn et al.19 were able to quantify the shrinkage of the corona thickness D of Cn-PEO5 micelles to be roughly 10% when heating from 20 °C to 60 °C. This heating induced shrinkage has a direct impact on the overlap concentration ϕ* since for C28-PEO5 ϕ* was determined from viscosity measurements at T = 15 °C, the equilibration process of the micelles however was carried out at T = 60 °C. Taking the shrinkage into account, the overlap concentration was re-calculated to be ϕ*(60 °C) ≈ 12.1%. The concentration ϕ** ≈ 34%, where the coronal star structure is supposed to disappear, was calculated from eqn (4). For the calculation values corrected for temperature effects of 12.1% for ϕ* and D(60 °C) = 76 Å, calculated with the experimental values of Rm and Rc from model fits at 0.25%, were used. Both ϕ* and ϕ** are shown as vertical dashed lines in Fig. 3, dividing the observed concentration range in dilute, semidilute, and concentrated region.
 | ||
| Fig. 3 Concentration dependence of Nagg as determined by freezing and diluting experiment (○) and crystal structure analysis (◇) normalized to the overlap concentration. Scaling behavior of Nagg according to eqn (3) assuming equilibrium aggregation number of Nagg = 100 in the dilute limit shown as red line. | ||
From Fig. 3 it can be seen that the data obtained from the freezing and diluting experiment covers essentially only the dilute region. Inside this region the aggregation number Nagg = 100 is constant within experimental uncertainty. This observation is in full agreement with the scaling law presented in eqn (7) which does not contain any concentration dependent term. The data from the crystal structure analysis span a concentration range from 7.3% to 72%, significantly expanding the investigated region up to 6·ϕ*, far beyond the concentrations accessible by the freezing and diluting experiment (see Fig. 3). The figure further reveals, that the calculated Nagg values from the crystal structure analysis are systematically higher than the values obtained by the freezing and diluting experiment. We explain this discrepancy by deviations from the perfect, homogeneous crystals assumed for the geometrical calculations. This discrepancy can be considered as a constant error which does not affect the observed trend of Nagg with increasing concentration. In fact, the Nagg values of both analysis show the same constant concentration behavior in the region where both methods overlap. This behavior continues until the concentration ϕ** is reached.
The constant behavior of Nagg in the semidilute region can now be compared to the scaling prediction for this concentration range. For this purpose we have calculated the concentration dependence of Nagg for our C28-PEO5–D2O system using ϕ** = 34% and an Nagg = 100 following eqn (3). The result of this calculation is shown as a red solid line in Fig. 3 revealing a complete disagreement with the experimental data.
At concentrations above ϕ** at ϕ = 50% and 72% Nagg clearly increases to 157 and 280, respectively. This increase is significantly larger than what is expected from the scaling theory (see eqn (3)) which predicts a weak power law dependence of Nagg3/4. It has been discussed by Zhulina et al.,53 that in this concentration range the system possibly changes the morphology of the micelles with increasing concentration. There is however no evidence for such a morphological change in the scattering data which clearly identify crystalline phases.
The clear disagreement of our results with the scaling predictions in semidilute and highly concentrated solutions requires a critical reflection of the validity of the experimental data. First of all we have to justify that the system is in full thermodynamic equilibrium. Therefore, we stress again that thermodynamic equilibrium at 60 °C can certainly be presupposed because of the known fast time scale for chain exchange as the elementary step to reach and attain equilibrium. Even when we take into account one order of magnitude slower chain exchange at higher concentrations as found by Choi et al.42 the sample preparation at 60 °C for more than 6 hours guarantees fully equilibrated systems for all concentrations.
We should further recall that the aggregation number of similar n-alkane-PEO–water systems was systematically measured by SANS and found to be independent of temperature between 20 °C to 60 °C.19 This is basically a consequence of the temperature independent interfacial tension γ between D2O and n-alkane in this temperature range, as already measured for the hydrocarbon PEP in water–N,N-dimethylformamide mixtures in ref. 15. Thus, a change of Nagg upon cooling to 15 °C due to changes of γ can be excluded. Hence, we can conclude that the micelles are in equilibrium at 60 °C and the single micellar structure is preserved at 15 °C.
We can compare our results additionally with the theoretical result by Grason33,54 which is based on mean field calculations. According to this theory, the micellar aggregation number in a fixed bcc structure is expected to increase linearly with concentration in the semidilute region above the critical concentration ϕ* where the micellar corona start to overlap. The system avoids this energetically unfavoured situation by reducing the number density of micelles leading to an increased mean aggregation number. When increasing the concentration even further, strong overlap of the corona forming polymer chains is unavoidable, such that it becomes preferable to reduce Nagg, increasing the lattice density but also reducing the strength of repulsions. Nevertheless, our experimentally observed Nagg dependence in both regions is inconsistent with theoretical predictions.
Finally, to discuss the clear disagreement of our results with the theory we recall that the scaling laws of eqn (3) were derived for the strong segregation limit (SSL) where the interfacial tension γ assumes large values and the core and corona blocks are highly stretched. Geometrically, this situation appears to be fulfilled. In order to proof the stretching of the n-alkane within the micellar core we have calculated the length of the C28H57 block in all trans conformation (contour length) by: lmax = 1.5 + 1.265(n − 1) = 35.7 Å, with n = 28 the number of carbons in the n-alkyl block.55 By comparing with the radius of the micellar core, Rc = 27 Å, we find that Rc ≃ 0.75·lmax. This indicates that the octacosanyl chain in the core is elongated but by far not fully stretched. The reduced length is due to several kinks along the chain and are equal to the dimensions found in a liquid like core, although it is known that long n-alkyl chains partly crystallize inside micellar cores.50 Following the latter result we may conclude that the concentration dependence of Nagg should follow the scaling laws predicted for the SSL regime.
However, when the interfacial tension exceeds a critical value γ* the system enters the super strong segregation limit (SSSL). In this region the core blocks are completely stretched meaning that spherical micelles cannot further grow as this would lead to an empty space in the center which is virtually impossible.39–41 Hence, Nagg becomes independent of γ but for the same reason also independent of polymer concentration ϕ. Taking into account that the interfacial tension between n-alkanes and water are very high, γ ≥ 50 mN m−1, and that the aggregation number is independent of temperature between 20 °C to 60 °C19 we might argue that our micelles need to be discussed in the SSSL regime even though geometrically this is not the case.
We should note that according to Semenov et al.39 micellar growth in the SSSL regime is still possible but can only occur by a one or two-dimensional growth leading to a shape transformation of the core from spherical to cylindrical or even disclike shape. This might be the case for the micelles at the two highest concentrations where considerable larger aggregation numbers were extracted from the crystal structure analysis. A direct observation of a morphological transition of the micellar cores cannot be deduced from our data as most of the scattering arises from the PEO corona which still remains spherical as the corona size is considerably larger than the core domain.
We should further note that the hydration of the PEO chain was assumed to be constant over the whole concentration range. Theory predicts a hydration level of two per EO monomer.56 Stoichiometrically only for the highest concentration at 72% this ratio cannot be reached any more. Hence, we may suppose a depletion of water molecules in particular close to the interface. This might have an effect on the aggregation behavior but cannot be quantified from our results.
Our results are furthermore in contrast to previous experimental results obtained by Puaud et al.28,29 who found a significant increase of the aggregation number with concentration when exceeding a critical concentration. Their results were measured on an amphiphilic block copolymer with a different hydrophobic block in water by light scattering after photochemical crosslinking the micellar core before diluting. For this polymer the observed increase of Nagg might be explained by the fact that the hydrophobic block carries polar chemical groups, e.g. ester linkages, leading to a much lower γ. Hence, this system follows the predictions of the SSL regime. On the other hand as stated by the authors the in situ cross linking process lead to aggregation numbers which are higher by almost a factor of 2 in dilute solution. The increase was explained by reorganization of micellar structure during cross-linking. What may happen at finite concentration is not known. Furthermore, an equilibrium mechanism for the reorganization was not given such that the resulting structures most likely reflect a non-equilibrium situation where a discussion within the scaling theories is not justified.
5 Conclusion
In summary, the C28-PEO5–water system of this work is considered to be an ideal model system because of the formation of well defined star-like micelles with comparably high aggregation numbers in dilute solution. The system further shows a temperature independent aggregation, and equilibrium kinetics which can be easily controlled in an experimentally convenient narrow temperature window between 20 °C to 60 °C. The results of the cooling and dilution experiment and crystal structure analysis of the C28-PEO5–water system show a completely different picture of the dependence of Nagg with increasing concentration than expected from scaling theories for star-like polymer micelles in the SSL regime and differ also from previous investigations on this topic.28,29 The observed constant Nagg in the semidilute concentration range may indicate that our micellar system under the experimental conditions already approaches the SSSL even though the size ratio Rc/lmax does not yet confirm fully elongated chains. We therefore may conclude that from experimental point of view the assignment to the SSL or SSSL regime is problematic as there is not a sharp transition between the two regimes.Acknowledgements
The authors gratefully thank Reidar Lund and Thomas Zinn for helpful discussion. This work is based upon experiments performed at the KWS-2 instrument operated by JCNS at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany.References
- I. W. Hamley, The Physics of Block Copolymers, Oxford University Press, Oxford, 1998 Search PubMed.
- P. Alexandridis and B. Lindman, Amphiphilic Block Copolymers: Self-Assembly and Applications, Elsevier Science B.V., Amsterdam, 2000 Search PubMed.
- Z. Tuzar and P. Kratochvil, Surf. Colloid Sci., 1993, 15, 1–83 CrossRef CAS.
- A. Halperin, M. Tirrell and T. Lodge, Adv. Polym. Sci., 1992, 100, 33–71 Search PubMed.
- G. Riess, Prog. Polym. Sci., 2003, 28, 1107–1170 CrossRef CAS.
- J.-F. Gohy, Adv. Polym. Sci., 2005, 190, 65–136 CrossRef CAS.
- R. Lund, L. Willner and D. Richter, Adv. Polym. Sci., 2013, 259, 51–158 CrossRef CAS.
- L. Leibler, H. Orland and J. C. Wheeleer, J. Chem. Phys., 1983, 79, 3550–3557 CrossRef CAS PubMed.
- J. Noolandi and K. M. Hong, Macromolecules, 1983, 16, 1443–1448 CrossRef CAS.
- R. Nagarajan and K. Ganesh, J. Chem. Phys., 1989, 90, 5843–5856 CrossRef CAS PubMed.
- A. Halperin, Macromolecules, 1987, 20, 2943–2946 CrossRef CAS.
- T. M. Birshtein and E. B. Zhulina, Polymer, 1989, 30, 170–177 CrossRef CAS.
- D. Izzo and C. M. Marques, Macromolecules, 1993, 26, 7189–7194 CrossRef CAS.
- L. Willner, A. Poppe, J. Allgaier, M. Monkenbusch, P. Lindner and D. Richter, Europhys. Lett., 2000, 51, 628–634 CrossRef CAS.
- R. Lund, L. Willner, J. Stellbrink, A. Radulescu and D. Richter, Macromolecules, 2004, 37, 9984–9993 CrossRef CAS.
- M. Laurati, J. Stellbrink, R. Lund, L. Willner, D. Richter and E. Zaccarelli, Phys. Rev. Lett., 2005, 94, 195504 CrossRef CAS.
- M. Laurati, J. Stellbrink, R. Lund, L. Willner, E. Zaccarelli and D. Richter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041503 CrossRef CAS.
- B. Lonetti, M. Camargo, J. Stellbrink, C. N. Likos, E. Zaccarelli, L. Willner, P. Lindner and D. Richter, Phys. Rev. Lett., 2011, 106, 228301 CrossRef CAS.
- T. Zinn, L. Willner, R. Lund, V. Pipich, M.-S. Appavou and D. Richter, Soft Matter, 2014, 10, 5212–5220 RSC.
- G. Grest, L. J. Fetters, J. Huang and D. Richter, Adv. Chem. Phys., 1996, 94, 67 CrossRef CAS PubMed.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CAS.
- J. Stellbrink, G. Rother, M. Laurati, R. Lund, L. Willner and D. Richter, J. Phys.: Condens. Matter, 2004, 16, S3821–S3834 CrossRef CAS.
- N. Hadjichristidis, H. Iatrou, S. Pispas and M. Pitsikalis, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 3211–3234 CrossRef CAS.
- G. A. McConnell, A. P. Gast, J. S. Huang and S. D. Smith, Phys. Rev. Lett., 1993, 71, 2102–2105 CrossRef CAS.
- T. P. Lodge, J. Bang, M. J. Park and C. Kookheon, Phys. Rev. Lett., 2004, 92, 145501 CrossRef.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- T. Nicolai, O. Colombani and C. Chassenieux, Soft Matter, 2010, 6, 3111–3118 RSC.
- F. Puaud, T. Nicolai, E. Nicol, L. Benyahia and G. Brotons, Phys. Rev. Lett., 2013, 110, 028302 CrossRef.
- F. Puaud, T. Nicolai, L. Benyahia and E. Nicol, J. Phys. Chem. B, 2013, 117, 12312–12318 CrossRef CAS PubMed.
- L. Willner, A. Poppe, J. Allgaier, M. Monkenbusch and D. Richter, Europhys. Lett., 2001, 55, 667–673 CrossRef CAS.
- R. Lund, L. Willner, D. Richter and E. E. Dormidontova, Macromolecules, 2006, 39, 4566–4575 CrossRef CAS.
- A. Halperin, Macromolecules, 2011, 44, 5072–5074 CrossRef CAS.
- M. Grason, J. Chem. Phys., 2007, 126, 114904 CrossRef PubMed.
- T. Zinn, L. Willner, R. Lund, V. Pipich and D. Richter, Soft Matter, 2012, 8, 623–626 RSC.
- T. Zinn, PhD thesis, Westfälische Wilhelms-Universität Münster, 2013.
- T. Zinn, L. Willner, D. Richter and R. Lund, ACS Macro Lett., 2015, submitted Search PubMed.
- H. Benoit and G. Hadziioannou, Macromolecules, 1988, 21, 1449–1464 CrossRef CAS.
- L. Willner, O. Jucknischke, D. Richter, J. Roovers, L.-L. Zhou, P. M. Toporowski, L. J. Fetters, J. S. Huang, M. Y. Lin and N. Hadjichristidis, Macromolecules, 1994, 27, 3821–3829 CrossRef CAS.
- A. N. Semenov, I. A. Nyrkova and A. R. Khokhlov, Macromolecules, 1995, 28, 7491–7500 CrossRef CAS.
- I. A. Nyrkova, A. R. Khokhlov and M. Doi, Macromolecules, 1993, 26, 3601–3610 CrossRef CAS.
- P. G. Khalatur, A. R. Khokhlov, I. A. Nyrkova and A. N. Semenov, Macromol. Theory Simul., 1996, 5, 749–757 CrossRef CAS PubMed.
- S.-H. Choi, F. S. Bates and T. P. Lodge, Macromolecules, 2011, 44, 3594–3604 CrossRef CAS.
- I. M. Krieger and T. J. Dougherty, Trans. Soc. Rheol., 1959, 3, 137–152 CrossRef CAS.
- A. Radulescu, V. Pipich, H. Frielinghaus and M.-S. Appavou, J. Phys.: Conf. Ser., 2012, 012026 CrossRef.
- C. Sommer, J. S. Pedersen and P. C. Stein, J. Phys. Chem. B, 2004, 108, 6242–6249 CrossRef CAS PubMed.
- A. Radulescu, N. K. Szekely, S. Polachovsky, M. Leyender, M. Amann, J. Buitenhus, M. Drochner, R. Engels, H. Frielinghaus, G. Kemmerling, P. Lindner, A. Papagiannopoulos, V. Pipich, L. Willner and D. Richter, J. Appl. Crystallogr., 2015 Search PubMed , submitted.
- J. S. Pedersen and C. Svaneborg, Curr. Opin. Colloid Interface Sci., 2002, 7, 158–166 CrossRef CAS.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134–146 CrossRef CAS.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- T. Zinn, L. Willner and R. Lund, Phys. Rev. Lett., 2014, 113, 238305 CrossRef CAS.
- P. G. Nilsson and B. Lindman, J. Phys. Chem., 1983, 87, 4756–4761 CrossRef CAS.
- R. P. Murphy, E. G. Kelley, S. A. Rogers, M. O. Sullivan and T. H. Epps, ACS Macro Lett., 2014, 3, 1106–1111 CrossRef CAS PubMed.
- E. B. Zhulina, M. Adam, I. LaRue, S. S. Sheiko and M. Rubinstein, Macromolecules, 2005, 38, 5330–5351 CrossRef CAS.
- The theoretical trend was derived for symmetric diblocks in a limit where the interfacial tension between insoluble block and solvent was assumed to be much smaller (10 mN m−1) than for the n-alkane/water with 50 mN m−1.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, Wiley Interscience, New York, 1980 Search PubMed.
- E. E. Dormidontova, Macromolecules, 2002, 35, 987–1001 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |


![[pentagon open]](https://www.rsc.org/images/entities/char_e1c1.gif)


