Tuning colloidal gels by shear

Abstract

Using a powerful combination of experiments and simulations we demonstrate how the microstructure and its time evolution are linked with mechanical properties in a frustrated, out-of-equilibrium, particle gel under shear. An intermediate volume fraction colloid–polymer gel is used as a model system, allowing quantification of the interplay between interparticle attractions and shear forces. Rheometry, confocal microscopy and Brownian dynamics reveal that high shear rates, fully breaking the structure, lead after shear cessation to more homogeneous and stronger gels, whereas preshear at low rates creates largely heterogeneous weaker gels with reduced elasticity. We find that in comparison, thermal quenching cannot produce structural inhomogeneities under shear. We argue that external shear has strong implications on routes towards metastable equilibrium, and therefore gelation scenarios. Moreover, these results have strong implications for material design and industrial applications, such as mixing, processing and transport protocols coupled to the properties of the final material.

---

1 Introduction

Improving material properties through intelligent design of their microstructure and molecular interactions is a central goal of materials science that requires an in-depth understanding of the fundamental physics involved. An additional control is provided by processing, i.e. the route followed in manufacturing or synthesizing a specific material, especially when out-of-equilibrium metastable states are involved. In mesoscopic soft matter systems, where building blocks self-assemble en route to thermodynamic equilibrium while affected by kinetic arrest,¹ external fields are quite common² and increasingly utilized in experimental studies.^3–5 Moreover, as structural changes occurring during processing significantly influence the end product, external fields such as shear may be utilized in smart applications of complex multicomponent materials ranging from flow of biological fluids,⁶ tissue engineering,⁷ food formulations⁸ and personal care products⁹ to drilling muds,¹⁰ ceramics¹¹ and high performance concretes.¹²

Due to their large size and easily tunable interactions colloids are ideal for studying several open condensed matter physics problems such as the glass transition and the interplay between thermodynamic phases and metastable, non-ergodic states¹³ which are ubiquitous in materials, industrial processes and biological systems. An additional parameter related to the glass transition and the jamming scenario is shear stress, which combined with temperature (or interparticle interactions) and volume fractions provides a generically unified jamming phase diagram.¹⁴ Again colloids arise as a prominent model system where a wealth of structural and dynamical phenomena¹⁵ such as shear induced melting (yielding),^16,17 slip,^18,19 shear banding,^20,21 ordering,^22,23 shear induced jamming²⁴ and frozen-in stresses²⁵ can be studied.

At low concentrations of attractive or charge stabilized particles, shear and flow may cause cluster break-up,^26–28 shear included aggregation leading to increased viscosity and elasticity^29–31 and delayed yielding³² or collapse of the gel network.^33,34 On the other hand at high particle volume fractions and/or attraction strengths colloids at rest acquire a variety of solid-like, non-ergodic states due to the formation of a microscopic network structure.^28,35–37 If, however, high enough stresses (or strains) are applied, the network will break, often in multiple steps due to the existence of spatial heterogeneities^17,38–41 and flow in a strongly non-Newtonean manner, also exhibiting significant thixotropy and ageing.^42,43 Preshear may affect mechanical properties such as the yield stress and viscoelastic moduli,^43,44 while depending on the shear rate, strong bond breaking or enhanced cluster formation is found in bulk,^6,45–47 2D,⁴⁸ or microchannels.⁴⁹ The elucidation of such rich flow response can be brought about only through the study of model systems with tunable interactions and by deploying a combination of experimental techniques and simulations. This may provide detailed information to guide the formulation of a comprehensive theoretical framework with predictive power. One of the most commonly used model systems for attractive particles is colloid–polymer mixtures where non-adsorbing polymer chains induce an attractive force between colloidal particles, with a strength and range that depend on the concentration and size of polymer chains, respectively.^50,51

In this paper we use a combination of rheology, rheo-confocal microscopy and computer simulations to demonstrate how the control of the externally imposed shear rate during rejuvenation (or processing) can tune the final structure and therefore mechanical properties of a model colloidal gel. Strong structural changes during flow as well as during gel reformation after flow cessation are corroborated by the interplay between shear and attractive forces. By computer simulation we find that structures created by shear may not be reproduced by instantaneous thermal quenching. Our findings have strong implications for material design and industrial processes, as they suggest how the implementation of well-defined modifications in mixing, processing and transport protocols of multicomponent systems can couple to, or alter the properties of final products.

2 Methods

For rheo-confocal measurements, we used concentrated suspensions of sterically stabilized poly(methyl methacrylate) (PMMA) with nearly hard-sphere particles of radius R = 830 nm (determined by confocal imaging) suspended in a density and refractive index matching the mixture of decalin and cyclobromoheptane. Depletion attractions were induced through the addition of non-adsorbing linear polystyrene (PS) chains with a molecular weight, M_w = 7 450 000 g mol⁻¹ and a radius of gyration, R_g = 113 nm. We used samples with a particle volume fraction ϕ = 0.44, as determined by Voronoi volumes and particle tracking,⁵² and a PS concentration, c_p = 0.0022 g ml⁻¹ resulting in an interparticle attraction at the contact of U(2R) ≃ −16k_BT and a range of attraction ξ ≃ 0.05 according to ref. 53. Rheological experiments were used to measure flow curves (steady state stress versus shear rate) and linear viscoelastic moduli while confocal microscopy under shear provided simultaneous structural analysis. An Anton-Paar MCR501 rheometer with cone-plate geometry (50 mm and 0.01 rad angle) coupled with a fast scanning VT-eye confocal unit (Visitech) mounted on an inverted microscope (Nikon) was used. The bottom glass coverslip was roughened by sintering a mixture of sand granules (>100 μm) and PMMA particles. Imaging was possible in the areas between the granules (≈1 mm) and measurements were acquired in imaging volumes with linear flow profiles. 3D images were taken after shear cessation, and the evolution of void structures was examined. The shear rates in rheo-confocal experiments correspond to local values determined from flow profiles prior to shear cessation and have an estimated 10% standard deviation.

Rheo-confocal measurements were complemented by conventional rheometry using roughened cone-plate geometries that prevent slips. The long-time rheological response was studied using PMMA particles with R = 400 nm (determined by light scattering) and PS chains with M_w = 283 300 g mol⁻¹ and R_g = 17 nm, dispersed in decalin. The polymer concentration, c_p = 0.0065 g ml⁻¹ at a particle volume fraction ϕ = 0.44, gives an attractive potential of U_dep(2R) ≃ −23.2k_BT and a range of attraction ξ ≃ 0.03.⁵³

For the cessation experiments, the samples were pre-sheared starting from the high shear rate (typically 100 s⁻¹), down to the shear rate in question, allowing for a steady state to be reached. As far as we have seen, both in experiments and simulations, the route followed to reach the final preshear rate after the high shear rate rejuvenation (i.e. directly or through a flow curve) did not affect the steady shear state reached during preshear.

In the case of rheo-imaging, although the size of the cone truncation gap was of the order of the roughness, most of the rheological torque arises from the outer part of geometry, where the actual gap is much larger. The corresponding confocal images were also taken towards the edge of the cone. Moreover, conventional rheology measurements verified the findings.

We also performed Brownian dynamics (BD) simulations that provide both mechanical information as well as detailed microstructure of the system under shear. Hard-sphere interactions were implemented using a potential-free algorithm⁵⁴ while attractions were included using an Asakura–Oosawa (AO) potential⁵⁰ with similar parameters as our experiments. The range of attraction used was ξ = 0.1 with the attraction strengths, U(2R) = −6, −10, −20 and −50k_BT. This allows a direct comparison between BD and experiments in terms of interactions, structure and stress response and examination of the validity of the Pe_dep scaling at various attraction strengths. In BD affine shear was applied on typically 5405 particles using periodic boundary conditions, while no crystallization was detected.

As BD simulations do not induce hydrodynamic interactions, there is a discrepancy with the short-time particle diffusion in a real experimental system. The latter is expected to be at least one order of magnitude smaller⁵⁵ in comparison with the free diffusion inside the highly concentrated clusters, in analogy with diffusion in a dense glass. Thus we scale the non-dimensional experimental Brownian time scale t_B, Pe (reflecting its scaled version, Pe_sc) and Pe_dep by an order of the magnitude correction factor of 10 throughout the figures. Moreover, although the simulation parameters are chosen to be as close as possible to the experiments, we expect experimental uncertainties in particle interactions (i.e. potential shape and depth) and the volume fraction to produce differences when performing comparisons. Configurations were visualized using the open source Visual Molecular Dynamics (VMD) program.⁵⁶

3 Results and discussion

3.1 Steady state under shear

We study gels in which particles aggregate due to a “depletion” attraction induced by non-adsorbing polymers.^50,51 Experiments and BD simulations probe the microscopic structure of such depletion gels during steady shear as a function of shear rate as well as the linear viscoelastic properties during restructuring after cessation of shear. Experimentally, our depletion gels consist of PMMA hard-spheres and PS linear chains in suspension at ϕ = 0.44 with an attraction strength well above the gelation threshold³⁷ while BD simulations⁵⁴ were conducted at similar Asakura–Oosawa (AO) interparticle potential⁵⁰ parameters. The steady state stress response of the gel at different shear rates, [small gamma, Greek, dot above], and typical slices of the microstructures are shown in Fig. 1 from rheo-confocal experiments and BD simulation data. Experiments and simulations show strikingly similar flow curves and structures under shear, verifying that BD, although lacking in full hydrodynamic interactions (HI) captures efficiently the fundamental macromechanical and microstructural response of the system. Without attractions, the effect of shear can be quantified by the non-dimensional Peclet number, 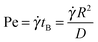, the product of the shear rate and the Brownian diffusion time, with the free diffusion coefficient, D = D₀ (, with R being the radius of the particle and η being the solvent viscosity) used in BD (in the absence of HI), while in experiments, the ϕ dependent short-time diffusion coefficient, D(ϕ), is used (the non-dimensional Peclet number is then denoted as Pe_sc).

Fig. 1 Normalized stresses as a function Pe for BD simulations (red circles) and of Pe_sc for experiments (black squares), along with confocal (top) and simulation (bottom) images of structures under flow with rates indicated using arrows in the main figure. Experiments shown are at a volume fraction ϕ = 0.44, a potential depth at the contact U_dep(2R) ≃ −16k_BT and a range of ξ ≃ 0.05 (Pe/Pe_dep ≃ 160). Simulations were set to ϕ = 0.44, U_dep(2R) = −20k_BT and ξ = 0.1 (Pe/Pe_dep ≃ 100). A power law slope of unity is shown for the higher rates (black line), while a power law fit discussed in the text is also shown.

Shearing at high Pe leads to a simple viscous stress response, where the stress increases linearly with the shear rate, indicating that a strongly shear-melted colloidal gel flows as a Newtonian fluid. The corresponding snapshots of the structure under shear show that the gel network and clusters are broken down completely and the particles are distributed randomly as expected in the equivalent volume fraction fluid of hard spheres.

At lower Pe, the flow curve tends to a yield stress plateau typical for a soft matter solid.^39,45 Slightly above the yield stress the sample exhibits plastic flow with the stress increasing weakly with the shear rate. Here both simulations and experiments reveal a shear thinning response with a sublinear power law increase of the stress with a power of about 0.32 for 5 ≲ Pe ≲ 500. Microscopic imaging of the system in this regime reveals a highly inhomogeneous microstructure with large empty voids. Their size decreases with the shear rate, suggesting that the shear thinning sublinear decrease of the apparent viscosity (equivalent to the stress increase) is due to a reduction of the cluster size with shear rate, in qualitative agreement with the behavior of lower volume fraction fractal clusters and gels.^26,27

When strong interparticle depletion forces are present, leading to clustering and gel formation, the [small gamma, Greek, dot above]-dependent structural changes can be attributed to the balance between shear and depletion attraction. An estimate of this is given by a modified Peclet number, Pe_dep, which reflects the ratio of shear to depletion forces³⁸

with U_dep(2R) being the potential at the contact and ξ being the range of attraction. For Pe_dep > 1, bonds between particles are expected to be ruptured by shear forces and attractions do not affect the structure, leading to liquid-like behavior. Conversely for Pe_dep < 1, the system is strongly affected by interparticle attractions, with shear enabling particles to explore configurational space and create compact clusters. Note that the ratio Pe/Pe_dep (= U_dep(2R)/2k_BTξ) depends only on the characteristics of the attraction potential and is independent of the shear rate.

3.2 Shear cessation

After cessation of shear (end of rejuvenation) the melted gel reforms, beginning from the steady-state structure created under shear. The linear viscoelastic properties evolve as shown in Fig. 2a, where G′ and G′′ are plotted for low and high shear rates, along with the corresponding confocal microscopy images (Fig. 2b) at 10t_B after shear cessation. An initial fast increase of both G′ and G′′ is followed by a slower evolution, indicative of further restructuring and gel coarsening. After a low shear rate preshear, the system almost instantaneously (for t ≲ 0.1t_B) acquires a solid like response with G′ > G′′, and then evolves weakly with time until an almost steady state is reached after about 10t_B. A preshear at high shear rates, however, is followed by a stronger increase of G′, starting from a liquid state but eventually creating a sample with stronger solid-like response, as evidenced by G′ increasing above the value following a weak shear rate rejuvenation.

Fig. 2 (a) Rheo-confocal experiments: time evolution of the linear viscoelastic moduli of a colloidal gel at 1 rad s⁻¹ (R = 830 nm, ϕ = 0.44, U_dep(2R) ≃ −16k_BT, ξ ≃ 0.05, Pe/Pe_dep ≃ 160) after cessation of shear rejuvenation at high and low shear rates, as indicated: G′ (solid symbols) and G′′ (open symbols); (b) the corresponding confocal images at t = 10t_B. (c) Rheological measurements of a similar colloidal gel at 10 rad s⁻¹ (ϕ = 0.44, U_dep(2R) ≃ −23.5k_BT, ξ ≃ 0.03 and Pe/Pe_dep ≃ 400) with smaller spheres (R = 400 nm) allowing the determination of long time behavior (only G′).

Confocal images provide valuable information on the microstructural evolution of the gel. After a low shear rate preshear, the gel remains highly heterogeneous, essentially retaining the steady state structure acquired during shear (Fig. 1). Higher shear rates show a continuous subtle evolution of the structure from a liquid-like to an interconnected network (see also ESI† confocal time-lapse movie). As inferred from the results shown in Fig. 1, the Pe regimes where different behaviors arise are correlated with the power-law slopes of the flow curve (Fig. 1). At high shear rates, where the stress increases linearly with the shear rate, extended restructuring is expected after shear cessation as interparticle attractions become important again and the gel gets reformed. However, around the yield stress plateau, plastic flow takes place, and particles are given ample time to reconfigure and compactify within clusters, while the system does not exhibit significant structural rearrangement after shear is stopped. Therefore by increasing Pe of preshear we observe a transition from a highly inhomogeneous gel created at low shear rates to a rather homogeneous network produced at high shear rates.

In Fig. 2c we present additional rheological data of a similar colloid–polymer gel using smaller particles. In agreement with the rheological trends inferred from the rheo-confocal experiments, the elastic modulus exhibits a moderate increase after weak preshear (Pe_dep < 1) in contrast to preshear at Pe_dep > 1, where stronger gel structures, with higher G′, are created at long times. For longer waiting times and for both cases, the viscoelastic moduli were frequency independent (1–10 rad s⁻¹), while the transient, full frequency dependence was less accessible due to time constraints.

These additional measurements also allow us to monitor the rheological evolution at longer times. It should be noted that although samples for confocal imaging are close to density matched, using micron size particles introduces gravitational effects that preclude measurements longer than those presented here. At significantly longer times, G′ and G′′ may start decreasing, especially in the cases where dense clusters are formed, due to sedimentation.

We monitor structural heterogeneity using a real-space variable, as the structure factor for such intermediate volume fraction gels is less sensitive in revealing structural changes. Here we use the void volume, VV, which quantifies the volume of empty space (voids) in the gel.⁵⁷ The VV of a point in space is defined as the volume of a sphere in contact with a particle surface, with the center of the sphere defining the position of the void in space. The probability density of the void volume, VVPDF, provides a quantitative measure of real-space heterogeneity (see ESI† figure). This analysis method was chosen over using a measure of the cluster size due to the ambiguity in defining the latter in a percolated gel.

In Fig. 3 we plot the VVPDF deduced from experiments and simulations after shear cessation and the time evolution of its average values, 〈VV〉. VVPDF values smaller than the particle size (VV < R³) represent gaps within close-packed areas, while higher values reflect large spatial heterogeneities (Fig. 3a and b). Confocal experiments and BD simulations show similar results: low shear rates produce highly heterogeneous systems, with large VVPDF values, in contrast to high shear rates, as is visually evident in Fig. 2b. By examining 〈VV〉 we may gauge the changes in heterogeneity with time, as shown in Fig. 3c and d, where lower shear rates are found to give rise to slower structural evolution than higher shear rates. Therefore, large structural heterogeneities are found to follow similar trends as the linear rheological properties of Fig. 2a and c. In the shear-thinning regime, at intermediate shear rates, 5 ≲ Pe ≲ 500, the void volume, or equivalently the average effective cluster volume, follows a power law decrease, 〈VV〉 ∝ Pe^{−0.63±0.06}, in agreement with the sublinear stress increase (power law slope ∼0.32) measured rheologically in the same regime (see Fig. 1).

Fig. 3 Void volume probability density functions from experiments (a) and BD simulations (b) at the steady state (at 10t_B) after cessation of high and low shear rate flow as indicated. Time evolution of 〈VV〉, normalized by the initial state values (at 2t_B), for high, low and intermediate rates from experiments (c) and BD simulations (d). Experiments are at ϕ = 0.44, U_dep(2R) ≃ −16k_BT and ξ ≃ 0.05 (Pe/Pe_dep ≃ 160). Simulations were set to ϕ = 0.44, U_dep(2R) = −20k_BT and ξ = 0.1 (Pe/Pe_dep ≃ 100).

3.3 Comparison to thermal quenching

We now discuss the transition from the low to the high preshear regime, and further compare with the structure of a quiescent gel thermally quenched from an equilibrium liquid state. While the experimental system is not strictly tunable by temperature, simulations allow for thermal quenching by scaling the interparticle potential. In Fig. 4 we plot the Pe dependence of 〈VV〉 for the gel during and after cessation of shear, and contrast it with 〈VV〉 of the quiescent gel, determined at long times, as a function of attraction strength. Pe_dep defines the transition from the low to the high shear rate regime. For Pe_dep > 1, homogeneous gels are formed after cessation of shear, very similar to those from thermal quenching, while the structure under shear approaches that of a simple liquid. On the other hand, for a preshear at Pe_dep < 1, larger voids are detected, and 〈VV〉 is found to be one or two orders of magnitudes higher than the liquid state value, defined by the average interparticle distance. The discrepancy in absolute values between experimental and simulation data seen in Fig. 4 is mainly attributed to small differences in volume fractions, interactions and time scales (and thus Pe). However it should be noted that the absence of HI in BD may also influence the gel formation processes and structural details as seen previously in similar non-equilibrium states.⁵⁸

Fig. 4 Average void volume, 〈VV〉, from confocal microscopy (black) and BD simulation (red) at ϕ = 0.44 under shear (stars, bottom axis) and after cessation (solid and open symbols, bottom axis) as a function of Pe. The blue solid line (top axis) represents 〈VV〉 from BD simulations (after 10t_B) when quenching an equilibrium fluid at different attraction strengths. The value of Pe_dep = 1 is indicated with a vertical black line. The power law fit indicated by the solid line is discussed in the text (see Table 1 for notations).

Table 1 Quantities plotted in Fig. 4 and 5a

Fig. 4 and 5a	During shear	After 0.1tB	After 10tB	After quench
Confocal		□	■
BD Sims

---

A comparison of instantaneously quenched quiescent gels may provide insights into the mechanisms of restructuring under shear. Quiescent samples exhibit an increase of structural heterogeneity approaching the gelation point and a further decrease to a constant value at large attraction strengths well inside the gel regime.³⁷ At the same ϕ, the maximum heterogeneity in the quiescent gel is quite smaller than that produced by low rate preshear, although after 10t_B the system has not yet fully reached the steady state (Fig. 4).

We further examine the average number of bonds between particles, defined as the number of particle neighbors within the depletion attraction range.⁵⁹ Even though the information provided is limited to short distances, it identifies particle clustering and provides a complementary view of structural heterogeneity. Due to precision constraints we apply this type of analysis only to BD simulation data. In Fig. 5a the average number of bonds is plotted versus Pe_dep during and after cessation of shear. After a low shear rate preshear, the number of bonds remains largely constant with time, similar to the behavior of 〈VV〉. As high shear rate rejuvenation causes a complete disintegration of clusters, the number of bonds upon shear cessation increases with time as the gel reforms, although the absolute number of bonds remains smaller after a low shear rate rejuvenation. In comparison, for the gel at rest, the number of bonds increases, reaching a maximum around gelation and subsequently drops to a constant at large attractions, similar to the behavior of 〈VV〉. Plotting the number of bonds as a function of the distance from the gelation point at U_dep(2R) = −4.6k_BT, we find a sigmoidal shape similar to the case under shear as a function of pre-shear rate (inset of Fig. 5a).

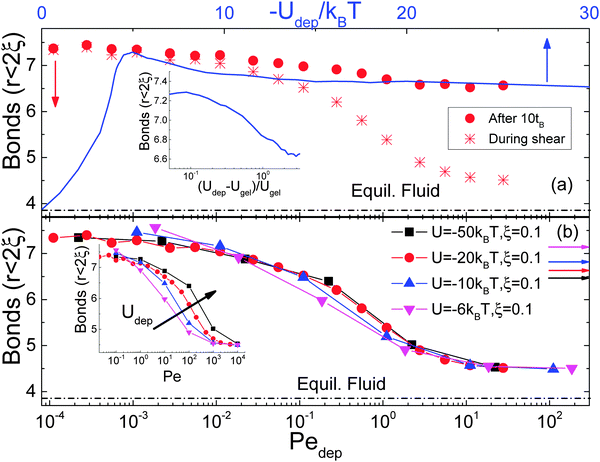Fig. 5 (a) Average number of bonds per particle (for r < 2(R + ξ)) as a function of Pe_dep from BD simulations (ϕ = 0.44, U_dep = −20k_BT and ξ = 0.1) during steady shear (stars, bottom axis) and after shear cessation (solid, bottom axis). The blue line (top axis) represents data from quenching an equilibrium fluid versus the attraction strength (after 10t_B) and as a function of the distance from gelation (inset). (b) BD data for sheared gels with ϕ = 0.44 at different attraction strengths as indicated versus Pe_dep calculated from eqn (1). The inset shows the same data as a function of Pe. Color coded horizontal arrows indicate the states produced from quenching an equilibrium fluid (see Table 1 for notations).

Although the number of bonds follows a similar trend with the void volume, both quantifying spatial heterogeneity, the main difference of the former is that its maximum value after low shear-rate rejuvenation is similar to that of the quiescent sample at the gel point. This is due to the fact that the two quantities reflect the structure at different length scales; VV reflects an average over all length scales whereas the average bond number pertains to distances within the range of attraction. Therefore, for a given volume fraction and average bond number, a narrow distribution of bonds per particle is produced from a more homogeneous interconnected network with a smaller 〈VV〉, corresponding to the peak in thermal quenching at rest. In contrast, a rather broad distribution of bond numbers reflects inhomogeneous percolated clusters with larger 〈VV〉, as detected at low preshear rates. Therefore, comparing quenching near gelation and preshearing at low rates, we find that although the average bonds are similar, the latter creates structures with larger voids and striking inhomogeneities.

Finally BD simulations with different depletion potentials provide further verification of the validity of Pe_dep scaling. As shown in Fig. 5b, the number of bonds under shear for various attraction strengths falls onto a single master curve versus Pe_dep, even though in the quenched gel at rest the average bond number depends on the depth of potential.

4 Discussion

Our findings suggests that by tuning the way a colloidal gel is sheared or mixed, one may vary its final structure and mechanical strength without the need for changing the interparticle potential, and furthermore allowing access to structures that may not be accessible by thermal quenching, although during such manipulation one has to preclude the interference from other forces such as gravity. The ability of shear to change particle configurations at large length-scales implies that it may also affect the gelation scenarios,^1,60 currently under intense investigation,^59,61–63 as found for gels under the influence of gravity, which showed enhanced phase separation.⁶⁴

Applying strong shear (high Pe_dep) has an effect equivalent to an instantaneous thermal quenching, promoting arrested phase separation, since upon shear cessation the system is a homogeneous fluid with strong attractive interactions present. On the other hand, weak shear (low Pe_dep), leads to lower free energy configurations corresponding to more compact clusters, akin of a low rate thermal quenching that would produce similar densification through Brownian motion. Although Brownian motion alone cannot create such compact structures on a reasonable time-scale (10t_B), the microstructure created under weak shear may bring the system closer to thermodynamic equilibrium. Even if interacting systems with simple short range attractions are unlikely to produce quiescent equilibrium gels,^1,59,61 we may expect that the application of shear can facilitate an approach to such scenarios in other systems. A major difference in the final state accessed via thermal quenching and shear should arise from the anisotropy associated with the latter and the accompanied residual stresses. It is clear from previous work on creep and recovery¹⁷ that after the application of shear, residual stresses remain constant, especially at low shear rates, as seen in hard sphere glasses.²⁵ This calls for a more extensive simulation study to compare thermal quenching with low shear rate shear-induced rejuvenation to unravel the underlying commonalities and differences. As a final note, in a reverse approach, one could infer the strength of interparticle interactions for a more complex attractive system by determining Pe_dep = 1, from either structural information under shear or by identifying the low to high shear rate viscosity transition through rheology.

5 Conclusions

The structural and rheological properties of intermediate volume fraction colloidal gels have been examined during steady-state shear flow and shear cessation using rheometry, confocal microscopy and Brownian dynamics simulations. Through structural analysis of the steady state, we find that a variation in the applied shear rate produces strong changes in the structure of the gels both during flow and gel reformation after flow cessation. Analysis of structural changes is carried out by determining the void distribution, a quantitative measure of spatial heterogeneity and the average number of interparticle bonds. At shear rates higher than Pe_dep, a non-dimensional shear rate representing the balance of shear and attractive interactions, particle networks and clusters break fully, whereas smaller rates produce large inhomogeneous structures due to compactification of clusters under shear. Such distinct microstructural starting states are the decisive factors for the evolution of the gel after shear cessation leading, at long times, to materials with different microstructures and mechanical properties. Gels reformed after strong shearing evolve into stronger solids with a relatively homogeneous structure, whereas the application of weak shear rates leads to gels with weaker elasticity and a highly heterogeneous microstructure.

We conclude that by tuning the way a colloidal gel is sheared or mixed, one may vary its final structure and mechanical strength, allowing access to structures with properties that may not be accessible by thermal quenching. By examining a well-defined model system, this work provides an understanding on gelation scenarios subject to mechanical perturbations and has strong implications for general industrial applications where variations in mixing, processing and transportation protocols alter the final materials' properties, as well as for users that rejuvenate products by shaking. Such controlled microstructural manipulation may be used in manufacturing of a diverse range of materials from controlled porosity and strength tissue scaffolds to high strength concrete formulations with desirable flow properties.

Acknowledgements

We thank A. B. Schofield for particle synthesis. We acknowledge funding from EU FP7-Infrastructures “ESMI” (CP&CSA-2010-262348), Greek projects Thales “Covisco” and Aristeia II “MicroSoft” and UK EPSRC (grant EP/D071070/1).

References

1. E. Zaccarelli, J. Phys.: Condens. Matter, 2007, 19, 323101.
2. P. Vukusic and J. Sambles, Nature, 2003, 424, 852–855.
3. K.-T. Wu, L. Feng, R. Sha, R. Dreyfus, A. Y. Grosberg, N. C. Seeman and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18731–18736.
4. L. Di Michele, F. Varrato, J. Kotar, S. H. Nathan, G. Foffi and E. Eiser, Nat. Commun., 2013, 4, 2007.
5. S. Rose, A. Prevoteau, P. Elziere, D. Hourdet, A. Marcellan and L. Leibler, Nature, 2014, 505, 382.
6. H. Chen, M. A. Fallah, V. Huck, J. I. Angerer, A. J. Reininger, S. W. Schneider, M. F. Schneider and A. Alexander-Katz, Nat. Commun., 2013, 4, 1333.
7. A. Zemel, I. B. Bischofs and S. A. Safran, Phys. Rev. Lett., 2006, 97, 128103.
8. R. Mezzenga, P. Schurtenberger, A. Burbidge and M. Michel, Nat. Mater., 2005, 4, 729–740.
9. C. Das, M. G. Noro and P. D. Olmsted, Phys. Rev. Lett., 2013, 111, 148101.
10. G. Maitland, Curr. Opin. Colloid Interface Sci., 2000, 5, 301–311.
11. H. Wyss, E. Tervoort and L. Gauckler, J. Am. Ceram. Soc., 2005, 88, 2337–2348.
12. E. Masoero, E. Del Gado, R. J.-M. Pellenq, F.-J. Ulm and S. Yip, Phys. Rev. Lett., 2012, 109, 155503.
13. P. N. Pusey, Liquids, Freezing and the Glass Transition, Elsevier Science Publishers, North-Holland, Amsterdam, 1991, pp. 763–942.
14. A. Liu and S. Nagel, Nature, 1998, 396, 21–22.
15. H. Lowen, Eur. Phys. J.: Spec. Top., 2013, 222, 2727–2737.
16. T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2770–2773.
17. K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676.
18. P. Ballesta, R. Besseling, L. Isa, G. Petekidis and W. C. K. Poon, Phys. Rev. Lett., 2008, 101, 258301.
19. J. R. Seth, L. Mohan, C. Locatelli-Champagne, M. Cloitre and R. T. Bonnecaze, Nat. Mater., 2011, 10, 838–843.
20. J. Dhont, M. Lettinga, Z. Dogic, T. Lenstra, H. Wang, S. Rathgeber, P. Carletto, L. Willner, H. Frielinghaus and P. Lindner, Faraday Discuss., 2003, 123, 157–172.
21. R. Besseling, L. Isa, P. Ballesta, G. Petekidis, M. E. Cates and W. C. K. Poon, Phys. Rev. Lett., 2010, 105, 268301.
22. B. Ackerson and P. Pusey, Phys. Rev. Lett., 1988, 61, 1033.
23. N. Koumakis, A. B. Schofield and G. Petekidis, Soft Matter, 2008, 4, 2008–2018.
24. D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Nature, 2011, 480, 355–358.
25. M. Ballauff, J. M. Brader, S. U. Egelhaaf, M. Fuchs, J. Horbach, N. Koumakis, M. Krüger, M. Laurati, K. J. Mutch, G. Petekidis, M. Siebenbürger, T. Voigtmann and J. Zausch, Phys. Rev. Lett., 2013, 110, 215701.
26. R. Sonntag and W. B. Russel, J. Colloid Interface Sci., 1986, 113, 399–413.
27. R. Wessel and R. Ball, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, R3008.
28. J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, 2012.
29. J. Guery, E. Bertrand, C. Rouzeau, P. Levitz, D. A. Weitz and J. Bibette, Phys. Rev. Lett., 2006, 96, 198301.
30. C. O. Osuji, C. Kim and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 060402.
31. A. Zaccone, D. Gentili, H. Wu, M. Morbidelli and E. Del Gado, Phys. Rev. Lett., 2011, 106, 138301.
32. S. B. Lindstrom, T. E. Kodger, J. Sprakel and D. A. Weitz, Soft Matter, 2012, 8, 3657–3664.
33. S. W. Kamp and M. L. Kilfoil, Soft Matter, 2009, 5, 2438–2447.
34. E. Secchi, S. Buzzaccaro and R. Piazza, Soft Matter, 2014, 10, 5296–5310.
35. Y.-L. Chen and K. S. Schweizer, J. Chem. Phys., 2004, 120, 7212.
36. S. A. Shah, Y. L. Chen, K. S. Schweizer and C. F. Zukoski, J. Chem. Phys., 2003, 119, 8747–8761.
37. M. Laurati, G. Petekidis, N. Koumakis, F. Cardinaux, A. B. Schofield, J. M. Brader, M. Fuchs and S. U. Egelhaaf, J. Chem. Phys., 2009, 130, 134907.
38. N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470.
39. M. Laurati, S. U. Egelhaaf and G. Petekidis, J. Rheol., 2011, 55, 673–706.
40. Z. Shao, A. S. Negi and C. O. Osuji, Soft Matter, 2013, 9, 5492–5500.
41. J. Kim, D. Merger, M. Wilhelm and M. E. Helgeson, J. Rheol., 2014, 58, 1359–1390.
42. D. Bonn and M. M. Denn, Science, 2009, 324, 1401–1402.
43. G. Ovarlez, L. Tocquer, F. Bertrand and P. Coussot, Soft Matter, 2013, 9, 5540–5549.
44. N. Y. Yao, C. P. Broedersz, M. Depken, D. J. Becker, M. R. Pollak, F. C. MacKintosh and D. A. Weitz, Phys. Rev. Lett., 2013, 110, 018103.
45. P. Ballesta, N. Koumakis, R. Besseling, W. C. K. Poon and G. Petekidis, Soft Matter, 2013, 9, 3237–3245.
46. L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16029–16034.
47. B. Rajaram and A. Mohraz, Soft Matter, 2012, 8, 7699.
48. K. Masschaele, J. Fransaer and J. Vermant, J. Rheol., 2009, 53, 1437–1460.
49. J. C. Conrad and J. A. Lewis, Langmuir, 2008, 24, 7628–7634.
50. S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255.
51. W. C. K. Poon, J. Phys.: Condens. Matter, 2002, 14, R859.
52. R. Besseling, L. Isa, E. R. Weeks and W. C. Poon, Adv. Colloid Interface Sci., 2009, 146, 1–17.
53. G. J. Fleer and R. Tuinier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041802.
54. D. R. Foss and J. F. Brady, J. Rheol., 2000, 44, 629–651.
55. A. Sierou and J. F. Brady, J. Fluid Mech., 2001, 448, 115–146.
56. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
57. M. D. Haw, Soft Matter, 2006, 2, 950–956.
58. A. Furukawa and H. Tanaka, Phys. Rev. Lett., 2010, 104, 245702.
59. J. C. F. Toledano, F. Sciortino and E. Zaccarelli, Soft Matter, 2009, 5, 2390–2398.
60. W. C. K. Poon and M. Haw, Adv. Colloid Interface Sci., 1997, 73, 71–126.
61. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503.
62. E. Zaccarelli and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15203–15208.
63. A. P. R. Eberle, N. J. Wagner and R. Castaneda-Priego, Phys. Rev. Lett., 2011, 106, 105704.
64. J. M. Kim, J. Fang, A. P. R. Eberle, R. Castañeda Priego and N. J. Wagner, Phys. Rev. Lett., 2013, 110, 208302.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm00411j

‡ Current address: School of Physics and Astronomy, University of Edinburgh, Mayfield Road, Edinburgh, EH9 3JZ, UK.

§ Current address: InProcess-LSP, Molenstraat 110, 5342 CC Oss, The Netherlands.

---