 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bijels stabilized using rod-like particles†
Niek
Hijnen
,
Dongyu
Cai
and
Paul S.
Clegg
*
School of Physics and Astronomy, University of Edinburgh, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK. E-mail: paul.clegg@ed.ac.uk
First published on 10th April 2015
Abstract
Bicontinuous interfacially jammed emulsion gels, in short ‘bijels’, rely on a trapped layer of colloidal particles for their stability. These structures have traditionally been created using spherical colloidal particles. Here we show for the first time the use of rod-shape particles to stabilize bijels. We show that domain size decreases more rapidly with particle concentration in the case of rods compared to spheres. Large-scale analysis and detailed examination of images show that the packing fraction of rods is much higher than expected, in part, due to the role of ‘flippers’.
Bijels are a new class of soft materials with two tortuous inter-penetrating fluid domains sharing an interface which is jammed with colloidal particles.1 They were predicted by computer simulations in 20052 and experimentally realized in 2007.3 The formation process of the bijel relies on the spinodal decomposition of a binary liquid mixture in presence of the colloidal particles (for different systems and approaches, see ref. 4–6). When equally wetted by the two emerging liquid phases (i.e. contact angle close to 90°), these particles are trapped on the percolating interface without imposing any preferred interfacial curvature. As a result of the jammed particles, coarsening of the spinodal structure slows to a stop, and the bijel, a soft solid, is formed. Bijels are not only interesting to physicists as a state trapped far from equilibrium, but also to a broader audience who are interested in new materials for potential applications. For example, the bijel has been suggested for application as a cross-flow microreaction medium.1 Additionally, selective polymerization of one of the fluid domains loaded with monomers followed by the removal of all liquids has been used to obtain porous polymeric materials without losing the original bijel structure.7,8
So far, it is known that the properties of bijels are crucially dependent on the colloidal particles including their size, concentration and particle–particle interactions.3,9 However, this has been established based on experiments with spherical particles alone. We anticipate that the shape of the particles will play a major role as well. Recently, Imperiali et al. reported the use of plate-shaped graphene oxide to arrest the bijel structure. They argued that the 2D nature of graphene oxide sheets led to the formation of highly elastic layers at the interface giving a different mechanism for arrest of the bijel structure in contrast to the jamming of spherical particles.10 Here, we focus on the use of 1D rod-like particles to stabilize bijels, which has not yet been explored experimentally. To maximize the removed area of liquid–liquid interface, the long axes of rods will lie parallel to the interface. We believe that rod-like particles will behave very differently from spherical particles, since they will have a preferred orientation with respect to cylindrical regions of interface and they tend to induce significant deformations of an otherwise flat interface, leading to strong capillary interactions.11,12 Another striking feature of colloidal rods at liquid–liquid interfaces is that, in response to compression, the rods can flip out of the plane, and also be expelled from the interface prior to buckling, contrasting with behaviour of spherical particles.13 Recently, computer simulations of bijels stabilized using rods,14–16 have shown that at constant particle number and volume fraction, increasing particle aspect ratio leads to smaller domains,14 furthermore rod-like particles allow the generation of more stable emulsions than spherical particles.16 In this Communication, we present the first experimental realization of bijels stabilized using colloidal rods. We have imaged the packing of the rods on the interface using confocal microscopy, and we compare, quantitatively, the role of particle shape in dictating final bijel structures. More broadly, the methodology presented in this study could be reproduced for exploring the structure of bijels arrested by even more exotic particles.
To realize the rod-stabilized bijels, a pair of partially miscible liquids (nitromethane (NM)–ethylene glycol (EG)17) was selected to host the akaganéite–silica core–shell rods. The phase diagram of NM and EG is shown in Fig. 1a. The preparation of the rods follows our method reported in ref. 18. Akaganéite cores provide the required shape, while the silica shells offer the essential functionality. For the purpose of imaging, only a thin inner layer of silica shell is labelled with Fluorescein isothiocyanate (FITC), leaving the surface chemistry of the outer unlabelled silica layer unaffected. The average dimensions of length (L) = 3.05 μm, diameter (D) = 0.32 μm, aspect ratio (AR) = 9.6 are determined by TEM e.g. image shown in Fig. 1e. The TEM image of Stöber silica particles used for comparison is also presented in Fig. 1b. These near-spherical particles have an average radius R = 0.37 μm and are labelled with Rhodamine B isothiocyanate (RITC).
 | ||
| Fig. 1 (a) The phase diagram of nitromethane (NM) and ethylene glycol (EG),19 with an arrow roughly indicating the temperature quench applied in experiments; TEM images of the (b) spheres and (e) rods used to produce NM–EG bijels; the confocal images of NM–EG bijels stabilized by (c) 3 vol% and (d) 5 vol% spheres, respectively; the confocal images showing the bijels stabilized by (f) 3 vol% and (g) 5 vol% rods. The scale bar is 50 micron. | ||
To create rod surfaces with equal wetting characteristics with the two solvents, the surface chemistry is tuned via a silanization reaction between the outer layer of silica and hexamethyldisiloxane (HMDS).17 To follow the changes in contact angle, bijel formation is attempted with every batch of modified rods using the quench route indicated by the vertical arrow in Fig. 1a. The aim of these experiments is to pinpoint the optimum concentration of HMDS to give bijel formation; the best surface treatments give rise to the bijels shown in Fig. 1f, g. These bijels were static and stable on the timescale of these experiments (at least 24 hours). The experimental details are available in ESI.† It can be seen that, when increasing the particle concentration from 3 to 5 vol%, rods take up more interfacial area, leading to smaller liquid domains, reflecting an earlier structural arrest of spinodal decomposition. For comparison, Fig. 1c, d show the bijels prepared with spherical Stöber silica particles. Here, the EG-rich channel is observed using Fluorescein dye. We note that volume per particle (Vparticle) is nearly the same for the rods and spheres, and this allows us to make a direct comparison of the domain sizes. It is clearly seen that rod-stabilized bijels exhibit much smaller domain sizes for similar particle concentration (comparing, in Fig. 1, image c and d with f and g, respectively). However, the particle shape does not result in an obvious change in domain shape. In water–2,6-lutidine bijels, the particle structure can remain intact after re-mixing of the liquids.9 The resulting material was termed a ‘monogel’. 20 min of aging is the key step for monogel formation, which drives particles to overcome the repulsive barrier into their primary van der Waals minimum. In contrast, successful monogel formation in NM–EG was here observed upon prolonged aging of samples. (Monogel formation has now also been observed in polymer-based bijels.20) The results presented in Fig. S4 (ESI†) indicate that the monogel is eventually formed with 19 days aging treatment. This is similar to the observation for sphere-based NM–EG bijels,8 in which the solvation of the HMDS graft layer by deprotonated NM molecules is regarded as a possible reason for an increased repulsive barrier. However, we still require a detailed understanding of why in NM–EG such long aging is required for monogel formation.
Next we consider the scaling of the domain size with particle concentration. In the following, ϕparticle refers to the volume fraction of rods (or spheres). For a fixed ϕparticle, the final domain size will depend solely on the effective area covered by the jammed layer of colloidal particles trapped at the interface. The situation can be approximated by a spherical droplet being fully covered by colloidal particles, which is contained within a liquid of a volume equal to that of the droplet.21 This is similar to spinodal decomposition, since the volumes of the two phases are roughly equal; the droplet diameter (L) represents the domain size. For the case of spherical particles that are neutrally wetted we find that
| L = 2vdsphere(ϕsphere)−1 | (1) |
Changing colloid shape from spheres to rods at fixed particle volume will change the above scaling relation. This reflects changes to both the area taken up by a single particle and the 2D packing fraction. For a clear comparison of the influence of particle shape alone, similar particle volume is important. Spheres with an equivalent volume per particle to the rods used would have a diameter of approximately 776 nm. With dsphere = 750 nm, the spheres used here are nearly perfect. The maximum packing fraction of sphero-cylinders of aspect ratio A on a flat interface (see ESI†) is: 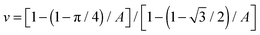 . Obviously, the change in the area taken up by single particles also depends on the aspect ratio. For instance, a neutrally wetted cylinder takes up twice as much interfacial area when its aspect ratio is increased from 1 to 8 at fixed volume. Using the same scenario as described above for spheres, to approximate the relation between domain size and colloid concentration, for cylindrical particles is found, where drod is the full width of a cylinder. Surprisingly, the particle aspect ratio only appears in the packing fraction.
. Obviously, the change in the area taken up by single particles also depends on the aspect ratio. For instance, a neutrally wetted cylinder takes up twice as much interfacial area when its aspect ratio is increased from 1 to 8 at fixed volume. Using the same scenario as described above for spheres, to approximate the relation between domain size and colloid concentration, for cylindrical particles is found, where drod is the full width of a cylinder. Surprisingly, the particle aspect ratio only appears in the packing fraction.
| L = ¾vdrod(ϕrod)−1 | (2) |
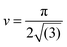 , the maximum packing of discs on a plane, and the experimentally determined particle diameter; the relation (1) can then be compared for these two samples. In previous experiments order of magnitude agreement was obtained.3 Of course, the pre-factor of the relation between L and ϕparticle depends on the shape of the domains, which was in this case approximated by a sphere. Other experimental factors introduce uncertainties including particle polydispersity, the fraction of particles trapped at the interface, and possible inhomogeneities in quench or particle distribution. Here, the slope found for spheres (1.44 μm) is in relatively good agreement with the value resulting from the relation (1) (1.36 μm) when using the current particle size. A similar result is found for a second batch of silica particles (labelled spheres 2).
, the maximum packing of discs on a plane, and the experimentally determined particle diameter; the relation (1) can then be compared for these two samples. In previous experiments order of magnitude agreement was obtained.3 Of course, the pre-factor of the relation between L and ϕparticle depends on the shape of the domains, which was in this case approximated by a sphere. Other experimental factors introduce uncertainties including particle polydispersity, the fraction of particles trapped at the interface, and possible inhomogeneities in quench or particle distribution. Here, the slope found for spheres (1.44 μm) is in relatively good agreement with the value resulting from the relation (1) (1.36 μm) when using the current particle size. A similar result is found for a second batch of silica particles (labelled spheres 2).
According to the graph in Fig. 2, plotting data against ϕcolloids−1 a slope of 0.87 μm is found for rod-stabilized bijels, compared to 1.44 μm for sphere-stabilized bijels. Based on the aspect ratio, v = 0.99 and drod determined with TEM, the relation (2) gives a value of 0.75 μm for the slope. This demonstrates a larger discrepancy with the experimental result than for the sphere-stabilized bijels. The difference is unlikely to originate from the assumed v for sphero-cylinders, as it can only be adjusted to lower values, resulting in a larger difference. The scaling relation suggests that v > 1. This could be related to the observation that, at the interface of the bijel, particles poke out and overlap. Their potential to reduce the interfacial area is thus not fully used, and the gain from changing particle shape is smaller than expected from simple geometrical arguments.
Our design of rods allows us to directly observe packing at the interface of the two continuous liquid domains. Images showing the packing of rods on droplets are provided in the ESI.† In the confocal images of the bijel with 2 vol% rods (Fig. 3(a)–(c)), the rods can be seen via the FITC fluorescence of the inner shell. Individual rods can be distinguished due to the inner fluorescent shells being separated by the thicker, unlabelled outer silica layers. Fig. 3(d) shows the confocal images of the bijels with 5 vol% rods using the combination of FITC fluorescence from the rods and Nile Red from the NM-rich phase which enhances the visualization of the rod packing. (Although combining channels reduces the visibility of gaps in the packing.) From these images, it is clear that there is no long-range translational or orientational ordering of the rods. On fluid necks there is some enhancement to rod alignment. This occurs both parallel and perpendicular to the length of the necks, which might well be related to whether a neck was stretched or compressed prior to structural arrest. We note that the ability of rods to align along a thinning neck results in some very thin liquid bridges (e.g.Fig. 3a).18 When the packing is studied more closely, it is found that several rods regularly form small side-by-side stacks, and significantly, often triangular gaps result from the random orientation of these tightly-packed structural elements. We also occasionally observe some tiny bright dots (as highlighted in Fig. 3b) which very likely indicate that some rods are sticking out of the interface and are even perpendicular to the interface.
It seems likely that rapid jamming is the main driving force behind the final arrangement of the rods. As a result the overall structure is mostly isotropic, and the packing contains many cases where particles are forced into energetically unfavourable arrangements. The latter includes flippers, and gives rise to gaps. Flippers have been observed for ellipsoidal particles at interfaces, just before a compressed monolayer buckles, and on droplets.13,23 The situation during domain coarsening involves the compression of a monolayer of rods at a curved interface. It is easy to imagine a scenario where two rods collide head-on, but still at an angle due to the curved interface, one of them might well end up on top of the other, and be forced off the interface. Apparently an event somewhat like this probably results in flippers, as well as less extreme arrangements. While flat interfaces induce bistable arrangements of jammed rods, either parallel or perpendicular to the interface, here we find some rods tilted to an intermediate extent which is probably related to the curvature of the interface. Furthermore, as has been shown recently for magnetic rods perturbed by an applied magnetic field perpendicular to the interface,24 flipping becomes more energetically expensive as the aspect ratio increases. Hence we believe that fewer flippers would be observed if we employed rods of even higher aspect ratio. This might mean that the interface separation would agree better with predictions at higher aspect ratios.
Naturally, the packing of the rods at the interface links to the scaling of the domain size with colloid concentration, as it determines how much of the interfacial area the rods effectively take up. Structural features such as the observed flippers, stacks and gaps are of importance here. Gaps would lower v, while particles sticking out of the interface would increase v. In both cases, the effect of the specific interfacial structuring on domain size scaling will be relatively small compared to the effect of changing the particle shape from spheres to rods. However, as discussed above, on a large scale, the shape of particles does not appear to play a significant role in changing the domain size of bijels. This reflects the overall isotropic organization of the rods at the interface, caused by a rapid jamming on the curved interface. Only on a smaller scale can the shape of the rods make a difference, where thin liquid bridges are a striking example. It appears that their ability to align does allow the stabilization of smaller necks.
Conclusions
In this study, bijels were created with colloidal rods (aspect ratio ≈ 10) and spheres (aspect ratio 1). After describing in some detail the route towards the preparation of rod-stabilized bijels, the scaling of the domain size with colloid concentration was presented and discussed. Since, due to their shape, the rods take up a larger area of the interface, jamming occurs at lower interface separations than with the same volume fraction of spheres. Scaling relations based on simple geometrical arguments show reasonable qualitative agreement. No clear difference in domain shapes could be pointed out between the two counterparts. This demonstrated that, on a large scale, the type of bijel structure is not significantly altered by changing spherical particles into rods. Thus, a different domain-size scaling is the main structural effect.After establishing this, confocal imaging was employed to elucidate packing of rods. Several characteristic structural features were identified. The packing contained side-by-side stacks of several particles, the formation of which could well have involved capillary interactions, judging from previous studies. Overall organization is isotropic due to a rapid jamming after phase separation, resulting in significant gaps where packing is frustrated, as well as some particles being partially ejected from the interface. In places very thin necks are observed, which are only a single rod wide. All of these features have consequences for the domain-size scaling. Particles flipping and being pushed off the interface undermines, if only slightly, the gain in packing efficiency given by changing spheres into rods.
Acknowledgements
We are grateful to Andrew Schofield for synthesizing the spherical silica particles and to Katherine Rumble for providing data for Fig. 2. This work was supported by the Marie Curie Initial Training Network COMPLOIDS no. 234810 and EPSRC grant EP/J007404/1.Notes and references
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132 RSC.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J. C. Desplat and M. E. Cates, Science, 2005, 309, 2198 CrossRef CAS PubMed.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966 CrossRef CAS PubMed.
- H.-J. Chung, K. Ohno, T. Fukuda and R. J. Composto, Nano Lett., 2005, 5, 1878 CrossRef CAS PubMed.
- H. Firoozmand, B. S. Murray and E. Dickinson, Langmuir, 2009, 25, 1300 CrossRef CAS PubMed.
- M. Cui, T. Emrick and T. P. Russell, Science, 2013, 342, 460 CrossRef CAS PubMed.
- M. N. Lee and A. Mohraz, Adv. Mater., 2010, 22, 4836 CrossRef CAS PubMed.
- M. N. Lee, J. H. J. Thijssen, J. A. Witt, P. S. Clegg and A. Mohraz, Adv. Funct. Mater., 2013, 23, 417 CrossRef CAS.
- E. Sanz, K. A. White, P. S. Clegg and M. E. Cates, Phys. Rev. Lett., 2009, 103, 255502 CrossRef PubMed.
- L. Imperiali, C. Clasen, J. Fransaer, C. W. Macosko and J. Vermant, Mater. Horiz., 2014, 1, 139 RSC.
- J. C. Loudet, A. Alsayed, J. Zhang and A. Yodh, Phys. Rev. Lett., 2005, 94, 018301 CrossRef CAS PubMed.
- E. P. Lewandowski, M. Cavallaro, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142 CrossRef CAS PubMed.
- M. G. Basavaraj, G. G. Fuller, J. Fransaer and J. Vermant, Langmuir, 2006, 22, 6605 CrossRef CAS PubMed.
- F. Günther, F. Janoschek, S. Frijters and J. Harting, Comput. Fluids, 2013, 80, 184 CrossRef.
- T. L. Cheng and Y. U. Wang, J. Colloid Interface Sci., 2013, 402, 267 CrossRef CAS PubMed.
- F. Günther, S. Frijters and J. Hartings, Soft Matter, 2014, 10, 4977 RSC.
- J. W. Tavacoli, J. H. J. Thijssen, A. B. Schofield and P. S. Clegg, Adv. Funct. Mater., 2011, 21, 2020 CrossRef CAS.
- N. Hijnen and P. S. Clegg, Chem. Mater., 2012, 24, 3449 CrossRef CAS.
- J. M. Sørenson and W. Arlt, in Liquid-liquid Equilibrium Data Collection, Ed. D. Behrens and R. Eckermann, Dechema, Frankfurt/Main, Germany, 1979, part 1, vol. 5, p. 29 Search PubMed.
- L. Bai, J. Fruehwirth, X. Cheng and C. W. Macosko, Soft Matter Search PubMed , submitted, http://arxiv.org/abs/1502.00165.
- E. M. Herzig, PhD thesis, University of Edinburgh, 2008, p. 112.
- W. S. Rasband, US National Institute of Health, Bethesda, Maryland, USA, 1997–2006, http://rsb.info.nih.gov/ij/ Search PubMed.
- B. Madivala, J. Fransaer and J. Vermant, Langmuir, 2009, 25, 2718 CrossRef CAS PubMed.
- B. J. Newton, K. A. Brakkeb and D. M. A. Buzza, Phys. Chem. Chem. Phys., 2014, 16, 26051 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm00265f |
| This journal is © The Royal Society of Chemistry 2015 |


