Smectic block copolymer thin films on corrugated substrates
Aldo D.
Pezzutti
,
Leopoldo R.
Gómez
and
Daniel A.
Vega
*
Instituto de Física del Sur (IFISUR), Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Universidad Nacional del Sur, Av. LN Alem 1253, 8000 Bahía Blanca, Argentina. E-mail: dvega@uns.edu.ar; Fax: +54-291-4595142; Tel: +54-291-4595101-2835
First published on 12th February 2015
Abstract
In this work we study equilibrium and non-equilibrium structures of smectic block copolymer thin films deposited on a topographically patterned substrate. A Brazovskii free energy model is employed to analyze the coupling between the smectic texture and the local mean curvature of the substrate. The substrate's curvature produces out-of-plane deformations of the block copolymer such that equilibrium textures are modified and dictated by the underlying geometry. For weak curvatures it is shown that the free energy of the block copolymer film follows a Helfrich form, scaling with the square of the mean curvature, with a bending constant dependent on the local pattern orientation. On substrates of varying mean curvature simulations show that topological defects are rapidly expelled from regions with large curvature. These results compare well with available experimental data of poly(styrene)-co-poly(ethylene-alt-propylene) smectic thin films.
1 Introduction
Due to their ability to generate ordered structures on the scale of tens of nanometers, block copolymers have emerged as attractive self-organized templates for cost-effective nanofabrication technologies.1,2 Their capacity to produce self-organized patterns with high resolution and compatibility with traditional processing techniques makes these systems useful as templates for diverse applications ranging from microelectronic and nanofluidic devices to ultrafiltration.3–9When block copolymers are confined to thin films, the morphologies are severely affected by the confining surfaces and the affinity of the individual blocks for the interfaces.10–17 Although block copolymer thin films can develop a wide diversity of morphologies, one of the most useful structures consists of quasi two-dimensional stripe patterns. Stripe patterns with smectic symmetry can be obtained through compositionally symmetric block copolymers or monolayers of cylinder-forming block copolymers combined with accurate control over the interaction between the blocks and the confining surfaces.3,11
One of the main drawbacks of using block copolymers in nanofabrication technologies is the lack of regularity in the textures, mainly due to the presence of different elastic disturbances of the ordered state, including long wave length undulations and a rich variety of defects like domain walls, disclinations, and dislocations (see Fig. 1). As the self-organization process involves a phase transition that can proceed via nucleation and growth or spinodal decomposition, in the absence of external fields the formation of defects in the smectic pattern is completely unavoidable.3 Although such defects can be reduced by thermal treatments and coarsening, it has been found that this process is prohibitively slow for most technological purposes.18–22
In the last few years much effort has been directed to the development of strategies to avoid the formation of defects. A variety of techniques, including chemoepitaxy, shear flow, electric fields, or a sweeping temperature gradient, have been employed to improve the degree of order in different block copolymer systems.23 One of the most successful methods to control long-range order and orientation involves the pre-treating of the substrate to create topographic structures (graphoepitaxy).24–30 Topographically patterned substrates with different features and symmetries have also been employed to obtain well ordered block copolymer thin films with hexagonal and smectic symmetries.31–37
Recently, it was experimentally observed that curved topographic substrates can be used to obtain well ordered textures of block copolymer thin films.38–40 It was found that the substrate's curvature plays a role similar to an external field, directing the self-assembly and leading to highly regular smectic textures.
Here we study the equilibrium configuration and dynamics of ordering of smectic thin films deposited on curved substrates. Even in very thin films, the role of the third spatial dimension (film thickness) cannot be neglected and there is natural coupling with any sort of out-of-flatness distortions. The effect of the film thickness on a curved substrate is emphasized in the scheme of Fig. 2, which compares the dominant features of a lamellar thin film lying on a cylindrical substrate. Note that in the configuration shown on the left panel of Fig. 2 where the lamellae are perpendicularly aligned with regard to the cylinder symmetry axis, the curvature does not affect the lattice constant of the texture. However, for other orientations there are regions simultaneously under compressional and dilational strain fields. As the different configurations of the pattern involve different degrees of deformation, the energy becomes dependent on the orientation of the texture with regard to the substrate.
In this work the coupling between the smectic texture and mean curvature of the substrate is analyzed through a Brazovskii free energy functional. In a strictly two-dimensional system the energy is independent of the specific orientation of the texture. However, due to the finite film thickness in curved space the smectic orientation couples with the mean curvature of the substrate and breaks the orientational symmetry found in flat systems, affecting both equilibrium configurations and dynamics of ordering.
This paper is organized as follows. In the next section, we discuss experimental results related to the equilibrium configurations observed in block copolymer thin films when deposited onto corrugated substrates. In Section 3 we introduce the Brazovskii free energy functional for smectic systems. Based on this model, in Section 4 we analyze equilibrium and non-equilibrium features of block copolymer smectic thin films deposited onto curved substrates and compare the results against available experimental data. Finally, in Section 5 we present the main conclusions of this work.
2 Experimental observations
The process of self-organization of a smectic system deposited onto a gently curved substrate was experimentally studied by Vega et al.40Fig. 3 shows experimental results for a 30 nm thick polystyrene-block-poly(ethylene-alt-propylene) block copolymer thin film deposited on a topographically patterned substrate. The figure shows a tapping-mode atomic force microscopy (AFM) height-phase image at intermediate annealing times (60 min at T = 373 K). The repeat spacing for the block copolymer is 19 nm while the substrate consists of a regular array of mesas separated by Gaussian-like bumps. The pitch of the substrate's features was fixed at 2.2 μm while the height of the bumps reaches 100 nm (see ref. 40 for more details). In this system, the analysis of the dynamics revealed that:1. During the early stage of coarsening the block copolymer microdomains show the characteristic fingerprint-like patterns observed in flat block copolymer thin films. At this stage the self-assembly process leads to patterns with a very short-ranged order and morphologies that are indistinguishable from those observed on unpatterned substrates.
2. Similar to flat systems, on curved backgrounds the evolution kinetics towards the equilibrium state also involve a slow coarsening process mediated by the diffusion and annihilation of disclinations.
3. The degree of smectic order becomes inhomogeneous as a consequence of the substrate's varying curvature (see Fig. 3). The ordered domains are located preferentially in the flatter regions of the substrate, where coarsening proceeds via the annihilation of multipoles of disclinations. Then, the dynamics of defect annihilation is conditioned by the interaction between the smectic phase and the substrate.
4. As the annealing time increases there is progressive coupling between the smectic orientation and the substrate topography. In the late stage of coarsening the perpendicular orientation of the smectic phase with regard to the substrate's crests is noteworthy and evidences a strong interaction between the block copolymer morphology and the substrate's topography.
Thus, the experiments show that the curvature of the substrate affects not only the equilibrium state but also the coarsening dynamics towards equilibrium. In curved systems one can expect that the energy of interaction between defects depends not only on the topological charge of the defects and the elastic constants of the smectic phase, but also on the local curvature. In this case, it is clear that the dynamics of defects must be strongly influenced by the underlying geometry of the substrate.
Previously, the effect of curvature on the equilibrium configuration of self-assembled columns constrained to lie on a curved substrate was theoretically studied by Santangelo et al.39 In that case, it was found that both the extrinsic and intrinsic curvatures of the substrate play an important role in determining the equilibrium configurations of columnar phases. However, since this model only accounts for the bending energy associated with the three-dimensional curvature of the columns and the compression energy which sets the average intercolumnar spacing, it is unable to describe the data shown in Fig. 3 (according to this model the parallel orientation of the smectic phase with regard to the substrate's crests in Fig. 3 is energetically favored over the observed configuration). In what follows we use a different free energy approach to understand the coupling between the smectic texture and the underlying curvature. The model is shown to reproduce most of the experimental observations discussed above.
3 Brazovskii model
The Brazovskii model has been employed in a variety of different phenomena involving pattern formation with strong wavelength selectivity. Examples of applications of this and similar models cover length scales ranging from atomistic to macroscopic systems. For example, it has been applied to describe pattern formation processes,41 grain boundary melting,42 defect dynamics,21,43–45 symmetry breaking phase transitions,46–49 block copolymers,2 Langmuir films50 and liquid crystals.51 This phase field approach naturally incorporates the dominant features of the topological defects and their interactions, and also accounts for the anisotropic features of systems developing smectic symmetry.According to the Brazovskii model,46,52 in the neighborhood of the critical line the phase behavior of different self-assembling systems can be described as:
 | (1) |
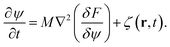 | (2) |
In order to explore the low energy states of block copolymer thin films lying on curved surfaces two key parameters must be taken into account: the film thickness and the interactions of the block copolymer with the substrate and air. Here we only consider the case where the film thickness h is small or similar to the characteristic wavelength λ of the lamellar structure and where the surface free-energy difference of the two blocks is small. Then, standing lamellae perpendicular to the substrate are energetically favored.
In flat space and critical conditions (ϕ0 = 0, τ ≤ 1), the phase separated structure can be well described within the one mode approximation, where ψ(r) ≃ ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(q0x). Here ψ0 and q0 are the amplitude and wave vector amplitude of the composition profile. This length scale selectivity emerges due to the competition between the gradient square term and the term involving the Laplacian operator in eqn (1). By minimizing F with respect to ψ0 and q0 it can be shown that the free energy density in flat systems f0 = F/V (V being the volume) becomes:
cos(q0x). Here ψ0 and q0 are the amplitude and wave vector amplitude of the composition profile. This length scale selectivity emerges due to the competition between the gradient square term and the term involving the Laplacian operator in eqn (1). By minimizing F with respect to ψ0 and q0 it can be shown that the free energy density in flat systems f0 = F/V (V being the volume) becomes:
 | (3) |
 and
and  .
.
In the present work eqn (2) is numerically solved on the different substrate geometries by using a finite difference algorithm, centered in space and forward in time.40,45 The most relevant features of a curved substrate can be expressed in terms of the mean curvature H and the Gaussian curvature K. In general, for every point P on the substrate there are two tangent circles with maximal and minimal radii of curvature R1 and R2, respectively. The mean curvature H and Gaussian curvature K at P are defined as  and K = k1k2, where ki = 1/Ri (i = 1, 2) is the principal curvature. In order to compare our results with the experiments, here we focus our attention on substrates with zero Gaussian curvature (K = 0). The initial liquid phase is modelled by random fluctuations in the order parameter ψ. The smectic was confined to ensure that the thin film thickness h remains constant. The temperature and compositional asymmetry were fixed at τ = 0.9 and ϕ0 = 0, respectively.
and K = k1k2, where ki = 1/Ri (i = 1, 2) is the principal curvature. In order to compare our results with the experiments, here we focus our attention on substrates with zero Gaussian curvature (K = 0). The initial liquid phase is modelled by random fluctuations in the order parameter ψ. The smectic was confined to ensure that the thin film thickness h remains constant. The temperature and compositional asymmetry were fixed at τ = 0.9 and ϕ0 = 0, respectively.
4 Coupling between smectic textures and mean curvature
Let us consider a lamellar thin film deposited on a cylindrical substrate of radius R (Fig. 2). When the system is on a curved substrate, the free energy f becomes dependent on the radius R of the substrate, the thin film thickness h, and orientation of the smectic with regard to the cylinder symmetry axis. In order to determine the energetic effects of these parameters, consider a system whose order parameter is described in cylindrical coordinates as:ψ(r,θ,z) = ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[q0(rθ cos[q0(rθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α) + z cos(α) + z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α))] sin(α))] | (4) |
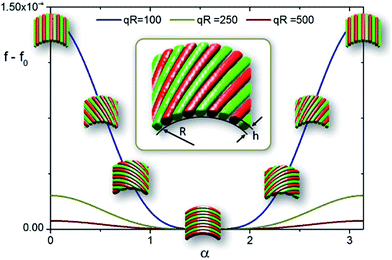 | ||
| Fig. 4 Free energy variations f − f0 of a smectic phase deposited onto a cylindrical substrate of radius R as a function of the smectic orientation with regard to the cylinder's symmetry axis α. Note that the free energy presents a minimum for α = π/2, which corresponds to the configuration depicted in the scheme of Fig. 2a. | ||
For the case of thin films (h/R ≪ 1, r ∼ R) the free energy density can be expanded in powers of h/R as (τ ≃ 1):
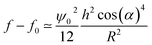 | (5) |
Fig. 4 shows the free energy density of ordered smectic thin films on cylindrical substrates of different curvatures as a function of the pattern orientation α. This figure clearly shows how the ground state configuration is affected by the substrate's curvature. Here, there is a strong energetic penalization for configurations departing from α = π/2 (pattern perpendicularly oriented with respect to the cylinder axis). Note also that the energy of the ground state grows as the curvature of the substrate increases (R decreases).
It is interesting to note here that the energetic penalization produced by the mean curvature eqn (5) has the form of a Helfrich free energy,53,54 widely used to study membranes and vesicles.55–60 According to the Helfrich theory, the elastic free energy of membranes can be written as:  , where H and K are respectively the mean and Gaussian curvatures, kb and kg are bending modulus and Gaussian rigidity respectively, and σ is the constant surface tension. As here we are focused in substrates where K = 0 and where the surface tension contribution is constant, the Helfrich model simply reduces to:
, where H and K are respectively the mean and Gaussian curvatures, kb and kg are bending modulus and Gaussian rigidity respectively, and σ is the constant surface tension. As here we are focused in substrates where K = 0 and where the surface tension contribution is constant, the Helfrich model simply reduces to:
 | (6) |
 | (7) |
As discussed in the introduction, the self-organization process involves a phase transition that can proceed via nucleation and growth or spinodal decomposition. In either case, the formation of defects at the early stage of relaxation is completely unavoidable. Fig. 5 shows the time evolution of an initially disordered system towards an ordered smectic pattern on a cylindrical substrate. In this figure panels (a) and (b) show the early and late time configuration of the smectic phase. At early times the system is disordered but with a very strong length scale selectivity, imposed by the competing short- and long-range interactions of block copolymers. Here as the smectic pattern is not-well developed there is no evident coupling with the underlying geometry. As time proceeds, the annihilation of topological defects produces the ordering of the smectic phase and the coupling with the mean curvature (Fig. 5b). Here there is a preferential ordering of the pattern because regions with a director orientation α ≠ π/2 are energetically penalized (Fig. 4), such that the pattern evolves towards the equilibrium state with α ∼ π/2 throughout the cylinder. This anisotropic ordering can also be clearly observed through orientational maps showing the local orientation of the smectic phase with regard to the cylinder's symmetry axis at early (Fig. 6a) and late times (Fig. 6b) (here the cylinder is unrolled for the better appreciation of the orientational maps). In flat systems the elastic energy associated with ±1/2 disclinations is invariant under rotations. However, in curved backgrounds the degree of bending depends upon their orientation with regard to the substrate features. Then, it can be expected that the orientation of the typical multipolar arrays of disclinations that drive the order in flat systems19 becomes coupled to the substrate topography. Fig. 6 also shows the Helfrich-like bending energy contribution maps (eqn (6)). Note that at early times the bending energy is roughly randomly distributed through the cylinder. On the other hand, at long annealing times there is a clear reduction of bending energy contribution while those regions containing defects are energetically penalized. Note also that the disclination array shown in this figure acquires a particular orientation, where the core of the +1/2 disclinations aligns along a direction of maximum curvature (z = constant).
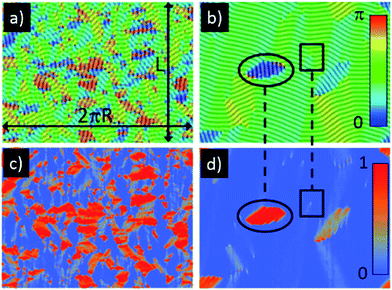 | ||
| Fig. 6 Pattern configurations (top panels) and Helfrich-like free energy maps (bottom panels) of a smectic phase deposited on a cylinder with a circular cross-section (the same configurations as shown in Fig. 5). Here L is the length of the cylinder and 2πR the arc-length of the circular cross-section. At early times (panels (a) and (c)), the Helfrich-like free energy contribution is roughly randomly distributed. At longer times (panels (b) and (d)), misaligned configurations are strongly penalized. The color maps indicate the local orientation of the smectic with regard to the cylinder's symmetry axis (top panels) and Helfrich-like free energy, normalized with (2/3)ψ02h2 (bottom panels). Here the presence of an array of disclinations and dislocations has been emphasized with an ellipse and a rectangle, respectively. | ||
In order to compare our model against the experimental results reviewed in Section 2, it would be more useful to consider substrates with varying mean curvature. For simplicity, here we consider corrugated substrates with Gaussian profile described as (see the inset of Fig. 7): R(x,y) = xi + yj + Γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x2/2)k, where Γ is a dimensionless constant that measures the deviation from flatness. The Gaussian curvature K for these substrates is zero and thus it is topologically equivalent to the experimental system shown in Fig. 3 and to flat space; there is no need for defects in the equilibrium state.61
exp(−x2/2)k, where Γ is a dimensionless constant that measures the deviation from flatness. The Gaussian curvature K for these substrates is zero and thus it is topologically equivalent to the experimental system shown in Fig. 3 and to flat space; there is no need for defects in the equilibrium state.61
During coarsening, we found that the system orders through the annihilation of dislocations and disclinations. Although in this case the order increases driven by the annihilation of arrays of defects, we can note that the curvature of the substrate acts as an external field that induces the preferential alignment of the lamellar pattern, in qualitative agreement with the experimental data shown in Fig. 3. This alignment can be observed in Fig. 7 which shows histograms of the orientation of the smectic pattern in the most curved region of the substrate (x = 0) at different annealing times. As observed in cylinders of constant mean curvature, at early times there is no coupling between the pattern and the mean curvature, such that all the orientations are equally probable and the distribution of orientations is flat (blue bars). However as the smectic order develops, it couples with the mean curvature, resulting in the growth of the energetically favored configuration with α = π/2 where the lattice distortion of the pattern is reduced (red and black bars).
For Gaussian substrates that involve small out of plane deformations, the mean curvature can be expressed as  . In these cases we can phenomenologically write a Helfrich-like free energy of the form (Fig. 8):
. In these cases we can phenomenologically write a Helfrich-like free energy of the form (Fig. 8):
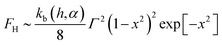 | (8) |
 | ||
Fig. 8 Cross-section of the substrate's height profile (z(x) = Γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(x2/2)), mean curvature (H) and Helfrich-like potential produced by the varying mean curvature (H2). exp(x2/2)), mean curvature (H) and Helfrich-like potential produced by the varying mean curvature (H2). | ||
Fig. 9 shows the pattern configuration of a smectic phase lying on a Gaussian substrate and the distribution of H2. This substrate reaches its maximum mean curvature along the directions defined by x = 0 and  (see also Fig. 8). Then, the smectic phase located in the neighborhood of these regions is subjected to the strong influence of the ordering field imposed by the Helfrich free energy and the mean curvature, energetically favouring configurations with local smectic orientations α ∼ π/2. Note in Fig. 9 that the perpendicular orientation of the smectic phase in the regions with the largest mean curvature is noteworthy and evidences a strong coupling between the block copolymer morphology and the substrate's topography. In addition, we have observed that the pattern located in the neighborhood of the regions with the largest mean curvature orders firstly, in agreement with the experimental results. Fig. 10 shows the block copolymer configuration observed after 90 min of annealing at T = 373 K. The preferential alignment of the smectic phase in the flatter regions and those with the largest values of H2 (green regions) is observed. In addition, the orientation of the 1/2 disclinations with regard to the substrate is observed. Clearly, this configuration of defects minimizes the elastic distortions associated with the out-of-plane deformations of the block copolymer thin film.
(see also Fig. 8). Then, the smectic phase located in the neighborhood of these regions is subjected to the strong influence of the ordering field imposed by the Helfrich free energy and the mean curvature, energetically favouring configurations with local smectic orientations α ∼ π/2. Note in Fig. 9 that the perpendicular orientation of the smectic phase in the regions with the largest mean curvature is noteworthy and evidences a strong coupling between the block copolymer morphology and the substrate's topography. In addition, we have observed that the pattern located in the neighborhood of the regions with the largest mean curvature orders firstly, in agreement with the experimental results. Fig. 10 shows the block copolymer configuration observed after 90 min of annealing at T = 373 K. The preferential alignment of the smectic phase in the flatter regions and those with the largest values of H2 (green regions) is observed. In addition, the orientation of the 1/2 disclinations with regard to the substrate is observed. Clearly, this configuration of defects minimizes the elastic distortions associated with the out-of-plane deformations of the block copolymer thin film.
 | ||
| Fig. 9 Pattern configurations and Helfrich-like free energy maps of a smectic phase deposited on a Gaussian bump. The color map representing H2 has been normalized with Γ2/4. | ||
5 Conclusions
In this work we have shown that due to the finite thickness of thin films the mean curvature of the underlying substrate may deeply affect the dynamics of coarsening and equilibrium configuration of block copolymers with smectic textures. For weakly curved substrates the free energy of the block copolymer film follows a Helfrich form, being proportional to the square of the mean curvature, with a bending constant dependent on the local pattern orientation. In good agreement with the experimental data, we observed that the dynamic coupling between the orientation of the smectic phase and the mean curvature of the substrate is dictated by the out-of-plane deformations of the block copolymer thin film. We can note that gently curved substrates combined with chemoepitaxy or graphoepitaxy would allow us to control the orientation and to improve the degree of order in different block copolymer systems. Finally, although here we only explored systems with smectic symmetry, the effect of the thin film thickness should be also important in block copolymers developing other self-assembled structures.Acknowledgements
We gratefully acknowledge helpful discussions with Richard Register and Paul Chaikin and the financial support from Universidad Nacional del Sur, the National Research Council of Argentina (CONICET) and ANPCyT (Argentina).References
- F. S. Bates and G. Fredrickson, Phys. Today, 1999, 52, 3238 CrossRef PubMed.
- I. W. Hamley, The physics of block copolymers, Oxford University, New York, 1998 Search PubMed.
- A. P. Marencic and R. A. Register, Annu. Rev. Chem. Biomol. Eng., 2010, 1, 277–297 CrossRef CAS PubMed.
- V. Pelletier, K. Asakawa, M. Wu, D. H. Adamson, R. A. Register and P. M. Chaikin, Appl. Phys. Lett., 2006, 88, 211114 CrossRef PubMed.
- M. Park, C. Harrison, P. M. Chaikin, R. A. Register and D. H. Adamson, Science, 1997, 276, 1401–1404 CrossRef CAS.
- M. Park, C. Harrison, P. M. Chaikin, R. A. Register and D. H. Adamson, Science, 2000, 290, 2126–2129 CrossRef.
- K. Naito, H. Hieda, M. Sakurai, Y. Kamata and K. Asakawa, Opt. Lett., 2002, 38, 1949–1951 CAS.
- D. E. Angelescu, J. H. Waller, D. H. Adamson, R. A. Register and P. M. Chaikin, Adv. Mater., 2004, 16, 1736–1740 CrossRef CAS.
- Y.-H. Hong, K. Asakawa, D. H. Adamson, P. M. Chaikin and R. A. Register, Opt. Lett., 2007, 32, 3125–3127 CrossRef CAS.
- M. Ma, K. Titievsky, E. L. Thomas and G. C. Rutledge, Nano Lett., 2009, 9, 1678–1683 CrossRef CAS PubMed.
- J. Y. Cheng, A. M. Mayes and C. A. Ross, Nat. Mater., 2004, 3, 823–828 CrossRef CAS PubMed.
- A. Tavakkoli, K. W. Gotrick, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Science, 2012, 336, 1294–1298 CrossRef PubMed.
- W. van Zoelen and G. ten Brinke, Soft Matter, 2009, 5, 1568–1582 RSC.
- J. Xu, T. P. Russell, B. M. Ocko and A. Checco, Soft Matter, 2011, 7, 3915–3919 RSC.
- S.-J. Jeon, G.-R. Yi and S.-M. Yang, Adv. Mater., 2008, 20, 4103–4108 CrossRef CAS.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A.-C. Shi, Phys. Rev. Lett., 2006, 96, 138306 CrossRef.
- A.-C. Shi and B. Li, Soft Matter, 2013, 9, 1398–1413 RSC.
- C. K. Harrison, D. H. Adamson, Z. Cheng, J. M. Sebastian, S. Sethuraman, D. A. Huse, R. A. Register and P. M. Chaikin, Science, 2000, 290, 1558–1560 CrossRef CAS.
- C. K. Harrison, Z. Cheng, S. Sethuraman, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011706 CrossRef.
- C. K. Harrison, D. E. Angelescu, M. Trawick, Z. Cheng, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Europhys. Lett., 2004, 67, 800–806 CrossRef CAS.
- D. A. Vega, C. K. Harrison, D. E. Angelescu, M. L. Trawick, D. A. Huse, P. M. Chaikin and R. A. Register, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061803 CrossRef.
- L. R. Gómez, E. M. Vallés and D. A. Vega, Phys. Rev. Lett., 2006, 97, 188302 CrossRef.
- S. B. Darling, Prog. Polym. Sci., 2007, 32, 1152–1204 CrossRef CAS PubMed.
- D. Sundrani, S. B. Darling and S. J. Sibener, Nano Lett., 2004, 4, 273–276 CrossRef CAS.
- J. Chai and J. M. Buriak, ACS Nano, 2008, 2, 489–501 CrossRef CAS PubMed.
- S. O. Kim, H. H. Solak, M. P. Stoykovich, N. J. Ferrier, J. J. de Pablo and P. F. Nealey, Nature, 2003, 424, 411–414 CrossRef CAS PubMed.
- D. Sundrani and S. J. Sibener, Macromolecules, 2002, 35, 8531–8539 CrossRef CAS.
- Y. S. Jung and C. A. Ross, Nano Lett., 2007, 7, 2046–2050 CrossRef CAS PubMed.
- Y. La, E. W. Edwards, S. Park and P. F. Nealey, Nano Lett., 2005, 5, 1379–1384 CrossRef CAS.
- I. Bita, J. K. W. Yang, Y. S. Jung, C. A. Ross, E. L. Thomas and K. K. Berggren, Science, 2008, 321, 939–943 CrossRef CAS PubMed.
- T. L. Chantawansri, A. W. Bosse, A. Hexemer, H. D. Ceniceros, C. J. García-Cervera, E. J. Kramer and G. H. Fredrickson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031802 CrossRef.
- L. R. Gómez and D. A. Vega, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031701 CrossRef.
- N. A. García, R. A. Register, D. A. Vega and L. R. Gómez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012306 CrossRef.
- N. A. García, A. D. Pezzutti, R. A. Register, D. A. Vega and L. R. Gómez, Soft Matter, 2015, 11, 898–907 RSC.
- D. Li, K. Liang and T. Gruhn, Macromol. Symp., 2014, 346, 22–31 CrossRef CAS.
- J. Li, H. Zhang and F. Qiu, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 18 CrossRef PubMed.
- L. Zhang, L. Wanga and J. Lin, Soft Matter, 2014, 10, 6713–6721 RSC.
- A. Hexemer, Ph.D. thesis, University of California, Santa Barbara, 2006.
- C. D. Santangelo, V. Vitelli, R. D. Kamien and D. R. Nelson, Phys. Rev. Lett., 2007, 99, 017801 CrossRef.
- D. A. Vega, L. R. Gómez, A. D. Pezzutti, F. Pardo, P. M. Chaikin and R. A. Register, Soft Matter, 2013, 9, 9385 RSC.
- K.-A. Wu and A. Karma, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 184107 CrossRef.
- J. Mellenthin, A. Karma and M. Plapp, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 184110 CrossRef.
- K. R. Elder, M. Katakowski, M. Haataja and M. Grant, Phys. Rev. Lett., 2002, 88, 245701 CrossRef CAS PubMed.
- A. D. Pezzutti, D. A. Vega and M. A. Villar, Philos. Trans. R. Soc., A, 2011, 369, 335 CrossRef CAS PubMed.
- A. D. Pezzutti and D. A. Vega, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011123 CrossRef.
- K. Yamada and S. Komura, J. Phys.: Condens. Matter, 2008, 20, 1 CrossRef.
- D. A. Vega and L. R. Gómez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 051607 CrossRef.
- A. D. Pezzutti, L. R. Gómez, M. A. Villar and D. A. Vega, Europhys. Lett., 2009, 87, 66003 CrossRef.
- R. K. W. Spencer and R. A. Wickham, Soft Matter, 2013, 9, 3373 RSC.
- A. Andelman, F. Brochard and J. Joanny, J. Chem. Phys., 1987, 86, 3673 CrossRef PubMed.
- J. Swift, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 14, 2274 CrossRef.
- S. A. Brazovskii, Soviet Physics – JETP, 1975, 41, 85 Search PubMed.
- J. M. Park and T. C. Lubensky, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 2648 CrossRef CAS.
- J. M. Park and T. C. Lubensky, J. Phys. I, 1996, 6, 493 CrossRef CAS.
- F. J. Solis, C. M. Funkhouser and K. Thornton, Europhys. Lett., 2008, 82, 38001 CrossRef.
- W. T. Gozdz and G. Gompper, Europhys. Lett., 2001, 55, 587 CrossRef CAS.
- C. M. Funkhouser, F. J. Solis and K. Thornton, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011912 CrossRef.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693 CAS.
- P. B. Canham, J. Theor. Biol., 1970, 26, 61 CrossRef CAS.
- O.-Y. Zhong-Can and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280 CrossRef.
- X. Xing, Phys. Rev. Lett., 2008, 101, 147801 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |






