Kinetics of colloidal deposition, assembly, and crystallization in steady electric fields†
Joseph A.
Ferrar
and
Michael J.
Solomon
*
Department of Chemical Engineering, University of Michigan, MI, USA. E-mail: mjsolo@umich.edu
First published on 16th March 2015
Abstract
We quantify and model the deposition and crystallization kinetics of initially dilute colloidal spheres due to application of a steady, direct current electric field in the thin gap between parallel electrodes. The system studied is poly(12-hydroxystearic acid) (PHSA)-stabilized poly(methyl methacrylate) (PMMA) spheres dispersed in a mixture of cyclohexylbromide (CHB), decalin, and a low concentration of the partially disassociating salt tetrabutylammonium chloride (TBAC). The temporal and spatial evolution of the colloidal volume fraction in the ∼1 mm gap between the electrodes is quantified under conditions of both deposition and relaxation by confocal laser scanning microscopy (CLSM). During deposition assembly, the spatial dependence of the colloid volume fraction approaches steady state at times between hundreds of minutes at the lowest electric field strength (as characterized by a Peclet number, Pe) and at tens of minutes at higher field strengths. During disassembly, the volume fraction relaxes nearly exponentially. The kinetics are modeled by adapting a treatment for sedimentation (Davis and Russel, Phys. Fluids A, 1989, 1, 82) to the case of steady electric fields. The model's predictions show good agreement with the measured kinetics at low Pe; however, agreement progressively deteriorates with increasing Pe. At low Pe the deposits are initially disordered. After an initial delay, 1D crystal growth propagates from the electrode surface at rates of several hundred nm min−1. The sharp crystal boundary propagates as a characteristic of constant colloidal volume fraction, consistent with an equilibrium crystalline phase transition. The results inform operational ranges for devices that produce active colloidal matter by reversible assembly.
Introduction
Colloidal crystal arrays with long-range positional order possess useful functional properties such as a photonic band gap,1 iridescence,1 and controllable porosity.1,2 Steady external fields – electric,3,4 gravitational,5–8 and shear9,10 – assist self-assembly by either concentrating particles to the point of a disorder-to-order phase transition or by accelerating the kinetics of this transition. Steady, direct current (DC) electric fields are of particular interest in this assembly process due to the fact that they are non-invasive, require only low power, and yield 3D assemblies.3 This method has recently been applied to generate reversible structural color in latex colloidal suspensions.11–15When a steady, uniform electric field, as generated by a Faradaic current, is applied to a dilute suspension of charged particles, the particles migrate toward an oppositely charged electrode via electrophoresis.3,16 The concentrated colloids form either ordered assemblies or amorphous deposits depending on the initial volume fraction of the suspension,6 the Peclet number,3,6 the suspension's compressibility and hydrodynamic interactions, and the time.3,9,10 Here the Peclet number is defined as Pe = (2U0R)/D0, where U0 is the free particle electrophoretic velocity, R is the sphere radius, and D0 is the Brownian diffusivity. Here U0 = f0εε0ζE/η, where ε is the dielectric constant of the solvent, ε0 is the vacuum permittivity, ζ is the particle zeta potential, E is the strength of the electric field, and f0 is a constant that ranges between 0.67 (Debye layer, κ−1 ≫ 2R) and 1 (κ−1 ≪ 2R).17E is equal to the field's current density (i) divided by the electrical conductivity (λ0) of the solvent; η is the viscosity of the solvent. Pe is the ratio of the electrophoretic velocity of a free particle, scaled by its characteristic length, to Brownian diffusivity.
Under the action of the uniform electric field, particles migrate toward the electrode and self-organize into deposits with a colloid volume fraction, ϕ, that varies with distance from the electrode. The spatially varying volume fraction generates a gradient in osmotic pressure. In the presence of the steady electric field, forces originating from both the applied field and the induced gradient in osmotic pressure therefore act upon the particles; it is their time-dependent balance that determines the kinetics of assembly. If the steady-state electric field is removed, the now unbalanced gradient in compressibility drives a flux of particles away from the electrode and back into the bulk region. The specific aim of this paper is to quantify and model the spatiotemporal behavior of the colloidal volume fraction during these two processes. Because of its relevance to applications, we pay special attention to the kinetic requirements for colloidal crystallization during the assembly process.
The rationale for the initial volume fraction, field strengths, Peclet numbers, and device gap that we select for study is that colloidal crystallization is induced rapidly (t ∼ tens to hundreds of minutes) in thin regions (hcrystal ∼ tens of microns) in geometries of small thickness (h ∼ 1 mm). These parameters define a range that is useful for applications.1,2 In addition, the thin geometries typical of direct current electric field assembly are an advantage for reversible assembly,3,13,15,18,19 because the smaller scales lead to accelerated assembly kinetics, which might potentially be exploited in applications such as switchable structural color,11–15 photonic materials,1 or in sensing.20 To produce these crystals at such conditions, it has been found that Pe ∼ 0.1–1.0 are needed.3,6 These physical parameters and deposition conditions contrast significantly with another common experiment – gravitational sedimentation – for which field-effects on colloidal crystallization have been studied. In sedimentation, colloidal crystallization is induced in thick regions (hcrystal ∼ 1 cm) from much larger initial heights (hinitial ∼ 101 cm and greater) and at much longer times (t ∼ several months).7,21,22
The steady-state density profile deduced from either sedimentation (of thick samples) or direct current electric fields (of thin samples) has been used to characterize the equation of state of different colloidal systems, including spheres at different electrolyte concentrations and rods of different aspect ratio.3,8,23 In these cases, measurements were performed at low Peclet numbers, experimental durations were long, and assembly kinetics were neither studied nor modeled. In addition, deposition kinetics have been studied in thick geometries over a range of Peclet numbers so as to understand conditions at which colloidal crystallization occurs.22
There is thus an unstudied parameter space of thin sample thicknesses, short deposition times, and small-applied field strengths that is of both scientific and technological interest. In this space, there is a potential operating window in which deposition would occur rapidly but colloidal crystallization would still be induced. The aim of this paper is to study this operating regime, and learn if the deposition and crystallization kinetics in it can be modeled by transport theory. Scientific questions in this regime are: (i) whether or not the continuum approximation implicit in colloidal transport theory can be applied in a regime in which the deposits are ∼50 μm in final height; (ii) whether or not applied field strengths are large enough to generate sufficient osmotic pressure to induce crystallization, yet small enough to avoid non-equilibrium effects such as jamming and vitrification; (iii) if available methods to parameterize the thermodynamic and hydrodynamic functions necessary to apply the transport theory are sufficient to model the complex kinetics that is observed for the times and field strengths of interest.
In this paper, the process in which particles move toward the electrode under the action of the applied field is called deposition. The process in which the colloids disassemble when the field is removed is called relaxation. We characterize the electric-field induced colloidal deposition and relaxation by measuring the spatial and temporal evolution of the volume fraction (ϕ) and the crystal thickness of the colloids from CLSM image analysis.24 The model system studied is an initially dilute suspension of poly(methyl methacrylate) spheres dispersed in a density and refractive index-matched solvent of cyclohexylbromide (CHB) and decalin. This system is commonly applied for direct visualization studies by confocal microscopy and is a model system for study of the phase behavior and dynamics of colloids.9,25,26 We predict the evolution of ϕ and crystallinity by adapting a one-dimensional model for sedimentation21,22 in a gravitational field in thick geometries (tens of cms) to the related case of an applied DC electric field in a thin geometry (1.15 mm). The comparison supports the applicability of the model, and indicates that optimal colloidal crystals are accessible by this simple technique if deposition is conducted at Pe ∼ 0.2 for durations on the order of an hour. Relaxation experiments and modeling show that this colloidal crystallization is rapidly reversible – with the accumulated deposits returning to an amorphous state within tens of minutes after the applied field is released. The results suggest that cycling between crystalline and amorphous states can be accomplished on scales of ∼120 min or longer by this method.
Materials & methods
Colloidal suspensions
Poly(12-hydroxystearic acid) (PHSA)-stabilized poly(methylmethacrylate) (PMMA) spheres of diameter 736 nm (+7.7% polydispersity) were synthesized following the methods of Antl et al.27 The particles contain Nile Red fluorescent dye and are imaged with a Nikon A1Rsi Confocal Laser Scanning Microscope (CLSM) (100× NA = 1.4 oil immersion objective). To ensure the presence of sufficient particle charge for deposition in the solvents of interest, a restabilization procedure was undertaken in which the particles were re-equilibrated with a concentration of PHSA ranging from equivalent to the concentration of particles to slightly greater than the concentration of particles over a period ranging from 2 to 3 days.28 The restabilized particles maintained their charge for several weeks. As needed, the procedure was repeated to reestablish the charge. After restabilization, the particles were dispersed in a density- and refractive index-matched mixture of 66 vol% cyclohexylbromide (CHB) and 34 vol% decalin at a volume fraction of 0.02.Solution conductivity, through tetrabutylammonium chloride (TBAC) electrolyte concentration, and applied current density were adjusted to produce four solutions whose direct current electric field assembly could be conducted at constant Pe of 0.14, 0.22, 0.80, and 1.07. These conditions bracket the operating range that yields both rapid deposition and high quality crystallization. The measured applied current density, particle zeta-potential, solvent electrical conductivity, TBAC concentration, and Debye length (κ−1) for each of the systems are reported in Table 1.
| System | [TBAC] (mM) | λ 0 (S m−1) | U 0/E (m2 s−1 V−1) | ζ (mV) | κ −1 (nm) | i (nA mm−2) | K 2,deposition | K 2,relaxation |
|---|---|---|---|---|---|---|---|---|
| Pe = 0.14 | 2 | 1.0 × 10−5 | (9.65 ± 2.61) × 10−10 | 90 | 42 | 0.51 | −1 | −6.55 |
| Pe = 0.22 | 1 | 4.5 × 10−6 | (7.16 ± 1.03) × 10−10 | 65 | 62 | 0.51 | −1 | −6.55 |
| Pe = 0.80 | 1 | 4.5 × 10−6 | (8.48 ± 1.36) × 10−10 | 65 | 62 | 1.53 | −1 | −6.55 |
| Pe = 1.07 | 1 | 4.4 × 10−7 | (3.33 ± 0.62) × 10−10 | 25 | 199 | 0.51 | −1 | −6.55 |
| Z(ϕ) | 1 | 4.5 × 10−6 | (6.92 ± 1.49) × 10−10 | 118 | 62 | 1.53 | −1 | −6.55 |
Other values reported in Table 1, and which are needed for the modeling are: (i) the free particle electrophoretic mobility (U0/E); (ii) K2, the estimated O(ϕ) correction to the particle velocity, U(ϕ) = U0(1 + K2(ϕ)) for the deposition and for the relaxation portions of the experiments.29–31K2 accounts for the effects of hydrodynamic interactions on field-induced particle convection, including the effects of backflow. We experimentally measure U0 for all deposition conditions from data collected at short times when the particle concentration is low; details of these measurements are included in the ESI.† The electric field strength (E) is characterized by the current density (i) and the solution conductivity, λ0, by E = i/λ0. The current density is the applied current per electrode cross-sectional area. The large ζ and κ−1 suggest that suspensions of the particles at high volume fraction might strongly interact thorough screened Coulombic interactions.
In electrophoresis, theory and experiment suggest that the effect of particle concentration on mobility is weaker than in sedimentation. Specifically, experiments suggest that K2 = −1 rather than K2 = −6.55 as for hard spheres in sedimentation, as indicated in Table 1. When the electric field is turned off, during relaxation, electrophoresis is no longer active. The particle mobility in this case is given by K2 = −6.55. Electrostatic interactions between the charged colloids do affect the concentration-dependent mobility; the estimated magnitude of this effect is explored in Fig. S5 (ESI†).32,33
DC electric field device for colloidal deposition
Fig. 1a is a schematic of the device used for DC electric field assembly of the colloids. The device consists of two plane parallel, glass electrodes, coated with indium tin oxide (ITO) as per Shah et al.3 and separated by a 1.15 mm thick glass spacer. The ITO coated surfaces are in contact with the suspension. A 5 mm circular hole is drilled into the center of the spacer to create a colloidal suspension chamber. This chamber holds approximately 23 μL of colloidal suspension and is sealed on either side by the electrodes with UV-curable glue. 19.6 mm2 of each electrode are exposed to the colloidal suspension. | ||
| Fig. 1 (a) Schematic of device used to apply DC electric fields to initially uniform suspensions of colloidal spheres. The device, developed by Shah et al.,3 has an electrode gap of 1.15 mm. (b) Current vs. time and (c) voltage vs. time plots for a galvanostatic electric field applied from 0–30 minutes and then removed from 30–90 minutes. | ||
The device is placed onto the stage of the CLSM (Nikon A1 Piezo z-drive) for direct visualization of deposition and disassembly. Both electrodes are connected to an Autolab PGSTAT 128N potentiostat/galvanostat. For deposition, we use galvanostatic (constant current, variable voltage) operation because it yields experiments at constant Pe. Then, the applied voltage progressively increases with time to compensate for the depletion of different electrochemically active species within the solvent.34 Upon completion of the deposition process, the current is turned off, and a constant electric potential of 0 Volts (V) is applied. This condition approximates the application of no power to the system, as the cell's (measured) open circuit voltage is very small (0.03 V). The voltage–current behavior observed for a particular experiment is shown in Fig. 1b and c.
Electrophoretic deposition and subsequent relaxation were imaged in a 2D plane oriented perpendicular to the device's electrodes. (Time-resolved 3D imaging was not possible because the large electrophoretic velocity of the particles caused sufficient displacement that particles locations could not be accurately determined by 3D image analysis.) To capture changes in colloidal volume fraction and crystallization with axial distance above the electrode, a time-series of images is acquired in a plane perpendicular to the electrode surface. The excitation was at 561 nm and the emission was collected from 570–620 nm. The image, of resolution 512 × 1593, is acquired as a set of line scans of length 15.93 μm, each separated by a vertical distance of 0.031 μm. The pixel size is 0.031 × 0.031 μm2, the image size is 15.93 × 49.50 μm2, and the frame rate is one every three seconds.
Image analysis, colloid volume fraction, and crystallization height
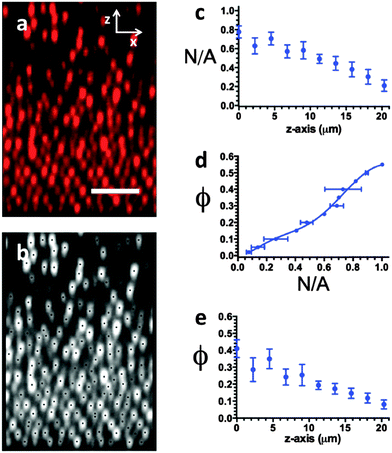
Fig. 2a is a typical image acquired during the electric field assembly. In this image the electrode surface is visible as a line at the bottom below which there are no colloids. In Fig. 2a, as is characteristic with all experiments performed, the colloidal volume fraction, ϕ, varies with distance above the electrode. There is little variability in ϕ along lines parallel to the electrode. The spatial dependence of the volume fraction, ϕ(z,t), is determined from the image time series, of which Fig. 2a represents one instance. Image analysis is by the algorithm of Crocker and Grier.24 Briefly, after a filtering step to smooth high frequency noise, pixels of the highest intensity in a spatial region of a dimension of approximately the particle diameter are identified as particle centroids. Thus, the image analysis yields the location of every particle identified within the image.Fig. 2b shows the particle centroids identified by the image analysis of Fig. 2a (the black dots represent identified particle centroids and are overlayed on top of a grayscale rendering of the original CLSM image). These centroids are located to precision of ±20 nm and ±77 nm in the tangential and axial directions, respectively, as found from image analysis of a specimen immobilized by photopolymerization. A check of the overlay image indicates the volume fraction found by image analysis is within 6% of the volume fraction expected based on the volume of the particles relative to the size of the imaged volume. Although we image ∼40 μm above the electrode, we limit our analysis to a region 20 μm above the electrode, due to imaging effects that may cause inaccuracies in particle identification at distances far from the coverslip.
The identified particles centroids are resolved into bins centered on different heights above the electrode. We take the distance of 4 layers of close-packed FCC particle layers (bin height = 4 × 0.767D = 2.26 μm) as the bin width and there are 10 of these vertical bins per image. The result is shown in Fig. 2c, which is the measure N(z)/A, or the number of particles per unit image area centered on each vertical height z. We transform N(z)/A to ϕ(z) by means of a calibration generated by CLSM measurements on 12 specimens of known volume fraction, as shown in Fig. 2d. To implement the calibration, we fit the Fig. 2d calibration curve to a high order polynomial. This method avoids the need to estimate the uncertain optical depth of field of the acquired 2D images.
Fig. 2e shows the final result of ϕ(z) for the colloidal suspension imaged in Fig. 2a. To observe the evolution of ϕ(z) in time, we repeat the image analysis and conversion from N(z)/A to ϕ(z) for each of the images in the time series used to capture the kinetics. To address noise in the time series, we take ϕ(z,ti) as the average of images in the time from ϕ(z,0.9ti) to ϕ(z,1.1ti). (For example, ϕ(z, t = 300 seconds) is an average of ϕ(z, 270 ≤ t ≤ 330 seconds).) We also report the standard deviation of frames as error bars on ϕ(z,t) plots. To capture any error associated with specimen-to-specimen variability, we also performed five replicate trials at the condition Pe = 1.07. The error bars reported on ϕ(z,t) plots at this condition therefore establish the contribution of replication error.
Kinetic modeling of deposition and relaxation
To model field-induced deposition and subsequent relaxation in a steady electric field, we adopt a one-dimensional colloidal transport model from the sedimentation literature.7 Specifically, the convective-diffusion equation for the volume fraction field is: | (1) |
Here U0 is the electric field-induced free particle electrophoretic velocity. The compressibility, Z(ϕ), is directly measured by the method discussed in the next section. K(ϕ) accounts for concentration effects on the colloidal mobility, U(ϕ)/U0 = K(ϕ). D0 is the Stokes–Einstein diffusivity, and Z(ϕ) is the compressibility factor of the suspension. In colloidal suspensions, Z(ϕ) = Π(ϕ)/nkT, which is a ratio of the suspension's ϕ-dependent osmotic pressure to the osmotic pressure of an ideal solution. Here, n = ϕ/Vparticle, or the number of particles per volume of suspension. Eqn (1) quantifies the effect the electric field (convective term) and gradients in osmotic pressure (diffusion term) have on ϕ(z,t). To model the retardation of particle mobility with concentration, we use the empirical function K(ϕ) = (1 − ϕ)−K2, with K2 as assigned in Table 1. Note that K2 varies between deposition (field on) and relaxation (field off) experiments because of the effect of the steady electric field on the concentration dependent mobility.29–31 The concentration-dependent mobility for the relaxation experiments is taken as that of amorphous hard spheres. Crystallinity and charge is known to affect the concentration-dependent mobility, and these effects have been studied by both experiment and theory.32,33,35 Fig. S5 (ESI†) explores how these effects change model predictions. Their effects are small for the systems and conditions studied here. Note that during relaxation, no electric field is applied and therefore U0 = 0; eqn (1) thus reduces to the diffusion equation.
Eqn (1) is solved numerically by the finite element method (FEM), implemented in COMSOL Multiphysics, for 1D transport with ϕ-dependent rates of convection and diffusion. The spatial domain is the gap between the device's electrodes (1.15 mm). There are two time domains: the time of particle deposition, tdep, and the time of particle relaxation, trel, which begins as soon as tdep ends. The initial condition is the initial volume fraction profile (ϕ(z, t = 0)) of the suspension, and the boundary conditions are no particle flux at either electrode. For deposition, ϕ(z, tdep = 0) = 0.02 at all positions within the sample. For relaxation, the initial condition ϕ(z, trel = 0) is as predicted by the model at the end of deposition – just before the field is turned off and the relaxation begins.
The spatial domain is divided into either 1000 or 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements, the time domains use steps of either 0.1 or 1 s, and the relative tolerance is varied between 0.01 and 0.05, depending on which of the above numerical parameter values allow for convergence of the numerical method. A coarser mesh in both time and space, as well as a greater relative tolerance, is needed for convergence as Pe increases. We assessed the effects of grid element number, time step, and tolerance on simulation results by changing grid element number and time step size by set factors (i.e. a factor of 10 at Pe = 0.14) and tolerance step sizes by a set factor (i.e. a factor of 5 at Pe = 0.14) and saw negligible differences in solutions to eqn (1).
000 elements, the time domains use steps of either 0.1 or 1 s, and the relative tolerance is varied between 0.01 and 0.05, depending on which of the above numerical parameter values allow for convergence of the numerical method. A coarser mesh in both time and space, as well as a greater relative tolerance, is needed for convergence as Pe increases. We assessed the effects of grid element number, time step, and tolerance on simulation results by changing grid element number and time step size by set factors (i.e. a factor of 10 at Pe = 0.14) and tolerance step sizes by a set factor (i.e. a factor of 5 at Pe = 0.14) and saw negligible differences in solutions to eqn (1).
Compressibility factor of charged colloidal suspensions
Modeling the kinetics of deposition and relaxation from eqn (1) requires Z(ϕ) for the charged suspensions studied. Recall that Z(ϕ) = Π(ϕ)/nkT. Π(ϕ) can be directly inferred from the equilibrium sedimentation profile as per the method of Piazza.8 For sedimentation, particles with a buoyant mass settle to a steady-state profile determined by hydrostatic equilibrium. For direct current electric field assembly, the equivalent expression is: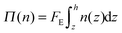 | (2) |
 | ||
| Fig. 3 Z(ϕ) from steady-state profile of ϕ(z). (a) PMMA spheres at ϕ0 = 0.01 were deposited in a steady (E = 340 V/m) field until a steady state in ϕ(z,t) was achieved. Scale bar is 5 μm. Eqn (2) was applied to these data to obtain Π(z), which is plotted as Z(ϕ) in b. The curve is the fit to eqn (3) with parameters as given in the text. | ||
In eqn (2), the force of the electric field on the particle, FE, depends on the Debye layer thickness relative to the particle size. In the Debye–Huckel limit for κD ≪ 1, FE is balanced by Stokes drag and is equal to 4πεε0ζRE where ε is the solvent dielectric constant, ε0 is the permittivity of free space, and E is the magnitude of the electric field.36 Here, FE in eqn (2) is directly characterized from the limiting behavior of the compressibility at vanishing volume fraction: Z(ϕ = 0) = 1. From this limiting behavior we characterize FE to be a factor of 1.86 less than the Debye–Huckel limit. That is, we implicitly use the ideal solution limit of the compressibility, as measured at equilibrium, to characterize the force of the electric field on a particle in the system.
To model the experimental Z(ϕ), we adopt the following continuous, differentiable function given by Peppin et al.37
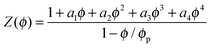 | (3) |
Results
Colloidal deposition and relaxation under a steady electric field
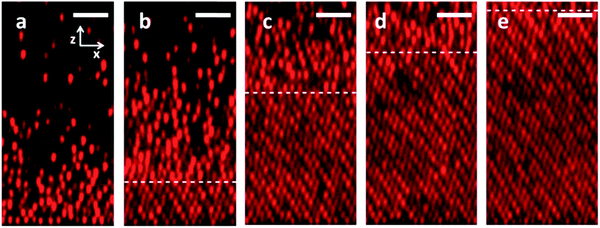
Fig. 4 reports images of colloidal deposition at a constant current density of 0.51 nA mm−2 (Pe = 0.22; Fig. 4a–e), as well as the subsequent relaxation of the assembled structure (Fig. 4f–j). A movie of the image time series is in the ESI† (Movie S1). Prior to application of the electric field (Fig. 4a), particles are homogeneously dispersed at an initial volume fraction of 0.02. Fig. 4b shows the sample after 30 minutes of electrophoretic deposition. A dense, amorphous deposit is observed at the electrode; the particle density decays with increasing distance from it. Fig. 4c shows the sample after 1 hour of deposition; colloidal crystallization is observed at this time. A sharp disorder-to-order transition is observed; the boundary spans the width of the entire image at a z-position of ∼7 microns above the electrode. Above this boundary, ϕ(z) varies rapidly with distance above the electrode. After two hours of deposition (Fig. 4d), the crystallization phase boundary has now propagated nearly to the top of the image and the particle density appears constant with distance above the bottom electrode. Fig. 4e shows the sample after 3 hours of particle deposition; an ordered crystal fills the entire imaged region. The density of this crystal appears slightly greater than the crystal observed at t = 2 h.The steady electric field is removed in the moments between Fig. 4e and f, and thus Fig. 4f shows the suspension at the onset of relaxation. In the absence of the applied electric field (Fig. 4g–j), particles diffuse away from the electrode toward the bulk solution. Fig. 4g shows the suspension after 5 minutes of relaxation. The deposit appears more disordered relative to the one observed in Fig. 4f; however, some order is still apparent throughout the sample. Fig. 4h shows the suspension after 15 minutes of relaxation. The particle number density is less than in the earlier frames, and crystalline order has vanished. Fig. 4i and j shows the sample after 30 and 90 minutes of relaxation – disorder and dilution due to diffusion of the particles away from the near-electrode region continues. During relaxation (field off), the particle density remains more uniform with distance above the electrode than during deposition, as evidenced by comparison of early time images of deposition (e.g.Fig. 4b) and late time images of relaxation (e.g.Fig. 4i).
Images of deposition and relaxation at the other Pe conditions studied can be found in ESI† (Fig. S1–S3). In each case, the deposition was continued until ϕ(z, t) attained steady state within the image area, which was approximately 40 μm above the electrode. This criterion yielded 420 minutes of deposition at Pe = 0.14, 180 minutes of deposition at Pe = 0.22, 90 minutes at Pe = 0.80, and 30 minutes at Pe = 1.07. Thus, particles deposit faster at higher Pe numbers.
The following qualitative effects are noted by comparing Fig. 4 and Fig. S1–S3 (ESI†). First, appreciable colloidal crystallization is observed at Pe = 0.14 (Fig. S1, ESI†) and Pe = 0.22 (Fig. 4 and Movie S1, ESI†). In both cases, crystallization is first observed at the electrode boundary. A front with crystal below and amorphous liquid above is established. The front propagates upward from the electrode surface. At Pe = 0.14, we observe high quality order of the crystal on a local scale; however, long-range order is imperfect – grain boundaries and stacking faults are observed. Comparable ordering is observed at Pe = 0.22. By comparison, little to no ordering was observed at Pe = 0.80 (Fig. S2, ESI†) and Pe = 1.07 (Fig. S3, ESI†).
Colloidal deposition and relaxation kinetics
Fig. 5 shows ϕ(z = 0, t), hereafter referred to as ϕelectrode(t), for all Pe conditions. ϕelectrode(t), is the largest particle density in the deposit at that time, and therefore is a characteristic measure of the deposition and relaxation dynamics. Data points represent experimental measurements, while curves represent solutions to eqn (1). The error bars represent the standard deviation of these time-averaged measurements. Recall that the Pe = 1.07 condition was replicated five times in order to quantify the error associated with sample-to-sample variability; in this case the data points are an average of these five separate, time-averaged measurements. | ||
| Fig. 5 Electrode volume fraction, ϕelectrode, as a function of time for (a) Pe = 0.14 (b) Pe = 0.22 (c) Pe = 0.80 and (d) Pe = 1.07. Data points are measured values and curves are solutions to eqn (1). Dotted curves are model solutions for a standard deviation above and below the measured colloidal velocity in the steady electric field, U0. | ||
The colloids deposit very rapidly at the onset of the steady electric field, and a corresponding increase in ϕelectrode at early deposition times is observed in all cases. Consistent with the images of Fig. 4 and Fig. S1–S3 (ESI†), we observe a plateau of measured ϕelectrode profiles at later deposition times, indicating that a steady state in ϕ(z,t) is approached. The solid curves are the solution to eqn (1) at each Pe using the average measured value of U0 for each condition from Table S1 (ESI†). The dotted curves are the solutions to eqn (1) for the upper and lower limits of the standard deviation in U0, also as reported in Table S1 (ESI†). Recall that U0 is the velocity of a dilute colloid at the applied field strength (Pe). It was characterized by direct measurement at early-time conditions (cf. ESI†).
Especially when the uncertainty in U0 is considered, the measured deposition kinetics are modeled to a fair degree by eqn (1). Specifically, the rapid deposition at high Pe is captured, and the steady-state volume fraction is well-modeled except at the highest Pe studied. At low Peclet number, the experiments show a somewhat faster deposition than the model predicts, even allowing for the uncertainty in U0. In addition, at the highest Peclet number, the steady-state volume fraction predicted by the transport model is greater than the measured steady-state volume fraction by a factor of 1.2. The effect of the error in U0 is more significant at Pe = 0.14 and Pe = 0.22 than at Pe = 0.80 and Pe = 1.07 even though, as can be seen in Table S1 (ESI†), the standard deviation of U0 measurements was similar across all Pe conditions. This sensitivity arises from the steepness of Z(ϕ) at high ϕ. As Pe increases, Z(ϕ) increases. In this region, a unit change (error) in Z(ϕ) has just a small effect on ϕ. Consequently, at low Pe modeling errors in ϕ are ∼5%. These errors reduce to ∼1% at the higher Pe number conditions. Thus, the effect of the uncertainty in U0 measurements has a greater effect on eqn (1)'s performance at lower Pe numbers than at higher Pe number.
There is a significant disagreement between the steady-state results for experiment and model at Pe = 1.07. A systematic difference between the equation of state (EOS), Π(ϕ), for the experiment and model is possible for this case. Specifically, the Debye length of the suspension from which the EOS was obtained is identical to the Debye length of the Pe = 0.22 and 0.80 conditions (62 nm), and very similar to the Pe = 0.14 conditions (42 nm) (Table S1, ESI†). However, the Debye length of the Pe = 1.07 suspension system is more than three times larger (199 nm). It is likely that the significant difference in Debye lengths between the Pe = 1.07 and the other systems explains some of the discrepancy between model and measurements at Pe = 1.07. That is, the larger diffuse double layer in the experiments would prevent the particles from packing as densely as the model – parameterized with a smaller diffuse double layer – would predict. (This effect is not accounted for by using an effective volume fraction based on the double layer thickness for the modeling. This approach likely fails because of the effects of double layer compression at high volume fraction.) Additionally, non-equilibrium effects, as addressed in the Discussion, might also lead to a discrepancy between model and experiment.
In Fig. 5, the electrode volume fraction declines during relaxation. Relaxation occurs very rapidly at the boundary between the dense deposit and the dilute bulk solution due to the large gradient in osmotic pressure at this boundary. Particles buried within the deposit remain kinetically trapped until the particles layered on top of them have diffused into the bulk solution. Once the deposit is sufficiently diluted by this initial mechanism, relaxation is slow because of the reduction in the magnitude of the osmotic pressure gradient. At long times, the volume fraction returns to the initial value of 2%; however, in all cases the relaxation volume fraction never decays below 15% in duration over which images were recorded. The transport modeling supports this initial fast relaxation followed by a slow return to homogeneity.
At Pe = 0.14 and 0.22, the measured relaxation kinetics are well modeled by eqn (1). The model's predictions reside near the upper limit of the error at early and intermediate times at Pe = 0.22, and are in good agreement at late times. At Pe = 0.80, the model lags the measured kinetics at early and intermediate times, but predictions and measurements are in better agreement at late times. At Pe = 1.07, the model significantly lags measured kinetics at all times, although the discrepancy is moderated at late times.
The model lags the measured kinetics at Pe = 1.07 due to the discrepancy in the initial condition. For the model, the ϕ(z, trel = 0) initial condition is as predicted by the model at the end of deposition – just before the field is turned off and the relaxation begins. The accuracy of this initial condition therefore depends on the accuracy of the model at late deposition times, which is itself in error, as discussed previously. The larger model initial condition has two effects that contribute to error in the relaxation. First, the number of colloids in the near wall region that must now diffuse away into the bulk is larger in the model than the experiment. Second, the osmotic pressure gradient available to drive colloids away from the near wall region is lower in the model than in the experiment because of the flat volume fraction profile in this region.
An interesting feature of the Fig. 5 results is the time scale required for appreciable deposition to occur. This time scale varies with Pe number. To further quantity this aspect of the deposition, Fig. 6 plots the time needed for ϕelectrode to reach 95% of its final value for each Pe condition, here called, tSS. This characteristic time is plotted for both the experiments and model. tSS decreases with Pe by approximately an order of magnitude from Pe = 0.14 to Pe = 1.07 for both experimental measurements and the model. At high Pe (Pe = 0.80 and 1.07), experiments and theory both predict a characteristic steady-state time between 10 and 20 minutes. At low Pe (Pe = 0.14 and 0.22), there is a discrepancy between the measured and modeled characteristic steady-state time. Measurements predict tSS = 65 minutes and 105 minutes for Pe = 0.14 and 0.22, respectively, while eqn (1) predicts tSS = 136 minutes and 360 minutes.
 | ||
| Fig. 6 Characteristic times of deposition (tSS) as a function of Pe. tSS is the time needed for ϕelectrode to reach 95% of its final value during deposition, as assessed from the results of Fig. 5. Blue data points are characteristic times for measurements, black data points are characteristic times for modeling. The curves are power laws: tSS(Pe) = 13.5 × Pe−1.091 for the measurements and, tSS(Pe) = 16.2 × Pe−1.568 for the model. | ||
The discrepancy in the model at low Pe potentially identifies errors in the characterization of the three material properties and functions that control the time scale for the field-assisted assembly. These parameters are the equation of state (Π(ϕ)), the sedimentation function, K(ϕ), and the electrophoretic velocity, U0. The first and last parameters were directly measured; K(ϕ) was taken from the literature. The agreement in measured Debye lengths between the particle–solvent systems used at low Pe (where there is a discrepancy in tSS) and at Pe = 0.80 (where the tSS prediction is accurate) indicate that Π(ϕ) is unlikely to be the cause of this discrepancy. To test if uncertainty in K(ϕ) might explain the discrepancy at low Pe, we varied K(ϕ) by varying the exponent, K2, and found only a small effect of this variation on the eqn (1) solutions (cf. Fig. S5, ESI†). However, as shown in Fig. 5, uncertainty in U0 has a significant effect on the performance of eqn (1) at low Pe numbers. Thus, small errors in U0 can significantly affect the tSS characterization at low Pe.
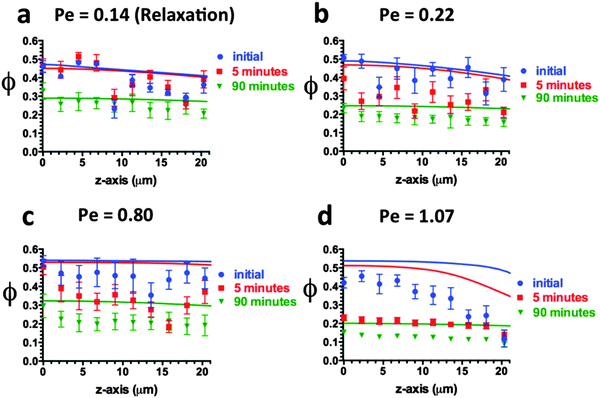
Fig. 7 and 8 report the spatial variation in the volume fraction at different time points and Pe conditions, for the cases of deposition and relaxation, respectively. The spatial range is 0 ≤ z ≤ 20 μm. Similar to ϕelectrode behavior observed in Fig. 5, particles accumulate very rapidly in the near-electrode region, especially at high Pe. The rate of deposition then slows due to (a) an increase in osmotic pressure as more particles deposit, and (b) retardation of particle mobility in the concentrated deposits. Specifically, significant increases in ϕ are seen across all positions within the first hour of deposition at Pe = 0.14 and 0.22, yet negligible changes in ϕ are seen in the last hour. Likewise, significant increases in ϕ are seen across all positions within the first 15 minutes of deposition at Pe = 0.80 and Pe = 1.07, yet little change in ϕ is observed in the last 30 minutes at Pe = 0.80 and in the last 10–15 minutes at Pe = 1.07. As a result of this kinetic behavior, ϕ(z) profiles become nearly flat at later times, especially at the lowest Pe. This behavior is a consequence of the divergent behavior of Z(ϕ) at high ϕ (Fig. 2b).
 | ||
| Fig. 7 ϕ(z,t) during deposition at (a) Pe = 0.14 (b) Pe = 0.22 (c) Pe = 0.80 and (d) Pe = 1.07. The curves are solutions to eqn (1). | ||
 | ||
| Fig. 8 ϕ(z,t) during relaxation at (a) Pe = 0.14 (b) Pe = 0.22 (c) Pe = 0.80 and (d) Pe = 1.07. The curves are solutions to eqn (1). | ||
The model's solutions (curves) show good agreement with experimental measurements (data points) at Pe = 0.14 (Fig. 7a) and Pe = 0.22 (Fig. 7b) at all positions and times. At Pe = 0.80 they agree with the experiments at low z-positions and all times (Fig. 7c). However, the agreement is only fair at higher z-positions and later times. At Pe = 1.07, the model's solutions are in good agreement with experimental measurements only at very early times – tdep = 1 minute – but then overshoot the measurements at all later positions and times (Fig. 7d).
Fig. 8 shows ϕ(0 ≤ z ≤ 20 μm, trel) at all Pe conditions. ϕ(z) profiles are relatively flat, independent of z-position, at all times during relaxation, as compared to their shape at early times during deposition. The measured volume fraction across all z-positions drops much more significantly in the first five minutes than in the remaining tens of minutes of relaxation, at Pe = 1.07. By comparison, the ϕ(z) profile at Pe = 0.14, 0.22, and 0.80 after 5 minutes of relaxation differs only marginally from the initial condition, because the top-most portion of deposits at these conditions (z ∼ 20 microns) are much denser at the onset of relaxation than are deposits at Pe = 1.07. Therefore, less time is required for particles to be released into the bulk fluid region at Pe = 1.07 than at the other Pe conditions. In Fig. 8, measured ϕ(z) profiles are somewhat noisy (i.e. jagged), at initial times, likely due to discretization effects; however, the level of agreement between model and experiment can still be assessed at later times.
The driving force for relaxation is the gradient in osmotic pressure between the dense deposit and the bulk fluid. As relaxation proceeds, this gradient diminishes, and thus, so does the rate of relaxation. At low volume fraction, a characteristic time scale for this relaxation is t ∼ H2/D0, where H is the ∼1 mm gap between the electrodes. The initial volume fraction in the electrode gap (2%), the ∼20% volume fraction after the initial rapid volume fraction depletion, and the 1 mm electrode gap suggest a deposit height that decays from h ∼ 100 microns in this slow relaxation period. Thus, given the free particle diffusivity of ∼0.265 μm2 s−1, the second step of the relaxation, when osmotic pressure gradients are low, requires a duration on the order of tens of days.
Propagation of crystallinity during deposition
The propagation of long-range, crystalline ordering is observed at Pe = 0.14 and 0.22. Little to no long-range order was observed at Pe = 0.80 or 1.07. At Pe = 0.14 and 0.22, the order is generated by the propagation of a crystalline front along an axis perpendicular to the electrode surface, as shown in Fig. 9a–e for Pe = 0.22. The dotted line indicates the position of the crystalline front. Such one-dimensional (1D) propagation of crystallization has been previously reported for the case of gravitational sedimentation.22 After the electric field is turned off, crystallinity persists near the electrode surface for tens of minutes. By 90 minutes, disorder has been reestablished at all axial positions.The position of the crystalline transition front (marked by the dotted line in Fig. 9a–e) – henceforth called hfront – is plotted in Fig. 10a and b for the Pe = 0.14 and 0.22 conditions, respectively. For both conditions, there is an onset period, of duration tens of minutes, during which crystallization is not observed, likely because the particles must concentrate sufficiently before crystal growth can occur. After this onset period, hfront grows at a nearly constant rate. Linear regression of the measurements yields a growth rate of 95 nm min−1 at Pe = 0.14 and 198 nm min−1 at Pe = 0.22. These rates are comparable to growth rates of ∼100–300 nm min−1 reported for sedimentation.22 Davis et al. modeled this propagation with classical nucleation theory. In this treatment, the rate at which amorphous particles add to the growing crystal depends on the difference in chemical potential between the crystalline and amorphous regions and the Brownian dynamics of the colloids at the conditions of the front.
The solid curves in Fig. 10a and b are loci in time and height of constant colloid volume fraction for the two Pe studied, as predicted by eqn (1). These model curves can be used to evaluate if the time-height dependence of the experiments correspond to a characteristic, constant volume fraction. At Pe = 0.14, the experimental hfront(t) is largely bounded by propagation characteristics of ϕ = 0.35 and ϕ = 0.37. At Pe = 0.22, hfront(t) approximately tracks the characteristic curve for ϕ = 0.33. Combining the two conditions, the crystal front maintains a volume fraction between ϕ = 0.33 and ϕ = 0.37.
To further investigate the possibility that the crystalline front propagates at a condition of nearly constant volume fraction, ϕ at each measured hfront position and time is plotted in Fig. 10c (Pe = 0.14) and d (Pe = 0.22) for the cases of both direct experimental characterization by image analysis (data points) and by the transport model (curves). The data points end at 20 μm, the upper limit at which ϕ was measured by image processing. Except at the initial point, the experimentally measured volume fraction of the crystal front is relatively flat for Pe = 0.14 and slightly decreasing for Pe = 0.22.
Fig. 10 therefore suggests that the volume fraction of colloids at the crystal front is constrained in a relatively narrow band centered on about ϕ = 0.34. This result is consistent with: (i) equilibrium fluid-crystalline phase transitions reported for PHSA–PMMA spheres of κR ∼ 6 in literature (ϕ ∼ 30%);38 (ii) our own equilibrium crystallization measurements for this colloid–solvent system, conducted in rectangular capillaries for a duration of two months.
The crystal front thus propagates along a characteristic of nearly constant volume fraction that is within the equilibrium coexistence region. Therefore, the rate of 1D crystalline growth can be predicted in DC electric field assembly by means of eqn (1) if this crystallization volume fraction has been independently measured. The crystallization comparison thus demonstrates the scope for using the model to directly predict the kinetics of time-dependent colloidal assembly by steady electric fields. What is required is measurement of the colloid equation of state (Fig. 3), the electrophoretic mobility at the condition of deposition (Table S1, ESI†), and the coexistence volume fraction of the system. Independent characterization of these material functions therefore yields, by means of eqn (1), a no adjustable parameter prediction of the deposition, assembly, and crystallization of the colloids in steady-electric fields.
Discussion
The results of this study address questions about the kinetics of colloidal assembly in steady electric fields, including the scope for their modeling by transport theory. Here we address: (i) if the continuum approximation inherent in eqn (1) is valid for the case of the thin ∼50 μm deposits generated here; (ii) if the operating window for deposition comprises a region in which crystallization can occur; (iii) if the available characterizations of the equation of state and electrophoretic velocity are sufficient to model the experimentally observed deposition structures.The continuum description of eqn (1) is potentially at odds with the fact that thin deposits were produced. Such thin deposits facilitate reconfiguration between crystalline and non-crystalline states, with cycle times ∼120 minutes observed in the experiments reported here. For these thin deposits, colloid volume fractions were determined as an average of intervals that were four particle layers deep. At this resolution scale it is arguable that effects of the discrete layers might invalidate continuity of the osmotic pressure and its gradients, which appear as terms in eqn (1). However, both the measured and modeled volume fraction profiles were found to vary smoothly, and the agreement between the two is fair to good. Thus, even though the deposits modeled are never more than about 100 particle layers thick, the continuum descriptions of eqn (1)–(3) are sufficient to capture the deposition and relaxation kinetics, even when crystalline deposits are formed at low Pe number. One case for which the ∼ four layer resolution limit might complicate interpretation of the measurements is for the behavior of the crystal front. The volume fraction of the front was consistent with reports of the equilibrium coexistence region. However, the spatial resolution of the volume fraction characterization is such that both amorphous and crystalline sides of the boundary contribute to the front volume fraction plotted in Fig. 10c and d. That is, the spatial resolution of the experiments was not sufficient to observe a discontinuity in the volume fraction at the front boundary, as would be expected for local equilibrium, and as has been seen for the case of sedimentation in thick specimens.8,23
The weakest electric fields applied (Pe = 0.14 and 0.22) were still large enough to generate sufficient osmotic pressure for crystallization. Eqn (1) predicts even greater propensity for crystallization at the two higher Pe studied, Pe = 0.80 and Pe = 1.07, because the osmotic pressures generated at the electrode by these applied field are even greater than the low Pe experiments. However, this expectation was not borne out by the experiments, because little to no colloidal crystallization was observed at these two high Pe number conditions. The presence of long-range crystalline ordering at low Pe numbers is consistent with other field-assisted assembly observations.3,6,9,22
For the higher Pe number experiments, the volume fraction of the deposit is lower than theory would predict. Moreover, although the measured volume fraction is in a region for which crystallization is observed at equilibrium, no order was found in the deposits. Non-equilibrium effects could modify the deposition in two ways. First, non-equilibrium effects could generate (metastable) structures that do not conform to the Fig. 3 equation of state. This effect would contribute to, for example, an observed volume fraction that was lower than predicted by eqn (1). Second, jamming or vitrification could prevent the initially amorphous deposits from transforming into crystalline structures at the volume fraction at which they are deposited. Fig. 5d appears to indicate that both effects are relevant to explaining the results at high Pe number.
The comparison between the measurements and model relies on the availability of accurate functions used by the model – U0, Π(ϕ), and K(ϕ). We first consider possible errors in K(ϕ). At low Pe the deposition leads to colloidal crystals; K(ϕ) in this case would differ from the functions used, which were taken as those for amorphous conditions. However, switching K(ϕ) to one appropriate for a periodic arrays of spheres has a negligible effect on the modeling solutions (cf. Fig. S5, ESI†).35 In addition, model results are comparatively insensitive to the parameterization of K(ϕ) during deposition because varying this function has little effect on eqn (1) solutions during deposition. However, the model results are sensitive to the functional form of K(ϕ) during relaxation (cf. Fig. S5, ESI†). Specifically, the K2 appropriate for electrophoretically deposited spheres (K2 = −1.0) captures the initial fast relaxation in density that is observed experimentally better than the value that should apply in the absence of an electric field (K2 = −6.55). This result is surprising, because voltage is not applied during relaxation. Either this agreement is coincidental or, alternatively, in the early period after the voltage is removed, there might be a residual electrophoretic driving force colloids away from the substrate, because of charged ionic species that would have accumulated at the surface.
Measurement errors in determining the equation of state, Π(ϕ), from the steady-state results such as Fig. 3 are, on the other hand, an important consideration for accurate modeling. Specifically, in the thin deposits (∼50 μm and less) of interest here, ϕ(z) decays from a high to low value in a very small region at the top of the deposit, as shown qualitatively in Fig. 3a. This physics translates into a sparse characterization of the equation of state at low volume fractions, as shown by the spacing of the datum points in Fig. 3b. The volume fraction region with high osmotic pressure does not suffer from this problem – this region of the equation of state is more densely populated with data. However, a different concern arises in this case – because the osmotic pressure is such a rapidly varying function here, the precision of the colloid volume fraction, as determined by the image analysis, could affect the accuracy of the equation of state. Additionally, the measured equation of state does not show evidence of a phase transition; it was probably not observed because of the rapid variation of Π(ϕ) in the thin sediment. Eqn (3)'s continuous behavior, as is required for our numerical methods, also does not show evidence of a phase transition. Model results are sensitive to the steepness of the divergence of Z(ϕ) at high volume fraction (cf. Fig. S6, ESI†), and this degree of steepness likely depends on the exact location of the phase coexistence boundary. These effects on the quality of the equation of state characterization are an important factor in the performance of the modeling.
Finally, direct measurement of U0 (cf. ESI†) from the deposition experiments themselves is recommended because it yields a characterization of U0 under the exact conditions of the field-assisted assembly. Even given this characterization, however, the sensitivity analysis plotted in Fig. 5 indicates that modest errors in the characterization of the particle's electrophoretic velocity become an important determinant of model performance at low Pe number conditions. Nevertheless, the fair to good agreement between modeling and experiments supports use of these methods to parameterize K(ϕ), Π(ϕ), and U0 in eqn (1) so as to predict deposition, relaxation, and crystallization kinetics by steady-electric fields.
The crystalline deposits produced at Pe = 0.14 and 0.22 were tens of microns thick; other work has shown that this thickness is sufficient for applications such as sensing and structural color.11–15,20 The time scales for deposition and relaxation, as well as for crystallization are also potentially sufficient for such applications. Dense deposits were achieved in tens or hundreds of minutes, and crystallization was observed in tens of minutes. Moreover, the strength of the steady electric field can be varied to control these times scales. The time needed to switch between crystalline and noncrystalline deposits is a key design parameter for applications of reversible assemblies. Our work shows that the steady-state electric fields used here can cycle between order and disorder on time scales ∼120 min. This work therefore delineates parameter ranges in which direct current electric field assembly can be used to generate time-dependent colloidal crystallization. It furthermore shows that eqn (1) may be used to model assembly dynamics in such devices and processes. Our method of characterizing crystallinity propagation through the position of hfront, while successful in quantifying crystal growth rates, does not characterize the quality of the crystalline structure. In future work, the application of local measures of bond orientation would be a possible way to address this question.9,39–41
We have therefore measured the assembly kinetics of charged colloids in steady electric fields. A one-dimensional transport model yields fair to good agreement with the measurements. Whereas little to no crystallization was observed at Pe = 0.80 and 1.07, crystalline order propagated upwards from the electrode at Pe = 0.14 and 0.22. The propagation was along a characteristic of constant volume fraction; the particular volume fraction of propagation was consistent with equilibrium measurements of fluid-crystal coexistence. By establishing operating ranges for colloidal deposition, assembly, and crystallization, and by demonstrating the connection of these phenomena to equilibrium thermodynamics and one-dimensional transport theory, the experiments and modeling inform the design of processes to generate colloidal materials that are active and reversible.
Acknowledgements
This work was supported by the National Science Foundation under Grant No. 0903629 and by the US Army Research Office under Grant Award No. W911NF-10-1-0518.References
- V. L. Colvin, MRS Bull., 2001, 26, 637–641 CrossRef CAS.
- H. Zhang, X. Yu and P. V. Braun, Nat. Nanotechnol., 2011, 6, 277–281 CrossRef CAS PubMed.
- A. A. Shah, H. Kang, K. L. Kohlstedt, K. H. Ahn, S. C. Glotzer, C. W. Monroe and M. J. Solomon, Small, 2012, 8, 1551–1562 CrossRef CAS PubMed.
- S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413–1418 RSC.
- D. Mukhija and M. J. Solomon, J. Colloid Interface Sci., 2007, 314, 98–106 CrossRef CAS PubMed.
- K. E. Jensen, D. Pennachio, D. Recht, D. A. Weitz and F. Spaepen, Soft Matter, 2013, 9, 320–328 RSC.
- K. E. Davis and W. B. Russel, Phys. Fluids A, 1989, 1, 82–100 CrossRef CAS PubMed.
- R. Piazza, Rep. Prog. Phys., 2014, 77, 056602 CrossRef PubMed.
- L. T. Shereda, R. G. Larson and M. J. Solomon, Phys. Rev. Lett., 2008, 101, 038301 CrossRef.
- B. J. Ackerson and P. N. Pusey, Phys. Rev. Lett., 1988, 61, 1033–1036 CrossRef CAS.
- A. C. Arsenault, D. P. Puzzo, I. Manners and G. A. Ozin, Nat. Photonics, 2007, 1, 468–472 CrossRef CAS.
- H. Fudouzi and T. Sawada, Langmuir, 2005, 22, 1365–1368 CrossRef PubMed.
- T. Gong, D. T. Wu and D. W. M. Marr, Langmuir, 2003, 19, 5967–5970 CrossRef CAS.
- F. Marlow, M. Muldarisnur, P. Sharifi, R. Brinkmann and C. Mendive, Angew. Chem., Int. Ed., 2009, 48, 6212–6233 CrossRef CAS PubMed.
- A. A. Shah, M. Ganesan, J. Jocz and M. J. Solomon, ACS Nano, 2014, 8, 8095–8103 CrossRef CAS PubMed.
- A. L. Rogach, N. A. Kotov, D. S. Koktysh, J. W. Ostrander and G. A. Ragoisha, Chem. Mater., 2000, 12, 2721–2726 CrossRef CAS.
- B. J. Kirby, Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices, reprint edn, 2013 Search PubMed.
- J. F. Bertone, P. Jiang, K. S. Hwang, D. M. Mittleman and V. L. Colvin, Phys. Rev. Lett., 1999, 83, 300 CrossRef CAS.
- P. Jiang, J. F. Bertone, K. S. Hwang and V. L. Colvin, Chem. Mater., 1999, 11, 2132–2140 CrossRef CAS.
- J. H. Holtz and S. A. Asher, Nature, 1997, 389, 829–832 CrossRef CAS PubMed.
- F. M. Auzerais, R. Jackson and W. B. Russel, J. Fluid Mech., 1988, 195, 437–462 CrossRef CAS.
- K. E. Davis, W. B. Russel and W. J. Glantschnig, J. Chem. Soc., Faraday Trans., 1991, 87, 411–424 RSC.
- R. Piazza, T. Bellini and V. V. Degiorgio, Phys. Rev. Lett., 1993, 71, 4267–4270 CrossRef CAS.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- Y. Kim, A. A. Shah and M. J. Solomon, Nat. Commun., 2014, 5, 3676 CAS.
- L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16029–16034 CrossRef CAS PubMed.
- L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, Colloids Surf., 1986, 17, 67–78 CrossRef CAS.
- Z. Zhang, P. Pfleiderer, A. B. Schofield, C. Clasen and J. Vermant, J. Am. Chem. Soc., 2011, 133, 392–395 CrossRef CAS PubMed.
- B. J. Marlow and R. L. Rowell, Energy Fuels, 1988, 2, 125–131 CrossRef CAS.
- H. Reiber, T. Koller, T. Palberg, F. Carrique, R. Ruiz and E. R. Reina, J. Colloid Interface Sci., 2007, 309, 315–322 CrossRef CAS PubMed.
- C. F. Zukoski and D. A. Saville, J. Colloid Interface Sci., 1987, 115, 422–436 CrossRef CAS.
- W. T. Gilleland, S. Torquato and W. B. Russel, J. Fluid Mech., 2011, 667, 403–425 CrossRef CAS.
- D. M. E. Thies-Weesie, A. P. Philipse, G. Nagele, B. Mandl and R. Klein, J. Colloid Interface Sci., 1995, 176, 43–54 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley and Sons, Hoboken, 2nd edn, 2001 Search PubMed.
- A. S. Sangani and A. Acrivos, Int. J. Multiphase Flow, 1982, 8, 343–360 CrossRef.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge Monographs on Mechanics, reprint edn, 1992 Search PubMed.
- S. S. L. Peppin, J. A. W. Elliott and M. Worster, J. Fluid Mech., 2006, 554, 147–166 CrossRef.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- D. J. Beltran-Villegas and M. A. Bevan, Soft Matter, 2011, 7, 3280–3285 RSC.
- D. D. Brewer and S. Kumar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022304 CrossRef.
- T. Solomon and M. J. Solomon, J. Chem. Phys., 2006, 124, 134905 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm02893g |
| This journal is © The Royal Society of Chemistry 2015 |