Open Access Article
Open Access ArticleDirect measurement of thermophoretic forces
Laurent
Helden
*a,
Ralf
Eichhorn
b and
Clemens
Bechinger
ac
a2. Physikalisches Institut, Universität Stuttgart, Pfaffenwaldring 57, 70550 Stuttgart, Germany. E-mail: L.Helden@physik.uni-stuttgart.de
bNORDITA, Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, SE-106 91 Stockholm, Sweden
cMax Planck Institut für Intelligente Systeme, Heisenbergstraße 3, 70569 Stuttgart, Germany
First published on 11th February 2015
Abstract
We study the thermophoretic motion of a micron sized single colloidal particle in front of a flat wall by evanescent light scattering. To quantify thermophoretic effects we analyse the nonequilibrium steady state (NESS) of the particle in a constant temperature gradient perpendicular to the confining walls. We propose to determine thermophoretic forces from a “generalized potential” associated with the probability distribution of the particle position in the NESS. Experimentally we demonstrate, how this spatial probability distribution is measured and how thermophoretic forces can be extracted with 10 fN resolution. By varying temperature gradient and ambient temperature, the temperature dependence of Soret coefficient ST(T) is determined for r = 2.5 μm polystyrene and r = 1.35 μm melamine particles. The functional form of ST(T) is in good agreement with findings for smaller colloids. In addition, we measure and discuss hydrodynamic effects in the confined geometry. The theoretical and experimental technique proposed here extends thermophoresis measurements to so far inaccessible particle sizes and particle solvent combinations.
1 Introduction
When colloidal particles dispersed in a liquid are exposed to a temperature gradient, they are subjected to thermophoretic forces which drives them towards one side of the gradient. Which side is favored depends on the ambient temperature and the details of particle solvent interactions.1,2 Thermophoresis has been employed for instance in thermal field flow fractioning to separate colloidal particles3 or in microscale thermophoresis to study protein interactions.4 Furthermore, in hydrothermal pore model systems, a combination of thermophoresis and convection led to an extreme accumulation of nucleotides, RNA and DNA and it is likely that this mechanism played a key role in the evolutionary building up of more complex structures.5To quantify thermophoresis of colloids, usually the stationary distribution of a particle ensemble governed by the interplay between thermophoresis in a temperature gradient and Brownian diffusion in a concentration gradient is analyzed by different optical techniques reviewed e.g. in ref. 6. This way the Soret coefficients of polystyrene particles of up to r = 1 μm radius have been characterized.7–9 For larger particles unfeasible long equilibration times and sedimentation effects restrain these ensemble based methods. Even for polystyrene, where sedimentation can be minimized by matching the density of particles and solvent, micron sized particles are notoriously difficult to measure.6
Here we propose a new strategy to characterize thermophoresis of larger (r > 1 μm) particles based on a single particle trajectory measurement. The probe particle is held by optical tweezers in a slit geometry over which a stable temperature gradient is applied. By adapting the strength of these optical tweezers, gravity or buoyancy effects can be compensated for rendering our method essentially independent of particle weight. This overcomes sedimentation problems and enables measurements with particles of larger sizes or composed of higher density materials like PMMA or melamine.
2 Experimental section
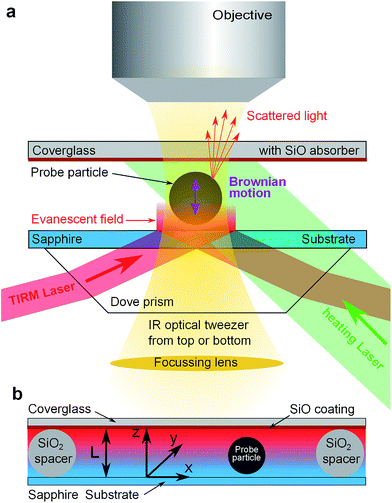
As experimental method we use total internal reflection microscopy (TIRM, see ref. 10 and 11 for a review). It is a single particle evanescent light scattering technique capable of measuring the trajectory of a spherical colloidal particle performing its Brownian motion in vicinity of a flat wall. In equilibrium TIRM is well established as a sensitive technique to measure double layer interactions, van der Waals forces and other particle wall interactions. The new idea to characterize thermophoresis is to apply TIRM in a non-equilibrium steady state (NESS) given by a constant temperature gradient and to develop a suitable scheme for data analysis in a NESS.As sketched in Fig. 1a, an evanescent field decaying into the solvent is created by total internal reflection of a laser beam (λ = 658 nm) at a substrate solvent interface. A single colloidal particle near the substrate will scatter light from this evanescent field. The scattered light intensity is then monitored through microscope optics (50×, NA = 0.55 objective) by a photomultiplier typically for time intervals of 15 to 30 minutes and sampling rates of 1 kHz. By converting scattering intensities to particle wall distances the trajectory of the particles motion perpendicular to the substrate is reconstructed. For analysis, data are processed into a histogram that is proportional to the probability density of finding the particle at a specific distance from the substrate. In the following Section 3 we will discuss how to interpret this probability density in a NESS. To restrict the lateral diffusion of probe particles and to exert additional light pressure onto the particle, two IR optical tweezers acting either from top (λ = 1064 nm) or bottom (λ = 1070 nm) onto the particle are implemented. Both tweezers are only slightly focused such that no detectable gradient forces act perpendicular to the surface.
For thermophoresis measurements, a stable temperature gradient has to be established in the sample cell. This is accomplished by a thin cell design (Fig. 1b) that allows considerable temperature gradients at only moderate temperature changes. It consists of a 1 mm thick sapphire substrate to ensure good thermal coupling to a heat sink, colloidal silica particles of 7.7 μm diameter as spacers to define the cell height L, and a 1 mm thick cover glass coated with about 1.8 μm SiO layer on the inner side of the cell. The thermally evaporated SiO coating serves as an (≈80%) optical absorber for green laser light (λ = 532 nm) while the TIRM detection wavelength (λ = 658 nm) and larger wavelength of optical tweezers are >95% transmitted. Thus the upper part of the cell above the probe particle can be heated by a slightly focused laser beam (≈200 μm beam waist) and the temperature at the absorber is tunable by laser power.
In each sample cell the temperature increase due to laser heating is estimated by the onset of water evaporation i.e. bubble formation at high laser powers (≈1 W). During this procedure care was taken not to superheat the water by using probe or spacer particles as nucleation sites. The procedure was crosschecked by determining the demixing temperature (34.0 °C) of a critical water 2,6-lutidine mixture in an identically build cell, where due to the spinodal demixing process superheating is impossible.12,13 Good agreement between both temperature estimates was found. Depending on the actual cell in use, heating of 0.10 to 0.15 K mW−1 at the upper cover glass is typical for the experiments.
For further analysis, heat distribution within the cell was modelled and computed by finite elements methods (COMSOL multiphysics using heat transfer model) taking into account the heat conductance and capacity of prism, substrate, water layer, particle, coverglass and 1 mm air above the cell. The copper housing of the cell was modelled as constant temperature boundary condition while for laser heating a Gaussian heating power profile within the SiO layer was assumed. The numerical results show that the temperature drop within the cell is not uniform due to the heat conductivity of the particle κp being different from that of the solvent κs. Within the confined geometry, we determine the temperature gradient over the probe particle from the temperature difference between the particle's top and bottom boundary divided by its diameter. For the case of a r = 2.5 μm polystyrene bead (κp = 0.13 W K−1 m−1) in water (κs = 0.6 W K−1 m−1), as studied in Section 5, we find that the temperature gradient within the particle is a factor 1.34 steeper than in an identical cell without particle. This factor is very similar to the renormalization factor 3κs/(2κs + κp) established for the temperature gradient in bulk systems (cf.eqn (24) of ref. 2). Also for melamine particles (κp = 0.45 W K−1 m−1), our numerical COMSOL simulations of the cell reveal a renormalization factor of 1.09, very close to the bulk value 3κs/(2κs + κp). Furthermore, within the parameter range of our experiments, we find only a weak dependence (≲5%) of this renormalization factor on particle size and z-position, indicating that the temperature distribution over the particle surface in our cell geometry is very similar to the one under bulk conditions. In the data analysis, we therefore neglect that weak size and position dependency of the temperature field. For determining the temperature difference over the sample cell, it has to be considered that the heat conduction of the sapphire substrate is not infinite. As a consequence, the temperature of the substrate at the sapphire–water interface Ts is not independent of laser heating and temperature gradient. According to our simulations, the change of Ts is, depending on details of cell design, about 1/3 of the total temperature rise. This is taken into account in our data analysis. Finally, the simulations show a linear dependence of the temperature gradient on laser power.
Due to the thermal expansion of water, the upper part of the water layer in the cell is less dense than the lower part. This together with the thin cell design effectively suppresses possible thermal convection within the cell. We have carefully checked that for the range of heating powers applied during the measurements thermal convection did not occur. Extending the above mentioned numerical simulations to include thermal expansion and the flow within the water layer (COMSOL nonisothermal flow model), we confirm that fluid velocities are below 0.1 nm s−1 at maximum applied temperature gradient. Corresponding Stokes drag on the particle is below 0.01 fN and thus orders of magnitude below TIRM force resolution. Signs of convection were actually only observed for extremely high laser powers leading to bubble creation.
As probe particles we used r = 2.5 μm radius polystyrene (Type 4205A, Duke Standards, Thermo Scientific, USA) and r = 1.35 μm COOH-functionalized melamine (MF-COOH-S1285, Microparticles GmbH, Germany) particles. Prior to use, dispersions were repeatedly washed with Millipore water and otherwise used as supplied. During assembly the cell is cleaned in a plasma cleaner and filled with a highly diluted aqueous dispersion of probe particles. The edges of the cell are sealed with UV curable glue. The whole cell is matched to a glass prism with immersion oil and housed in a copper frame with windows above the cell and below the prism to allow optical access to the sample. The copper frame also contains water pipes connected to a flow thermostat such that the cells ambient temperature can be adjusted in the range of 5…55 °C.
3 Model and theory
In this section we outline the standard phenomenological description of thermophoresis and adapt it to the confined geometry and particle wall interactions relevant for the present experiment. In particular we demonstrate how to extract thermophoretic forces and the Soret coefficient ST from single particle measurements.We describe the probability density p = p(x, y, z, t) for finding a particle at position (x, y, z) in the sample cell at time t by the Fokker–Planck equation 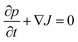 , with the probability current J = (Jx, Jy, Jz). In the present experimental setup, J contains contributions from deterministic forces (particle–wall interactions and external forcing by optical tweezers and gravity), thermophoretic drift and thermal noise effects. We define the coordinate system in such a way, that the z-axis is oriented along the temperature gradient (i.e. perpendicular to the sapphire substrate) and its origin is located at the sapphire–water interface (see Fig. 1b). Thus the two walls (sapphire substrate and cover glass) with their different temperatures are located at z = 0 and z = L and the x–y plane is parallel to the substrate. Since the optical tweezers confine the particle motion in the x and y directions, and we are only interested in the motion perpendicular to the wall (z direction), we can integrate out the x and y components in the Fokker–Planck equation to obtain
, with the probability current J = (Jx, Jy, Jz). In the present experimental setup, J contains contributions from deterministic forces (particle–wall interactions and external forcing by optical tweezers and gravity), thermophoretic drift and thermal noise effects. We define the coordinate system in such a way, that the z-axis is oriented along the temperature gradient (i.e. perpendicular to the sapphire substrate) and its origin is located at the sapphire–water interface (see Fig. 1b). Thus the two walls (sapphire substrate and cover glass) with their different temperatures are located at z = 0 and z = L and the x–y plane is parallel to the substrate. Since the optical tweezers confine the particle motion in the x and y directions, and we are only interested in the motion perpendicular to the wall (z direction), we can integrate out the x and y components in the Fokker–Planck equation to obtain
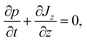 | (1) |
The probability current Jz along the temperature gradient can be written as
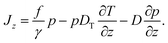 | (2) |
The force f in the first term contains all particle wall interactions, light forces from the optical tweezers and gravity; γ is the viscous friction coefficient. The second term is the standard phenomenological ansatz for the thermophoretic drift being proportional to the temperature gradient with DT as a phenomenological coefficient quantifying the thermophoretic effects.2,6,14 The last term represents thermal diffusion with Einstein's diffusion constant D = kBT/γ. The details connected with the specific form of the thermal noise term with the space-dependent diffusion coefficient being written in front of the gradient ∂/∂z are discussed in the Appendix.
In the following, we are interested in the non-equilibrium steady state (NESS) where thermophoretic effects are balanced by external forces and diffusion currents so that Jz = 0. The current-free solution of eqn (2) reads
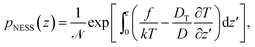 | (3) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) is chosen such that
is chosen such that 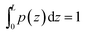 .
.
Following the procedure in ref. 15, we define the generalized “pseudopotential”15,16 as the negative logarithm of the steady-state distribution,
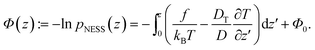 | (4) |
The offset Φ0 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) is due to normalization; it is irrelevant for the spatial dependence and thus will be omitted in the following. The generalized potential is composed of two space-dependent contributions
is due to normalization; it is irrelevant for the spatial dependence and thus will be omitted in the following. The generalized potential is composed of two space-dependent contributions
| Φ(z) = Φf(z) + ΦT(z). | (5) |
The first part
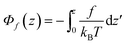 | (6) |
| T(z) = Ts + θz | (7) |
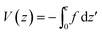 ,
,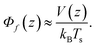 | (8) |
This relation is exact in case of an equilibrium situation, i.e. where there are no temperature variations over the sample cell, θ = 0.
The second part in eqn (4),
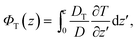 | (9) |
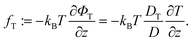 | (10) |
A simplification based on a small gradient expansion as we performed it for Φf is not easily possible due to the a priori unknown temperature dependence of the coefficient DT/D.
It is obvious, however, that in thermal equilibrium with ∂T/∂z = θ = 0 we have fT = 0 and thus ΦT = 0 (again, up to an irrelevant constant). Using eqn (5) and (8), we find Φ = V(z)/kBTs and, finally, from eqn (4)
V(z) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) peq(z), peq(z), | (11) |
4 Data evaluation
As already mentioned in Section 2, the probability density p(z) for finding the particle at distance z from the substrate can be extracted from the TIRM scattering intensities. Performing such a TIRM measurement without applying a temperature gradient, allows to deduce the potential V(z) viaeqn (11) to quantify particle–wall interactions and the external forces due to the optical tweezers and gravity.In our experiments, the temperature gradient θ is below 1 K μm−1 so that θL/Ts ≲ 0.025 (with L = 7.7 μm and Ts = 300 K) is indeed negligibly small. As shown above [see eqn (8)], such small temperature variations do not interfere with the potential forces due to V(z). We can therefore determine the “thermophoretic potential” ΦT from the stationary distribution pNESS in a given (weak) temperature gradient by using [cf.eqn (4), (5) and (8)]
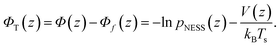 | (12) |
A central quantity for characterizing thermophoretic effects is the Soret coefficient ST = DT/D. According to eqn (10) it is related to the “thermophoretic force” and the generalized “thermophoretic potential” by
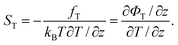 | (13) |
The Soret coefficient can therefore be measured from the stationary particle distribution pNESS observed in a weak temperature gradient θ (with θL/Ts ≪ 1) by making use of the relations (12), (13), after V(z) has been determined in an independent equilibrium measurement [eqn (11)]. We remark that Parola and Piazza in ref. 14 suggested a relation analogous to eqn (13) for determining the Soret coefficient, however derived directly from hydrodynamic forces on the particle due to thermophoretic effects and without taking into account other conservative forces.
5 Results and discussion
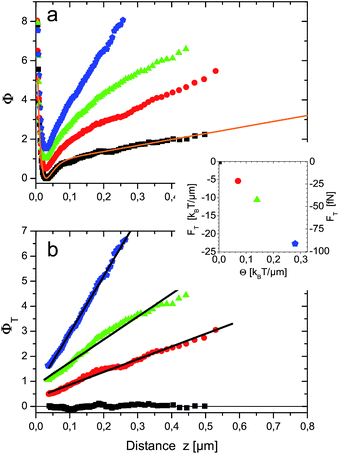
Typical TIRM measurements for different temperature gradients are shown in Fig. 2a. Without temperature gradient, the equilibrium potential V(z)/kBTs = Φf(z) (black squares) is obtained. For z < 30 nm it exhibits a steep repulsion which is due to screened Coulomb interactions between the negatively charged surfaces of sapphire substrate and sulfate terminated polystyrene particle. For larger distances up to about 150 nm a potential well of 0.8 kBT depth is observed. This can be attributed to attractive van der Waals forces. Towards larger distances the potential has a constant slope that reflects the buoyancy of the particle and additional light forces of optical tweezers. The entire potential is well fitted by the function Φfit(z) = 16.50 exp(−z/10 nm) − 6.53 exp(−z/21.91 nm) + 3.05 nm−1z + 0.35 displayed as orange line in Fig. 2a.The first term accounts for electrostatic interactions according to Debye–Hückel theory. The fitted Debye length of 10 nm is attributed to the counterions in the thin sample cell. The second term describes the van der Waals attraction by an empirical exponential formula given in eqn (5) of ref. 17. The last two terms incorporate light pressure and gravity. In the following Φfit(z) is used to subtract ΦT(z) from Φ(z) in the presence of temperature gradients [cf.eqn (12)]. The result is shown in Fig. 2b for z ≳ 30 nm, i.e. the position of the potential minimum. The pure thermophoretic potentials ΦT obtained at different temperature gradients are, within errors, linear functions of distance. This means that the probe particle experiences a constant thermophoretic force within the distance range sampled. For bulk measurements this is certainly expected. However, in the vicinity of a surface it is worthwhile to discuss the different contributions to fT (eqn (10)), in particular due to the hydrodynamic wall effects altering the diffusion coefficient D(z).
Close to a wall the hydrodynamic friction coefficient γ of a spherical colloidal particle is changed drastically (it even becomes anisotropic) compared to the bulk value γ0 = 6πνr (ν being the fluid viscosity) given by Stokes' solution. By Einstein's relation D(z) = kBT(z)/γ(z) also the Brownian diffusion coefficient for diffusion perpendicular to the wall D(z) acquires a pronounced distance dependence. Exploiting, as before, that the temperature variations over the sample cell are small in our experiments, θL/Ts ≪ 1, we can neglect the space-dependence of temperature and find in lowest order D(z) = kBTs/γ(z). The effects of hydrodynamic corrections in the friction and (normal) diffusion coefficient close to the walls can therefore be considered to be unaffected by the (weak) temperature gradients. The theoretical prediction for the normal diffusion coefficient is displayed in Fig. 3 as orange line. It has been calculated by Brenners formula18 and its extensions for a thin slit between two walls,19,20 which represents the actual experimental situation. The inset predicts that in the experimental slit geometry diffusion is at maximum only 23% of the bulk diffusion coefficient D0 = kBTs/(6πνr).
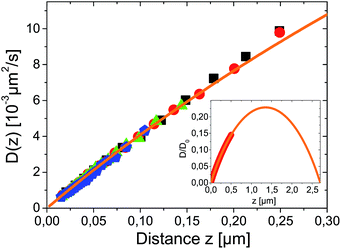 | ||
| Fig. 3 Measured spatial dependence of Brownian diffusion coefficient for different temperature gradients θ = 0.00, 0.07, 0.14 and 0.27 K μm−1 for black squares, red circles, green triangles and blue pentagons respectively. D(z) was derived from the same data as used for Fig. 2 and symbols correspond. The orange line is a fit to theory given in ref. 19 calculated for r = 2.5 μm particle in a L = 7.7 μm slit with D0 as only fitting parameter. The inset shows the theoretical prediction for D(z) on a larger scale with the range of experimental data marked as thick red line. | ||
Experimentally, the spatially resolved diffusion coefficient can be extracted from dynamical analysis of TIRM-data according to a procedure described in ref. 21. It is shown as symbols in Fig. 3. For all temperature gradients data are in remarkable agreement. This proves that the Brownian motion is completely independent of thermophoretic effects. Since ∂ΦT/∂z is constant within the experimentally accessible distance range, it follows from eqn (10) that DT(z) has the same distance dependence as D(z) and the Soret coefficient ST = DT(z)/D(z) is constant i.e. independent of z.
The magnitude of the thermophoretic force, i.e. the negative slopes of the fitted (black) lines in Fig. 2b, also depends linearly on the temperature gradient, as shown in the inset of Fig. 2b. This experimental observation confirms the usual assumption that thermophoretic velocities (and forces) are proportional to the temperature gradient and ST is independent of the temperature gradient. It also imparts an impression on the magnitude of thermophoretic forces which are here in the range of about 20–100 fN.
While ST does not depend on temperature gradient, a characteristics of thermophoresis is its pronounced dependence on the absolute temperature. It has been shown that for many substantially different dispersed systems, like polystyrene nanoparticles, Lysozyme micelles, DNA etc.1,9,22,23 the temperature dependence of the Soret coefficient follows a common empirical fitting formula introduced by Iacopini and Piazza,23
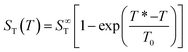 | (14) |
Fig. 4 shows the temperature dependence of ST for probe particles of different material. As an example of particles that due to their size and strong sedimentation (density ρMF = 1.51 g cm−3) are difficult (if not impossible) to access with other techniques, we present data for r = 1.35 μm melamine particles (triangles) with carboxyl terminated surface. Qualitatively, they follow the temperature dependence given by eqn (14) with a remarkably high T* = 43.5 °C. Hence at room temperature they have a negative ST and belong to the rare group of thermophilic particles.
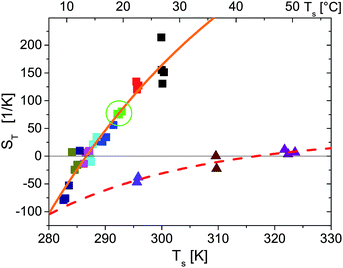 | ||
| Fig. 4 Temperature dependence of Soret coefficient obtained for different ambient temperatures (indicated by different colors), temperature gradients and particle types (indicated by symbol types). Square symbols are for a r = 2.5 μm polystyrene probe particle. In particular green squares marked by a circle correspond to the data shown in Fig. 2. Triangles are for a r = 1.35 μm melamine particle. The spread of the symbols for equal ambient temperature along the temperature axis is due to increasing substrate temperatures Ts for increasing temperature gradients as mentioned in the main text. The lines are fits to eqn (14). For polystyrene particles (full orange line) S∞T = 583 K−1, T* = 286.6 K, T0 = 40.6 K and melamine particles (dashed red line) S∞T = 36.0 K−1, T* = 316.7 K, T0 = 27.3 K. | ||
S
T(T) for r = 2.5 μm polystyrene particles also accords with eqn (14). Even the temperature of sign reversal is in good agreement with previous results for considerably smaller polystyrene particles of 53 nm to 253 nm radius where T* ≃ 12 °C ≙ 285.2 K is reported.9 Comparing the absolute values of ST for the r = 253 nm particles in these measurements and for the 10 times larger polystyrene particles in the present experiment, we find in our experiments that ST is two orders of magnitude larger. This certainly exceeds the linear prediction for the size dependence of ST found for smaller particles measured in ref. 9 and expected from theories of thermophoresis based on a flow field around the particle.2,6,24 While in our experiments no salts or surfactants where added, dispersions of ref. 9 were treated with Triton X100 surfactant and experiments where performed in a density matched H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D2O mixture containing 1 mM Tris–HCl pH 7.8 buffer and 10 mM NaCl. These different condition certainly question the comparability of both measurements even though T* known to depend sensitively on the particle–solvent interface1 is quite similar.
D2O mixture containing 1 mM Tris–HCl pH 7.8 buffer and 10 mM NaCl. These different condition certainly question the comparability of both measurements even though T* known to depend sensitively on the particle–solvent interface1 is quite similar.
In experiments with r = 1.25 μm polystyrene particles (data not shown) measured under same conditions as the r = 2.5 μm particles, we find a 4–5 times smaller ST which corresponds to a nonlinear scaling of ST with particle radius. This contrasts with the majority of experiments reported in the literature (see ref. 6 for a review), but a quadratic size dependence for ST is found in ref. 7 and 8. Such a quadratic dependence is theoretically supported by thermodynamic arguments7,8 in a parameter range where STrθ ≪ 1. However, in our experiments the combination of ST, particle size and temperature gradients STrθ ≈ 5…100 largely exceeds the applicability of this theory.
Finally, if we presume a driving mechanism for thermophoretic motion that creates a flow field around the particle and in bulk results in a linear size dependence of ST,2,6,24 it is to be expected, that the pronounced influence of confining surfaces on hydrodynamics shown in Fig. 3 will not only influence the Brownian diffusion but also the thermophoretic propulsion itself.25,26 On a length-scale of the order of the particle radius, i.e. for distances considerably larger than those sampled in Fig. 2, this would lead to a spatial variation of thermophoretic forces. If this is indeed the case, comparison with bulk measurements and furthermore the concept of ST (which should be a particle property, independent of distance from boundaries) is inappropriate in confined geometries. A distance dependence of thermophoretic forces could also explain measurements showing a size dependence of ST which is stronger than linear within this hydrodynamic concept. These issues will be in the focus of our further research.
6 Conclusions
In conclusion we have demonstrated the applicability of TIRM in NESS-systems and pointed out a suitable scheme for data analysis. The origin of nonequilibrium is a temperature gradient that drives a thermophoretic motion of micron sized colloidal particles. Thermophoretic forces have been defined and directly measured with a precision in the 10 fN range. In good qualitative agreement with existing measurements for smaller polystyrene particles we measured the temperature dependence of ST for polystyrene particles. Influences of the confined geometry on D, DT and ST were discussed. This might have important consequences for the applicability of thermophoresis in microfluidic devices. Furthermore we demonstrated the potential of the method to characterize micron sized particles with higher densities with respect to their thermophoretic properties by determining ST(T) for melamine particles in agreement with the empirical formula by Iacopini and Piazza.23 The new technique not only makes a larger variety of microparticles accessible to thermophoretic measurements, but also opens up a route for generalization to different solvents like alcohols, hydrocarbons and other unpolar liquids. This might allow to study the dependence of thermophoresis on detailed particle solvent interaction in the near future.Appendix
In this Appendix, we discuss the details associated with formulating overdamped Brownian motion in an inhomogeneous thermal environment with space-dependent diffusion coefficient in the context of thermophoresis. For simplicity we restrict ourselves to one spatial dimension which is denoted by z (as in the main text). We furthermore omit any deterministic forces, so that the probability current Jz for the particles in a dilute suspension consists of a thermophoretic part proportional to the gradient of temperature T = T(z) and a diffusive part proportional to the gradient of the probability density p = p(z, t),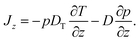 | (15) |
This description represents the standard form used in the thermophoretic literature,2,6,14 based on the reciprocal formulation of heat and particle currents driven by temperature and density gradients.27 The so-called “thermal diffusion coefficient” DT essentially quantifies the effects of the thermal gradient on a thin layer at the particle–solvent interface, where interfacial tension gradients parallel to the temperature gradient drive thermophoretic particle motion.2,6 The strength of the diffusion term is given by the diffusion coefficient D = kBT/γ.
Our main concern in this Appendix is the specific form of this diffusion term. In thermophoresis, T and thus γ and D are position-dependent. It is therefore not clear that −D∂p/∂z is the “correct” form to describe particle diffusion in such inhomogeneous thermal environment or if additional “spurious” drift terms would have to be added in eqn (15).28–34 This problem is per se not related to thermophoretic mechanisms as sketched above, but has a different origin rooted essentially in the mathematical description of Brownian motion. It is connected to the so-called Itô–Stratonovich dilemma for the stochastic Langevin equation associated with eqn (15).35–38 In fact, as fluid viscosity changes with temperature, the friction coefficient γ depends on particle position as well. In our experimental setup, where we measure thermophoresis close to the substrate surface in a slit geometry (see Fig. 1), γ even acquires an additional effective dependence on the wall distance z by hydrodynamic effects39† In other words, variations of D with position z are the result of separate dependencies of T and γ on z. It is well-known28,29,32,34,38 that under such conditions, the correct form of the diffusion term is −(1/γ)∂(kBTp)/∂z, so that we would have to write
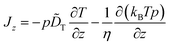 | (16) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T as compared to eqn (15). This particular form of the diffusion term results from performing the overdamped limit in the full-fledged particle equations of motion including the velocity degrees of freedom (after the white noise limit has been performed first).
T as compared to eqn (15). This particular form of the diffusion term results from performing the overdamped limit in the full-fledged particle equations of motion including the velocity degrees of freedom (after the white noise limit has been performed first).
We can easily bring eqn (16) into the form eqn (15) by identifying DT = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T + kB/γ. Based on an alternative physical reasoning, the additional “correction” term kB/γ has been discussed in ref. 40 to be related to the osmotic pressure in dilute suspensions.
T + kB/γ. Based on an alternative physical reasoning, the additional “correction” term kB/γ has been discussed in ref. 40 to be related to the osmotic pressure in dilute suspensions.
The corresponding difference between the Soret coefficients ST = DT/D and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T/D is 1/T. Typical values of ST for colloidal beads are of the order of 0.1 K−1 to 1 K−1 (ref. 1, 2 and 9) (or even several ten or hundred per Kelvin for micron-sized particles as measured here), so that around room temperature this difference is expected to be negligibly small, except maybe in temperature regions close to the sign change of ST.
T/D is 1/T. Typical values of ST for colloidal beads are of the order of 0.1 K−1 to 1 K−1 (ref. 1, 2 and 9) (or even several ten or hundred per Kelvin for micron-sized particles as measured here), so that around room temperature this difference is expected to be negligibly small, except maybe in temperature regions close to the sign change of ST.
We finally remark that a third variant for the diffusion term has been discussed briefly in ref. 14, namely −∂(Dp)/∂z. In principle, this prescription amounts to yet another definition for the thermophoretic coefficient in the probability current
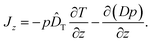 | (17) |
However, as we have pointed out above, this form of the diffusion term is not correct if γ depends on position z; the difference to the correct form −(1/γ)∂(kBTp)/∂z in eqn (16) is an unphysical drift-like term p(D/γ)(∂γ/∂z). In case the friction coefficient γ depends on space only due to changes of fluid viscosity with temperature, this term may be hidden in ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) T, as by comparison with eqn (16) we can write
T, as by comparison with eqn (16) we can write ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T =
T = ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) T − (D/γ)(∂γ/∂T), or, comparing with eqn (15), DT =
T − (D/γ)(∂γ/∂T), or, comparing with eqn (15), DT = ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) T + kB/γ − (D/γ)(∂γ/∂T). For water around room temperature the corresponding “correction” −(1/γ)(∂γ/∂T) in the Soret coefficient is of the order of 0.02 K−1 and thus for colloidal particles probably negligibly small in most cases.
T + kB/γ − (D/γ)(∂γ/∂T). For water around room temperature the corresponding “correction” −(1/γ)(∂γ/∂T) in the Soret coefficient is of the order of 0.02 K−1 and thus for colloidal particles probably negligibly small in most cases.
Summarizing, for modeling thermophoresis in dilute particle suspensions, one should either use eqn (15) or (16) for the probability current, while eqn (17) is physically questionable. The deviation between eqn (15) and (16) is compensated by slightly different definitions of the “thermal diffusion coefficient”, DTvs. ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) T. They differ in the contribution kB/γ, which is related to the temperature dependence of the osmotic pressure in dilute suspensions.40 Given, however, that the formulation of thermophoretic effects is connected to the reciprocity of heat and mass flow in temperature and density gradients,27 the standard representation eqn (15) is preferable.
T. They differ in the contribution kB/γ, which is related to the temperature dependence of the osmotic pressure in dilute suspensions.40 Given, however, that the formulation of thermophoretic effects is connected to the reciprocity of heat and mass flow in temperature and density gradients,27 the standard representation eqn (15) is preferable.
Acknowledgements
We thank Daniele Vigolo and Alois Würger for stimulating discussions and Daniel Maier for COMSOL simulations. R.E. acknowledges financial support by the Swedish Science Council under the grant 621-2013-3956.References
- S. Iacopini, R. Rusconi and R. Piazza, Eur. Phys. J. E, 2006, 19, 59–67 CrossRef CAS PubMed.
- A. Würger, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- J. C. Giddings, Science, 1993, 260, 1456–1465 CAS.
- C. J. Wienken, P. Baaske, U. Rothbauer, D. Braun and S. Duhr, Nat. Commun., 2010, 1, 100 CrossRef PubMed.
- P. Baaske, F. M. Weinert, S. Duhr, K. H. Lemke, M. J. Russell and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9346–9351 CrossRef CAS PubMed.
- R. Piazza and A. Parola, J. Phys.-Cond. Matt., 2008, 20, 153102 CrossRef.
- S. Duhr and D. Braun, Phys. Rev. Lett., 2006, 96, 168301 CrossRef.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS PubMed.
- M. Braibanti, D. Vigolo and R. Piazza, Phys. Rev. Lett., 2008, 100, 108303 CrossRef.
- D. C. Prieve and N. A. Frej, Langmuir, 1990, 6, 396–403 CrossRef CAS.
- J. Y. Walz, Curr. Opin. Colloid Interface Sci., 1997, 2, 600–606 CrossRef CAS.
- C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516–519 CrossRef CAS.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172–175 CrossRef CAS PubMed.
- A. Parola and R. Piazza, Eur. Phys. J. E, 2004, 15, 255–263 CrossRef CAS PubMed.
- V. Blickle, T. Speck, U. Seifert and C. Bechinger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 060101(R) CrossRef.
- T. Speck and U. Seifert, Europhys. Lett., 2006, 74, 391–396 CrossRef CAS.
- M. A. Bevan and D. C. Prieve, Langmuir, 1999, 15, 7925–7936 CrossRef CAS.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS.
- L. Lobry and N. Ostrowsky, Phys. Rev. B, 1996, 53, 12050–12056 CrossRef CAS.
- T. Benesch, S. Yiacoumi and C. Tsouris, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021401 CrossRef.
- R. J. Oetama and J. Y. Walz, J. Colloid Interface Sci., 2005, 284, 323–331 CrossRef CAS PubMed.
- S. A. Putnam, D. G. Cahill and G. C. L. Wong, Langmuir, 2007, 23, 9221–9228 CrossRef CAS PubMed.
- S. Iacopini and R. Piazza, Europhys. Lett., 2003, 63, 247–253 CrossRef CAS.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- J. Morthomas and A. Wuerger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 051405 CrossRef.
- M. Yang and M. Ripoll, Soft Matter, 2013, 9, 4661–4671 RSC.
- S. DeGroot and P. Mazur, Non-Equilibrium Thermodynamics, Dover, 1995 Search PubMed.
- D. Ryter, Z. Phys. B - Cond. Matt., 1981, 41, 39–42 CrossRef.
- J. Sancho, M. San Miguel and D. Dürr, J. Stat. Phys., 1982, 28, 291–305 CrossRef.
- N. van Kampen, Z. Phys. B - Cond. Matt., 1987, 68, 135–138 CrossRef.
- M. E. Widder and U. M. Titulaer, Physica A, 1989, 154, 452–466 CrossRef.
- A. Jayannavar and M. C. Mahata, Pramana J. Phys., 1995, 45, 369–376 CrossRef.
- A. Lau and T. Lubensky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011123 CrossRef CAS.
- S. Hottovy, G. Volpe and J. Wehr, J. Stat. Phys., 2012, 146, 762–773 CrossRef.
- N. van Kampen, J. Stat. Phys., 1981, 24, 175–187 CrossRef.
- N. van Kampen, Stochastic Processes in Physics and Chemistry, North Holland, Amsterdam, 2007 Search PubMed.
- J. Sancho, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 062102 CrossRef CAS.
- M. Yang and M. Ripoll, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062110 CrossRef.
- J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Kluwer, Dordrecht, 1983 Search PubMed.
- S. Fayolle, T. Bickel and A. Würger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041404 CrossRef.
Footnote |
| † In the current experimental situation with temperature variations of at most a few degrees Kelvin within the sample cell, the corresponding changes in viscosity are below 10% and thus are negligible in comparison with the hydrodynamic wall effects, see also Fig. 3. |
| This journal is © The Royal Society of Chemistry 2015 |