Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing the stability of spontaneously self-assembled vesicles – the effect of polymer architecture†
Katharina
Bressel
* and
Michael
Gradzielski
*
Technische Universität Berlin, Stranski Laboratorium für Physikalische und Theoretische Chemie, Straße des 17. Juni 124, 10623 Berlin, Germany. E-mail: katharina.bressel@tu-berlin.de; michael.gradzielski@tu-berlin.de
First published on 4th February 2015
Abstract
The formation of stable vesicles with a controlled size and high stability is an important matter due to their wide application in pharmaceutical and detergency formulations and as drug delivery vehicles. One can control the size of spontaneously formed vesicles in mixtures of zwitterionic and anionic surfactants by the admixture of small amounts of an amphiphilic copolymer of the PEO-PPO-PEO type. Of course, this effect should depend largely on the molecular architecture of the copolymer employed which was varied systematically in this work, and the temporal evolution of aggregate size and final structure was followed by means of DLS and three main effects could be observed. First the size of the formed vesicles is the larger the higher the molecular weight (MW) of the polymer and the higher the polymer concentration. Secondly the amount of copolymer required to induce long time stability is inversely proportional to the fraction of PEO in the polymer. Finally the architecture for a given MW and PEO/PPO ratio has no effect on the vesicle structure but their structure is directly controlled by the length of the PPO block of the copolymer. Thereby by appropriate choice of type and amount of PEO-PPO-PEO copolymer one can exert comprehensive control over size and stability of unilamellar vesicles.
1 Introduction
Vesicles have been studied extensively in the past due to their applications in pharmaceutical formulations1–3 and as model systems for biological membranes.4,5 They are also interesting as delivery systems for active agents encapsulated either in their aqueous interior or in their hydrophobic bilayer,6–9 and are suitable to interact with biological membranes and to introduce drugs into living cells.10–13 Unilamellar vesicles can be prepared in a number of ways from lamellar phases, for instance by external forces like sonification14 or extrusion.15–18 However, particularly interesting are spontaneously forming vesicles as they are observed in catanionic19–28 and zwitanionic29–34 systems, but also in mixtures of anionic surfactants with a cosurfactant,35 in systems of anionic surfactants, where repulsion between the head groups is screened by the presence of salts,36,37 or in mixtures of phospholipids with largely different lengths of the alkyl chains.38 In general, the vesicle properties depend strongly on the choice of surfactants. Key points in that context are the ways of preparation and the long-time stability of these unilamellar vesicles as frequently they are metastable structures that are kinetically stabilized and with their properties depending on the preparation history.39 When vesicles are prepared by mixing two micellar solutions, the vesicle formation takes place via a disc-like micellar state (while below the cmc may proceed via a torus-like state40), where small discs are formed shortly after mixing stock solutions of both surfactants. These discs grow until vesicles are energetically more favoured compared to these discs which then close to form spherical shells. The energetic conditions for vesicle formation are well understood. The maximum radius of disc-like micelles can be derived from the total energy F of the bent disc, which is a sum of the contribution from the disc rim (line tension) and from the bending energy of the bilayer (eqn (1)) with c being the bilayer curvature of the lens (for a spherically symmetric deformation), c0 the spontaneous curvature (will be 0 for symmetric bilayers), the length of the disc rim l, the line tension λ, the mean bending modulus κ and the Gaussian modulus![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) .41–44
.41–44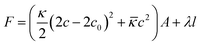 | (1) |
That leads to the maximum disc radius Rdisc,max. given by eqn (2) beyond which discs will spontaneously close to form vesicles.
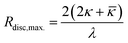 | (2) |
This process was described theoretically41,44–49 and for the case of mixing anionic surfactants with cationic or zwitterionic surfactants was studied in detail by time-resolved small angle X-ray scattering (SAXS) for mixtures of TDMAO (tetradecyldimethylamine oxide) and various anionic perfluoro surfactants49–53 and for mixtures of TTAOH (tetradecyltrimethylammonium hydroxide) and TexaponN(70)-H (laureth sulfuric acid).54
Since the vesicle size and polydispersity in these systems are determined by the kinetics of the process and the cut-off radius for the disc growth, the idea to modify the vesicle properties by influencing the formation process is obvious43 and corresponding experiments were successfully performed using an amphiphilic polymer of the Pluronic type as admixture.55 Addition of L35 led to a modified mechanism of vesicle formation. The idea is, that the hydrophobic part of the copolymer becomes incorporated into the micellar disc rim, thereby leading to a decrease in the line tension. Highly time-resolved SAXS measurements that followed the mixing process of TDMAO and LiPFOS (lithium perfluorooctylsulfonate) in a stopped-flow device showed that the addition of L35 allowed to have systematic control of the size of the formed vesicles. The higher the polymer concentration in the mixture the lower the line tension, what led to a prolonged disc growth and a delayed vesicle formation at larger disc sizes. Thus the vesicle size can be controlled by the polymer concentration and these experiments also showed enhanced vesicle stability presumably due to steric interactions between the polymers.55 However, in particular the long time stability of unilamellar vesicles is a very important property and should depend to a large extent on the type of amphiphilic copolymer employed.
Accordingly, in this work we studied the effect of a systematic variation of the polymer architecture on the formation process by following the hydrodynamic radius by time resolved dynamic light scattering (DLS). The aim was to determine the function of the hydrophobic and the hydrophilic part of the polymer on the process and to find a recipe that gives the required type and concentration of polymer for the desired vesicle size and stability, as it is of central importance for the general applicability of the concept of polymer controlled vesicles. For that purpose we applied polymers of the Pluronic type (PEO-PPO-PEO) with varying total polymer length and varying ratio between the length of the hydrophobic and the hydrophilic part (thereby changing the hydrophilicity of the amphiphilic copolymer). We also compared L35 to 10R5, which have the same number of EO and PO units but a hydrophilic core with hydrophobic end caps instead of a hydrophobic core with hydrophilic end caps, and thereby investigate the effect of the molecular architecture.
2 Experimental section
2.1 Materials
Tetradecyldimethylamine oxide (C14H29(CH3)2NO, TDMAO) was kindly provided by Stepan (Stepan Company, Northfield, Illinois, USA) as a 25% TDMAO solution in water named Ammonyx M. This solution was freeze-dried and used without further purification. Lithium perfluorooctylsulfonate (C8F17SO3Li, LiPFOS, >96%) was purchased from TCI Europe and used without further purification. Pluronics L35 (EO11PO16EO11, L35), 10R5 (PO8EO22PO8, 10R5), F38 (EO46PO16EO46, F38), F88 (EO102PO41EO102, F88), F108 (EO132PO52EO132, F108) were kindly given by BASF SE (Ludwigshafen, Germany) and used without further purification.All samples were prepared from stock solutions. The surfactant stock solutions and polymer-surfactant stock solutions were prepared by dissolving an adequate amount of surfactant or surfactant with polymer in water filtered twice by a Millipore water filter.
Samples were prepared from stock solutions by mixing pure LiPFOS surfactant solutions with TDMAO solutions that contained the polymers. Samples for measurements performed in the stopped-flow were prepared directly from stock solutions in the stopped-flow. Samples for measurements performed in the ALV-Goniometer system were prepared by choosing adequate amounts of stock solutions by weight and by mixing both components by vigorous shaking directly before the measurement.
2.2 Kinetic dynamic light scattering measurements (DLS)
Time dependent Dynamic Light Scattering (DLS) measurements were performed with a high time resolution (2 s) covering a time range of up to a maximum of 30 min with a combined stopped-flow-DLS device, where the DLS detection was home-made (see below).Sample preparation was carried out using a BioLogic SFM-400 with a rectangular Hellma QS quartz cell (FC-15 cell) with an inner diameter of 1.5 mm provided by BioLogic and by sequential mixing of up to four solutions. Before mixing, these solutions were stored in thermostated reservoirs and were then pushed by step motors in controlled ratios and with a controlled flow rate through high efficiency mixers into the observation cell. Then the flow was stopped by a hard stop and the measurement started simultaneously by an electronic trigger. The length of the pathway to the cuvette defines the initial age of the sample and this dead time depends on the filling volume and the flow rate. To ensure efficient mixing the last mixer located directly under the observation cell was a high density mixer, which allows blockage of convection created by temperature and density effects, instead of the conventionally used Berger ball mixer. For all experiments the flow rate was set to 7 mL s−1 and the dead volume in combination with the high density mixer is 51.3 μL leading to a dead time of 7.3 ms.
The sample was illuminated with a frequency doubled diode pumped Nd-Yag laser with a wavelength of 532 nm and an output power of 20 mW (Compass 215M-20, Coherent). The intensity of the scattered light was collimated under 90° by a combination of a fibre collimator (60FC, Schäfter and Kirchhoff) and a single mode glass fibre cable (SMC, Schäfter and Kirchhoff) and recorded by a single photon counting module (Count-250C-FC, Laser Components). A Flex02-1D digital correlator was used to process the signal.
Measurements for longer times covering a time range of 30 s up to 12 days were performed with an ALV/CGS-3 Goniometer system with a 22 mW HeNe-Laser (λ = 622.8 nm) and employing a pseudo cross-correlation under a scattering angle of 90°. The samples were prepared 30 s before the first measurements and thermostated at 25 °C in a toluene bath during the measurement.
Intensity autocorrelation data from DLS measurements were evaluated with monoexponential fits (eqn (3)). With increasing time for samples, where ageing was observed (for low polymer content), a small shoulder could be observed in the correlation functions, that indicates the presence of large aggregates. In that case the data were evaluated with double exponential fits (eqn (4)). An example is given in the ESI material (Fig. S.1†).
g(2)(τ) = 1 + β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Γτ) exp(−Γτ) | (3) |
g(2)(τ) = 1 + (β1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Γ1τ) + β2 exp(−Γ1τ) + β2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Γ2τ))2 exp(−Γ2τ))2 | (4) |
The translational diffusion coefficient was calculated by using the relation DT = Γ/q2, with Γ being the relaxation rate of the exponential fit, and q being the magnitude of the scattering vector (q = 4πn/λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2) with refractive index n, wavelength of the light λ, and scattering angle θ). The hydrodynamic radius Rh was calculated from the translational diffusion coefficient DT by employing the Stokes-Einstein-relation (eqn (5)) with the Boltzmann constant kB, temperature T, and viscosity of the solvent η.
sin(θ/2) with refractive index n, wavelength of the light λ, and scattering angle θ). The hydrodynamic radius Rh was calculated from the translational diffusion coefficient DT by employing the Stokes-Einstein-relation (eqn (5)) with the Boltzmann constant kB, temperature T, and viscosity of the solvent η.
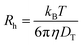 | (5) |
In the analysis the hydrodynamic radii were determined from the faster relaxation rate since the slower relaxation rate only appeared, when ageing took place and represents large vesicles or agglomerates produced by ageing.
Of course, it has to be noted the eqn (5) is originally valid for dilute diffusing particles and the radii obtained by us on the vesicle systems are apparent hydrodynamic radii. However, if we describe the vesicle–vesicle interactions by a hard-sphere potential and following the work by Phillies56 one arrives at a ratio between real (D0) and apparent hydrodynamic radius close to one, as depicted in Fig. S.2.† Similarly even if one considers electrostatic forces for the colloidal interaction between the vesicles the effect on the apparent hydrodynamic radius should be small. In general, the apparent diffusion coefficient is described by:
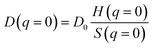 | (6) |
3 Results and discussion
Gaining control about the kinetics of the vesicle formation process offers a new way to tailor the size and stability of vesicles. This should be applicable in general to vesicle systems, where the vesicle formation takes place via a disc-like intermediate state. This can usually be expected in catanionic or zwitanionic systems, that are prepared by mixing two micellar solutions and where correspondingly a jump-wise change of the spontaneous curvature is to be expected.For that purpose a LiPFOS solution was mixed with a TDMAO solution with varying polymer content. The total surfactant concentration in the mixture was 50 mM and the ratio between TDMAO and LiPFOS was 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 since this ratio had been proven before to deliver very monodisperse vesicles.51 To study the evolution of aggregates in the mixtures the hydrodynamic radius was measured as a function of time. As the amphiphilic copolymer is the key component for controlling structure and stability in this study we aimed at elucidating the effect of its architecture on this stabilizing property. For that purpose we varied the arrangement of the EO/PO units for constant sum formula, the EO/PO ratio, i.e., the hydrophilicity of the polymeric surfactant, and its total length.
45 since this ratio had been proven before to deliver very monodisperse vesicles.51 To study the evolution of aggregates in the mixtures the hydrodynamic radius was measured as a function of time. As the amphiphilic copolymer is the key component for controlling structure and stability in this study we aimed at elucidating the effect of its architecture on this stabilizing property. For that purpose we varied the arrangement of the EO/PO units for constant sum formula, the EO/PO ratio, i.e., the hydrophilicity of the polymeric surfactant, and its total length.
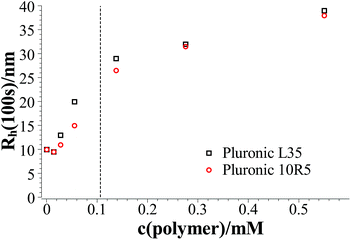
3.1 Pluronic L35 vs. Pluronic 10R5
First we studied the effect of molecular architecture without modifying the ratio of EO/PO in the copolymer and the total molecular weight. For that purpose we chose L35 and 10R5, which differ with respect to the arrangement of hydrophilic and hydrophobic block. Both polymers have the same number of PO and EO units, but while L35 has a hydrophobic core and two hydrophilic chains, in the case of 10R5 this architecture is reversed. L35 has the average structure EO11-PO16-EO11 and 10R5 that of PO8-EO22-PO8.Fig. S.3† shows the time dependent development of the hydrodynamic radii of aggregates in the system TDMAO-LiPFOS + 10R5 for different polymer concentrations. Both systems show an increase of the hydrodynamic radius (when compared after some minutes) with increasing polymer content and for both systems the hydrodynamic radius increases shortly after mixing (within the first 20–50 s). The observed increase is due to the growth process of the disc-like micelles, that precedes the vesicle formation. Afterwards a further increase in the vesicle size due to ageing can be observed. For polymer concentrations ≥0.1375 mM the hydrodynamic radius reaches a plateau after about 100 s and then remains constant for a longer period of time, i.e., the vesicles can be considered as colloidally stable. That means for polymer contents of ≥0.1375 mM the expected vesicles can be efficiently stabilised by the polymer. For L35 the vesicle radius stays constant for a period of at least 2 weeks (our experimental observation time) while for 10R5 after reaching the plateau still a slight increase of the vesicle radius can be observed which means that the 10R5 is somewhat less effective in long term stabilization. This could be associated with the fact that the EO22 chain that is anchored on both ends within the vesicle bilayer is protruding less far out into the aqueous solution than a single EO11 chain, and in addition their number is twice that high for L35.
Fig. 1 shows the development of the hydrodynamic radius Rh for both polymers and they have the same effect on the aggregates. The vesicles reach the same radius for similar polymer concentrations and the process of vesicle formation shows a very similar time-dependent behaviour.
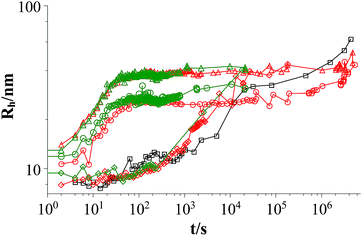 | ||
Fig. 1 Time dependent development of the hydrodynamic radius Rh comparing L35 and 10R5 at two different polymer concentrations (mixture: TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) 50 mM + polymer, 25 °C); black squares: mixture without polymer, red symbols: mixture with L35, green symbols mixture: with 10R5, diamonds: c(polymer) = 0.01375 mM, circles: c(polymer) = 0.1375 mM, triangles: c(polymer) = 0.55 mM (results from static light scattering are given in Fig. S.6†). 45) 50 mM + polymer, 25 °C); black squares: mixture without polymer, red symbols: mixture with L35, green symbols mixture: with 10R5, diamonds: c(polymer) = 0.01375 mM, circles: c(polymer) = 0.1375 mM, triangles: c(polymer) = 0.55 mM (results from static light scattering are given in Fig. S.6†). | ||
Fig. 2 shows the hydrodynamic radii of the vesicles in solution for all polymer contents after 100 s, where the plateau region begins for polymer contents of ≥0.1375 mM. In the graph two regions can be observed. In the area for a polymer content of 0–0.055 mM the hydrodynamic radius of the aggregates increases strongly with the polymer content while in the area for a polymer content of ≥0.1375 mM this dependency is less pronounced. The first area is the area where relatively fast ageing can be observed while the vesicles in the second area stay stable for at least two weeks. In total it is found that the L35 and 10R5 show no significant difference in their behaviour, i.e., the order of the EO and PO blocks has no significant influence on the vesicle size and the stability, and what counts is only the total composition of the copolymer.
3.2 Pluronic L35 vs. Pluronic F38 – hydrophilicity
The two polymers L35 and F38 are both PEO-PPO-PEO copolymers and have and the same PPO block of 16 monomer units but with 46 EO units (L35: 11 EO units) on each side the hydrophilic part of the F38 has a significantly longer EO block and therefore is a much more hydrophilic polymer surfactant. In addition, the longer EO block should also introduce more pronounced steric repulsion.The overall behaviour of the evolution of the hydrodynamic radii for F38 addition is similar to that observed with L35. Comparing the hydrodynamic radii in both systems 100 s after mixing no significant difference between both polymers can be observed (see Fig. S.4†). This leads to the conclusion, that the decrease in the line tension is the same for L35 and F38. This is not surprising since the hydrophobic parts in both polymers are the same and in the proposed mechanism the hydrophobic part of the polymer is supposed to be responsible for the decrease in the line tension.
However, in the system with L35 stabilisation is only observed for polymer concentrations ≥0.1375 mM while in the system with F38 stabilisation is already achieved for 0.055 mM. Since the hydrophilic chains are longer in F38 than in L35 apparently they are more efficient in covering the vesicle and lead to a more pronounced steric stabilisation, i.e. vesicle stability depends on the length of the EO block.
3.3 Pluronic F38, F88, and F108-polymer length
The next systematic copolymer variation was then a change of the total molecular weight while keeping the EO/PO ratio constant. By comparing the polymers F38, F88 and F108 we stay at a fixed ratio of PO and EO units (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) and vary the total molecular weight from 4700 g mol−1 to 14
21) and vary the total molecular weight from 4700 g mol−1 to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 g mol−1 (F38: EO46-PO16-EO46, F88: EO102-PO41-EO102, and F108: EO132-PO52-EO132). As the comparison of L35 and F38 showed no effect of the EO block length on the vesicle radius and mainly the stability was affected, here mainly the effect of the length of the PPO block should be probed.
600 g mol−1 (F38: EO46-PO16-EO46, F88: EO102-PO41-EO102, and F108: EO132-PO52-EO132). As the comparison of L35 and F38 showed no effect of the EO block length on the vesicle radius and mainly the stability was affected, here mainly the effect of the length of the PPO block should be probed.
Fig. 3 and 4 show the time dependent development of the hydrodynamic radii in the systems TDMAO-LiPFOS + F38 (F88, F108). Comparing the hydrodynamic radius 100 s after mixing in the three different systems as a function of the polymer concentration shows a strong increase of the hydrodynamic radius with the polymer length (see Fig. 5). For the same polymer number density (Fig. S.5†) in the mixture the formed vesicles are larger the longer the polymer chain is, which is interesting as the PPO block is quite long (6.4, 16.4, and 20.8 nm stretched length for F38, F88 and F108, respectively) compared to the bilayer thickness. That means a larger polymer leads to a stronger decrease in the line tension of the discs and a stronger anchoring within the vesicle bilayers. Since an increase in the length of the hydrophilic chain did not have an effect on the vesicle radius it can be concluded, that the increase in the vesicle radius is caused by the hydrophobic part of the polymer. An explanation is that the polymers orientate themselves along the disc rim, so that with increasing length of the hydrophobic part of the polymer less molecules are needed to cover the disc rim thereby causing a higher decrease of the line tension per polymer molecule (see Fig. 6 and S.5†). This agrees with the observation that L35, F38 and 10R5 that all possess similarly sized short PPO blocks show an almost identical effect on the size change of the vesicles (Fig. 5), i.e. this effect seems to be controlled by the hydrophobic PPO part.
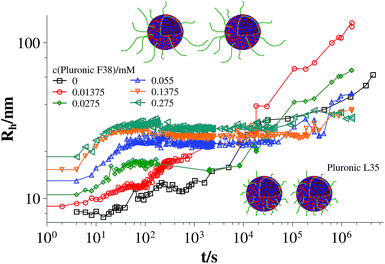 | ||
Fig. 3 Time dependent development of the hydrodynamic radius Rh (mixture: TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) 50 mM + F38, 25 °C) (results from static light scattering are given in Fig. S.7†). 45) 50 mM + F38, 25 °C) (results from static light scattering are given in Fig. S.7†). | ||
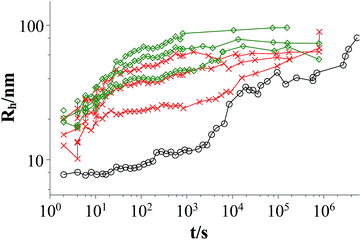 | ||
Fig. 4 Time dependent development of the hydrodynamic radius Rh; mixtures: TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) 50 mM: black circles; TDMAO 45) 50 mM: black circles; TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) 50 mM + F88 (0.0137 mM, 0.0275 mM, 2.75 mM), 25 °C, red crosses; TDMAO 45) 50 mM + F88 (0.0137 mM, 0.0275 mM, 2.75 mM), 25 °C, red crosses; TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45) 50 mM + F108 (0.0137 mM, 0.055 mM, 0.275 mM), 25 °C, green diamonds (results from static light scattering are given in Fig. S.8†). 45) 50 mM + F108 (0.0137 mM, 0.055 mM, 0.275 mM), 25 °C, green diamonds (results from static light scattering are given in Fig. S.8†). | ||
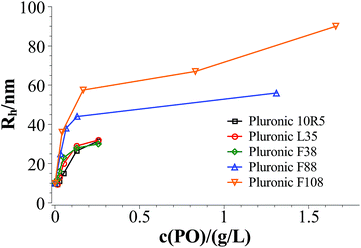 | ||
| Fig. 5 Hydrodynamic radius 100 s after mixing in the systems TDMAO-LiPFOS + F38, F88, and F108 at 25 °C. | ||
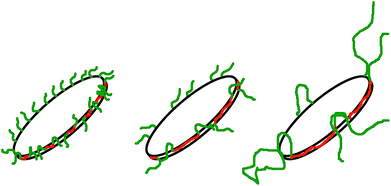 | ||
| Fig. 6 Polymers with a larger hydrophobic part are more effective in stabilising the disc, so that less polymer is necessary to achieve higher disc radii. | ||
On the other hand comparing the time dependent development of the hydrodynamic radius in different systems with polymers of different hydrophilic chain length, it can be seen that the longer the hydrophilic part is the lower is the number concentration of polymer needed to reach the plateau area in the DLS measurements, i.e. to achieve long-time stability (Fig. 7a). It is interesting to note that the total amount of EO units in the mixture is rather similar for all the copolymers studied, irrespective of the length of the EO chains (Fig. 7b), i.e., apparently the most important quantity that controls the stability is the total amount of EO in the stabilizing polymer shell.
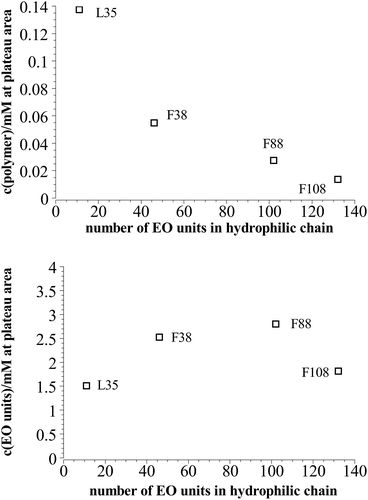 | ||
| Fig. 7 Polymer content where the plateau area in the DLS measurements is reached in dependency of the length of the hydrophilic part in the polymer at 25 °C. | ||
In the following we want to estimate the polymer concentration at which the vesicle bilayer can be expected to be fully covered. The steric hindrance of PEO chains attached to an vesicle surface can be described using the concept of de Gennes.58 It assumes that at low polymer density on the vesicle surface the PEO chains are in a mushroom-like conformation each PEO chain covering an area AEO-chain according to eqn (7).
| AEO-chain = π(Nk3/5lk)2 | (7) |
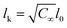 being the Kuhn length of the polymer, l0 the length of a monomeric unit,
being the Kuhn length of the polymer, l0 the length of a monomeric unit, 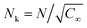 the number of Kuhn units, and N the number of monomeric units. The characteristic ratio C∞ is 5.2 for PEO, as determined from scattering experiments.59 It has to be noted, that the formulas given above are only strictly valid for N → ∞ which is not the case here. So the calculation has to be considered as an estimation. In principle the area occupied on the vesicle surface by the PEO chains per polymer molecule has to be doubled for L35, F38, F88, and F108 since these polymers have two PEO chains. On the other hand the hydrophilic coils can appear on both sides of the vesicle bilayer, so that the area has to be divided by two again and that both effects cancel out. When two vesicles approach each other the polymer coils from both vesicles have to be taken into account so that upon contact a layer of interdigitated polymer mushrooms from both surfaces is formed. So the area occupied on the vesicle surface by the PEO chains per polymer molecule has to be doubled again to take into account the polymer coils coming from both vesicles leading to AEO = 2πNk6/5lk2.
the number of Kuhn units, and N the number of monomeric units. The characteristic ratio C∞ is 5.2 for PEO, as determined from scattering experiments.59 It has to be noted, that the formulas given above are only strictly valid for N → ∞ which is not the case here. So the calculation has to be considered as an estimation. In principle the area occupied on the vesicle surface by the PEO chains per polymer molecule has to be doubled for L35, F38, F88, and F108 since these polymers have two PEO chains. On the other hand the hydrophilic coils can appear on both sides of the vesicle bilayer, so that the area has to be divided by two again and that both effects cancel out. When two vesicles approach each other the polymer coils from both vesicles have to be taken into account so that upon contact a layer of interdigitated polymer mushrooms from both surfaces is formed. So the area occupied on the vesicle surface by the PEO chains per polymer molecule has to be doubled again to take into account the polymer coils coming from both vesicles leading to AEO = 2πNk6/5lk2.
From the polymer concentration cpolymer and the corresponding hydrodynamic vesicle radius Rh the area A that is available for each polymer molecule on the vesicle surface can be calculated by eqn (8) where ϕ (for calculation see ESI†) is the volume fraction of amphiphilic material, c(pol) is the polymer concentration, and vves,shell ≈ 4πRh2d is the volume of the vesicle shell.
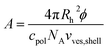 | (8) |
From A = AEO the concentration cpol,stab can be calculated, where the whole vesicle surface is covered with polymer coils, when two vesicles approach each other, so that vesicle fusion is hindered and stabilisation can be expected according to eqn (9) with d = 3.2 nm.
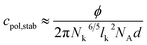 | (9) |
Fig. 8 shows that the values for cpol,stab determined from measurements and from theoretical considerations are pretty similar except for L35 where Nk = 5 is very low.
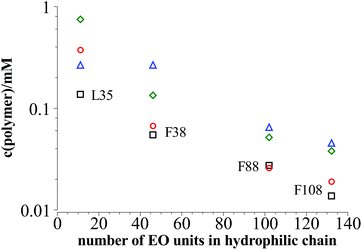 | ||
| Fig. 8 Black squares: polymer content where the plateau area in the DLS measurements is reached in dependency of the length of the hydrophilic part in the polymer at 25 °C; red circles: polymer concentration cpol,stab where vesicle stabilisation can be expected according to eqn (9); green diamonds: concentration of polymer saturation caused by dense packing of PEO mushrooms on top of the vesicle bilayer; blue triangles: concentration of polymer saturation caused by dense packing of PPO in the vesicle bilayer. | ||
Similar calculations can give the concentration where the vesicle surface is saturated with polymer. Here the effect from the PEO chains and from the PPO chains has to be taken into account.
If the PEO chains remain in the mushroom conformation on the vesicle surface then full coverage of the surface can be assumed for 2cpol,stab. On the other hand when squeezing the chains together they can form brushes so that the concentration of saturation can be much higher.
Compressing the PPO chains that form a self-avoiding random 2-dim-coil in the vesicle surface is not so easily possible. The Flory exponent for a two dimensional geometry is ν = 3/4 instead of ν = 3/5 for a 3-dim-coil so that the area occupied by each PPO chain in the surface is πNk3/2lk2 with Nk = 7, 7, 18, and 23 being the number of Kuhn units in L35, F38, F88, and F108. Analogous calculations to eqn (9) lead to the concentration of polymer saturation in the vesicle as given as blue triangles in Fig. 8.
3.4 Energetic stabilisation by polymer addition
The polymer stabilises the vesicles against ageing by fusion processes. From the kinetics an additional activation energy EA,pol due to the presence of the polymer can be determined. For its quantification the kinetic rate constant in the system with polymer has to be compared to the kinetic rate constant in the system without polymer.In the system TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55
LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45, 50 mM) the time dependent evolution of the z-average of the vesicle size RZ was analysed with eqn (10) developed by von Smoluchowski, where the vesicle fusion is governed by diffusion and where the same kinetic constant K is assumed for all vesicle sizes.60,61
45, 50 mM) the time dependent evolution of the z-average of the vesicle size RZ was analysed with eqn (10) developed by von Smoluchowski, where the vesicle fusion is governed by diffusion and where the same kinetic constant K is assumed for all vesicle sizes.60,61
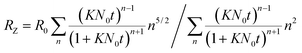 | (10) |
Fig. 9 shows that the growth process can not be described by one kinetic constant but that the kinetic constant must depend on the vesicle size (dark green line). To introduce the size dependency of K into eqn (10), an empirical approach was used for K as given in eqn (11) that describes an easier fusion for smaller vesicles, which can be ascribed to the fact that with increasing curvature of the membrane its energy per area increases. For m we assumed a constant value of 2 that would correspond to a situation where the activation energy EA depends directly on the bending energy of the fusing vesicles (as given by eqn (12),42 where C is the energy of a transitional state for fusion and Afus is the area involved in the fusion step, and Rv is the vesicle radius). It can be stated that eqn (12) is at best a very rough approximation for the real situation but in agreement with our experimental observation (where it should be noted that the fits are not very sensitive to the choice of m, but, of course, without having a size dependence of the rate constant, m = 0, one would have a largely different behaviour, as seen by the green solid line in Fig. 9).
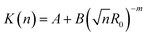 | (11) |
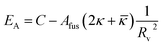 | (12) |
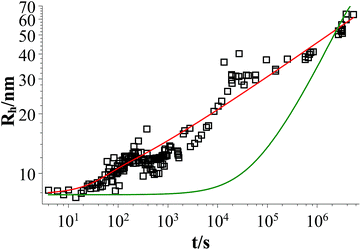 | ||
Fig. 9 Time dependent evolution of the z-average of the vesicle size Rh for a sample of TDMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LiPFOS (55 LiPFOS (55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45, 50 mM) (black open squares), fit with eqn (10) (dark green line), and fit with eqn (10) taking eqn (11) into account (red line). 45, 50 mM) (black open squares), fit with eqn (10) (dark green line), and fit with eqn (10) taking eqn (11) into account (red line). | ||
Eqn (10) together with eqn (11) does now describe the overall growth process as shown in 9 (red line).
The same analysis with eqn (10) and (11) was carried out for the mixtures with L35 so that for every polymer concentration K was determined as a function of the radius. The additional activation energy EA,pol of the vesicle fusion process caused by the polymer can be calculated from the kinetic rate constant in the systems with polymer Kpol and without polymer Kpure by eqn (13) at the initial vesicle in the system with polymer Rh,ini to ensure comparability between both systems. It has to be noted that the characteristic time for the vesicles to remain stable at the beginning of the vesicle growth process can not be compared for different polymer concentrations since the kinetic rate constant strongly depends on the vesicle radius and since the characteristic time includes the initial vesicle number density that decreases with the vesicle size.
 | (13) |
E A,pol increases significantly above a polymer concentration of 0.1375 mM from 0kBT to 3kBT. So when the polymer completely covers the vesicle surface the vesicles are stabilised by an additional activation energy for vesicle fusion of 3kBT (Fig. 10).
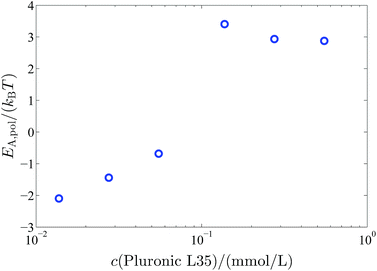 | ||
| Fig. 10 Additional activation energy EA,pol for the vesicle fusion caused by the polymer coverage of the vesicles in dependency on the polymer concentration. | ||
4 Conclusion
In this work we studied the influence of polymers of the Pluronic type (PEO-PPO surfactants) with different molecular architecture on the vesicle formation in a zwitanionic model system, where vesicle formation takes place via disc-like micelles after mixing two micellar solutions. Vesicle formation is controlled by the ratio between the bending elasticity of the bilayer and the line tension of the disc rim, where in particular the latter is modulated by the presence of the amphiphilic copolymer, which allows to control the size of the formed vesicles. In addition, a pronounced increase of vesicle stability is observed beyond a threshold concentration of copolymer. The aim of this work was to elucidate the effect of the polymer architecture and to give detailed information about how the hydrophobic and the hydrophilic parts of the polymers influence the initial vesicle size and stability, so that the vesicle properties can be controlled by appropriate choice of polymer type and concentration.Accordingly in our investigation the length of the hydrophilic part and the hydrophobic part of the polymer were varied and a conventional Pluronic with a hydrophobic core was compared to a Pluronic with a reversed geometry with a hydrophilic core. Time resolved DLS measurements, that allowed to follow the formation process and to determine the long time stability, led to three conclusions.
First comparing L35(EO11PO16EO11), F38(EO46PO16EO46), F88(EO102PO41EO102), and F108(EO132PO52EO132) we could show that, apart from the amount of added copolymer, mainly the length of the hydrophobic part of the polymer is responsible for the vesicle size. It lowers the line tension of the disc-like micelles by accumulating in the disc rim and the higher the amount of hydrophobic material incorporated in the disc rim the lower the line tension. Presumably the PPO chains are oriented along the disc rim, as this location is not only favourable for the relatively long PO blocks but with their two EO blocks they also have a much bulkier head group, which can be well accommodated in the rim. The longer the PO block the more stable the disc and the larger are the vesicles that are formed after spontaneous closure.
In contrast, the hydrophilic part of the polymer is responsible for the stability of the vesicles. The longer the PEO chain the lower the polymer concentration needed to prevent vesicle ageing. However, the scaling is such that the onset of colloidal stability is simply determined by the total concentration of EO units in the stabilizing PEO shell. The point where vesicle stabilization sets in is in good agreement with the polymer concentration estimated for having dense packing in the vesicle bilayer (assuming a mushroom configuration for the PEO blocks protruding into the aqueous surroundings).
Thirdly hardly any difference could be observed between polymers with a hydrophobic core or a hydrophilic core, when they have the same number of EO and PO units. Only the long-term stability of the vesicles is somewhat reduced for the case of the inverse Pluronic, which can be attributed to the lower number of EO chains and their lower extension into the surrounding aqueous phase.
Hence gaining control over the vesicle formation process by addition of amphiphilic polymers of the Pluronic type, offers a new and versatile mechanism to tailor the size and, in particular, the stability of vesicles. Depending on copolymer architecture and concentration one has wide control over the vesicle properties. In order to achieve the demanded vesicle properties only small amounts of these nontoxic, cheap and easily available polymers have to be added and this study gives the information, which polymer type and concentration will lead to the desired vesicle structures.
In summary, the addition of copolymer of the PEO/PPO type constitutes an elegant way of controlling the size and stability of spontaneously forming unilamellar vesicles. This can be achieved by adding rather small amounts of appropriately chosen copolymer, where the controlling ability and stability effects become more pronounced for longer chain copolymers. This is an important finding as it allows to form tailor-made unilamellar vesicles, an ability that is frequently required for their application in colloidal formulations, for pharmacy, cosmetics or detergency.
Acknowledgements
This research work was partially financially supported by the German Research Council (DFG) within the framework of the priority program SPP 1273 “Kolloidverfahrenstechnik” (GR1030/7-1 and 2). M. Medebach is thanked for helping with the time-resolved DLS set-up.References
- J. H. Felgner, R. Kumar, C. N. Sridhar, C. J. Wheeler, Y. J. Tsai, R. Border, P. Ramsey, M. Martin and P. L. Felgner, J. Biol. Chem., 1994, 269, 2550–2561 CAS.
- R. Langer, Science, 1990, 249, 1527–1533 CAS.
- D. Needham and M. W. Dewhirst, Adv. Drug Delivery Rev., 2001, 53, 285–305 CrossRef CAS.
- C. Dietrich, L. Bagatolli, Z. Volovyk, N. Thompson, M. Levi, K. Jacobson and E. Gratton, Biophys. J., 2001, 80, 1417–1428 CrossRef CAS.
- D. Papahadjopoulos and N. Miller, Biochim. Biophys. Acta, Biomembr., 1967, 135, 624–638 CrossRef CAS.
- C. L. Apel, D. W. Deamer and M. N. Mautner, Biochim. Biophys. Acta, Biomembr., 2002, 1559, 1–9 CrossRef CAS.
- G. Cevc, Crit. Rev. Ther. Drug Carrier Syst., 1996, 13, 257–388 CrossRef CAS PubMed.
- P. P. Ghoroghchian, J. J. Lin, A. K. Brannan, P. R. Frail, F. S. Bates, M. J. Therien and D. A. Hammer, Soft Matter, 2006, 2, 973–980 RSC.
- R. Langer, Science, 2001, 293, 58–59 CrossRef CAS PubMed.
- G. Betageri and D. Parsons, Int. J. Pharm., 1992, 81, 235–241 CrossRef CAS.
- O. C. Farokhzad and R. Langer, ACS Nano, 2009, 3, 16–20 CrossRef CAS PubMed.
- Y. Geng, P. Dalhaimer, S. Cai, R. Tsai, M. Tewari, T. Minko and D. E. Discher, Nat. Nanotechnol., 2007, 2, 249–255 CrossRef CAS PubMed.
- M. R. Prausnitz, S. Mitragotri and R. Langer, Nat. Rev. Drug Discovery, 2004, 3, 115–124 CrossRef CAS PubMed.
- J. B. Huang and G. X. Zhao, Colloid Polym. Sci., 1995, 273, 156–164 CAS.
- M. Hope, M. Bally, G. Webb and P. Cullis, Biochim. Biophys. Acta, Biomembr., 1985, 812, 55–65 CrossRef CAS.
- R. C. MacDonald, R. I. MacDonald, B. P. Menco, K. Takeshita, N. K. Subbarao and L.-R. Hu, Biochim. Biophys. Acta, Biomembr., 1991, 1061, 297–303 CrossRef CAS.
- L. D. Mayer, M. J. Hope and P. R. Cullis, Biochim. Biophys. Acta, Biomembr., 1986, 858, 161–168 CrossRef CAS.
- F. Olson, C. A. Hunt, F. C. Szoka, W. J. Vail and D. Papahadjopoulos, Biochim. Biophys. Acta, Biomembr., 1979, 557, 9–23 CrossRef CAS.
- F. Antunes, R. Brito, E. Marques, B. Lindman and M. Miguel, J. Phys. Chem. B, 2007, 111, 116–123 CrossRef CAS PubMed.
- L. L. Brasher and E. W. Kaler, Langmuir, 1996, 12, 6270–6276 CrossRef CAS.
- B. A. Coldren, H. Warriner, R. van Zanten, J. A. Zasadzinski and E. B. Sirota, Langmuir, 2006, 22, 2465–2473 CrossRef CAS PubMed.
- M. Dubois, B. Demé, T. Gulik-Krzywicki, J.-C. Dedieu, C. Vautrin, S. Desért, E. Perez and T. Zemb, Nature, 2001, 411, 672–675 CrossRef CAS PubMed.
- J. Hao, H. Hoffmann and K. Horbaschek, Langmuir, 2001, 17, 4151–4160 CrossRef CAS.
- E. W. Kaler, A. K. Murthy, B. E. Rodriguez and J. A. N. Zasadzinski, Science, 1989, 245, 1371–1374 CAS.
- E. W. Kaler, K. L. Herrington, A. K. Murthy and J. A. N. Zasadzinski, J. Phys. Chem., 1992, 96, 6698–6707 CrossRef CAS.
- S. B. Lioi, X. Wang, M. R. Islam, E. J. Danoff and D. S. English, Phys. Chem. Chem. Phys., 2009, 11, 9315–9325 RSC.
- E. F. Marques, O. Regev, A. Khan, M. da Graça Miguel and B. Lindman, J. Phys. Chem. B, 1998, 102, 6746–6758 CrossRef CAS.
- R. Talhout and J. B. F. N. Engberts, Langmuir, 1997, 13, 5001–5006 CrossRef CAS.
- K. Bressel, S. Prévost, M.-S. Appavou, B. Tiersch, J. Koetz and M. Gradzielski, Soft Matter, 2011, 7, 11232–11242 RSC.
- W. Guo, E. K. Guzman, S. D. Heavin, Z. Li, B. M. Fung and S. D. Christian, Langmuir, 1992, 8, 2368–2375 CrossRef CAS.
- H. Hoffmann, D. Gräbner, U. Hornfeck and G. Platz, J. Phys. Chem. B, 1999, 103, 611–614 CrossRef CAS.
- C. Wolf, K. Bressel, M. Drechsler and M. Gradzielski, Langmuir, 2009, 25, 11358–11366 CrossRef CAS PubMed.
- L. Zhai, J. Zhang, Q. Shi, W. Chen and M. Zhao, J. Colloid Interface Sci., 2005, 284, 698–703 CrossRef CAS PubMed.
- L. M. Zhai, X. J. Tan, T. Li, Y. J. Chen and X. R. Huang, Colloids Surf., A, 2006, 276, 28–33 CrossRef CAS PubMed.
- M. Gradzielski, J. Phys.: Condens. Matter, 2003, 15, R655–R697 CrossRef CAS.
- N. Vlachy, M. Drechsler, J.-M. Verbavatz, D. Touraud and W. Kunz, J. Colloid Interface Sci., 2008, 319, 542–548 CrossRef CAS PubMed.
- A. Renoncourt, N. Vlachy, P. Bauduin, M. Drechsler, D. Touraud, J.-M. Verbavatz, M. Dubois, W. Kunz and B. W. Ninham, Langmuir, 2007, 23, 2376–2381 CrossRef CAS PubMed.
- M.-P. Nieh, T. A. Harroun, V. A. Raghunathan, C. J. Glinka and J. Katsaras, Phys. Rev. Lett., 2003, 91, 158105 CrossRef.
- M. Gradzielski, Eur. Phys. J.: Spec. Top., 2012, 213, 267–290 CrossRef CAS.
- J. Gummel, M. Sztucki, T. Narayanan and M. Gradzielski, Soft Matter, 2011, 7, 5731–5738 RSC.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- W. Helfrich, J. Phys., 1986, 47, 321–329 Search PubMed.
- P. Fromherz, Chem. Phys. Lett., 1983, 94, 259–266 CrossRef CAS.
- A. Shioi and T. A. Hatton, Langmuir, 2002, 18, 7341–7348 CrossRef CAS.
- D. D. Lasic, Biochem. J., 1988, 256, 1–11 CAS.
- J. Leng, S. Egelhaaf and M. Cates, Biophys. J., 2003, 85, 1624–1646 CrossRef CAS.
- J. Leng, S. U. Egelhaaf and M. E. Cates, Europhys. Lett., 2002, 59, 311–317 CrossRef CAS.
- H. Noguchi and G. Gompper, J. Chem. Phys., 2006, 125, 164908 CrossRef PubMed.
- A. J. O'Connor, T. A. Hatton and A. Bose, Langmuir, 1997, 13, 6931–6940 CrossRef.
- M. Gradzielski, I. Grillo and T. Narayanan, Prog. Colloid Polym. Sci., 2004, 129, 263–271 Search PubMed.
- K. Bressel, M. Muthig, S. Prévost, I. Grillo and M. Gradzielski, Colloid Polym. Sci., 2010, 288, 827–840 CAS.
- T. M. Weiss, T. Narayanan, C. Wolf, M. Gradzielski, P. Panine, S. Finet and W. I. Helsby, Phys. Rev. Lett., 2005, 94, 038303 CrossRef CAS.
- T. Weiss, T. Narayanan and M. Gradzielski, Langmuir, 2008, 24, 3759–3766 CrossRef CAS PubMed.
- S. Schmölzer, D. Gräbner, M. Gradzielski and T. Narayanan, Phys. Rev. Lett., 2002, 88, 258301 CrossRef.
- K. Bressel, M. Muthig, S. Prévost, J. Gummel, T. Narayanan and M. Gradzielski, ACS Nano, 2012, 6, 5858–5865 CrossRef CAS PubMed.
- G. D. J. Phillies, Macromolecules, 1984, 17, 2050–2055 CrossRef CAS.
- M. Gradzielski and H. Hoffmann, J. Phys. Chem., 1994, 98, 2613–2623 CrossRef CAS.
- P. G. de Gennes, Macromolecules, 1980, 13, 1069–1075 CrossRef CAS.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1997, 38, 2885–2891 CrossRef CAS.
- M. Von Smoluchowski, Kolloid-Z., 1917, 21, 98–104 CrossRef.
- M. Von Smoluchowski, Phys. Z., 1916, 17, 585–599 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and preparation procedures; instrumentational details about the stopped-flow device and the DLS; analysis of DLS data; additional graphs. See DOI: 10.1039/c4sm02746a |
| This journal is © The Royal Society of Chemistry 2015 |