Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effects of globotriaosylceramide tail saturation level on bilayer phases†
Weria
Pezeshkian
ab,
Vitaly V.
Chaban
a,
Ludger
Johannes
c,
Julian
Shillcock
d,
John H.
Ipsen
a and
Himanshu
Khandelia
*a
aCenter for Biomembrane Physics (MEMPHYS), Department of Physics, Chemistry and Pharmacy (FKF), University of Southern Denmark, Campusvej 55, 5230 Odense M, Denmark. E-mail: hkhandel@sdu.dk
bTRANSPOL Molecular Neurobiochemistry, RUHR UNIVERSITAT BOCHUM, Bochum, Germany
cU1143 INSERM-UMR3666 CNRS, Institut Curie, 26 Rue DUlm, 75248 Paris Cedex 05, France
dEcole Polytechnique Fèdèrale De Lausanne (EPFL), 1015 Lausanne, Switzerland
First published on 16th December 2014
Abstract
Globotriaosylceramide (Gb3) is a glycosphingolipid present in the plasma membrane that is the natural receptor of the bacterial Shiga toxin. The unsaturation level of Gb3 acyl chains has a drastic impact on lipid bilayer properties and phase behaviour, and on many Gb3-related cellular processes. For example: the Shiga toxin B subunit forms tubular invaginations in the presence of Gb3 with an unsaturated acyl chain (U-Gb3), while in the presence of Gb3 with a saturated acyl chain (S-Gb3) such invagination does not occur. We have used all-atom molecular dynamics simulations to investigate the effects of the Gb3 concentration and its acyl chain saturation on the phase behaviour of a mixed bilayer of dioleoylphosphatidylcholine and Gb3. The simulation results show that: (1) the Gb3 acyl chains (longer tails) from one leaflet interdigitate into the opposing leaflet and lead to significant bilayer rigidification and immobilisation of the lipid tails. S-Gb3 can form a highly ordered, relatively immobile phase which is resistant to bending while these changes for U-Gb3 are not significant. (2) At low concentrations of Gb3, U-Gb3 and S-Gb3 have a similar impact on the bilayer reminiscent of the effect of sphingomyelin lipids and (3) At higher Gb3 concentrations, U-Gb3 mixes better with dioleoylphosphatidylcholine than S-Gb3. Our simulations also provide the first molecular level structural model of Gb3 in membranes.
Introduction
Glycosphingolipids (GSLs) are a class of lipids consisting of a ceramide linked to a carbohydrate moiety and are abundant in the outer leaflet of the plasma membrane. They are involved in many biological processes including macromolecular recognition, intracellular protein uptake and cell adhesion (reviewed in ref. 1). Globotriaosylceramide (Gb3) is an interesting GSL lipid which is required for the binding of Shiga toxin to the host cell membrane and the toxin's subsequent internalization into the cell.2,3 Gb3 is over-expressed in metastatic colon cancer and its presence is sufficient for epithelial cells to be invasive.4 The high expression of Gb3 in invasive colon cancer cells suggests a possible route to target and detect these cells.4,5 The Gb3-binding B-subunit of Shiga toxin (STxB) has also been used to target defined antigens to dendritic cells for the induction of a therapeutic immune response against cancer or intracellular pathogens.6–8STxB binds up to 15 Gb3 lipids on the surface of the host cell membrane9 and allows the intracellular transport of the toxin via the retrograde route.2 STxB can also bind to, aggregate and form clusters on model membranes composed of dioleoylphosphatidylcholine (DOPC) and porcine Gb3, and if the membrane tension is sufficiently low, it drives the model membrane to invaginate and form tubular invaginations.2,10–12 The Gb3 lipid is a large and chemically diverse molecule. It contains three sugar moieties, αGal(1–4) βGal(1–4) βGlc, which are connected to a ceramide. The acyl chain structure of this ceramide varies in different Gb3 species and the saturation level of this acyl chain affects many Gb3 involving processes. For example binding of STxB to a bilayer composed of dioleoylphosphatidylcholine (DOPC) and Gb3 with saturated acyl chains does not lead to the formation of tubular invaginations, whereas invagination occurs for unsaturated Gb3.2,11,13,14 Also, a lipid bilayer containing DOPC, sphingomyelin, cholesterol and Gb3 phase separate into a liquid ordered (lo) and a liquid disordered (ld) phase at room temperature. Phase behaviour of such a bilayer is strongly influenced by STxB clustering as well as the saturation levels and length of the Gb3 fatty acyl chain.11,13,15 Recently, the condensation of phospholipid–Gb3 monolayers was studied, using X-ray reflectivity and grazing incidence X-ray diffraction. The capacity of Gb3 to condense the monolayers was strongly affected by unsaturation levels of its acyl chain.16
Despite the important cellular roles of Gb3 and its significant impact on the physical behaviour of the lipid bilayers, it has not been studied by simulations before. Therefore, we use all-atom MD simulations to investigate a mixed bilayer of DOPC and Gb3 with two different acyl chain compositions, Gb3-22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 (Gb3 with a saturated acyl chain with 22 carbon atoms) and Gb3-22
0 (Gb3 with a saturated acyl chain with 22 carbon atoms) and Gb3-22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Gb3 with an unsaturated acyl chain with 22 carbon atoms and a trans-double bound in C13–C14). We refer to the saturated and unsaturated versions of Gb3 as S-Gb3 and U-Gb3, respectively. The simulations reveal two important features of the Gb3 structure which strongly affect lipid bilayer physical properties. First: Gb3 fatty acyl chains from one leaflet interdigitate into the opposite monolayer leading to a reduction in chain fluctuations, ordering of all fatty acyl chains in the bilayer and result in a bilayer with higher bending resistance. Second: the degree of the Gb3 acyl chain saturation influences the phase behaviour of the bilayer where for fully saturated acyl chains an ordered phase was observed. Our simulations can explain several experimental observable processes, which we present in the Discussion section of the report.
1 (Gb3 with an unsaturated acyl chain with 22 carbon atoms and a trans-double bound in C13–C14). We refer to the saturated and unsaturated versions of Gb3 as S-Gb3 and U-Gb3, respectively. The simulations reveal two important features of the Gb3 structure which strongly affect lipid bilayer physical properties. First: Gb3 fatty acyl chains from one leaflet interdigitate into the opposite monolayer leading to a reduction in chain fluctuations, ordering of all fatty acyl chains in the bilayer and result in a bilayer with higher bending resistance. Second: the degree of the Gb3 acyl chain saturation influences the phase behaviour of the bilayer where for fully saturated acyl chains an ordered phase was observed. Our simulations can explain several experimental observable processes, which we present in the Discussion section of the report.
Methods, force field and systems
Methods
We performed all-atom MD simulations of mixtures of DOPC and Gb3 lipids using GROMACS17–20 software and the CHARMM36 force field (FF).21,22 The Gb3 molecule had a C18 sphingosine tail and either a 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 acyl tail (S-Gb3) or a 22
0 acyl tail (S-Gb3) or a 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 acyl tail unsaturated at C13 (U-Gb3). For all systems, at least 100 water molecules (The TIP3P solvent model23) per lipid were present (some simulations were repeated using the TIPS3P water model,24 and the differences in the results were within the range of error bars). Na and Cl ions corresponding to a biological concentration of 150 mmol were present. Electrostatic interactions were treated with particle-mesh Ewald (PME) with a short range cutoff 1.2 nm, and van der Waals interactions were switched off between 1.0 and 1.2 nm. The system temperature was kept constant at 37 °C using Nose–Hoover temperature coupling.25,26 Bonds containing hydrogen atoms were constrained using the LINCS algorithm.27 Parrinello–Rahman barostat pressure coupling28,29 was applied on all systems after equilibrating the systems with Berendsen pressure coupling.30 The leap frog integrator was used with a timestep of 2 fs.
1 acyl tail unsaturated at C13 (U-Gb3). For all systems, at least 100 water molecules (The TIP3P solvent model23) per lipid were present (some simulations were repeated using the TIPS3P water model,24 and the differences in the results were within the range of error bars). Na and Cl ions corresponding to a biological concentration of 150 mmol were present. Electrostatic interactions were treated with particle-mesh Ewald (PME) with a short range cutoff 1.2 nm, and van der Waals interactions were switched off between 1.0 and 1.2 nm. The system temperature was kept constant at 37 °C using Nose–Hoover temperature coupling.25,26 Bonds containing hydrogen atoms were constrained using the LINCS algorithm.27 Parrinello–Rahman barostat pressure coupling28,29 was applied on all systems after equilibrating the systems with Berendsen pressure coupling.30 The leap frog integrator was used with a timestep of 2 fs.
Force field parameters for Gb3
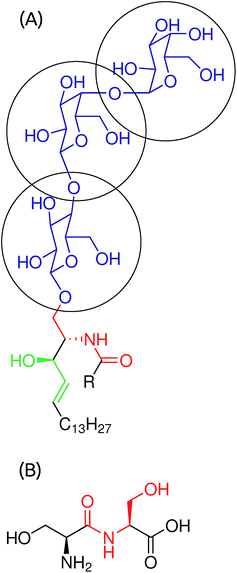
The Gb3 lipid contains three sugar moieties, αGal(1–4), βGal(1–4) and βGlc (Blue segment of Fig. 1A), which are connected to ceramide. The sugar moiety was described by the CHARMM36 FF for carbohydrates.31–35 Point electrostatic charges needed for HO–CH2–CH–CH–CH2–… (Green segment of Fig. 1A) are not provided in the CHARMM36 FF. As point electrostatic charges are unknown for the HO–CH2–CH–CH–CH2–… moiety of Gb3, we have performed electronic structure calculations for a set of similar systems to obtain information on the electron density distribution. All-electron Möller–Plesset second-order perturbation theory, MP2, was used. The wave function was constructed using the 6-311G basis set. Polarization and diffuse functions were added to this basis set. Additionally, polarization and diffuse functions were added to all hydrogen atoms. A strict self-consistent field convergence criterion of 10–9 Ha was applied. Geometries of the molecules were optimized at the same level of theory prior to the computation of the electrostatic potential (ESP). The ESP, derived from the electronic structure, was reproduced using a set of point charges centered on each atom, including hydrogen atoms. The atom spheres were defined according to the CHELPG scheme.36 The calculations were performed using the GAUSSIAN 09 program.37 We considered 4 model compounds, (1) CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2–OH, (2) CH3–CH2–CH2–OH, (3) CH3–CH
CH–CH2–OH, (2) CH3–CH2–CH2–OH, (3) CH3–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH3 and (4) CH3–CH
CH–CH3 and (4) CH3–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–CH2–OH. The inclusion of enumerated compounds into consideration was necessary to ensure reasonable transferability of the assigned charges. Please refer to the ESI† for a more detailed description of the development of the force field. The derived charges are summarized in Table 1. The HO–CH2–CH–NH–C
CH–CH2–OH. The inclusion of enumerated compounds into consideration was necessary to ensure reasonable transferability of the assigned charges. Please refer to the ESI† for a more detailed description of the development of the force field. The derived charges are summarized in Table 1. The HO–CH2–CH–NH–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety (Red segment of Fig. 1A and B) was described using serine–serine peptide bond parameters in the CHARMM36 FF for proteins. Finally, the fatty acid chains were described by the CHARMM36 FF for lipids.
O moiety (Red segment of Fig. 1A and B) was described using serine–serine peptide bond parameters in the CHARMM36 FF for proteins. Finally, the fatty acid chains were described by the CHARMM36 FF for lipids.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) γCH3
γCH3
| Atoms | Charge |
|---|---|
| OH | −0.70 |
| HO | +0.40 |
| αC | +0.55 |
| H1 | −0.05 |
| βC | −0.30 |
| H2 | +0.10 |
| γC | −0.10 |
| H3 | +0.10 |
Simulated systems
Details of all simulated systems are present in Table 2. Five different Gb3 concentrations in a DOPC bilayer, 0, 12, 25, 50, and 100 percent, were simulated. Two extra simulations to investigate the phase separation tendency of Gb3 were performed (Table 2). For systems 1–9, initial configurations were built by placing all DOPC lipids on a lattice and then a sufficient amount of the DOPC lipids was randomly replaced by Gb3 lipids to the desired concentration. The number of Gb3 lipids in both the monolayers is equal. For Gb3 domain simulations (systems 10 and 11), 16 DOPC lipids were replaced by 16 Gb3 lipids in the middle of the upper mono-layer of the bilayer.| System | DOPC/Gb3 | Na/Cl | Solvent | Time (ns) |
|---|---|---|---|---|
| 0% Gb3 | 128/0 | 24/24 | 9088 | 380 |
| 12% U-Gb3 | 176/24 | 37/37 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689 689 |
320 |
| 12% S-Gb3 | 176/24 | 36/36 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625 |
330 |
| 25% U-Gb3 | 96/32 | 25/25 | 9359 | 325 |
| 25% S-Gb3 | 96/32 | 23/23 | 8784 | 250 |
| 50% U-Gb3 | 64/64 | 19/19 | 7350 | 380 |
| 50% S-Gb3 | 64/64 | 17/17 | 6354 | 520 |
| 100% U-Gb3 | 0/128 | 45/45 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671 671 |
200 |
| 100% S-Gb3 | 0/128 | 36/36 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611 611 |
200 |
| U-Gb3 domain | 322/16 | 74/74 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612 612 |
400 |
| S-Gb3 domain | 322/16 | 62/62 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
400 |
Results
The last 200 ns of the simulation outputs were used for data analysis. We performed an initial check on our simulation methodology by measuring the structural properties of a pure DOPC bilayer, and found that they are in good agreement with previous results from experiments and other simulations. In particular, the area per lipid and bilayer thickness were 64.7 ± 1.2 Å2 and 36.4 ± 0.6 Å, which are close to the literature results of 68.0 Å2 and 36.6 Å (ref. 38) extracted from simulations. Experimental values are 67.4 Å2 (ref. 39) for the area per lipids and 36.1, 36.7 and 37.6 at 45, 30, and 15 °C,40,41 respectively for the membrane thickness. The area and thickness are the two key mechanical properties that characterise a planar bilayer. The area per lipid responds sensitively to the lipid phase, and the thickness influences the membrane curvature modulus that governs its thermal fluctuations. Our results show that these mechanical properties strongly depend on the membrane composition and the structural details of the Gb3 acyl chains.The rest of the paper is organized as follows. First, we report on the area and thickness using several different techniques for accurate measurement of the area per molecule. We then explore the influence of the Gb3 on the membrane dynamical properties, and measure the lipid tail order parameters, fatty acid tilt distributions, lipid diffusion, rotational correlation times and the tendency of Gb3 to phase separate. All of these properties are found to be sensitive to the Gb3 concentrations and the degree of Gb3 acyl chain saturation. In the Discussion section, we elaborate upon the main findings, and show how the simulations explain several previously unexplained experimental observations with regard to membrane invagination induced by Shiga toxins and the phase behaviour induced by Gb3.
Area per lipid and membrane thickness
We used three different methods to calculate the area per lipid.| System | a p (Å2) | a (Å2) | a v (DOPC/Gb3) | L m (Å) |
|---|---|---|---|---|
| 0 Gb3 | 64.7 ± 1.2 | 65.3 ± 0.9 | 64.7/— | 36.4 ± 0.6 |
| 12 S-Gb3 | 61.6 ± 0.8 | 61.9 ± 0.7 | 62.9/54.8 | 38.9 ± 0.5 |
| 12 U-Gb3 | 62.2 ± 0.8 | 62.9 ± 0.8 | 63.0/53.8 | 38.6 ± 0.5 |
| 25 S-Gb3 | 59.2 ± 1.0 | 60.4 ± 0.7 | 61.1/53.7 | 38.2 ± 0.6 |
| 25 U-Gb3 | 60.0 ± 1.0 | 61.7 ± 1.1 | 62.0/55.7 | 37.4 ± 0.5 |
| 50 S-Gb3 | 47.2 ± 0.4 | 50.8 ± 1.2 | 49.3/45.6 | 43.1 ± 0.3 |
| 50 U-Gb3 | 54.1 ± 1.0 | 55.0 ± 1.0 | 55.7/50.5 | 39.0 ± 0.5 |
| 100 U-Gb3 | 53.2 ± 0.5 | 58.0 ± 1.0 | — | — |
| 100 S-Gb3 | 52.6 ± 0.5 | 60.0 ± 1.0 | — | — |
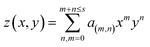 | (1) |
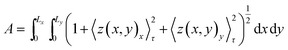 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y)〉τ is a time average of the function A(x,
y)〉τ is a time average of the function A(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y) in a specific time period, τ, (we have used τ = 20 ns) that minimizes the effects of membrane protrusions and shape fluctuations due to thermal fluctuations. z(x,
y) in a specific time period, τ, (we have used τ = 20 ns) that minimizes the effects of membrane protrusions and shape fluctuations due to thermal fluctuations. z(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y)x and z(x,
y)x and z(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y)y are partial derivatives of the function z(x,
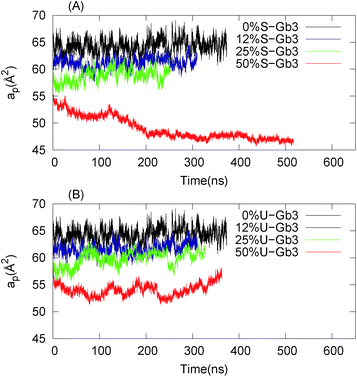
y)y are partial derivatives of the function z(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y) with respect to x and y, respectively. For most of the systems (except for pure U-Gb3 or S-Gb3) the polynomial method gives similar values for area per lipid as the previous methods (Table 3). However, for the pure systems, the polynomial method extracts a higher value for the area per lipid, indicating that the pure Gb3 bilayers are not planar (Fig. 2C and D). In general, the increase in Gb3 concentration results in decreases in area per lipid and tighter bilayer packing (a similar result was observed experimentally16). The decrease in the area per lipid comes from two sources: increase in the amount of Gb3 which has a smaller area per lipid or a change in the membrane phase behaviour, from a disordered to an ordered phase. At low Gb3 concentration, the first effect plays a major role, because the area per lipid (av) for Gb3 remains constant while the av for DOPC changed because the number of the DOPC lipids in contact with Gb3 increased. However, at high S-Gb3 concentrations, the Gb3av is lowered significantly which indicates a change in the phase state of the bilayer. We will elaborate on this in the subsequent sections.
y) with respect to x and y, respectively. For most of the systems (except for pure U-Gb3 or S-Gb3) the polynomial method gives similar values for area per lipid as the previous methods (Table 3). However, for the pure systems, the polynomial method extracts a higher value for the area per lipid, indicating that the pure Gb3 bilayers are not planar (Fig. 2C and D). In general, the increase in Gb3 concentration results in decreases in area per lipid and tighter bilayer packing (a similar result was observed experimentally16). The decrease in the area per lipid comes from two sources: increase in the amount of Gb3 which has a smaller area per lipid or a change in the membrane phase behaviour, from a disordered to an ordered phase. At low Gb3 concentration, the first effect plays a major role, because the area per lipid (av) for Gb3 remains constant while the av for DOPC changed because the number of the DOPC lipids in contact with Gb3 increased. However, at high S-Gb3 concentrations, the Gb3av is lowered significantly which indicates a change in the phase state of the bilayer. We will elaborate on this in the subsequent sections.
Chain order parameter
The orientational order of lipid chains is described by a deuterium order parameter which is given as: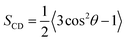 | (3) |
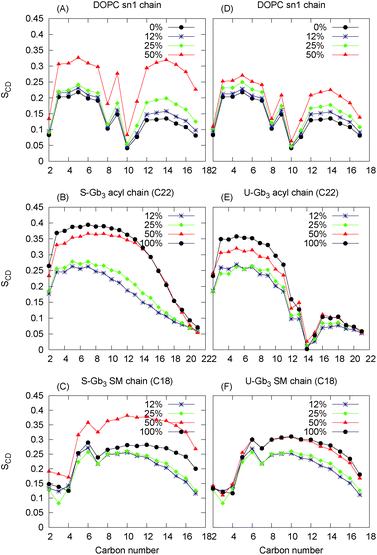 | ||
| Fig. 4 Deuterium order parameter for Gb3 chains and DOPC sn1 chains: left panels are for the mixture of DOPC with S-Gb3 (A–C) and right pan are for the mixture of DOPC with U-Gb3 (D–F). | ||
The very high order parameter for 50% S-Gb3 indicates that this system is in an ordered phase state. The transition of this system from an initially disordered state to an ordered state can be observed from the distinct differences in the Voronoi diagrams at the beginning (Fig. 9A in the ESI†) and the end of the simulation (Fig. 9B in the ESI†). In the ordered state, many lipids acquire a very low area per lipid, depicted by dark blue colors. It is important to note that S-Gb3 orders the nearby DOPC acyl chains, whereas increasing the concentration of U-Gb3 only has a small effect on the DOPC lipids, even up to 50% U-Gb3. The behaviour of the order parameter for the sphingosine chain of Gb3 in the low concentration regime is in good agreement with previous simulations of sphingomyelin lipids.45
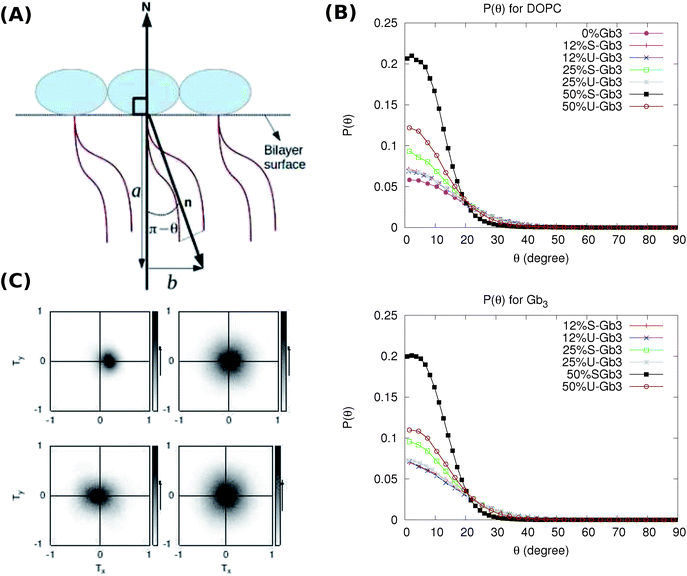
Lipid tilt
Tilt of the hydrophobic chains of lipid with respect to the bilayer normal is a characteristic parameter of the internal structure of the membrane in ordered phases. In the ld phase, the average tilt is zero in the absence of constraints which is imposed by external objects (for example proteins). Changes in the lipid tilt are associated with energy cost and coupled to the membrane bending energy.46The average orientation of the lipid chains is determined by the lipid tail director vector, n (Fig. 5A). Deviation of n from the bilayer normal (N) is quantified by the tilt vector (m) which is given as:
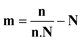 | (4) |
The probability of finding a lipid with a tilt angle between θ1 and θ2 (in the ld phase, the tilt is independent of ϕ because of the rotational symmetry) is given by:
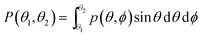 | (5) |
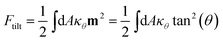 | (6) |
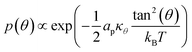 | (7) |
Such a deviation, and thus an ordered phase is observed at high concentrations of S-Gb3 (Fig. 5B). Also, the higher peaks of the profiles containing high percentages of S-Gb3 correspond to a larger value for κθ and a more rigid bilayer. Thus, the increase in Gb3 concentration rigidifies the bilayer, particularly for S-Gb3. To further visualise the tilt in the systems, a 2D tilt distribution map of the director vector density (ρ(Tx,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ty)) was made. ρ(Tx,
Ty)) was made. ρ(Tx,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ty) was measured as the time average of the number of lipids whose director vector projection on the membrane plane is equal to Txi + Tyj. Fig. 5C shows the 2D tilt distribution map for different systems. For 50% S-Gb3, the maximum peak is a bit shifted from the center, implying an overall non-zero average tilt for the system.
Ty) was measured as the time average of the number of lipids whose director vector projection on the membrane plane is equal to Txi + Tyj. Fig. 5C shows the 2D tilt distribution map for different systems. For 50% S-Gb3, the maximum peak is a bit shifted from the center, implying an overall non-zero average tilt for the system.
Diffusion coefficient
Lipid diffusion constants for different systems were measured by evaluating the root mean-square deviation and using the Einstein relationship. The values are given in Table 4. High concentrations of Gb3 resulted in lower lateral diffusion coefficients of the lipid in the bilayer plane. At low concentrations, the values are close to the expected values for fluid lipid bilayers (around 8 μm2 s−1 for DOPC47). Beyond 12.5% Gb3, the diffusion of DOPC is significantly lowered by S-Gb3 and to a lesser degree by U-Gb3.| System | DOPC μm2 s−1 | Gb3 μm2 s−1 |
|---|---|---|
| 0 Gb3 | 5.5 ± 0.8 | — |
| 12 U-Gb3 | 3.7 ± 0.4 | 3.3 ± 0.7 |
| 12 S-Gb3 | 3.2 ± 0.5 | 3.0 ± 0.7 |
| 25 U-Gb3 | 2.4 ± 0.1 | 2.3 ± 0.2 |
| 25 S-Gb3 | 1.2 ± 0.2 | 2.0 ± 0.2 |
| 50 U-Gb3 | 1.8 ± 0.1 | 1.3 ± 0.2 |
| 50 S-Gb3 | 0.3 ± 0.1 | 0.4 ± 0.1 |
| 100 U-Gb3 | — | 0.3 ± 0.2 |
| 100 S-Gb3 | — | 0.4 ± 0.3 |
Effects of Gb3 fatty acid chain length disparity
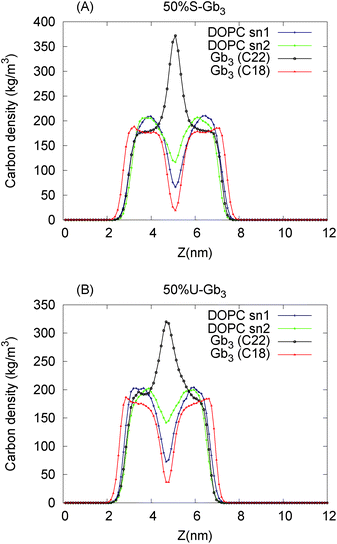
The Gb3 lipid has a big length mismatch in its two hydrocarbon tails. The sphingosine chain has 18 carbon atoms while the acyl chain contains 22 carbon atoms. Three different states for such a chain mismatch have been suggested, which under some conditions could lead to interdigitation between the hydrocarbons of the two opposite monolayers and drive the system in a new phase state.48 In the mixed systems, the shorter Gb3 chain (sphingosine chain) is packed end to end with DOPC chains, while the Gb3 acyl chain from both the leaflets penetrate the hydrocarbon region of the opposite monolayer, more so for S-Gb3 (Fig. 2). The peak in the Gb3 acyl chain density profile (Fig. 6) shows interdigitation between the acyl chains of the two opposing monolayers. The higher peak of S-Gb3 compared to that of U-Gb3 shows that it is more favourable for S-Gb3 to interdigitate into the other monolayer. Similar results are observed for lower Gb3 concentrations (data not shown).Lipid rotation
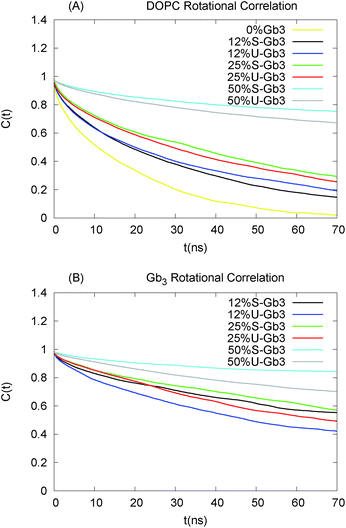
Lipid rotation around the bilayer normal is one of the slower degrees of freedom of the lipids in a lipid bilayer. The two-time correlation function for lipid rotation is defined as| Cθ(t0) = 〈Rθ(t)Rθ(t + t0)〉 | (8) |
Phase separation and mixing of Gb3 in a DOPC lipid bilayer
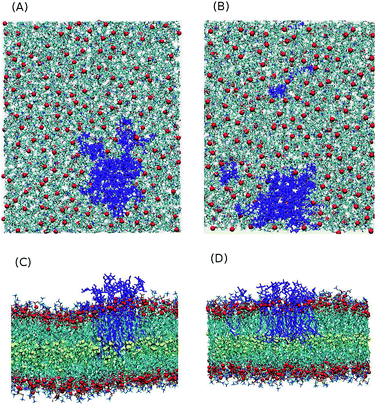
The time and length scales accessible to atomistic MD simulations are in the order of μs and 10 s of nm using present soft/hardware. It is difficult to study the complete spontaneous phase separation of lipid mixtures without resorting to coarse-grained techniques. To deal with this, instead of waiting for the system to phase separate, a phase separated system was created and the number of mixed lipids was considered. The initial configuration contains 16 Gb3 lipids (for both S-Gb3 and U-Gb3) in a patch embedded into one monolayer of a DOPC bilayer. The simulation was then run for 400 ns.Two U-Gb3 lipids mixed in the DOPC bilayer after 400 ns (Fig. 8B), while no mixing was observed for S-Gb3 for the same simulation time (Fig. 8A). Thus, we can hypothesize from the data that U-Gb3 has a higher affinity to mix with DOPC, compared to S-Gb3. This effect could be because of the height mismatch between DOPC and S-Gb3 (Fig. 8C and D) and/or because of unfavourable contacts between the saturated acyl chain of the S-Gb3 and the unsaturated DOPC chains.
The method above does not quantify phase behaviour accurately, but does provide a comparison between the mixing rates of S-Gb3 and U-Gb3.
Discussion
The Gb3 carbohydrate moiety, which is identical in all Gb3 types, is essential for Shiga toxin binding to a cell membrane and its subsequent internalization into the host cell.9 However, different types of Gb3 behave differently in the Gb3 involving processes. The most notable example is the inability of STxB to induce tubular membrane invagination upon binding to S-Gb3 on the surface of a DOPC model membrane. On the other hand, STxB bound to U-Gb3 on the surface of a DOPC model membrane induces tubular invaginations.2,12 Thus, STxB binding to the membrane is insufficient for the formation of membrane tubular invagination and the presence of a specific Gb3 species is required.We have used all-atom MD simulations to investigate the effects of varying the Gb3 concentration as well as the degree of unsaturation of its acyl chains on the physical properties of DOPC lipid bilayers. Our results reveal two important features of the Gb3 structure that strongly affect the structure and dynamics of the lipid bilayers when it is present at high concentrations. (1) The Gb3 chain length mismatch results in interdigitation of the longer chain into the opposite monolayer and in subsequent reduction in lipid fatty acid chain fluctuations, and ordering of all bilayer chains. The effect is stronger for S-Gb3 compared to U-Gb3. (2) The degree of Gb3 acyl chain saturation influences the affinity of Gb3 lipids to mix or demix in DOPC lipid bilayers.
The Gb3 concentration is low in the experiments (up to 10%).2,12 However, considering that each STxB molecule can bind up to 15 Gb3 lipids, it is reasonable to think that the Gb3 concentration is high (up to 40%) under the protein. Combining this assumption with the fact that STxB proteins cluster on the surface of a membrane,2,11 a high concentration of Gb3 is expected in the domains enriched by STxB that modifies the local bilayer structure. This argument and the simulation results provide the following insights into several experimental observations:
(a). Binding of STxB to a bilayer containing S-Gb3 and DOPC does not drive the membrane to invaginate:2 we hypothesise that invagination will not occur when STxB is bound to an ordered phase. A high energetic cost must be borne to bend such a rigid bilayer which cannot be compensated by the system. Such an ordered and rigid bilayer is observed at a high concentration of S-Gb3 in our simulations, as shown in Fig. 5. A similar lo phase is present in a phase-separated lipid bilayer composed of DOPC, sphingomyelin, cholesterol and porcine Gb3. Binding of STxB to the lo phase of this membrane does not induce tubular invagination.11 On the other hand, U-Gb3 does not form a rigid bilayer, and thus membrane invagination can occur without incurring the high bending energy penalty. Experiments also show that tubular invagination is observed upon STxB binding to a membrane containing only DOPC and U-Gb3, which does not exhibit the lo phase.11
(b). For lipid bilayers containing DOPC, sphingomyelin, cholesterol and Gb3-C24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, which are phase separated at room temperature, no change in the area percentage of the lo phase was observed upon STxB binding experimentally:13 we have shown that S-Gb3 tends to remain phase separated in such a DOPC bilayer. Thus, SGb3 is probably already in a phase separated state in the mixed bilayer even before STxB binds. Thus, STxB binds to the lo phase, and no further changes occur in the system.
0, which are phase separated at room temperature, no change in the area percentage of the lo phase was observed upon STxB binding experimentally:13 we have shown that S-Gb3 tends to remain phase separated in such a DOPC bilayer. Thus, SGb3 is probably already in a phase separated state in the mixed bilayer even before STxB binds. Thus, STxB binds to the lo phase, and no further changes occur in the system.
(c). Increase in membrane height due to protein clustering:11Table 3 shows that the membrane thickness increases with increasing Gb3 concentration. The change is particularly significant at high S-Gb3 concentrations.
(d). The condensation of phospholipid–Gb3 monolayers at high Gb3 concentrations:16 increasing the Gb3 concentration induces a progressively lower area per lipid and a dramatic reduction was observed at high S-Gb3 concentrations (Table 3). In the experiments a similar impact for S-Gb3 was observed.16
Our results suggest that the STxB binding to a lipid bilayer indirectly influences the properties of the lipid bilayer by clustering and accumulating Gb3 underneath the protein aggregate. Invagination is not induced when Gb3 is saturated, because S-Gb3 forms a rigid immobile phase resistant to bending whilst the unsaturated version does not. Our results provide several hypotheses which can resolve some of the unexplained experimental observations with regard to the phenomenon of membrane invagination induced by Shiga toxins. Further investigation is needed to validate these hypotheses.
Acknowledgements
The research leading to these results has received funding from the European Community's Seventh Framework Programme (FP7/2007–2013) under the grant agreement number TRANSPOL-264399. Some parts of the computations were carried out on the Horseshoe clusters at the SDU node for the Danish Center for Scientific Computing (DCSC). We acknowledge that the results of this research have been achieved using the PRACE-2IP project (FP7 RI-283493) resource ARCHER based on the United Kingdom at https://www.archer.ac.uk/. HK is funded by a Lundbeckfonden Young Investigator Grant. The LJ group was supported by the European Research Council advanced grant (project 340485), Agence Nationale pour la Recherche (ANR-09-BLAN-283 and ANR-11 BSV2 014 03), and Human Frontier Program organization (RGP0029/2014C101).References
- B. Maggio, M. L. Fanani, C. M. Rosetti and N. Wilke, Biochim. Biophys. Acta, 2006, 1758, 1992–1944 Search PubMed.
- W. Römer, L. Berland, V. Chambon, K. Gaus, B. Windschiegl, D. Tenza, M. Aly, V. Fraisier, J. Florent, D. Perrais, C. Lamaze, G. Raposo, C. Steinem, P. Sens, P. Bassereau and L. Johannes, Nature, 2007, 450, 670–675 CrossRef PubMed.
- T. Eierhoff, B. Bastian, R. Thuenauer, J. Madl, A. Audfray, S. Aigal, S. Juillot, G. Rydell, S. Muller, S. de Bentzmann, A. Imberty, C. Fleck and W. Romer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12895–12900 CrossRef CAS PubMed.
- O. Kovbasnjuk, R. Mourtazina, B. Baibakov, T. Wang, C. Elowsky, M. A. Choti, A. Kane and M. Donowitz, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 19097–19092 CrossRef PubMed.
- L. Johannes and D. Decadin, Gene Ther., 2005, 12, 1360–1368 CrossRef CAS PubMed.
- F. Sandoval, M. Terme, M. Nizard, C. Badoual, M. Bureau, L. Freyburger, O. Clement, E. Marcheteau, A. Gey, G. Fraisse, C. Bouguin, N. Merillon, E. Dransart, T. Tran, F. Quintin-Colonna, G. Autret, M. Thiebaud, F. Suleman, S. Riffault, T. Wu, O. Launay, C. Danel, J. Taieb, J. Richardson, L. Zitvogel, W. Fridman, L. Johannes and E. Tartour, Sci. Transl. Med., 2013, 5, 172ra20 Search PubMed.
- H. Pere, Y. Montier, J. Bayry, N. Merillon, F. Quintin-Colonna, E. Dransart, C. Badoual, A. Gey, P. Ravel, F. Sandoval, C. Guerin, O. Adotevi, Y. Lone, L. Ferreira, B. Nelson, D. Hanahan, W. Fridman, L. Johannes* and E. Tartour*, Blood, 2011, 118, 4853–4862 CrossRef CAS PubMed.
- O. Adotevi, B. Vingert, L. Freyburger, P. Shrikant, Y. Lone, F. Quintin-Colonna, N. Haicheur, M. Amessou, A. Herbelin, P. Langlade-Demoyen, W. Fridman, F. Lemonnier, L. Johannes* and E. Tartour*, J. Immunol., 2007, 179, 3371–3379 CrossRef CAS.
- H. Ling, A. Boodhoo, B. Hazes, M. D. Cummings, G. D. Armstrong, J. L. Brunton and R. J. Read, Biochemistry, 1998, 37, 1777–1788 CrossRef CAS PubMed.
- D. G. Pina, L. Johannes and M. A. Castanho, Biochim. Biophys. Acta, 2007, 1768, 628–636 CrossRef CAS PubMed.
- B. Windschiegl, A. Orth, W. Römer, L. Berland, B. Stechmann, P. Bassereau, L. Johannes and C. Steinem, PLoS One, 2009, 4, e6238 Search PubMed.
- M. Safouane, L. Berland, A. Callan-Jones, B. Sorre, W. Römer, L. Johannes, G. E. S. Toombes and P. Bassereau, Traffic, 2010, 11, 1519–1529 CrossRef CAS PubMed.
- O. M. Schütte, A. Ries, A. Orth, L. J. Patalag, W. Römer, C. Steinem and D. B. Werz, Chem. Sci., 2014, 5, 3104–3114 RSC.
- D. J. Chinnapen, W. Hsieh, Y. te Welscher, D. Saslowsky, L. Kaoutzani, E. Brandsma, L. D'Auria, H. Park, J. Wagner, K. Drake, M. Kang, T. Benjamin, M. Ullman, C. Costello, A. Kenworthy, T. Baumgart, R. Massol and W. Lencer, Dev. Cell, 2012, 23, 573–586 CrossRef CAS PubMed.
- V. Solovyeva, L. Johannes and A. C. Simonsen, Soft Matter, 2015, 11, 186–192 RSC.
- E. B. Watkins, H. Gao, A. J. C. Dennison, N. Chopin, B. Struth, T. Arnold, J.-C. Florent and L. Johannes, Biophys. J., 2014, 107, 1146–1155 CrossRef CAS PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model, 2001, 7, 306–317 CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- P. Bjelkmar, P. Larsson, M. A. Cuendet, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2010, 6, 459–466 CrossRef CAS.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, J. R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. R. III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplu, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, A. DiNola and J. R. Haak, J. Phys. Chem. B, 1984, 81, 3684–3690 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Noséa and M. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- O. Guvench, S. Greene, G. Kamath, J. Brady, R. Venable, R. Pastor and A. J. MacKerell, J. Comput. Chem., 2008, 29, 2543–2564 CrossRef CAS PubMed.
- O. Guvench, E. R. Hatcher, R. M. Venable, R. W. Pastor and A. J. MacKerell, J. Chem. Theory Comput., 2009, 5, 2353–2370 CrossRef CAS PubMed.
- E. P. Raman, O. Guvench and A. J. MacKerell, J. Phys. Chem. B, 2010, 114, 12981–12994 CrossRef CAS PubMed.
- O. Guvench, S. S. Mallajosyula, E. P. Raman, E. Hatcher, K. Vanommeslaeghe, T. J. Foster, F. W. Jamison and A. J. MacKerell, J. Chem. Theory Comput., 2011, 7, 3162–3180 CrossRef CAS PubMed.
- S. S. Mallajosyula and A. J. MacKerell, J. Phys. Chem. B, 2011, 115, 11215–11229 CrossRef CAS PubMed.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian-09 Revision D.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- J. P. M. Jambeck and A. P. Lyubartsev, J. Chem. Theory Comput., 2012, 8, 2938–2948 CrossRef.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef PubMed.
- J. Pan, S. Tristram-Nagle, N. Kučerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2005, 208, 193–202 CrossRef PubMed.
- G. Lukat, J. Krüger and B. Sommer, J. Chem. Inf. Model., 2013, 53, 2908–2925 CrossRef CAS PubMed.
- J. Seelg, Q. Rev. Biophys., 1977, 3, 353–418 CrossRef.
- J. Douliez, A. Léonard and E. J. Dufourc, Biophys. J., 1995, 68, 1727–1739 CrossRef CAS PubMed.
- J. Aittoniemi, P. S. Niemelä, M. T. Hyvönen, M. Karttunen and I. Vattulainen, Biophys. J., 2007, 92, 1125–1137 CrossRef CAS PubMed.
- M. Hamm and M. M. Kozlov, Eur. Phys. J. E, 2000, 3, 323–335 CrossRef CAS.
- G. Lindblom and G. Orädd, Biochim. Biophys. Acta, 2009, 1788, 234–244 CrossRef CAS PubMed.
- I. W. Levin, T. E. Thompson, Y. Barenholz and C. Huang, Biochemistry, 1985, 24, 6282–6286 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm02456g |
| This journal is © The Royal Society of Chemistry 2015 |