Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlled motion of Janus particles in periodically phase-separating binary fluids
Takeaki
Araki
* and
Shintaro
Fukai
Department of Physics, Kyoto University, Sakyo-ku, Kyoto 606-8502, Japan. E-mail: araki@scphys.kyoto-u.ac.jp
First published on 7th April 2015
Abstract
We numerically investigate the propelled motions of a Janus particle in a periodically phase-separating binary fluid mixture. In this study, the surface of the particle tail prefers one of the binary fluid components and the particle head is neutral in the wettability. During the demixing period, the more wettable phase is selectively adsorbed to the particle tail. Growths of the adsorbed domains induce the hydrodynamic flow in the vicinity of the particle tail, and this asymmetric pumping flow drives the particle toward the particle head. During the mixing period, the particle motion almost ceases because the mixing primarily occurs via diffusion and the resulting hydrodynamic flow is negligibly small. Repeating this cycle unboundedly moves the Janus particle toward the head. The dependencies of the composition and the repeat frequency on the particle motion are discussed.
1 Introduction
Self-propelled motions of micro- and nano-particles have attracted much interest from a wide range of viewpoints. They will provide us with important applications, such as nanomachines and drug delivery.1–8 Recently, focus has been on their collective dynamics because they are very fascinating in a growing field of non-equilibrium physics, i.e., active matter.9–13 Self-propelled particles use some energy or nutrients to generate the self-propulsion force. For example, biological molecules, such as ATPase and myosin, convert chemical energy to mechanical motion through chemomechanical coupling.14 In non-biological systems, Marangoni effect can induce spontaneous motions of liquid droplets.15,16Janus particles, which have heterogeneous surface properties, are often employed as artificial self-propelled systems.17,18 For example, the self-propelled motions are modelled by asymmetric nanoparticles partially coated with platinum. The catalytic decomposition of hydrogen peroxide, which occurs selectively on the Pt-surface, drives the nanoparticles.1,2,5,19,20 Interfacial phoretic effects21,22 are another possible mechanism of micro-swimmers.17 Jiang et al. demonstrated that a Janus particle can create an asymmetric temperature gradient around it in a defocused laser beam. The induced gradients lead to spontaneous drift motions of the Janus particles.7 Also, local heating by illumination light induces active motions of Janus particles in a binary mixture of lower critical solution temperature.23,24
Besides the thermo- and diffusio-phoresis motions,7,23,24 Janus particles can move in phase-separating binary mixtures because of the coupling between the wetting and phase separation.25,26 The phase separation of binary fluid mixtures has been well studied.27–29 During the later stage of the phase separation, the domain patterns grow with time. The particles in the phase-separating mixtures are trapped in one of the phases or at the interfaces. Even when Brownian motions and external forces are absent, the particles move with the resulting coarsening of the domain patterns.30–33 Because the Janus particles have asymmetric wettability, we expect that their motions also become asymmetric. The direction of the asymmetric motion will more or less depend on the particle direction. Janus particles with two distinct wettabilities are occasionally used as surfactants to stabilize the phase-separated domains.34–36 In the final stage of the phase separation, the particle motions will be frozen.
In this article, we demonstrate a possible mechanism of spontaneous motions of a Janus particle in periodically phase-separating mixtures. By continually varying the temperature or pressure slightly above and below the transition point, one can cause periodic processes of phase separation and mixing.37–40 By resetting the binary mixtures to the one-phase state, we expected that we could continuously propel the particle. Here, we examine this expectation by means of numerical simulations. The dependencies of the particle motion on the average composition and the duration of the cycle are discussed.
In Section 2, we explain our numerical model, which is based on the fluid particle dynamics method.41,42 Numerical results are shown and are discussed in Section 3. We summarize our study and discuss some remarks in Section 4.
2 Model and simulation
2.1 Free energy functional
We consider the case in which a spherical Janus particle is suspended in a binary mixture. The surface of the particle is heterogeneous in wettability. For numerical simulations, dealing with the particle in a continuous manner is convenient. We express it with a smooth shape function as41,42 | (1) |
Here, r is the coordinate in a lattice space and R is the position of the particle in an off-lattice space. a is the radius of the particle and d represents the width of the smooth interface. In the limit of d → 0, ψ is unity and zero in the interior and exterior of the particle, respectively. We also define the surface distribution as ψs = |∇ψR|.
The free energy function comprises two parts:32,43,44
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix + mix + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sur. sur. | (2) |
The first part ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) mix is the mixing free energy given by
mix is the mixing free energy given by
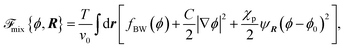 | (3) |
fBW(ϕ) = ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ), ϕ + (1 − ϕ)ln(1 − ϕ) + χϕ(1 − ϕ), | (4) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) sur is the surface free energy, which is given by
sur is the surface free energy, which is given by
 | (5) |
 | (6) |
 | ||
| Fig. 1 (a) A sketch of a spherical particle with a heterogeneous surface. The orientation is described by a unit vector n. We set W0 = −1 and W1 = 1 in eqn (6), so that we have W = 0 and W = −2 at the two poles. We refer to the pole with W = 0 as the “head” and the other one as the “tail”. The particle head is neutral in wettability and the tail prefers component A. (b) A typical phase diagram of a binary fluid mixture. We change the χ parameter by using a square wave function of t. Phase separation occurs during the period with χ = χd. However, when χ = χm, the phase-separated domains are mixed. | ||
2.2 Time development equations
The hydrodynamic equation for the flow field v is given by | (7) |
Here ρ is the material density. In this work, we assume that all the materials have the same density. Σ is the viscous stress tensor, which is given by
| Σ = η{∇v + (∇v)T}. | (8) |
In the spirit of fluid particle dynamics (FPD), we assume that the viscosity η depends on the particle distribution as41,42
| η(r) = η0 + ΔηψR(r), | (9) |
f is the force field stemming from the particle interactions and is given by
 | (10) |
 | (11) |
The particle motions are caused by the hydrodynamic flow and their kinetics are described as
 | (12) |
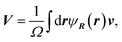 | (13) |
 | (14) |
Furthermore, the time development equation of the concentration field is
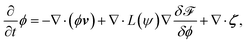 | (15) |
2.3 Numerical simulations
We numerically solve the above equations using the Maker and Cell method with a staggered grid.45 We discretize the space by d and set v0 = d3 and C = d2. Also, we set the particle radius to a = 6d. The simulation box is a three-dimensional system (643) with periodic boundary conditions. The time increment is 0.005t0, where t0 is a typical diffusion time defined by t0 = d2T/L0. For the wettability, we set W0 = −1 and W1 = 1 in this study. Hence, the head of the particle is neutral in the wettability and the tail prefers the component of large ϕ (see Fig. 1(a)). Hereafter, we describe the more and less wettable components as A and B, respectively. The viscosity parameters in eqn (8) are η0 = ρL0/T and Δη = 49η0. In eqn (3), we set ϕ0 to be equal to the average composition, 〈ϕ〉, and χp = 20. Because Reynold numbers in colloidal systems are very small, we iterate to integrate eqn (7) without updating R, n, and ϕ until |ρ(∂/∂t + v·∇)v| becomes less than 10−3η0L0/(T0d3). The intensity of the thermal fluctuation is given by 〈ζi(r,t)ζj(r′,t′)〉 = 0.05TL(ψ)δ(r − r′)δ(t − t′)δij, where i and j stand for x, y and z.2.4 Periodic phase separation
To induce periodic phase separation, we change the χ parameter uniformly in space using square wave functions of time (see Fig. 1(b)). tm and td denote the durations for mixing and demixing, respectively. We also define tt = tm + td. For simplicity, because we consider mixtures near the phase-separation point, we assume that the other physical parameters are constant, independent of χ. In durations of mtt ≤ t < mtt + tm, χ is fixed at χm below the critical point. Here, m is an integer. The phase-separated domains will be mixed during these times. In mtt + tm ≤ t < (m + 1)tt, we retain χ at χ = χd, above the critical point, so that phase separation proceeds in the bulk. Throughout the simulations presented in this article, we fix the χ parameters to χd = 2.7 and χm = 1.3. In the demixing periods with χd, the coexistence concentrations of A- and B-rich phases are ϕ ≅ 0.893 and 0.107, respectively. The correlation length, also referred to as the interface thickness, is . However, during the mixing periods with χm, the correlation length is given by
. However, during the mixing periods with χm, the correlation length is given by  .
.
3 Results and discussions
3.1 Domain patterns
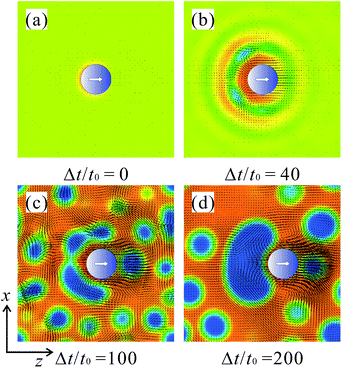
Fig. 2 shows snapshots of the domain patterns in the case of tm = td = 100t0. The snapshots were obtained at t = 200t0 and t = 1000t0, which correspond to the times when the first and fifth demixing periods are just completed, respectively. The average concentrations, 〈ϕ〉, of component A are (a) 0.3, (b) 0.5, and (c) 0.7. In the demixing periods with χd, the volume fractions of the A-rich phase are (a) 24.6%, (b) 50% and (c) 75.4%, respectively. The light blue surfaces represent the isosurfaces of ϕ = 0.5 and the dark blue sphere represents the Janus particle. At t = 0, the particle is directed toward the z-axis, i.e., n(t = 0) = (0, 0, 1). In each case, we observed that the particle follows the background flows, which are caused by the interface tensions during the phase separations. The mechanisms of the particle motions are discussed below. | ||
| Fig. 2 Snapshots of a Janus particle in periodically phase-separating binary fluids. The average concentrations of the more wettable phase are (a) 〈ϕ〉 = 0.3, (b) 〈ϕ〉 = 0.5, and (c) 〈ϕ〉 = 0.7. | ||
3.2 Particle trajectories
Fig. 3 shows typical trajectories of the Janus particle from t = 0 to t = 104t0 in the binary mixtures of different concentrations. The time intervals are tm = td = 500t0. The trajectories show that the particle tends to move directionally toward the particle head. Because the particle surface has a heterogeneous affinity to the components, the phase separation proceeds asymmetrically around the particle. This asymmetry of the phase separation dynamics may cause the directional motion of the Janus particle. Interestingly, the particle moves toward its head in all the mixtures. Fig. 3 also indicates that the trajectories are not completely straight. The degree of the directionality and the particle speed depend on parameters such as the average concentrations and the time intervals.Fig. 4(a) and (b) show the temporal changes in the trajectory length and velocity toward the head. Since the particle orientation, n, changes with time, the trajectory length d‖ and the velocity V‖ toward the particle orientation are calculated as
 | (16) |
| V‖(t) = V(t)·n(t). | (17) |
Positive and negative values of V‖ represent the forward and backward motions of the particle position, respectively. In Fig. 4, the time intervals are set to tm = td = 103t0. Here, each curve was obtained from one simulation run. We simulated nine average concentrations from 〈ϕ〉 = 0.1 to 0.9. In the mixtures of 〈ϕ〉 ≤ 0.1 and 〈ϕ〉 ≥ 0.8, we did not observe any drastic motion of the particle; hence, their curves have not been included in Fig. 4. Also, we did not plot the curves for the mixtures of 〈ϕ〉 = 0.4 and 〈ϕ〉 = 0.6 because they essentially demonstrate behaviors similar to those with the symmetric mixture 〈ϕ〉 = 0.5.
In Fig. 4(a), the trajectory lengths indicate stepwise motions. The particle is almost fixed in the mixing periods. However, during the demixing periods, the particle shows forward displacements. By repeating these cyclic motions, the particle continuously propels in a periodically phase-separating binary mixture. The displacement in each cycle is of the order of the particle diameter. Although the onsets of the motion in the demixing periods are not clearly seen in Fig. 4, the detailed analyses indicate that the particle does not start moving simultaneously with the quenching into the demixing states. It moves most largely after a certain incubation time ti, which is discussed later.
The cyclic behaviors are also clearly displayed in the particle velocity. After the initial incubation time in each demixing period, the particle velocity shows large positive values. After this transient deterministic motion, the velocity decreases gradually with some fluctuations. In particular, it can have negative values in more symmetric mixtures, with 〈ϕ〉 = 0.5. A similar stepwise motion is observed in a system where a Janus particle with metallic surfaces is trapped at a liquid–air interface.20 The particle's stepwise motion is due to spontaneous cyclic bursts of bubbles. In our system, the stepwise motion is due to the controlled changes of the interaction parameter.
Fig. 5(a) and (b) show the temporal changes of the average-concentration differences and the velocity intensities. They are calculated as
| 〈Δϕ2〉 = Ωt−1∫dr(ϕ − 〈ϕ〉)2, | (18) |
| 〈v2〉 = Ωt−1∫drv2, | (19) |
Fig. 6(a) and (b) show plots of the averaged speeds toward the particle head, 〈V‖〉, and perpendicular to it, 〈V⊥〉, as a function of the time interval. Here, we set tm = td for simplicity. The parallel and perpendicular velocities in the m-th cycle are defined as
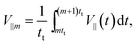 | (20) |
 | (21) |
From these, the averaged velocities 〈V‖〉 and 〈V⊥〉 are obtained by averaging M = 10 cycles as
 | (22) |
In Fig. 6(a), each curve of 〈V‖〉 is non-monotonic with maxima. The maxima peaks suggest that we can choose efficient time intervals for propelling the particle. As discussed above, the hydrodynamic flow has not developed yet in the early stage of the demixing periods. In the cases of small time intervals, the phase-separating times are too short for the hydrodynamic flows to develop sufficiently; hence, the particle is not dragged, implying that we have to maintain the system in the phase-separated state till the conclusion of the early stage te. However, for large time intervals, the average speed along the orientation becomes low. In the mixtures of 〈ϕ〉 = 0.2, 0.3, and 0.7, the parallel speed becomes largest at approximately td ≅ te. Thus, larger time intervals are not needed for propelling the particle with high speeds. However, in the symmetric mixture (〈ϕ〉 = 0.5), the parallel speed becomes largest around td ≈ 200t0, which is larger than the duration of an early stage te. This is attributed to large background flows emerging from other domains near the particle, as discussed below.
As has been shown in Fig. 3, we observe the particle fluctuations, which are characterized by the perpendicular motion 〈V⊥〉 in Fig. 6(b). The particle changes its orientation and the resulting direction of the particle motion. Thus, similar to the 〈V⊥〉 changes, the temporal changes of the orientation are also considered as a measure of the particle fluctuation. Fig. 7(a) demonstrates the autocorrelation of the orientation vector. It is calculated as
 | (23) |
 , which is calculated for M = 10 as
, which is calculated for M = 10 as | (24) |
 | (25) |
As shown in Fig. 6(b) and 7(b), both 〈V⊥〉 and  are large for large values of td, in contrast to those for small td. In the demixing periods, the phase separation proceeds throughout the bulk. The fluctuations of the particle motions and orientation stem from the hydrodynamic flows accompanied by the spontaneous growth of the domains surrounding the particle. These background flows are independent of the particle; thus, they disturb the particle motion and change its orientation. Therefore, if we use large time intervals, the particle motion is likely to deviate from the straight line along the initial orientation n(t = 0). As suggested in Fig. 6 and 7, the ratios 〈V⊥〉/〈V‖〉 and
are large for large values of td, in contrast to those for small td. In the demixing periods, the phase separation proceeds throughout the bulk. The fluctuations of the particle motions and orientation stem from the hydrodynamic flows accompanied by the spontaneous growth of the domains surrounding the particle. These background flows are independent of the particle; thus, they disturb the particle motion and change its orientation. Therefore, if we use large time intervals, the particle motion is likely to deviate from the straight line along the initial orientation n(t = 0). As suggested in Fig. 6 and 7, the ratios 〈V⊥〉/〈V‖〉 and  increased slightly with td. Also, in this sense, the large time interval is not preferred for the controlled propulsions.
increased slightly with td. Also, in this sense, the large time interval is not preferred for the controlled propulsions.
Fig. 6(a) shows that the propelling speed is higher in the symmetric mixtures (〈ϕ〉 = 0.5) than in the asymmetric mixtures. However, the fluctuations of the particle motion are also large as shown in Fig. 6(b) and 7(b). Therefore, the symmetric mixtures are not suitable for keeping the straight line motions. The particle moves largely; however, its motion easily loses the directionality with time. Furthermore, in the asymmetric mixtures, the fluctuations of the particle motion and the orientation are relatively small for the preferred td; thus, the asymmetric mixtures are more suitable to control the particle motions. We consider the mechanisms of the propelled motions in the two types of asymmetric mixtures separately.
3.3 The wettable component-rich mixture
Fig. 8 shows the patterns of the evolutions of the concentration and flow field in the mixture of 〈ϕ〉 = 0.7. As shown in Fig. 3, the particle moves rather straightforward. In the early stage of the phase separation during the demixing periods, the A-rich phase wets the half-portion of the particle and a wetting layer is formed on it. Because of the directional fluxes of the A-component toward the surface, the A-component is depleted near the outside of this first wetting layer. This accumulated layer structure is similar to the oscillating profiles of the concentration field near a flat wall or a particle with a homogeneous surface.47,48 To compensate for the depleted region, non-spherical droplets of the B-rich phase are formed as shown in Fig. 8(b). The droplets grow near the surface via coagulation and coalescence. Because the processes of coagulation and coalescence occur asymmetrically near the particle tail, the associated hydrodynamic flow likely pushes the particle toward the particle head. This process is shown in Fig. 8(c) and (d). During the phase separation, many small droplets of the B-rich phase are also formed in the bulk. They grow to their typical sizes with time via coalescence and coagulation, or evaporation and condensation processes.27,29 Around coalescing droplets, other hydrodynamic flows are induced, which disturb the particle motion. The disturbing flows are relatively weaker; thus, the particle motion remains straightforward, in contrast to that in the symmetric mixtures.The mixture of 〈ϕ〉 = 0.8 should be phase-separated at equilibrium, when χ = χd(= 2.7). However, because the nucleation rate is very small, the time intervals we employed (td ≤ 103t0) were not sufficient to induce the phase separation. Thus, we did not observe any motion of the Janus particle in the mixture of 〈ϕ〉 ≥ 0.8.
3.4 The wettable component-deficient mixture
The motions in the B-rich mixtures are highly directed toward the particle orientation as shown in Fig. 3 and 6. Fig. 9 shows the pattern evolutions of the concentration and flow field in the mixture of 〈ϕ〉 = 0.3. In the early stages of the phase separation, a cap-shaped domain of the A-rich phase emerges from the wettable portion of the particle surface. It covers a large amount of the interfacial area, although its volume is not so large. Then, it tends to change its shape to a sphere for reducing the interfacial energy after the early stage of the phase separation. This process induces a pumping hydrodynamic flow around the tail of the Janus particle and the resulting pumping flow pushes the particle toward the head as shown in Fig. 9(c) and (d). The decay time of the localized pumping flow, th, is estimated as th ≈ ηa/σ, where σ is the interface tension.The mixtures of 〈ϕ〉 = 0.3 and 0.7 have the same stability for the phase separation in the bulk. Because the tail of the particle prefers component A, this asymmetry leads to the difference in the particle motions between the 〈ϕ〉 = 0.3 and the 〈ϕ〉 = 0.7 cases. Fig. 6(a) shows that the highest parallel speed in the 〈ϕ〉 = 0.7 mixture is approximately twice of that in the 〈ϕ〉 = 0.3 case. However, Fig. 6(c) indicates that the ratio 〈V⊥〉/〈V‖〉 in the 〈ϕ〉 = 0.7 case is also approximately twice of that in the 〈ϕ〉 = 0.3 case at the maximum parallel speed. Also, Fig. 6(a) shows that the standard deviations of V⊥m for the 〈ϕ〉 = 0.3 mixture are smaller than those for the 〈ϕ〉 = 0.7 case. The particle is suggested to move more steadily and smoothly in the 〈ϕ〉 = 0.3 mixture. Thus, we conclude that the B-rich mixtures are more preferred to induce more straight motions.
The stability for the bulk phase-separation in the mixture of 〈ϕ〉 = 0.2 is the same as that in the 〈ϕ〉 = 0.8 case. However, we have not observed any motions in the 〈ϕ〉 = 0.8 mixture, although the particle moves straightforward in the 〈ϕ〉 = 0.2 case. This difference suggests that the domain formation in the mixture of 〈ϕ〉 = 0.2 is attributed to the heterogeneous nucleation at the particle surface.49 As the average concentration approaches the binodal line, the thermal nucleation rate in the bulk is strongly decreased.29 However, the rate of heterogeneous nucleation on the wetting surface is large enough to induce it during our demixing periods. Because the number of surrounding droplets is decreased, particle motion becomes more straightforward in more asymmetrically B-rich mixtures (see the case of 〈ϕ〉 = 0.2 in Fig. 6).
In both cases, the hydrodynamic flow around the particle tail pushes the particle toward the head. In this sense, our particle motion may be compared to that of a pusher in the active matter field.11 However, more detailed analyses on the flow pattern are required before this conclusion can be derived.
3.5 Roles of mixing periods
Fig. 4(a) and (b) indicate that the particle does not show any large changes of the position and orientation during the mixing periods. This is because diffusion dominates the mixing but it does not contribute to the particle motion. However, here, we should note that the mixing periods are very important for resetting the binary mixtures. As noted above, the hydrodynamic flow caused by the interface tension is large in the demixing periods, whereas it is small in the mixing periods. This difference in the hydrodynamic flows present between the mixing and demixing periods induces the continuous propelled motion of the Janus particle.In the above simulations, we set tm = td for simplicity. However, considering whether this mixing interval is sufficient to reset the binary mixtures is important. The characteristic length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) of the phase-separated domain increases with time algebraically. In the symmetric mixture, a bicontinuous pattern is formed and the domain grows obeying28
of the phase-separated domain increases with time algebraically. In the symmetric mixture, a bicontinuous pattern is formed and the domain grows obeying28
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (t) ≈ cσt/η. (t) ≈ cσt/η. | (26) |
However, in the asymmetric mixtures, the minority phase forms droplets. The droplets grow with time via coalescence and coagulation as27,29
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (t) ≈ c′(Tt/η)1/3. (t) ≈ c′(Tt/η)1/3. | (27) |
Here, c and c′ are non-dimensional numbers, which depend on the volume fractions. Then, the characteristic length at the ends of the demixing periods would be given by ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (td). If the volume fraction is quite small, the droplets grow via the nucleation and growth mechanism, and the above scaling relationship (eqn (27)) is replaced by
(td). If the volume fraction is quite small, the droplets grow via the nucleation and growth mechanism, and the above scaling relationship (eqn (27)) is replaced by ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (t) ∝ (L0σt)1/3. Because its growth exponent is the same as that of eqn (27), we consider only cases described by eqn (27) above.
(t) ∝ (L0σt)1/3. Because its growth exponent is the same as that of eqn (27), we consider only cases described by eqn (27) above.
In the mixing periods, these phase-separated domains should be dissolved into a homogeneous state via diffusion. The diffusion time is estimated as tdif ∼ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (td)2/Dm, where Dm = 2L0(χsp − χm)/T is the diffusion constant at χ = χm and χsp is the interaction parameter at the spinodal point. When the time interval of the mixing period is longer than the diffusion time, the system can be reset for the next demixing period. However, if tdif ≪ tm, the mixtures show non-steady states37–40 and the particle would not move directionally. The condition tdif ≪ tm is rewritten as tm ≫ (T/η)2/3td2/3/Dm for the droplet patterns and tm≫ (σ/η)2td2/Dm for the bicontinuous patterns. If we set td ≫ (T/η)2Dm−3, we have tdif ≪ td in the asymmetric mixtures. Therefore, long annealing times for the mixing are not required. The total time interval tt = tm + td can be reduced to tt ≅ td.
(td)2/Dm, where Dm = 2L0(χsp − χm)/T is the diffusion constant at χ = χm and χsp is the interaction parameter at the spinodal point. When the time interval of the mixing period is longer than the diffusion time, the system can be reset for the next demixing period. However, if tdif ≪ tm, the mixtures show non-steady states37–40 and the particle would not move directionally. The condition tdif ≪ tm is rewritten as tm ≫ (T/η)2/3td2/3/Dm for the droplet patterns and tm≫ (σ/η)2td2/Dm for the bicontinuous patterns. If we set td ≫ (T/η)2Dm−3, we have tdif ≪ td in the asymmetric mixtures. Therefore, long annealing times for the mixing are not required. The total time interval tt = tm + td can be reduced to tt ≅ td.
4 Summary and remarks
We proposed a possible mechanism of propelled motions of Janus particles in periodically phase-separating binary mixtures using numerical simulations. Because the particle has an asymmetric surface in wettability, phase separation proceeds heterogeneously around the particle. The resulting asymmetric hydrodynamic flow leads to directional motions of the particle. After a usual one-step quench, the directional motion slows down and will stop eventually. By changing the interaction parameter, the phase-separated system recovers to a one-phase mixing state. Therefore, under periodic changes of the interaction parameter, we can induce a continuous motion along the particle orientation.We found that the particle propels more directionally in asymmetric binary mixtures. In symmetric mixtures, the hydrodynamic flow emerging from other domains surrounding the particle is so large that it disturbs the directional motions of the Janus particle. We also found that the propelling speed and the directionality depend on the frequency of the change in the interaction parameter. In the cases of short time intervals, the hydrodynamic flow does not develop well and it cannot drive the particle. However, in the cases of long time intervals, the hydrodynamic flows from the surrounding domains disturb the directional motion. We can efficiently move the particle in the intermediate time intervals, which are comparable to the characteristic time of the spinodal decomposition or nucleations in the early stage of the phase separation. The pumping hydrodynamic flow that is localized around the particle decays with the relaxation time th. th is of the order of ηa/σ. The interval of the demixing period should be larger than ti + th. However, the large time interval for the demixing periods leads to the loss of the directionality as discussed above. Thus, the most efficient time interval would be td ≈ ti + th. The displacement of the particle in each cycle is of the order of the particle diameter. Then, the maximum particle speed could be increased to V ∼ a/(ti + th).
Unfortunately, the simulations performed in this study are limited owing to the numerical costs. We need to deepen our understanding of the propelled motions of such a Janus particle, and hope that we will present a report on them in the near future. We make some critical remarks to improve our study as follows.
(1) In this article, we show only the simulations with the particle diameter 2a = 12d. Here, d is comparable to the correlation length, hence our particle is rather small. In actual phase-separating mixtures, such small particles would show drastic Brownian motions and the directional motions we discovered might be smeared out. Our preliminary simulations with larger particles indicated that the displacement of the particle in each cycle is of the order of the particle size. In other words, they suggest that the particle speed can be increased linearly with its size by employing appropriate temporal changes of the interaction parameter.
(2) The wettability of our particle changes smoothly on the surface (see eqn (6)). However, an actual Janus particle usually has two distinct surfaces and the wettability changes abruptly at the equator. Instead of eqn (6), we performed some simulations with an alternate surface function given by
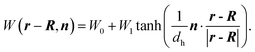 | (28) |
Here, dh is introduced to avoid the singularity at the equator of the Janus particles. A particle described by eqn (28) with small dh would behave more realistically. The preliminary simulations using eqn (28) with dh = 0.05 demonstrated essentially similar results to those using eqn (6). This similarity can be derived from the fact that our particle motions are induced by the secondary effect of the phase separation, i.e., the asymmetric growth of the hydrodynamic flow around the particle. Thus, we consider that our findings are robust for the heterogeneous surface pattern. To improve the efficiency of the particle motions, simulations with a variety of surface structures would be interesting.
We consider that the propelled motions in this article are robust also for the details of the free energy function. We numerically confirmed that the particle moves in the same way in binary mixtures described by the Ginzburg–Landau free energy instead of eqn (4).
(3) The easiest method to realize our findings in actual systems would be a direct observation of them with an optical microscope equipped with a temperature control hot stage.40 However, changing the temperature with high frequencies might be experimentally difficult because the thermal diffusion constant is finite. To induce a high speed propulsion, large differences of the temperature from the binodal point are preferred for both the mixing and demixing periods. However, for deep quenches in the demixing periods, the incubation times for the phase separation would be reduced up to microscopic timescales.
Pressure control50 is considered to be an alternative method to induce continuous propulsions. The combination of temperature control and illumination-induced phase separation would also be able to induce periodic phase separation with high speeds.23,24 In this study, we employ only the square waves of the interaction parameter to induce periodic phase separation. We should perform more simulations with other types of wave functions to find more efficient propulsion schemes.
(4) In our model, particle motion is caused by the hydrodynamic flow. However, studying the behaviors of a Janus particle in solid mixtures where v = 0 would also be interesting. In such mixtures, the particle motion is caused by the thermodynamic forces (∝∇δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) /δϕ). Because the coarsening behavior of the phase separation domain pattern depends on the fluidity of the mixtures (see eqn (26) and (27)), whether our findings are applicable to the solid mixture is not trivial.
/δϕ). Because the coarsening behavior of the phase separation domain pattern depends on the fluidity of the mixtures (see eqn (26) and (27)), whether our findings are applicable to the solid mixture is not trivial.
(5) Because the intensity of the hydrodynamic flow is proportional to 1/η0 (see eqn (7)), we expected that the particle speed is also proportional to 1/η0. However, our simulations with different solvent viscosities indicated that V‖ is approximately proportional to 1/η0 in symmetric mixtures, whereas it is approximately independent of η0 in asymmetric mixtures (not shown here). This is because the rate-limiting process of the phase separation in asymmetric mixtures is the nucleation and growth of the minority phase; their rates are dominated by the diffusion constant, not the solvent viscosity. Thus, the results reported in this article are not quantitatively universal. They will depend on the system parameters such as the solvent viscosity and interface tension. Although we consider that the propelled motion in periodic phase separation can be qualitatively realized in actual systems, we have to perform more simulations with wide ranges of system parameters.
For simplicity, we also assumed a constant viscosity η0 in the surrounding fluids. However, the solvent viscosity is generally a function of the local composition. As noted above, the particle speed depends on the solvent viscosity in symmetric mixtures; thus, studying the influences of the viscosity difference would also be interesting.
A Time development of total free energy
The total free energy including the kinetic energy is considered. Using eqn (2), it is given by | (29) |
Its time development is
 | (30) |
After some calculations, we obtain
 | (31) |
 | (32) |
 | (33) |
Then, we finally obtain
 | (34) |
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) decreases with time only via diffusion and viscous dissipation.
decreases with time only via diffusion and viscous dissipation.
Acknowledgements
The authors thank H. Tanaka for his helpful comments. We started this work following his original ideas on this research topic. This work was supported by KAKENHI (no. 24540433, 23244088 and 25000002) and the JSPS Core-to-Core Program “International research network for non-equilibrium dynamics of soft matter”. The computational work was performed using the facilities at the Supercomputer Center, Institute for Solid State Physics, University of Tokyo. This research was also partly supported by CREST, JST.References
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. St. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed.
- W. F. Paxton, S. Sundararajan, T. E. Mallouk and A. Sen, Angew. Chem., Int. Ed., 2006, 45, 5420–5429 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. Roper, M. L. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- J. R. Howse, R. A. L. Jones, A. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
- R. Laocharoensuk, J. Burdick and J. Wang, ACS Nano, 2008, 5, 1069–1075 CrossRef PubMed.
- S. Sundararajan, P. E. Lammert, A. W. Zudans, V. H. Crespi and A. Sen, Nano Lett., 2008, 8, 1271–1276 CrossRef CAS PubMed.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef.
- R. Kapral, J. Chem. Phys., 2013, 138, 020901 CrossRef PubMed.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS.
- D. Helding, Rev. Mod. Phys., 2001, 73, 1067–1141 CrossRef.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. Aditi Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef PubMed.
- M. E. Cates, Rep. Prog. Phys., 2012, 75, 042601 CrossRef CAS PubMed.
- M. Schliwa and G. Woehlke, Nature, 2003, 422, 759–765 CrossRef CAS PubMed.
- K. Nagai, Y. Sumino, H. Kitahata and K. Yoshikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 065301(R) CrossRef.
- S. Yabunaka, N. Yoshinaga and T. Ohta, J. Chem. Phys., 2012, 136, 074904 CrossRef CAS PubMed.
- R. Golestanian, T. B. Liverpool and A. Ajdari, New J. Phys., 2007, 9, 126 CrossRef.
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef.
- N. K. Reddy and C. Clasen, Korea Aust. Rheol. J., 2014, 26, 73–79 CrossRef PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef.
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810–8815 RSC.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- J. W. Cahn, J. Chem. Phys., 1977, 66, 3667–3672 CrossRef CAS PubMed.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- K. Binder and D. Stauffer, Phys. Rev. Lett., 1974, 33, 1006–1009 CrossRef.
- E. D. Siggia, Phys. Rev. A, 1979, 20, 595–605 CrossRef CAS.
- A. Onuki, Phase Transition Dynamics, Cambridge Unversity Press, Cambridge, 2002 Search PubMed.
- H. Tanaka, A. J. Lovinger and D. D. Davis, Phys. Rev. Lett., 1994, 72, 2581–2584 CrossRef CAS.
- V. V. Ginzburg, G. Peng, F. Qiu, D. Jasnow and A. C. Balazs, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4352–4359 CrossRef CAS.
- T. Araki and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061506 CrossRef.
- M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138 RSC.
- B. P. Binks and P. D. I. Fletcher, Langmuir, 2001, 17, 4708–4710 CrossRef CAS.
- N. Glaser, D. J. Adams, A. Bòker and G. Krausch, Langmuir, 2006, 22, 5227–5229 CrossRef CAS PubMed.
- M. Huang, Z. Li and H. Guo, Soft Matter, 2012, 8, 6834–6845 RSC.
- A. Onuki, Prog. Theor. Phys., 1982, 67, 1740–1755 CrossRef.
- A. Onuki, Phys. Rev. Lett., 1982, 48, 753–756 CrossRef CAS.
- M. Joshua, W. I. Goldburg and A. Onuki, Phys. Rev. Lett., 1985, 54, 1175–1177 CrossRef CAS.
- H. Tanaka and T. Sigehuzi, Phys. Rev. Lett., 1995, 75, 874–877 CrossRef CAS.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS.
- H. Tanaka and T. Araki, Chem. Eng. Sci., 2006, 61, 2108–2141 CrossRef CAS PubMed.
- T. Araki and H. Tanaka, J. Phys.: Condens. Matter, 2008, 20, 072101 CrossRef.
- A. Furukawa, A. Gambassi, S. Dietrich and H. Tanaka, Phys. Rev. Lett., 2013, 111, 055701 CrossRef.
- F. H. Harlow and J. D. Welch, Phys. Fluids, 1965, 8, 2182–2189 CrossRef PubMed.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 1998, 81, 389–392 CrossRef CAS.
- H. Tanaka and T. Araki, Europhys. Lett., 2000, 51, 154–160 CrossRef CAS.
- A. Karim, J. F. Douglas, G. Nisato, D.-W. Liu and E. J. Amis, Macromolecules, 1999, 32, 5917–5924 CrossRef CAS.
- D. Winter, P. Virnau and K. BInder, Phys. Rev. Lett., 2009, 103, 225703 CrossRef.
- M. Shibayama, K. Isono, S. Okabe, T. Karino and M. Nagao, Macromolecules, 2004, 37, 2909–2918 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |