Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Topological energy storage of work generated by nanomotors
Fabian
Weysser
a,
Olivier
Benzerara
a,
Albert
Johner
ab and
Igor M.
Kulić
*a
aInstitut Charles Sadron, CNRS-UdS, 23 Rue du Loess, BP 84047, 67034 Strasbourg Cedex 2, France. E-mail: kulic@unistra.fr
bDepartment of Physics, Sejong University, Seoul 143-743, South Korea
First published on 8th December 2014
Abstract
Most macroscopic machines rely on wheels and gears. Yet, rigid gears are entirely impractical on the nano-scale. Here we propose a more useful method to couple any rotary engine to any other mechanical elements on the nano- and micro-scale. We argue that a rotary molecular motor attached to an entangled polymer energy storage unit, which together form what we call the “tanglotron” device, is a viable concept that can be experimentally implemented. We derive the torque–entanglement relationship for a tanglotron (its “equation of state”) and show that it can be understood by simple statistical mechanics arguments. We find that a typical entanglement at low packing density costs around 6kT. In the high entanglement regime, the free energy diverges logarithmically close to a maximal geometric packing density. We outline several promising applications of the tanglotron idea and conclude that the transmission, storage and back-conversion of topological entanglement energy are not only physically feasible but also practical for a number of reasons.
I. Introduction
Molecular machines are everywhere around us and run our lives on the sub-cellular scale. Throughout evolution, Nature has come up with many practical and robust nano-machine designs, from DNA copying and protein producing machines to muscle driving nano-scale walkers. To mimic Nature and maybe even outperform it in some tasks seems to be humanity's undeclared goal in this century. What was science-fiction a decade ago takes shape in the physical reality as we speak. However, building functional, task performing nano-assemblies with comparable features as macro-scale machines still meets large obstacles. In particular, at the present stage it is virtually impossible to apply our machine building intuition gathered on the macroscopic scale. Interlocked motors with gears and wheels, connected with force transmitting chains and belts form the practical basis for most large scale mechanical devices. And yet they appear like a very awkward, hard to realize way to build nano-machines in the fluctuating realm of the soft and small.While the motif of a classical rotary wheel is rare in Nature,1 it is occasionally utilized in some branches of life. For instance, bacteria's rotary flagellar engines enable them to move through their fluid environments. However, to benefit from their flagellar rotor the bacteria had to come up with a clever and efficient way to couple it to their environment. In their case, the task is fulfilled by a sophisticated filamentous helical coil – the flagellum. The latter acts as a screw propeller, transmitting the motor rotation into translation and propulsion through the surrounding viscous fluid.
Thus, we could conclude that the problem in utilizing wheels, gears and rotors on the nano-scale in Nature is not the rotary engine mechanism itself. The difficulty lies rather in establishing an efficient and flexible transmission mechanism of the rotary movement to its surroundings.
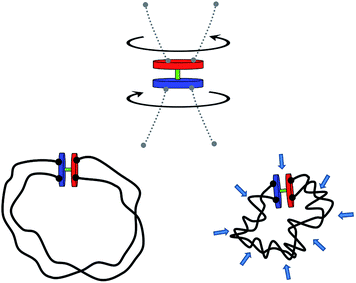
In this report, we propose such a transmission mechanism that could be beneficial on the nano-scale. In particular, we will discuss a simple, generic way to implement a coupling of virtually any existing rotary nano- and microengines to their surroundings. The central idea that we want to advance is that of torque transmission by the process of topological entanglement of polymer chains attached to the active rotary device (motor), cf., Fig. 1. Such a motor equipped with a topological energy storage device we will in the following – alluding to the idea of entanglement – simply call the “tanglotron”.
The concept of the tanglotron is related to the previously proposed idea of molecular motors operating in closed ring geometries2 combined with the natural idea of attaching polymer side chains for topologically trapping and preserving motor rotations. Numerous rotary engines exist in Nature3 with the most prominent examples being ATP-synthase,4,5 the flagellar motor of bacteria6 and various DNA-topoisomerases.7 Several artificial directed rotors based on various operational principles have been developed.3,8–11 New rotary engine designs continue to be conceptually proposed and still light up our imagination in nano-engineering.2,12
The circularly rotating geometry of these numerous nano-engines is particularly suitable for generating entanglements and contraction in gel like materials. The effect of entanglement on the visco-elastic behavior of polymer gels and networks is a classical problem in polymer science.13–15 In a typical polymer melt, passively responding to sudden external strains, polymer entanglements are created and destroyed in a dynamic fashion, by the process of polymer “reptation”. It is well-established that during mechanical shearing of a dense melt of long polymers, the relaxation of transient polymer entanglements is also the main contribution to dynamic stress relaxation.13–15 In this sense the concept of dynamic, transient entanglements is at the core of polymer physics.
The problems of fixed (permanent) topological entanglements have also attracted much theoretical interest. Simplified two dimensional models for the entanglements of flexible polymer chains have been developed in the past16–19 (reviewed in ref. 20) as well as more realistic but analytically less tractable 3 dimensional models have been considered.21,22 Motivated by single DNA molecule probing experiments23 applying torques on the molecular scale by magnetic tweezers, the problem of DNA supercoiling,24 DNA braiding26 and its untwisting25 has been studied theoretically.
The idea of actively utilizing gel's permanent topology to tune and tweak its mechanical properties reaches quite far into the past. “Topological gels” containing sliding link pulley-like mechanisms were envisioned theoretically,13,27 long before their experimental manufacturing (chemical synthesis) could be realized in practice.28
Since the advent of DNA based life, living organisms naturally utilize the principle of topological energy storage.7,29,30 In particular, DNA double strand twisting and supercoiling are known to energetically shift the threshold for DNA opening and gene transcription as well as to provide an additional energy source for genome folding and compaction in prokaryotic organisms like bacteria. Besides DNA, other natural filaments, like single actin rings, are known to display similar supercoiling behavior.31 Beyond its obvious usefulness in natural processes, DNA supercoiling has also been suggested as a mechanism for processing information and performing simple computational tasks.32
In this article opening the topic, we will focus on some central physical features associated with the tanglotron. In particular, we will study the problem of energy storage in the form of topological polymer-entanglements. We will derive the “equation of state” of the tanglotron and show that its torque-entanglement relationship can be understood by simple geometrical and statistical mechanics arguments. We conclude the article by outlining several benefits of actually building a tanglotron device, including possible applications from artificial muscles to nano-actuators for DNA nano-assemblies.
II. Topological battery: storage of entanglement energy
Let us consider a synthetic system shown in Fig. 1, consisting of an active rotary motor unit and two chains connecting the stator and the rotor of the device. In this section, we will first focus on the conceptual questions resulting from Fig. 1. These will be:When the motor unit operates by n turns how much energy is stored in its polymer chains?
How many topological entanglements (links) can be injected at a given maximal motor torque?
By how much do the chains of length L collapse when loaded with n entanglements?
Is there an upper topological storage capacity of the chains and how many topological links do fit inside for a given chain length L?
A. Tanglotron simulated
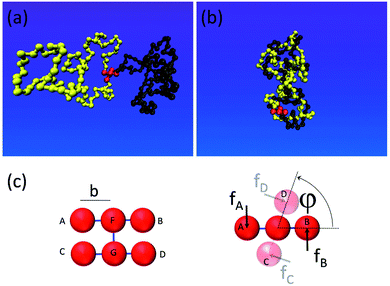
To gain insight into the system shown in Fig. 1, we set up a molecular dynamics simulation implementing the motor unit (red) and the topological container consisting of two long flexible polymer chains. The monomers within the chains interact purely repulsively by a Lennard-Jones short-range excluded volume interaction. The latter is strong enough to prevent them from crossing through each other on relevant simulation timescales. Thus, entanglements, once formed by motor rotation, are unable to dissipate by simple chain crossing. The motor unit consists of 6 beads connected as shown in Fig. 2c: the rotor and the stator both consist of 3 beads and are driven by a quadruplet of forces acting at beads A, B, C and D perpendicular to the motor axis F–D as well as to the stator (C–G–D) and the rotor axes (A–F–B).33 To ensure the rigid geometry of the motor, an additional angular stiffness term is added ensuring the orthogonality of the axis FG on the stator and rotor.When acted upon the forces f, as shown in Fig. 2c, such a configuration is both net force-free and (external) torque free. And yet the device generates a relative internal torque M = fb between its stator and rotor part. The mutual excluded volume interactions of the 6 motor beads are inactivated to prevent steric hindrance of the stator with rotor and to allow a free motor rotation. The 6 rotor beads only interact with the chain particles to prevent accidental chain disentanglement.
The simulated tanglotrons with varying chain lengths of N = 100, 200 and 400 particles per chain show an interesting trend, cf.Fig. 3. When actuated even with moderate torques M of around 2kT, the conformation of the chains starts to change in a dramatic manner. Their radius of gyration Rg(M) consistently collapses from their initial unperturbed value Rg0 to a plateau value Rg∞ ≈ Rg0/2. The threshold torque Mcrit ≈ 2kT leads to a strong chain entanglement which brings the chains closer together, leading to an effective compression of the tanglotron unit.
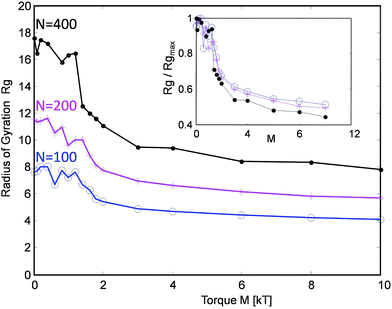 | ||
| Fig. 3 The radius of gyration of the tanglotron particle as a function of the maximal torque generated by the motor for three different chain lengths. | ||
The chain collapse is brought about by the increase of the mean motor angle 〈φ(M)〉 and the associated inter-chain linking number 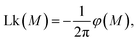 cf.Fig. 4. The latter grows with the increasing motor torque in an interesting manner. At small torques up to M ≈ 1kT, there is little or no change of Lk. At slightly larger torques up to about 5kT, the linking number starts to grow quickly. At larger values, it saturates to a plateau value Lkmax. The evolution of Lk for different chain lengths scales linearly with the maximal plateau value, which itself is proportional to the total chain length N, as further discussed below (cf. also Fig. 7).
cf.Fig. 4. The latter grows with the increasing motor torque in an interesting manner. At small torques up to M ≈ 1kT, there is little or no change of Lk. At slightly larger torques up to about 5kT, the linking number starts to grow quickly. At larger values, it saturates to a plateau value Lkmax. The evolution of Lk for different chain lengths scales linearly with the maximal plateau value, which itself is proportional to the total chain length N, as further discussed below (cf. also Fig. 7).
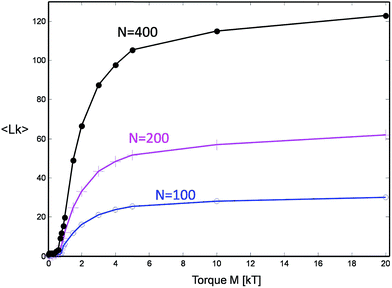 | ||
| Fig. 4 The number of stored topological links (linking number Lk) for three chain lengths as a function of applied motor torque. | ||
Interestingly, the chains collapse quickly to about 50% of their size even at low torques M ≈ 2kT and one sees very little evolution in size beyond that. At the same time, the entanglement Lk (cf.Fig. 4) continues to grow up to M ≈ 10kT. This indicates that already in the weak entanglement regime the chains are strongly compacted on the large scale. Beyond that the process of compaction is more subtle, happens on smaller scales down to the monomer size, but reflects in Rg only very weakly.
B. Stored free energy
By inverting the M vs. Lk(M) relationship, we can extract the effective free energy of the system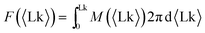 | (1) |
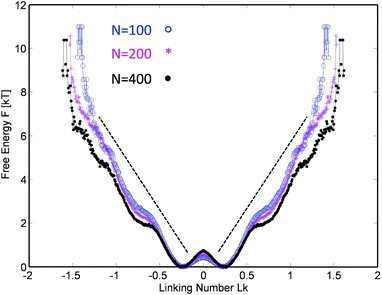
This procedure is equivalent to performing a Legendre transform on the Gibbs potential 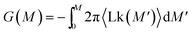 and applies where the fluctuations of Lk are small or negligible. We cross-check it in the appendix against a direct measure of the free energy from the probability distribution of Lk for small Lk. The result plotted in Fig. 5 shows a remarkable behavior. Most notably, at small Lk the free energy is proportional to the number of links. Due to symmetry, the free energy is the same for the positive and negative linking numbers of the same magnitude. This symmetry and the linear (rather than a quadratic) growth slightly away from zero lead to an apparent non-analytic cusp of F(Lk) at Lk = 0.
and applies where the fluctuations of Lk are small or negligible. We cross-check it in the appendix against a direct measure of the free energy from the probability distribution of Lk for small Lk. The result plotted in Fig. 5 shows a remarkable behavior. Most notably, at small Lk the free energy is proportional to the number of links. Due to symmetry, the free energy is the same for the positive and negative linking numbers of the same magnitude. This symmetry and the linear (rather than a quadratic) growth slightly away from zero lead to an apparent non-analytic cusp of F(Lk) at Lk = 0.
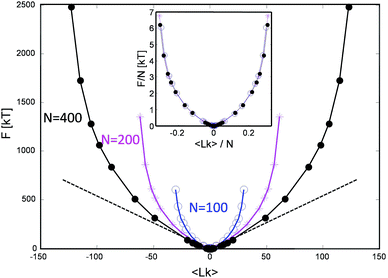 | ||
| Fig. 5 The stored entanglement free energy as a function of the number of stored topological links/turns (linking number Lk) for three chain lengths. | ||
The result is reproducible and very similar for all chain lengths. What does this mean? The result indicates that at low linking number density, the topological links behave as discrete particle-like entities, with a certain chemical potential μ = F(1) for their injection. This leads to a formal cusp of the free-energy extrapolated towards Lk = 0. That observation agrees with the common polymer-physics intuition that, at low density, each entanglement costs a small amount of energy comparable to kT. This very reasonable assumption common in the literature13–15 comes from the fact that all free energies are entropic in nature and the only energy scale is the thermal one. However there could be a geometric prefactor to this energy scale. Indeed from the free energy slope at Lk = 0, we find μ ≈ 6kT i.e. each complete topological link (at low density) costs roughly that amount. This value of μ is compatible with the direct measure of the free energy at low link presented in the Appendix.
Interestingly, in the large Lk regime, after the initial linear growth, F(Lk) begins to shoot up steeply. This behavior can be understood as densely packed links start to strongly interact with each other. Eventually the chains are expected to reach a densest topological packing state, corresponding to roughly ≈4 beads per turn on each chain. This result is analogous to previous computer studies on the optimal packing of inflating torus knots39 as well as mechanical 2 ply structures40 at vanishing temperature. There, as in our case, the geometry and the excluded volume of the chains prevent any further topological packing beyond the densest packing limit (cf. below).
III. Tanglotron's equation of state
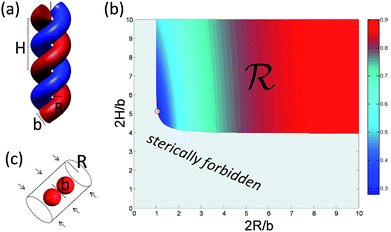
To understand deeper the high entanglement regime, which is most relevant for free-energy storage, let us take the simplest phenomenological approach and consider a tightly packed helix of radius R and a pitch height H shown in Fig. 6a.The helix with the inclination angle 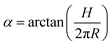 has a length per turn
has a length per turn 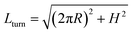 and the linking number per monomer is given by:
and the linking number per monomer is given by:
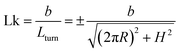 | (2) |
In the following, we conveniently scale the radius and pitch 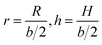 by the actual radius of the monomer b/2. In Fig. 6b, we have evaluated numerically the region of geometrically admissible helix pitches and radii satisfying the condition of mutual non-penetration of the two chains. We obtain that the state with maximum packing density (the bluest region) has h = h0 ≈ 5.3 and r = r0 ≈ 1.06. The maximal linking number density resulting from these values is |Lkmax|/N ≈ 0.25. This energy minimizing state would be ideally assumed for a perfect (double polymer) helix at zero temperature T = 0 if fluctuations can be neglected.
by the actual radius of the monomer b/2. In Fig. 6b, we have evaluated numerically the region of geometrically admissible helix pitches and radii satisfying the condition of mutual non-penetration of the two chains. We obtain that the state with maximum packing density (the bluest region) has h = h0 ≈ 5.3 and r = r0 ≈ 1.06. The maximal linking number density resulting from these values is |Lkmax|/N ≈ 0.25. This energy minimizing state would be ideally assumed for a perfect (double polymer) helix at zero temperature T = 0 if fluctuations can be neglected.
However at any finite temperature, the mutual entropic confinement effects of the two polymer chains become the dominant effect, preventing further entanglement before the contact is established. In the limit of a tightly packed helical arrangement, the chain monomers start to dramatically loose their translational entropy. In particular, the motions in the radial direction of the helical arrangement become strongly prohibited by the geometric constraints. To model this behavior let us consider the twisting energy per monomer E = Etot/N that can be expressed as
| E = −2πMLk. | (3) |
To obtain the Gibbs potential G(M) (Gibbs free energy), ideally, we should integrate the partition function over all possible configurations weighted according to their Lk. This procedure is not analytically tractable due to the subtle nature of the linking number which is a double integral over the two chains in the most general case. Instead we chose to integrate over all possible helices, whose Lk obeys a simple expression. This is physically justified as at high torque helices are indeed the preferred shapes.
In the limit of strong entanglement, each monomer starts to behave as an independent entity and we can approximate the Gibbs potential per monomer by
Gmon(M) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zmon Zmon | (4) |
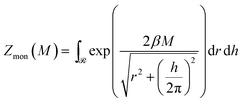 | (5) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) of the configurational space where the excluded volume constraint is satisfied (cf.Fig. 6b). For large M, the main contribution to the partition function comes from a certain corner of the helix configurational space with the lowest energy E(h, r) (cf. circle in the blue region of Fig. 6b). There the partition function can be evaluated numerically, but it is conceptually more illuminating to estimate it by an approximate argument. For that we replace the exact boundary of the region
of the configurational space where the excluded volume constraint is satisfied (cf.Fig. 6b). For large M, the main contribution to the partition function comes from a certain corner of the helix configurational space with the lowest energy E(h, r) (cf. circle in the blue region of Fig. 6b). There the partition function can be evaluated numerically, but it is conceptually more illuminating to estimate it by an approximate argument. For that we replace the exact boundary of the region ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) by its two asymptotes given by r = 1 and h = 4, corresponding to two extreme types of self-contacting helices with R = b/2, H ≫ R and H = 2b, H ≪ R, respectively. For large torques βM ≫ 1, we expand the exponent in Zmon
by its two asymptotes given by r = 1 and h = 4, corresponding to two extreme types of self-contacting helices with R = b/2, H ≫ R and H = 2b, H ≪ R, respectively. For large torques βM ≫ 1, we expand the exponent in Zmon![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) around these values using h = 4 + δh and r = 1 + δr with δh, and δr ≪ 1. In this way, we easily obtain
around these values using h = 4 + δh and r = 1 + δr with δh, and δr ≪ 1. In this way, we easily obtain| Zmon(M) ∝ (βM)−2e2πγβM | (6) |
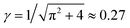 . The Gibbs potential G(M) (Gibbs free energy) is then given by
. The Gibbs potential G(M) (Gibbs free energy) is then given byGmon(M) ≈ −2πMγ + 2kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Mβ) ln(Mβ) | (7) |
The mean linking number per monomer 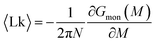 is then given by the elegant expression
is then given by the elegant expression
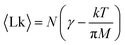 | (8) |
The first term γ is the maximal entanglement packing density while the second term is the “squeeze-out” of monomer's 2 degrees of freedom (H and R) by the applied torque. In our simple approximate model γ = γsimple = 0.27 but in principle this value can be different, in fact larger, due to more optimal packing possible for two chains. If we allow for a slight adjustment of the γ term due to such effects, we obtain very good agreement with the simulation data, cf.Fig. 7.
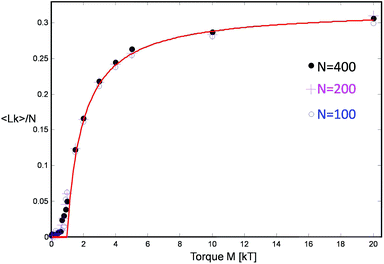 | ||
| Fig. 7 The linking number Lk per unit length for three chain lengths as a function of applied motor torque and the comparison with the theoretical model (red curve) cf.eqn (8). | ||
The somewhat higher packing density of γ = 0.32 likely originates from a symmetry breaking along the helix similar to the one found by Pieranski for extremely knotted torus knots.39 Indeed for very large torques M > 10kT, this type of dense zig-zag helix arrangement, where strand 1 first wraps around 2 one round, while 2 remains straight, and then they switch roles, can be also observed in our simulation snapshots, cf.Fig. 2b.
An approximate value of the free energy F(Lk) which is a function of Lk (rather then applied torque) can be obtained by Legendre transform of the Gibbs potential and reads
 | (9) |
A simple estimate of the free energy density stored in the tanglotron (over a volume Rg3) for torques M of order of 10kT, for the chain-lengths considered here (N = 100–400), leads to typical values between 100 MPa and 1 GPa. The typical elastic moduli should be well beyond those of typical polymer gels but in the same range and comparable to those of proteins. Injecting entanglements even at moderate motor torques should therefore lead to a strong rigidification of the tanglotron's chains, comparable to those introduced in peptides by non-covalent bonds.
A. The scaling picture: the blob double helix
The upper considerations in the high entanglement regime suggest a surprisingly simple picture of how the entanglement energy is stored for low entanglement densities. If we look back to the inset of Fig. 5, where the entanglement density (per monomer) and free energy per monomer are plotted for three chain lengths, we can make an interesting observation. For all entanglement densities, the energy densities collapse onto a single curve. That is, the monomers seem to behave on average as identical entities with the same energy content per monomer, with no signs of explicit system size dependence. The corresponding free energy is extensive in the system size N.This is an indication that we could make a simple blob-argument even for a small entanglement case by replacing what were single beads with size b in the high-entanglement limit by blobs of size l > b carrying each ∼kT of energy. A chain of such l− blobs is now packed in such a manner to mimic the previous case of the densest helical packing of single beads in the high-entanglement limit. To inject a single entanglement, we need then roughly ∼3–4 blobs per chain, which amounts to a free energy cost of 6–8kT per single entanglement. This expectation is in surprisingly close agreement with the chemical potential μ ≈ 6kT per entanglement estimated from the simulations. This suggests that the simple “blob-helix” model predicts the behavior of the free energy even for moderate entanglement.
The observation that at intermediate densities a single entanglement costs a fixed amount of energy deserves a few comments. Note that a similar behavior of the free energy as a function of Lk, F(Lk) ∝ |Lk|, has been observed by Marko22 for two entangling mutually pinned DNA rings with excluded volume. A related study by Walter et al.21 on flexible chains (with excluded volume) wrapping around a bar also finds a transition from a Gaussian F(Lk) ∝ Lk2 scaling to a weaker power law F(Lk) ∝ |Lk|α with α not far from unity and with a typical cross-over occurring at Lk ∼ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N. In our current case, such Gaussian behavior is difficult to observe, as it is masked by another effect: the mutual entropic hindrance of the two chains at the motor junction for Lk = 0. The latter gives rise to an inverted quadratic behavior around 0 and to additional shallow minima in the free energy, cf.Fig. 9 in the Appendix. Furthermore, it is interesting to note that the constant free energy per entanglement found by Marko of 3.6kT per entanglement is comparable to, yet roughly two times smaller than the μ ≈ 6kT we find here. The reason can be found in the fact that Marko's Monte Carlo study measures the contribution of arbitrary complex catenanes while in our case only toroidal inter-chain braids are generated by the nature of motor unit rotation. Restricting the type of entanglement (from arbitrary to toroidal ones) to a subset obviously increases the free energy per entanglement in agreement with the larger value we find.
N. In our current case, such Gaussian behavior is difficult to observe, as it is masked by another effect: the mutual entropic hindrance of the two chains at the motor junction for Lk = 0. The latter gives rise to an inverted quadratic behavior around 0 and to additional shallow minima in the free energy, cf.Fig. 9 in the Appendix. Furthermore, it is interesting to note that the constant free energy per entanglement found by Marko of 3.6kT per entanglement is comparable to, yet roughly two times smaller than the μ ≈ 6kT we find here. The reason can be found in the fact that Marko's Monte Carlo study measures the contribution of arbitrary complex catenanes while in our case only toroidal inter-chain braids are generated by the nature of motor unit rotation. Restricting the type of entanglement (from arbitrary to toroidal ones) to a subset obviously increases the free energy per entanglement in agreement with the larger value we find.
IV. Discussion
In this report, we have considered the energy storage capacity and configurational properties of a rotary motor unit self-connected with two entangling polymer chains – the “tanglotron” device. The tanglotron principle is scalable and rather flexible. Several motor candidates, including artificial ones like the Feringa rotary engine10 (driven by light) or biological ones like ATP synthase4 (supplied with excess ATP), can be utilized.The basic energy “currency” that we propose here for storage and transmission is the topological link. This entity has a number of interesting and useful properties including:
(1) A fine grained and tunable elementary “quantum” of (free) energy. For a low link density, we expect a few kTs per entanglement.
(2) For higher densities, the links strongly interact which increases their energy to larger values. This might be advantageous in some situations where larger free energies per turn are required.
(3) The topological links are easy to store and can be specifically transported to the location where they can be utilized, i.e. to a free energy consumer. They directly interact with the mechanical degrees of freedom of the consumer, but being topological rather than strict geometric entities, they do so without a strong dependence on the environmental constraints.
(4) The topo-links are stable, long lived topological objects. They do not simply vanish into the solution but rather remain localized in the device. Therefore they can intermittently store and buffer the mechanical work produced by a motor and become utilized at a later time point by a consumer. In this sense, they can act as a “time-scale bridge” or “time-gear” bridging the otherwise vastly different conformational relaxation timescales of the motor and the consumer.
(5) The energy of the entanglements can be additionally further tuned under appropriate solvent conditions. It can be increased by charging the chains in an identical manner (positive or negative) or can be decreased by increasing the chains' affinity as compared to the solvent, i.e. making them less soluble.
V. Outlook
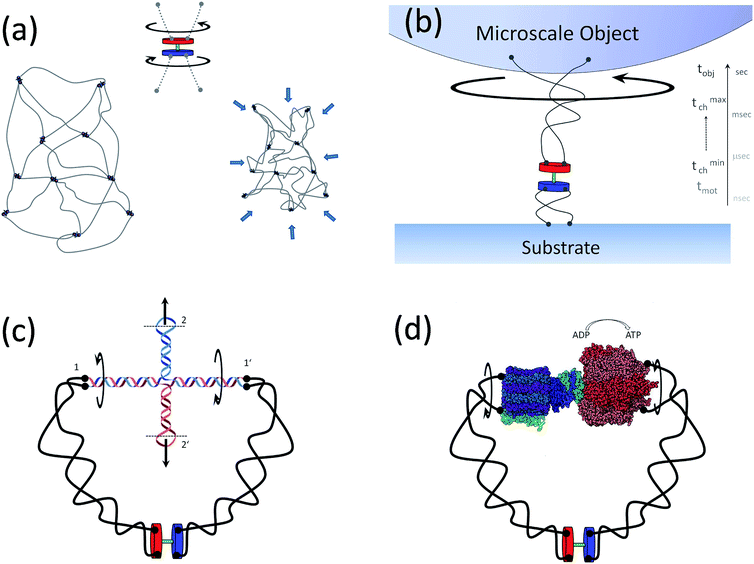
A rather non-exhaustive list of potential tanglotron related applications, giving us a flavor of its utility is outlined in Fig. 8a–d. Examples include the following aspects which are interesting to mention:Application 1 (artificial muscle material, see Fig. 8a): an obvious generalization consisting of tanglotrons cross-linked in a fully reticulated gel – the “topo-gel” deserves separate consideration. However it is intuitively clear that upon motor operation such a gel will collapse by the same order of magnitude as the single “topo-core” (tanglotron) particle, namely around 50 percent in each spatial direction. Both in the topo-gel and in the topo-core particle, the particular arrangement of the stator-rotor of the motor unit and its connectivity established by the polymer chains ensure that the construct acts as a topo-mechanical battery.
Notably, by the action of one small fraction of the whole system mass (the rotary motors) acting as an “enzymatic” element, the system (the polymer gel) is progressively converted, via the process of topological “charging”, into an energy enriched contracted structure. Such a gel would operate as an artificial muscle, although only in one direction (contraction). To make the contraction reversible, a second passive topology-dissipating unit could be inserted to counteract the action of the motor unit.
Application 2 (motion amplification, see Fig. 8b): a tanglotron can move objects billions of times heavier than itself. The fast elementary stepping of the motor unit, which occurs typically in nanoseconds to microseconds, would be dramatically suppressed by any rigid coupling to a much bigger object, like the slowly rotating macroscopic bead shown in Fig. 3. However, the situation is much more hopeful when the motor is coupled to the “consumer” through the two soft polymer chains. The latter have a broad distribution of relaxation timescales, with the shortest ones typically overlapping with the motor stepping timescales. The topological links injected by the rotor are transiently buffered in the polymer chains to be utilized in the bead rotation on much longer time-scales (seconds).
Application 3 (linear actuation and DNA interfacing, see Fig. 8c): the rotary motion can be simply transformed into linear actuation. This can happen e.g. via a DNA cruciform structure coupled to the polymer chains. In this way, the tanglotron device can principally bridge to any DNA nano-assembly via the end loops of the cruciform at connections 2 and 2′. The DNA nano-assembly realm34–38 is a very promising target and a possible “killer-application” for the tanglotron device.
Application 4 (mechanochemical coupling to reactions, see Fig. 8d): the tanglotrons should also optimally allow the release of the stored stress by coupling the dissipation of the entanglements to a chemical reaction. This can be done also in a useful manner. The motor unit can be directly coupled to “energy consumers”, like for instance distant catalytic centers. One curious, but feasible consumer would for instance be an ATP-synthase – the cellular enzyme synthesizing ATP from the proton-motive force across cellular membranes. The transmembrane proton-drive subunit of the ATP-synthase can be replaced by a tanglotron, i.e. a distant rotary motor, softly coupled by polymer chains. Interestingly, in the reverse direction, supplying the synthase with excess ATP makes it itself a rotary motor unit which can be used as an ATP-driven rotor drive of the tanglotron unit.
VI. Conclusions
A tanglotron (cf.Fig. 1) is a molecular device that converts repetitive cyclic motion into polymer self-entanglement. As a consequence, it induces a large polymer contraction and stores topo-mechanical energy in this process. The tanglotron's chains can act as a practical energy conversion and storage unit as well as a long range energy transmission medium. The tanglotron can be seen as an active topological nanoscale gear that acts as a soft and “geometry insensitive” nano-mechanical element able to adapt to any relative reorientation and repositioning of the motor and “consumer”. What is transmitted are topological entanglements, entities which are robust under geometric transformations. An effective transmission of rotation from a (fast) molecular engine device to a (slow) “consumer” element can only work if there is some form of intermediate mechanical energy storage, i.e. an efficient buffering of energy. This task can be practically fulfilled by the topological entanglement unit of the tanglotron.It will be the central future challenge to synthesize realizations of tanglotrons, to characterize the chemical, thermodynamical and mechanical properties of such novel molecular devices and explore their utility as universal driving components of future smart materials.
Appendix: the free energy at zero torque
It is interesting to reinvestigate the wedge-like behavior of the free energy by another method that allows us to further zoom into the region around Lk = 0. At vanishing torque, i.e. when the motor is free to rotate, the probability density p(φ) of the motor angle φ (i.e. its histogram of values) can be used to extract the free energy fromF(Lk) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(Lk) + const. p(Lk) + const. | (10) |
The result plotted in Fig. 9 shows similar wedge like behavior around Lk = 0 as shown in Fig. 5. However it displays some more interesting fine details. In particular, it shows that the naively expected orientation φ = 0 is not preferable. Instead, there are two close symmetric minima at around φ ≈ ±π/2, induced by the mutual entropic hindrance of the two polymer chains coming out from the motor unit. At φ = 0, the chains would emerge very close to each other giving rise to mutual entropic forces, thus pushing the preferred motor angle slightly away from 0. At larger values Lk ∼ 1 (φ ∼ 2π), the free energy grows linearly, with a slight modulation due to inter-chain steric hindrance, displaying a similar slope of ∼6kT per turn found in the main text.
Acknowledgements
The authors thank Quan Li, Gad Fuks, Hendrik Meyer, Nicolas Giuseppone, Joachim Wittmer, Justin Foy, and Falko Ziebert for fruitful discussions.References
- R. Dawkins, Why don't animals have wheels?, Sunday Times, November 24, (1996) Search PubMed.
- I. M. Kulić, R. Thaokar and H. Schiessel, Twirling DNA rings – Swimming nanomotors ready for a kickstart, Europhys. Lett., 2005, 72, 527 CrossRef.
- V. Balzani, A. Credi and M. Venturi, Molecular Devices and Machines, Wiley-VCH, 2003 Search PubMed.
- J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman, 5th edn, 2002 Search PubMed.
- H. Noji, R. Yasuda, M. Yoshida and K. Kinosita, Direct observation of the rotation of F1-ATPase, Nature, 1997, 386, 299–302 CrossRef CAS PubMed.
- H. C. Berg and R. A. Anderson, bacteria swim by rotating their flagellar filaments, Nature, 1973, 245, 380 CrossRef CAS.
- A. Maxwell and A. D. Bates, DNA topology, Oxford University Press, 2005 Search PubMed.
- C. Mao, W. Sun, Z. Shen and N. C. Seeman, A nanomechanical device based on the B–Z transition of DNA, Nature, 1999, 397, 144–146 CrossRef CAS PubMed.
- H. Yan, X. Zhang, Z. Shen and N. C. Seeman, A Robust DNA Mechanical Device Controlled by Hybridization Topology, Nature, 2002, 415, 62–65 CrossRef CAS PubMed.
- N. Koumura, R. W. J. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Light-driven monodirectional molecular rotor, Nature, 1999, 401, 152–155 CrossRef CAS PubMed.
- T. R. Kelly, H. De Silva and R. A. Silva, Unidirectional rotary motion in a molecular system, Nature, 1999, 401, 150 CrossRef CAS PubMed.
- J.-M. Lehn, Conjecture: Imines as Unidirectional Photodriven Molecular Motors—Motional and Constitutional Dynamic Devices, Chem.–Eur. J., 2006, 12, 5910–5915 CrossRef CAS PubMed.
- P. G. de Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca, 1979 Search PubMed.
- P. G. De Gennes, Entangled polymers, Phys. Today, 1983, 36(6), 33–31 CrossRef CAS PubMed.
- M. Doi and S. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1999 Search PubMed.
- F. Spitzer, Some Theorems Concerning 2-Dimensional Brownian Motion, Trans. Amer. Math. Soc., 1958, 87, 187–197 Search PubMed.
- S. Prager and H. L. Frisch, Statistical Mechanics of a Simple Entanglement, J. Chem. Phys., 1967, 46, 1475 CrossRef CAS PubMed.
- S. F. Edwards, Statistical mechanics with topological constraints: I, Proc. Phys. Soc., 1967, 91, 513 CrossRef CAS.
- J. Rudnick and Y. Hu, The winding angle distribution of an ordinary random walk, J. Phys. A: Math. Gen., 1987, 20, 4421–4438 CrossRef.
- A. Grosberg and H. Frisch, Winding angle distribution for planar random walk, polymer ring entangled with an obstacle, and all that: Spitzer–Edwards–Prager–Frisch model revisited, J. Phys. A, 2003, 36, 8955 CrossRef.
- C. Walter, G. T. Barkema and E. Carlon, The equilibrium winding angle of a polymer around a bar, J. Stat. Mech.: Theory Exp., 2011, P10020 CrossRef.
- J. F. Marko, Linking topology of tethered polymer rings with applications to chromosome segregation and estimation of the knotting length, Phys. Rev. E, 2009, 79, 051905 CrossRef.
- T. R. Strick, J.-F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, The Elasticity of a Single Supercoiled DNA Molecule, Science, 1996, 29, 1835 Search PubMed.
- J. F. Marko and E. D. Siggia, Fluctuations and supercoiling of DNA, Science, 1994, 265, 506 Search PubMed; J. F. Marko and E. D. Siggia, Statistical mechanics of supercoiled DNA, Phys. Rev. E, 1995, 52, 2912 CrossRef CAS.
- J.-C. Walter, M. Baiesi, E. Carlon and H. Schiessel, Unwinding Dynamics of a Helically Wrapped Polymer, Macromolecules, 2014, 47, 4840 CrossRef CAS.
- J. F. Marko, Supercoiled and braided DNA under tension, Phys. Rev. E, 1997, 55, 1758 CrossRef CAS.
- R. C. Ball, M. Doi, S. F. Edwards and M. Warner, Elasticity of entangled networks, Polymer, 1981, 22, 1010–1018 CrossRef CAS; P. G. de Gennes, Sliding gels, Physica A, 1999, 271, 231–237 CrossRef.
- A. Harada and M. Kamachi, Complex formation between poly(ethylene glycol) and a-cyclodextrin, Macromolecules, 1990, 23, 2821–2823 CrossRef CAS; Y. Okumura and K. Ito, The polyrotaxane gel: a topological gel by figure-of-eight cross-links, Adv. Mater., 2001, 13, 485–487 CrossRef.
- T. C. Boles, J. H. White and N. R. Cozzarelli, Structure of plectonemically supercoiled DNA, J. Mol. Biol, 1990, 213(4), 931–951 CrossRef CAS.
- N. R. Cozzarelli, T. Christian-Boles, and J. H. White, Primer on the topology and geometry of DNA supercoiling, DNA Topology and its Biological Effects, 1990, pp. 139–184 Search PubMed.
- T. Sanchez, I. M. Kulić and Z. Dogic, Circularization, Photomechanical Switching, and a Supercoiling Transition of Actin Filaments, Phys. Rev. Lett., 2010, 104, 098103 CrossRef CAS.
- I. M. Kulić, Evaluating polynomials on the molecular level – a novel approach to molecular computers, Biosystems, 1998, 45, 45 CrossRef.
- The “rotor” and “stator” are identical and can be seen interchangably, as none of them is static and there is only relative motion between them induced by M.
- N. C. Seeman, Nanotechnology and the double helix, Sci. Am., 2004, 290(6), 64–75 CrossRef CAS PubMed.
- W. K. Paul, Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440, 297–302 CrossRef PubMed.
- F. C. Simmel and Y. Krishnan, Nucleic Acid Based Molecular Devices, Angew. Chem., Int. Ed., 2011, 50, 3124 CrossRef PubMed.
- S. M. Douglas, H. Dietz, T. Liedl, B. Hogberg, F. Graf and W. M. Shih, Self-assembly of DNA into nanoscale three-dimensional shapes, Nature, 2009, 459, 414 CrossRef CAS PubMed; H. Dietz, S. M. Douglas and W. M. Shih, Folding DNA into Twisted and Curved Nanoscale Shapes, Science, 2009, 325, 725 CrossRef PubMed.
- B. Yurke, A. J. Turberfield, A. P. Mills, F. C. Simmel and J. L. Neumann, A DNA-fuelled molecular machine made of DNA, Nature, 2000, 406, 605 CrossRef CAS PubMed; S. F. Wickham, J. Bath, Y. Katsuda, M. Endo, K. Hidaka, H. Sugiyama and A. J. Turberfield, A DNA-based molecular motor that can navigate a network of tracks, Nat. Nanotechnol., 2012, 7, 169 CrossRef PubMed.
- P. Pieranski, In search of ideal knots. In: Ideal Knots, Series on Knots and Everything, ed. A. Stasiak, V. Katritch and L. H. Kauffman, World Scientific, Singapore, 1998, vol. 19, pp. 20–41 Search PubMed.
- S. Neukirch and G. H. M. Van der Heijden, Geometry and Mechanics of Uniformn-Plies: from Engineering Ropes to Biological Filaments, J. Elastoplast., 2002, 69, 41–72 CrossRef.
- Note that our calculations in this section are specialized to high link densities and describe the simulation results accurately at high torques, above the inflection point in the Lk vs. M curve (Fig. 7), for M > 1.5kT. At low torques, the helix parameters show large fluctuations and the polymer connectivity becomes an issue. Nevertheless, the theoretical curve represented in Fig. 7 and complemented by zero response below M = kT/(πγ) ≈ kT nonetheless fairly accounts for the simulated equation of state.
| This journal is © The Royal Society of Chemistry 2015 |