Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sorting of integral membrane proteins mediated by curvature-dependent protein–lipid bilayer interaction
Bojan
Božič
a,
Sovan L.
Das
b and
Saša
Svetina
*ac
aInstitute of Biophysics, Faculty of Medicine, University of Ljubljana, Ljubljana, Slovenia. E-mail: sasa.svetina@mf.uni-lj.si
bDepartment of Mechanical Engineering, Indian Institute of Technology, Kanpur 208016, India
cJožef Stefan Institute, Ljubljana, Slovenia
First published on 21st January 2015
Abstract
Cell membrane proteins, both bound and integral, are known to preferentially accumulate at membrane locations with curvatures favorable to their shape. This is mainly due to the curvature dependent interaction between membrane proteins and their lipid environment. Here, we analyze the effects of the protein–lipid bilayer interaction energy due to mismatch between the protein shape and the principal curvatures of the surrounding bilayer. The role of different macroscopic parameters that define the interaction energy term is elucidated in relation to recent experiment in which the lateral distribution of a membrane embedded protein potassium channel KvAP is measured on a giant unilamellar lipid vesicle (reservoir) and a narrow tubular extension – a tether – kept at constant length. The dependence of the sorting ratio, defined as the ratio between the areal density of the protein on the tether and on the vesicle, on the inverse tether radius is influenced by the strength of the interaction, the intrinsic shape of the membrane embedded protein, and its abundance in the reservoir. It is described how the values of these constants can be extracted from experiments. The intrinsic principal curvatures of a protein are related to the tether radius at which the sorting ratio attains its maximum value. The estimate of the principal intrinsic curvature of the protein KvAP, obtained by comparing the experimental and theoretical sorting behavior, is consistent with the available information on its structure.
Introduction
“Membrane curvature is a vital property of cells: many cellular processes, such as cell migration, cell division, or endocytosis crucially depend on membrane remodeling reactions, but the understanding how cells change the shape of their membranes is still at an early stage”.1 The molecular basis of membrane curvature control resides in integral membrane and membrane bound proteins that are sensitive to membrane curvature,2 as their energy and conformational state depend on the surrounding membrane curvature.3 If mobile, such proteins distribute on membranes with variable curvatures in an inhomogeneous manner.4In a recent experiment,5 the membrane curvature dependent lateral distribution of the integral membrane protein potassium channel KvAP has been studied quantitatively. A biophysical system has been used, in which a narrow membrane tube, the tether, is pulled by optical tweezers out of an aspirated giant unilamellar vesicle (GUV) and kept at a constant length (Fig. 1a). Tether radius has been established according to the requirements of the mechanical equilibrium and monitored by changing the aspiration pressure and consequently, membrane lateral tension. In this system, there are essentially two spatially separated regions of significantly different curvatures, a highly curved tether and a practically flat GUV. The corresponding protein densities and their ratio have been measured using the intensities of fluorescent dye molecules to tag the proteins. Further, by measuring the density of lipids, the tether radius, and hence the curvature, was determined independently. The key result of the study was the measured dependence of the sorting ratio, i.e., the ratio between the KvAP density (protein per lipid) on the tether and the GUV, on the tether curvature. KvAP density on the highly curved membrane of the tether was larger than on the vesicle main body. The similar experimental technique was also employed in the studies of curvature sensitivity of different BAR proteins.6–8
The experimental observations on the curvature dependent lateral sorting of membrane proteins can be interpreted by taking into consideration the effect of membrane proteins on membrane spontaneous curvature.9 The corresponding models are conceptually simple, and their variants are often used in interpretations of membrane curvature establishment and sensing. Aimon and coworkers5 interpreted their main result on the basis of a similar model proposed by Markin.10 In this model, it was asserted that proteins because of their intrinsic shape cause a modification of membrane bending constant and spontaneous curvature. The redistribution of proteins was explained by spatial variation of protein density yielding the match between local membrane spontaneous curvature and local membrane curvature, which gives rise to the minimum of the total membrane bending energy.
An alternative approach to study the effects of the protein–lipid bilayer interaction on the behavior of membranes with embedded proteins is to introduce a term for the strength of interactions between the protein and the membrane, which is a function of curvature.11–13 The parameters of this interaction term are defined in a general way so that they may represent different underlying physical or chemical mechanisms giving rise to the curvature dependent protein–lipid bilayer interaction. Few such mechanisms are, for example, the perturbed bending energy of the surrounding bilayer,3 locally modified lipid composition in multicomponent lipid bilayers,14 or the protein elasticity.15 The macroscopic parameters of the protein–lipid bilayer interaction can be viewed as a possible link between the microscopic and macroscopic properties of membranes. On one hand, the determination of their magnitude could be the target of molecular simulations on how curvature is sensed or generated by proteins,16,17 while on the other hand it is of interest to reveal in what way they define membrane macroscopic behavior. It has been shown that the approach to be employed here is more general than the spontaneous curvature model because the latter represents its limit at small interaction constants.12,13
This study will focus on the interaction of an embedded membrane protein with the surrounding lipid moiety expressed as the contribution to the membrane energy. We shall assume that proteins are rigid and mobile, and that they behave like a two-dimensional gas. By assuming that the protein is rigid, we are neglecting its internal degrees of freedom. In this limit, the sensing of membrane curvature is manifested by the lateral occupancy of proteins being enhanced in membrane regions that are favorable to their intrinsic shape and diminished in regions of unfavorable shape. We shall investigate how these parameters are manifested in the tether pulling experiment of protein curvature sensing.5 In view of the promising perspective of this experiment in the characterization of curvature forming and sensing properties of membrane proteins, we shall perform a detailed analysis of the information on the protein–lipid bilayer interaction that can be obtained from the determination of the dependence of the sorting ratio on the tether curvature. The analysis will be guided by the observation on the transmembrane protein KvAP5 but is meant to be valid also for other proteins. We will draw some conclusions about the underlying structural features of KvAP.
The analysis
We shall first define the energy terms that constitute the free energy of the treated system. In the next two subsections, we shall reveal the constants that define the protein density ratio in the case that all proteins have the same transmembrane orientation, first in the limit of low protein density and then for their finite density. In a separate subsection, we shall show the consequences of a bidirectional orientation of a given protein. In the last subsection, it will be shown how the constants that define the protein density ratio relate to the parameters of the protein–lipid bilayer interaction term.(i) Free energy of membrane embedded proteins
The energy contribution due to protein–lipid bilayer interaction is, in the limit of rigid protein surface, the consequence of the mismatch between local membrane principal curvatures and the intrinsic principal curvatures of the protein.11,12 The intrinsic principal curvatures of the protein refer to the shape of the part of the protein which is in contact with the lipid bilayer. The general expression for the corresponding energy term has been derived18 and can be written as | (1) |
The lateral distribution of proteins can be obtained by minimizing the sum of the free energies for the tether compartment (denoted by index “t”) of radius Rt and the GUV, which can be assumed to be practically flat with H ≈ 0. For the tether C1 = 1/Rt and C2 = 0, thus Ht = 1/(2Rt). A representative simple model for the vesicle is a flat surface with Hr = 0 (denoted by index “r”), with a very large area occupied by proteins of a constant density serving as the reservoir from which the thin tether is pulled out and kept at a constant length so that its area is relatively small (Fig. 1b). The free energy relevant for the treated system involves the interaction energies for the two compartments Np,iEi (with i = r or t, Np,i the number of proteins and Ei defined by eqn (1)) and the corresponding contributions due to the entropy of mixing proteins and lipids. We approximate the latter contributions by a free energy term due to the entropy of the proteins
 | (2) |
(ii) Unidirectional transmembrane protein orientation – small protein density
We first treat the system in which all inclusions have the same transmembrane orientation. The behavior of this system is governed essentially by six parameters (cf.eqn (1) and (2)), the four parameters of the interaction term (Hm, ΔHm, κ, κ*), the area of the protein (ap) and the reservoir protein number density (mp,r = Np,r/Ar) (density in the following). It turned out that it is possible to unravel how the parameters appearing in the interaction term (eqn (1)) relate to different characteristic features of the system's behavior by determining the sorting ratio, i.e., the ratio between the protein densities in the compartments “t” and “r” (denoted by Ŝ),† for dilute protein solution (or by taking ap = 0). The entropy term eqn (2) reduces in this limit to the entropy term of the ideal gas. The sorting ratio Ŝ is then obtained from the requirement of the equality of protein chemical potentials in the tether and the reservoir and is, according to eqn (8) in Kralj-Iglič and coworkers,18 equal to | (3) |
 | (4) |
The modified Bessel function of the first kind and of order zero 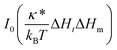 appears in eqn (3) as a result of averaging in the tether compartment over all possible angles ω.18,21 In eqn (3), it is also taken into account that the corresponding value of this modified Bessel function for the reservoir is unity because of ΔHr = 0. By inserting Ht = ΔHt = 1/(2Rt) into eqn (3) and (4), we obtain for the protein density ratio
appears in eqn (3) as a result of averaging in the tether compartment over all possible angles ω.18,21 In eqn (3), it is also taken into account that the corresponding value of this modified Bessel function for the reservoir is unity because of ΔHr = 0. By inserting Ht = ΔHt = 1/(2Rt) into eqn (3) and (4), we obtain for the protein density ratio
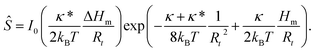 | (5) |
We first show that the function describing the dependence of the sorting ratio Ŝ on the tether curvature 1/Rt depends only on two independent constants related to the protein mean curvature and the protein anisotropy. By conveniently defining these constants to be directly related to the protein properties Hm and ΔHm as
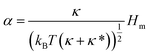 | (6) |
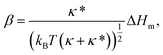 | (7) |
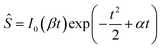 | (8) |
 | (9) |
Function Ŝ exhibits a maximum at t = te, which is the solution of the equation obtained by requiring that the derivative of Ŝ defined by eqn (8) by t equals zero,
| βI1(βte) + I0(βte)(−te + α) = 0. | (10) |
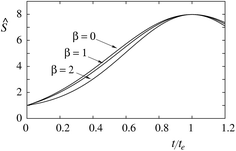
It is instructive already in the limit of low protein density (mp,r ≈ 0) to evaluate the relation between the constants α and β and measurable properties of the sorting ratio curve Ŝe. When β = 0, we have (see eqn (10)) te,0 = α0, which gives  . When β ≠ 0 the same sorting ratio Ŝe,0 can be reached at smaller values of the constant α (Fig. 3a), whereas the scaled tether curvature te for which the maximal Ŝ is realized shifts to larger values (Fig. 3b). The slope of the Ŝ(t/te) curve at small values of tether curvature, which at β = 0 is equal to α0, decreases with β (Fig. 2).
. When β ≠ 0 the same sorting ratio Ŝe,0 can be reached at smaller values of the constant α (Fig. 3a), whereas the scaled tether curvature te for which the maximal Ŝ is realized shifts to larger values (Fig. 3b). The slope of the Ŝ(t/te) curve at small values of tether curvature, which at β = 0 is equal to α0, decreases with β (Fig. 2).
(iii) Unidirectional transmembrane protein orientation – finite protein density
The sorting ratio Ŝ (eqn (5)) obtained in the limit of low protein density (mp,r ≈ 0) does not depend on the protein density on the flat vesicle region (reservoir) and therefore does not represent the observed behavior, which shows the diminishing of Ŝ(1/Rt) at the higher protein density.5 Such behavior can be ascribed to finite protein sizes, which affect the system through the entropy contribution to its free energy as considered here by eqn (2). The corresponding generalization of the equilibrium condition (eqn (8)) obtained by the requirement of the equality of protein chemical potential in the reservoir and the tether can be expressed in terms of the protein concentration of the reservoir (mp,r) and the density ratio as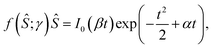 | (11) |
 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) from what we demonstrate here.
γ) from what we demonstrate here.
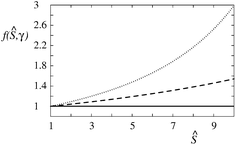 | ||
| Fig. 4 Function f(Ŝ;γ) for values of the area exclusion constant γ = 0 (solid line), 0.02 (dashed line), and 0.04 (dotted line). | ||
The area exclusion constant γ has an effect on the dependence of Ŝ on curvature. In Fig. 5 it is shown by two representative examples how it affects this dependence by keeping the maximum sorting ratio Ŝe constant, and appropriately adjusting constants α and β. The protein in Fig. 5a is considered to be isotropic (β = 0) and the protein in Fig. 5b to be anisotropic (with α = β). It can be seen that at finite values of the constant γ, the curves are running above the curve at γ = 0. The effect of γ in isotropic and anisotropic cases is practically similar. This can also be inferred from the appearance of γ only on the left hand side of eqn (11).
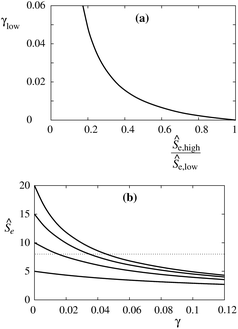
The Ŝ(1/Rt) curves measured at different protein densities also provide information about the corresponding values of the constants α, β and γ. This will be illustrated by taking into consideration that these curves are measured at two reservoir protein densities as it was presented by Aimon and coworkers.5 The available data in this case include the two maximum sorting ratios, Ŝe,high for the higher and Ŝe,low for the lower reservoir protein density, and the ratio between the reservoir densities mp,r,high/mp,r,low. Because the constant γ is proportional to the reservoir density, the latter ratio also gives us the ratio γhigh/γlow. From eqn (11) it follows that for given values of the constants α and β we have
| f(Ŝe,low;γlow)Ŝe,low = f(Ŝe,high;γhigh)Ŝe,high. | (13) |
Eqn (13) can be used, by choosing Ŝe,low and γhigh/γlow, to determine which value of γlow corresponds to a given value of the ratio Ŝe,high/Ŝe,low. The corresponding dependence is presented in Fig. 6a for Ŝe,low = 8 and γhigh/γlow = 10. From the measured value of γlow, it is then possible by the use of eqn (11) and (12), or equivalently Fig. 6a, to extract the values of the constants α and β analogously to the corresponding description in the subsection (ii). As an example, we take β = 0. Then, from the theoretical Ŝe(γ) curve and known Ŝe(γlow) we obtain the sorting ratio at γ = 0 (Ŝe,0) and thus the constant α from eqn (8). To illustrate this, we plot in Fig. 6bŜe(γ) for different values of Ŝe,0. The sought Ŝe,0 corresponds to the curve which intersects the dotted Ŝe = 8 line at γ = γlow.
(iv) Bidirectional orientation of transmembrane proteins
In previous subsections, we have discussed the case of a single integral membrane protein species whose molecules are oriented across the membrane in one direction only. That is, they induce curvature of one sign only (either positive or negative). In this subsection, we will look into the case when molecules of the transmembrane protein are oriented in both ways. We will consider them as two different species (“+” and “−”). We take that in the GUV (or flat membrane) the densities of proteins with positive and negative orientation are mp,r+ = νmp,r and mp,r− = (1 − ν)mp,r, respectively, so that mp,r = mp,r+ + mp,r−, where ν is the fraction of protein molecules of positive orientation. Then, ν = 1 implies GUV has proteins with positive orientation only (see subsections (ii) and (iii)), and ν = 0 denotes that all the proteins present have negative orientation. In the corresponding interaction terms (cf.eqn (1)), both the intrinsic mean and deviatoric curvatures of these species will have the same magnitude, but they will differ by a sign (Hm+ = −Hm and ΔHm+ = −ΔHm−). Furthermore, the proteins have the same area ap. As a result we have α+ = −α− = α, and β+ = −β− = β. The entropic contribution to free energy given by eqn (2) gets modified into | (14) |
In analogy, with the case of protein molecules having the same transmembrane orientation, the free energy of this more general system has to be minimized with respect to the equilibrium distribution between the tether and flat membrane compartments of both species. The equilibrium equations analogous to eqn (11) are then
 | (15) |
 | (16) |
 | (17) |
From eqn (17), it can be concluded that bidirectional orientation affects the behavior of the system at the level of the interaction term. Therefore, it is sufficient to investigate its consequences in the limit of dilute proteins when f(Ŝ;γ) = 1. As an example of the basic behavior of the system due to the bidirectional orientation, we present in Fig. 7a the sorting of Ŝ+ = mp,t+/mp,r and Ŝ− = mp,t−/mp,r of the positively and negatively oriented proteins, respectively, for ν = 0.5 and β = 1. Here, ν = 0.5 implies that initially in the flat membrane the two types of proteins have been present in equal amounts. With increasing curvature (positive) of the tether, we observe that the proteins with positive orientation enrich in the tether and the negatively orientated proteins get depleted from the tether. The same has also been observed for other values of ν as well. The behavior for ν = 0.5 has also been demonstrated by Aimon and coworkers.5 We also present the sorting for different values of the fraction ν in Fig. 7b–d for β = 0, 1, and 2, respectively. Decreasing values of ν imply increasing fraction of protein with negative orientation. The results and the scenario for ν = 1 are the same as that considered for the proteins with the same orientation, presented in subsections (ii) and (iii) and Fig. 2. We observe that the behavior of the sorting ratio curve for different β is similar for all values of ν. Moreover, with increasing β the effect of ν diminishes and with decreasing ν the effect of β on sorting reduces.
The values of the scaled mean intrinsic curvature α of proteins and scaled tether radius te corresponding to the maximum sorting ratio also depend on the fraction ν. We demonstrate that α decreases and te increases with β for all values of ν considered, which is consistent with Fig. 3a and b for ν = 1. In Fig. 8, we also present the variation of the ratio α/te with ν. For β = 0 the ratio α/te is almost (but not exactly) equal to one for all ν. For nonzero β, the ratio decreases with ν. This implies that the tether curvature required to attain a specified maximum sorting is larger. Further, both α and te decrease with ν (that is with enrichment of proteins of positive orientation in the GUV). When only the proteins with negative orientation are present in the flat membrane (that is ν = 0), the density ratio Ŝ decreases with tether curvature. However, if the membrane with negative curvature is present, enrichment occurs, and for maximum sorting, the tether curvature te is negative.
 | ||
| Fig. 8 Dependence of the ratio α/te corresponding to Ŝe = 8 on ν for β = 0 (solid line), 1 (dashed line), and 2 (dash-dot line). | ||
(v) Determination of the parameters of the protein–lipid bilayer interaction
The next step of the analysis is to extract from the values of the constants α, β and γ, all available information about the parameters of the interaction term, eqn (1). The expressions for the mean protein principal curvature and the difference between protein principal curvatures are obtained by dividing eqn (6) and (7), respectively, by eqn (9) for t = te, and denoting the tether radius at the maximum sorting as Rt,e. The obtained expressions are | (18) |
 | (19) |
The structural features of the protein, Hm and ΔHm, in eqn (18) and (19) are related to the experimentally obtained value of Rt,e and from the above fit values of te, α and β. However, the interaction term eqn (1) involves more parameters than can be extracted from the Ŝ(t/te) curves. In eqn (18) and (19), the unknown parameter is the ratio κ*/κ. It can be concluded that it is possible to obtain by the described procedure only the combinations of Hm and ΔHm that give the same Ŝ(t/te) dependence.
It is noteworthy that the curvature at which the ratio Ŝ attains the maximum does not depend on the strength of the protein–lipid bilayer interaction expressed by the parameters κ and κ*. These parameters instead affect the magnitude of Ŝe.
Discussion
Biological membranes are lipid based but crowded by many different proteins and protein complexes serving different functions, among which are the establishment of membrane curvature and its sensing. Effects of proteins on the latter can be treated theoretically at various structural levels, from molecular or atomistic to macroscopic. Here, we pursued the macroscopic approach by using a set of phenomenological parameters that define the protein–lipid bilayer interaction caused by the mismatch between the intrinsic principal curvatures of the protein and the principal curvatures of membrane. Proteins were assumed to be rigid. The crucial parameters of the corresponding interaction term (eqn (1)) are the principal curvatures of the shape of the protein that is in contact with the surrounding lipid molecules. These curvatures are in a mismatch with the principal curvatures C1 and C2 that a membrane would have at the position of a protein in its absence. This formulation implies that while due to a protein the curvature of the surrounding membrane is modified, this modification decays into the bulk membrane curvatures C1 and C2 within a relatively short characteristic distance. The validity of the approach thus depends on how much is this characteristic distance smaller than the average closest distance between proteins.The effects of protein shape have also been considered by other researchers, who assumed that it modifies membrane local spontaneous curvature. The predictions of the spontaneous curvature and protein–lipid bilayer interaction term approaches look similar; however, they differ in details. In the limit of weak interaction constant, the model based on the interaction term reduces13 into the spontaneous curvature model; therefore, it can be considered to be more general. The qualitative difference between the two approaches comes to light particularly at small protein concentrations. Due to the curvature dependent interaction term the curvature differences are sensed even by a single protein, whereas in the spontaneous curvature approach the membrane curvature must first be formed, which requires the presence of a considerable number of molecules, and only then the curvature is felt by the additional proteins. In the tether pulling experiment, as will be demonstrated later, this feature is reflected in the initial slope of the sorting curve.
The general analysis on which parameters of the treated protein–lipid bilayer interaction term can be extracted from measured dependence of the sorting ratio on tether curvature showed the system behavior to be defined by the protein mean curvature constant α and the protein anisotropy constant β based on the parameters of the interaction term (eqn (1)) and the area exclusion constant γ arising from the entropy contribution to the system's free energy. The first two constants are related to the mean protein intrinsic principal curvature and to the difference between protein intrinsic principal curvatures, respectively.
We analyzed the dependence of the sorting ratio on the constants α, β and γ. The main feature of the sorting ratio curve is that there exists a tether radius at which this ratio is maximal. This implies that at the maximal sorting, the mismatch between the tether curvature and the protein intrinsic curvatures is least. The same maximum sorting ratio can be attained by many combinations of the constants α, β and γ, appearing at different tether radii. At a specified tether radius, the sorting ratio of isotropic protein is higher than that in the case of anisotropic protein. Further, the tether radii at which the sorting ratio is maximal are determined only by the constants α and β whereas the maximum sorting ratio depends also on the constant γ. As an important indicator of the protein isotropy features, we identified the slope of the sorting ratio curve at small tether curvature, which for more anisotropic proteins is lower (Fig. 2). This initial slope does not depend on the constant γ (Fig. 5). Consequently, the effect of the area exclusion constant γ on the sorting ratio curve of isotropic and anisotropic proteins is almost the same (Fig. 5). It is also notable that the bidirectional orientation effect of the proteins is manifested at the level of the protein–phospholipid membrane interaction term only (eqn (17)).
The above general conclusions will be illustrated by the analysis of the expression for the protein–lipid bilayer interaction18 in view of recent experiments exploring the effect of membrane curvature on the distribution of proteins over the variably curved vesicle membrane.5 X-ray structural studies of the open state of KvAP show22 that this tetrameric channel is 4-fold symmetric, which indicates that β = 0. It is possible, from the experimental value of Ŝe at two protein densities and the Ŝ(t/te) dependence, to obtain reasonable values of the remaining parameters α and γ. The measured points of the KvAP sorting ratio, denoted by Aimon and coworkers5 as S, we transformed into the true KvAP sorting ratio (Ŝ) by the relationship
 | (20) |
 | ||
| Fig. 9 Comparison of the predictions of the presented model for the values of the area exclusion constant γ = 0.015 (upper curve) and γ = 0.15 (lower curve) and constant α = 2.15 with the experimentally measured dependence of the sorting ratio Ŝ on tether curvature for potassium channel KvAP obtained by Aimon and coworkers.5 The experimental points (the mean values, the median values and the standard deviations) are from the work of Aimon and coworkers5 and recalculated according to eqn (20), by taking mp,r,low = 162 μm−2, mp,r,high = 1777 μm−2 and ap = 45 nm2. Dashed lines represent the fit obtained by the model developed by Aimon and coworkers.5 | ||
Through eqn (18) and (19), the interaction parameters κ and κ*, and the protein shape determinants Hm and ΔHm, are related to the constants α and β. However, the number of parameters of the interaction term (κ, κ*, Hm, ΔHm) is larger than the number of constants that determine the dependence of the sorting ratio on the tether curvature (α and β). Consequently, by measuring only this dependence the interaction parameters are undeterminable. It is nevertheless possible to make plausible estimates. For example, by assuming κ = κ* the principal curvatures of the protein KvAP are predicted (eqn (18)) to be equal to 1/Rt,e, which is ≈0.1 nm−1. This value corresponds to the radius of curvature of the slope in the paddle shape of KvAP presented in Fig. 4E of Cuello and collaborators (also reproduced in Fig. 10).23 Within the indeterminacy of the ratio κ*/κ, the intrinsic principal curvature of the isotropic protein KvAP obtained by measuring the sorting ratio was found to be consistent with the X-ray diffraction obtained shape of one of this protein's conformations. Corresponding intrinsic spontaneous curvature of this protein (cp = 2Hm) is thus predicted to be 1/5 nm−1, which is five times higher than the value presented by Aimon and collaborators.5
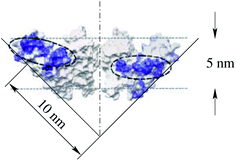 | ||
| Fig. 10 Estimate of the intrinsic principal curvature of the paddle shape of KvAP as presented in Fig. 4E of Cuello and collaborators.23 | ||
As it was demonstrated, by the analysis of the observed dependence of the sorting ratio on the tether curvature, it is possible to extract a few model parameters. These parameters could then be used to obtain a consistent picture about the functioning of a studied membrane protein in conjunction with other structural level studies. For example, the microscopic theories could within the context of this study contribute by estimating the ratio κ*/κ, whereas structural studies could provide an estimate of protein principal curvatures.
The present analysis was based on the protein–lipid bilayer interaction and assuming proteins to be rigid. The treatment of proteins as rigid entities is from the point of view of a systematic development of a general model an approximation. However, it can be considered as a useful intermediate step also in situations when it is necessary to take into account protein internal degrees of freedom. For example, in a protein exhibiting different conformational states with different intrinsic curvatures the present model could be generalized by defining, for each of these states, a separate interaction term. Analogous generalization could also be made for proteins with finite compressibility. Moreover, the attractive/repulsive interaction between proteins and between protein and lipids may play a significant role, in addition to the area exclusion effect considered here, at higher protein concentrations. It will be therefore of interest to extend the studies of membrane curvature effects by including these other features of the system.
Acknowledgements
This work was supported by the Slovenian research agency through the research program P1-0055 and in part by the Project of Knowledge Innovation program (PKIP) of Chinese Academy of Sciences, grant no. KJCX2.YW.W10. S. L. Das acknowledges financial support from Department of Science and Technology, Government of India, through grant no. DST/ME/20120003.References
- C. Mim and V. M. Unger, Trends Biochem. Sci., 2012, 37, 526–533 CrossRef CAS PubMed.
- T. Baumgart, B. R. Capraro, C. Zhu and S. L. Das, Annu. Rev. Phys. Chem., 2011, 62, 483–506 CrossRef CAS PubMed.
- R. Phillips, T. Ursell, P. Wiggins and P. Sens, Nature, 2009, 459, 379–385 CrossRef CAS PubMed.
- R. Parthasathy and J. T. Groves, Soft Matter, 2007, 3, 24–33 RSC.
- S. Aimon, A. Callan-Jones, A. Berthaud, M. Pinot, G. E. S. Toombes and P. Bassereau, Dev. Cell, 2014, 28, 212–218 CrossRef CAS PubMed.
- P. Singh, T. Mahata, T. Baumgart and S. L. Das, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051906 CrossRef.
- B. Sorre, A. Callan-Jones, J. Manzi, B. Goud, J. Prost, P. Bassereau and A. Roux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 173–178 CrossRef CAS PubMed.
- C. Zhu, S. L. Das and T. Baumgart, Biophys. J., 2012, 102, 1837–1845 CrossRef CAS PubMed.
- J. Zimmerberg and M. M. Kozlov, Nat. Rev. Mol. Cell Biol., 2006, 7, 9–19 CrossRef CAS PubMed.
- V. S. Markin, Biophys. J., 1981, 36, 1–19 CrossRef CAS.
- S. Svetina, V. Kralj-Iglič and B. Žekš, in Biophysics of Membrane Transport, ed. J. Kuczera and S. Przestalski, 1990, vol. II, pp. 139–155 Search PubMed.
- V. Kralj-Iglič, S. Svetina and B. Žekš, Eur. Biophys. J., 1996, 24, 311–321 CrossRef.
- B. Božič, V. Kralj-Iglič and S. Svetina, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041915 CrossRef.
- N. S. Mueller, R. Wedlich-Söldner and F. Spira, Mol. Membr. Biol., 2012, 29, 186–196 CrossRef CAS PubMed.
- S. Perutková, V. Kralj-Iglič, M. Frank and A. Iglič, J. Biomech., 2010, 43, 1612–1617 CrossRef PubMed.
- H. Cui, C. Mim, F. X. Vázquez, E. Lyman, V. M. Unger and G. A. Voth, Biophys. J., 2013, 104, 404–411 CrossRef CAS PubMed.
- F. X. Vázquez, V. M. Unger and G. A. Voth, Biophys. J., 2013, 104, 396–403 CrossRef PubMed.
- V. Kralj-Iglič, V. Heinrich, S. Svetina and B. Žekš, Eur. Phys. J. B, 1999, 10, 5–8 CrossRef.
- T. L. Hill, An Introduction to Statistical Thermodynamics, Addison-Wesley Publishing Company, Inc., USA, 1962, ch. 16 Search PubMed.
- P. Mahata and S. L. Das, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062713 CrossRef.
- J. B. Fournier, Phys. Rev. Lett., 1996, 76, 4436–4439 CrossRef CAS.
- Y. Jiang, A. Lee, J. Chen, V. Ruta, M. Cadene, B. T. Chait and R. MacKinnon, Nature, 2003, 423, 33–41 CrossRef CAS PubMed.
- L. G. Cuello, D. M. Cortes and E. Perozo, Science, 2004, 306, 491–495 CrossRef CAS PubMed.
Footnote |
| † This notion (Ŝ) is chosen here to distinguish the defined ratio between the protein areal densities in the tether and flat GUV from the defined sorting ratio S by Aimon and coworkers,5 measuring the ratio between the amount of protein per lipid in both compartments. |
| This journal is © The Royal Society of Chemistry 2015 |