Open Access Article
Open Access ArticleAtomistic simulation for coil-to-globule transition of poly(2-dimethylaminoethyl methacrylate)†
Sa Hoon
Min
a,
Sang Kyu
Kwak
*b and
Byeong-Su
Kim
*ac
aDepartment of Energy Engineering, School of Energy and Chemical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 689-798, Korea
bDepartment of Chemical Engineering, School of Energy and Chemical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 689-798, Korea. E-mail: skkwak@unist.ac.kr; Tel: +82-52-217-2514
cDepartment of Chemistry, School of Natural Science, Ulsan National Institute of Science and Technology (UNIST), Ulsan 689-798, Korea. E-mail: bskim19@unist.ac.kr; Tel: +82-52-217-2923
First published on 28th January 2015
Abstract
The coil-to-globule transition of poly(2-dimethylaminoethyl methacrylate) (PDMAEMA) in aqueous solution was investigated by all-atomistic molecular dynamics simulations. The polymer consistent force field (PCFF) was applied to the PDMAEMA model with a proper protonation state. The structural analysis indicates a distinct difference in the hydration state of particular functional groups of PDMAEMA as well as in the conformational state of PDMAEMA below and above the lower critical solution temperature (LCST). In particular, by monitoring the motion of water molecules, we observe that water molecules in the vicinity of the carbonyl group are relatively restricted to the motion in the globule state due to the extended relaxation time of hydrogen bonds among water molecules. The degree of protonation was also adjusted to study the effect of protonation on the conformational state of PDMAEMA.
Introduction
The transition between coil and globule states is a fundamental phenomenon in polymer chains. The conformational state of polymer chains in a good solvent exhibits a well expanded coil structure, while that in a poor solvent undergoes a collapse into a globule structure, due to the energetic difference in the interaction between the polymer and solvent molecules.1,2 It has been observed that thermo-responsive polymers also show a similar conformational transition under the same solvent condition when changing the temperature through their lower critical solution temperature (LCST).3–5 Among these polymers, poly(N-isopropylacrylamide) (PNIPAM), a representative thermo-responsive polymer, has been well studied by means of theoretical calculations6–9 as well as experimental methods10–12 to explore the conformational transition behaviour in an aqueous solution through the LCST whose range includes the human body temperature.Recently, molecular dynamics (MD) simulations have been applied to observe what happens in the coil-to-globule transition of PNIPAM at the atomic level using diverse force-fields. The optimized-potentials-for-liquid-simulations (OPLS) force-field has been successfully used by Spohr's group to investigate the LCST of multiple chains as well as a single chain of PNIPAM in water, showing that the polar amide group could be a temperature-sensitive region for the coil-to-globule transition.13 In addition, they have modelled a PNIPAM-grafted cylindrical pore14 and graphene-like nanosheets connected with PNIPAM15 to predict the temperature-responsive properties on the inner surface functionalized pore and on the conceptual nanoengines, respectively, by the assisted model building with the energy refinement (AMBER) 94 force-field. In other examples, with this force-field, Longhi et al. reported the microscopic details between a 50-mer of PNIPAM and water molecules below and above the LCST,16 and Du et al. also reported the effect of salt on the LCST of PNIPAM by calculating the radius of gyration (Rg) and the radial distribution function (RDF) between atoms in PNIPAM and the salt cations.17 The DREIDING force-field was applied to study the PNIPAM-grafted silicon substrate for understanding the deswelling process above the LCST.18
In particular, Mancini's group have mainly focused on the polymer consistent force field (PCFF) to simulate the coil-to-globule transition of a 30-mer of PNIPAM in water.19–21 They observed a polymer chain length dependence on the conformational transition, indicating that short PNIPAM oligomers such as 3-, 5-, and 10-mer did not change their conformation significantly. Moreover, their studies revealed that there was a distinct difference in the hydrogen bond (H-bond) strength between PNIPAM–water and water–water below and above the LCST by analysing the H-bond autocorrelation functions and the vibrational spectra of the water molecules.20,21 These simulation results are in good agreement with the experimental observation, and give an insight into the structural and dynamic correlations between the polymer and water molecules below and above the LCST. Even though it could not elucidate the exact mechanism of the coil-to-globule transition, it would help to understand a possible driving force for the transition.
Poly(2-dimethylaminoethyl methacrylate) (PDMAEMA), a weak cationic polyelectrolyte, has been widely used as non-viral gene delivery vectors with buffering capacity and low cytotoxicity.22–26 In contrast with PNIPAM, PDMAEMA is another class of thermo-responsive polymer whose phase transition is also affected by the pH of solutions, resulting from the protonation–deprotonation of the tertiary amine group in PDMAEMA.27–31 Copolymerization with the DMAEMA monomer makes it possible to design multi-responsive polymeric micelles where PDMAEMA plays a crucial role in thermo- and pH-responsiveness, simultaneously.32–37 It has been considered that this can be applied in the smart drug delivery system.38,39 Furthermore, PDMAEMA has provided the opportunities for the functionalization of the dual responsiveness on nanomaterials such as nanoparticles,40,41 nanoclay,42 fullerene,43 and graphene.44
Owing to the protonation of amine groups, the conformational transition of PDMAEMA in aqueous solution is a more complicated phenomenon than the PNIPAM case. Thus, it is still challenging to study its coil-to-globule transition, causing the thermo- and pH-responsive properties. Plamper's group recently reported the role of the carbonyl group and polymer backbone in the conformational transition with fluorescence spectroscopy.45 However, the coil-to-globule transition of PDMAEMA with temperature changes has not been studied yet by the all-atomistic MD simulation, which can provide insights into the origin of the conformational transition, despite numerous theoretical studies on PNIPAM.
In this study, we perform MD simulations for the first time to investigate the coil-to-globule transition of PDMAEMA in the aqueous phase through a model system established for a 30-mer of PDMAEMA in water with a proper protonation state. The MD simulations were employed to observe the coil-to-globule transition of PDMAEMA at three different temperature regimes. The structural correlations between PDMAEMA and water molecules were analysed for both the coil and globule states. In particular, we monitored the motion of water molecules in the vicinity of the specific functional groups in PDMAEMA to calculate the dynamic properties of water, such as the residence time and the H-bond relaxation time around PDMAEMA to account for the origin of the coil-to-globule transition in PDMAEMA. The degree of protonation of PDMAEMA was also adjusted to investigate the effect of protonation on the conformational state.
Method
Force-field and polymer modelling
For the all-atomistic model of PDMAEMA, the PCFF46–48 as an ab initio based class II force-field was chosen because it has been successfully applied in the coil-to-globule transition of polymers19–21 as well as the prediction for the physical properties of polymers.49,50 The potential energy of the system can be calculated as a summation of valence interactions, valence cross-terms, and non-bonding interactions by the following eqn (1). Detailed energy expressions for each potential are described in the ESI.†| Etotal = Ebond + Eangle + Etorsion + Eoop + Ecross-term + ECoulomb + EvdW | (1) |
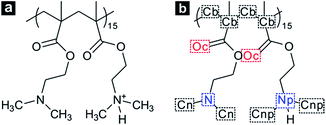
In the case of a short polymer chain, it is considered that there is a limitation in conformational transition of polymers.19,51 Thus, we modelled a single PDMAEMA chain comprised of 30 monomer units, which is long enough to form both the coil and globule structure depending on temperature changes.51 In addition, the atactic form was applied to the PDMAEMA model to reproduce the general PDMAEMA chain.52,53 The protonation state of PDMAEMA varies with the pH of the solution due to the protonation–deprotonation of the nitrogen atom in the dimethylamino (DMA) group. Recent experimental studies suggest the pH-dependent protonation properties, indicating that PDMAEMA is completely protonated at a low pH level and can be deprotonated with increasing pH of the solution.29,52 In particular, the degree of protonation of PDMAEMA is known to be about 0.5 at neutral pH, owing to the pKa of 7.0–7.3 for PDMAEMA.29 To simulate the coil-to-globule transition of PDMAEMA in neutral water, these protonation states were employed in a 30-mer of PDMAEMA model by an alternate protonation, as shown in Fig. 1. The degree of protonation was further adjusted to achieve pH-dependent transition behaviour of PDMAEMA.
Simulation details
All of the MD simulation studies were performed with the LAMMPS code (http://lammps.sandia.gov)54 and the GPU-accelerated package.55 The PCFF was used for both PDMAEMA and water molecules19,56,57 in a cubic simulation box with the periodic boundary conditions for all directions. The simulations were calculated with the isothermal–isobaric (NPT) ensemble, and the target temperature and pressure were maintained by using the Nose–Hoover thermostat and barostat with damping relaxation times of 1 and 2 ps, respectively. A cutoff of 9.5 Å was applied to calculate the pairwise interactions, and the long-range electrostatic interactions were evaluated using the particle–particle particle–mesh (PPPM) method with an RMS accuracy of 10−4. The bond lengths and angles for the molecules were not constrained, thus a time step of 1 fs with a velocity-Verlet scheme was employed for the integration of motion.A single PDMAEMA chain with a fully extended backbone was placed in a simulation box with 9000 water molecules, resulting in the initial density of about 1.0 g cm−3. For the protonated PDMAEMA, appropriate counterions (Cl−) were added to neutralize the simulation system. The initial topologies and force-field parameters were built by Materials Studio®, and were converted into the LAMMPS-readable format. After energy minimization for unfavourable geometry of initial topologies, short simulations consisting of a 100 ps canonical (NVT) ensemble followed by a 900 ps NPT ensemble under atmospheric pressure were carried out at 283 K for the initial equilibrium of the system. Long NPT simulations of 30 ns for the production runs were performed at three different temperatures of 283, 303, and 338 K in order to investigate the coil-to-globule transition depending on temperature. The structural and dynamical analyses were performed using the VMD package.58
Results and discussion
Structural analysis
In aqueous solution, PDMAEMA exhibits a phase separation behaviour induced by the conformational transition with an LCST around 40 °C, which can be affected by the molecular weight, solution pH, and concentration.30 Thus, the MD simulations were carried out at 283 and 303 K, i.e. below the LCST, and at 338 K, i.e. above the LCST of PDMAEMA. During the simulation, the system temperature was well maintained by the Nose–Hoover thermostat (Fig. S1†). Fig. 2a shows the time evolution of the radius of gyration (Rg) for PDMAEMA at three different temperature conditions. Rg which represents the dimension of a polymer chain is calculated by averaging the mass-weighted distance of each atom from the center-of-mass position of the group of atoms: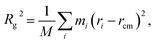 | (2) |
 | ||
| Fig. 2 Time evolution of (a) the radius of gyration, Rg, and (b) the water accessible surface area, WASA, for PDMAEMA at 283 K (blue), 303 K (green), and 338 K (red). | ||
Indeed, the equilibrium morphologies of PDMAEMA are consistent with each Rg and WASA as shown in Fig. 3. After the production runs for 30 ns, coil states of PDMAEMA with a partially linear structure are observed at 283 and 303 K, and a globule state with a compact configuration is observed at 338 K. These structural properties represent a distinct difference in the domain size of PDMAEMA through the LCST. From the atomic viewpoint, we further focused on the structural features between PDMAEMA and water molecules in the coil and globule states.
The radial distribution function (RDF) makes it possible to calculate the probability of finding atom i at a distance r from atom j, meaning the local structure between atoms i and j. The RDF can be defined by eqn (3),
 | (3) |
Fig. 4a and b display the RDFs of the carbon (Cn) and nitrogen (N) atom in the unprotonated DMA group to the oxygen (Ow) atom in water, respectively. While there were no significant differences in the intensity between the RDF peak at 283 and 303 K, the RDFs at 338 K showed a considerable decrease in the intensity compared with that below the LCST. By integrating the RDFs, the number of water molecules (Nw) was calculated for the first and second hydration shells surrounding the two different DMA groups of PDMAEMA, as presented in Table 1. The Nw in the second hydration shell as well as the first hydration shell of Cn and N was significantly reduced by >35% at 338 K. It indicates that the unprotonated DMA groups of PDMAEMA tend to be shielded from water molecules in its globule state, since the probability of finding water molecules remarkably decreases from Cn and N atoms above the LCST.
| Temperature (K) | N w | ||
|---|---|---|---|
| First shellb | Second shellc | ||
| a The Nw is calculated from the last 10 ns trajectory. b Integration from zero to the first minimum of each RDF. c Integration from the first minimum to the second minimum of each RDF. | |||
| Cn | 283 | 8.47 ± 0.28 | 30.49 ± 0.74 |
| 303 | 8.11 ± 0.23 | 29.33 ± 0.56 | |
| 338 | 5.18 ± 0.31 | 19.83 ± 1.01 | |
| N | 283 | 0.36 ± 0.03 | 17.26 ± 0.49 |
| 303 | 0.33 ± 0.02 | 16.73 ± 0.34 | |
| 338 | 0.20 ± 0.02 | 11.05 ± 0.57 | |
| Cnp | 283 | 9.15 ± 0.07 | 32.93 ± 0.16 |
| 303 | 9.09 ± 0.06 | 33.12 ± 0.20 | |
| 338 | 8.68 ± 0.07 | 31.94 ± 0.20 | |
| Np | 283 | 1.06 ± 0.01 | 21.91 ± 0.12 |
| 303 | 1.04 ± 0.01 | 22.06 ± 0.16 | |
| 338 | 1.02 ± 0.01 | 21.43 ± 0.16 | |
| Oc | 283 | 1.98 ± 0.02 | |
| 303 | 1.88 ± 0.04 | ||
| 338 | 1.53 ± 0.04 | ||
In Fig. 4c, it can be seen that the intensities of the RDFs between the carbon (Cnp) atom in the protonated DMA group and Ow increase in comparison with that between Cn and Ow (Fig. 4a), and the Nw in the first and second hydration shell is also found to be higher for all temperature ranges. In addition, the peak positions of the RDFs are slightly shifted toward smaller distance by 0.3 Å. It suggests that the methyl groups in the protonated DMA group have a stronger interaction with water molecules than those in the unprotonated DMA group, due to the change of partial charge by the protonation. Fig. 4d also represents an increase in the intensities of the RDFs between the nitrogen (Np) in the protonated DMA group and Ow, compared with Fig. 4b. In particular, sharp peaks located at 2.7 Å were observed, resulting from the H-bond between Np and Ow atoms, while there were only weak shoulder peaks in the N–Ow RDFs at the same position. It also reveals a distinct difference between the number of water molecules in the first hydration shell of N and Np, which can be related to water molecules participating in the H-bond to each DMA group. Interestingly, in the case of the protonated DMA group, the RDFs above the LCST are almost similar to those below the LCST. The intensities of the RDFs do not decrease much even in its globule state, suggesting that the structural correlation between the protonated DMA group and water molecules remains stable regardless of the conformational states. In other words, the protonated DMA groups are not shielded from water molecules even in the globule state. The Nw also exhibits a slight decrease (<5%) for the first and second hydration shells of Cnp and Np at 338 K. Moreover, the contour plots of the protonated DMA group show the steady state values of RDF over the simulation time in contrast with the other functional groups. It supports the fact that the protonated DMA groups are not consistently shielded from water molecules during the coil-to-globule transition.
Fig. 4e and f exhibit the RDFs between the carbonyl oxygen (Oc) and Ow, and between the backbone carbon (Cb) and Ow, respectively. As with the unprotonated DMA group, the intensity of the RDFs for the carbonyl group and polymer backbone decreased above the LCST. Due to the absence of a clear second minimum of the Oc–Ow RDFs, we only calculated the Nw in the first hydration shell of Oc which decreased by 23% at 338 K, compared with that at 283 K. This expulsion of water in the vicinity of the carbonyl group and polymer backbone during the course of coil-to-globule transition has also been similarly observed in MD simulations of PNIPAM.14,18,19
Overall, judging from the RDFs, we observe that the structural correlation between the DMA groups and water is affected by the protonation. Each DMA group in the coil state of PDMAEMA maintains the microstructure with water molecules. However, in the globule state (i.e., above the LCST), the unprotonated DMA groups are mainly shielded inside the globule state, while the protonated DMA groups are exposed on the surface of the globule state. Moreover, the carbonyl group and backbone of PDMAEMA also lose their contact with water molecules in the globule state.
This interesting conformational transition of PDMAEMA was also revealed by the pairwise energy during the production run. Fig. 5a shows the time averaged intramolecular pairwise energies of PDMAEMA. The coil states of PDMAEMA mostly maintained its self-interaction energy, indicating that there was not an appreciable change in the intramolecular structure. However, owing to the conformational change, the self-interaction energy gradually increased through the globule transition and was well converged as shown in the extension of the simulation (Fig. S3†). In the case of the intermolecular pairwise energy between PDMAEMA and water, the pairwise energy decreases with increasing temperature, as shown in Fig. 5b. The pairwise energy of the coil state was further reduced compared to the thermal effect. This decrease in the interaction energy between PDMAEMA and water molecules also supports the fact that the functional groups in PDMAEMA are shielded from water molecules above the LCST.
 | ||
| Fig. 5 Time series of (a) the intramolecular pairwise energies of PDMAEMA and (b) the intermolecular pairwise energies between PDMAEMA and water at 283, 303, and 338 K. | ||
H-bond analysis
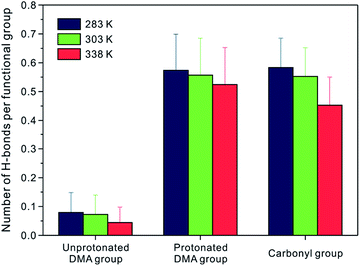
In the structural analysis of the coil and globule state of PDMAEMA, there is a difference not only in the dimension of PDMAEMA but also in the microstructure of water molecules in the vicinity of the functional groups. Since it has been discussed that the H-bond plays an important role in the coil-to-globule transition of a single chain of PNIPAM,16,19 we focused on the unprotonated DMA, protonated DMA, and carbonyl group, which can participate in the formation of H-bonding. The H-bond in this study was defined by using the geometric criteria of the donor and acceptor. Among the atoms in the candidate group for the H-bond, a pair can be considered to participate in H-bond formation if the distance between the donor and acceptor is less than 3.6 Å, and the angle between hydrogen-donor and donor–acceptor is less than 30°, simultaneously. The number of H-bonds was averaged for the last 10 ns of the production run.Fig. 6 shows the number of H-bonds per each functional group between the specific functional groups (i.e., the unprotonated DMA, the protonated DMA, and the carbonyl group) and water molecules, respectively. It can be seen that there are few H-bonds between the unprotonated DMA group and water. At 283 K, only 8% of the unprotonated DMA groups form an H-bond with water molecules, suggesting that the unprotonated DMA group is a poor H-acceptor for H-bond. However, owing to the polar nature of the protonated DMA group and the carbonyl group, 57% of Np and 58% of Oc atoms have H-bonds with water molecules. At 303 K, which is still in a coil state, the decrease in the number of H-bonds is insignificant for all functional groups. It is noteworthy that the number of H-bonds between the protonated DMA group and water molecules almost remains the same in the globule state. It indicates that the protonated DMA group maintains the H-bonds to water as well as the microstructure with water molecules regardless of the conformational state. On the other hand, the number of H-bonds for N–Ow and Oc–Ow pairs decreases by 44% and 22% in the globule state, respectively. These decreases in the number of H-bonds well correlate with that in the Nw for the first hydration shell of the N–Ow and Oc–Ow RDFs, as shown in Fig. 4, which show a 43% and 23% reduction in the Nw at 338 K, respectively. Thus, the water molecules in the first hydration shell particularly involved in H-bonds to each functional group.16 Note that the unprotonated DMA group hardly participates in H-bond to water molecules. The difference between the total number of H-bonds for the N–Ow pair at 283 and 338 K is as little as 0.5, whereas that for the Oc–Ow pair at 283 and 338 K is about 3.9. Therefore, we can conclude that the carbonyl group in PDMAEMA shows a considerable decrease in the number of H-bonds through the coil-to-globule transition.
Previous studies on PNIPAM have shown that the intrachain H-bonds between the amide nitrogen and the carbonyl oxygen in PNIPAM exist in its globule state, and can play a crucial role in the interaction for the coil-to-globule transition.13,20 In a stark contrast, we found interestingly that the intrachain H-bonds in PDMAEMA rarely existed (<0.1%) in its globule state. Although the atomistic simulation in this study is limited to the polymer length of 30-mer, which can lead to enhanced steric hindrance for the intramolecular H-bond, it suggests that the intrachain H-bond between the protonated DMA group and the carbonyl group is not a dominant factor for the coil-to-globule transition of PDMAEMA.
To investigate more detailed motion of water molecules surrounding the unprotonated DMA, protonated DMA, and carbonyl group, additional NPT simulations of 200 ps were sequentially performed five times from the last trajectories at each temperature, with the time interval of 0.01 ps for sampling. The H-bond relaxation time can be calculated for the H-bond not only between PDMAEMA and water but also among water molecules in the vicinity of the functional groups of PDMAEMA from the normalized time correlation function (TCF) as shown below,
| cx(t) = 〈hij(t)hij(t0)〉/〈hij(t0)hij(t0)〉 | (4) |
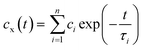 | (5) |
 | (6) |
Fig. 7a–c exhibit the relaxation behaviour of the H-bond between PDMAEMA and water. It is observed that the relaxation of H-bonds decays faster with increasing temperature due to the thermal energy. Among the three different functional groups, the cpw(t) of the unprotonated DMA group shows the fastest decay with the mean relaxation time of the H-bond between PDMAEMA and water (τpw) below 1 ps at all temperature conditions, as summarized in Table 2. It suggests that the H-bond between the unprotonated DMA nitrogen and water oxygen has poor stability. The relaxation behaviour of the cpw(t) of the protonated DMA group and the carbonyl group is much slower than that of the unprotonated DMA group, indicating that the functional groups maintain stable H-bonds to water molecules. The τpw of the protonated DMA group is always larger than that of the carbonyl group, but the difference diminishes with increasing temperature, for example, at 338 K, the difference is only 0.3 ps.
| Functional group | Temperature (K) | H-bond relaxation timea (ps) | |
|---|---|---|---|
| τ pw | τ ww | ||
| a The mean H-bond relaxation time is calculated by multi-exponential fitting the H-bond TCF. b τ pw and τww are the mean relaxation time of the H-bond between PDMAEMA and water, and among water molecules in the vicinity of each functional group, respectively. | |||
| Unprotonated DMA | 283 | 0.76 ± 0.38 | 1.38 ± 0.06 |
| 303 | 0.38 ± 0.06 | 0.88 ± 0.02 | |
| 338 | 0.24 ± 0.03 | 0.61 ± 0.01 | |
| Protonated DMA | 283 | 6.39 ± 0.94 | 1.23 ± 0.05 |
| 303 | 5.40 ± 0.71 | 0.81 ± 0.01 | |
| 338 | 3.04 ± 0.26 | 0.54 ± 0.01 | |
| Carbonyl | 283 | 4.27 ± 0.36 | 1.37 ± 0.04 |
| 303 | 3.55 ± 0.31 | 0.96 ± 0.02 | |
| 338 | 2.70 ± 0.48 | 0.68 ± 0.02 | |
Fig. 7d–f represent the relaxation behaviour of the H-bond among water molecules in the vicinity of each functional group. Comparing the cww(t) of two different DMA groups, the cww(t) of the unprotonated DMA groups, contrary to the cpw(t), decays more slowly than that of the protonated DMA group at all temperature ranges. The mean relaxation time of the H-bond among water molecules (τww) in the vicinity of the unprotonated DMA group is also slightly longer by about 12% than that of the protonated DMA group at 283 and 338 K. It indicates that the unprotonated DMA group acts more as a hydrophobic solute by disturbing the H-bond exchange among water molecules, resulting in the longer τww in the vicinity of the unprotonated DMA group.61 The cww(t) of the carbonyl group surprisingly shows a decaying behaviour similar to that of the unprotonated DMA group at 283 K. Moreover, at higher temperatures (303 and 338 K), the cww(t) decays even slower than that of the unprotonated DMA group, as shown in Fig. 7d and f. The τww in the vicinity of the carbonyl group is longer by about 18% and 26% than that of the protonated DMA group in the case of 303 and 338 K, respectively. We observe that the H-bond exchange among water molecules in the vicinity of the carbonyl group is mostly restricted in the globule state, with the longest H-bond relaxation time of 0.68 ps. Although the carbonyl group maintains the H-bond to water molecules, the extended τww in the vicinity of the carbonyl group can be associated with the polymer backbone near the carbonyl group, similar to the unprotonated DMA group.
Residence time
The motion of water molecules near the functional groups in PDMAEMA is also monitored to calculate the residence time, representing how long a water molecule will stay within a specific region. The residence time of water molecules in the vicinity of each functional group is calculated from the another TCF,| rj(t) = 〈pi(t)pi(t0)〉j/〈pi(t0)pi(t0)〉j | (7) |
Fig. 8 displays the residence TCF of water molecules in the vicinity of each functional group. The residence time of water molecules decreases with increasing temperature due to the thermal energy. Compared with the unprotonated DMA group, the residence TCF of water molecules in the vicinity of the protonated DMA group, rNp(t), decreases slowly, meaning that the water molecules stay longer around the protonated DMA group. However, there is no significant difference between the decreasing rate of rN(t) and rNp(t) with temperature change. In the case of the carbonyl group, we observe that the rOc(t) shows a slower decay than the rNp(t) at 303 and 338 K, while the rOc(t) shows a slightly faster decay than the rNp(t) at 283 K.
To understand this different tendency of the decay in the residence time for each functional group, we also calculated the residence time of water molecules in the first hydration shell, as shown in Table 3. It can be seen that the residence time of water molecules in the first hydration shell well correlates with its relaxation time of the H-bond between PDMAEMA and water, τpw. Since the motion of water molecules in the first hydration shell of each functional group is highly influenced by the strength of H-bonds between them, the residence time of the first hydration shell is obviously proportional to τpw. It is quite surprising to observe that the residence times in the vicinity of the carbonyl group at 303 and 338 K are 4.00 and 3.05 ps, respectively, which are longer than those of the protonated DMA group, even though the residence time of water in the first hydration shell of the protonated DMA group is much longer. It is considered that this unusual residence time of water molecules in the vicinity of the carbonyl group is caused by the relatively low decreasing rate of the τpw of the carbonyl group and by the extended τww in the vicinity of the carbonyl group.
| Functional group | Temperature (K) | Residence timea (ps) | |
|---|---|---|---|
| First shell | Up to 6.1 Å | ||
| a The residence time is calculated by integrating the residence TCF. | |||
| Unprotonated DMA | 283 | 0.25 ± 0.01 | 3.56 ± 0.12 |
| 303 | 0.22 ± 0.01 | 2.82 ± 0.03 | |
| 338 | 0.18 ± 0.00 | 2.11 ± 0.07 | |
| Protonated DMA | 283 | 2.82 ± 0.16 | 4.95 ± 0.20 |
| 303 | 2.37 ± 0.20 | 3.71 ± 0.11 | |
| 338 | 1.55 ± 0.05 | 2.87 ± 0.02 | |
| Carbonyl | 283 | 1.47 ± 0.05 | 4.78 ± 0.10 |
| 303 | 1.32 ± 0.09 | 4.00 ± 0.08 | |
| 338 | 1.05 ± 0.01 | 3.05 ± 0.07 | |
From the H-bond relaxation time and the residence time of water molecules it may be concluded that the water molecules near the carbonyl group are restricted in motion with fewer opportunities for the exchange of H-bonds. Although water molecules are also expelled from the unprotonated DMA groups which show the hydrophobic effect with the extended τww in the vicinity, the water dynamics surrounding the carbonyl group indicates a more restricted structure and temperature-sensitive behaviour compared with that surrounding the other functional groups, as the temperature increases. Thus, it can be suggested that the carbonyl group in PDMAEMA is more responsible for the coil-to-globule transition, involving the exclusion of water molecules with an entropic effect. This is consistent with the recent experimental study of Thavanesan et al.,45 who reported that the change in solvation of the carbonyl group and backbone mainly leads to the phase transition of PDMAEMA.
Protonation of the DMA group
The degree of protonation was adjusted to investigate the effect of protonation on the conformational state of PDMAEMA where the DMA groups were fully protonated or unprotonated. According to the pKa value of PDMAEMA, the DMA groups almost appear in the form of protonation and deprotonation under acidic conditions and basic conditions, respectively.29Fig. 9 shows the Rg of PDMAEMA with the fully protonated and unprotonated state of the DMA groups. The fully protonated PDMAEMA maintained the coil state through the production run at both 283 and even 338 K with a mean Rg of 16.8 and 16.9 Å for the last 10 ns, respectively. On the other hand, from the initial equilibrium step, the fully unprotonated PDMAEMA chain collapsed into a globule state with a mean Rg of about 10 Å, even at 283 K. It implies that PDMAEMA would be a water-soluble polyelectrolyte or becomes insoluble in water at the low and high pH conditions, respectively, and this is in good agreement with the experimental behaviour of PDMAEMA.29,43 | ||
| Fig. 9 Time evolution of the radius of gyration, Rg, for PDMAEMA with the fully protonated (red), partially protonated (green), and unprotonated (blue) state at (a) 283 K and (b) 338 K. | ||
The Rg values reveal that the fully protonated and unprotonated PDMAEMA prefer to be in the coil and globule state regardless of temperature changes, respectively. As expected, the N–Ow RDF for the fully unprotonated PDMAEMA shows a slight decrease in the intensity between the RDF peak at 283 and 338 K, as shown in Fig. 10a, indicating that the unprotonated DMA group maintains its hydration state. Fig. 10b displays the Oc–Ow RDF of the fully unprotonated PDMAEMA. Interestingly, it can be seen that the intensity of the Oc–Ow RDF decreases significantly at 338 K, with a decrease in Nw in the first hydration shell of Oc by 19%. A similar phenomenon is found in the fully protonated PDMAEMA, as shown in Fig. 10c and d. The Nw in the first hydration shell of Oc is reduced by 16% in the fully protonated PDMAEMA at 338 K, while that of Np is only reduced by 5%.
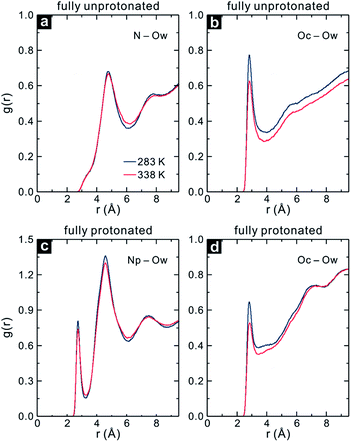 | ||
| Fig. 10 RDFs of the (a) N and (b) Oc atom in the fully unprotonated PDMAEMA, and (c) Np and (d) Oc atom in the fully protonated PDMAEMA to water oxygen (Ow) at 283 and 338 K. | ||
Even though the fully unprotonated and protonated PDMAEMA maintain their conformational states, water molecules are still expelled from the vicinity of the carbonyl group with increasing temperature, irrespective of the protonation state of PDMAEMA. Thus, it is quite obvious that the carbonyl group plays a crucial role in the coil-to-globule transition in PDMAEMA. Moreover, it can be suggested that the DMA group can affect the solvation behaviour of PDMAEMA with the degree of its protonation in solution, resulting in the pH-responsive property of PDMAEMA.
Conclusions
In this study, MD simulations have been successfully employed to observe the coil-to-globule transition of PDMAEMA in water and to understand the conformational state of PDMAEMA with atomic level at three different temperatures. The structural analysis, such as the Rg and WASA, as well as the pairwise energy analysis indicate that PDMAEMA shows a distinct conformational change through the LCST. The structural correlations between PDMAEMA and water were investigated to explore the hydration behaviour of the functional groups in the coil and globule state of PDMAEMA. From the RDFs of the functional groups in PDMAEMA it is observed that the protonated DMA group maintained its hydration state even in the globule state, while the unprotonated DMA group and the carbonyl group tended to lose their contact with water molecules. This expulsion of water molecules in the functional groups leads to the decrease in the number of H-bonds between each functional group and water. In particular, it is found that the carbonyl group shows a significant decrease in the number of H-bonds toward water molecules in the globule state.The motion of water molecules was further analysed to understand the conformational transition by monitoring the dynamic properties of water molecules in the vicinity of each functional group in detail. The residence time shows that the water molecules in the vicinity of the carbonyl group are more restricted in motion than other functional groups, with increasing temperature. This extended residence time results from the relatively low decreasing rate of the relaxation time of the H-bond between the carbonyl group and water, and from the extended relaxation time of the H-bond among water molecules in the vicinity of the carbonyl group. Therefore, our simulations suggest that the motion of water molecules near the carbonyl group is restricted with fewer H-bond exchange rates, which could be one of the possible driving forces for the coil-to-globule transition by the entropic effect.
The degree of protonation of the DMA group affects the solvation behaviour of PDMAEMA, resulting in its pH-responsiveness. Although the solvation behaviour of PDMAEMA depending on the degree of protonation is beyond the scope of this study, we note that the fully unprotonated and protonated PDMAEMAs maintain globule and coil states, respectively, regardless of temperature changes. The expulsion phenomenon of water molecules in the vicinity of the carbonyl group is also observed in the case of the fully unprotonated and protonated PDMAEMA, and it thus supports the role of each functional group in the conformational transition in PDMAEMA.
Acknowledgements
We thank the supercomputing resources of the UNIST Supercomputing Center. This work was supported by the National Research Foundation of Korea grant funded by the Korean Government (2010-0028684) and by the basic science research program (2013R1A1A2007491) through the National Research Foundation of Korea in the Ministry of Education, Science and Technology.Notes and references
- P. J. Flory, J. Chem. Phys., 1949, 17, 303–310 CrossRef CAS PubMed.
- F. Brochard and P. G. De Gennes, Macromolecules, 1977, 10, 1157–1161 CrossRef CAS.
- H. Feil, Y. H. Bae, J. Feijen and S. W. Kim, Macromolecules, 1993, 26, 2496–2500 CrossRef CAS.
- E. S. Gil and S. M. Hudson, Prog. Polym. Sci., 2004, 29, 1173–1222 CrossRef CAS PubMed.
- E. A. Clark and J. E. G. Lipson, Polymer, 2012, 53, 536–545 CrossRef CAS PubMed.
- T. M. Birshtein and V. A. Pryamitsyn, Macromolecules, 1991, 24, 1554–1560 CrossRef CAS.
- T. Hoare and D. McLean, Macromol. Theory Simul., 2006, 15, 619–632 CrossRef CAS.
- T. Koga, F. Tanaka, R. Motokawa, S. Koizumi and F. M. Winnik, Macromolecules, 2008, 41, 9413–9422 CrossRef CAS.
- Y. Tamai, H. Tanaka and K. Nakanishi, Macromolecules, 1996, 29, 6750–6760 CrossRef CAS.
- X. Wang, X. Qiu and C. Wu, Macromolecules, 1998, 31, 2972–2976 CrossRef CAS.
- Y. Zhang, S. Furyk, L. B. Sagle, Y. Cho, D. E. Bergbreiter and P. S. Cremer, J. Phys. Chem. C, 2007, 111, 8916–8924 CAS.
- J.-F. Lutz, O. Akdemir and A. Hoth, J. Am. Chem. Soc., 2006, 128, 13046–13047 CrossRef CAS PubMed.
- M. Alaghemandi and E. Spohr, Macromol. Theory Simul., 2012, 21, 106–112 CrossRef CAS.
- M. Alaghemandi and E. Spohr, RSC Adv., 2013, 3, 3638–3647 RSC.
- M. Alaghemandi and E. Spohr, Chem. Phys. Lett., 2013, 581, 80–84 CrossRef CAS PubMed.
- G. Longhi, F. Lebon, S. Abbate and S. L. Fornili, Chem. Phys. Lett., 2004, 386, 123–127 CrossRef CAS PubMed.
- H. Du, R. Wickramasinghe and X. Qian, J. Phys. Chem. B, 2010, 114, 16594–16604 CrossRef CAS PubMed.
- S. G. Lee, T. A. Pascal, W. Koh, G. F. Brunello, W. A. Goddard and S. S. Jang, J. Phys. Chem. C, 2012, 116, 15974–15985 CAS.
- S. A. Deshmukh, S. K. R. S. Sankaranarayanan, K. Suthar and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 2651–2663 CrossRef CAS PubMed.
- S. A. Deshmukh, S. K. R. S. Sankaranarayanan and D. C. Mancini, J. Phys. Chem. B, 2012, 116, 5501–5515 CrossRef CAS PubMed.
- S. A. Deshmukh, Z. Li, G. Kamath, K. J. Suthar, S. K. R. S. Sankaranarayanan and D. C. Mancini, Polymer, 2013, 54, 210–222 CrossRef CAS PubMed.
- X. Jiang, M. C. Lok and W. E. Hennink, Bioconjugate Chem., 2007, 18, 2077–2084 CrossRef CAS PubMed.
- C. V. Synatschke, A. Schallon, V. Jérôme, R. Freitag and A. H. E. Müller, Biomacromolecules, 2011, 12, 4247–4255 CrossRef CAS PubMed.
- C. Zhu, S. Jung, S. Luo, F. Meng, X. Zhu, T. G. Park and Z. Zhong, Biomaterials, 2010, 31, 2408–2416 CrossRef CAS PubMed.
- S. Agarwal, Y. Zhang, S. Maji and A. Greiner, Mater. Today, 2012, 15, 388–393 CrossRef CAS.
- H. Y. Cho, A. Srinivasan, J. Hong, E. Hsu, S. Liu, A. Shrivats, D. Kwak, A. K. Bohaty, H.-J. Paik, J. O. Hollinger and K. Matyjaszewski, Biomacromolecules, 2011, 12, 3478–3486 CrossRef CAS PubMed.
- J.-F. Gohy, S. Antoun and R. Jérôme, Macromolecules, 2001, 34, 7435–7440 CrossRef CAS.
- G. Liu, D. Wu, C. Ma, G. Zhang, H. Wang and S. Yang, ChemPhysChem, 2007, 8, 2254–2259 CrossRef CAS PubMed.
- H. Lee, S. H. Son, R. Sharma and Y.-Y. Won, J. Phys. Chem. B, 2011, 115, 844–860 CrossRef CAS PubMed.
- V. Bütün, S. Armes and N. Billingham, Polymer, 2001, 42, 5993–6008 CrossRef.
- F. A. Plamper, A. Schmalz, M. Ballauff and A. H. E. Müller, J. Am. Chem. Soc., 2007, 129, 14538–14539 CrossRef CAS PubMed.
- X. Liu, P. Ni, J. He and M. Zhang, Macromolecules, 2010, 43, 4771–4781 CrossRef CAS.
- E. Betthausen, M. Drechsler, M. Förtsch, F. H. Schacher and A. H. E. Müller, Soft Matter, 2011, 7, 8880–8891 RSC.
- H. Bao, L. Li, L. H. Gan, Y. Ping, J. Li and P. Ravi, Macromolecules, 2010, 43, 5679–5687 CrossRef CAS.
- X. Han, X. Zhang, H. Zhu, Q. Yin, H. Liu and Y. Hu, Langmuir, 2013, 29, 1024–1034 CrossRef CAS PubMed.
- F. A. Plamper, J. R. McKee, A. Laukkanen, A. Nykänen, A. Walther, J. Ruokolainen, V. Aseyev and H. Tenhu, Soft Matter, 2009, 5, 1812–1821 RSC.
- S. B. Lee, A. J. Russell and K. Matyjaszewski, Biomacromolecules, 2003, 4, 1386–1393 CrossRef CAS PubMed.
- X. J. Loh, S. J. Ong, Y. T. Tung and H. T. Choo, Polym. Chem., 2013, 4, 2564–2574 RSC.
- W. Wu, J. Liu, S. Cao, H. Tan, J. Li, F. Xu and X. Zhang, Int. J. Pharm., 2011, 416, 104–109 CrossRef CAS PubMed.
- A. P. Majewski, A. Schallon, V. Jérôme, R. Freitag, A. H. E. Müller and H. Schmalz, Biomacromolecules, 2012, 13, 857–866 CrossRef CAS PubMed.
- Z. Dong, H. Wei, J. Mao, D. Wang, M. Yang, S. Bo and X. Ji, Polymer, 2012, 53, 2074–2084 CrossRef CAS PubMed.
- J. Niskanen, M. Karesoja, T. Rossi and H. Tenhu, Polym. Chem., 2011, 2, 2027–2036 RSC.
- S. Dai, P. Ravi, C. H. Tan and K. C. Tam, Langmuir, 2004, 20, 8569–8575 CrossRef CAS PubMed.
- J. M. Bak, T. Lee, E. Seo, Y. Lee, H. M. Jeong, B.-S. Kim and H. Lee, Polymer, 2012, 53, 316–323 CrossRef CAS PubMed.
- T. Thavanesan, C. Herbert and F. A. Plamper, Langmuir, 2014, 30, 5609–5619 CrossRef CAS PubMed.
- H. Sun, J. Comput. Chem., 1994, 15, 752–768 CrossRef CAS.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Phys. Chem., 1995, 99, 5873–5882 CrossRef CAS.
- S. Yang, S. Yu, W. Kyoung, D. Han and M. Cho, Polymer, 2012, 53, 623–633 CrossRef CAS PubMed.
- X. P. Chen, C. A. Yuan, C. K. Y. Wong, S. W. Koh and G. Q. Zhang, Mol. Simul., 2011, 37, 990–996 CrossRef CAS.
- A. K. Tucker and M. J. Stevens, Macromolecules, 2012, 45, 6697–6703 CrossRef CAS.
- B. Tangeysh, M. Fryd, M. A. Ilies and B. B. Wayland, Chem. Commun., 2012, 48, 8955–8957 RSC.
- J. Niskanen, C. Wu, M. Ostrowski, G. G. Fuller, S. Hietala and H. Tenhu, Macromolecules, 2013, 46, 2331–2340 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. M. Brown, P. Wang, S. J. Plimpton and A. N. Tharrington, Comput. Phys. Commun., 2011, 182, 898–911 CrossRef CAS PubMed.
- F. S. Emami, V. Puddu, R. J. Berry, V. Varshney, S. V. Patwardhan, C. C. Perry and H. Heinz, Chem. Mater., 2014, 26, 2647–2658 CrossRef CAS.
- W. Li, J. Chem. Phys., 2013, 138, 014106 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- A. Shrake and J. A. Rupley, J. Mol. Biol., 1973, 79, 351–371 CrossRef CAS.
- A. Luzar, J. Chem. Phys., 2000, 113, 10663–10675 CrossRef CAS PubMed.
- H. Xu and B. J. Berne, J. Phys. Chem. B, 2001, 105, 11929–11932 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The potential energy components of the PCFF, average temperatures of PDMAEMA and water molecules, radius of gyration for replica simulations, intramolecular pairwise energy of PDMAEMA in the extension of the production run, and total system energies. See DOI: 10.1039/c4sm02242d |
| This journal is © The Royal Society of Chemistry 2015 |