Structural and mechanical properties of cardiolipin lipid bilayers determined using neutron spin echo, small angle neutron and X-ray scattering, and molecular dynamics simulations
Jianjun
Pan
*a,
Xiaolin
Cheng
bc,
Melissa
Sharp
d,
Chian-Sing
Ho
a,
Nawal
Khadka
a and
John
Katsaras
*efg
aDepartment of Physics, University of South Florida, Tampa, FL 33620, USA. E-mail: panj@usf.edu
bOak Ridge National Laboratory, Oak Ridge, TN 37831, USA
cDepartment of Biochemistry and Cellular and Molecular Biology, University of Tennessee, Knoxville, TN 37996, USA
dEuropean Spallation Source ESS AB, Lund, Sweden
eNeutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA. E-mail: katsarasj@ornl.gov
fDepartment of Physics and Astronomy, University of Tennessee, Knoxville, TN 37996, USA
gJoint Institute for Neutron Sciences, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
First published on 29th October 2014
Abstract
The detailed structural and mechanical properties of a tetraoleoyl cardiolipin (TOCL) bilayer were determined using neutron spin echo (NSE) spectroscopy, small angle neutron and X-ray scattering (SANS and SAXS, respectively), and molecular dynamics (MD) simulations. We used MD simulations to develop a scattering density profile (SDP) model, which was then utilized to jointly refine SANS and SAXS data. In addition to commonly reported lipid bilayer structural parameters, component distributions were obtained, including the volume probability, electron density and neutron scattering length density. Of note, the distance between electron density maxima DHH (39.4 Å) and the hydrocarbon chain thickness 2DC (29.1 Å) of TOCL bilayers were both found to be larger than the corresponding values for dioleoyl phosphatidylcholine (DOPC) bilayers. Conversely, TOCL bilayers have a smaller overall bilayer thickness DB (36.7 Å), primarily due to their smaller headgroup volume per phosphate. SDP analysis yielded a lipid area of 129.8 Å2, indicating that the cross-sectional area per oleoyl chain in TOCL bilayers (i.e., 32.5 Å2) is smaller than that for DOPC bilayers. Multiple sets of MD simulations were performed with the lipid area constrained at different values. The calculated surface tension versus lipid area resulted in a lateral area compressibility modulus KA of 342 mN m−1, which is slightly larger compared to DOPC bilayers. Model free comparison to experimental scattering data revealed the best simulated TOCL bilayer from which detailed molecular interactions were determined. Specifically, Na+ cations were found to interact most strongly with the glycerol hydroxyl linkage, followed by the phosphate and backbone carbonyl oxygens. Inter- and intra-lipid interactions were facilitated by hydrogen bonding between the glycerol hydroxyl and phosphate oxygen, but not with the backbone carbonyl. Finally, analysis of the intermediate scattering functions from NSE spectroscopy measurements of TOCL bilayers yielded a bending modulus KC of 1.06 × 10−19 J, which was larger than that observed in DOPC bilayers. Our results show the physicochemical properties of cardiolin bilayers that may be important in explaining their functionality in the inner mitochondrial membrane.
1. Introduction
Cardiolipin (CL) lipids are a group of anionic phospholipids that are found predominantly in the inner mitochondrial membrane (IMM) of eukaryotic cells,1 and in the plasma membranes of certain bacteria.2 Unlike common phospholipids, CL is composed of two phosphate moieties, each attached to two hydrocarbon chains via a glycerol backbone. CL's peculiar structure restricts phosphate mobility, reduces headgroup area, and promotes the tendency for forming non-lamellar phases.2,3 CL plays an important role in the IMM of eukaryotes, including: (1) supporting the activation of mitochondrial related enzymes; (2) disrupting4 or promoting5 supramolecular organization; and (3) increasing mitochondria membrane electronegativity which leads to programmed cell death.6,7 In addition, defects in CL remodeling can cause detrimental diseases such as Barth syndrome.8 More details about the physiological importance of CL can be found in recent review articles.2,9–11To understand CL's functionality, elucidating its detailed physicochemical properties through the use of model CL bilayers is essential. To date, only a handful of experimental results detailing the structure and organization of CL bilayers exist, including reports about headgroup orientation, thermotropic phase behavior, and the lamellar/non-lamellar phase transition (see review article2 and the references therein). Both coarse-grained and atomistic molecular dynamics (MD) simulation studies of CL bilayers have been carried out.12–20 However, the lack of experimental data needed for comparison has hampered the development of CL force fields. In the present study we used different contrast small angle neutron and X-ray scattering (SANS and SAXS, respectively), neutron spin echo (NSE) spectroscopy, and all-atom MD simulations to characterize the structural and mechanical properties of a fluid phase tetraoleoyl cardiolipin (TOCL) bilayer. Specifically, we developed a scattering density profile (SDP) model to jointly refine SANS and SAXS data. Bilayer structural parameters were then determined from SDP model analysis, along with component distributions, including volume probability (vP), one-dimensional electron density (ED) and neutron scattering length density (NSLD). We also performed five sets of area-constrained MD simulations. Model free comparison to experimental scattering data revealed the best simulated bilayer, from which detailed atomic interactions and the area compressibility modulus KA were determined. We also calculated the bending modulus KC of TOLC bilayers by analyzing the intermediate scattering functions from NSE measurements using a Zilman–Granek (ZG) model.21
2. Materials and methods
2.1 Small angle neutron and X-ray scattering
Synthetic TOCL lipid (sodium salt) was purchased from Avanti Polar Lipids (Alabaster, AL) and used as received. The molecular volume of TOCL was determined using an Anton-Paar DMA5000 vibrating tube density meter (Graz, Austria).22 For SANS experiments (Oak Ridge national Laboratory), 50 nm sized unilamellar vesicles (ULVs) were prepared by mixing 30 mg of TOCL lipid powder with 1.0 ml D2O water, followed by freeze–thaw cycling. The lipid dispersion was extruded using an Avanti mini-extruder. The resulting ULV solution was aliquoted into three microcentrifuge tubes, and diluted to different neutron external contrast conditions (i.e., 100, 70 and 50% D2O). The final lipid concentration was about 10 mg ml−1. ULVs for SAXS experiments (Cornell High Energy Synchrotron Source) were prepared in a similar manner, but using H2O water instead. All scattering experiments were performed at 30 °C. Details regarding sample preparation, experimental procedures and data reduction can be found in ref. 23–26.2.2 Neutron spin echo spectroscopy
50 nm sized ULVs suspended in 100% D2O were prepared as described for the small angle scattering experiments. NSE spectroscopy measurements were performed at the Spallation Neutron Source (SNS), Oak Ridge National Laboratory. SNS is a time-of-flight neutron source, and two ranges of wavelengths (5–8 Å and 8–11 Å) were used to cover a range of Fourier time τ from 30 ps to 82 ns, and a q-range from 0.05 to 0.16 Å−1. ULVs taken up in 3 mm thick Hellma quartz cells were placed in a temperature-controlled sample holder. Graphite foil was used to determine the instrumental resolution, and pure D2O water was used for background subtraction. The collected data were binned to yield four q-values per scattering angle, resulting in a total of 16 q-values. For a given q, the final output from the NSE measurement is the intermediate scattering function, S(q, τ)/S(q, 0). The bilayer bending modulus KC can be calculated from the intermediate scattering function using the ZG model:21| S(q, τ)/S(q, 0) = exp{−[Γ(q)τ]2/3}, | (1) |
| Γ(q) = 0.025ε(kBT/KC)1/2(kBT/η)q3, | (2) |
2.3 Molecular dynamics simulations
Initial coordinates for a TOCL bilayer made up of 100 lipids were generated by Packmol.28 Lipid hydrogen atoms were explicitly included (all-atom model), in addition to 5778 water molecules and counterions to neutralize the system. MD simulations were performed using NAMD 2.9 (ref. 29) and the CHARMM 36 lipid force field.30,31 Periodic boundary conditions were applied. For each system, atomic coordinates were first minimized using the conjugated gradient algorithm for 5000 steps, followed by 2 ns of equilibration in a constant particle number, pressure, and temperature (NPT) ensemble. Equilibrium was determined by monitoring the system's area per lipid and the root-mean-square deviation (RMSD). In all simulations, the van der Waals (vdW) interactions were truncated via a potential-based switching function used by X-PLOR. Starting from a switching distance of 10.5 Å, the vdW potential was brought smoothly to 0 at the cutoff distance of 12 Å. Electrostatic interactions were treated using the particle-mesh Ewald (PME) method with a 1.0 Å grid spacing.32,33 The r-RESPA multiple-time-step method34 was employed with a 2 fs time step for bonded, and 2 and 4 fs time steps for short-range non-bonded and long-range electrostatic interactions, respectively. The bonds between hydrogen and other atoms were constrained using the SHAKE algorithm.35We first simulated the TOCL bilayer using the NPT ensemble for 50 ns. Langevin dynamics were used to maintain a constant temperature of 303 K, while the Nosé-Hoover Langevin-piston algorithm36,37 was used to maintain a constant pressure of 1 bar. The z-axis was allowed to expand and contract independently of the x–y plane (semi-isotropic pressure coupling). The resulting lipid area was 122.5 Å2. This simulation was used to guide the development of an SDP model for subsequent analysis of SAXS and SANS data. An additional five sets of constant particle number, area, normal pressure and temperature (NAPnT) simulations were performed, where the average area per lipid was constrained to 127.2, 129.2, 131.2, 133.2 or 135.2 Å2, while the z-axis was allowed to expand and contract in order to maintain a constant Pn. Starting configurations for these simulations were selected snapshots from the NPT trajectory, with lipid areas close to their target values. The production run length for each of these simulations was between 101 and 132 ns. Only the final 50 ns of each trajectory were used for data analysis. For each of the area-constrained simulations, the surface tension γ was calculated from the difference between the normal and lateral components of the pressure tensor.38,39
The CHARMM-GUI Membrane Builder40 was used to generate coordinates for a dioleoyl phosphatidylcholine (DOPC) bilayer containing a total of 244 lipids. The entire system contained 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 408 water molecules. Simulations of DOPC followed the same procedures as those outlined for TOCL bilayers. The DOPC bilayer was first simulated using the NPT ensemble for 40 ns. The resulting lipid area was 67.5 Å2. Subsequently, five additional sets of NAPnT simulations were performed where the average lipid area was constrained to 63.4, 65.4, 67.4, 69.4 or 71.4 Å2. The production run length for each of these simulations was between 86 and 93 ns. All simulations were conducted on the Hopper supercomputer located at the National Energy Research Scientific Computing Center (NERSC).
408 water molecules. Simulations of DOPC followed the same procedures as those outlined for TOCL bilayers. The DOPC bilayer was first simulated using the NPT ensemble for 40 ns. The resulting lipid area was 67.5 Å2. Subsequently, five additional sets of NAPnT simulations were performed where the average lipid area was constrained to 63.4, 65.4, 67.4, 69.4 or 71.4 Å2. The production run length for each of these simulations was between 86 and 93 ns. All simulations were conducted on the Hopper supercomputer located at the National Energy Research Scientific Computing Center (NERSC).
3. Results and discussion
3.1 Constructing SDP model
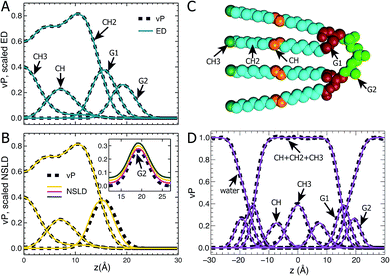
Following our previous studies of phosphatidylcholine (PC),23,41 phosphatidylglycerol (PG),25,42 and phosphatidylserine (PS)26 bilayers, the SANS and SAXS data for TOCL ULVs were analyzed using the SDP model shown in Fig. 1A. The four oleoyl chains of TOCL were parsed into three components, depending on the number of hydrogens associated with each carbon atom, namely, the terminal methyl (CH3), methylene (CH2) and unsaturated methine (CH) groups. The amphiphilic headgroup was parsed into the backbone carbonyl (G1), and a G2 group which is comprised of the two phosphates and the glycerol hydroxyl linkage. The reason for not separating the phosphate and glycerol linkage is because of their positional overlap, as indicated by our MD simulations. This complicates the determination of component volumes for the phosphate and glycerol linkage from MD simulations.43 On the other hand, our previous studies of PG and PS lipids indicate that both two-Gaussian (2G) and three-Gaussian (3G) headgroup models yield similar lipid bilayer structures.25,26,42 Based on these observations, we decided to use the 2G headgroup model to jointly refine the SANS and SAXS data.The SDP model is based on the concept that the bilayer's component ED and NSLD can be described by its volume probability vP. However, this is not always the case, as was previously demonstrated by a study of DOPC bilayers.41 The overall vP of the phosphate and choline moieties does not coincide with the overall ED and NSLD. This therefore necessitates separating the choline and phosphate into two components.41 To check whether the proposed SDP model (Fig. 1) is suitable for the TOCL bilayer, we show component vP together with the corresponding ED (Fig. 1B) and NSLD (Fig. 1C) distributions. For each component, good overlap is observed between its vP and the scaled ED (Fig. 1B) – the scaling factor is the ratio of the component volume and the component electron number. This indicates that each component's ED can be well represented by its vP.
For components in the hydrocarbon chain region (i.e., CH3, CH2 and CH), good overlap is obtained between their vPs and the corresponding NSLDs (Fig. 1C). However, some discrepancy was observed between G1's vP and its NSLD. Such a discrepancy also exists in the SDP models for PC, PG and PS bilayers.25,26,41 On the other hand, the difference is smaller than the typical positional uncertainties (∼0.5 Å) obtained from SDP model analysis. Therefore, we adopted the same grouping method for G1, as was used previously. For the G2 component, the glycerol linkage contains a hydroxyl which undergoes hydrogen exchange with the water solvent, making G2's NSLD dependent on D2O concentration.26,44 The inset to Fig. 1C compares G2's vP and its NSLDs at the three D2O concentrations used in our SANS measurements. It is clear that G2's vP overlays with the three sets of NSLDs, lending support for the G2 grouping used.
The grouping of atoms shown in Fig. 1C enables component vPs, and consequently their EDs and NSLDs, to be represented by analytical functions (Fig. 1D). Specifically, four Gaussian functions are used to describe components CH3, CH, G1 and G2; the summation of CH, CH2 and CH3 in the hydrocarbon chain region is represented by a symmetrical error function; and the water vP is obtained by subtracting the lipid's vP from unity.25,26,41 It is clear that component vPs can be well represented by these analytical functions. The goal of SDP model analysis is to determine a set of parameters describing these analytical functions by minimizing the difference between model form factors calculated from these analytical functions, and the experimental SANS and SAXS data.26
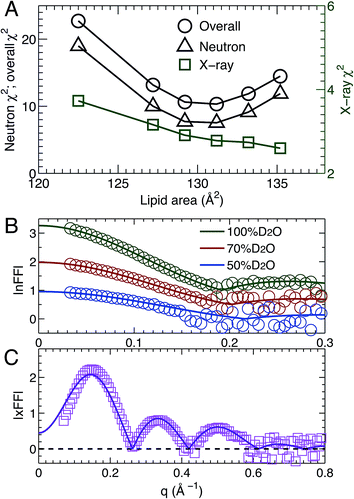
3.2 SDP analysis
Using the described SDP model we simultaneously fit three sets of different contrast SANS data and one set of SAXS data. The best fitting results are shown in Fig. 2. It is clear that the model form factors (solid lines in Fig. 2A and B) agree very well with the experimental data (open symbols). The corresponding component EDs (Fig. 2C) and NSLDs (Fig. 2D) were calculated from the vPs in Fig. 2E. Based on parameters describing the analytical functions representing component vPs, the structural properties of the TOCL bilayer are determined. They include the overall bilayer thickness DB, the bilayer hydrocarbon chain thickness 2DC, the distance between electron density maxima DHH, and the lipid area A. It should be noted that DB is given by the Gibbs dividing surface, which divides the water distribution into two equal parts (Fig. 2E). 2DC is defined by the full width of the error function, which is comprised of the CH, CH2 and CH3 components (Fig. 2E). A is related to either DB or 2DC through volumetric information, that is A = DB/2VL (VL is the lipid volume) or A = (VL − VHL)/DC (VHL is the headgroup volume).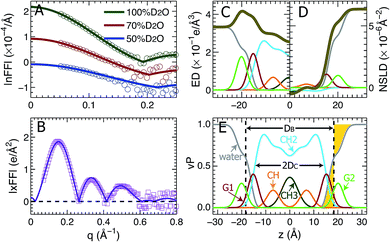 | ||
| Fig. 2 Simultaneously refining different contrast SANS and SAXS data using the SDP model. (A) Neutron form factors at three external D2O concentrations – data are shifted vertically for clarity. (B) X-ray form factor. (C) and (D) are the component ED and NSLD distributions of one bilayer leaflet. (E) Component vPs obtained from best fits to the data. They are used to calculate the EDs and NSLDs in (C) and (D), respectively. The overall bilayer thickness DB is defined by the Gibbs dividing surface (vertical dashed line), and the hydrocarbon chain thickness 2DC is represented by the full width of the error function describing the sum of the CH3, CH2 and CH components. Color scheme is the same as in Fig. 1. | ||
Table 1 contains several important TOCL bilayer structural parameters, which were calculated from the best SDP fit shown in Fig. 2. The total lipid volume VL, which was obtained from density measurements, and the lipid headgroup volume VHL were fixed during data analysis. A value of 490 Å3 for VHL was used, which was estimated from MD simulations of the TOCL bilayer and a tetramyristoyl cardiolipin (TMCL) bilayer (data not shown). This value is slightly smaller than a recently reported headgroup volume of 506.8 Å3 for TMCL.45 To assess the effect of VHL on bilayer structure, we performed additional SDP analysis by varying VHL by ±10%. The resultant lipid area A changed by only 0.2%, a difference which is negligible compared to the 2% upper bound limit in uncertainty associated with SDP analysis. Note that the small effect of VHL on lipid bilayer structure using SDP analysis was also observed for a PS bilayer.26
| TOCL (MD) | TOCL (SDP) | DOPC (SDP) | |
|---|---|---|---|
| V L (Å3) | 2400 | 2380 | 1303 |
| V HL (Å3) | 493 | 490 | 331 |
| D B (Å) | 36.6 | 36.7 | 38.7 |
| D HH (Å) | 37.4 | 39.4 | 36.7 |
| 2DC (Å) | 29.1 | 29.1 | 28.8 |
| A (Å2) | 131.2 | 129.8 | 67.4 |
Table 1 also lists structural parameters of a TOCL bilayer calculated from MD simulations with the average lipid area constrained to 131.2 Å2, and a DOPC bilayer which was determined using a similar SDP analysis.41 For the TOCL bilayer, MD simulations and SDP analysis yielded similar overall bilayer and hydrocarbon chain thicknesses. This is understandable since the simulation was performed at a lipid area (i.e., 131.2 Å2) close to that obtained from SDP analysis (i.e., 129.8 Å2) – the simulation also generated a lipid volume close to the experimental value. The largest discrepancy resides in the distance between the electron density maxima DHH. SDP analysis suggested a DHH that is 2.0 Å larger than what simulation predicted. This difference may explain the discrepancies between the simulation and experimental form factors in the following section.
Since DOPC contains two oleyol chains and TOCL contains four oleoyl chains, it is interesting to compare their bilayer structures. The last two columns in Table 1 show that the average cross-sectional area of the oleoyl chain in TOCL (32.5 Å2) is smaller than for DOPC (33.7 Å2). This is consistent with TOCL's larger hydrocarbon chain thickness, assuming the same molecular volume for the oleoyl chains in TOCL and DOPC bilayers. The larger 2DC for TOCL also explains its larger DHH, which is primarily determined from the position of the electron dense phosphate group. On the other hand, TOCL exhibits a smaller overall bilayer thickness DB than DOPC. This is mainly due to TOCL's smaller volume for each phosphate moiety, when compared to DOPC (i.e., 245 Å3 for TOCL versus 331 Å3 for DOPC). It is noteworthy that the larger DHH for the tetraoleoyl TOCL, compared to the dioleoyl DOPC, is consistent with a recent study which compared the structures of dimyristoyl PC (DMPC) and tetramyristoyl PC (TMCL) bilayers.45
3.3 Model-free evaluation of simulated bilayers
MD simulations are useful in revealing detailed molecular features within a lipid bilayer, assuming that the simulated bilayer is able to reproduce experimental observations. One way to validate simulations is to use a model free comparison between form factors calculated from simulated bilayers and the experimental ones shown in Fig. 2.25,26,46 Such comparisons were performed for the six sets of simulations with different lipid areas. The goodness of the comparison is given by χ2, which describes the difference between the simulation and experimental form factors.25,26,46Fig. 3A shows χ2 for individual neutron and X-ray form factors, and the overall χ2 which sums the neutron and X-ray χ2. Because there are three sets of neutron data, but only one X-ray data set, the neutron χ2 is larger than the X-ray χ2. In addition, the neutron χ2 is U-shaped, while the χ2 for X-rays decreases continuously with increasing lipid area. The overall χ2 behavior resembles that of the neutron χ2. The smallest overall χ2 was obtained near the lipid area predicted by SDP analysis. Fig. 3B and C show the detailed comparison between the best simulated bilayer with the smallest χ2 (i.e., A = 131.2 Å2) and the experimental form factors. It is clear that good agreement is obtained for the neutron data. However, noticeable differences are observed in the case of the X-ray form factor, especially in the region of the first lobe. This indicates that further improvements to the force fields describing CL bilayers are needed.3.4 Lipid bilayer area compressibility KA
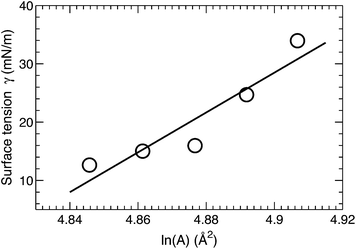
A surface tension γ was applied in order to constrain the average lipid area to a desired value. The magnitude of γ needed to displace the lipid area by a constant value is quantified by the lateral area compressibility modulus KA, which can be calculated from KA = ∂γ/∂(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A).46 For the five area-constrained simulations, the surface tensions and the corresponding lipid areas are shown in Fig. 4. A linear fit to the data resulted in a KA of 342 mN m−1. This value is smaller than that reported by two earlier simulations, which calculated KA by quantifying lipid area fluctuations.12,18 The larger values from these simulations may be attributed to their smaller lipid areas, which can in turn suppress lateral area fluctuations. As a control, we also simulated a DOPC bilayer at different lipid areas. The calculated KA is 320 mN m−1 (data not shown), which is close to the 321 mN m−1 obtained using the fluctuation expression, but greater than the 277 mN m−1 value calculated by the surface tension versus lipid area relationship.47 Our slightly larger KA for the tetraoleoyl TOCL bilayer, compared to the dioleoyl DOPC bilayer, implies that the glycerol linkage sterically hinders the two phosphate moieties, thus making it difficult for TOCL's four chains to compress against each other.2,3 On the other hand, the difference is small, implying that the restriction is not pronounced. This is consistent with the not too different chain cross-sectional areas for TOCL and DOPC bilayers shown in Section 3.2.
A).46 For the five area-constrained simulations, the surface tensions and the corresponding lipid areas are shown in Fig. 4. A linear fit to the data resulted in a KA of 342 mN m−1. This value is smaller than that reported by two earlier simulations, which calculated KA by quantifying lipid area fluctuations.12,18 The larger values from these simulations may be attributed to their smaller lipid areas, which can in turn suppress lateral area fluctuations. As a control, we also simulated a DOPC bilayer at different lipid areas. The calculated KA is 320 mN m−1 (data not shown), which is close to the 321 mN m−1 obtained using the fluctuation expression, but greater than the 277 mN m−1 value calculated by the surface tension versus lipid area relationship.47 Our slightly larger KA for the tetraoleoyl TOCL bilayer, compared to the dioleoyl DOPC bilayer, implies that the glycerol linkage sterically hinders the two phosphate moieties, thus making it difficult for TOCL's four chains to compress against each other.2,3 On the other hand, the difference is small, implying that the restriction is not pronounced. This is consistent with the not too different chain cross-sectional areas for TOCL and DOPC bilayers shown in Section 3.2.
Based on the polymer brush model,27 the bilayer bending modulus KC is related to the area compressibility modulus by KA = 24 KC/(2DC)2. Substituting KA (obtained from our surface tension calculation) and the hydrocarbon chain thickness 2DC (obtained from SDP analysis), the predicted KC turns out to be 1.2 × 10−19 J. We will compare this value to the bending modulus obtained from NSE analysis in Section 3.6.
3.5 Molecular interactions inferred from the “best” simulated bilayer
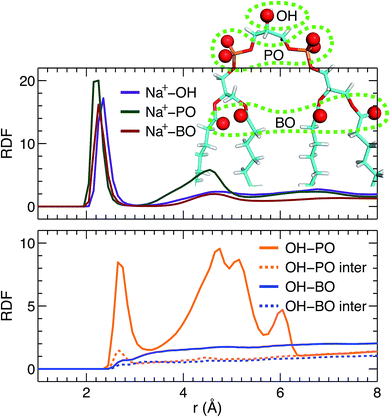
Direct comparison without any model intervening between the simulation and experimental form factors indicates that the simulated bilayer with an average lipid area of 131.2 Å2 agrees best with the experimental data. Here we show Na+ cation-lipid and lipid–lipid interactions based on the best simulated bilayer by calculating volume-averaged radial distribution functions (RDFs). We first calculated the RDF for Na+ ions with respect to three types of lipid oxygen atoms, namely, the hydroxyl oxygen of the terminal glycerol linkage (OH), the four phosphate non-ether oxygens (PO), and the four backbone carbonyl oxygens (BO). The results are shown in Fig. 5A. Well-resolved peaks are identified near 2.3 Å for all oxygens. Moreover, based on the magnitude of the RDF peaks, and the fact that there is only one OH, but four oxygens for the PO and BO groups, the Na+ ions interact most strongly with the glycerol linkage OH. Surprisingly, Na+ ions interact similarly with the phosphate PO and the backbone BO. This observation is very different from our previous study of a PS bilayer, where Na+ ions interacted weakly with the backbone carbonyl oxygen.26 One explanation for this is that the smaller headgroup per phosphate in TOCL provides less coverage for the backbone oxygens, exposing them to water and Na+ ions.48 The presence of strong interactions between cations and CL headgroups is consistent with other simulations.19In addition to ion–lipid interactions, we also explored the role of lipid–lipid interactions in mediating TOCL bilayer organization. RDFs between the glycerol linkage OH, and the phosphate PO and the backbone carbonyl BO are shown in Fig. 5B. The dashed lines are the calculated inter-lipid pairs, while the solid lines include both the inter- and intra-lipid pairs. It is clear that OH interacts with PO by forming hydrogen bonds, as indicated by the RDF peaks near 2.7 Å. Moreover, intra-lipid hydrogen bonding is preferred over inter-lipid. This may be related to the lipid's bulky tetra-chain configuration which impairs the inter-lipid association between the OH and PO groups in adjacent lipids. For the RDF between OH and PO, additional broad peaks were observed at larger distances, which likely reflect the presence of inter-lipid interactions. For interactions between OH and BO, no discernable RDF peaks were identified, indicating no preferred interactions between the pair. This is primarily due to the restricted motion of the glycerol OH,48 making it difficult for OH to approach the backbone BO which resides at the interface between the headgroup and the hydrocarbon chains. Our inter- and intra-lipid hydrogen bonding between the glycerol OH and phosphate PO is consistent with earlier simulations.14,18 This observation is also supported by Fourier transform infrared (FTIR) spectroscopy measurements.49 The authors remarked that the hydrogen bonding within CL headgroups provides a structural framework that may be important for conducting protons in the IMM. Hydrogen bonding is also in-line with the speculated role of CL as a proton trap for oxidative phosphorylation.50 It is interesting to note that our recent study of a PS bilayer revealed similar inter-lipid hydrogen-bonding interactions.26 It is conceivable then that the observed lipid–lipid interactions, which are weak or absent in neutral PC lipid bilayers, may be important for the specific functions played by these minority lipids.
3.6 Neutron spin echo spectroscopy and bilayer bending modulus
NSE spectroscopy is a powerful technique capable of studying dynamical properties of soft materials through the so-called intermediate scattering function. For example, NSE has been successfully applied in determining the bending moduli KC of various model membrane systems, such as vesicles composed of pure lipids with different hydrocarbon chain composition,51 lipids with and without cholesterol,52 lipids with an antimicrobial peptide,53 and oriented multibilayers,54 to name a few.As described in the Materials and Methods, by changing the scattering angle and the wavelength band, the intermediate scattering function S(q, τ)/S(q, 0) is obtained at discrete q values as a function of Fourier time τ. An example of the normalized intermediate scattering functions at six scattering vectors is shown in Fig. 6A. Using eqn (1) the data points at each q were fitted by a stretched exponential decay curve (solid lines). It is clear that the intermediate scattering functions are well modeled by the stretched exponential decay over the entire Fourier time regime. This indicates that the obtained NSE signal is dominated by membrane fluctuations in the q range studied. Moreover, the relaxation rate Γ(q) increases with q. This is shown in Fig. 6B, where Γ(q) is plotted as a function of q3. A linear fit to the data results in a slope b of 7.1 ± 0.2 Å3 ns−1. Based on the ZG model (eqn (2)), b is related to the bilayer's bending modulus KC. Taking the viscosity η of D2O to be 0.9759 cP at 30 °C,55 and the coefficient ε to be one (i.e., KC ≫ kBT), the calculated KC is 9.5 × 10−19 J with an uncertainty of σ(KC) = 2 KCσ(b)/b = 5.4 × 10−20 J. This KC is much larger than that of a typical lipid bilayer.27 The abnormally large KC derived from the ZG model has been attributed by neglecting local dissipation within the bilayer.51–53,56 To compensate for the dissipation, an effective viscosity ηeff, which is three times that of the bulk solvent viscosity, was introduced.51,53 One explanation for the altered viscosity is that the properties of water near the bilayer interface could be modified by molecular interactions (e.g., hydrogen bonding and electrostatic interactions) formed between the amphiphilic lipids and the interfacial water molecules. On the other hand, the choice of ηeff was mainly geared to reconciling differences between NSE results and those from other experimental approaches.51,57 Substituting ηeff into eqn (2), the new bending modulus becomes: KC = (1.06 ± 0.06) × 10−19 J. This value is close to the prediction in Section 3.4, which was calculated from the simulation-derived area compressibility modulus KA and a polymer brush model.
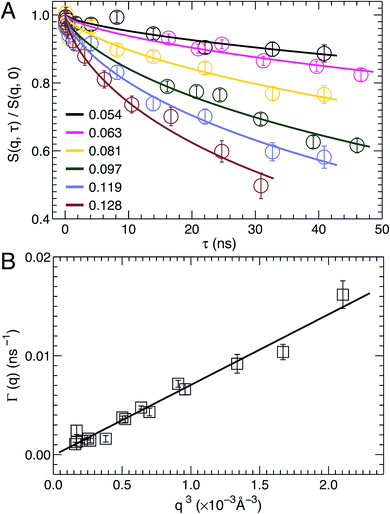 | ||
| Fig. 6 (A) Stretched exponential decays of NSE intermediate scattering functions S(q, τ)/S(q, 0) at selected scattering vectors q. For each curve, the corresponding q is shown in the figure legend. Analytical fits using eqn (1) are shown as solid lines. (B) The relaxation rate Γ(q) obeys the universal scaling law, Γ(q) ∼ q3. This is confirmed by a linear fit (solid line) to the data, which has a slope b of 7.1 ± 0.2 Å3 ns−1. | ||
In addition to scaling the solvent viscosity, the dissipation within a lipid bilayer can also be accounted for by considering that when a bilayer is bent, one monolayer is stretched and the other is compressed.58 This leads to an inter-monolayer friction which damps the fluctuation in the density difference between the coupled monolayers.58 The effective bending modulus KCeff from NSE measurements (eqn (2)) is then contributed by the usual hydrodynamically damped bending mode and the slipping mode damped by inter-monolayer friction:56,58KCeff = KC + d2KA, where d is the distance between the monolayer neutral plane (no compression or stretching) and the bilayer center.56,58,59 The physical basis of the substitution has been discussed by Watson and Brown.56 Using the polymer brush model mentioned above,27 we have KCeff = KC [1 + 24(d/2DC)2]. The difficulty associated with this method is how to determine the location of the neutral plane. Since DOPC and TOCL bilayers have a similar hydrocarbon chain thickness (Table 1), we assume the neutral plane is located similarly in the two bilayers, namely at d = 16.4 Å.53 This results in KC = (1.10 ± 0.06) × 10−19 J, which is in good agreement with the value obtained from scaling the solvent viscosity.
Recently, DMPC and TMCL bilayers were compared using X-ray diffuse scattering.45 The authors reported that the bending modulus KC for TMCL bilayers is about 50% larger than that of DMPC. For DOPC, the reported KC ranges from 7.6 × 10−20 J (ref. 60) to 8.5 × 10−20 J (ref. 27), depending on the experimental technique used. Our calculated KC for TOCL bilayers, using the ZG model and an effective viscosity, is 29–45% larger compared to previously reported KC for DOPC bilayers. X-ray diffuse scattering also predicted a KC of 7.5 × 10−20 J for the TMCL bilayer,45 a value smaller than that of the TOCL bilayer. The same trend is observed when comparing the two-chain PC lipid bilayers, that is the KC of DMPC is smaller than that of DOPC.27
4. Conclusions
In the present study we used scattering experiments and MD simulations to study the various structural and mechanical properties of a TOCL bilayer. In particular, an SDP model was developed based on MD simulations to jointly refine different contrast SANS and SAXS data. This resulted in detailed component vP, ED and NSLD profiles, as well as lipid bilayer structural parameters. The hydrocarbon chain thickness 2DC and the distance between electron density maxima DHH were found to be larger than those of the corresponding DOPC bilayer, while TOCL's overall bilayer thickness DB is smaller, primarily due to its smaller headgroup volume per phosphate. The cross-sectional area per oleoyl chain is also smaller for the TOCL bilayer, compared to DOPC. Area stretching moduli KA for TOCL and DOPC bilayers were determined by simulating at different lipid areas. It was found that the KA for TOCL (342 mN m−1) is slightly larger than that for DOPC (320 mN m−1). By directly comparing simulation and experimental form factors, we identified the best simulated bilayer from which detailed atomic interactions within a TOCL bilayer were determined. We found that Na+ cations interact most strongly with the glycerol hydroxyl linkage, followed by the phosphate and backbone carbonyl oxygens. The glycerol hydroxyl also forms intra- and inter-lipid hydrogen bonds with the phosphate oxygen, but not with the backbone carbonyl oxygen. The bending modulus KC of TOCL bilayers was determined using NSE spectroscopy measurements and the ZG model. Compared to DOPC bilayers, KC was found to be larger for TOCL. We believe that the physicochemical properties of a TOCL bilayer reported here may be important for elucidating the functionality of cardiolipin lipids in the IMM.Abbreviations
| TOCL | Tetraoleoyl cardiolipin |
| NSE | Neutron spin echo |
| DOPC | Dioleoyl phosphatidylcholine |
| CL | Cardiolipin |
| TMCL | Tetramyristoyl cardiolipin |
| DMPC | Dimyristoyl phosphatidylcholine |
| PC | Phosphatidylcholine |
| PG | Phosphatidylglycerol |
| PS | Phosphatidylserine |
| IMM | Inner mitochondrial membrane |
| SANS | Small angle neutron scattering |
| SAXS | Small angle X-ray scattering |
| MD | Molecular dynamics |
| SDP | Scattering density profile |
| vP | Volume probability |
| ED | Electron density |
| NSLD | Neutron scattering length density |
| ZG model | Zilman–Granek model |
| ULV | Unilamellar vesicle |
| SNS | Spallation neutron source |
| RDF | Radial distribution function |
Acknowledgements
Part of the research conducted at ORNL's High Flux Isotope Reactor (IPTS 7168) and Spallation Neutron Source (IPTS 5975 and IPTS 6192) was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy. CHESS is supported by the NSF & NIH/NIGMS via NSF award DMR-1332208. Part of the computation used the resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231. J. Katsaras is supported through the Scientific User Facilities Division of the DOE Office of Basic Energy Sciences (BES), and from the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory (ORNL), managed by UT-Battelle, LLC, for the U.S. Department of Energy (DOE) under contract no. DE-AC05-00OR2275. J. Pan is supported by a startup fund from the University of South Florida.References
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS PubMed.
- R. N. A. H. Lewis and R. N. McElhaney, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2069–2079 CrossRef CAS PubMed.
- P. R. Allegrini, G. Pluschke and J. Seelig, Biochemistry, 1984, 23, 6452–6458 CrossRef CAS.
- V. Betaneli, E. P. Petrov and P. Schwille, Biophys. J., 2012, 102, 523–531 CrossRef CAS PubMed.
- D. Acehan, A. Malhotra, Y. Xu, M. D. Ren, D. L. Stokes and M. Schlame, Biophys. J., 2011, 100, 2184–2192 CrossRef CAS PubMed.
- B. Heit, T. Yeung and S. Grinstein, Am. J. Physiol., 2011, 300, C33–C41 CrossRef CAS PubMed.
- M. Crimi and M. Degli Esposti, Biochim. Biophys. Acta, Mol. Cell Res., 2011, 1813, 551–557 CrossRef CAS PubMed.
- A. J. Chicco and G. C. Sparagna, Am. J. Physiol.: Cell Physiol., 2007, 292, C33–C44 CrossRef CAS PubMed.
- Z. T. Schug and E. Gottlieb, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2022–2031 CrossRef CAS PubMed.
- S. M. Claypool, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2059–2068 CrossRef CAS PubMed.
- M. Schlame and M. D. Ren, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 2080–2083 CrossRef CAS PubMed.
- M. Dahlberg and A. Maliniak, J. Phys. Chem. B, 2008, 112, 11655–11663 CrossRef CAS PubMed.
- S. Poyry, T. Rog, M. Karttunen and I. Vattulainen, J. Phys. Chem. B, 2009, 113, 15513–15521 CrossRef CAS PubMed.
- T. Rog, H. Martinez-Seara, N. Munck, M. Oresic, M. Karttunen and I. Vattulainen, J. Phys. Chem. B, 2009, 113, 3413–3422 CrossRef CAS PubMed.
- M. Dahlberg and A. Maliniak, J. Chem. Theory Comput., 2010, 6, 1638–1649 CrossRef CAS.
- M. A. Kiebish, R. Bell, K. Yang, T. Phan, Z. D. Zhao, W. Ames, T. N. Seyfried, R. W. Gross, J. H. Chuang and X. L. Han, J. Lipid Res., 2010, 51, 2153–2170 CrossRef CAS PubMed.
- N. Khalifat, J. B. Fournier, M. I. Angelova and N. Puff, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2724–2733 CrossRef CAS PubMed.
- D. Aguayo, F. D. Gonzalez-Nilo and C. Chipot, J. Chem. Theory Comput., 2012, 8, 1765–1773 CrossRef CAS.
- T. Lemmin, C. Bovigny, D. Lancon and M. Dal Peraro, J. Chem. Theory Comput., 2013, 9, 670–678 CrossRef CAS.
- S. Poyry, O. Cramariuc, P. A. Postila, K. Kaszuba, M. Sarewicz, A. Osyczka, I. Vattulainen and T. Rog, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 769–778 CrossRef CAS PubMed.
- A. G. Zilman and R. Granek, Phys. Rev. Lett., 1996, 77, 4788–4791 CrossRef CAS PubMed.
- J. J. Pan, X. L. Cheng, F. A. Heberle, B. Mostofian, N. Kucerka, P. Drazba and J. Katsaras, J. Phys. Chem. B, 2012, 116, 14829–14838 CrossRef CAS PubMed.
- N. Kučerka, M. P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef PubMed.
- F. A. Heberle, J. J. Pan, R. F. Standaert, P. Drazba, N. Kucerka and J. Katsaras, Eur. Biophys. J., 2012, 41, 875–890 CrossRef CAS PubMed.
- N. Kučerka, B. W. Holland, C. G. Gray, B. Tomberli and J. Katsaras, J. Phys. Chem. B, 2012, 116, 232–239 CrossRef PubMed.
- J. J. Pan, X. L. Cheng, L. Monticelli, F. A. Heberle, N. Kucerka, D. P. Tieleman and J. Katsaras, Soft Matter, 2014, 10, 3716–3725 RSC.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- S. E. Feller, D. X. Yin, R. W. Pastor and A. D. MacKerell, Biophys. J., 1997, 73, 2269–2279 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- J. Sonne, F. Y. Hansen and G. H. Peters, J. Chem. Phys., 2005, 122, 124903 CrossRef PubMed.
- O. Berger, O. Edholm and F. Jahnig, Biophys. J., 1997, 72, 2002–2013 CrossRef CAS PubMed.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef PubMed.
- J. J. Pan, F. A. Heberle, S. Tristram-Nagle, M. Szymanski, M. Koepfinger, J. Katsaras and N. Kucerka, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 2135–2148 CrossRef CAS PubMed.
- H. I. Petrache, S. E. Feller and J. F. Nagle, Biophys. J., 1997, 72, 2237–2242 CrossRef CAS PubMed.
- J. Pan, D. Marquardt, F. A. Heberle, N. Kucerka and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2966–2969 CrossRef CAS PubMed.
- A. L. Boscia, B. W. Treece, D. Mohammadyani, J. Klein-Seetharaman, A. R. Braun, T. A. Wassenaar, B. Klosgen and S. Tristram-Nagle, Chem. Phys. Lipids, 2014, 178, 1–10 CrossRef CAS PubMed.
- Q. Waheed and O. Edholm, Biophys. J., 2009, 97, 2754–2760 CrossRef CAS PubMed.
- A. R. Braun, J. N. Sachs and J. F. Nagle, J. Phys. Chem. B, 2013, 117, 5065–5072 CrossRef CAS PubMed.
- R. N. Lewis, D. Zweytick, G. Pabst, K. Lohner and R. N. McElhaney, Biophys. J., 2007, 92, 3166–3177 CrossRef CAS PubMed.
- W. Hubner, H. H. Mantsch and M. Kates, Biochim. Biophys. Acta, 1991, 1066, 166–174 CrossRef CAS.
- T. H. Haiens and N. A. Dencher, Febs Lett., 2002, 528, 35–39 CrossRef.
- Z. Yi, M. Nagao and D. P. Bossev, J. Phys.: Condens. Matter, 2009, 21, 155104 CrossRef PubMed.
- L. R. Arriaga, I. Lopez-Montero, F. Monroy, G. Orts-Gil, B. Farago and T. Hellweg, Biophys. J., 2009, 96, 3629–3637 CrossRef CAS PubMed.
- J. H. Lee, S. M. Choi, C. Doe, A. Faraone, P. A. Pincus and S. R. Kline, Phys. Rev. Lett., 2010, 105, 038101 CrossRef PubMed.
- M. C. Rheinstadter, W. Haussler and T. Salditt, Phys. Rev. Lett., 2006, 97, 048103 CrossRef PubMed.
- C. H. Cho, J. Urquidi, S. Singh and G. W. Robinson, J. Phys. Chem. B, 1999, 103, 1991–1994 CrossRef CAS.
- M. C. Watson and F. L. H. Brown, Biophys. J., 2010, 98, L9–L11 CrossRef CAS PubMed.
- S. Komura, T. Takeda, Y. Kawabata, S. K. Ghosh, H. Seto and M. Nagao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 041402 CrossRef CAS.
- U. Seifert and S. A. Langer, Europhys. Lett., 1993, 23, 71–76 CrossRef.
- E. Evans and A. Yeung, Chem. Phys. Lipids, 1994, 73, 39–56 CrossRef CAS.
- J. Pan, S. Tristram-Nagle, N. Kucerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |