Colloidal particles in blue phase liquid crystals

Abstract

We study the effect of disorder on the phase transitions of a system already dominated by defects. Micron-sized colloidal particles are dispersed chiral nematic liquid crystals which exhibit a blue phase (BP). The colloids are a source of disorder, disrupting the liquid crystal as the system is heated from the cholesteric to the isotropic phase through the blue phase. The colloids act as a preferential site for the growth of BPI from the cholesteric; in high chirality samples BPII also forms. In both BPI and BPII the colloids lead to localised melting to the isotropic, giving rise to faceted isotropic inclusions. This is in contrast to the behaviour of a cholesteric LC where colloids lead to system spanning defects.

---

1 Introduction

Colloid–liquid crystal composites are an exciting class of responsive, soft materials. Colloidal particles mixed into liquid crystals create defects in the (ideally defect free) ordered phase. The form of the defects is dependent on the particle size, the alignment of the mesogens at the particle surface and how strongly this alignment is enforced (the anchoring strength). Colloids tend to aggregate in order to share defects and minimise the disruption of the ordered phase. Structures including lines,¹ plates² and 3d colloidal glasses³ are formed. An even richer range of colloidal structures are observed when the liquid crystal is chiral.^4,5

One such chiral liquid crystal phase is the cholesteric blue phase. The blue phases of chiral liquid crystals consist of an ordered array of defect lines. They only exist in a narrow range of temperatures and chiralities between the isotropic and cholesteric phase due to the delicate balance between satisfying an increased degree of twist at the expense of the formation of defect lines. Depending on the temperature and chirality, these defect lines form either a cubic lattice in blue phase one (BPI) and blue phase two (BPII) and an amorphous network in blue phase three (BPIII).⁶

Simulation work^7,8 has suggested that the cubic structure of the blue phase lattice could be used as a template to assemble 3d photonic crystals and other switchable opto-electronic structures. In particular varying the size of colloids in composite blue phase-colloidal particle photonic crystals is predicted to alter the photonic band gap.⁸ However, the addition of particles to a BP raises the question of how the particles will interact with a phase already dominated by defects. For small particles with weak surface anchoring such as those used by Cordoyiannis et al.⁹ the particles are assumed to contribute to the stability of the blue phase by occupying the defect cores of an undistorted blue phase lattice as in simulation.¹⁰ For particles much larger than the defect lines, it is clearly essential to be able to visualise what happens close to the particle surfaces.

When the particle size and anchoring strength are considered a rich variety of colloidal structures are observed, depending on the anchoring strength at the colloid surface. Recent simulation results¹¹ have shown that the occupation of an undistorted lattice is an ideal case. For weak anchoring at the particle surface, the blue phase lattice acts as a template for the colloids, but as the anchoring strength increases the colloids' own defects become dominant and the blue phase lattice is distorted.

There have been only limited experiments on micron-sized colloidal particles in blue phases.¹² These studies have focused on the ability of colloidal particles to increase the (temperature) existing range of the blue phase. They show that for micron-sized colloidal particles there is only a negligible increase in blue phase stability. There are no published images showing the changes to the ordered state due to colloids dispersed within the blue phase. In this study we use confocal microscopy to observe large (r = 1.5 μm) colloidal particles dispersed in a cholesteric blue phase in order to explore the influence of the colloids on the behaviour of the blue phases.

We build on previous studies of these colloidal particles dispersed within cholesteric and nematic liquid crystals both in the bulk¹³ and at interfaces.^14,15 The colloids have strong planar anchoring at their surface and form flat plates perpendicular to the helical axis in the cholesteric phase.

In order to prepare a blue phase we take the liquid crystal through a phase transition with the colloids already dispersed. Colloidal particles introduce disorder, which has a significant effect on phase transitions.¹⁶ It has been shown that the addition of quenched disorder effectively smooth out a first order phase transition, making it second order above a certain degree of randomness.¹⁷ The theory of disorder in liquid crystals has been applied successfully to the case of aerosils dispersed in nematics,^18,19 smectics^20,21 and nematics confined within random pore glasses.²² An extensive review can be found in Popa-Nita et al.²³ Further, Cordoyiannis et al.⁹ reported that the particles affect the nature of phase transitions, in particular the transitions from the isotropic phase to the BP. The transitions become broader and “smear out” with increased concentrations of nano-particles.

The effect of disorder on phase transitions from more ordered to less ordered phases is pertinent to systems beyond the liquid crystal colloid composite reported here. In the field of nuclear reactor materials, the presence of a disordered phase between an ordered phase and the melt has been shown to confer increased stability and resistance to radiation damage.²⁴ The melting behaviour of inclusions in metallic systems is of interest for engineering applications and is often difficult to observe in situ.²⁵

Below, we explore how a system already dominated by defects responds to disorder. We observe micron-sized colloidal particles dispersed in a blue phase exhibiting LC. The effect of particles on the behaviour of the liquid crystal on heating from the cholesteric phase through the blue phase to the isotropic is explored. We observe that well ordered BPI and BPII form in the presence of colloids, but subsequently localised melting occurs.

2 Materials and methods

The liquid crystal is a three-component commercial mixture. It consists of two nematic liquid crystals, 5CB (Aldrich) and a fluorinated nematic mixture, JC1041-XX (Chisso). Finally a chiral dopant, ZLI-4572 (Merck) is added to create a chiral nematic liquid crystal. Varying the concentration of the chiral dopant varies the pitch of the liquid crystal. The composition and estimated pitch length of the liquid crystals used in these studies can be found in Table 1. This was calculated using values for the helical twisting power of ZLI-4572 given by Yan et al.²⁶ Short pitch mixtures exhibit both BPI and BPII. Long pitch mixtures exhibit only BPI. The three components were mixed by stirring overnight until uniform.

Table 1 The chiral dopant concentrations used in this study

Mixture	Concentration of chiral dopant	Pitch length
Long pitch	7%	0.40 μm ± 0.01 μm
Short pitch	10%	0.29 μm ± 0.01 μm

---

Colloidal particles, fluorescein isothiocyanate (FITC)-labelled melamine with carboxylate-modified surfaces, were purchased from Fluka, r = 1.5 μm. These were dried under vacuum at 40 °C overnight prior to use. The colloidal particles were dispersed in the cholesteric phase of the liquid crystal mixture under stirring, sonication (via an ultrasound bath VWR Ultrasonic Cleaner) and vortex mixing. Care was taken to ensure that the liquid crystal did not enter the isotropic phase. Cooling from the isotropic phase in the presence of particles can result in the formation of a cellular solid.²⁷ Once the samples were uniform (confirmed via visual inspection and microscopy) they were used immediately. If samples were stored then the colloidal particles were re-dispersed prior to use. This dispersion method was chosen over a co-solvent transfer method to avoid the risk of contamination. The final volume fraction was 3%.

To explore the effect of particle size some experiments were performed with r = 0.5 μm (FITC)-labelled melamine, carboxylate-modified colloids also from Fluka.

Once the colloidal particles were uniformly dispersed samples were loaded into glass capillaries (0.05 × 1 × 50 mm) or hand built sample cells via capillary action. The cells were sealed using silicone vacuum grease (Dow Corning) and used immediately.

Blue phases are only prepared by heating from the cholesteric phase as the colloidal particles rapidly sediment out from the isotropic phase. When blue phases are prepared by heating, the elastic nature of the cholesteric and blue phases prevents the colloidal particles from sedimentation. Bulk samples of colloidal particles in the cholesteric phase are stable to sedimentation for months.

Some preliminary experiments were performed using an Instec Hotstage in conjunction with a confocal microscope to allow the colloidal particles to be imaged in three dimensions.

To allow a greater control of heating rate a custom heating stage was constructed. The temperature is controlled using a Lakeshore 331 temperature controller to ±0.005 °C. Samples were mounted in the hotstage using heat sink paste (RM) to ensure good thermal contact. A lid was placed over the sample inside the stage body to increase thermal stability. Once mounted, the sample was heated rapidly (10 °C min⁻¹) to within 5 °C of the blue phase transition. The heating rate was then decreased to 1 °C min⁻¹. For the final stage (within approximately 1 °C of the transition) the heating rate was decreased further to 0.1 °C min⁻¹. During heating, time lapse images were recorded using a Zeiss Observer.Z1 inverted confocal microscope in conjunction with a Zeiss LSM 700 scanning system and a 20× NA = 0.8 objective. The FITC in the colloids was excited using a 488 nm diode laser. The transmission signal from the laser was also recorded. Once the blue phase transition was observed the temperature was maintained constant until the transition was complete. Further heating and cooling of the sample was then performed within the blue phase to study the effect of colloidal particles. The temperature was recorded digitally via an adapted LabView application provided by Lakeshore.

3 Results and discussion

3.1 Colloidal particles in the cholesteric phase

Colloidal particles mixed into cholesteric liquid crystals have been shown to stabilise the oily streak network forming a colloidal particle stabilised defect gel.⁵ Colloidal particles with planar alignment form flat sheets perpendicular to the helical axis.¹³ In this study a similar behaviour is observed; flat plates of colloidal particles are found surrounded by defects and always at the junction of oily streaks as can be seen from Fig. 1. On heating towards the blue phase transition the oily streak network undergoes significant rearrangement. This rearrangement of defects results in some movement of the associated colloidal particles. However, on average, the colloidal particles remain in flat plates perpendicular to the helical axis and surrounded by defect lines. This was confirmed using confocal microscopy in conjunction with the Instec stage.

Fig. 1 (a) Colloidal particles in the oily streak network. A composite confocal microscopy image of the fluorescent signal from the colloidal particles (green) held in the oily streak network (grey imaged in transmission with crossed polarisers) of the cholesteric. Scale bar 100 μm (b) blue phase I (c) blue phase II scale bars 50 μm.

3.2 Cholesteric to blue phase transition

In the absence of colloids. In the absence of colloids the oily streak network and other defects present in the cholesteric act as nucleation sites for the blue phase. In Fig. 2(a) a sample with a dense oily streak network and no colloidal particles is heated rapidly (5 °C min⁻¹ and then 1 °C min⁻¹) to close to the blue phase transition temperature. This rapid heating ensures that the defect network does not have time to anneal. On heating through the transition the oily streak defects thicken as the blue phase grows from the cores (Fig. 2(b) and (c)). The blue phase grows outwards from the defects with islands of aligned cholesteric texture (Fig. 2(d)), the last to disappear.

Fig. 2 The transition from cholesteric to blue phase in a planar cell. These images were taken using a confocal microscope between crossed polarisers. False colour has been used to enhance contrast. (a) The cell has not been annealed prior to use. Oily streak defects (dark purple) are present in the cholesteric. (b–e) The blue phase (purple with a rough texture) grows from the defects leaving islands of (orange and smooth) cholesteric. (f) These eventually disappear leaving the sample with a rough texture. The initially defected regions are still visible as the blue phase grains have different orientations here. Scale bars 50 μm.

The observation that the blue phase grows preferentially from preexisting defects, either in the form of oily streaks or defects surrounding colloidal particles is unsurprising. The formation of BPI from a uniformly aligned cholesteric requires the formation of a lattice of defects. When the cholesteric already possesses defects it is likely that there is a lower cost for defect formation and the blue phase can preferentially grow from the defect regions. The blue phase which grows from these regions exhibits a range of colours; indicating different alignments of the ordered BPI grains as in Fig. 4. This is in contrast to BPI in regions where the parent cholesteric had uniform alignment. In the aligned regions the blue phase has a single colour indicating that the grains have similar alignments.

Fig. 3 The transition from cholesteric to blue phase in the presence of colloidal particles. (a) Prior to the transition, colloidal particles are held in the oily streak network, the thick dark lines. (b) Blue phase starts to grow from these lines making them thicker. (c) The blue phase (pale) continues to grow from the defects, leaving islands of the dark ordered cholesteric phase. These islands gradually shrink. (d) Eventually colloidal particles are left embedded in a blue phase. Darker shading indicates where the principle defects were as the blue phase had a greater choice of alignment in these regions. Scale bars 50 μm.

Fig. 4 Polarising optical microscopy of a time sequence (constant temperature) cholesteric to blue phase transition with colloids of 1 μm. The previously defected regions become blue phase with different orientations (colours) of grains. Scale bars 20 μm.

The transition from the cholesteric to blue phase takes around a minute to complete. We measured the speed at which the blue phase expands into the aligned cholesteric manually using ImageJ. The phase fronts which advance from the defects into the aligned cholesteric move at 0.5 ± 0.1 μm s⁻¹. This is slow compared to velocities reported for nematic isotropic fronts ∼100 μm s⁻¹ (ref. 28) reflecting the highly visco-elastic nature of the cholesteric and blue phases. During these transitions the temperature changes at a maximum rate of 0.1 °C min⁻¹ and by at most 0.1 °C (due to lag in the temperature stage). Even if the temperature stage is set to hold at a given temperature once the transition is under way it continues to completion. We do not see the coexistence of long lasting cholesteric blue phase.

Simulation studies by Henrich et al.²⁹ predict that homogeneous nucleation of a BP from a uniformly aligned cholesteric forms a disordered blue phase lattice similar in nature to BPIII rather than the equilibrium structure of either BPI or BPII. These disordered structures are kinetically stabilised. Experimentally, as seen here, it appears that heterogeneous nucleation from defects is more likely and these disordered structures are avoided.

In the presence of colloids. In the presence of colloids the particles stabilise the oily streak network⁵ pinning it in place. Colloidal particles are themselves surrounded by defects in the cholesteric phase¹³ as can be seen from Fig. 1 and 3(a). All of these defects act as nucleation sites for the blue phases, which can be seen to grow from the colloidal particles and the oily streaks simultaneously, Fig. 3(b). As in the case with no dispersed colloidal particles, the islands of aligned cholesteric between defects are the last to transition to the blue phase, Fig. 3(c). The particles have little influence on the cholesteric to blue phase transition, other than increasing the stability of the oily streak network which acts as a nucleation site from the blue phase. The velocity of the phase fronts is unaffected by the presence of colloids.

3.3 Blue phase to isotropic transition

Adding colloidal particles to a blue phase liquid crystal has a clear effect on the kinetics of the phase transition between the blue phase and the isotropic phase. They also lead to a shift in the transition temperature.

Low chirality samples. As discussed in the previous section, colloidal particles and their associated defects act as nucleation sites for the blue phase. In low chirality samples once the sample is in BPI the colloidal particles are observed to be surrounded by uniform BPI, Fig. 3(d). On further heating but at temperatures below the final melting point dark regions are observed around the colloidal particles. Colloidal particles within these regions move due to Brownian motion indicating that locally the elastic modulus is lower. Very occasionally dark regions without colloidal particles can be observed once the temperature is increased further. This is rare, typically blue phases melt from the regions around colloidal particles which grow to fill the whole sample. Finally, the whole blue phase melts. The dark regions become completely black. This indicates that the regions are present through the full height of the sample. Colloidal particles within these black regions sediment through the isotropic phase onto the sample boundaries.

High chirality samples. In samples with higher chirality the liquid crystal can exhibit both BPI and at slightly higher temperatures BPII. The presence of colloidal particles has no discernible effect on the BPI to BPII phase transition, Fig. 5. Unlike the cholesteric to BPI transition there is no evidence of nucleation from the colloidal particles or BPI grain boundaries. Once the sample is heated further in BPII, dark regions similar to those seen in lower chirality samples surround the colloidal particles, Fig. 5(d). The transition temperatures of these phenomena with reference to the cholesteric to BPI transition can be found in Table 2. We note, Fig. 5 and 7 show an indication of BPI and BPII grain sizes, which are unaffected by the presence of colloids.

Fig. 5 Transmission images with crossed polarisers. (a) Colloidal particles in BPI. (b) Transition from the blue phase I to blue phase II (c) further heating towards the isotropic in the presence of colloidal particles leads to the BPII coarsening. (d) Melted regions surrounding colloidal particles. Scale bars 50 μm.

Table 2 Table of appearance temperatures of the various transitions with reference to the cholesteric to BPI transition

Chirality	Total range of blue phases	Transition to BPII	Temperature below BP to isotropic transition at which melted regions containing colloids appear	Temperature below BP to isotropic transition at which melted regions without colloids appear
Low	0.49 ± 0.03 °C	Not seen	0.34 ± 0.01 °C	0.16 ± 0.02 °C, 3 observations
High	0.66 ± 0.08 °C	0.24 ± 0.01 °C	0.29 ± 0.02 °C	Not seen

---

Fig. 6 Composite confocal images of colloidal particles (green) surrounded by faceted inclusions in (a) BPII scale bar 20 μm and (b) BPI. Scale bar 50 μm.

Fig. 7 Composite confocal images of colloidal particles (green) in (a) blue phase I (grey scale) and (b) blue phase II. Scale bars 50 μm.

3.4 The phase of the inclusions

Once the melted regions have appeared, colloidal particles are free to move within them. Colloidal particles do not leave the dark regions. If dark regions shrink, due to a temperature fluctuation, clusters of colloidal particles become more compact indicating a phase separation. There are two candidate phases which exist at higher temperatures than BPI and BPII which have reduced birefringence. These are BPIII and the isotropic phase.

BPIII, an isotropic disordered lattice of defects,³⁰ is only weakly birefringent and appears as a blue fog in polarising optical images. The materials used in our study do not exhibit BPIII in the absence of colloidal particles. However, given that nano-particles have been shown to stabilise BPIII³¹ and disordered blue phases have been shown to appear at phase transitions²⁹ and in the presence of colloidal particles,¹¹ a disordered blue phase cannot immediately be discounted as a candidate for the dark regions.

A more compelling reason to conclude that the dark regions are composed of the isotropic phase is that the colloidal particles move in these regions. BPI and BPII are visco-elastic in character.^32,33 The cholesteric phase and BPIII are highly viscous and possess a similar viscosity to one another (η = 0.1 Pa s).³⁴ The isotropic phase is a Newtonian fluid. Using particle tracking routines in IDL developed by E. Weeks and others³⁵ we measured the mean squared displacement of the colloidal particles within these dark regions and extract a diffusion constant. From this we calculated the associated viscosity of the melted regions to be η = 0.005 ± 0.002 Pa s. This is the same order of magnitude as that of 5CB at the same temperature in the isotropic phase, 0.016 Pa s implying that the dark regions are inclusions of the isotropic phase. The final value of the diffusion coefficient extracted from the particle tracking results must be used cautiously as the equations used to extract the diffusion coefficient are not applicable to partially ordered fluids. However, the fact that the colloids move at all in these regions and are stationary in both the cholesteric and blue phases is highly suggestive that the region is in the isotropic phase given the difference in viscosity between the LC and isotropic phases.

The presence of the isotropic phase close to the colloidal particles suggests that colloidal particles act as nucleation sites for the isotropic phase. There is only limited work on the effect of large colloidal particles on an ordered blue phase. Simulations of small colloidal particles with weak or zero surface anchoring dispersed in blue phases find that they are localised at the defect junctions⁷ of a cubic blue phase. However, this arrangement is extremely sensitive to the anchoring strength and size of the colloidal particles. For even moderate adjustments the blue phase defect structure becomes disordered.¹¹ Ravnik et al.³⁶ performed simulations on micron size colloidal particles in confinement. They find that for finite anchoring strength at the colloidal particle surface the colloidal particles are surrounded by a cage of defects.

Transition temperatures. Table 2 shows the transition temperatures of the low and high chirality blue phase with colloids with reference to the cholesteric to blue phase transition temperature. There is no significant difference in the range of existence of the blue phase with and without colloids.

We also record the appearance temperature of dark regions which appear below the bulk blue phase to isotropic transition with reference to the (bulk) blue phase to isotropic temperature. It should be stressed that these regions appear below the bulk transition temperature and remain local to the colloidal particles. They do not grow further if the temperature is maintained constant. The temperature must be increased in order for the bulk blue phase to melt. The vast majority of these regions are observed to appear close to colloidal particles, however a small number are observed without colloidal particles. No such regions are observed in samples without colloidal particles.

The presence of the dark regions suggests that we have entered a biphasic region of the phase diagram, with a colloid rich disordered phase coexisting with a colloid poor blue phase. We do not see coexistence between the blue phase and isotropic on heating in the absence of colloids. However, the blue phase to isotropic transition is first order and coexistence between the blue phase and isotropic has been observed using calorimetry³⁷ and using microscopy on cooling from the isotropic phase.³⁸ This would suggest that the colloidal particles increase the temperature range of coexistence between the blue phase and the isotropic.

Studies of disorder in nematic systems have shown that the presence of disorder lowers the nematic–isotropic transition temperature. This appears to be the case here, as the temperature of the cholesteric to blue phase and the blue phase to isotropic transitions are lower close to colloidal particles which act as regions of disorder.

The fact that the colloidal particles expand phase coexistence between the blue phase and the isotropic might lead us to expect that they would also promote coexistence between BPI and BPII. However, we do not observe such coexistence. We propose a tentative explanation; the region around the colloidal particles will have a higher concentration of defects than the rest of the sample regardless of the nature of the blue phase. These defects do not have the structure of either blue phase and so present no advantage for the nucleation of the higher temperature ordered phase. On a more fundamental level it suggests to us that the picture of disorder enhancing phase coexistence at first order phase transitions¹⁷ is unhelpful in the BPI to BPII case.

3.5 Facets

The faceted nature of the melted regions as shown in Fig. 6 shows that they are constrained by the elastic anisotropy of the embedding blue phase. Faceted regions are larger and more clearly visible in BPII. In BPII the grain size of the blue phase is significantly larger than the faceted regions. Facets within a grain have the same orientation. In BPI the grain size is typically smaller than the melted regions, facets are more irregular and do not have an obvious orientation. There are also more preferential directions for faceting due to the bcc symmetry of BPI. The orientation of the melted region is independent of the orientation of the underlying colloidal cluster.

The facets are extremely temperature sensitive. Very small temperature fluctuations (smaller than the stability of the temperature stage) can cause the facets to round off and disappear. Facets can reappear at later times in response to temperature fluctuations.

The interfacial tension between the blue phase and the isotropic phase is anisotropic. This is demonstrated most clearly by the fact that mono-crystals of the blue phase grown by slowly cooling from the isotropic phase exhibit clear facets which reflect the underlying symmetry of the blue phase.⁶ Careful study of the nature of these facets was used to determine the symmetries of the blue phases.⁶

In the case we study, inclusions of the isotropic phase are embedded in a polycrystalline blue phase. At equilibrium the inclusions need to minimise their surface energy for a given volume whilst minimising distortions in the surrounding lattice. In an elastically isotropic medium all inclusions will be spherical, minimising the surface area. In an elastically anisotropic medium facets form, these reflect the symmetry of the surrounding medium, as can be seen from the different facet symmetries in the two blue phases.

Other systems, principally metal alloys exhibit faceted inclusions embedded in the polycrystalline bulk material. Studies of liquid lead inclusions in an aluminium matrix have shown that above a certain inclusion size facets are observed.²⁵ There is an energy cost associated with deforming the flat facet into a curved interface. This cost is associated with the nucleation of steps on the flat interface and it scales with the inclusion radius. The faceted form of the inclusion is shown to be metastable. On heating, facets round off but reform on cooling although with a much more rounded form. The authors suggest that the spherical shape is in fact the equilibrium shape and that faceted inclusions are kinetically arrested. Heating increases the atomic mobility and allows the facets to round off. For our blue phase samples, even where flat facets are present the corners remain rounded with a radius of curvature of 5 ± 1 μm (measured manually using ImageJ).

The faceted inclusions of the isotropic phase in our sample are observed to round on heating. Given the soft nature of the system the degree of heating required to round off a facet is very small, less than the temperature variability of our sample stage. Faceted regions fluctuate in size and facets appear and disappear in response to very small temperature changes. The fluctuations indicate that the activation energy to create steps in a blue phase interface is very small. This is in agreement with the observation that faceted mono-crystals of the blue phase can only be grown at very slow cooling rates (∼0.01 °C min⁻¹).³⁸

3.6 Local melting

The relationship between the area of the melted region and the area occupied by the enclosed colloidal particles is not straightforward. The area and shape of the melted regions are extremely temperature sensitive and fluctuate within the temperature variability of the sample stage. We measure the maximum extent of the melted regions at a temperature below the BP to isotropic transition and compare it to the number of enclosed colloidal particles.

Melted regions are selected by hand using ImageJ.³⁹ As colloidal particles are clustered, there is insufficient resolution to extract individual colloidal particle coordinates so a coarse-grained approach was adopted. The fluorescent signal from the colloidal particles was smoothed, a threshold applied and the clusters of colloidal particles identified as regions of connected pixels using in-built IDL routines. The values of the threshold and smoothing as well as the minimum region size are optimised to ensure that all colloids are identified without the inclusion of artefacts. The area of each colloidal particle region is calculated.

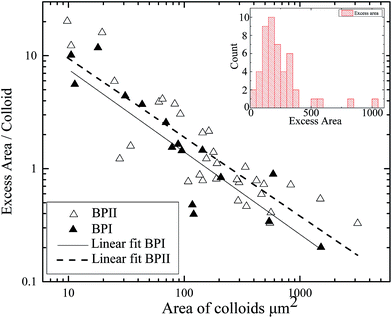
The colloidal particle areas and the areas of the associated melted regions are compared. Specifically, we compare the excess melted region (the area of melted region minus the area of the associated colloidal particles) with the area of the underlying colloidal particles. Colloidal particles are found in flat sheets so the area of the fluorescent signal is a good proxy for the number of colloidal particles. The results can be found in Fig. 8. The excess area is inversely proportional to the number of colloidal particles over two decades of area. This indicates that the melted region associated with a colloidal particle cluster is independent of the cluster size and roughly constant. The size of the melted regions and their associated colloidal clusters are essentially uncorrelated as can be seen in Fig. 9.

Fig. 8 The excess area of melted regions per colloidal particle compared to the area of the underlying colloidal particles. The lines are linear fits through the two datasets, they have slopes of −0.6 and −0.7. Inset is a histogram of the excess areas.

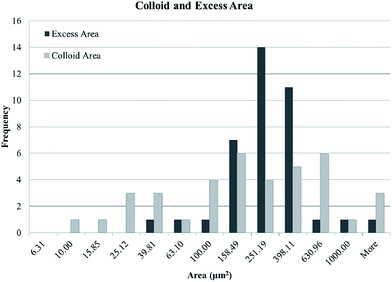Fig. 9 Histograms of the excess area of melted regions compared to the area of the underlying colloidal particles. The bins are logarithmic in width.

The extent of these melted regions beyond their associated colloidal particles is independent of the number of colloidal particles in the associated aggregate and whether the surrounding medium is BPI or BPII. The former observation would seem to contradict a heterogeneous nucleation mechanism. In heterogeneous nucleation the energy balance is between the energy saving of having a volume of lower energy phase balanced by the cost of the surface between the two phases. The presence of an impurity can reduce the second cost by removing a portion of the interface thus reducing the energy barrier to nucleation. If we apply this logic to our system then the larger aggregates with a larger surface area would therefore preferentially nucleate a larger volume of isotropic phase than small aggregates, which is not the case as shown in Fig. 8.

A tentative explanation is as follows; the surface tension of the BP–isotropic interface is manifestly anisotropic, as shown by the faceted inclusions discussed above and the faceted nature of blue phase crystals grown by cooling from the isotropic phase. There are different energy costs associated with each of the “crystal” orientations. At the size of melted regions that we can observe, this additional anisotropic term appears to dominate over any effects mediated by the colloidal particle surfaces. The elasticity of the surrounding medium is more significant at this length scale than the effects due to the surface area of the inclusions. The elastic anisotropy of the blue phase may influence to the extent that a melted region can grow into an ordered blue phase if it is not in a favourable orientation.

3.7 Particle size

The particle size and the anchoring type and strength at the particle surfaces have a significant effect on the behaviour of colloidal particles dispersed within all liquid crystal phases.^12,40,41 In the case of the blue phase, experiments have shown that increasing the particle size decreases blue phase stability.¹² In our case we have used large colloids in order to be able to unambiguously explore their arrangements with respect to the liquid crystal phase. A limited set of experiments were performed with colloids of r = 0.5 μm. The behaviour observed was qualitatively the same as the larger colloids (see ESI†). This is perhaps unsurprising as previous experimental¹² and theoretical studies⁷ have shown that the change in behaviour with respect to stability occurs when colloids are smaller than the unit cell size.

4 Conclusions

Colloidal particles with planar surface anchoring do not hinder the formation of BPI from the cholesteric. Indeed, the colloids and their associated defects act as nucleation sites for BPI. Once formed the BP texture is unperturbed, and the BP grain size is unaffected by the presence of particles. This holds in BPI where the grain size is typically smaller than the colloidal inclusion and in BPII where the grains are frequently much larger than the colloids.

The presence of colloids has no observable effect on the transition from BPI to BPII (where both exist). However, the colloids do have a profound effect on the transition from the BP to the isotropic. They cause localised melting of the blue phase to the isotropic at temperatures below the bulk BP–isotropic transition temperature. The shapes of the locally melted regions are anisotropic, suggesting that the anisotropic nature of the blue phase-isotropic surface tension influences the shape of the melted regions. In contrast to particles dispersed in a cholesteric liquid crystal, where colloids are held within a system spanning oily streak network,⁵ this melting is a purely local phenomenon: it is unaffected by the BP grain size. Compared to the cholesteric, there are no associated non local defects, equivalent to the oily streaks.

Colloidal particles have previously been shown to create defects in ordered chiral phases.^7,41–43 It is possible that for the cholesteric to blue phase transition these defects act as nucleation sites for the higher temperature, defect dominated blue phase. Within the blue phases, recent simulation work¹¹ has shown that particles with strong surface anchoring disrupt the blue phase lattice, this disruption may favour melting to the isotropic. This simulation is with particles which are smaller than the BP unit cell. For larger particles, a cage of disordered defects is observed.⁷ In both cases the disorder is local to the particle as observed in our experiments.

The area of the melted region per colloid is independent of the size of the colloidal cluster, we conclude that energetics is not strongly influenced by the particle surfaces. Instead this suggests that the area of the melted region is controlled by the anisotropic blue phase–isotropic surface tension rather than by a simple heterogeneous nucleation mechanism. There is no difference in the melted area per colloids between inclusions in the two blue phases. These behaviours are in marked contrast to research where nano particles extend the range of these subtle phases.

Acknowledgements

This work was funded by EPSRC grant EP/G03673X/1. We thank O. Henrich and J. Lintuvuori for helpful discussions.

References

1. J. C. Loudet, P. Barois and P. Poulin, Nature, 2000, 407, 611–613.
2. T. Araki and H. Tanaka, Phys. Rev. Lett., 2006, 97, 127801.
3. T. A. Wood, J. S. Lintuvuori, A. B. Schofield, D. Marenduzzo and W. C. K. Poon, Science, 2011, 334, 79–83.
4. U. Tkalec, M. Ravnik, S. Copar, S. Zumer and I. Musevic, Science, 2011, 333, 62–65.
5. M. Zapotocky, L. Ramos, P. Poulin, T. C. Lubensky and D. A. Weitz, Science, 1999, 283, 209–212.
6. P. Oswald and P. Pieranski, Nematic and Cholesteric Liquid Crystals, Taylor and Francis, 2005.
7. M. Ravnik, G. P. Alexander, J. M. Yeomans and S. Žumer, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5188–5192.
8. M. Stimulak and M. Ravnik, Soft Matter, 2014, 10, 6339–6346.
9. G. Cordoyiannis, V. S. Rao Jampani, S. Kralj, S. Dhara, V. Tzitzios, G. Basina, G. Nounesis, Z. Kutnjak, C. S. Pati Tripathi, P. Losada-Pérez, D. Jesenek, C. Glorieux, I. Muševič, A. Zidanšek, H. Ameinitsch and J. Thoen, Soft Matter, 2013, 9, 3956.
10. M. Ravnik, G. P. Alexander, J. M. Yeomans and S. Zumer, Faraday Discuss., 2010, 144, 159–169.
11. K. Stratford, O. Henrich, J. S. Lintuvuori, M. E. Cates and D. Marenduzzo, Nat. Commun., 2014, 5, 3954.
12. I. Dierking, W. Blenkhorn, E. Credland, W. Drake, R. Kociuruba, B. Kayser and T. Michael, Soft Matter, 2012, 8, 4355.
13. N. Hijnen, T. A. Wood, D. Wilson and P. S. Clegg, Langmuir, 2010, 26, 13502–13510.
14. A. C. Pawsey, J. S. Lintuvuori, T. A. Wood, J. H. J. Thijssen, D. Marenduzzo and P. S. Clegg, Soft Matter, 2012, 8, 8422–8428.
15. J. S. Lintuvuori, A. C. Pawsey, K. Stratford, M. E. Cates, P. S. Clegg and D. Marenduzzo, Phys. Rev. Lett., 2013, 110, 187801.
16. M. Plischke and B. Bergersen, Equilibrium Statistical Physics, World Scientific, 1994.
17. A. Nihat Berker, Phys. A, 1993, 194, 72–76.
18. G. S. Iannacchione, C. W. Garland, J. T. Mang and T. P. Rieker, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 5966–5981.
19. A. Hourri, T. Bose and J. Thoen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 051702.
20. P. S. Clegg, R. J. Birgeneau, S. Park, C. W. Garland, G. S. Iannacchione, R. L. Leheny and M. E. Neubert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 031706.
21. M. K. Ramazanoglu, P. S. Clegg, R. J. Birgeneau, C. W. Garland, M. E. Neubert and J. M. Kim, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 061706.
22. Liquid Crystals in Complex Geometries, ed. G. P. Crawford and S. Žumer, Taylor and Francis, 1996.
23. V. Popa-Nita, I. Gerlic and S. Kralj, Int. J. Mol. Sci., 2009, 10, 3971–4008.
24. K. Sickafus, R. Grimes and J. Valdez, Nat. Mater., 2007, 6, 217–223.
25. H. Gabrisch, L. Kjeldgaard, E. Johnson and U. Dahmen, Acta Mater., 2001, 49, 4259–4269.
26. J. Yan and S.-T. Wu, Opt. Mater. Express, 2011, 1, 1527.
27. V. Anderson, E. Terentjev, S. Meeker, J. Crain and W. C. K. Poon, Eur. Phys. J. E, 2001, 4, 11–20.
28. J. Cleaver and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S1901–S1909.
29. O. Henrich, K. Stratford, D. Marenduzzo and M. E. Cates, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13212–13215.
30. O. Henrich, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2011, 106, 107801.
31. E. Karatairi, V. Tzitzios, G. Nounesis, G. Cordoyiannis, J. Thoen, C. Glorieux and S. Kralj, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041703.
32. K. Negita, Liq. Cryst., 1998, 24, 243–246.
33. O. Henrich, K. Stratford, P. V. Coveney and M. E. Cates, Soft Matter, 2013, 9, 10243–10256.
34. R. N. Kleiman, D. J. Bishop, R. Pindak and P. Taborek, Phys. Rev. Lett., 1984, 53, 2137–2140.
35. R. Besseling, L. Isa, E. R. Weeks and W. C. K. Poon, Adv. Colloid Interface Sci., 2009, 146, 1–17.
36. M. Ravnik, J.-i. Fukuda, J. M. Yeomans and S. Žumer, Soft Matter, 2011, 7, 10144–10150.
37. J. Thoen, Phys. Rev. A, 1988, 37, 1754.
38. R. Barbet-Massin, P. Cladis and P. Pieranski, Phys. Rev. A, 1984, 30, 1161.
39. W. S. Rasband, ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, http://imagej.nih.gov/ij/, 1997–2014.
40. H. Stark, Phys. Rep., 2001, 351, 387–474.
41. J. S. Lintuvuori, K. Stratford, M. E. Cates and D. Marenduzzo, Phys. Rev. Lett., 2010, 105, 178302.
42. V. S. Jampani, M. Škarabot, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031703.
43. J. S. Lintuvuori, D. Marenduzzo, K. Stratford and M. E. Cates, J. Mater. Chem., 2010, 20, 10547.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm02131b

‡ Present address, Rowett Institute of Nutrition and Health, Greenburn Road, Bucksburn, Aberdeen, AB21 9SB, UK.

---